Understanding Glycomechanics using Mathematical Modeling: A review of current approaches to simulate cellular glycosylation reaction networks

Abstract

Following the footsteps of genomics and proteomics, recent years have witnessed the growth of large-scale experimental methods in the field of glycomics. In parallel, there has also been growing interest in developing Systems Biology based methods to study the glycome. The combined goals of these endeavors is to identify glycosylation dependent mechanisms regulating human physiology, check-points that can control the progression of pathophysiology, and modifications to reaction pathways that can result in more uniform biopharmaceutical processes. In these efforts, mathematical models of N- and O-linked glycosylation have emerged as paradigms for the field. While these are relatively few in number, nevertheless, the existing models provide a basic framework that can be used to develop more sophisticated analysis strategies for glycosylation in the future. The current review surveys these computational models with focus on the underlying mathematics and assumptions, and with respect to their ability to generate experimentally testable hypotheses.

INTRODUCTION

Glycosylation is a common post-translational modification that affects the function of most eukaryotic proteins ^{59, 61}. These post-translationally modified glycoproteins function as cell signaling, structural and adhesion molecules. In addition, mammals have also evolved specialized families of carbohydrate or glycan binding proteins that interact with specific glycoconjugates. These include lectins that carry specific carbohydrate recognition domains (CRDs) and glycosaminoglycan (GAG)-binding proteins containing clusters of positively charged amino acids, which recognize the negatively charged GAGs. Together, the glycoconjugates and glycan binding proteins participate in diverse processes including protein folding, cell growth and development, apoptosis, immunity and cancer metastasis ⁶¹.

Glycoproteins contain one of thirteen different monosaccharides linked to eight types of amino acids (Table 1, ⁵⁵). Based on this, although a large combination of glycosidic bonds can be expected to initiate glycoconjugate synthesis, certain classes of these linkages are more prevalent in nature. These glycoconjugates are classified based on the type of linkage between the glycans and the aglycone. In the case of glycoproteins, N- and O-linked glycans are common modifications that are observed in nature. Such glycans are attached to a majority of mammalian transmembrane or secreted proteins. N-glycosylation is commonly initiated by the attachment of β-linked N-Acetylglucosamine (GlcNAc) to Asparagine (N) residues in the Asn-Xaa-Ser/Thr (Xaa ≠ Pro) sequons of proteins. O-glycosylation, on the other hand, is typically initiated by α-linked N-Acetylgalactosamine (GalNAc) at hydroxyl groups located on Serine (Ser) or Threonine (Thr) residues.

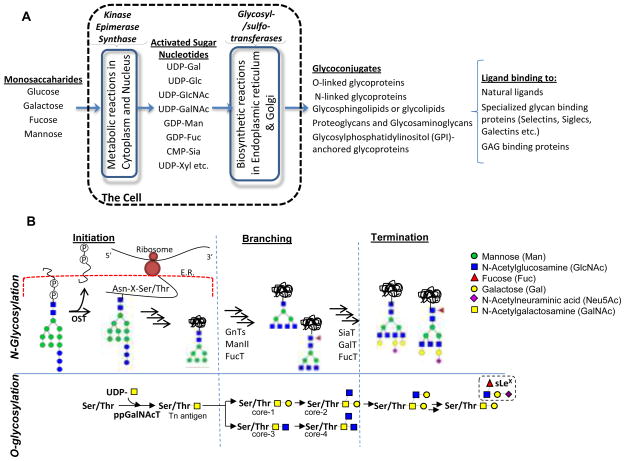
Glycoconjugates are formed as a result of complex biochemical reaction networks that involve various families of intra-cellular enzymes including transferases, isomerases, kinases and epimerases (Figure 1A). In the first set of metabolic reactions that occur in the cell cytoplasm and nucleus, simple monosaccharides are converted into activated sugar-nucleotides or isomerized into other sugar types via a series of metabolic reactions. Sugar-nucleotides formed in this manner are transported to the endoplasmic reticulum and Golgi where biosynthetic reactions mediate the formation of glycoconjugates. In the second set of biochemical reactions, the glycosyltransferases mediate the transfer of monosaccharides from activated sugar-nucleotides to protein and lipid acceptors. These glycosyltransferases are an important class of ~200 enzymes that constitute ~1% of the human genome ⁵⁷.

Figure 1. Overview of the glycosylation process.

A. Two types of reaction networks (shown in blue box) contribute to glycoconjugate biosynthesis. These include metabolic reactions that result in sugar-nucleotide synthesis, and glycosylation reactions that result in glycoconjugate assembly. Once formed the glycosylated macromolecules interact with a variety of ligands including glycan binding proteins. Such interactions regulate cell function. B. Overview of N- and O-glycosylation processes divided into the chain initiation, branching and termination steps. Mathematical models for each of these steps/modules is described in this manuscript.

Traditional ‘reductionist’ approaches study the function of each biochemical reaction described in the preceding sections one at a time, and these studies are often carried out in reconstituted systems that do not completely mimic the in vivo situation. To gain insight into the complex enzymatic reactions and interactions in situ, recent years have witnessed the development of mathematical models. These computer simulations aim to identify chemical reaction kinetic principles that are applicable to the study of glycans, with the goal of providing basic mathematical equations and dimensionless parameters describing this process. They also aim to integrate heterogeneous dynamic data into quantitative predictive models in order to determine critical rate limiting steps that represent targets of intervention/drug-development. Finally, they generate experimentally testable hypotheses that can lead to greater biochemical insight.

In the current article, we summarize quantitative models and analysis methods that have been applied to study glycosylation, with focus on N- and O-linked glycosylation of glycoproteins (Figure 1B). These models study either the initiation, branching or termination steps of the glycosylation process. As shown in the schematic, N-glycosylation is initiated by the en bloc transfer of a 14-monosaccharide unit from a lipid like precursor Dol-P to Asn-Xaa-Ser/Thr on the newly translated protein by oligosaccharyltransferase (OST). Subsequent modification of this unit by glycosidases and transferases results in the folded protein that has branched N-glycans, typically bi-, tri- or tetra- antennary structures. In the final step, the individual branches may be extended by addition of N-Acetyllactosamine units (Galβ1,4GlcNAc) and they may be capped by sialic acid (typically Neu5Ac) and fucose (Fuc) residues. O-glycosylation proceeds differently from N-glycosylation in that it is initiated by the transfer of a single GalNAc residue to Ser/Thr on the protein by enzymes belonging to the ppGalNAcT (polypeptide GalNAc-transferase) family. Subsequently, O-glycans form one of eight ‘core’ structures, four of which are shown in Figure 1B. These structures are extended and terminated similar to N-glycans in the final step. Besides providing an overview of past efforts that model O- and N-glycosylation, the current work also describes Systems Biology based principles that may form the foundation for model and code development in the future.

N-LINKED GLYCOSYLATION

Glycosylation at a particular site is heterogeneous. There is interest in understanding the factors regulating such heterogeneity both due to the biological importance of this process and also due to biotechnology applications that demand stringent control on the glycan profile of pharmaceuticals ^{2, 18}. For N-glycans, glycan heterogeneity is described at two levels: macroheterogeneity, which describes the absence or presence of a glycan at a given site, and microheterogeneity, which describes the variability in the identity of the oligosaccharide at a given position. Mathematical models applied to study the mechanism of N-glycosylation including steps regulating heterogeneity are described in the following sections.

I. Initiation and macroheterogeneity

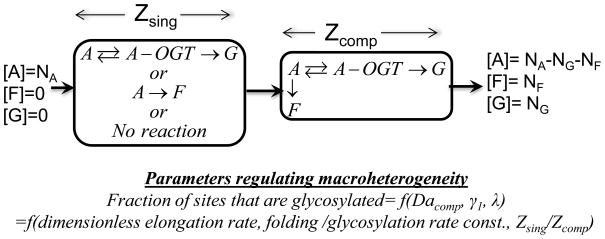
Macroheterogeneity is regulated by the efficiency of the en bloc transfer of a 14-monosaccharide module (Glc₃Man₉GlcNAc₂) from the lipid-like molecule Dol-P to target protein. This transfer occurs on the luminal side of the endoplasmic reticulum (ER) membrane and it is mediated by the enzyme oligosaccharyltransferase (OST). In one of the first examples of a mathematical model that studied glycosylation, Shelikoff et al. ⁵² analyzed this first step. Here, the authors considered the competition between the protein folding event that may ‘hide’ the Asparagine site where glycosylation occurs and the glycosylation process that occurs on the nascent, unfolded co-translating protein ⁴⁴. Based on experimental data that suggest that the initiation of N-glycosylation occurs in a brief time window prior to protein folding ²⁶, the investigators consider the region proximal to the OST reaction site to be composed of two zones. In the first zone, either folding or glycosylation individually occur (Z_sing). In the second, these two processes compete with each other (Z_comp) (Figure 2). By considering the folding event to proceed via a first order process and glycosylation to follow the Michaelis-Menten kinetics, the authors characterize the fraction or extent of glycosylation based on three dimensionless parameters that relate to: i) the rate of protein synthesis and elongation, ii) the relative rates of glycosylation and folding, and iii) the relative sizes of the compartments, Z_sing and Z_comp. The work predicts that the extent of macroheterogeneity can be regulated by both controlling the protein translation rate and the activity of the OST complex. While qualitative trends are established, a quantitative comparison with experimental data on fraction site occupancy is absent.

Figure 2. Initiation of N-Glycosylation.

Native protein (A) enters the endoplasmic reticulum (ER) at a concentration N_A. This protein may be either folded (F) or glycosylated (G) in the ER lumen in a section called Z_sing. Following this, in a second region called Z_comp, folding and glycosylation compete for the substrate emerging from the previous section. In both compartments, folding is modeled as a first order rate with rate constant k_fold, while glycosylation follows the Michaelis-Menten kinetics with parameters and K_M k_gly. This results in a change in the relative concentrations of aglycosylated [A], folded [F] and glycosylated [G] proteins.

II. Branching by N-acetylglucosaminyltransferases

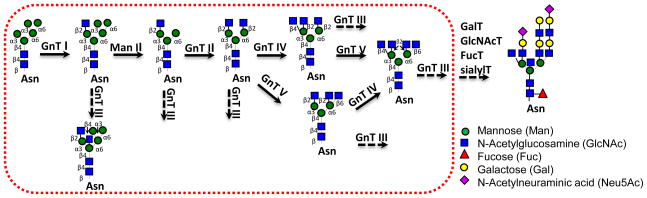
The 14 monosaccharide unit transferred in the initial glycosylation step undergoes a series of reactions that result in the creation of high mannose, hybrid and complex N-glycans ^{24, 51}. An important step in this glycan maturation process involves the action of five N-acetylglucosaminyltransferases (GnTI-V) that contribute to the formation of branched N-glycan structures (Figure 3). During this process, three glucose residues and one mannose are removed from Glc₃Man₉GlcNAc₂ in the ER. The Man₈GlcNAc₂-Asn thus formed enters the Cis-Golgi where it is further trimmed to form Man₅GlcNAc₂-Asn. The overall glycan at this point is an oligomannose. Glycan branching mediated by GlcNAc primarily occurs in the medial-Golgi. In this process, the first attachment of GlcNAc is mediated by the enzyme GnTI. The action of mannosidase-II then results in a substrate for GnTII (Figure 3). This biantennary N-glycan may be further modified by enzymes GnTIV and GnTV to result in tri- and tetra-antennary structures. The enzyme GnTIII, responsible for modifying nongalactosylated hybrid and complex oligosaccharides, results in the attachment of β1,4 linked GlcNAc to the core mannose. This ‘bisecting GlcNAc’ prevents further branching of the N-glycan by GnTII, GnTIV and GnTV at any point in the process.

Figure 3. N-glycosylation branching and extension.

Red box shows the ‘Central Reaction Network’ that regulates the branching pattern of N-linked glycans. Each of the branches starts with a GlcNAc residue (blue box) and it is called an antennae. This branching primarily occurs in the medial-Golgi compartment. In later compartments, branched glycans are acted upon by other enzymes including Gal-, GlcNac-, sialyl- and fucosyl- transferases to result in complex glycans. An example of a complex N-glycan, a tetraantennary oligosaccharide, is shown on the right side.

The first network based model of glycosylation simulated the above N-glycan branching process using a series of Ordinary Differential Equations (ODEs) ⁶⁰. As in several subsequent publications ^{13, 25, 60}, individual reactions were expressed as two-substrate bi-bi reactions, or alternatively as single-substrate enzymatic reactions (Figure 4A). Model parameters for these equations (like the Michaelis-Menten constant, K_M) are derived from independent enzymology experiments that appear in literature. In addition to the five GnTs highlighted in Figure 3, the model also considers two additional mannosidases and one galactosyltransferase. Together, this results in a reaction network with 8 enzymes, 33 species, and 33 reactions. Immunoelectron microscopy studies suggest that these enzymes are localized in multiple compartments ^{38, 43}. As a result, the authors simulated each of the 33 reactions in four 2.5μm³ CSTRs (continuous stirred tank reactors) located in series. These reactors represent the cis-, medial-, trans-, and trans-Golgi network. The residence time for each compartment was set to ~5 min.

Figure 4. Rate equations.

A variety of mathematical equations have been used in models that simulate glycosylation. A. The first set illustrates an extension of the Michaelis-Menten equation. Here, the enzyme E_m binds an array of acceptors (A_k; k=1..z). The velocity of formation of the reaction product (P_j) is illustrated using either single-substrate or two-substrate equations. B. A series of generalized mass action equations (instead of a distinct solution in panel A) can be used to describe the rate of product formation. Here, UDP-D_i binds enzyme prior to the acceptor since the concentration of UDP-D_i in Golgi is in the 1–10mM range. Also, rebinding of product to enzyme is allowed, and thus the sequential bi-bi reaction (panel A) is modified. C. Since acceptor concentration is less than K_M^A (K_M with respect to acceptor) in many instances, the reaction equation can be linearized as illustrated.

Overall, by addressing the process of glycan transport between compartments and biochemical reaction processes, this work sets the framework for modeling glycosylation which was subsequently used by many other investigators ^{13, 25, 27, 29, 35}. Upon parameterizing the simulation using experimental data from Chinese Hamster Ovary (CHO) cells, the model predicted a distribution of complex-galactosylated glycoforms with different numbers of antennae that were largely consistent with recombinant proteins produced in this cell system ^{19, 54, 63}. The system of equations also served the function of simulating qualitative trends in the oligosaccharide distribution when one or more enzymes were overexpressed. In studies that assess the effect of overexpression and redistribution of N-acetylglucosaminyltransferase GnTIII, the model suggests that a competition between GnTIII, Mannosidases II and GnTII regulates the distribution of bisected-complex sugars.

III. Ultrasensitivity in response to hexosamine flux

Coupling in silico modeling with experiments, Lau et al. ²⁷ extended the approach initiated by Umana and Bailey ⁶⁰ to demonstrate ultrasensitivity in the N-glycan branching pathway. In this regard, ultrasensitivity is a stimulus-response behavior of some biological systems where the response rises sharply over a relatively narrow range of stimulus ¹⁵. The model simulated by these authors, included two well-mixed compartments (medial and trans-Golgi) and 14 types of N-glycans. Since the authors, considered that significant product inhibition may occur throughout the pathway due to binding between the reaction product and enzymes, they simulate the network using a series of elemental reaction equations (Figure 4B) instead of the Michaelis-Menten equation of Umana and Bailey (Figure 4B). Considering all the intermediates formed, as a result of this approach, this model has 143 species in two compartments and a host of kinetic parameters. Most, but not all, parameters were mined from literature.

Mathematical modeling simulates the effect of increasing extra-cellular GlcNAc concentration on cell function and compares computational results with wet-lab experiments that study the same perturbation. The in silico baseline Golgi UDP-GlcNAc concentration is set at 1.5mM (10 times cytosolic levels) under conditions where the membrane UDP-GlcNAc antiport channel is functioning at near maximum velocity ⁴². Increasing media GlcNAc concentration from 0–50mM proportionally increases UDP-GlcNAc Golgi concentration from 1.5–6mM. Wet lab experiments under identical conditions show that increasing the hexosamine (GlcNAc) flux regulates the heterogeneity of N-glycans on surface proteins, some of which include growth factors receptors (TGFβR, EGFR). Increased N-glycan branching results in the presentation of greater number of antennae that are terminated by Galactose. This enhances surface receptor binding to galectin-3, a soluble multivalent glycan binding protein. As a result of enhanced receptor binding, galectin-3 lattices then restrict receptor endocytosis and it augments signaling via corresponding growth factor pathways. Further, the response to increasing GlcNAc concentration varies depending on the multiplicity of N-linked glycans on receptors ^{23, 65}. ‘Growth arresting’ receptors with fewer N-glycans exhibiting a switch-like/ultrasensitive response to increasing GlcNAc concentration. ‘Growth promoting’ receptors, which typically have more N-glycans, display a hyperbolic or saturation-type response. Using mathematical modeling, the authors suggest that such ultrasensitivity is a robust system property brought about by two conditions: i) A sequential increase in K_M from GnT-I to -V for Golgi enzyme reactions ^{50, 58}, and ii) Removal of intermediate products in this reaction pathway. Thus, hexosamine flux regulation in cells may be a highly evolved control mechanism for regulating transition in cells from growth to arrest. Further, the pattern of N-Glycan branching also plays a key role during epithelial to mesenchymal transition, a step regulating the metastasis of cancer. Whether similar processes regulate the formation and function of other families of glycoconjugates remains to be determined.

IV. Terminal modification and microheterogeneity

In addition to glycan branching studied in the previous section, extensions by N-acetyllactosamine chains ([Galβ1,4GlcNAcβ]_n), sialylation, fucosylation and sulfation are additional terminal modifications to N-glycans that regulate glycan microheterogeneity (Figure 3). There is enhanced interest in studying this aspect, in part, due to the realization that asialoglycoprotein receptors in hepatocytes called the Aswell-Morell receptors regulate the half-life of both therapeutic glycoproteins and cells by clearing desialylated entities that have exposed galactose (Gal) residues from circulation ^{45, 53}. Terminal modifications of N- and O-glycans are also critical for recognitions by glycan binding proteins ⁶¹.

Krambeck and Betenbaugh addressed this challenge by extending the model of Umana and Bailey (1997) to include all glycosylation steps, starting from the high mannose structure all the way to terminal sialylation ²⁵. By including 11 enzyme activities, including some with different isoforms, these authors account for extension of antennae by the addition of N-acetyllactosamine, fucosylation, galactosylation and sialylation. While not all combinations of theoretically possible N-glycans are considered, the inclusion of these different enzymes results in a large network with 7,565 glycans and 22,871 reactions. To handle this combinatorial explosion in reactants and products, the authors provide rule based definitions for various enzymes, and methods to solve the large system of equations using the constrained Newton-Raphson method. The overall modeling approach is partially validated by comparing the in silico glycan distribution with experimentally measured glycans reported for recombinant human thrombopoietin expressed in CHO cells ¹⁷. Similar to the result by Monica et al. ³⁵, the authors show that protein productivity and carbohydrate distribution can be independently regulated to a certain extent. Upon increasing protein concentration to 1000 μM, however, a decrease in the degree of sialylation was noted. By analysis of this model, it is apparent that critical branch points exist in the networks that determine the distribution of fluxes and products emerging from the entire network. Overall, the model includes a very large number of glycan structures, only a small fraction of which are detected in typical experimental glycan profiling studies. Despite this limitation, this approach does provide a useful computational tool that can be used for N-glycan engineering, in order to produce proteins with targeted distribution of glycoforms.

V. Reactor configurations for modeling glycosylation

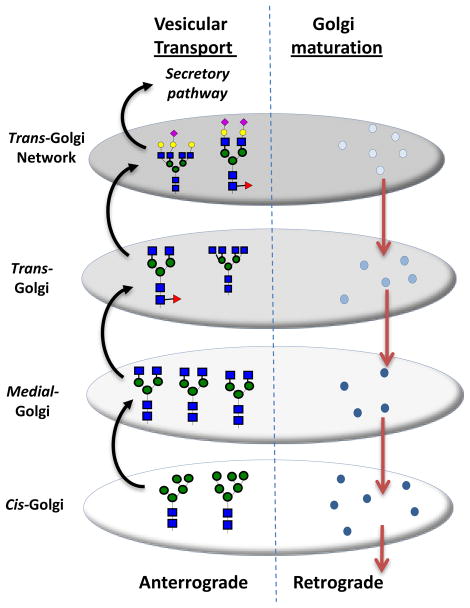
The mechanism regulating glycoprotein transport through the Golgi and the effect of this transport mechanism on glycan structure remains to be determined. While recent visualization methods including live-cell imaging and super-resolution microscopy are starting to reveal new details, a universal model remains elusive ⁹. Two classical models of Golgi transport, include the vesicular transport and cisternal progression/maturation model (Figure 5) ^{30, 31}. In vesicular transport model, the different stacks of cisternae (stack of disc-shaped membranes) are stationary while the cargo or protein buds from one compartment to another. In contrast, in the Golgi maturation model, the secretory cargo is stationary while the compartments themselves transform from the early cisternae to late cisternae.

Figure 5. Glycoprotein transport in Golgi.

In the vesicular transport model, proteins bud from early cisternae to later compartments while the enzymes themselves are stationary. In the Golgi maturation model, the protein is stationary while the cisternae themselves mature from early to late stage.

Hossler et al. ¹³ propose that, from the engineering perspective, vesicular transport can be modeled as a series of CSTRs while Golgi maturation resembles a single plug-flow reactor (PFR) or a series of PFRs in series. While the glycoprotein is acted upon by different enzymes in both reactors, individual proteins remain in specific compartments for variable times in the well-mixed reactor, while the residence time is identical for all proteins in a PFR. Thus, glycan microheterogeneity should be less in the PFR configuration. The overall model simulated by these authors, resembles that developed by Krambeck and Betenbaugh (2005) ²⁵. Unlike Krambeck who examined CSTRs, however, Hossler studied reaction kinetics in both PFRs and CSTRs. The simulation results highlight the importance of spatial enzyme distribution in the Golgi since the products formed in a single PFR was dramatically different from that of four PFRs in series. In the latter case, the four reactors are considered to represent the cis-, medial-, trans-, and the trans-Golgi network, each with its own enzyme composition ^{4, 38, 43}. The difference between 4 PFRs in series versus 4 CSTRs in series was less dramatic, though at low residence times, as anticipated, the glycan mixtures was more heterogeneous in the CSTRs in series configuration compared to the PFRs in series model. Large amounts of unprocessed high mannose structures were formed in the PFR model in this case due to incomplete processing in the first reactor, and this is reminiscent of experimental observations by others ⁵⁴. Overall, it appears that neither the CSTR nor PFR model is ideally suited to explain all experimental observations reported in literature. Also, the authors suggest that effectively channeling reactions to a single N-glycan product is a non-trivial task that requires either changing the expression/levels of multiple enzymes in cells, or domain engineering of luminal regions of glycosyltransferases to alter enzyme spatial distribution ⁵.

O-LINKED GLYCOSYLATION

The most common type of O-glycosylation is initiated by the attachment of GalNAc to Ser/Thr residues by a family of ~20 Golgi resident enzymes called UDP-GalNAc:polypeptide α-N-acetylgalactosaminyltransferases, ppGalNAcT. These enzymes transfer a GalNAc residue from UDP-GalNAc to Ser or Thr (Figure 1B). Like N-linked glycosylation, this process of O-glycosylation may also be divided into three steps that include: i. Initiation of glycosylation by the transfer of GalNAcα to Ser/Thr on the peptide by one of the ppGalNAcTs; ii. Branching which involves the synthesis of one of eight O-glycan core structures (core-1 to core-8) ²⁹; and iii. Extension and termination which results in the fully synthesized O-glycan. Mathematical models for O-linked glycosylation are not as well developed as similar efforts for N-glycosylation. Some efforts have been undertaken to study the initiation and extension steps, and these are reviewed here.

I. Initiation by ppGalNActransferases

While the peptide consensus sequences for N-glycosylation (Asn-Xaa-Ser (Xaa≠Pro)) and O-xylosylation (acidic-acidic-Xaa-Ser-Gly-Xaa-Gly) are known, a consensus sequence for the initiation of O-linked glycosylation is not established ⁶¹. Gerken and colleagues have studied this aspect by experimentally measuring the rate of attachment of GalNAcα to both natural glycoproteins and peptide libraries ^{10, 11}. Experimental data were fit to the kinetic model below, to determine the effect of neighboring residues on the initiation of O-glycosylation:

$$\text{d}{[\text{OG}]}_i/\text{d}t=k_{(\text{Ser}\text{or}\text{Thr})}f{(\text{OG}+\text{OH})}_{I}g{(\text{Pro},\text{Glu},\text{Arg})}_i{[\text{OH}]}_i$$

In this expression, [OH]_i and [OG]_i represent the concentration of unglycosylated and glycosylated residues on the peptide. k_{(Ser or Thr)} represents the first order rate constant for Ser/Thr glycosylation. f(OG+OH)_i captures the effect of neighboring residues that are glycosylated (plus or minus three residues from the site of glycosylation) on the initiation step, and g(Pro, Glu, Arg) is a weighting function that accounts for the effect of neighboring proline or charged residues (glutamic/aspartic acid or arginine/lysine/histidine). A negative value implies that the proximal residues inhibit glycosylation, while a positive value implies that they promote glycosylation.

This analysis shows that some ppGalNAcTs prefer to glycosylate peptides that were previously glycosylated while others are inhibited by prior glycosylation. The presence of proline at 1–3 amino acids from the site of glycosylation favors glycosylation for most ppGalNAcTs, possibly due to a conserved Trp in some of these enzymes. While Pro, Val, Ile and Tyr at the C-terminus favor glycosylation, the preference appears to vary with ppGalNAcT. Further, some enzymes favor an acidic substrate, while others favor a basic substrate. Overall, although this data fitting approach does not strictly constitute a ‘systems approach’, however, it does represent the state-of-the-art in efforts to model the initiation of O-glycosylation.

II. Subset modeling applied to model O-linked glycosylation

Much of the data on glycosyltransferase specificity comes from biochemical/enzymology based studies performed in reconstituted systems ^{33, 57}. While this is an excellent starting point for computational modeling, in situ enzyme-substrate specificity and kinetics may be different. In addition, in situ, not all substrates that appear to be structurally similar may be reacted upon to the same extent by a given enzyme. In order to partially account for this effect, the concept of ‘subset modeling’ is introduced²⁹.

Subset modeling is a heuristic approach that is used to fit experimentally measured glycan distribution data to an in silico model. Here, first, all enzymes that can potentially participate in the synthesis of the glycans detected in wet-lab studies are enumerated, based on prior knowledge of biochemistry. Next, a ‘master pathway’ is generated that includes all possible reactions catalyzed by these enzymes. In order to account for enzyme-substrate specificity that may favor some reactions over others, one or more species and associated reactions in the master pathway are deleted to create smaller reaction networks that are called ‘subset models’. By this process, even a relatively small master pathway with 20 species and 28 reactions can result in over 800 subset models ²⁹. Each of these models is then fit to experimental data using global and local optimization methods. Enzymatic reactions are linearized in order to reduce computational expense (Fig. 4C). This is a reasonable approach since the Golgi sugar-nucleotide donor concentration is typically high in the mM range and acceptor concentration is less than the reaction K_M ^{1, 51}. Those in silico subset models that ‘best fit’ the experimental data are then ranked and selected. Cluster and principal component analysis is performed on these best fits to identify common features that are central to the glycosylation process. Sensitivity analysis is performed to generate testable-hypothesis that can be used to refine the model using additional experimentation.

TOWARDS A STRUCTURED VIEW OF GLYCOSYLATION

Glycan synthesis is the result of a modular process that is driven by the action of a variety of glycosidases and glycosyltransferases (²⁰, Figure 1A). This is true not only for glycoproteins, but also for glycosaminoglycans and glycolipids. In addition to the conventional view that considers reactions mediated by these enzymes as being unidirectional, recent evidence suggests that this process can be reversible under some circumstances ^{3, 39, 64}. Further extra-cellular glycosidases and glycosyltransferases exist in human physiology (e.g. in blood) which may sculpt, cell-surface or extra-cellular glycan structures dynamically ^{57, 61}. Finally, a variety of regulatory mechanisms control the expression of glycosyltransferases and other enzymes participating in carbohydrate synthesis and this increases the complexity of the reaction system. A generalized modeling framework that can incorporate these features will be advantageous since it is difficult for any single laboratory to model and experimentally validate each of these modules. Further, while current models in this field largely examine individual enzymatic reactions and glycan structure outcomes, the incorporation of cell/tissue level function is likely to necessitate multi-scale, coarse-grain modeling that will benefit from a structured approach.

The need for structured modeling to analyze the glycome is recognized by manuscripts in the field that have developed rule based descriptions of glycosyltransferase activity ^{25, 29}. While such definitions enable automated construction of glycosylation reaction networks, the methodologies proposed thus far are not exhaustive. For example, the 9-digit code used by Krambeck and Betenbaugh ²⁵ cannot be used to describe all N-glycan structures and they do not describe glycosidic bond linkage information. Thus, when modeling CHO cell line data, differences in sialic acids are not easily distinguished. The work by Liu et al. ²⁹ overcomes this limitation but it is also not tailored to describe all families of glycans in a machine readable format.

To facilitate streamlined, modular model construction and sharing, the field of Systems Biology has developed various markup languages that enable machine-readable reaction networks. This includes the Systems Biology Markup Language (SBML) ¹⁶. Graphical representation of these models is possible using Molecular Interaction Maps (MIMs), System Biological Graphical Notation (SBGN) and other programs ^{22, 28}. Further, over 150 software packages (listed at www.sbml.org) have been developed for the simulation and post-simulation analysis of SBML based models. To complement this development, the field of glycobiology has also witnessed the development of XML (eXtensible Markup Language) based descriptions or schemas of glycan structures, including Glyde-II and GlycoCT ^{12, 47}. Recent databases developed in this field also focus on structured presentation of experimental tools and data ^{7, 34, 40, 62}. The complementary development of XML based representation along with data repositories is likely to enhance efforts to develop structured/mechanistic mathematical models that can query and exploit these databases. To this end, computational standards that link parallel developments in the field of Systems Biology and Carbohydrate Biochemistry are necessary. Rudimental efforts in this direction are already underway with models of glycosylation reaction networks being described using SBML notation ²⁹.

One aspect that is likely to facilitate structured modeling is the standardization of object oriented coding methods for the construction of glycosylation reaction networks. Based on the models reviewed in this article, Figure 6 provides potential class definitions that may be used in the future (adapted from ref. ²⁹). This includes the ENZYME class that contains details on enzyme-acceptor/substrate specificity, the REACTION class that defines the rate and type of reaction between acceptor (GLYCAN) and DONOR in the presence of ENZYME, the COMPARTMENT class that describes all reactions in a given cellular or extra-cellular section, and the SYSTEM class that encompasses the entire interactome. Some of the models described in this manuscript can thus be studied by modifying the ENZYME class to fit experimental data. In other cases, different types of reactor configurations can be simulated by varying the COMPARTMENT definition.

Figure 6. Class diagram.

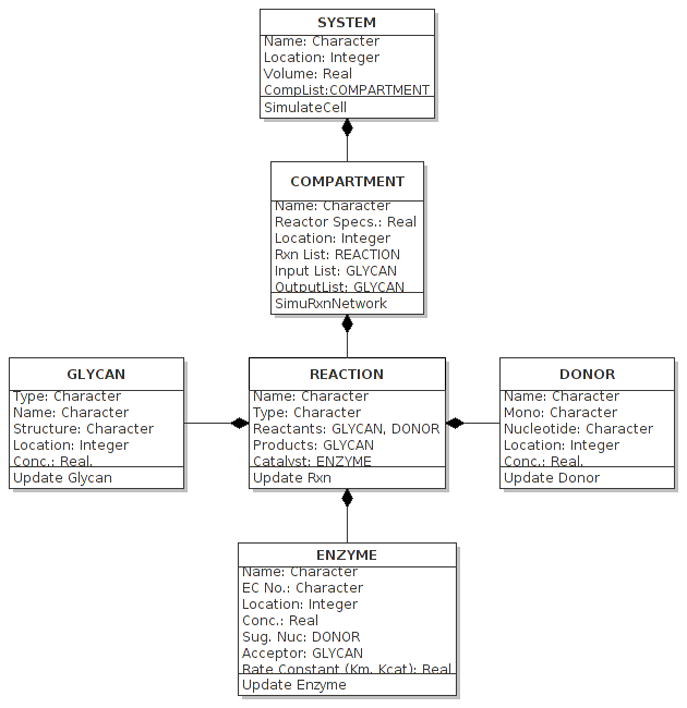
Object oriented programming (OOP) can describe selected fields and methods in classes including GLYCAN, DONOR, ENZYME, REACTION, COMPARTMENT and SYSTEM.

CONCLUSIONS

There is growing use of Bioinformatics and Systems Biology based approaches to study the glycome, i.e. the carbohydrate ensemble that composes the cells. These glycan structures are critical components that regulate the function or mechanics of cells. In the context of inflammation, it has been shown that the inhibition of biochemical reaction pathways that contribute to the formation of O-glycosylated structures leads to reduced selectin mediated cell adhesion under hydrodynamic shear or fluid flow conditions ^{6, 32, 48}. This then results in the reduced presence of transmigrated leukocytes at sites of inflammation in vivo. The progression of cancer is also accompanied by the development of aberrant glycan structures, and efforts are currently underway to target such carbohydrates to reduce disease footprint ⁸. Finally, it is well known that stage specific glycan structures accompany stem cell development ⁵⁶. In the field of Regenerative Medicine also, engineering specific carbohydrate structures on mesenchymal stem cells has been shown to enhance the homing of these cells to sites of therapy ^{21, 46, 49}. In all these disparate applications, a quantitative understanding of biochemical reaction pathways leading to cellular glycosylation can help define novel strategies that improve outcome. The role of mathematical modeling in such efforts is to apply quantitative engineering analysis to reveal causal relationships that cannot be determined by the application of traditional, qualitative approaches in biochemistry or cell biology.

The focus of the current review is primarily on the ‘bottom-up’ modeling approach, which constructs models of biochemical reaction networks based on experimental data collected in simple/reconstituted systems. While these models are simulated by solving a series of ordinary differential equations, it is apparent that Boolean network analysis and stochastic simulations of such networks can also be performed. The former approach may be useful when limited information on network structure is known, while the latter can be useful for simulating glycan macro/micro-heterogeneity. Further, to complement this approach, it is possible to develop ‘top-down’ approaches based on the collection of high-throughput datasets using methods that include, but are not limited to, mass spectrometry, gene arrays, and glycan microarrays (reviewed in ref. ^{14, 41}). In this case, analysis methods may focus on statistical approaches like singular value decomposition, hierarchical clustering and partial least-square regression to derive the biochemical reaction network structure. In addition, post-simulation analysis methods can be applied to analyze both ‘bottom-up’ and ‘top-down’ models to reveal various properties of these networks including robustness, oscillation, bistability and modularity (reviewed in ref. ^{36, 37}).