Abstract
Natural killer (NK) cells are innate lymphocytes that mediate early host defense against viruses, such as cytomegalovirus. Interleukin 15 (IL-15) is upregulated during viral infections and drives the expansion of NK cells. However, the influence of IL-15 on murine NK cell division and death rates has not been quantitatively studied. Therefore, we developed a series of two-compartment (representing quiescent and dividing NK cell subpopulations) mathematical models, incorporating different assumptions about the kinetic parameters regulating NK cell expansion. Using experimentally derived division and death rates, we tested each model’s assumptions by comparing predictions of NK cell numbers with independent experimental results and demonstrated that the kinetic parameters are distinct for non-dividing and dividing NK cell subpopulations. IL-15 influenced NK cell expansion by modulating recruitment and division rates to a greater extent than death rates. The observed time delay to first division could be accounted for by differences in the kinetic parameters of non-dividing and dividing subsets of NK cells. Although the duration of the time delay to first division was not significantly influenced by IL-15, the recruitment of non-dividing NK cells into the replicating subpopulation increased with higher IL-15 concentrations. Our model quantitatively predicted changes in NK cell accumulation when IL-15 stimulation was reduced, demonstrating that NK cell divisional commitment was interrupted when cytokine stimulation was removed. In summary, this quantitative analysis reveals novel insights into the in vitro regulation of NK cell proliferation and provides a foundation for modeling in vivo NK cell responses to viral infections.
Keywords: IL-15, mathematical model, NK cells, proliferation
Introduction
Natural killer (NK) cells are innate lymphocytes that recognize transformed or infected cells rapidly without prior sensitization. They are particularly important in early host resistance against viral pathogens while the adaptive immune system is being marshaled (1–3). NK cells are stimulated by cytokines (e.g., IL-15 and IL-12) as well as by direct recognition of infected or transformed cells through activation receptors, resulting in cytolysis of the abnormal cells and the production of immunomodulatory cytokines (e.g., IFNγ).
In addition to these effector functions, NK cells rapidly proliferate during viral infections, resulting in increased NK cell numbers (4–7). This NK cell expansion is driven by pro-proliferative cytokines, such as IL-15, which are up-regulated during viral infections (6, 8–9). Exogenous IL-15 or overexpression of IL-15 in transgenic mice also stimulates NK cell proliferation, resulting in elevated NK cell numbers (6, 10). The NK cell proliferative response during viral infections can be divided into three distinct phases: 1) early, nonselective cytokine-driven NK cell proliferation, 2) preferential proliferation of a subset of NK cells expressing activation receptors that recognize infected cells, and 3) resolution of proliferation and contraction of the expanded NK cell numbers (5, 7, 9). In addition to driving viral-induced NK cell proliferation, IL-15 plays an important role in NK cell development, survival, and homeostasis (11–14). Dysregulation of NK cell proliferation and homeostasis can result in abnormally low levels of NK cells (13–15) or in lymphoproliferative disorders, such as chronic NK cell lymphocytosis (CNKL) (16–18).
The fundamental understanding garnered from qualitative models describing NK cell proliferation based on experimental studies (for example (5–7)) can be substantially enriched and extended by quantitative insights from mathematical models. For example, Gett and colleagues established a mathematical framework of how T cells integrate signaling from cytokine, costimulatory, and T cell receptors (19), and three subsequent models built on this work to provide insight into the kinetic parameters controlling T cell proliferation (20–22). Furthermore, a recent study utilized mathematical modeling to characterize the integration of activation and inhibitory receptor signaling by Vav1 in the regulation of NK cell cytotoxicity (23).
Although mathematical models have been used to study T cell proliferation in vitro, no work has been done to determine how NK cell proliferation responses are quantitatively regulated. We had previously developed an in vitro CFSE-based assay of NK cell proliferation that was able to replicate the first two phases of viral-induced NK cell proliferation (7), and we were interested in using experimentally determined rate constants from this system in mathematical modeling to develop a more quantitative understanding of the kinetic parameters controlling NK cell proliferation. In this study, we present a novel two-compartment mathematical model to investigate the influence of IL-15 on the kinetic parameters governing NK cell proliferation and expansion. We demonstrate the model’s ability to predict changes in NK cell expansion that were verified with independent experiments. Observations from this model provide novel insights into the factors regulating cytokine-driven NK cell proliferation.
Materials and Methods
Mice
Female C57BL/6 (B6) mice were obtained from the National Cancer Institute (Charles River, MA). They were maintained under specific pathogen-free conditions and used between 8 and 16 weeks of age. All experiments were conducted in accordance with institutional guidelines for animal care and use.
Cell preparation and culture
Single cell suspensions were prepared from whole spleens using standard techniques (7). Splenic NK cells were enriched from approximately 2.5% to 45–60% of lymphocytes following negative selection with magnetic beads (Miltenyi, CA). Enriched NK cells were labeled with 0.25 µM CFSE (Molecular Probes, OR) for 7 min at 37°. The reaction was quenched by adding RPMI 1640 medium supplemented with 10% fetal calf serum, and the cells were subsequently incubated for 30 min at 37°. The CFSE-labeled splenocytes were plated in 96-well plates (2.5 × 104 NK cells/well) and cultured for 4 days with various concentrations of murine IL-15 (Peprotech, NJ).
Quantifying the NK cell population
Cells harvested from the 96-well plates at different time points were blocked with 2.4G2 (anti-Fcγ II/III receptor) supernatant prior to being labeled with anti-CD3 (145-2C11) and anti-NK1.1 (PK136) antibodies (eBioscience, CA). NK cells were identified as CD3-NK1.1+ lymphocytes and enumerated with calibration beads (Spherotech, IL) in conjunction with 7-aminoactinomycin (7-AAD) (BD Pharmingen, CA). Flow cytometry analysis was performed with a FACScalibur flow cytometer (BD Pharmingen), and the data were analyzed with FlowJo (Tree Star, OR), Origin 7.5 (OriginLab, MA) and Mathematica 7.0 (Wolfram, IL).
Estimating cell numbers and division progression
Precursor cohort analysis was conducted, as previously described (19–22), using OriginPro 7.5 software. Briefly, a Levenberg-Marquardt algorithm was used to determine distinct Gaussian distributions representing cell cohorts with the same division history in the CFSE intensity histogram. The ratios of the area under each Gaussian distribution to the total area under the CFSE intensity histogram were used in calculating the distribution of NK cells in each distinct division. Precursor numbers were then calculated by dividing the number of cells present in division i by a factor of 2i.
Cytokine reduction
After NK cells were stimulated with 25 ng/ml of IL-15 for 48 hours, the majority of the IL-15 containing media inside each well was extracted. Approximately 30 µL of media was left covering the NK cells at the bottom of each well. 220 µL of media without IL-15 was slowly added to prevent disruption of the NK cell cluster. This resulted in a final calculated concentration of 3 ng/ml IL-15. The NK cells were then cultured for an additional 48 hours, and cell numbers were assessed periodically. In mock cytokine reduction experiments, the majority of the media was removed and 220 µL of media containing 25 ng/ml of IL-15 was slowly added, maintaining an IL-15 concentration of 25 ng/ml.
Quality of prediction calculation
The quality of simulations and predictions from each mathematical model was assessed by computing the normalized root mean square deviation (NRMSD) between model computations and observed experimental values. The sum of squared deviations (SSD) at different time points were computed, and NRMSD was calculated as a percentage value by the following formula: . A NRMSD value of 0% indicated absolute agreement between model computations and experimental results. Greater differences between model results and experimental data were reflected in higher NRMSD values.
Models for NK cell proliferation
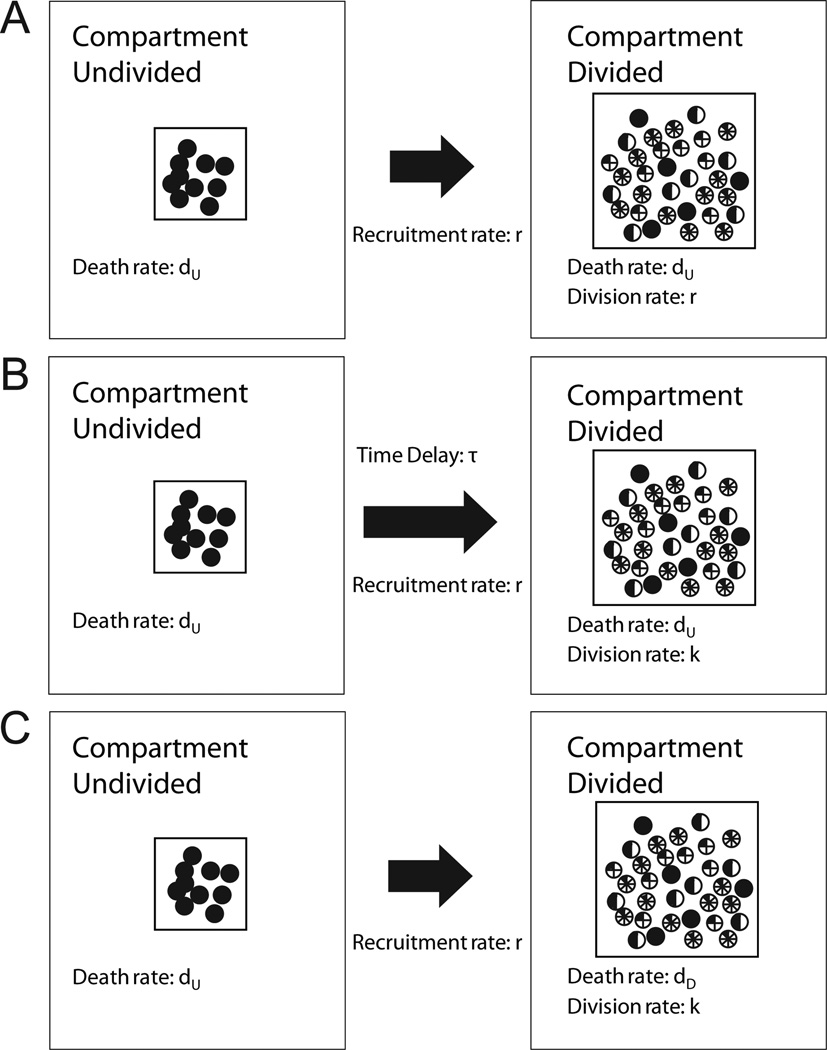
We hypothesized that quiescent NK cells had kinetic parameters distinct from those of actively dividing NK cells. Therefore, we devised a model that separated NK cells into two subsets or compartments: undivided (compartment U) and divided (compartment D) cells. Division and death rates were used to characterize the changes in the NK cell population in each compartment. Since division by compartment U cells represented recruitment into compartment D, the division rate of compartment U cells was equivalent to the recruitment rate. Three models were developed using systems of ordinary differential equations to solve for the number of cells in both compartments and to test the validity of the two-compartment hypothesis (Fig. 1).
| Model 1 |
| Model 2 |
| Model 3 |
Figure 1. Graphical representation of two-compartment models of cytokine-driven NK cell expansion.
Undivided and divided subpopulations of NK cells were denoted as compartments U and D, respectively. The recruitment rate and division rate were denoted by r and k, the rates of cell death in compartments U and D were represented by dU and dD, and the time delay was denoted by τ. A, In model 1, the death rates between the two compartments were identical and the recruitment rate and division rates were also identical. B, In model 2, the death rates between the two compartments were identical but the recruitment rate and division rate were distinct. In addition, Model 2 incorporated an explicit time delay before cells initiated division. C, In model 3, the recruitment rate, division rate, and the death rates between the two compartments were distinct, and no explicit time delay was included.
In these equations, r was the rate with which compartment U cells were recruited to compartment D, dU was the death rate of compartment U cells, τ was the time delay to first division, and k and dD were the division and death rates of compartment D cells. (Mathematical symbols are defined in Table I.) The estimates r, dU, τ, and k were obtained through precursor cohort analysis (19–20, 22). The estimate for dD was derived using r, dU, and k. CU and CD were the total number of cells in compartment U and D, respectively. Initially, CU(0) was equal to the number of live NK cells at the start of the experiment, and CD(0) was equal to zero.
Table I.
Definitions of mathematical symbols
| Parameters used in the model: | |
|---|---|
| CU | total number of cells in undivided compartment |
| CD | total number of cells in divided compartment |
| dU | death rate of cells in the undivided compartment |
| dD | death rate of cells in the divided compartment |
| k | division rate of cells in the divided compartment |
| r | recruitment rate of cells in the undivided compartment |
| τ | apparent time delay to first division |
| Derived quantities: | |
| f0(t) | frequency distribution of precursors that divided 0 times |
| fi(t) | frequency distribution of precursors that divided i times |
| M(t) | mean division number of NK cells the divided compartment |
| m(t) | mean division number of precursors whose progeny are in the divided compartment |
| N0 | number of cells that have not divided |
| N1 | number of cells that have divided once, determined from flow cytometry and precursor cohort analysis |
| N1* | theoretical number of cells that divided once, calculated using r, k, and τ |
| Ni | number of cells that divided i times |
| n0 | number of precursor cells that have not divided |
| n1 | number of precursor cells that have divided once |
| ni | number of precursor cells that have divided i times |
| ntotal | total number of precursor cells |
CFSE histogram simulations
Simulated CFSE histogram profiles were generated from the differential equation predictions in our model using Matlab (Mathworks, MA). The experimental profile of NK cells after CFSE labeling was used as the initial cell distribution. CFSE data is organized by the flow cytometer into 1024 bins, corresponding to an intensity range of 1 to 10,000. The natural CFSE decay over the initial twenty-four hours following CFSE labeling was accounted for in the simulation and resulted in the histograms shifting to a mean CFSE intensity of 1000 to 2000. (During this initial observed decay, no dilution due to cell division occurred). Corresponding to the limits of flow cytometer detection, up to 8 cycles of cell division were experimentally analyzed (20). Model differential equations were used with experimentally derived parameters to estimate cell distributions at specific time intervals. The number of NK cells that were recruited from the undivided compartment to the divided compartment, the number of NK cells that continued to divide, and the number of dead cells were calculated. These changes in the NK cell population were applied to the corresponding CFSE intensity bins using Matlab to define the simulated CFSE histograms at specific time-points.
Results
IL-15 stimulation directly augments NK cell proliferation kinetics
We used 3H-thymidine incorporation experiments to determine the appropriate range of IL-15 concentrations with which to study in vitro NK cell proliferation. 3H-thymidine incorporation began to increase at 3 ng/ml IL-15 and approached maximum response levels at 200 ng/ml (Fig. S1).
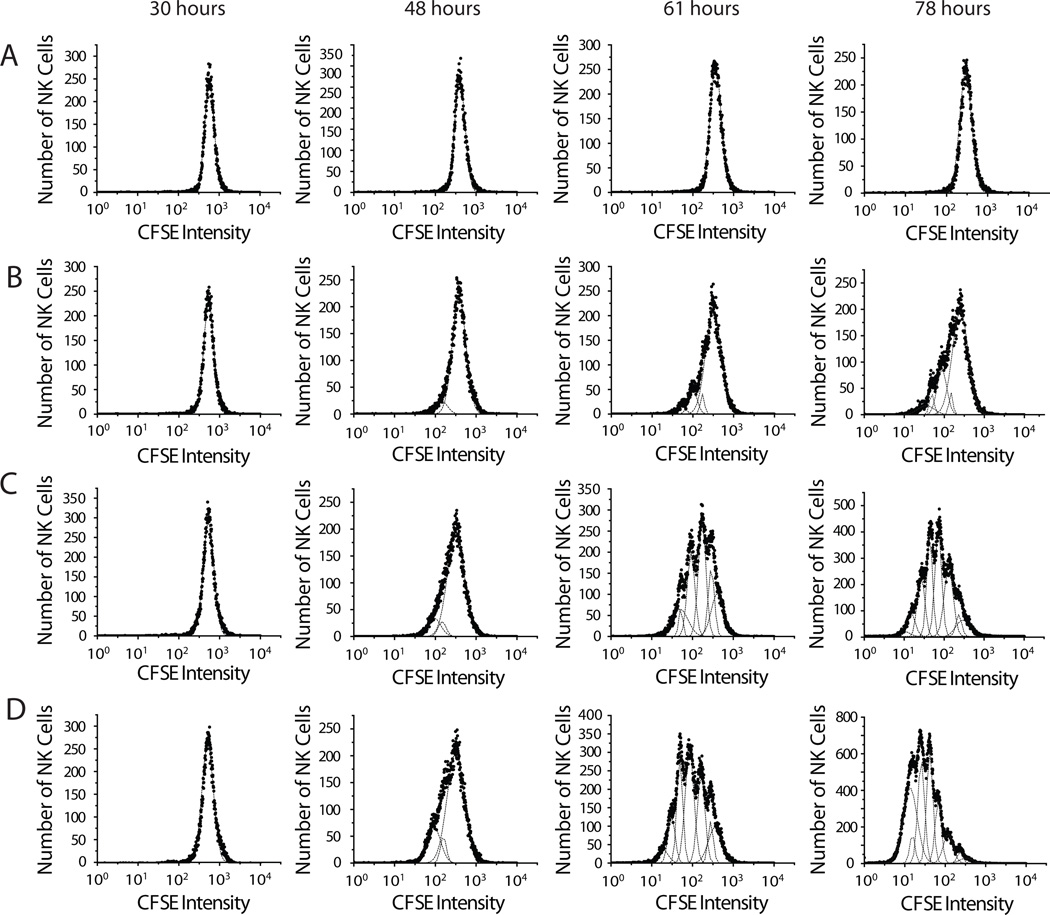
Based on these results, soluble IL-15 was added to CFSE-labeled NK cell cultures at concentrations of 3, 9, 25, and 75 ng/ml. NK cell numbers were assessed with flow cytometry at defined time points. Representative NK cell CFSE intensity histograms are shown for 30, 48, 61 and 78 hours in Figure 2. During the first 30 hours of cell culture, no cell divisions were observed at any of the four IL15 concentrations. Even after 78 hours, negligible cell division was seen in NK cells incubated in 3 ng/ml of IL-15, and the CFSE intensity distribution consisted of a single Gaussian peak (Fig. 2A). Following stimulation with 9 ng of IL-15/ml, a subset of NK cells divided up to 4 times; however, the majority of the NK cell population remained quiescent. Therefore, although the recruitment rate from the non-dividing subpopulation of NK cells into the dividing population was greater following stimulation with 9 ng/ml than with 3 ng/ml, it remained relatively low. As IL-15 concentrations increased to 25 and 75 ng/ml, NK cells manifested progressively more divisions (Fig. 2C–D), reflected in increased CFSE dilution with multiple Gaussian peaks. After stimulation with higher IL-15 concentrations, a larger fraction of NK cells were found in later cohorts. This observation suggests that the division rate increased with increasing IL-15 concentration, but it is not possible to empirically distinguish the influence of division and death rates on the observed expansion of NK cells. To address this issue, we utilized a mathematical modeling approach incorporating two compartments representing quiescent and dividing subsets of NK cells.
Figure 2. NK cell proliferation in vitro was dependent on IL-15 concentrations.
NK cells (7-AAD−NK1.1+CD3− lymphocytes) were enumerated at specific time-points following incubation with IL-15. The binned cell counts were plotted on a semi-log scale CFSE intensity histogram to show CFSE dilution in cells stimulated by IL-15 at concentrations of 3 ng/ml (A), 9 ng/ml (B), 25 ng/ml (C) and 75 ng/ml (D). Data shown represented samples collected at 30 h (column 1), 48 h (column 2), 61 h (column 3) and 78 h (column 4) following in vitro IL-15 stimulation. The number of cells in each CFSE intensity bin were represented as filled circles in each histogram. CFSE intensity histograms were modelled using a Levenberg-Marquardt algorithm and partitioned into a series of curves described by Gaussian distributions (representing cohorts of NK cells with the same division history). The total area under the CFSE intensity curve and the area under each Gaussian curve were computed and used to calculate NK cell numbers from each cohort, Ni(t). Results are representative of three to four independent experiments.
Two-compartment models
Three models were proposed to interpret and analyze the quantitative experimental data. Model 1 was designed to test the validity of the two-compartment hypothesis. In model 1, the division rate of compartment D cells was equal to the recruitment rate of compartment U cells, and the death rates in both compartments were identical (Fig. 1A), representing essentially a single compartment system (20, 22). In contrast, model 2 included a distinct division rate for compartment D cells and an explicit time delay to first division (Fig. 1B). The time delay to first division accounted for the observed lag in transition of NK cells from compartment U to compartment D. Model 3 incorporated distinct death rates in both compartments as well as distinct recruitment rate in compartment U and proliferation rate in compartment D. Model 3 tested the hypothesis that an explicit time delay was not necessary to account for the observed delay to cell recruitment in the context of distinct proliferation and death rates in compartments U and D (Fig. 1C).
Model parameter estimation
Model parameter estimates were derived from CFSE experimental results using precursor cohort analysis. Cell division resulted in multiple CFSE “peaks” in CFSE histograms secondary to diluted CFSE in each generation of daughter cells. Each peak represented a cohort of cells that had divided the same number of times. These cohorts could be mathematically represented as a series of Gaussian distributions of CFSE intensities. Ni(t) was defined as the number of cells in the ith cohort, and the values of Ni(t) were determined as described in methods. CU was equal to the number of cells in the initial undivided cohort N0.
CD (the total number of cells in compartment D) was equal to the sum of cells in all subsequent cohorts:
To determine the number of precursor cells (ni) from which the divided cohorts originated, the cell numbers in each cohort were divided by 2i.
At the beginning of each experiment when all cells were in compartment U and no cells had divided, the precursor number n0 was equal to the number of cells in compartment U.
The starting NK cell population consisted of a finite number of precursors. After accounting for the decrease in precursors due to serial doubling, the only change to the precursor cell number was through cell death. Therefore, the rate of decrease in total precursor numbers over time was used to calculate an estimate of the death rate in compartment U (dU):
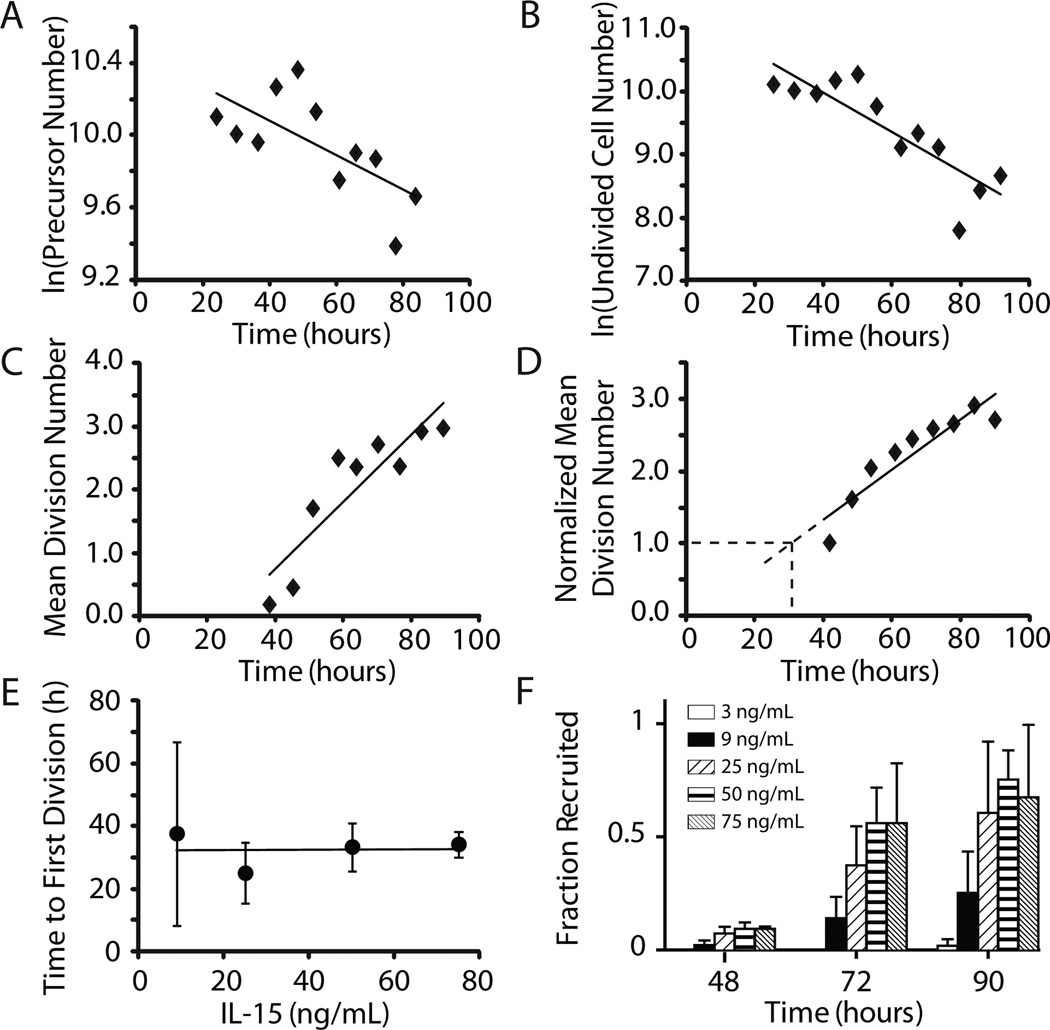
The term ntotal(t) represented the total number of precursors in the NK cell population at time t. Therefore, the slope of the linear regression of the ln[ntotal(t)] vs. t plot provided an estimate of dU (Fig. 3A).
Figure 3. Derivation of recruitment rate, division rate, death rates, time delay, and fractional recruitment.
Representative graphs of estimation methods are shown for one experiment with IL-15 at 75 ng/ml. A, The number of precursor cells ntotal(t) was computed using precursor cohort analysis. The slope of the natural log of total precursor cells vs. time was used to estimate the exponential death rate of precursor cells, d0. B, The number of cells in compartment U decreases over time due to recruitment to compartment D and death. The recruitment rate, r, was calculated as the difference between the rate of change of undivided cells (calculated from the slope of natural log of undivided cells vs. t) and d0. C, The slope of the mean division number (M(t)) vs. time was used to determine the division rate for dividing cells (compartment D), k. D, The time delay, τ, was estimated by calculating the time at which the mean division number of precursor cells excluding undivided precursors, m(t), was equal to 1. E, Mean time delay to first division +/− SD at IL-15 concentrations of 9 (n=3), 25 (n=4), 50 (n=2) and 75 (n=3) ng/ml is shown plotted vs. IL-15 concentration. The line represents linear regression of the average τ values (y = 0.007x + 32.5). F, Fractional recruitment is shown in bars representing the fraction of precursors whose progeny are in compartment D to the total precursors at IL-15 concentrations of 3 (n=3), 9(n=3), 25 (n=4), 50 (n=2) and 75 (n=3) ng/mL at time-points 48, 72 and 90 h.
The recruitment rate of compartment U cells was calculated by tracking the changes in the number of undivided cells over time, because the rate of change in the number of undivided cells was the sum of recruitment and death rates.
The recruitment rate of undivided cells (r) was therefore equal to the difference between the slope of the linear regression of ln[CU(t)] vs. t and dU (Fig. 3B).
The division rate of compartment D cells (k) was estimated using cell numbers from each cohort and the statistical concept of expected value (20). The value of N0 decreased with recruitment and death rates, as noted in the following equation.
N0 represented the number of undivided cells while Ni represented the number of cells that had divided i times. Therefore, the average number of divisions that cells in compartment D had completed at time t (M(t)) could be calculated as follows:
M(t) increased with time, and the slope of M(t) vs. t was equal to the rate of division of cells in compartment D (Fig. 3C).
Analysis of CFSE histograms in multiple experiments (Fig. 2) revealed minimal NK cell division at 30 hours regardless of the IL-15 concentration. The time delay (τ) characterizing this prolonged time to first division was calculated by extrapolating the time at which the mean division number of precursor cells excluding undivided precursors, m(t), was equal to 1 (i.e., the average time to first division). The mean division number of precursor cells was calculated using the frequency distribution of precursor cells, fi(t) (i.e., the precursors that have divided i times as a fraction of total precursor numbers). The concept of fi(t) was based on normalized cohort cell numbers as described by De Boer and colleagues (20, 22).
m(t) was the sum of the product of precursor frequency distribution and precursor division number, excluding non-dividing precursors using the factor 1-f0(t).
The time delay (τ) was estimated as the time at which m(t) = 1 in a plot of m(t) vs. t (Fig. 3D).
The values of τ ± SD calculated at 9, 25, 50, and 75 ng IL-15/ml are shown in Fig 3E. The average time delay to first division based on these experimental results was 32.5 hours and appeared relatively independent of IL-15 concentration. However, the values calculated at 9 ng/ml IL-15 demonstrated substantial variability suggesting that the time delay may be prolonged at lower IL-15 concentrations.
In contrast to the time delay, the fractional recruitment of NK cells from compartment U to compartment D increased with increasing IL-15 concentrations (Fig. 3F). The fractional recruitment was defined as the ratio of precursors whose progeny were in compartment D to total precursors and was calculated by accounting for the fraction of precursors that remained in compartment U.
Fractional recruitment was dependent on IL-15 concentration with an increasing fraction of the precursor NK cells in compartment U recruited to compartment D as IL-15 levels increased (Fig. F); however, fractional recruitment appeared to plateau as IL-15 concentrations rose higher than 50 ng/ml.
Although cell death was not directly measured in the CSFE experiments, the death rate of compartment D cells (dD) was estimated by comparing the theoretical (N1(t)*) and observed (N1(t)) number of cells that had completed one cell division. The theoretical value N1(t)*, describing cells recruited from compartment U to compartment D that had completed one division at time t, was calculated using the recruitment rate r and division rate k, assuming no cell death in compartment D. Given a time delay of τ, the number of cells that had not been recruited and remain in compartment U was
Similarly, after time t, the number of cells that had not been recruited was
The non-recruited cells consisted of quiescent and dead cells. If no recruitment occurred, the number of non-recruited cells would remain constant over time. Therefore, the change in the number of non-recruited cells was equal to the number of recruited cells. CU(0)e−rτ was used because recruitment was only appreciable after the apparent time delay period. Therefore, the number of cells recruited into compartment D at time t was
The theoretical number of cells in first division at time t must account for cells in compartment D that may have divided more than once by subtracting
Thus, for t > τ, the theoretical number of cells in division 1 (N1(t)*) was represented as
The observed value N1(t) was equal to the number of cells in the first division at time t. Therefore, the death rate in compartment D (d1) could be approximated from the slope of the linear regression of vs. time. The values of dD at different IL-15 concentrations are listed in Table II.
Table II.
Kinetic parameter estimates obtained by analysis of independent CFSE experimentsa
| IL-15 = 3 ng/ml | IL-15 = 25 ng/ml | IL-15 = 75 ng/ml | IL-15 = 9 ng/ml | IL-15 = 50 ng/ml | ||
|---|---|---|---|---|---|---|
| Mean ± SD | Mean ± SD | Mean ± SD | Estimate | Estimate | ||
| d0 × 10−2 | h−1 | 0.25 ± 0.19 | 0.69 ± 0.49 | 1.2 ± 0.39 | 0.38 | 1.0 |
| d1 × 10−2 | h−1 | 2.4 ± 1.6 | 4.0 ± 0.7 | 1.3 | 3.4 | |
| r × 10−2 | h−1 | 0.0067 ± 0.01 | 2.0 ± 1.1 | 2.4 ± 1.2 | 0.93 | 2.2 |
| k × 10−2 | h−1 | 6.1 ± 2.5 | 7.1 ± 2.6 | 2.8 | 6.8 |
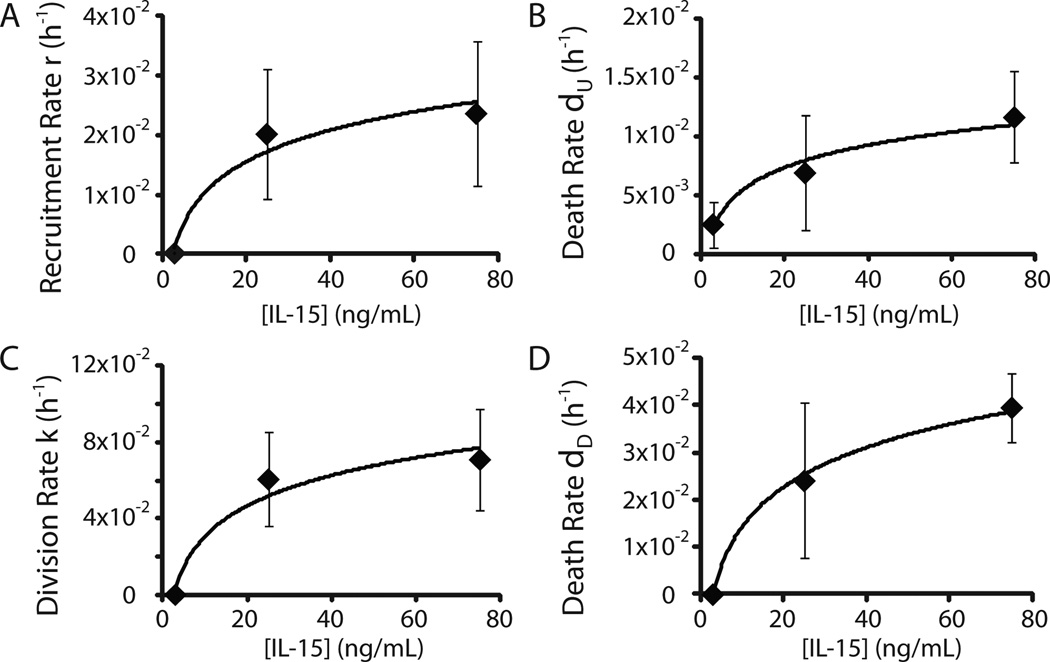
Kinetic parameter values at IL-15 concentrations of 3, 25 and 75 ng/ml were estimated as illustrated in Fig. 3. These estimates represent average values from 3 independent experiments. d0 was the exponential death rate of precursor cells in all the models; d1 was the exponential death rate of cells that were actively dividing, (described in model 3 as the cells in compartment 1); r was the recruitment rate of precursors to compartment 1;. k was the division rate of cells in compartment 1 (described in Models 2 and 3). Parameter estimates obtained from experiments with 3, 25 and 75 ng/ml of IL-15 were used to derive logarithmic functions describing the dependence of the specific kinetic parameters on IL-15 concentrations (Fig. 5). Predicted parameter values for NK cells stimulated by 9 and 50 ng/ml IL-15 were estimated from these functions.
The parameter estimates derived from CFSE experiments with 3, 25, and 75 ng/ml of IL15 are shown in Table II. Due to minimal cell division and transition to compartment D, only dU and r could be calculated for experiments using 3 ng/ml of IL-15. At higher IL-15 concentrations, the proliferation rate of dividing NK cells (k) was three-fold higher than the recruitment rate (r) of quiescent NK cells, suggesting that NK cells divide at a faster rate once they start to proliferate (Table II). Moreover, dividing NK cells also had higher death rates than quiescent NK cells following stimulation with either 25 or 75 ng/ml of IL-15. Dead NK cells could also be directly identified by the uptake of 7-aminoactinomycin (7-AAD, a fluorescent molecule that intercalates in double-stranded DNA but does readily pass through cell membranes). Estimates of death rates based on enumeration of 7-AAD+ NK cells over time were consistent with our conclusion that NK cells stimulated with 75 ng/ml IL-15 had higher death rates than NK cells stimulated with 25 ng/ml IL-15 (Fig. S2).
Model simulation of experimental data
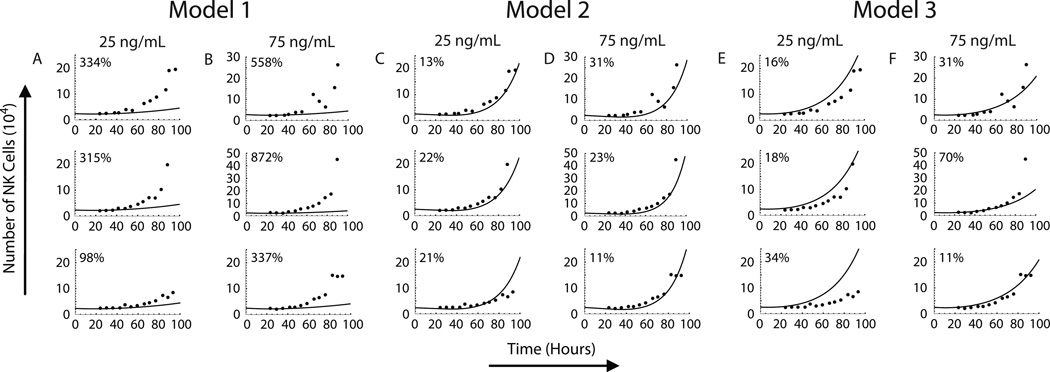
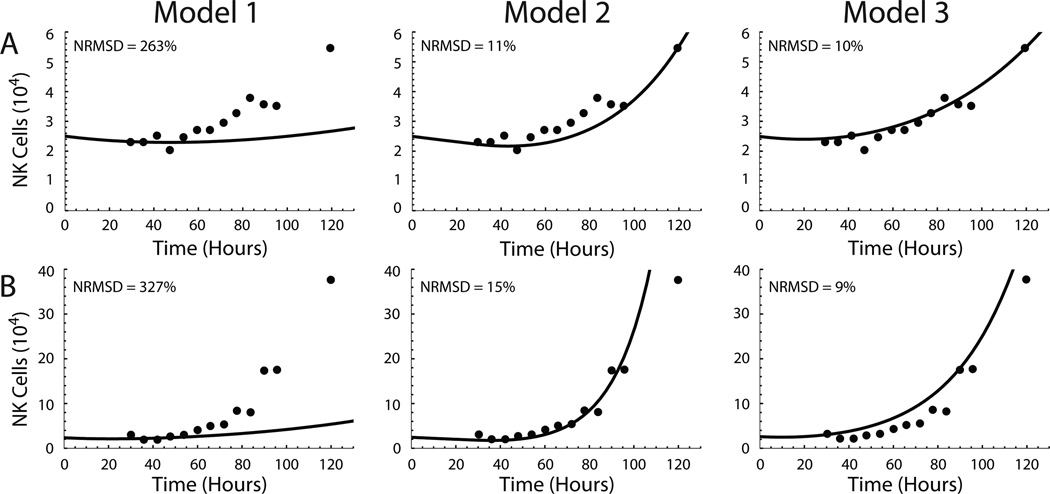
These experimentally derived proliferation and death rates were utilized in models to evaluate hypotheses about cytokine-driven NK cell proliferation. The model simulations of NK cell accumulation over 100 hours were compared with experimental data from three independent experiments at 3, 25, and 75 ng/ml IL-15 (Fig. 4). Consistent with our experimental results (Fig. 2A), no NK cell expansion was predicted to occur following stimulation with 3 ng/ml of IL-15 stimulation (data not shown). Model 1 utilized identical proliferation and death rates in compartments U and D (i.e., k = r and dD = dU). The significant differences between the model 1 simulation and experimental results (Figs. 4A–B) support the hypothesis that quiescent and dividing NK cells have distinct kinetic parameters. In contrast, the simulation results in models 2 and 3 were much closer to experimental values at both IL-15 concentrations (Figs. 4C–F), as quantified by the normalized root mean square deviation (NRMSD) values. The similarity between the quality of the predictions from models 2 and 3 when compared with experimental data suggests that differences in the recruitment rate, division rate, and distinct death rates between quiescent and dividing NK cells (model 3) are sufficient to account for the observed initial lag in proliferation without the incorporation of an explicit time delay (model 2).
Figure 4. Comparison of model predictions of NK cell expansion with experimental data.
Utilizing experimentally derived kinetic parameters, model predictions of NK cell accumulation over time (black line) following stimulation with 25 ng/ml (A, C and E) and 75 ng/ml (B, D, and F) of IL-15 are shown in comparison to experimental NK cell numbers (filled circles) from three independent experiments. The three experiments are arranged in individual rows, and the simulation results from Model 1 (A and B), Model 2 (C and D) and Model 3 (E and F) are plotted in columns of two. The normalized root mean square deviation (NRMSD; shown in the upper left of each plot) was calculated as a quantitative measure of the accuracy of model simulations.
Model predictions of NK cell expansion under different IL-15 stimulation conditions
The ability to simulate experimental results is critical for a mathematical model, but the true test of this approach is in accurately predicting results under experimental conditions not used in deriving the parameter values. Therefore, we used parameter estimates determined from CFSE experiments with 3, 25, and 75 ng/ml of IL-15 to generate logarithmic equations that defined the kinetic parameters as functions of IL-15 concentration (Fig. 5). These functions were used to interpolate parameter values at different IL-15 concentrations, including 9 and 50 ng/ml (Table II).
Figure 5. Dependence of proliferation and death kinetic parameters on IL-15 concentrations.
The kinetic parameters A) r (recruitment rate), B) dU (death rate in compartment U), C) k (division rate in compartment D), and D) dD (death rate in compartment D) were estimated from NK cells stimulated with 3, 25 and 75 ng/ml IL-15 in three independent experiments. The mean values +/− SD were plotted against IL-15 concentrations. Logarithmic functions were derived to describe each parameter’s dependence on IL-15.
The predicted kinetic parameters at 9 and 50 ng/ml of IL-15 were then utilized to calculate NK cell expansion in all three models, and the predictions were compared with results obtained from independent experiments (3 experiments with 9 ng IL-15/ml and 2 with 50 ng IL-15/ml; Fig. 6). Model 1 was unable to accurately predict NK cell expansion at either concentration of IL-15 (Fig. 6A & B), affirming the hypothesis that quiescent and dividing NK cells have distinct proliferation and death kinetics. In contrast, the predictions of model 2 and 3 were comparable with much lower NRMSD values. Given that model 3 could predict NK cell expansion as well as model 2 at IL-15 concentrations of 9, 25, 50, and 75 ng/ml, we concluded that the presence of distinct proliferation and death rates in the two-compartment NK cell proliferation model is sufficient to eliminate the necessity of incorporating an explicit time delay. Supporting this conclusion, model 3 was able to accurately predict mean division numbers of NK cells at specific time-points over the course of the experiment (Fig. S3A). Therefore, we utilized model 3 in the following work.
Figure 6. Model predictions of NK cell expansion at IL-15 concentrations not used in deriving the kinetic parameters.
The kinetic parameter values for IL-15 stimulation at 9 and 50 ng/ml were estimated from logarithmic functions derived from experimental data with IL-15 concentrations of 3, 25, and 75 ng/ml IL-15 (Fig. 5A–D). The interpolated parameter estimates (shown in Table II) were used in the three models to predict NK cell expansion under stimulation with IL-15 concentrations of 9 and 50 ng/ml. The predictions (black lines) were compared with independent data (filled circles) from experiments with 9 ng/ml IL-15 (A, representative of 3 experiments) or 50 ng/ml IL-15 (B, representative of 2 experiments). The normalized root mean square deviation (NRMSD) is shown in the upper left of each plot.
Robust model predictions under dynamic cytokine stimulation conditions
Our two-compartment model was able to accurately predict the expansion of NK cells in response to a variety of steady-state IL-15 concentrations (Figs. 4 and 6). However, in vivo IL-15 concentrations during stimuli such as viral infections are not static (6, 9) but rather are elevated and then return to baseline homeostatic levels. Therefore, we tested the robustness of our model in predicting NK cell numbers under conditions in which IL-15 stimulation was reduced to basal levels (3 ng/ml) after 48 hours of stimulation with 25 ng/ml IL-15.
We hypothesized that the reduction of IL-15 levels would gradually modulate the kinetic parameters controlling NK cell expansion to values consistent with the new cytokine concentration. We estimated the length of time taken for cellular behavior to transition between the two IL-15 concentrations to be approximately 12 hours based on the following assumptions: 1) equilibration of IL-15 levels between the new media and the fluid remaining around the cell pellet would occur over a relatively short period of time, given a moderate amount of mixing when the new fluid was added, 2) approximately four hours would be required to reach steady-state levels of receptor occupancy at the new equilibrium IL-15 concentrations based on receptor-level modeling of soluble IL-15 binding to IL-15 receptors on cell surfaces (following the approach outlined in (24); data not shown), and 3) cells already in the process of dividing would be minimally affected by changes in cytokine stimulation. Proliferating NK cells require at least six hours to complete a division cycle (see Fig. 2C where NK cells stimulated with 25 ng/ml IL-15 undergo up to 5 rounds of division in approximately 30 hours after the they are recruited into the proliferating pool). We made the simplifying assumption that the temporal impact of the changing cytokine levels on cells already committed to dividing could be approximated by the time required for the cells in compartment D to undergo on average 0.5 divisions (M(t)=0.5). Given that M(t) = kt and that k at 25 ng/ml of IL-15 was 0.061 (Table II), the time for M(t) to equal 0.5 would 8 hours. Taking these three observations into account, we incorporated into the model the assumption that the IL-15-dependent kinetic parameters would vary as the effective concentration of IL-15 decreased linearly from the initial IL-15 concentration to the new concentration over a 12-hour period.
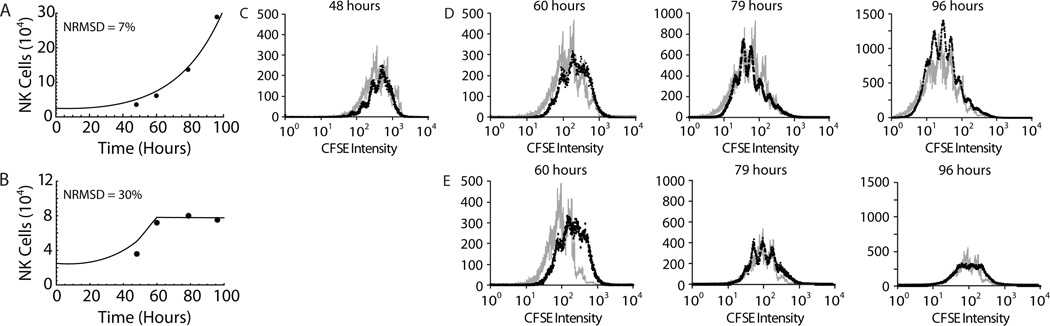
With this modification, the model was able to accurately account for the expansion of NK cells under mock cytokine exchange and IL-15 reducing conditions when compared with independent experimental data (Fig. 7). The ability of the model to accurately predict NK cell numbers during mock exchange experiments (25 ng/ml of IL-15 media replaced at 48 hours with 25 ng/ml of IL-15 media; Fig. 7A) demonstrated that the removal and replacement of media did not alter NK cell proliferation kinetics. When the IL-15 concentration was reduced to 3 ng/ml after 48 hours of stimulation with 25 ng/ml of IL-15, model predictions accurately accounted for the slowing and subsequent plateauing of NK cell expansion (Fig. 7B). The model was also able to approximate the decreased mean division numbers of NK cells in the cytokine reduction group compared to the mock exchange group observed during the experiments (Fig. S3B). In addition, the model could predict the distribution of undivided and divided NK cells into distinct division cohorts. Indeed, model-simulated histograms of NK cell division cohorts compared favorably with CFSE histograms from mock exchange (Fig. 7C & D) and cytokine exchange (Fig. 7C & E) experiments. Consistent with experimental results, the simulated histograms of NK cell division cohorts representing the cytokine reduction experiments had fewer cells in cohorts which had undergone more than four divisions in addition to fewer NK cells overall (Fig. 7E). In summary, our two-compartment model was capable of robust predictions of both overall NK cell numbers and population distributions under changing IL-15 conditions.
Figure 7. Model predictions of the impact of cytokine reduction on NK cell expansion.
We modeled NK cell expansion following a decrease in IL-15 levels after 48 h of stimulation with 25 ng/ml IL-15 by incorporating a linear change in cytokine concentration over a 12 h period into model 3. A and B, Model predictions (black lines) compared well with experimental results (filled circles) during both A) mock exchange experiments where media containing 25 ng/ml of IL-15 was replaced with media containing 25 ng/ml of IL-15 and B) cytokine reduction experiments where the IL-15 concentration was reduced from 25 ng/ml to 3 ng/ml. C, Model-simulated histograms of NK cell division cohorts (gray) closely approximated experimental CFSE histograms (black) at 48 hours, prior to either mock exchange or cytokine reduction experiments. D and E, Model-simulated histograms of NK cell division cohorts compared favorably with experimental CFSE histograms from mock exchange (D) or cytokine reduction (E) experiments at 60, 79 and 96 hours following media exchange at 48 hours. Results are representative of two independent experiments.
Discussion
To characterize NK cell proliferation and expansion, we developed a two-compartment mathematical model distinguishing quiescent and dividing populations of NK cells and used it to quantitatively investigate the proliferative response of NK cells to IL-15 stimulation in vitro. To our knowledge, this is the first work to quantitatively study the impact of IL-15 on the kinetic parameters (e.g., recruitment rate) governing cytokine-driven NK cell proliferation. In contrast to earlier modeling work on T cell proliferation that relied primarily on parameter estimates based on multi-parameter, nonlinear curve fitting of experimental data (20–22), we directly derived rate constants describing recruitment, proliferation, and death rates within each compartment from experimental data. The predictions from our model were tested and verified in independent experiments. The analysis of the model provided a number of unique insights into the factors controlling cytokine-driven NK cell proliferation: 1) IL-15 modulated recruitment and division rates to a greater extent than death rates, 2) increasing IL-15 concentrations paradoxically led to higher death rates in dividing NK cells, 3) the observed time delay to first division was not significantly influenced by IL-15 concentrations and could be directly accounted for by differences in the kinetic parameters of non-dividing and dividing subsets of NK cells, 4) the recruitment of non-dividing NK cells into the replicating pool increased with higher IL-15 concentrations, and 5) NK cell divisional commitment was interrupted when cytokine stimulation was removed.
IL-15 drives NK cell expansion by modulating proliferation rates (including recruitment rate from compartment U) and death rates. Both the proliferation and death rate of dividing cells increased with increasing IL-15 concentrations. However, increasing IL-15 had a greater impact on the proliferation rate than on the death rate (Table II), resulting in a net increase in NK cells as IL-15 concentrations increased. Although IL-15 is known to support NK cell survival (11–12), our model parameter derivation found higher death rates as the IL-15 concentration increased (Table II), suggesting that rapidly proliferating NK cells undergo higher rates of death than quiescent cells. This conclusion was supported by estimates of NK cell death rates based on direct enumeration of 7-AAD+ NK cells (Fig. S2). It is possible that this observation reflects physical constraints and/or increased cell-cell contact within the expanding cell mass of dividing cells rather than an inherent feature of IL-15-driven NK cell proliferation; however, experiments varying the NK cell density support the conclusion that replicating NK cells have a higher death rate than quiescent NK cells (Fig. S4). Although unexpected, this observation is consistent with previous reports that the rate of T cell death is dependent on cell division number (22) and that rapidly dividing T cells are more susceptible to apoptosis (25–27).
Our model demonstrates that several characteristics of NK cell proliferation are similar to those of T cell proliferation. For example, our work found that the observed time delay to first division (τ) is relatively insensitive to IL-15 concentration (although more variability was seen at low IL-15 concentrations). This is consistent with the observation that varying IL-2 stimulation did not alter the average time to first division for CD3-stimulated T cells (21–22). In contrast, the fractional recruitment (i.e., the proportion of cells entering first division) of both NK and T cells increased with increasing pro-proliferative cytokines (IL-15 for NK cells and IL-2 for T cells) (21–22).
However, in a number of other ways, our model demonstrates that the proliferative behavior of NK cells is distinct from T cells. Our work confirms results from previous NK cell studies that pro-proliferative cytokine stimulation is sufficient to drive significant NK cell expansion (6–7, 9) in contrast to T cells. Although T cells, to a certain extent, do undergo “bystander proliferation” (cytokine-driven division in the absence of signaling through their T cell receptor (28–29)), previous in vitro studies have found minimal proliferation with IL-2 alone (19, 21). In addition, our experiments demonstrate that NK cell divisional commitment is dynamic and can be interrupted when the cytokine milieu changes. This observation contrasts with previous reports that once CD8 T cells are stimulated, they enter into an apparent program of division and divide at least seven times without further antigen stimulation (30–31). However, one caveat in this comparison is that the CD8 T cell studies were done with T cells stimulated through the T cell receptor, while our studies of NK cells used stimulation solely by pro-proliferative cytokines and not through their activation receptors.
In summary, the combination of mathematical modeling and experimental observations allows the systematic interrogation of the influence of IL-15 on NK cell proliferation. Our quantitative study of the kinetic parameters controlling cytokine-driven NK cell proliferation and expansion demonstrated several similarities between NK and T cell proliferative behavior, but it also identified a number of differences between NK and T cell proliferation. In addition to the insights garnered about IL-15-driven NK cell proliferation, our model provides the basis for future studies incorporating signaling through NK cell activation receptors. A more complete understanding of the factors governing NK cell proliferation and homeostasis may lead to novel therapies to modulate NK cells in clinically relevant settings such as intractable viral infections or NK cell lymphoproliferative disorders.
Supplementary Material
Acknowledgments
This research was supported by NIAID R01 AI078994 and AI073552 grants and a Basil O’Connor award from the March of Dimes.
Footnotes
The authors have no relevant financial disclosures
References
- 1.Orange JS. Human Natural Killer Cell Deficiencies. Current Opinion in Allergy and Clinical Immunology. 2006;6:399–409. doi: 10.1097/ACI.0b013e3280106b65. [DOI] [PubMed] [Google Scholar]
- 2.Bukowski JF, Woda BA, Welsh RM. Pathogenesis of murine cytomegalovirus infection in natural killer cell-depleted mice. Journal of Virology. 1984;52:119–128. doi: 10.1128/jvi.52.1.119-128.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.French AR, Yokoyama WM. Natural Killer Cells and Viral Infections. Current Opinion in Immunology. 2003;15:45–51. doi: 10.1016/s095279150200002x. [DOI] [PubMed] [Google Scholar]
- 4.Biron CA, Turgiss LR, Welsh RM. Increase in NK cell number and turnover rate during acute viral infection. Journal of Immunology. 1983;131:1539–1545. [PubMed] [Google Scholar]
- 5.Dokun AO, Kim S, Smith HR, Kang HS, Chu DT, Yokoyama WM. Specific and nonspecific NK cell activation during virus infection. Nature Immunology. 2001;2:951–956. doi: 10.1038/ni714. [DOI] [PubMed] [Google Scholar]
- 6.Nguyen KB, Salazar-Mather TP, Dalod MY, Van Deusen JB, Wei XQ, Liew FY, Caligiuri MA, Durbin JE, Biron CA. Coordinated and distinct roles for IFN-αβ, IL-12 and IL-15 regulation of NK cell responses to viral infection. Journal of Immunology. 2002;169:4279–4287. doi: 10.4049/jimmunol.169.8.4279. [DOI] [PubMed] [Google Scholar]
- 7.French AR, Sjolin H, Kim S, Koka R, Yang L, Young DA, Cerboni C, Tomasello E, Ma A, Vivier E, Karre K, Yokoyama WM. DAP12 signaling directly augments proproliferative cytokine stimulation of NK cells during viral infections. Journal of Immunology. 2006;177:4981–4990. doi: 10.4049/jimmunol.177.8.4981. [DOI] [PubMed] [Google Scholar]
- 8.Orange JS, Biron CA. Characterization of Early IL-12, IFN-alphabeta, and TNF Effects on Antiviral State and NK Cell Responses During Murine Cytomegalovirus Infection. Journal of Immunology. 1996;156:4746–4756. [PubMed] [Google Scholar]
- 9.Geurs TL, Zhao YM, Hill EB, French AR. Ly49H engagement compensates for the absence of type I interferon signaling in stimulating NK cell proliferation during murine cytomegalovirus infection. Journal of Immunology. 2009;183:5830–5836. doi: 10.4049/jimmunol.0901520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fehniger TA, Suzuki K, Ponnappan A, Van Deusen JB, Cooper MA, Florea SM, Freud AG, Robinson ML, Durbin J, Caligiuri MA. Fatal leukemia in interleukin 15 transgenic mice follows early expansions in natural killer and memory phenotype CD8+ T cells. Journal of Experimental Medicine. 2001;193:219–231. doi: 10.1084/jem.193.2.219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cooper MA, Bush JE, Fehniger TA, Van-Deusen JB, Waite RE, Liu Y, Aguila HL, Caligiuri MA. In vivo evidence for a dependence on interleukin 15 for survival of natural killer cells. Blood. 2002;100:3633–3638. doi: 10.1182/blood-2001-12-0293. [DOI] [PubMed] [Google Scholar]
- 12.Ranson T, CA V, Corcuff E, Richard O, Muller W, Di Santo JP. IL-15 is an essential mediator of peripheral NK cell homeostasis. Blood. 2003;101:4887–4893. doi: 10.1182/blood-2002-11-3392. [DOI] [PubMed] [Google Scholar]
- 13.Kennedy MK, Glaccum M, Brown SN, Butz EA, Viney JL, Embers M, Matsuki N, Charrier K, Sedger L, Willis CR, Brasel K, Morrissey PJ, Stocking K, Schuh JC, Joyce S, Peschon JJ. Reversible Defects in Natural Killer and Memory Cd8 T Cell Lineaages in Interleukin 15-Deficient Mice. Journal of Experimental Medicine. 2000;191:771–780. doi: 10.1084/jem.191.5.771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lodolce JP, Boone DL, Dassopoulos T, Chai S, Swain RE, Trettin S, Ma A. Interleukin-15 Receptor Maintains Lymphoid Homeostasis by Supporting Lymphocyte Homing and Proliferation. Immunity. 1998;9:669–676. doi: 10.1016/s1074-7613(00)80664-0. [DOI] [PubMed] [Google Scholar]
- 15.Kim S, Lizuka K, Aguila HL, Weissman IL, Yokoyama WM. In Vivo Natural Killer Cell Activities Revealed by Natural Killer Cell-Deficient Mice. PNAS. 2000;97:2731–2736. doi: 10.1073/pnas.050588297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tefferi A, Li CY, Witzig TE, Dhodapkar MV, Okuno SH, Phyliky RL. Chronic Natural Killer Cell Lymphocytosis: a Descriptive Clinical Study. Blood. 1994;84:2721–2725. [PubMed] [Google Scholar]
- 17.French AR, Kim S, Fehniger TA, Pratt JR, Yang L, Song YJ, Caliguri MA, Yokoyama WM. Chronic Lymphocytosis of Functionally Immature NK Cells. Journal of Allergy. Clinical Immunology. 2007;120:924–931. doi: 10.1016/j.jaci.2007.05.022. [DOI] [PubMed] [Google Scholar]
- 18.Lima M, Almeida J, Montero AG, Teixeira MA, Queiros ML, Santos AH, Balanzatequi A, Estevinho A, Alquero MC, Barcena P, Fonseca S, Amorim ML, Cabeda JM, Pinho L, Gonzalez M, San Miguel J, Justica B, Orfao A. Clinicobiological, Immunophenotypic, and Molecular Characteristics of Monoclonal CD56−/+dim Chronic Natural Killer Cell Large Granular Lymphocytosis. American Journal of Pathology. 2004;165:1117–1127. doi: 10.1016/s0002-9440(10)63373-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gett AV, Hodgkin PD. A cellular calculus for signal integration by T cells. Nature Immunology. 2000;1:239–244. doi: 10.1038/79782. [DOI] [PubMed] [Google Scholar]
- 20.De Boer RJ, Ganusov VV, Milutinovic D, Hodgkin PD, Perelson AS. Estimating lymphocyte division and death rates from CFSE data. Bulletin of Mathematical Biology. 2006;68:1011–1031. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- 21.Deenick EK, Gett AV, Hodgkin PD. Stochastic model of T cell proliferation: A calculus revealing IL-2 regulation of precursor frequencies, cell cycle time, and survival. Journal of Immunology. 2003;170:4963–4972. doi: 10.4049/jimmunol.170.10.4963. [DOI] [PubMed] [Google Scholar]
- 22.Ganusov VV, Dejan Milutinovic, De Boer RJ. IL-2 regulates expansion of CD4+ T cell populations by affecting cell death: insights from modeling CFSE data. Journal of Immunology. 2007;179:950–957. doi: 10.4049/jimmunol.179.2.950. [DOI] [PubMed] [Google Scholar]
- 23.Mesecke S, Urlaub D, Busch H, Eils R, Watzl C. Integration of Activating and Inhibitory Receptor Signaling by Regulated Phosphorylation of Vav1 in Immune Cells. Science Signaling. 2011;4:ra36. doi: 10.1126/scisignal.2001325. [DOI] [PubMed] [Google Scholar]
- 24.Fallon EM, Lauffenburger DA. Computational Model for Effects of Ligand/Receptor Binding Properties on Interleukin-2 Trafficking Dynamics and T Cell Proliferation Response. Biotechnology Progress. 2000;16:905–916. doi: 10.1021/bp000097t. [DOI] [PubMed] [Google Scholar]
- 25.Asquith B, B JA, Ganusov VV, Macallan DC. Lymphocyte Kinetics in Health and Disease. Trends in Immunology. 2009;30:182–189. doi: 10.1016/j.it.2009.01.003. [DOI] [PubMed] [Google Scholar]
- 26.Boehme SA, Lenardo MJ. Propriocidal Apoptosis of Mature T Lymphocytes Occurs at S Phase of the Cell Cycle. European Journal of Immunology. 1993;23:1552–1560. doi: 10.1002/eji.1830230724. [DOI] [PubMed] [Google Scholar]
- 27.Macallan DC, A B, Irvine AJ, Wallace DL, Worth A, Ghattas H, Zhang Y, Griffin GE, Tough DF, Beverley PC. Measurement and Modeling of Human T Cell Kinetics. European Journal of Immunology. 2003;33:2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]
- 28.Tough DF, Borrow P, Sprent J. Induction of Bystander T Cell Proliferation by Viruses and Type I Interferon in vivo. Science. 1996;272:1947–1950. doi: 10.1126/science.272.5270.1947. [DOI] [PubMed] [Google Scholar]
- 29.Murali-Krishna K, Altman JD, Suresh M, Sourdive D, Zajac A, Ahmed R. In Vivo Dynamics of Anti-viral CD8 T Cell Responses to Different Epitopes. An Evaluation of Bystander Activation in Primary and Secondary Responses to Viral Infection. Advances in Experimental Medicine. Biology. 1998;452:123–142. doi: 10.1007/978-1-4615-5355-7_14. [DOI] [PubMed] [Google Scholar]
- 30.Kaech SM, Ahmed R. Memory CD8+ T cell differentiation: initial antigen encounter triggers a developmental program in naive cells. Nature Immunology. 2001;2:415–422. doi: 10.1038/87720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wong P, Pamer EG. Cutting Edge: Antigen-Independent CD8 T Cell Proliferation. Journal of Immunology. 2001;166:5864–5868. doi: 10.4049/jimmunol.166.10.5864. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.