Single stranded DNA translocation of E. coli UvrD monomer is tightly coupled to ATP hydrolysis

Abstract

E. coli UvrD is an SF1A helicase/translocase that functions in several DNA repair pathways. A UvrD monomer is a rapid and processive single-stranded (ss) DNA translocase, but is unable to unwind DNA processively in vitro. Based on data at saturating ATP (500 μM) we proposed a non-uniform stepping mechanism in which a UvrD monomer translocates with biased (3′ to 5′) directionality while hydrolyzing 1 ATP per DNA base translocated, but with a kinetic step-size of 4–5 nucleotides/step, suggesting a pause occurs every 4–5 nucleotides translocated. To further test this mechanism we examined UvrD translocation over a range of lower ATP concentrations (10–500 μM ATP), using transient kinetic approaches. We find a constant ATP coupling stoichiometry of ~1 ATP/DNA base translocated even at the lowest ATP concentration examined (10 μM) indicating that ATP hydrolysis is tightly coupled to forward translocation of a UvrD monomer along ssDNA with little slippage or futile ATP hydrolysis during translocation. The translocation kinetic step size remains constant at 4–5 nucleotides/step down to 50 μM ATP, but increases to ~7 nucleotides/step at 10 μM ATP. These results suggest that UvrD pauses more frequently during translocation at low ATP, but with little futile ATP hydrolysis.

Introduction

E. coli UvrD is an SF1A helicase and single-stranded (ss)DNA translocase that functions in DNA repair pathways, such as nucleotide excision repair¹ and methyl-directed mismatch repair², and in the replication of some plasmids³. UvrD can also displace the DNA replication termination protein, Tuss, from its double strand (ds) DNA recognition sequence Ter⁴ and RecA from ssDNA⁵. Genetic studies suggest that the RecA protein displacement function of UvrD is important for its anti-recombinase activity^{6; 7; 8}. Whereas a UvrD monomer is capable of processive ssDNA translocation, UvrD must at least dimerize in order to form a helicase that will unwind DNA processively enough to unwind even an eighteen base pair duplex^{9; 10}. Studies of the structurally similar E. coli Rep helicase have shown that the Rep monomer can also translocate along ssDNA rapidly and processively, but that DNA unwinding by the Rep monomer is auto-inhibited by its 2B sub-domain¹¹. Based on this it is possible that a similar auto-inhibitory mechanism may explain why a UvrD monomer is not a processive helicase.

We previously determined a minimal kinetic mechanism for ssDNA translocation by a UvrD monomer at saturating ATP concentrations using single round fluorescence stopped-flow methods¹⁰ monitoring UvrD translocation, dissociation and ATP hydrolysis¹². The translocation kinetics can be described by a simple sequential n-step kinetic mechanism, which assumes that a series of identical rate-limiting “translocation steps” are repeated until the monomer dissociates or reaches the 5′ end of the ssDNA. Analysis of the kinetics of translocation suggests a model in which a UvrD monomer moves an average of ~4–5 nucleotides (termed the translocation kinetic step-size) between two successive rate-limiting steps^{10; 13}. However, a study of the extent of ATP hydrolysis during translocation revealed an ATP coupling stoichiometry of ~ 1 ATP per nucleotide translocated, suggesting a non-uniform (or discontinuous) stepping mechanism for UvrD translocation. In this mechanism a UvrD monomer rapidly translocates 4–5 nt, hydrolyzing 1 ATP/nucleotide, followed by a slow step that limits the overall rate of translocation¹². This model assumes ATP hydrolysis is tightly coupled to ssDNA translocation. Alternatively, if ATP hydrolysis is not tightly coupled to translocation, i.e., there is some futile ATP hydrolysis occurring in the cycle, then a simpler translocation mechanism without a periodic slow step could be operative.

Here we determine the ATP coupling stoichiometry of UvrD monomer translocation and the kinetic step size for translocation over a range of lower ATP concentrations in order to determine whether ATP hydrolysis is tightly coupled to translocation. We find that the ATP coupling stoichiometry remains constant (0.8–0.9 ATP/DNA base translocated) even at the lowest ATP concentration measured (10 μM) indicating that ATP hydrolysis is tightly coupled to unidirectional translocation along the ssDNA, consistent with the non-uniform mechanism proposed previously¹².

Results

UvrD monomer translocation kinetic step size increases with decreasing ATP concentration

In the non-uniform stepping model for UvrD monomer translocation along ssDNA UvrD takes 4–5 rapid, 1 nucleotide steps, hydrolyzing one ATP per step, followed by a slow step that limits the overall rate of translocation. Since each of the rapid steps requires ATP binding and hydrolysis, ATP binding should eventually become rate limiting for translocation at some low ATP concentration. In this limit, the kinetic step size should decrease, approaching a limiting value of ~ 1 nucleotide (Figure S1(a, b)). The data suggesting a non-uniform stepping model were obtained at saturating ATP concentrations and was based on the assumption that ATP hydrolysis is tightly coupled to translocation (i.e., no futile ATP hydrolysis occurred). To test this prediction and the assumption of tight coupling, we examined UvrD monomer translocation along ssDNA for a range of lower ATP concentrations.

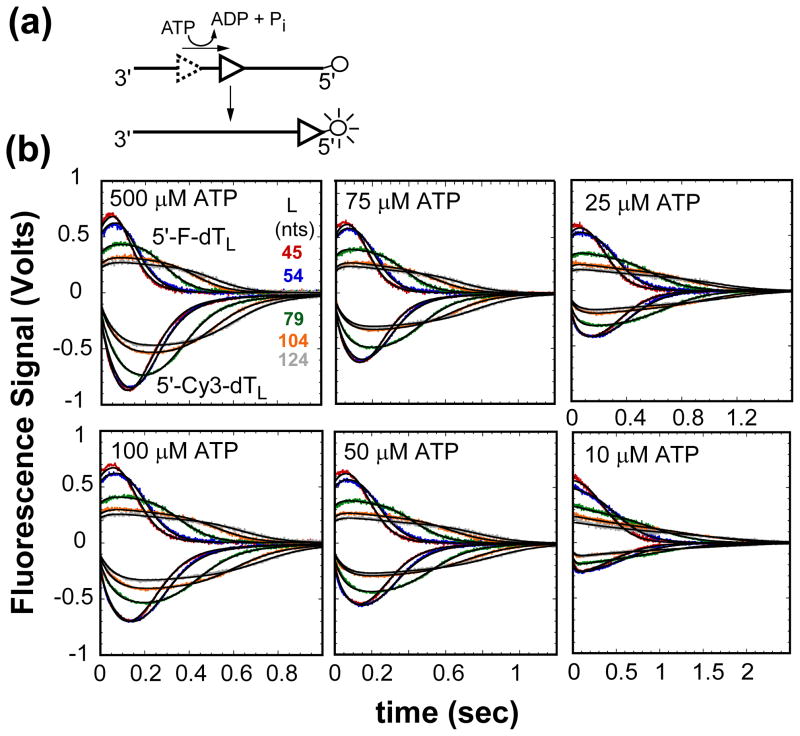
The methods used to examine the kinetics of UvrD monomer translocation along ssDNA have been described¹⁰ and are depicted in Figure 1(a). In this stopped-flow assay an oligodeoxythymidylate labeled at the 5′-end with Cy3 or fluorescein is combined with UvrD in buffer T₂₀ at 25°C under conditions of 2-fold molar excess of ssDNA molecules to ensure a monomer of UvrD is bound to the ssDNA. Our previous studies^{10; 12; 14} have shown that UvrD monomer binding to ssDNA occurs randomly. The translocation reaction is initiated by mixing the UvrD:ssDNA complex with buffer T₂₀, ATP, MgCl₂ (2 mM, final), and heparin (4 mg/ml, final). When the UvrD monomer reaches the 5′-labeled end of the ssDNA, the fluorescence intensity of the fluorophore is either enhanced in the case of Cy3 or quenched in the case of fluorescein¹⁰. Any UvrD that dissociates from the ssDNA either during translocation or after reaching the 5′-end of the ssDNA is trapped by excess heparin and prevented from rebinding to the ssDNA, thus ensuring “single round” conditions. Dissociation of UvrD from the 5′-end of the ssDNA results in a decrease in Cy3 fluorescence or increase in fluorescein fluorescence.

Figure 1.

Kinetics of UvrD monomer translocation monitored by the arrival of UvrD at the 5′-end of fluorescently labeled (dT)_L as a function of ATP concentration. (A)- Cartoon depicting translocation assay. UvrD (triangle) binds randomly to ssDNA. Upon addition of ATP UvrD translocates 3′ to 5′ along the ssDNA. When UvrD reaches the 5′-end with a covalently attached fluorophore it either quenches or enhances the fluorescence of the fluorophore. (B)- UvrD is pre-incubated with either excess 5′-Cy3-dT_L or 5′-F-dT_L in T₂₀ buffer then rapidly mixed with ATP, MgCl₂, and heparin in T₂₀ buffer at 25°C to initiate translocation. The top portion of each panel has the time courses for translocation on Cy3 labeled ssDNA and the bottom portion has the time courses for translocation on fluorescein labeled ssDNA at the given ATP concentration. The smooth black curves are simulations using eq. (1) and the best-fit parameters determined from a combined global NLLS analysis of the time courses (Table 1).

Figure 1(b) shows UvrD translocation/dissociation time courses obtained with a series of oligodeoxythymidylates labeled at the 5′-end with Cy3 (5′-Cy3-(dT)_L) or fluorescein (5′-F-(dT)_L) (L = 44, 54, 79, 104, and 124 nucleotides (nts)) and at several ATP concentrations (10–500 μM). These time courses show the characteristic profiles indicative of directional ssDNA translocation of an ensemble of UvrD monomers that are initially bound randomly along the ssDNA at the start of the reaction^{10; 12; 14; 15}. The average time required to reach the maximum fluorescence signal change increases with increasing ssDNA length, L, reflecting the translocation process. The time courses also broaden with increasing ssDNA length since the initial random distribution of UvrD bound to (dT)_L broadens with increasing ssDNA length^{10; 13}. For a given DNA length, as the ATP concentration decreases the maximum signal change decreases and the time courses also broaden, reflecting both a lower processivity and slower rate of translocation. Global analysis of these time courses using an n-step sequential model can yield estimates of the translocation stepping rate constant, k_t, the kinetic step-size, m, and the processivity, although this requires independent knowledge of the dissociation rate constant, k_d, for UvrD from internal sites within the ssDNA^{10; 12}.

UvrD monomer dissociation rate from internal ssDNA sites

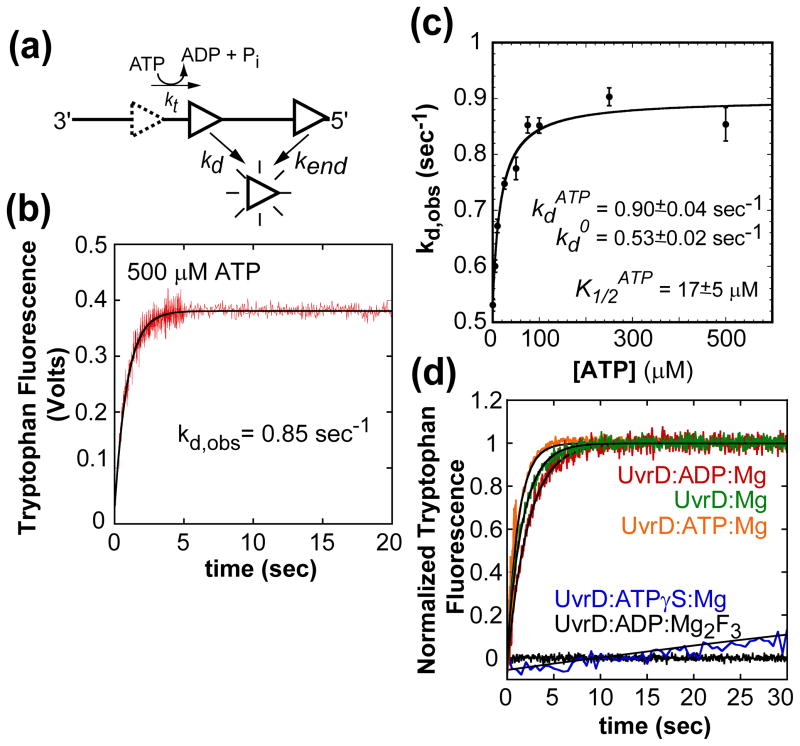
We determined the rate constant for UvrD monomer dissociation from internal ssDNA sites (k_d) using poly(dT) since (dT)_L was used for the translocation experiments. UvrD dissociation was monitored by the increase in the intrinsic UvrD tryptophan fluorescence upon dissociation from poly(dT) as shown in Figure 2(a)¹⁰. We used poly(dT) stocks that had been fractionated (see Materials and Methods) (average lengths of 1,500 ± 50 and 3,500 ± 100 nucleotides) to eliminate shorter lengths to insure that the rate constant reflects dissociation from internal sites¹⁰. UvrD was pre-bound to poly(dT) (1 monomer per 400 nucleotides) in buffer T₂₀ and dissociation was initiated by mixing with buffer T₂₀ containing ATP (500 μM), MgCl₂ (2.0 mM) and heparin (4 mg/mL). The resulting single exponential time course (Figure 2(b)) yields k_d = 0.85 ± 0.04 s⁻¹ for both poly(dT) samples in good agreement with previous measurements using even longer poly(dT)¹². UvrD dissociation rates were measured as a function of ATP concentration (no ATP, 10, 25, 50, 75, 100, 250, and 500 μM) and were all well described by a single exponential (data not shown). The observed dissociation rate constant increases with ATP concentration reaching a plateau at 0.83–0.85 sec⁻¹ (Figure 2(c)). Therefore, UvrD monomer dissociation is slow in the absence of ATP (0.54 sec⁻¹) and increases with increasing ATP concentration. Interestingly, UvrD monomer dissociation is slower in the absence of nucleotide (0.58 ± 0.02 s⁻¹) or presence of ADP (0.42 ± 0.02 s⁻¹) and even slower with non-hydrolysable ATPγS (0.005 ± 0.001 s⁻¹) or the transition state analog Mg₂F₃ADP (Figure 2(d)), indicating that UvrD dissociation is faster in the ADP:P_i or P_i bound state.

Figure 2.

UvrD monomer dissociation kinetics from internal sites of ssDNA during translocation as a function of ATP concentration. (A)- Cartoon depicting assay for UvrD dissociation during ssDNA translocation. (B)- Time course of UvrD monomer (25 nM, post mix) dissociation from poly(dT) (10 μM nts, post mix) (1.5 ± 0.05 kb), (buffer T₂₀, 500 μM ATP, 2 mM MgCl₂, and 4 mg/ml heparin, 25°C) fit to a single exponential. (C)- The observed k_d as a function of ATP concentration fit to a hyperbola, fit parameters shown in plot. The dissociation time courses at each ATP concentration were fit to a single exponential (data not shown). (D)- Time courses of UvrD dissociation from ssDNA in the absence of nucleotide, ADP, ATPγS, and ADP:Mg₂F₃ fit to a single exponential. The observed k_d^{No Nucleotide}= 0.58 ± 0.02, k_d^ADP= 0.42 ± 0.02, and k_d^ATPγS= 0.005 ± 0.001.

Kinetic parameters for UvrD monomer translocation

Global nonlinear least squares analysis of the data in Figure 1(b) for both sets of translocation time courses (Cy3 and fluorescein) at each ATP concentration using the sequential n-step kinetic model (eq. (1), see Figure S2) was used to determine the best-fit translocation kinetic parameters, k_t, m, d, and n as described¹⁰, where k_t is the stepping rate constant, m is the translocation kinetic step size, d is the UvrD monomer contact size on the ssDNA and n is the maximum number of steps taken to reach the 5′-end of a given length of ssDNA. We note that analysis of these time courses, where UvrD initiates translocation from random positions along the ssDNA, using a semi-quantitative time-to-peak analysis results in an over estimate of the macroscopic translocation rate and thus was avoided¹⁶. The kinetic parameters in the sequential n-step kinetic model, k_t, m, d, and n were assumed to be fluorophore independent, whereas k_c and k_end, which describe UvrD monomer dissociation from the 5′-end of the ssDNA, were floated for each fluorophore.

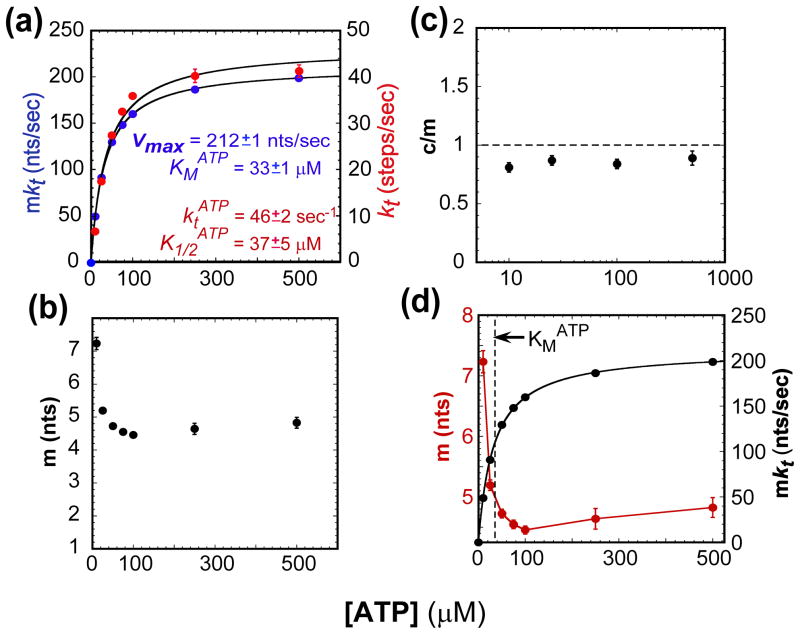
The UvrD monomer translocation stepping rate constant, k_t, and macroscopic rate (mk_t) both increase hyperbolically with ATP concentration (Figure 3(a)). The ATP dependence of the macroscopic rate is well described by the Michaelis-Menten equation with the maximum translocation rate approaching 211 nts/sec and K_M^ATP = 33 μM. In the presence of 4 mg/mL heparin, the UvrD monomer translocation processivity, P = mk_t/(mk_t + k_d) (in nucleotide units), decreases with decreasing ATP concentration from an average of (1−P)⁻¹ =(241 ±1) nts before dissociation at saturating ATP to an average of (74 ± 1) nts at 10 μM ATP (Figure S3(a)). This drop in processivity reflects a decrease in the macroscopic translocation rate and is not due to a higher dissociation rate since the dissociation rate is actually lower in the absence of ATP (Figure 2(c)).

Figure 3.

The ATP concentration dependence of select kinetic parameters for UvrD monomer translocation along ssDNA. (A)- The observed rate-limiting stepping rate constant (k_t) and macroscopic translocation rate (mk_t) as a function of ATP fit to a hyperbola and Michaelis-Menten, respectively; fit parameters shown in plot. (B)- The observed translocation kinetic step size (m). (C)- ATP coupling stoichiometry (c/m). (D)- Comparison of the trends in the kinetic step size (m) and macroscopic translocation rate (mk_t).

At each ATP concentration, the maximum number of translocation steps, n, increases linearly with increasing ssDNA length, L, as shown in Figure S3(b). The translocation kinetic step size, m, and the contact size, d, at each ATP concentration was determined by fitting the data in Figure S3(b) to the relationship, n = (L−d)/m. The UvrD monomer contact size, d, remains relatively constant, at ~8–10 nts, for all ATP concentrations (Table 1). The translocation kinetic step size remains fairly constant at 4–5 nt/step from 500 μM to 50 μM ATP, but increases to ~7nt/step at 10 μM ATP (Figure 3(b)). This trend is opposite to that expected for the discontinuous stepping model where the kinetic step size should approach a value of 1 nt. The he increase in the kinetic step size occurs when the ATP concentration is below the K_M for ATP, suggesting that the larger kinetic step size is linked to an increase of ATP-free UvrD in the ssDNA bound UvrD population (Figure 3(d)).

Table 1. UvrD monomer ssDNA translocation kinetic parameters as a function of ATP concentration.

(T₂₀ buffer, 2.0 mM MgCl₂, and 4 mg/ml heparin at 25°C)

Translocation Kinetic Parameters	ATP (μM)
	10	25	50	75	100	250	500
kt (kinetic steps sec−1)	6.7±0.1	17.5±0.3	27.4±0.5	32.5±0.5	35.9±0.5	40±1	41±1
kd (sec−1)	0.67±0.01	0.75±0.01	0.77±0.02	0.85±0.01	0.85±0.01	0.90±0.02	0.85±0.03
Dissociation from 5′-endA
kc (sec−1) Fluorescein	36±4	20±1	17.8±0.5	17.2±0.4	16.0±0.3	13.7±0.3	13.9±0.3
Cy3	49±7	25±2	26±1	27±1	24±1	25±3	25±3
kend (sec−1) Fluorescein	22±1	6.3±0.3	4.5±0.1	3.7±0.1	3.4±0.1	2.8±0.1	3.0±0.1
Cy3	2±1	3±1	3±2	2.5±1	0.6±0.1	2±1	1.1±0.8
Tryptophan	44±8	34±4	---	---	19±1	---	18±1
ka (ATP UvrD−1 sec−1)	0	10±19	---	---	63±13	---	53±19
c (ATP kinetic-step−1)	5.8±0.1	4.5±0.1	---	---	3.8±0.1	---	4.3±0.1
r	8±1	2.5±0.2	1.9±0.1	1.9±0.1	1.4±0.1	1.4±0.3	1.4±0.3
m (nts kinetic-step−1)	7.2±0.2	5.2±0.1	4.7±0.1	4.5±0.1	4.5±0.1	4.6±0.2	4.8±0.2
d (contact size, nts)	7.3±0.8	9.6±0.4	10.2±0.3	10.1±0.4	9.6±0.3	9.5±0.7	9.3±0.7
c/m (ATP nt−1)	0.81±0.04	0.87±0.04	---	---	0.84±0.04	---	0.89±0.06
mkt (nts sec−1)B	48.8±0.6	90.9±0.7	129±1	148±1	160±1	186±1	199±1
1/(1−P) (nts)	74±1	122±1	168±1	174±1	189±1	207±1	241±1

^ADissociation from the 5′-end in the translocation assay is fluorophore dependent and is a two step process defined by k_c and k_end. In the absence of fluorophore dissociation from the 5′-end can be modeled as a single step (k_end, Tryptophan, see Figure S5).

^BMacroscopic translocation rate.

P Is the translocation processivity where $P=\frac{{mk}_t}{{mk}_t+k_d}$ (in nucleotide units). 1/(1−P) is the average number of nucleotides translocated before dissociation from the ssDNA under the experimental conditions.

The reported error represents ± 1 σ determined from a 100 cycle Monte Carlo simulation

ATP hydrolysis is tightly coupled to translocation at all ATP concentrations

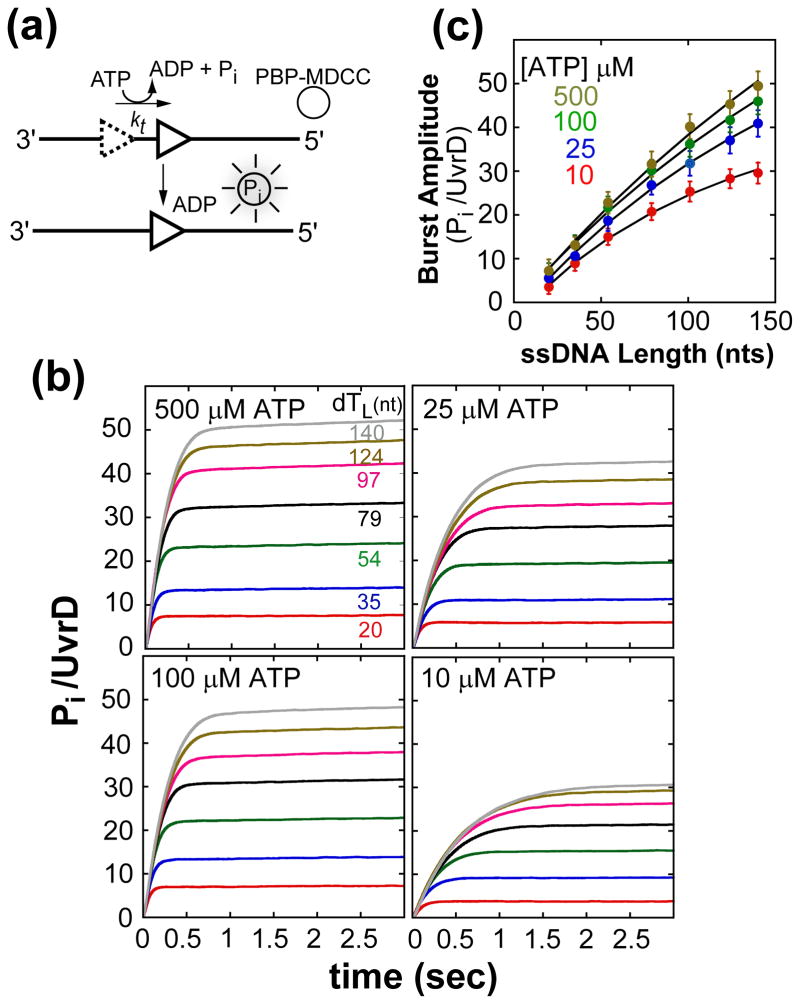
ATP hydrolysis during UvrD monomer translocation was measured using a fluorescent assay (Figure 4(a)) that monitors production of inorganic phosphate, P_i, using a fluorescence E. coli phosphate binding protein (PBP-MDCC)^{17; 18}. The assay was modified to include heparin as a trap for free UvrD, minimizing rebinding of UvrD¹². Figure 4(b) shows time courses of P_i production resulting from UvrD monomer translocation along a series of (dT)_L substrates (L= 20, 35, 54, 79, 97, 124, and 140 nucleotides) at 10, 25, 100, and 500 μM ATP. UvrD was pre-incubated with (dT)_L in buffer T₂₀ and then mixed with buffer T₂₀ containing ATP, MgCl₂, heparin and PBP-MDCC. Each time course shows an exponential increase in P_i production, the amplitude of which increases with increasing ssDNA length, consistent with ATP-dependent translocation of UvrD monomers along ssDNA^{12; 13}. This is followed by a slow linear increase in P_i production, which reflects a small fraction of UvrD that can rebind to the ssDNA and hydrolyze additional ATP¹². As the ATP concentration decreases the P_i production for each length decreases consistent with a lower translocation processivity.

Figure 4.

Kinetics of ATP hydrolysis during UvrD monomer translocation at different ATP concentrations. (A)- Cartoon depicting P-release assay for monitoring ATP hydrolysis during UvrD (triangle) translocation. (B)- Time courses of P_i production during UvrD monomer translocation along (dT)_L. UvrD was pre-incubated with excess (dT)_L and translocation initiated by the addition of ATP, Mg²⁺, heparin, and PBP-MDCC at 25°C. Time courses were corrected for contaminating phosphate (P_i) and converted to P_i/UvrD monomer (see Material and Methods). Curves (L = 54–124 nts) used 300 nM (dT)_L, and curves (L = 20 and 35 nts) used 1.0 μM (dT)_L at the given ATP concentrations to saturate UvrD. (C)- Dependence of the normalized burst phase amplitude (P_i/UvrD monomer) on ssDNA length, L, at each ATP concentration analyzed using eq. (4), where P, m, d, r and k_end were constrained to the values determined independently (Table 1) while c and k_a were floated. The black curves are the best-fit to the data (see Table 1 for c and k_a values).

The total moles of P_i produced per mole of UvrD monomer as a function of ssDNA length is plotted in Figure 4(c). Note that since the processivity is low at the lower ATP concentrations, the plots of these data show increased non-linearity. As a result, these data must be analyzed using the full expression for the amount of ATP hydrolyzed as a function of length given by eq. (4) to determine the number of ATP hydrolyzed per kinetic step, c¹². Analysis of the data using a semi-quantitative duration analysis ¹⁸ or taking a limiting slope result in overestimates of the macroscopic translocation rate and underestimates the ATP coupling stoichiometry¹² (Figure S4(a–c)). The translocation kinetic parameters, k_t, k_d, m, d, and k_end, determined independently at each ATP concentration by monitoring UvrD arrival at the 5′-end (Figure 1) (Table 1) were constrained and c and k_a were determined as fitting parameters. In order to obtain an estimate of k_a, the rate constant for UvrD monomer ATP hydrolysis at the 5′-end, k_end in the absence of fluorophore was determined independently at each ATP concentration (Figure S5(a, b)). The number of ATP hydrolyzed per kinetic step, c, determined from NLLS analysis of the data in Figure 4(c), combined with the kinetic step-size, m, yields the ATP coupling stoichiometry, c/m, the number of ATP molecules hydrolyzed per nucleotide translocated per UvrD monomer. Figure 3(c) shows that c/m has values of ~0.8–0.9 ATP molecules hydrolyzed per nucleotide translocated per UvrD monomer and changes very little over the range of ATP concentrations examined. The fact that the ATP coupling stoichiometry is near unity and shows no significant increase at low ATP concentration suggests that UvrD does not undergo significant slippage (backward movement) or futile hydrolysis. Either of these would result in an increase in coupling stoichiometry.

Slipping, pausing, or static disorder in the translocation rate can yield a larger apparent translocation kinetic step size

The increase in the apparent translocation kinetic step size with decreasing ATP concentrations suggests that the discontinuous stepping model is not completely applicable at these lower ATP concentrations. As noted above, the simple model predicts that the step size should eventually approach unity when ATP binding becomes rate limiting. Single molecule studies have shown that some nucleic acid motors can display pausing or slippage^{19; 20}. In addition, single molecule studies of helicases and ssDNA translocation by PcrA have observed a persistent variation in the unwinding and/or translocation rates among individual enzymes, often referred to as static disorder^{21; 22; 23; 24; 25}. These observations suggest slipping, pausing, or static disorder in the rate within the nucleic acid enzyme population could be present.

The discontinuous stepping model assumes a series of n irreversible kinetic steps occur with rate constant, k_t, whose rate is limited by the slowest process in translocation cycle. In addition, k_t is assumed to be the same for all translocases in the population^{10; 12}. To address this further, we consider how four types of heterogeneity in k_t might influence the value of the apparent kinetic step size. First, we consider simple heterogeneity where the value of k_t can vary for each step within some Gaussian distribution around the average value of k_t. Such kinetic heterogeneity is expected for any exponential process. Second, we consider the effects of pausing of the translocase. Third, we consider slippage (backward movement) of the translocase. Fourth, we consider the effects of persistent heterogeneity or static disorder, in which the average value of k_t differs significantly among enzyme molecules within the population^{25; 26; 27}.

To assess how these phenomena affect the translocation kinetic parameters measured in our ensemble experiments we simulated time courses of translocase arrival at the 5′-end of the DNA and ATP hydrolysis during translocation where we included that the translocase has a finite probability to slip backward along the ssDNA, pause, or possess static disorder in translocation rates among the enzyme population (see Materials and Methods). The resulting simulated time courses were then analyzed with the n-step sequential model (see representative fits, Figure S6(a-d)) to determine the macroscopic translocation rate, the translocation kinetic step size and ATP coupling stoichiometry. In the case of pausing we examined two cases: one in which ATP hydrolysis occurs during the pause, i.e., futile ATP hydrolysis occurs, and one in which ATP hydrolysis is required for recovery from the pause. For each simulation the translocase is assumed to hydrolyze one ATP per nucleotide translocated.

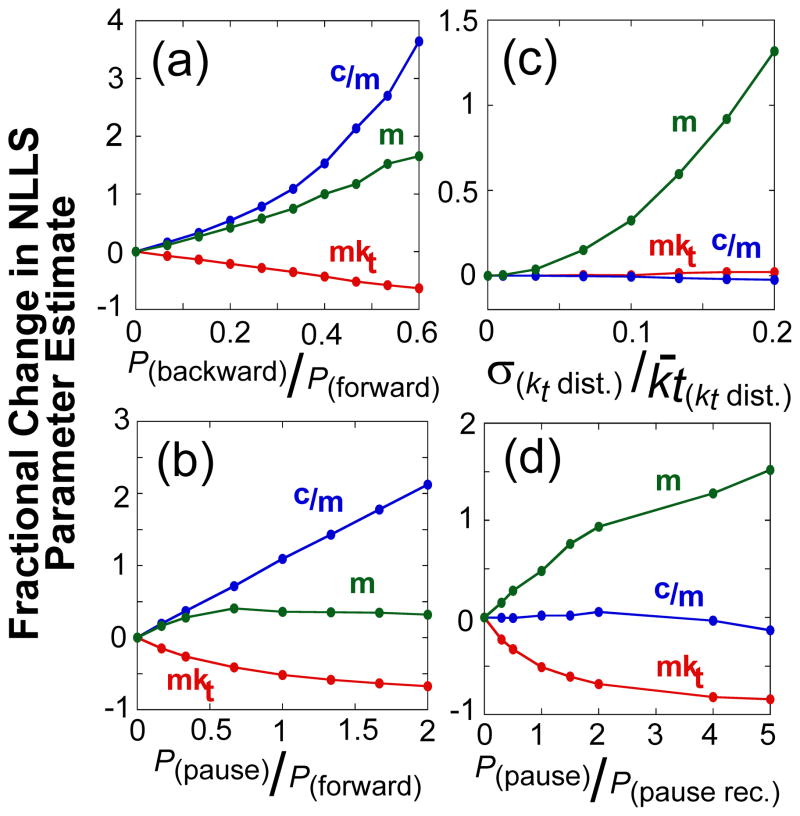
Figure 5 shows the effects of slippage (panel (a)), pausing (panels (b) and (d)), and static disorder (panel (c)) on the kinetic parameters (mk_t, m, and c/m) that we obtain from global analysis of a set of simulated ensemble translocation experiments. In each case, the apparent translocation kinetic step size is overestimated, but to different extents, as the probability of slippage or pausing increases or as the extent of static disorder increases. However, the other kinetic parameters (mk_t and c/m) are generally affected differently in each case; for example, in the cases where ATP hydrolysis does not always result in forward motion along the ssDNA, as for slippage (panel (a)) or futile hydrolysis during a pause (panel (b)), the ATP coupling stoichiometry, c/m, increases as the probability of these events increase. However, when ATP hydrolysis is required for recovery from a pause (panel (d)), or when static disorder is present in the population (panel (c)), the ATP coupling stoichiometry is not affected. As expected, the macroscopic translocation rates (mk_t) are slower when slippage or pausing occurs.

Figure 5.

The dependence of the estimates of kinetic parameters for DNA translocation on the presence of slipping, pausing, and static disorder in the translocase population. Simulated translocation time courses with translocase pausing, slipping, and static disorder were analyzed with the n-step model (see Materials and Methods). The data are plotted as the fractional change in the value of the fit parameter determined in the presence of the kinetic heterogeneity from the value determined in the absence of the kinetic heterogeneity as a function of the ratio of specific probabilities used in the simulations, unless otherwise noted: macroscopic translocation rate (mk_t, red), ATP coupling stoichiometry (c/m, blue), and kinetic step size (m, green). (A)- The effect of backward motion. (B)- The effect of pausing with futile ATP hydrolysis. (C)- The effect of a distribution of inter-enzyme translocation rates (static disorder). The fractional change in the fit parameter is plotted as a function of the ratio of the standard deviation of the distribution to its mean. (D)- The effect of random pauses of varying duration. Here the probability of pausing was kept constant, equal to the probability of stepping forward, but the probability of recovering from the paused varied. The fractional change in the fit parameter is plotted as a function of the ratio of the probability of pausing to the probability of recovering from the pause.

Since our experimental measure of ATP coupling stoichiometry, c/m, remains constant over a broad range of ATP concentrations (Figure 3(c)), slippage or futile ATP hydrolysis during a pause cannot explain the increase in the apparent kinetic step size. In the following experiments, we test if pausing without futile ATP hydrolysis could explain the increase in the kinetic step size.

The increase in translocation kinetic step size at low ATP is consistent with UvrD pausing

Our experimental results show that the large increase in the apparent kinetic step size occurs when the ATP concentration is below the apparent K_m^ATP for ATP (Figure 3(d)). These are clearly conditions in which the population of nucleotide free UvrD is increased. In fact, the observed k_d under these conditions approaches the k_d obtained in the absence of nucleotide. Our analysis of the simulated time courses indicate that pausing of UvrD without futile ATP hydrolysis would have no effect on the ATP coupling stoichiometry, but can result in a larger apparent kinetic step size.

To test whether increased pausing at low ATP concentrations could explain the increase in the apparent kinetic step size we performed a set of translocation experiments including ADP in the solution and varying the ADP/ATP ratio. By including a competitive amount of ADP in solution, more pauses should be induced in the UvrD population due to the competitive binding of ADP to the single nucleotide binding site on the UvrD monomer. UvrD monomers bound with ADP cannot translocate (paused) while UvrD monomers bound with ATP can translocate. After dissociation of ADP the UvrD monomer can either rebind ADP remaining paused, or bind ATP and resume translocation. UvrD translocation was examined using 5′-F-dT_L (L: 45, 54, 64, 79, 84, 97, 104, and 124) by pre-incubating UvrD with excess 5′-F-dT_L in buffer T₂₀ and rapidly mixed with an ADP:ATP mixture, MgCl₂, and heparin at 25°C in buffer T₂₀ to initiate translocation.

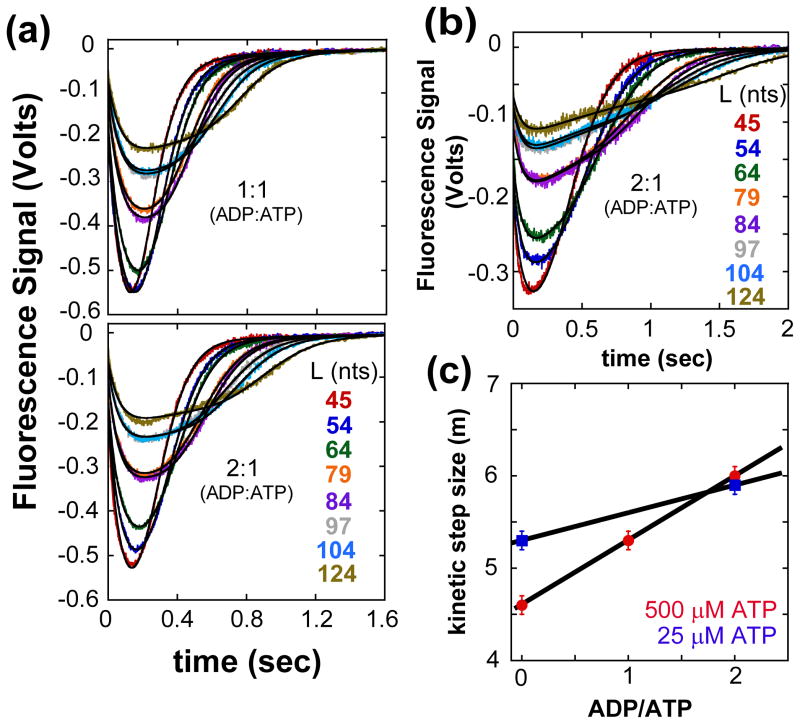
The translocation time courses from these mixed ADP/ATP experiments are shown in Figure 6(a), (b) and (c) for 1:1 and 2:1 ADP:ATP ratios at saturating ATP (0.5 mM) and low ATP (25 μM). The black traces are simulations using the best fit parameters obtained by globally fitting the time courses at each ratio of ADP:ATP to the sequential n-step model (eq. (2) for a single fluorophore). The UvrD monomer dissociation rate constant from internal ssDNA sites was determined at each ADP:ATP ratio and constrained in the global analysis (Table 2) (Figure S7). In all cases, the translocation kinetic step size increased as the ADP:ATP ratio increased (Figure 6(c)), consistent with increased pausing resulting in an inflated kinetic step size. As expected, the macroscopic translocation rate also decreased at the higher ADP:ATP ratios (Table 2). Furthermore, the UvrD monomer dissociation rate constant, k_d, decreased at the higher ADP:ATP ratios, approaching the value of k_d for the UvrD monomer in the presence of only ADP (Figure 2(d)). Hence, it is likely that the increased apparent kinetic step size determined at low [ATP] results from a significant contribution from paused UvrD.

Figure 6.

Kinetics of UvrD monomer translocation monitored by the arrival of UvrD at the 5′-end of 5′-F-(dT)_L in the presence of different molar ratios of ADP:ATP. UvrD is pre-incubated with excess 5′-F-dT_L in T₂₀ buffer then rapidly mixed with ATP, ADP, MgCl₂, and heparin in T₂₀ buffer at 25°C to initiate translocation. (A)- Translocation time courses at 1:1 and 2:1 ADP:ATP concentration ratios at a constant ATP concentration of 500 μM ATP. (B)- Translocation time courses at 2:1 ADP:ATP concentration ratio at constant ATP concentration of 25 μM ATP. The smooth black curves are simulations using eq. (2) and the best-fit parameters determined from a combined global NLLS analysis of the time courses (Table 2). (C)- The observed translocation kinetic step size as a function of ADP:ATP ratio. The kinetic step size was determined as in Figure S2A.

Table 2. UvrD monomer ssDNA translocation kinetic parameters in presence of different ADP:ATP molar ratios.

(T₂₀ buffer, 2.0 mM MgCl₂, and 4 mg/ml heparin at 25°C)

Translocation Kinetic ParametersA	ADP:ATP
	(500 μM ATP)			(25 μM ATP)
	0:1	1:1	2:1	0:1	2:1
kt (kinetic steps sec−1)	42±1	28.3±0.5	20.3±0.5	15.6±0.4	10.8±0.3
kd (sec−1)	0.88±0.05	0.77±0.02	0.52±0.03	0.68±0.02	0.62±0.01
Dissociation from 5′-end
kc (sec−1) Fluorescein	13.6±0.1	13.9±0.3	15.9±0.1	13.5±0.2	15.7±0.3
kend (sec−1) Fluorescein	2.8±0.2	2.3±0.1	1.34±0.03	1.02±0.01	0.73±0.02
r	1.3±0.1	1.7±0.1	2.5±0.2	1.8±0.1	2.7±0.1
m (nts kinetic-step−1)	4.6±0.1	5.2±0.1	6.0±0.1	5.3±0.1	5.9±0.1
d (contact size, nts)	13±2	13.5±0.3	13±2	16±1	17±2
mkt (nts sec−1)B	194±1	148±1	122±1	83±1	63.5±0.5
1/(1−P) (nts)	221±1	193±1	236±1	123±1	103±1

^AParameters determined from global NLLS analysis using a single set of ssDNA labeled with fluorescein.

^BMacroscopic translocation rate. P is as defined in Table 1.

The reported error represents ± 1 σ determined from a 100 cycle Monte Carlo simulation.

Discussion

UvrD monomer ATP hydrolysis is tightly coupled to unidirectional translocation along ssDNA

The ATP coupling stoichiometry (c/m), the average number of ATP hydrolyzed per nucleotide translocated, is an important mechanistic feature of a translocase motor indicating how well the catalytic cycle of ATP hydrolysis is coupled to physical translocation along ssDNA under a given set of conditions. Loose coupling (c/m > 1) indicates that multiple rounds of ATP hydrolysis occur on average to translocate 1 nt. Thermal or ‘Brownian’ ratchet models for ssDNA translocation as proposed for the SF2 NS3h helicase^{28; 29} predict loose coupling between ATP hydrolysis and translocation. This arises since thermal fluctuations of the translocase move it stochastically forward or backward along the ssDNA. Indeed a large ATP coupling stoichiometry (~5 ATP/nt) has been measured for NS3h translocation on either ssDNA or ssRNA using bulk assays at low salt concentrations²⁹. However, single molecule studies measuring NS3 monomer RNA and DNA unwinding^{30; 31} and bulk assays measuring NS3h ssDNA and ssRNA translocation³² at higher salt concentrations suggest a smaller coupling stoichiometry (1–0.5 ATP/nt). In contrast, for a translocase with tight coupling (c/m ≤ 1), every round of ATP hydrolysis results in unidirectional translocation along the ssDNA; this is a hallmark of inchworm stepping models. In inchworm stepping models proposed for SF1 helicases/translocases, ATP binding and hydrolysis alter the relative ssDNA affinities of the 1A and 2A motor domains allowing the 2A domain to move forward followed by the 1A domain^{33; 34}.

ATP coupling stoichiometries for ssDNA translocation have been reported for the SF1 DNA helicases: PcrA¹⁸, UvrD¹², and RecD³⁵ and the SF2 helicases: NS3h, NS3-4A²⁹ and BLM³⁶. Except for NS3h, the ATP coupling stoichiometries determined at saturating ATP concentrations are near ~1 ATP/nt, suggesting tight coupling between ATP hydrolysis and directional translocation. This observation along with structural models of the helicase bound to nucleic acid have been used to support the inchworm stepping model for translocation^{33; 34}. However, at saturating ATP in bulk solution assays one cannot assess if the helicase pauses or slips backward along the ssDNA. By examining the observed ATP coupling stoichiometry over a range of ATP concentrations, our results show that ATP hydrolysis is indeed tightly coupled to UvrD translocation. The ATP coupling stoichiometry during UvrD monomer translocation along ssDNA remained constant at ~ 0.8–0.9 ATP/nt translocated between 10–500 μM ATP (Figure 3(c)). This suggests that UvrD translocates with little backward slippage or futile ATP hydrolysis, since either of those processes would result in an ATP coupling stoichiometry exceeding unity (Figure 5(a, b)). The tight coupling between ATP hydrolysis and translocation provides strong evidence for an inchworm stepping mechanism and is not consistent with a Brownian ratchet.

Interpretation of the observed kinetic step size and implications for the mechanism of UvrD monomer translocation

A discontinuous stepping model was proposed to explain the large UvrD monomer translocation kinetic step size and the small (~1) ATP coupling stoichiometry¹². In this model the UvrD monomer takes 4–5 rapid one nucleotide steps each coupled to hydrolysis of one ATP, followed by a slow step or pause that limits the overall rate of translocation. As the ATP concentration decreases into a range where ATP binding should become rate-limiting, the model predicts that the kinetic step size should decrease approaching a value of 1 nt (Figure S1(a, b)). In addition to the ATP coupling stoichiometry, we also determined the translocation kinetic step size over a range of ATP concentrations and found that the kinetic step size remains relatively constant at 4–5 nts down to 50 μM ATP, but increases to a value near 7 nts at 10 μM ATP. Our simulations and subsequent experiments at different ATP:ADP ratios suggest that this increase in the kinetic step size results from an increase in pausing by UvrD, but without futile ATP hydrolysis (Figures 5(d) and 6(c)). This increase in UvrD pausing at low ATP concentrations could mask the expected decrease in the kinetic step size. However, the observation that the kinetic step size remains constant at 4–5 nucleotides over a wide range of [ATP] suggests that this large kinetic step size may be mechanistically significant and not the result of static disorder in the enzyme population.

Unfortunately, our results do not enable us to distinguish whether the kinetic step size of 4–5 nts at ATP concentrations greater than 50 μM represents an overestimate due to the presence of static disorder in the UvrD population or whether this reflects a true mechanistic feature of the stepping mechanism of UvrD. A recent single molecule study of ssDNA translocation by a PcrA monomeric translocase suggests that the large (4–5 nucleotide) observed kinetic step size measured in ensemble studies³⁷ may represent an overestimate due to the presence of static disorder. Analysis of single-molecule translocation time courses of individual PcrA monomers are consistent with a smaller one nt step size; however, when the data for all molecules are analyzed as an ensemble a larger step size is observed (~3 nts)²⁵. Another observation that may indicate the UvrD kinetic step size is inflated is that at saturating ATP a smaller translocation kinetic step size (~1 nt) is observed for UvrD when it initiates translocation from a 5′-ss/dsDNA junction rather than from random internal sites within the ssDNA¹⁴. The smaller kinetic step size suggests either that UvrD utilizes a different stepping mechanism when initiating translocation from a 5′-ss/dsDNA junction or possibly that UvrD binding to the junction minimizes static disorder in the UvrD population¹⁴. Further work using single molecule methods is needed to understand whether static disorder in these enzyme populations is an intrinsic feature of the enzyme mechanism.

Materials and Methods

Buffers and Reagents

Buffers were prepared with reagent grade chemicals using distilled water, further deionized with a Milli-Q purification system (Millipore Corp., Bedford, MA) and were filtered through 0.2 micron filters. Buffer T₂₀ is 10 mM Tris-HCl (pH 8.3 at 25°C), 20 mM NaCl, and 20 % (v/v) glycerol (enzyme grade). Storage buffer is 20 mM Tris-HCl (pH 8.3 at 25°C), 200 mM NaCl, 50 %(v/v) glycerol (enzyme grade), 1 mM EDTA, 0.5 mM EGTA, and 25 mM 2-mercaptoethanol. Storage minimal buffer is 20 mM Tris-HCl (pH 8.3 at 25°C), 200 mM NaCl, and 50 % (v/v) glycerol (enzyme grade). ssDNA buffer is 10 mM Tris-HCl (pH 8.3 at 25°C) and 50 mM NaCl. Heparin buffer is 19 mM Tris-HCl (pH 8.3 at 25°C), 40 mM NaCl, 2 mM MgCl₂, and 40 % (v/v) glycerol (enzyme grade). PBP-MDCC buffer is 10 mM Tris-HCl (pH 8.0 at 25°C) and 1 mM MgCl₂. PBS buffer is 10 mM Potassium Phosphate buffer (pH 7.0), 100 mM NaCl. MgCl₂ stock concentrations were determined by refractive index ¹².

Heparin (sodium salt) (catalog no. H-3393) stocks were dialyzed vs. Heparin buffer at 4°C and concentrations determined as described ³⁸. 5′-adenosine triphosphate (ATP) stocks (40–50 mM) were prepared in 50 mM NaOH, pH adjusted to 7.0, stored at −20°C and concentrations determined in PBS buffer (ε_260nm = 15340 M⁻¹cm⁻¹)³⁹. 7-Methylguanosine (7-MEG) stocks in Milli-Q water were stored at −20°C and concentrations determined spectrophotometrically (ε_{256 nm} = 13300 M⁻¹cm⁻¹)¹². Nucleoside phosphorylase (PNPase) stocks (500-units/mL) were flash-frozen with liquid N₂ and stored at −80°C. 7-diethylamino-3((((2-maleimidyl)-ethyl)amino)carbonyl)coumarin (MDCC) (Invitrogen, Carlsbad, CA) was dissolved in N,N-dimethylformamide and concentrations determined spectrophotometrically in methanol (ε_{419 nm} = 49300 M⁻¹ cm⁻¹).

Enzymes and DNA

E. coli UvrD was purified and its concentration determined as described ⁴⁰ and was stored at −20°C in minimal storage buffer for up to six months without loss of translocation activity. E. coli phosphate binding protein A197C (PBP) was purified (>96% purity) as described ¹⁷, and its concentration determined in PBP buffer (ε_{280 nm} = 6.16(± 0.12) × 10⁴ M⁻¹cm⁻¹). PBP was labeled with a coumarin derivative, MDCC, and purified as described (15).

(dT)_L and (dT)_L labeled with fluorescein or Cy3, were synthesized and purified as described 41, dialyzed vs. 10 mM Tris-HCl, pH 8.3, and stored at −20°C and concentrations determined spectrophotometrically ¹⁰. Poly(dT) (Midland Certified Reagents, Inc., Midland, TX) was fractionated by size-exclusion chromatography as described ¹⁰, dialyzed into ssDNA buffer and stored at −20°C. The average lengths of poly(dT) were estimated from weight average sedimentation coefficients determined in 10 mM KPO₄, pH 7.4, 1 M NaCl, 20°C, as described ^{10; 42}.

Stopped-flow Experiments

Experiments were performed in buffer T₂₀ at 25°C using an SX18MV stopped-flow (Applied Photophysics Ltd., Leatherhead, UK). In translocation experiments UvrD was pre-incubated with ssDNA in one syringe and reactions initiated by 1:1 mixing with buffer T₂₀ plus 0.5 mM ATP, 2 mM MgCl₂, and 4 mg/mL heparin. All concentrations given are the final concentrations after mixing in the stopped-flow.

UvrD monomer-ssDNA dissociation kinetics from ssDNA internal sites

Dissociation kinetics were monitored by the increase in UvrD tryptophan fluorescence 12 (λ_ex = 280 nm, λ_em >350 nm). The dissociation rate constant from internal ssDNA sites, k_d, during UvrD translocation was measured using poly(dT) (average length 1.5 kb). In experiments measuring the dissociation rate constant of different UvrD monomer:nucleotide complexes from ssDNA UvrD (25 nM) was pre-incubated (5 min at 4°C) with poly(dT) (10 μM nts) in the presence or absence of saturating ADP and ATPγS (1 mM) and MgCl₂ (2.0 mM) in T₂₀ buffer then rapidly mixed with T₂₀ buffer plus heparin (4 mg/ml). To form the UvrD:ssDNA:ADPMg₂F₃ complex UvrD, ADP, poly(dT), and MgCl₂ as above where incubated in the presence of 5 mM NaF in T₂₀ buffer for 10 min at 4°C then rapidly mixed with T₂₀ buffer plus heparin as above. Dissociation time courses were fit to a single exponential where the k_obs = k_{d, obs} during translocation in the presence of ATP or k_d of specific UvrD monomer:nucleotide complexes.

Kinetics of UvrD monomer translocation

UvrD monomer translocation kinetics were measured under single round conditions (no rebinding of UvrD to ssDNA) using a fluorescent stopped-flow assay to monitor the arrival of UvrD at the 5′-end of the DNA using both 5′-Cy3-(dT) and 5-F-(dT)_L as described^{10; 12}. Fluorescein fluorescence was excited at 492 nm and emission monitored at >520 nm. Cy3 fluorescence was excited at 515 nm and emission monitored at >570 nm.

The time courses determined with 5′-Cy3-(dT)_L and 5-F-(dT)_L were analyzed globally using an n-step sequential model, eq. (1), to obtain fluorophore independent estimates of the translocation kinetic parameters using NLLS analysis as described^{10; 12}.

$$f(t)=\frac{A}{1+nr}{\text{L}}^{-1}(\frac{1}{s+k_c}\left(1+\frac{k_{t}r}{s+k_d}\left(1-{\left(\frac{k_t}{s+k_t+k_d}\right)}^n\right)\right)\times \left(1+\frac{f_{\mathit{end}}^{\ast }{k}_c}{f_{\mathit{end}}\left(s+k_{\mathit{end}}\right)}\right)+\sum _{i=1}^j\left(r\frac{f_i}{f_{\mathit{end}}}\right)\frac{k_t+k_d+s-k_t{\left(\frac{k_t}{s+k_t+k_d}\right)}^{n-i}}{\left(k_d+s\right)\left(k_t+k_d+s\right)})$$ (1)

Time courses determined at different ADP:ATP molar ratios were globally analyzed using the same model, but with eq. (2) for a single fluorophore ¹⁰.

$$f(t)=\frac{A}{1+nr}{\text{L}}^{-1}\left(\frac{1}{s+k_c}\left(1+\frac{k_{t}r}{s+k_d}\left(1-{\left(\frac{k_t}{s+k_t+k_d}\right)}^n\right)\right)\times \left(1+\frac{f_{\mathit{end}}^{\ast }{k}_c}{f_{\mathit{end}}\left(s+k_{\mathit{end}}\right)}\right)\right)$$ (2)

Kinetics of inorganic phosphate production

The time course of ATP hydrolysis was monitored in the stopped-flow as an increase in PBP-MDCC fluorescence due to binding of phosphate (P_i)¹² (λ_ex =430 nm, λ_em > 450 nm). Prior to each experiment, the stopped-flow syringes and flow lines were treated with a P_i-MOP (10 mM Tris-HCl, pH 8.0, 300 μM 7-MEG, and 0.2 units/mL PNPase) for 15 min to remove contaminating P_i 17 and then rinsed with buffer T₂₀. The MOP was not included in the experiments. UvrD-(dT)_L complexes in buffer T₂₀ were pre-incubated on ice for 5 min, loaded into one syringe and incubated for 5 min at 25°C. A solution of PBP-MDCC, ATP, heparin, and MgCl₂ in buffer T₂₀ was loaded into the other syringe and incubated for 15 min at 25°C. A control time course, conducted without ssDNA, was subtracted from each time course to correct for the presence of contaminating phosphate. PBP-MDCC fluorescence enhancement was converted to [P_i] after calibration in the stopped-flow using [NaH₂PO₄] standards. The amount of [P_i] produced per UvrD monomer in the burst, A, was determined by fitting each time course to eq. (3).

$$\frac{P_i}{\mathit{UvrD}}=A\left(1-{exp}^{-k_{\mathit{obs}}t}\right)+k_{ss}t$$ (3)

The burst phase amplitude, A (P_i per UvrD monomer), was plotted vs. ssDNA length, L, and fit to eq. (4) to determine c and k_a using Scientist (Micromath, St. Louis, MO), while the parameters k_t, k_d, k_end, r, m, and d were constrained to the values determined from the translocation experiments (Table 1).

$$\left[\mathit{ADP}(L)\right]=\frac{I(0)}{1+\left(\frac{L-d}{m}\right)r}\left[\frac{\mathit{rcP}(L+d(P-1)-LP+mP(P^{\frac{L-d}{m}}-1)}{m{(P-1)}^2}+\frac{k_a(k_d+k_{t}r(1-P^{\frac{L-d}{m}})}{k_d{k}_{\mathit{end}}}\right]$$ (4)

UvrD monomer dissociation rate constant from the 5′-end of ssDNA in the absence of fluorophore

The dissociation rate constant from the 5′-end, k_end, was determined in the absence of fluorophore¹². We monitored UvrD dissociation kinetics from a series of defined length (dT)_L substrates at 10, 25, 100, and 500 μM ATP. With the short (dT)_L molecules, each time course has contributions both from UvrD dissociation from internal sites, k_d, as well as the 5′ end, k_end. Time courses for UvrD dissociation were obtained for (dT)_L with L= 54, 79, 84, 97, 101, 104, and 124 nts, monitoring UvrD fluorescence, although only data for (dT)₅₄, (dT)₇₉, (dT)₁₀₄, and (dT)₁₂₄ are shown in Figure S5. UvrD was pre-incubated with excess ssDNA in T₂₀ buffer then rapidly mixed with ATP, MgCl₂ and heparin in T₂₀ buffer at 25°C to initiate translocation. The average time for dissociation decreases with decreasing ssDNA length reflecting the increasing contribution from UvrD monomers bound at the 5′ ends, which dissociate with a faster rate than UvrD bound at internal sites.

UvrD dissociation from all seven lengths of (dT)_L were analyzed by global NLLS analysis using eq. (5), based on n-step sequential mechanism (Figure S1), where f(t) is the time dependent

$$f(t)=\frac{A}{(1+nr)}{L}^{-1}\left(\frac{1}{s}\left(\frac{k_{d}r\left(n\left(k_d+s\right)+k_t\left({\left(\frac{k_t}{k_t+k_d+s}\right)}^n-1\right)\right)}{{\left(k_d+s\right)}^2}+\frac{k_{\mathit{end}}}{s+k_{\mathit{end}}}\left(1+\frac{k_{t}r}{s+k_d}\left(1-{\left(\frac{k_t}{s+k_t+k_d}\right)}^n\right)\right)\right)\right)$$ (5)

fluorescence signal for free UvrD (P_f) ¹³. For this, k_t, k_d, r and n were constrained to the values determined from analysis of the translocation experiments conducted with fluorescently labeled ssDNA (Table 1), while k_end was assumed to be the same for each (dT)_L and obtained as a fitting parameter. The parameter A was allowed to float for each (dT)_L. The black curves in figure S5 are simulations using eq. (5) and the best-fit parameters (Table 1). The observed k_end increase as the ATP concentration is lowered, suggesting the UvrD monomer rapidly dissociates from the 5′-end when not bound with nucleotide.

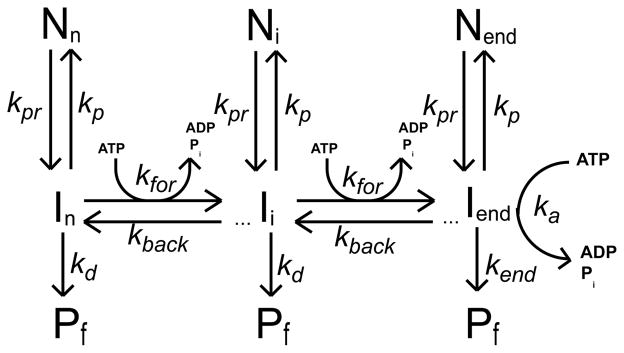
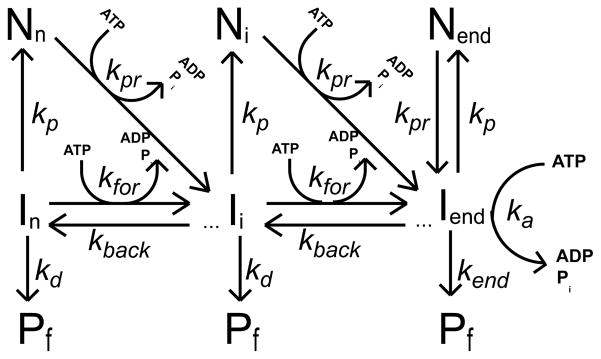
Translocation Simulations with pausing, backward motion, and static disorder

Monte Carlo simulation programs were written in the C computer language and compiled with the Microsoft Visual Studio .NET 2003 C compiler on a Windows XP workstation. In these simulations the motion of the translocase along the DNA was determined according to the probabilities that were assigned to various outcomes with corresponding average rate constants for forward motion, k_for, backward motion, k_rev, dissociation, k_d, pause, k_p, and pause recovery, k_pr, shown in schemes 1 and 2. In both schemes the translocase is initially randomly bound i translocation steps away from the 5′-end, with concentration, I_i. The number of translocation steps, i, is constrained (1 ≤ i ≤ n), where n is the maximum number of translocation steps needed for a translocase bound initially at the 3′ end to move to the 5′ end of a DNA that is L nucleotides long. Each step along the DNA occurs in a 1 nt increment. In both schemes, the hydrolysis of a single ATP molecule is associated with each motion of the translocase forward one step along the DNA; however, we also allowed the hydrolysis of a single ATP molecule when the translocase slipped backward (ATP induced slip) and entered a pause (N_i) (futile hydrolysis). Analysis of simulated time courses where ATP hydrolysis is not coupled to backward slipping produce the same qualitative trends in the fitted translocation parameters as shown in Figure 5, but not with as high an increase in the ATP coupling stoichiometry (data not shown). When the protein reaches the 5′-end of the DNA it continues to hydrolyze ATP with an associated rate constant k_a and dissociates from the DNA with rate constant k_end.

Scheme 1.

Scheme 2.

We assumed that the protein would dissociate from the DNA during a pause with the same probability that it would dissociate from the DNA during translocation. We note varying the probability of protein dissociation from the DNA during the pause had no effect on the qualitative trends of the fitted translocation parameters (data not shown). Upon dissociation from the DNA (either during translocation, during a pause, or from the 5′ end of the DNA), the translocase was not allowed to rebind the DNA and thus all simulations correspond to translocation events that are single-turnover with regard to DNA binding.

In order to examine the effects of static disorder in translocation rates we simulated a series of time courses in which the microscopic translocation rate constant (k_for) of an individual enzyme was sampled from a Gaussian distribution of possible rate constants, and this translocation rate constant remained constant for the entire translocation of that protein along the DNA.

We tested two different ATP-dependent pause recovery pathways, one where pause recovery was not coupled to translocation, but requires ATP hydrolysis (scheme 1) and the other where pause recovery is coupled to ATP-dependent translocation (scheme 2). Under the conditions tested both schemes produce similar qualitative trends in the fitted parameters shown in Figure 5. However, if the probability of pausing in scheme 1 is high relative to the probability for forward translocation, then one will obtain a higher ATP coupling stoichiometry when the probability of pause recovery is high, due to futile ATP hydrolysis (data not shown). This is not the case for scheme 2, since ATP hydrolysis during pause recovery is coupled to forward translocation. In these simulations the probability of entering a pause was kept constant, equal to the probability of stepping forward (average time = 0.033 sec), while the probability of pause recovery was varied, resulting in average pause durations ranging from 0 to 0.2 sec.

The corresponding kinetic parameters obtained from simulations in which no heterogeneity in translocation is present are: k_for = 30 step/s, k_d = 0.5 s⁻¹, k_end = 2 s⁻¹, c = 1 ATP/step and m = 1 nt/step. Similar trends were obtained using other probabilities for k_t, k_d and k_end (data not shown). Each simulation produced time courses for translocase arrival at the 5′-end and ATP hydrolysis during translocation corresponding to 5 lengths of DNA: 15, 30, 45, 53, and 60 nt. The multiple time courses for protein translocation on DNA, each corresponding to a different length of DNA, were analyzed globally using Eqs. (6) and (7) (derived from the n-step sequential model, Figure S2) and standard NLLS algorithms to obtain estimates of the translocation kinetic parameters¹³. In these equations, k_t, k_d, k_end, c, and r were constrained to be global parameters (independent of DNA length); n and A were allowed to float for each time course^{10; 12}.

$$f_{5^{\prime }}(t)=\frac{A}{1+n\ast r}{L}^{-1}\left[\frac{1}{s+k_{\mathit{end}}}\ast \left(1+\frac{k_t\ast r}{s+k_d}\left(1-{\left(\frac{k_t}{s+k_t+k_d}\right)}^n\right)\right)\right]$$ (6)

$$\mathit{ADP}(t)=\frac{I(0)}{1+n\ast r}{L}^{-1}\left[\frac{1}{s}\left(\frac{c\ast k_t\ast r\ast \left(n(k_d+s)+k_t\left({\left(\frac{k_t}{k_t+k_d+s}\right)}^n-1\right)\right)}{{(k_d+s)}^2}+\frac{k_a\left(1-\frac{k_t\ast r\left({\left(\frac{k_t}{k_t+k_d+s}\right)}^n-1\right)}{k_d+s}\right)}{k_{\mathit{end}}+s}\right)\right]$$ (7)

In the NLLS analysis, the parameter k_d was constrained to the input value. We also simulated dissociation time courses from an infinite lattice (no 5′ or 3′-end) to determine the observed dissociation rate constant, k_d,obs, for a given set of simulation conditions. The simulated dissociation time courses were quantitatively described by a single exponential where k_d,obs = k_d¹³(data not shown). Constraining the parameter k_d in the NLLS analysis to the value of k_d,obs did not affect the qualitative trends in the fitted translocation parameters. The parameter I(0) was set equal to unity since all protein in our simulations was initially bound to the DNA. All other parameters were determined directly from the NLLS analysis. The kinetic step-size of translocation was then subsequently determined from a linear least squares analysis of the dependence of n on L according to n = (L−d)/m ¹³.

All NLLS analyses were performed using Conlin ⁴³ kindly provided by Dr. Jeremy Williams. The software library CNL50 (Visual Numerics Incorporated, Houston, TX) was used for the numerical calculation of the inverse Laplace transform.

Highlights.

• How does the UvrD monomer translocate along single-stranded DNA?

• ATP hydrolysis is tightly coupled to forward motion of UvrD at low and high [ATP].

• The kinetic step size increases when the [ATP] drops below 50 μM.

• UvrD pausing and/or static disorder may explain the large kinetic step size.

• UvrD moves along ssDNA using a stepping mechanism and can enter paused states.

Abbreviations

SF1A

super family one type A DNA helicase

ssDNA

single-stranded DNA

dsDNA

double-stranded DNA

dT

deoxythymidylate

ATP

adenosine triphosphate

ADP

adenosine diphosphate

ATPγS

adenosine gammathiotriphosphate

PBP

phosphate binding protein

MDCC

7-diethylamino-3((((2-maleimidyl)-ethyl)amino)carbonyl)coumarin

P_i

inorganic phosphate

SF2

super family two DNA helicase

ssRNA

single-stranded RNA

nt

nucleotide

7-MEG

seven methylguanosine

PNPase

Nucleoside phosphorylase

NLLS

nonlinear least squares analysis

EDTA

ethylenediaminetetraacetic acid

EGTA

ethylene glycol tetraacetic acid