Morphological and kinematic basis of the hummingbird flight stroke: scaling of flight muscle transmission ratio

Abstract

Hummingbirds (Trochilidae) are widely known for their insect-like flight strokes characterized by high wing beat frequency, small muscle strains and a highly supinated wing orientation during upstroke that allows for lift production in both halves of the stroke cycle. Here, we show that hummingbirds achieve these functional traits within the limits imposed by a vertebrate endoskeleton and muscle physiology by accentuating a wing inversion mechanism found in other birds and using long-axis rotational movement of the humerus. In hummingbirds, long-axis rotation of the humerus creates additional wing translational movement, supplementing that produced by the humeral elevation and depression movements of a typical avian flight stroke. This adaptation increases the wing-to-muscle-transmission ratio, and is emblematic of a widespread scaling trend among flying animals whereby wing-to-muscle-transmission ratio varies inversely with mass, allowing animals of vastly different sizes to accommodate aerodynamic, biomechanical and physiological constraints on muscle-powered flapping flight.

1. Introduction

Hummingbirds have been dubbed ‘vertebrate insects’ owing to the evolutionary convergence of wing kinematics and the similarity in overall body size of the smallest hummingbirds and the largest flying insects [1]. Indeed, wing loading, wing beat frequency and hovering flight behaviours of hummingbirds are more typical of flying insects such as fruit flies (Drosophila spp.) than of birds [2]. Additionally, early cinematographic investigations of hummingbird flight revealed an inverted or highly supinated wing during upstroke [3], similar to that of many insects, allowing hummingbirds to generate aerodynamic lift in both downstroke and upstroke [4]. In insects, active wing inversion must originate at the wing base because the wings have no distal joints. However, flying vertebrates have muscles and skeletal joints throughout their wings and may flex or rotate different segments according to aerodynamic demands. Thus, the source of wing inversion in the hummingbird flight stroke remains uncertain but is hypothesized to occur at the wrist [3] or shoulder [5].

Hummingbirds power their insect-like wing motions using flight muscle strains of approximately 11 per cent [6], similar to those reported for moths of similar body size [7] but much less than the strains of up to 40 per cent reported in other bird species [8]. Hummingbirds likely use small muscle strains compared with other birds because their high flapping frequencies would otherwise lead to high strain rates and reduce flight muscle power output via the intrinsic force–velocity properties of muscle [9]. Using smaller overall muscle fibre strains alleviates this problem but creates another. Because hummingbirds flap their wings through similar arcs compared with other birds (approx. 120°), they must convert these small muscle strains into large amplitude wing motions, probably requiring changes to the wing skeleton and flight stroke.

Here, we use high-speed three-dimensional X-ray videography to show how hummingbirds create insect-like flapping flight in a vertebrate musculoskeletal system, inverting their wings during upstroke and accommodating high frequency, small amplitude muscle strains. We further show that changes in the wing-to-muscle-transmission ratio, which help hummingbirds accommodate small muscle strains and power their flight, are part of a general trend in flying animals ranging in size from fruit flies (1 µg) to large birds (5 kg).

2. Material and methods

(a). Animals

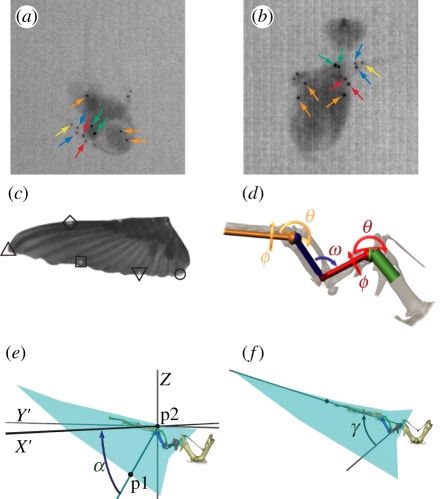
Three female and one male ruby-throated hummingbirds (Archilochus colubris, 3.4 ± 0.2 g) were captured using nectar-feeding traps at Harvard University's Concord Field Station (CFS). During the 4 days of flight recording following capture, the birds were maintained at the CFS in individual 0.4 × 0.3 × 0.45 m cages with artificial nectar provided ad libitum in the form of Nektar-Plus (NEKTON; Günter Enderle, Pforzheim, Baden-Württemberg, Germany) or a sucrose solution (20%, mass : volume). Prior to X-ray videographic recording (see below), the birds were marked with 13 0.3-mm diameter (0.1 mg) platinum beads glued to the skin surface overlying the wing skeleton and body. Markers overlying the wing skeleton were placed on the dorsal and ventral aspects of the left shoulder and left elbow, on the leading and trailing edge sides of the left manus and at the tip of the left manus (figure 1a,b). Three markers were placed on the manus of right wing, two markers were placed along the vertebral column and a final marker on the keel of the sternum. Additionally, six white 1.0 mm diameter acrylic paint markers (5 µg) were placed on the wings along the leading and trailing edges (figure 1c). Following the recordings and removal of markers, two of the birds were released to the wild. The remaining two were sacrificed via an overdose of isoflurane inhalant for scanning in a micro computed tomography (µCT) system.

Figure 1.

Hummingbird kinematic markers and methods: (a) and (b) show original X-ray video images of the hummingbird from an overhead and lateral view, respectively. Arrows indicate the location of the different platinum markers; orange arrows point to the three body markers, green indicate the left wing shoulder markers, red the elbow markers, dark blue the manus markers and yellow the manus tip marker. The right wing markers are not indicated. (c) Planar view of the left wing and indicates the location of the different wing markers as follows: the filled diamond lies on the distal leading edge, the filled circle at the wing-tip, the open square at the tip of the fourth primary, the open diamond at the tip of the first secondary and the open circle at the tip of the fourth secondary. (d) Kinematic chain segments and joints used to model the movements of the hummingbird wing skeleton and their rotations, θ (spherical rotation), ϕ (long-axis rotation) and ω (polar rotation). The shoulder and wrist joints have three degrees of freedom while the elbow has one. (e) Calculation of angle α, the local supination angle of the wing. p1 is a trailing edge wing marker, p2 the nearest point on the leading edge of the wing, and X′ lies perpendicular to gravity and parallel to the projection of p1–p2 in the horizontal plane. (f) Calculation of angle γ, the angle between the long axis of the humerus and the leading edge of the wing.

(b). X-ray videography

The hummingbirds were trained to fly in a 0.4 × 0.4 × 0.5 m netted enclosure and to feed from a 5 ml syringe filled with Nektar-Plus placed within the recording volume. The birds were recorded at 1000 Hz using two X-ray videography systems each composed of a Photron 1024 PCI camera (Photron USA Inc., San Diego, CA, USA) coupled to an X-ray C-arm system (Model 9400, OEC-Diasonics Inc., remanufactured by Radiological Imaging Services) and five visible-light video cameras (shutter speed 1/5000 s): one Photron SA-3, one Photron 1024 PCI, one Photron 1280 PCI and two Phantom v. 7.1 (Vision Research Inc., Wayne, NJ, USA). The X-ray and light-video cameras were calibrated using direct linear transformation following pre-processing of the X-ray images to remove all optical distortion introduced by the multiple lenses and image intensifier [10]. Mean re-projection error across all X-ray and visible-light markers was 1.3 ± 1.0 (mean ± s.d.) pixels. The X-ray C-arms were set to emit at 79 kVp and 10 mA.

The small size, low density and rapid movement of the hummingbird wing skeleton did not permit the use of either marker-based or feature-based alignment of three-dimensional bone models to X-ray images as described elsewhere [10]. Nevertheless, the X-ray markers are a substantial improvement over visible-light high-speed videography studies of hummingbirds because the X-ray system allows markers to be placed against the wing bones rather than on the externally visible feather surfaces. This distinction is particularly critical for examination of the humerus, which lies at the interface of the wing and body contour feathers and is hidden within them during portions of the stroke cycle. Additionally, the X-ray markers are never obscured by changes in wing or body orientation and position. The X-ray wing markers, in conjunction with the visible-light markers attached to the wing leading and trailing edge, served as inputs to a kinematic chain analysis (below). The X-ray and wing markers were digitized using custom software in Matlab 2010a (Mathworks, Natick, MA, USA) [10].

(c). Wing motion analysis

We analysed wing motion in the hummingbird by fitting an idealized set of joints and rigid links—a serial kinematic chain [11] (figure 1d)—to the platinum markers. The kinematic chain models the hummingbird wing skeleton as a ball and socket joint at the shoulder connected to a hinge [12] (confirmed by mechanical testing of a hummingbird wing) at the elbow and to a second ball and socket at the wrist (figure 1d). Our automated analysis routine placed the joint centres at the midpoint of each of the joint marker pairs running along the left wing at the shoulder, elbow and manus. The movements of the chain were constructed by working from the proximal to distal joints and finding the spherical (θ) and long-axis rotations (ϕ) at the ball and socket joints and the polar (ω) rotation at the hinge joint that brought the joint marker pair and the two next most proximal joint centre into a least-squares fit with their position in a canonical pose, in this case mid-downstroke. The rotations were then applied to the joint in question, moving all more distal markers and components of the kinematic chain. The fitting process was then repeated at the next most proximal joint and re-initiated in subsequent video frames.

We used the resulting time-varying joint rotation angles and kinematic chain to measure the contribution of different joint movements to overall wing translation and supination. This was performed by reversing the rotation at the joint in question in the observed complete wing motion. The contribution of that joint movement was then measured as the difference between marker movements between the complete and partial chains. Contributions to wing translation were computed as the difference in the length of the path travelled by each marker. Contributions to wing supination were assessed from differences in wing supination angle α, calculated as described below.

The spanwise rotation or supination angle α of the wing was calculated for each of the three trailing edge wing points (figure 1c) as the angle between the global horizontal plane and a ray beginning at the trailing edge point, and making a perpendicular intersection with a second ray running from the shoulder joint centre to the marker at the tip of the manus (figure 1e). Thus, the supination of the wing could be calculated from the raw marker positions or from the marker positions following application of a partial or complete kinematic chain. We also quantified humeral orientation with respect to the wing as the angle between the humerus and the leading edge of the wing (γ, figure 1f). Lastly, wing-tip speed was calculated from the first derivative of a quintic spline fit through the observed wing-tip positions and smoothed by the local three-dimensional position uncertainty [13]. Digitizing, X-ray reconstruction and kinematic calculations were performed using matlab. Details of this analysis, including an assessment of its sensitivity to marker movement on the skin overlaying the skeleton, an important source of error [14] in analyses such as this one, are presented in the electronic supplementary material, appendix [15].

(d). µCT scans

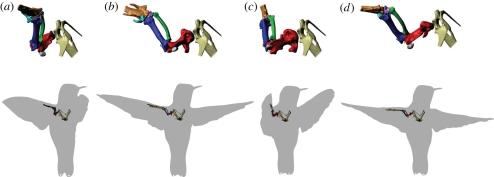
Two of the hummingbirds were scanned in a µCT (HMX ST225, X-Tek Systems Ltd.) and the scans analysed using mimics 13 (Materialize, Leuven, Belgium). During the scans, one bird was posed in a mid-downstroke wing configuration (electronic supplementary material, figure S1); the other bird was posed in mid-upstroke. The resulting three-dimensional bone models were then repositioned in maya (Autodesk, San Rafael, CA, USA) according to the kinematic chain results to show how the skeleton might have moved, allowing assessment of the anatomical feasibility of these movements (figure 2).

Figure 2.

The estimated position and orientation of the hummingbird shoulder and proximal forelimb bones through a complete stroke cycle in hovering flight: (a) beginning of downstroke, (b) mid-downstroke, (c) end of downstroke, (d) middle of upstroke. Key to colours: red, humerus; dark blue, ulna; green, radius; magenta, radiale; light blue, ulnare; gold, manus; grey, sesamoid bones; tan, incompletely measured medial and distal elements. The upper row contains a magnified view of the left shoulder while the lower row shows the shoulder girdle and left wing positioned within the silhouette of the bird. All views are from a point slightly above, behind and to the right of the bird. The position of the bones was determined by the marker-based kinematic chain analysis, referenced from their position in the mid-downstroke pose (b), which served as the base orientation in constructing the kinematic chain and was also the pose of the bird in the µCT scan used to generate the bone models.

(e). Comparative analysis of wing-to-muscle-gear ratio

To compare the overall relationship between wing movement and muscle shortening created by the hummingbird wing skeleton and flight stroke, we collected a variety of muscle strain, morphological and flapping kinematic data from previously published studies for 22 species of flying insects and birds spanning seven orders of magnitude of body mass (electronic supplementary material, table S2). From these muscle and kinematic data, we computed a wing-to-muscle-transmission ratio, or velocity ratio, as

2.1

where β is the flapping arc and ɛ is muscle strain. In cases where more data were available, we calculated alternate expressions for transmission ratio that include wing and fascicle length, see electronic supplementary material for details. We also estimated the strain rate of the flight muscles of these different animals as

2.2

this expression assumes a sinusoidal muscle strain cycle at flapping frequency n.

Scaling trends in these comparative results were analysed using model 1 (linear least-squares) regressions against body mass; we assumed that uncertainty in T and 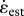was much greater than that of body mass. Given the mixture of homologous and non-homologous flight systems in the dataset, we provide complementary independent contrasts analysis in the electronic supplementary material, appendix [15].

3. Results

Our stereo X-ray kinematic measurements (figure 3 and table 1; electronic supplementary material movies S1–S3) revealed that hummingbird wing supination during upstroke is largely due to rotation in the wrist, which accounts for more of the supination movements than any other single skeletal element we tracked and, for markers on the fourth primary and first secondary, contributed more than the sum of the shoulder and elbow joints. However, much of wing supination in the fourth primary could not be assigned to any of the skeletal elements, suggesting substantial deformation of feathers and wing soft tissue in response to inertial and aerodynamic forces, similar to passive wing supination observed in fruit flies [15]. Additionally, some of this distal wing supination may also reflect rotation in the distal phalanges, which have particularly smooth and flat articulations ([3]; electronic supplementary material, figure S1) but were not marked and could not be tracked in our recordings.

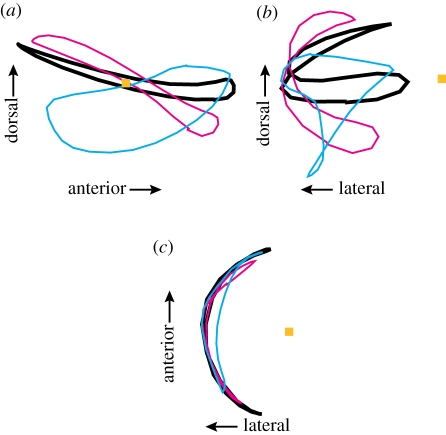
Figure 3.

The path of the left wing-tip for one hummingbird flap from (a) lateral, (b) rear and (c) overhead viewpoints. The shoulder position is indicated with an orange square and the path of the wing-tip is shown by the heavy black line. The cyan line shows the tip path if the humeral long-axis rotation angle ϕ is held constant at its mid-downstroke value throughout the flap but humeral rotation angle θ and all other kinematic chain angles allowed to vary. The magenta line shows the wing-tip path if humeral rotation angle θ is held constant but all other angles, including humeral long-axis rotation angle ϕ are allowed to vary. See electronic supplementary material, movies S1–S3 for an animation of the wing movement without contributions from all measured joints.

Table 1.

Contribution to hummingbird wing supination and flapping movement of joint, by wing location. α, supination; θ, spherical rotation; φ, long-axis rotation; ω, polar rotation, n.a., not applicable; —, contribution less than standard deviation. All values mean ± s.d., n = 4 birds.

	supination				flapping movement
	shoulder	elbow	wrist	unknown	shoulder		elbow	wrist
	α	α	α	α	θ	Φ	ω	θ	φ	unknown
fourth secondary	23 ± 9°	—	13 ± 3°	28 ± 8°	35 ± 6%	—	6 ± 2%	—	18 ± 3%	45 ± 6%
first secondary	22 ± 9	—	36 ± 16	40 ± 11	27 ± 3	—	3 ± 1	4 ± 3%	27 ± 9	33 ± 10
fourth primary	17 ± 9	—	45 ± 14	75 ± 12	23 ± 2	16 ± 5%	4 ± 2	11 ± 7	14 ± 8	33 ± 5
leading edge	n.a.	n.a.	n.a.	n.a.	23 ± 2	40 ± 5	10 ± 4	14 ± 5	—	11 ± 3
tip	n.a.	n.a.	n.a.	n.a.	21 ± 1	31 ± 2	—	14 ± 7	—	22 ± 2

As predicted from prior anatomical studies [3], long-axis rotation of the humerus (ϕ, figure 1d) plays a key role in the hummingbird flapping cycle (figures 2 and 3), providing the largest single contribution to the movement of the wing-tip and distal leading edge (table 1 and electronic supplementary material, movie S1–S3). Removal of this movement from the kinematic chain also substantially changes the shape of the wing-tip trajectory (figure 3). Spherical rotation at the shoulder also contributed to wing movement, particularly at proximal and trailing edge locations but has less effect on the wing-tip trajectory. In contrast, the effects of flexion and rotation at the elbow and wrist on translational wing movement were generally small.

We compared A. colubris humeral long-axis rotation magnitude, timing and contribution to wing movement with results from earlier studies of starlings and pigeons. The magnitude of humeral rotation in A. colubris (figures 2 and 3; approx. 80°) was slightly less than the 80–90° reported for pigeons and starlings with flight muscles stimulated in situ [16], 85° estimated from cineradiographic records of starlings flying in a wind tunnel [17] and 120° measured via scientific rotoscoping of pigeon cineradiographs [14]. However, the contribution of humeral rotation to total wing-tip movement was 18 per cent in starlings (also estimated from cineradiographic records, n = 1), compared with 52 per cent for the hummingbirds.

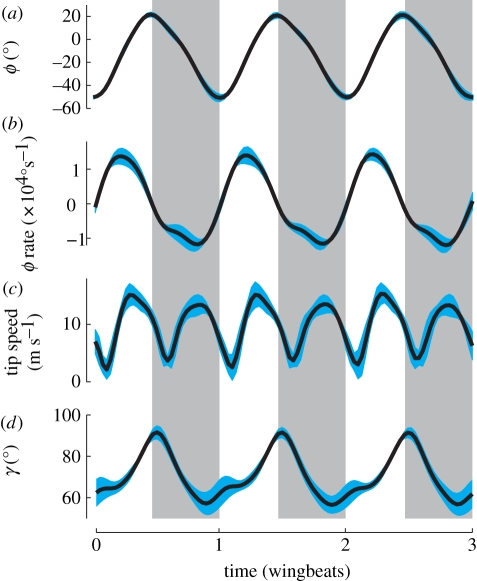
The enhanced contribution of humeral rotation to wing movement in hummingbirds is due to changes in the orientation of the bone and the timing of its rotation. We measured humeral orientation as angle γ (figure 1f). At a γ = 90°, humeral rotation only contributes to translational movement of the wing, whereas at γ = 0° humeral rotation produces solely wing supination or pronation. In A. colubris, γ ranged from 92 ± 3° to 57 ± 6° (mean ± s.d., n = 4) during the stroke cycle (figure 4d), compared with a range of 46–36° for the starling (n = 1). Additionally, A. colubris humeral rotational velocity was greatest near the mid-downstroke and mid-upstroke (figure 4c); in the starling and pigeon, humeral rotation occurs primarily at the end of upstroke and end of downstroke [16].

Figure 4.

Average kinematics for three wing beats from four hummingbirds: (a) ϕ, humeral long-axis orientation, (b) long-axis rotation rate, (c) wing-tip speed and (d) γ, the angle between the humerus and the leading edge of the wing (figure 1). Downstroke is indicated by the vertical shaded regions, the blue shaded margins of the curves show ± 1 s.d. n = 4 birds. Wing beat frequency was 43 ± 5 Hz.

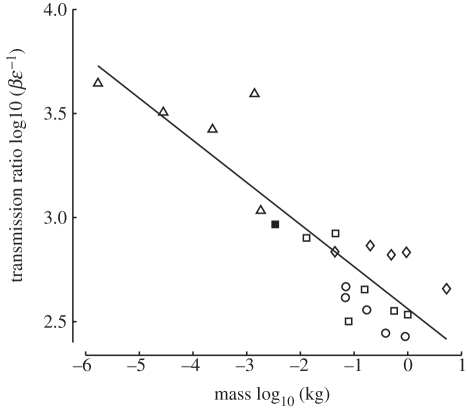
The combination of large flapping amplitude and small muscle strain reported for hummingbirds results in a higher wing-to-muscle-transmission ratio T than was calculated for any other bird (electronic supplementary material, table S2). However, the observed T for hummingbirds is not unusual given their body size as T was found to vary as mass^−0.20 (r² = 0.77, p = 9.38e − 8) among the 22 species of insects and birds in our comparative dataset (figure 5). In contrast, the estimated muscle strain rate 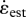did not vary significantly with body size (mass^−0.04, r² = 0.16, p = 0.063). The independent contrast results for T did not differ in slope from the model 1 regression [15], but those for 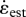showed a significant reduction with size (mass^−0.12, r² = 0.40, p = 0.0015).

Figure 5.

Transmission ratio, the ratio of wing flapping amplitude to muscle strain, was found to vary proportional to mass^−0.20 (r² = 0.77, p = 9.38e − 8) among a variety of insect and bird species. The transmission ratio of the hummingbird species examined here, Archilochus colubris, was larger than that of any other bird but is not particularly unusual in the context of this broad scaling relationship. Although these data include two closely related groups, a phylogenetically based regression analysis produced a nearly identical scaling relationship [15] (filled square, A. colubris; circles, Corvidae; diamonds, Phasianidae; open squares, other birds; triangles, insects).

4. Discussion

We found that hummingbirds enable one aspect of their insect-like flight stroke—a highly supinated and aerodynamically active wing in upstroke—by rotation at the wrist and possibly even more distal skeletal elements. This is in agreement with hypotheses based on anatomy and external kinematics from Stolpe & Zimmer [3] but contra those of Karhu [5]. The wrist-based wing movement likely represents an extension of the mechanism used by other bird species during low speed tip-reversal type upstrokes [18,19], where the distal wing is rotated by more than 90° from its orientation in mid-downstroke. In hummingbirds, reduction in the relative size of the proximal skeletal elements of the hummingbird wing compared with other birds [20] allows wrist supination to affect a much larger fraction of wing area than in larger birds.

Another insect-like aspect of the hummingbird flight stroke—the combination of a high wing beat frequency, large flapping amplitude and small muscle strain—is facilitated by the high muscle to wing transmission ratio T of the hummingbird wing skeleton. Specifically, the hummingbird humerus is oriented nearly perpendicular to the leading edge and rotates about its long axis during the stroke, with maximum rotational velocities (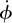) occurring at mid-stroke and coincident with maximum wing-tip velocity (figure 4). Thus, hummingbirds turn the long-axis rotational movement used by other birds to rapidly shift the wing between downstroke and upstroke postures [18] into a means for driving the wing through the middle of each upstroke and downstroke. Using humeral long-axis rotation to enhance wing movement greatly increases the hummingbird T in comparison with other larger birds. This mechanism also helps explain the evolutionary trend towards a more axial position of the humeral head in hummingbird evolution [5]. A more axial position facilitates enhanced wing-tip movement via long-axis humeral rotation.

The comparative analysis of transmission ratio (figure 5) reveals that, although the particular adaptation exhibited by A. colubris of augmenting flapping via humeral rotation is unusual among birds, its result is entirely consistent with trends across a wide range of vertebrate and invertebrate flying animals. This trend likely arises as a biomechanical accommodation of aerodynamic and physiological constraints on muscle-powered flapping flight. Because aerodynamic forces are proportional to the product of wing area and wing velocity squared, which is itself a function of wing length, flapping amplitude and flapping frequency, smaller animals must flap their wings at higher frequencies to support body weight [21,22]. Accordingly, flapping frequency scales proportional to mass^−0.24 (r² = 0.80, p = 2.34e − 8) in the set of animals for which muscle strains were recorded (electronic supplementary material, table S2). If T were constant, then the higher flapping frequencies exhibited by smaller animals would demand equally higher muscle strain rates, resulting in a reduced capacity for muscle power output [9]. By gearing the mechanical link between flight muscle and wing movement, animals can use muscle strain rates appropriate for high power output. Thus, hummingbirds use muscle strain rates [23] similar to those of other birds, helping them produce mass-specific muscle aerobic power outputs comparable with or greater than larger birds [24–26]. This change in T with size helps us explain how flying animals are able to maintain a nearly constant power to mass ratio over a wide range of body sizes [27,28] despite decreases in flapping frequency with size, which would otherwise predict flight muscle power scaling proportional to mass^2/3 [29]. The T may also help explain some other known scaling anomalies in animal flight such as the positive allometric scaling of wing skeleton length with respect to wing length in birds [30] because positive allometry in the wing skeleton would reduce the transmission ratio, helping produce the effect observed here. However, compensation for decreases in flapping frequency via increases in strain rate [31] and decreases in transmission ratio cannot continue indefinitely. Flight muscles remain limited by the maximum feasible strains and perhaps by the geometries required to achieve extremely high or low transmission ratios. Accordingly, transmission ratio scaling likely operates in conjunction with changes to muscle maximum shortening velocity, which scales proportional to mass^−0.12 in vertebrate flight muscle [32], the same scaling relationship revealed in our independent contrasts analysis of estimated strain rate in vertebrate and invertebrate flight muscle [15]. Future examination of the skeletal geometries and estimated wing-to-muscle-transmission ratios of large, prehistoric flapping flyers may provide insight into the limits of these trends and the degree to which the flight behaviour of these animals was limited by muscle physiology. Examination of large extant hummingbird species may reveal the limits of the particular mechanism we highlight here—humeral long-axis rotation—used to achieve high transmission ratios in this group.