Individual variation and the resolution of conflict over parental care in penduline tits

Abstract

Eurasian penduline tits (Remiz pendulinus) have an unusually diverse breeding system consisting of frequent male and female polygamy, and uniparental care by the male or the female. Intriguingly, 30 to 40 per cent of all nests are deserted by both parents. To understand the evolution of this diverse breeding system and frequent clutch desertion, we use 6 years of field data to derive fitness expectations for males and females depending on whether or not they care for their offspring. The resulting payoff matrix corresponds to an asymmetric Snowdrift Game with two alternative evolutionarily stable strategies (ESSs): female-only and male-only care. This, however, does not explain the polymorphism in care strategies and frequent biparental desertion, because theory predicts that one of the two ESSs should have spread to fixation. Using a bootstrapping approach, we demonstrate that taking account of individual variation in payoffs explains the patterns of care better than a model based on the average population payoff matrix. In particular, a model incorporating differences in male attractiveness closely predicts the observed frequencies of male and female desertion. Our work highlights the need for a new generation of individual-based evolutionary game-theoretic models.

1. Introduction

Decisions about parental care are among the most important life-history decisions that animals face. Across vertebrates, a diversity of parental care systems exists, ranging from cooperative breeding with biparental care and helpers, such as in meerkats (Suricata suricatta [1]) and long-tailed tits (Aegithalos caudatus [2]), to limited (or no) parental care, such as in precocial birds and many fish species [3–5]. The fitness consequences of parental care decisions depend on the social and non-social environment [3,5–7], and strongly reflect the trade-off between investment in the current brood and investment in future survival and reproduction [3,8,9]. Although both parents have a shared interest in their current brood, there is conflict between them because each individual would prefer its mate to provide the majority of parental care [5,9,10].

Evolutionary game theory is a powerful approach for studying cooperation and conflict in a coherent framework [11,12], and it has often been used to model parental care decisions [13–18]. With a few notable exceptions [19,20], most published parental care models are conceptual and not directly tailored to a specific empirical system. Attempts to test theoretical predictions have focused primarily on biparental care, examining how a parent responds to its local circumstances and the parental effort of its mate [21–23]. Realistic game-theory models for the interactions between parents involved in biparental care have to consider how such behavioural interactions may depend on individual traits and environmental variables, and how the outcome of the interactions may change over time. This makes the models and their solutions inherently intricate [13,16]. Furthermore, model predictions are often sensitive to their specific assumptions [13]; so, for accurate tests of care models, it is particularly important to validate the underlying theoretical assumptions.

Testing models of parental care might be easier in systems that are not restricted to biparental care, but have a polymorphic pattern of care. In systems with uniparental care by either the male or the female parent, for instance, a decision about parental care may be more manifest than in systems with biparental care (e.g. desert the offspring versus a mere reduction in feeding rates, respectively), and the consequences more pronounced (e.g. sequential reproduction with multiple mates within one season versus resources saved for winter survival and/or reproduction in a following breeding season). Therefore, in systems with uniparental care, one may be better able to quantify individual-based reproductive payoffs associated with a given strategy. Several species of vertebrates exhibit a combination of male-only, female-only and biparental care within the same population [24–26]. Here, we focus on the Eurasian penduline tit (Remiz pendulinus), in which male-only care, female-only care and biparental desertion all occur within the same population [27,28]. Full incubation and feeding of nestlings are carried out by only one parent. In our study population in southern Hungary, 45 per cent of all nests are cared for by the female alone, 16.7 per cent are cared for by the male alone and 38.3 per cent are deserted by both parents [29]. Biparental care is never observed. Despite large geographical distances and substantial variation in breeding density and other ecological variables, this pattern of care is consistent across five populations of penduline tits in distant locations in Europe [29] (electronic supplementary material, figure S1).

The diverse care pattern in penduline tits, in particular the high frequency of nest desertion, is probably the result of sexual conflict between the two parents [28,30,31]. One parent is able by itself to incubate the clutch and feed all the nestlings until independence [32,33], giving each parent an incentive to desert the nest. Nest desertion puts the deserted partner in a difficult situation (a ‘cruel bind’ [34]): even if uniparental care is costly, the deserted partner has a strong incentive to stay, because deserting as well would condemn the offspring to death. Nevertheless, the deserted partner may also leave the nest if desertion is associated with higher fitness expectations than continuing to care for the current brood [35]. Game-theory models show that sexual conflict over parental care can indeed result in biparental desertion, or in uniparental care and an associated arms race for being the first to desert [36].

Our objective here is to apply these game-theoretic concepts to a particularly well-studied wild population of Eurasian penduline tits, in which males and females may have up to six mates in a single breeding season [28]. Based on 6 years of data from this population, we estimate for both males and females the fitness consequences of caring for the offspring or deserting the nest. Using these estimates, we calculate a payoff matrix, from which we derive the evolutionarily stable strategy (ESS) for each sex. We show that the resulting ESS predictions do not explain the variation in parental care observed in the field. We argue that this is because the average payoff matrix for the population gives a poor representation of the conflict faced by each pair of penduline tits, which is likely to depend on their individual characteristics. We therefore investigate the possibility that variation in care patterns is caused by individual variation in payoffs [37]. By incorporating individual variation, we can account better for population-level patterns of parental care. Finally, we incorporate an individual plumage trait, male ‘mask’ size, which may be associated with such individual variation in payoffs as it predicts the likelihood for males to desert the clutch [38,39]. This further improves the predicted population-level patterns of care. Throughout, we discuss the difficulties of applying simple payoff matrices to real populations with substantial individual variation, and argue that evolutionary models should aim to take a more realistic approach by modelling individual variation.

2. Estimating payoffs

(a). Study site and data collection

We studied Eurasian penduline tits during the breeding season between April and August in six consecutive years (2002–2007) at a 1321 ha fishpond system, Fehértó, in southern Hungary (46°19′ N 20°6′ E). Each year, 41–116 ringed males and 15–51 ringed females bred at this site [28]. The male bias in the number of ringed individuals reflects the fact that females are more difficult to trap than males, rather than a genuine bias in population sex ratio. Males were usually trapped before incubation using mist nets, whereas females were usually trapped at the nest during incubation. We searched for nest-building penduline tits and then visited each nest roughly every 2 days [40] to determine the date of nest initiation, date of pair formation, number of eggs (between the sixth and the ninth day after the start of incubation; median, eighth day), date of desertion, identity of the parent attending the nest and the number of nestlings (10 days after hatching of the first egg; the number of nestlings on the tenth day after hatching is highly correlated with the number of fledglings [39,40]). Adults were trapped and ringed with one metal ring and a unique combination of three colour rings (A. C. Hughes, Middlesex, UK). Standard biometric measurements were taken, as well as digital photographs of each side of the bird's head to quantify the size of the eye-stripe or ‘mask’, which previously we found to indicate male attractiveness (see [38,39] for details). The pattern of nest desertion in our population did not differ between nests where neither parent was trapped and those where at least one of the parents was trapped (multinomial logistic regression: χ² = 3.932, d.f. = 2, p = 0.140, n = 389 nests), suggesting that trapping did not influence the probability of desertion. Adult return rates between years are low (5% for males, 2% for females [41]). To avoid pseudoreplication, we randomly selected data from only one season per colour-ringed individual, giving a total sample of 337 nests from 172 individuals. The composition of pairs was nearly always different between subsequent clutches: out of 194 colour-ringed pairs that produced a clutch between 2002 and 2007, only six pairs (3.1%) kept the same mate between successive nests (for further details on fieldwork, see Szentirmai et al. [28]). The pattern of parental care for these six pairs (50% female-only care, 10% male-only care and 40% biparental desertion) did not appear to differ from that observed at the population level.

(b). Fitness consequences of care and desertion

Throughout this paper, we focus on parental care or desertion decisions concerning each individual's first breeding attempt in the season. Since incubation and nestling feeding take about 34 days [42], caring for the first brood severely constrains the opportunities for subsequent breeding (table 1a). To estimate the contribution of the first clutch to parental fitness, we calculated the average number of eggs and nestlings for all nests that were initiated before 6 June, depending on the parental care category (female-only care, male-only care and biparental desertion) of the nest (table 1a). The cut-off date corresponds to the midpoint of the interval between the nest initiation date of the first and second nest of ringed males (mean ± s.d. between males: 3 June ± 22.7 days, n = 267 males; and 8 June ± 21.1 days, n = 101 males, respectively). If a given individual had more than one nest before 6 June, we selected only the earliest nest in the season as its first nest.

Table 1.

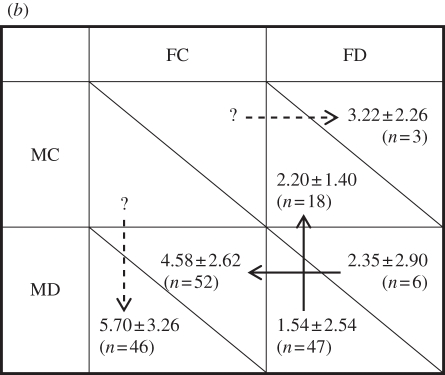
(a) Summary of breeding parameters of Eurasian penduline tits in southern Hungary: number of eggs and nestlings produced in all first nests (including those of both ringed and unringed individuals) of the breeding season, with sample size (number of nests) between parentheses; the probability for ringed individuals to have at least one more successful breeding attempt after the first successful nest (‘successful’ meaning that pair formation and egg laying took place); the number of subsequent successful breeding attempts; the total number of eggs and nestlings produced in all subsequent nests; and the seasonal reproductive output (mean ± s.d.). Standard deviation of the total number of nestlings represents the pooled standard deviations of the first and subsequent nests. (b) Population strategy-dependent seasonal reproductive payoffs for males and females: mean number of nestlings ± s.d. for males (below the diagonal) and females (above the diagonal) given the parental category of their first nest in the breeding season (n is the number of individuals). FC, female care; FD, female desertion; MC, male care; MD, male desertion. Arrows point from smaller to larger payoffs, representing the direction in which selection for a parental care strategy would act. Dashed arrows indicate our assumption that unilateral desertion always yields a higher fitness payoff than caring (see §3b); continuous arrows are based on observed values. This matrix is consistent with that of the Snowdrift Game (see table 2e). n is the number of individually marked males or females, whereas sample sizes at the first nests of the season (in parentheses) are the number of nests including those of both ringed and unringed individuals. Sample sizes for the former may be larger than that for first nests only, because reproductive success for some nests was estimated using population means for a given strategy (see §2b).

		female-only care		male-only care		biparental desertion
(a)		♂	♀	♂	♀	♂	♀
first	no. of eggs	6.37 ± 1.16 (41)		3.17 ± 1.27 (12)		2.84 ± 1.27 (51)
	no. of nestlings	3.63 ± 2.00 (40)		2.20 ± 1.40 (10)		0 ± 0 (65)
subsequent	p-value	0.74	0.38	0.06	0.67	0.34	0.83
	no. of nests	1.46 ± 1.39	0.58 ± 0.91	0.06 ± 0.24	0.67 ± 0.58	1.17 ± 1.20	1.33 ± 0.82
	no. of eggs	6.34 ± 6.05	2.61 ± 3.97	0.06 ± 0.24	2.91 ± 2.90	4.49 ± 4.66	7.12 ± 5.00
	no. of nestlings	2.07 ± 2.58	0.95 ± 1.70	0 ± 0	1.02 ± 1.77	1.54 ± 2.54	2.35 ± 2.90
total	no. of nestlings	5.70 ± 3.26	4.58 ± 2.62	2.20 ± 1.40	3.22 ± 2.26	1.54 ± 2.54	2.35 ± 2.90
	n	46	52	18	3	47	6

Our data on first clutches are in line with previous studies of penduline tits [28,29]. Nest desertion takes place during the egg-laying phase. If the male deserts first, the female often lays two or three additional eggs, so that female-only cared clutches are significantly larger than those cared for by males and those deserted by both parents (table 1a). In biparentally deserted nests, all offspring die, whereas offspring survival (i.e. survival from hatching until 10 days after hatching) does not differ between male-only and female-only cared clutches (binary logistic regression including parental care category, clutch size, egg-laying date, year and the interaction between parental care category and clutch size as fixed effects: χ² = 1.458, p = 0.227, n = 142 nests; Á. Pogány, R. E. van Dijk, P. Horváth & T. Székely 2008, unpublished data). The reproductive success of males may be inflated (or deflated) by the occurrence of extra-pair young; in this system, about 24 per cent of all offspring are sired by an extra-pair male [43]. However, the percentage of extra-pair young does not differ between nests cared for by the male and those deserted by him, nor between nests cared for by the female and those deserted by her [43]. Therefore, extra-pair paternity is unlikely to bias our results.

The data on first broods within a season were based on 115 nests for which the parental care category was known. For 172 ringed birds (111 males and 61 females) involved in successful breeding attempts at these nests, the parental care category of their first nest of the season could be determined (‘successful’ meaning that pair formation and egg laying took place). For each combination of sex (male, female) and parental care category (male-only care, female-only care and biparental desertion), we calculated the percentage of birds involved in a second successful breeding attempt and the mean number of subsequent nests established by those birds. Males may only care for one brood in a breeding season, whereas females may care for up to two broods. The difference between males and females in the probability of having a subsequent successful nest after providing parental care (0.06 for males versus 0.38 for females; table 1a) is largely due to the fact that males often care near the end of the breeding season [28,44]. Additionally, males who deserted their first nest were less likely to have a subsequent successful nest if the female had also deserted (p = 0.34) than if she had stayed behind to provide care (0.74; table 1a). This might suggest that males at nests that are biparentally deserted are of lower quality and/or less attractive. However, mask size was not different between males whose nest was deserted by both parents and males at nests where either the male or the female provided care (binary logistic regression: model effect estimate ± s.e. = 1.025 ± 0.912, Wald statistic = 1.262, d.f. = 1, p = 0.261, n = 88 males). Tarsus length, wing length and body mass of males were also not different between these two categories of nests (p > 0.331). Additionally, at the second nest in a season, the pattern of parental care for males was not different from that observed at the population level (table 3b) if his first nest was cared for by the female (χ² = 0.211, p = 0.900, n = 34 males) or was biparentally deserted (χ² = 1.186, p = 0.553, n = 31 males). This suggests that the breeding experience of males did not predict the likelihood of biparental desertion of a subsequent nest.

Table 3.

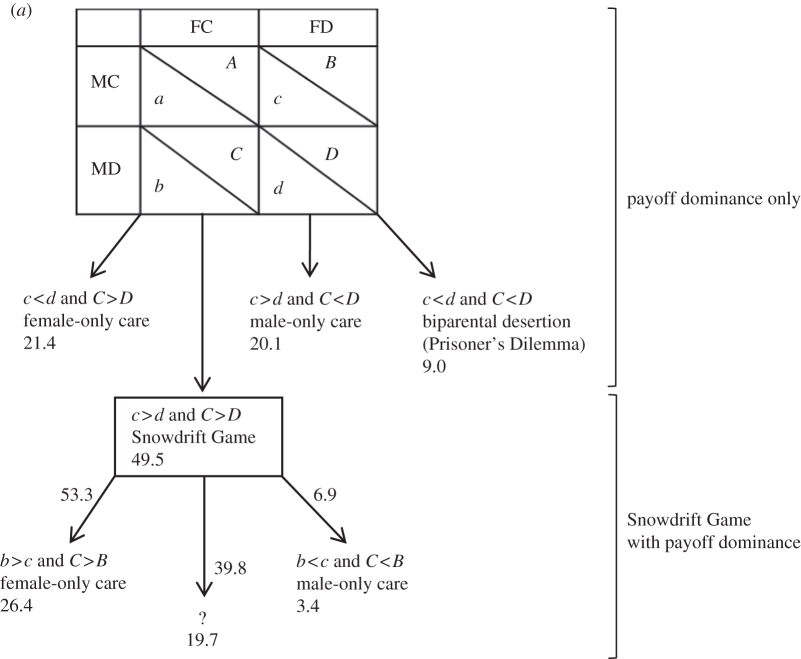
(a) Payoff requirements, parental care evolutionarily stable strategies (ESSs) and the probability (%) for each ESS. The question mark (?) indicates the percentage of pairs involved in a Snowdrift Game for which neither of the two ESSs (male-only care or female-only care) was payoff-dominant. (b) The expected population strategy for three different assumptions for ‘?’, i.e. the sum of the proportion predicted by payoff dominance and the proportion predicted by the Snowdrift Game.

(b)	female-only care (%)	male-only care (%)	biparental desertion (%)
observed parental care ± CI (n = 534 pairs)	47.4 ± 8.6	13.5 ± 6.0	39.1 ± 8.4
if ? = biparental desertion	47.8 (21.4 + 26.4)	23.5 (20.1 + 3.4)	28.7 (9.0 + 19.7)
if ? = female-only care	67.5 (21.4 + 26.4 + 19.7)	23.5 (20.1 + 3.4)	9.0 (9.0)
if ? = 50% male-only care and 50% female-only care	57.6 (21.4 + 26.4 + 9.9)	33.4 (20.1 + 3.4 + 9.9)	9.0 (9.0)
if ? = biparental desertion and attractive males desert	49.1 (24.4 + 24.7)	8.6 (7.5 + 1.1)	42.3 (22.6 + 19.7)

Based on all penduline tits within a category (i.e. including those birds that did not establish a second nest), we calculated the average number of eggs and nestlings produced during subsequent breeding attempts (table 1a). If the number of eggs and/or nestlings could not be determined, it was estimated as the population mean of nests with the corresponding parental care category (male-only care: 3.67 eggs and 2.22 nestlings; female-only care: 5.80 eggs and 3.07 nestlings; biparental desertion: 2.93 eggs and 0 nestlings; n_eggs = 371 nests and n_nestlings = 194 nests). Overall, we estimated reproductive success for 77 of 339 clutches (22.7%) and for 33 of 336 broods (9.8%).

Finally, we calculated the seasonal reproductive output for each parental category, by adding up the average number of nestlings in the first and subsequent nests (table 1a). To check the consistency of our calculations of parental strategy-dependent seasonal reproductive output, we also determined the total number of nestlings produced over the season by the 172 ringed penduline tits, separately for males and females in each care category of their first nest. For all six categories, the reproductive output of the colour-ringed penduline tits that we followed throughout the breeding season was almost identical to that in table 1a.

3. Game-theoretic analysis

(a). No individual variation in payoffs

The seasonal reproductive output given in the penultimate row of table 1a corresponds to the total number of nestlings shown in the payoff matrix for the parental care categories in table 1b. A male who cared for the offspring in his first nest produced more nestlings over the course of the season (2.20 ± 1.40) than a male whose first nest was biparentally deserted (1.54 ± 2.54; Mann–Whitney U-test: U = 257.5, p = 0.009, n = 65, Cohen's d = 0.878, 1 − β = 0.88). In contrast, a female who cared for the offspring in her first nest did not produce significantly more nestlings over the course of the season (4.58 ± 2.62) than a female whose first nest was biparentally deserted (2.35 ± 2.90; U = 93.5, p = 0.108, n = 58, d = 1.120, 1 − β = 0.70). Note, however, that we had only six females in the latter category.

Pairs rarely produced multiple clutches together (see §2a [39]). We therefore assume that penduline tits play a single-shot game with two alternative actions: care or desert. An influential single-shot game from the game-theoretic literature is the Prisoner's Dilemma. In this game, each player may either cooperate or defect, but the best response to any action by the opponent is to defect [45–48]. Thus, the Prisoner's Dilemma characterizes a situation in which cooperative behaviour is vulnerable to exploitation by non-cooperators, eventually leading to an equilibrium in which no one cooperates. Despite the high frequency of nest desertion in penduline tits, table 1b suggests that desertion is not the dominant strategy: if the male deserts, the female does best by caring, whereas if the female deserts, the male does best by caring. Thus, penduline tits do not appear to be playing a Prisoner's Dilemma at the population level.

An alternative possibility is the Snowdrift Game, in which cooperation is beneficial for both players but the costs of cooperating depend on the opponent's strategy [49–51]. This is also true for parental care. Because parental care is an asymmetric game between two types of players, namely males and females, the game in table 1b may reflect an asymmetric Snowdrift Game (cf. ‘Battle of the Sexes’ [52]). Although in asymmetric games an ESS can never be a mixed strategy [53], the asymmetry (male versus female) may be used to settle the conflict: each of the ESSs, corresponding to the two forms of unilateral cooperation (i.e. male-only care and female-only care), may be viewed as a convention. Although either convention is evolutionarily stable once it is adopted by the whole population, the problem of which one will be reached in the course of evolution remains. Both players agree that unilateral cooperation would be best, but they differ in which of the two ESSs they prefer.

If one of the ESSs is payoff-dominant [54]—in that the payoff to each player is at least as great as the payoff it would get at the alternative ESS—then an obvious solution is to adopt that ESS. In terms of the average reproductive payoffs in our dataset, female-only care is more profitable for both sexes than male-only care (table 1b), and thus female-only care is the payoff-dominant ESS. However, the predicted outcome of female-only care is inconsistent with the observed behaviour. Why is it that some pairs exhibit male-only care, when female-only care apparently gives a higher payoff for both sexes? And if the parents coordinate their actions, why do we still observe such a high frequency of biparental desertion (28–44%; electronic supplementary material, figure S1)?

(b). Individual variation in payoffs

Because individuals vary in their fitness prospects, a payoff matrix based on reproductive outputs averaged across the whole population may provide a poor framework for understanding conflict resolution within individual pairs. Although at a population level penduline tits appear to be playing a Snowdrift Game, individual pairs of birds may differ in their payoffs from particular actions and may bargain an outcome depending on their individual traits (and their particular environmental circumstances). Within each pair, individual characteristics such as attractiveness or condition are likely to affect the payoff for a given parental category. If a male is attractive, for instance, his female partner may be more willing to care for his offspring [55], while the male may benefit more from desertion by finding a new mate more rapidly than a less attractive male. Similarly, males may be more willing to care for the offspring of fecund females, while those females may be better at producing additional clutches. But accounting for such individual differences to generate precise, pair-specific predictions of the outcome of individual conflicts over parental care is a very difficult task.

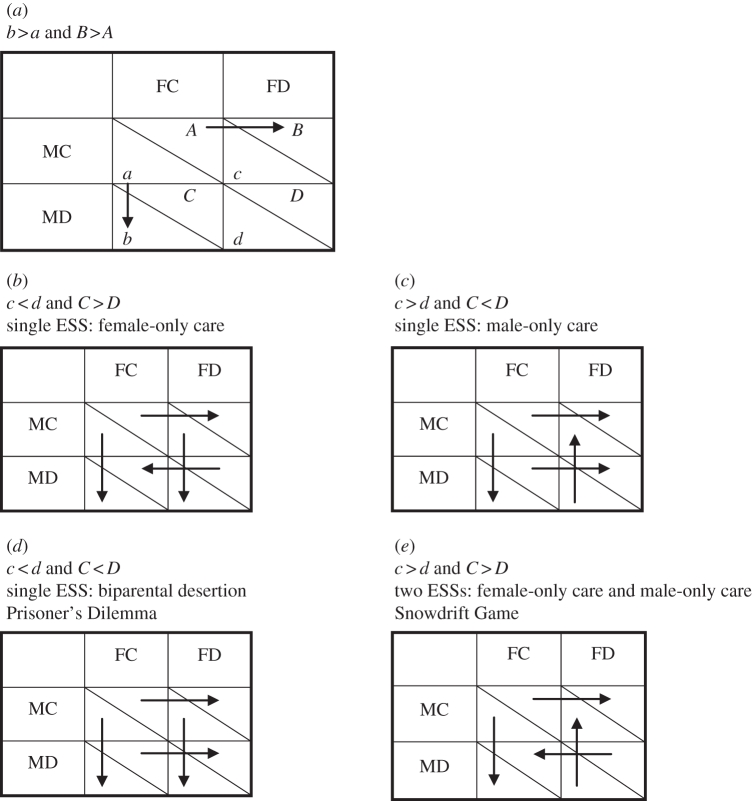
Nevertheless, using the available field data on reproductive output for three of the categories (though never biparental care) for some of the birds may allow us to generate more accurate predictions than when we consider only the population average payoff matrix. Here, we use an approach based on bootstrapping. The game played by each pair is represented by the general payoff matrix shown in tables 2a and 3a. Note that in our study population not a single case of biparental care was observed at the 534 nests we investigated; so the payoffs A and a cannot be estimated for any individual. Instead, we assume that unilaterally deserting a caring partner always yields a higher fitness payoff than caring (i.e. b > a and B > A). For all other outcomes (male-only care, female-only care and biparental desertion), we allow the expected payoffs to vary between individuals.

Table 2.

Reproductive payoff matrices. For comparing alternative actions, arrows point from smaller to larger payoffs (indicating the expected direction of selection). (a) Generic version; our central assumption is that unilateral desertion yields a higher payoff for the deserting partner (both male and female) than biparental care (a behaviour we never observed in our population), i.e. b > a and B > A. (b–e) Four specific scenarios for the different relationships between the payoffs when caring alone (c for males, C for females) and when both parents desert (d for males, D for females).

For most pairs, we lack individual payoffs for both the male and the female; so, as an approximation, we used a bootstrapping approach to generate a large sample of payoff matrices from the field data. This involved randomly drawing (with replacement) from the observed individual payoff values (seasonal number of nestlings) for each parental care category for males and females. Each bootstrapped matrix was composed of the following values randomly drawn from the corresponding observed payoffs: one b value drawn from the n = 46 observed male payoffs under female-only care; one c value from the n = 18 male payoffs under male-only care; one d value from the n = 47 male payoffs under biparental desertion; one B value from the n = 3 female payoffs under male-only care; one C value from the n = 52 female payoffs under female-only care; and one D value from the n = 6 female payoffs under biparental desertion. To each of these values, we added a small amount drawn from a random normal distribution with mean 0 and s.d. 0.01. This was to preclude the occurrence of tied payoffs, which would otherwise be common in the biparental desertion category since many of these individuals produced no offspring in the breeding season. We repeated this process until we had generated 5000 unique bootstrapped matrices from the field data.

There are four possibilities (table 2b–e) for the type of parental care game being played by a pair, determined by the particular values of c, d, C and D:

1. c < d and C > D: a game in which female-only care is the only ESS;

2. c > d and C < D: a game in which male-only care is the only ESS;

3. c < d and C < D: a Prisoner's Dilemma where biparental desertion is the only ESS; or

4. c > d and C > D: a Snowdrift Game with two ESSs (male-only care and female-only care).

On the basis of our bootstrapped matrices, 21.4 per cent of nests are predicted to have female-only care (case (i)), 20.1 per cent male-only care (case (ii)) and 9 per cent biparental desertion (case (iii)), while the remaining 49.5 per cent of pairs will be involved in a Snowdrift Game (case (iv)) from which any of the three outcomes may result (table 3a). In the Snowdrift Game, we assume that if one of the two ESSs is payoff-dominant, this is the one the pair will adopt. Thus, we assume that female-only care results when b > c and C > B (26.4% of the bootstrapped matrices, in addition to those from case (i)) and that male-only care results when b < c and C < B (3.4% of the bootstrapped matrices, in addition to those from case (ii); table 3a). For 19.7 per cent of the bootstrapped matrices, the male and female are involved in a Snowdrift Game in which neither equilibrium is payoff-dominant. We consider three possible scenarios for how the conflict is resolved at these nests:

• —Both parents desert the nest. This scenario predicts an additional 19.7 per cent of nests with biparental desertion (table 3b).

• —The parents adopt the solution that is payoff-dominant at the population level, namely female-only care (table 1b). This scenario predicts an additional 19.7 per cent of nests with female-only care (table 3b).

• —The two ESSs are adopted with equal probability, resulting in female-only care at half of these nests and male-only care at the remaining half [40]. This scenario predicts an additional 9.9 per cent of nests with female-only care and an additional 9.9 per cent of nests with male-only care (table 3b).

Of these three scenarios for resolving the Snowdrift Game in the absence of payoff dominance, the first (biparental desertion) best predicts the observed patterns of care, as this provides the closest match to the pattern of parental care observed in our study population (table 3b). The predicted frequencies of female-only care (47.8%) and biparental desertion (28.7%) are within the natural ranges (electronic supplementary material, figure S1), although it overestimates the frequency of male-only care (23.5%, table 3b). This model, based on individual variation, is therefore broadly consistent with the observed patterns of care in our study population, and provides a better fit than the earlier model based on the average payoff matrix for the population (§3a), which predicted female-only care at all nests.

To test how individual characteristics may influence the resolution of conflict over care, we ran our bootstrapped model again on a reduced sample of males, for whom we knew the size of the mask (n = 30, n = 10 and n = 40 males whose first nest in the season was cared for by the female, cared for by the male or biparentally deserted, respectively). Males with larger masks are more attractive [38] and more likely to desert [39], whereas the female's decision to care or desert does not appear to be influenced by the size of her partner's mask [39]. We therefore assumed that all males with a larger-than-average mask (i.e. greater than 1.30 cm²; n = 120 males) would desert, whereas for males with smaller masks we assumed that payoff dominance and the Snowdrift Game would determine parental care as outlined in table 3a. The predictions of parental care from this model accounting for individual variation in attractiveness closely resemble the observed pattern of parental care in penduline tits (table 3b).

4. Discussion

We found no evidence that penduline tits are playing a Prisoner's Dilemma, despite the high frequency of biparental desertion. At the population level, the payoff matrix based on seasonal reproductive success is most consistent with an asymmetric Snowdrift Game with two alternative ESSs: female-only care and male-only care. Female-only care is the payoff-dominant ESS, but this fails to predict the patterns of care in the wild, where more than half of the nests are either cared for by the male (13.5%) or deserted by both parents (39.1%). We argue that the population payoff matrix is of little use in explaining observed patterns of care because expected reproductive payoffs are likely to vary between individuals, and therefore different pairs may be playing very different games when deciding whether to care or desert.

Our individual-based approach predicts a mixture of parental care strategies, with frequencies of female-only care and biparental desertion that fall within the observed range in natural populations (table 3b, electronic supplementary material, figure S1). Although largely consistent with observed frequencies of parental care, our first model overestimates the frequency of male-only care and underestimates the occurrence of biparental desertion compared with the empirical dataset (table 3b). In many ways, this mismatch is not surprising, given that we have payoffs only for a subset of individuals in specific situations. Furthermore, we lack information on the extent to which an individual's expected payoffs are correlated across the three different situations (male-only care, female-only care and biparental desertion), and on the correlation between the male and female payoffs of each pair. Such information is largely beyond our reach, even for such an intensively studied field system as this penduline tit population. Nevertheless, our approach based on bootstrapped individual payoffs highlights the importance of considering individual variation when predicting the behaviour of individual pairs instead of applying more conceptual models like the Prisoner's Dilemma.

The significant deviation of this model from the empirically observed pattern of care could be partly owing to stochastic factors affecting some of the payoffs based on small sample sizes. This may, for example, have been responsible for the overestimate of the occurrence of male-only care, which was derived from only n = 18 payoffs for males and n = 3 for females. But the fact that males are more likely to provide care nearer the end of the breeding season (yet without entailing biparental care [27,43]), for instance, suggests that there are other factors besides just the strategy-dependent payoffs that are important in determining which parent will provide care and which will desert.

The discrepancy between predicted and observed patterns of care may be partly ascribed to individual differences, such as individual quality or environment [37]. To some extent, we took these individual-specific effects into account by replacing the average fitness payoffs at a population level with individual payoffs. However, a correlation between individual traits and the different adopted strategies may cause a consistent bias in the exact payoffs. Attractive males, for instance, may desert not only when their partner stays behind to care for the offspring but also when the partner already has deserted (as predicted in a Prisoner's Dilemma), whereas a less attractive male may be better off caring for the offspring in the latter case (as predicted in a Snowdrift Game). Such covariance of individual traits with parental care strategies is likely to influence the outcome of conflict over parental care. In our final model, we accounted for some potential correlations between individual traits and reproductive payoffs by including the effect of male attractiveness on the decision to care or desert, based on our findings from earlier work [38,39]. We showed that this substantially improved our model's predictions, bringing them closely in line with the empirically observed pattern of care.

We assumed that the parents play a single-shot game because normally each pair breeds together only once in a breeding season, but in reality they are unlikely to play a strictly single-shot game. Parents may interact multiple times and repeatedly assess each other's quality before they decide whether to care for the offspring or desert. Such interactive ‘negotiation’ behaviour probably influences decisions over parental care [56]. However, although the male's own parental care decisions are known to be associated with his body condition or attractiveness, we have no evidence that these male traits influence the parental care decisions of females [38,44,57]. Additionally, it is worth noting that Eurasian penduline tit parents spend little time together at the nest during the period before desertion, making detailed monitoring of each other's behaviour, such as has been suggested for St Peter's fish [20], unlikely [44]. Nevertheless, the interaction between individual traits and environmental variables (e.g. mating opportunities) may be complex, and experimental manipulations would be useful for investigating systematically how these factors combine to influence patterns of parental care.

Balshine-Earn & Earn [20] also showed in their model that natural variation between individuals and in the environment could promote the coexistence of different forms of parental care (see also McNamara et al. [48]). A spatially heterogeneous distribution of strategies, such as desertion in high-quality habitats and care in poor habitats, or vice versa, could potentially confound the outcome of our analyses. Although it has been suggested that spatially diverse environments might favour multiple coexisting strategies [47], in earlier work we found no relationship between parental care category and habitat characteristics [41]. Nonetheless, it would be worthwhile to investigate the possibility that mating opportunities might be spatially structured in some way, perhaps resulting in spatial variation in deserting strategies. Such extrinsic factors, the reputation of the players in the game and occasional mistakes made by those players may all influence conflict resolution and allow multiple strategies to persist [12,48,50,58].

In conclusion, we have shown that the resolution of conflict over care is highly variable and may be strongly influenced by individual differences in the expected reproductive payoffs for each male–female pair. Using a population payoff matrix to predict the behaviour of individual pairs has severe limitations, because this is likely to be a poor representation of the particular conflict faced by each pair. We recommend the use of individual-specific information on the reproductive consequences of care decisions to obtain more accurate predictions of population-level patterns of parental care.