Quantification of the Kinetics and Extent of Self-Sorting in Three Dimensional Spheroids

Abstract

The self-sorting of cells into distinct compartments in three-dimensional (3D) microtissues is a process critical to developmental biology, cancer metastasis, and tissue engineering. Although self-sorting has been studied since the 1950s, little quantitative data exist that describe this dynamic process. Here, we describe a recently developed assay designed to quantify the extent and kinetics of self-sorting in 3D. Mixtures of fluorescently labeled normal human fibroblasts (NHF) and hepatocyte (H35) cells were fluorescently labeled, red and green respectively, and seeded onto micro-molded non-adhesive hydrogels. The cells self-assembled into a spheroid and self-sorted with NHFs forming the central core and H35s forming the outer shell. A time course of fluorescent images was used to analyze the ratio of red (NHFs) and green (H35s) fluorescence in concentric hollow cylinders throughout a spheroid and was statistically compared with the fluorescent ratio of the perfectly sorted spheroid. We found that NHFs and H35s, at a 1:1 ratio, sorted to a final extent of 88±3% at an initial rate of 0.36±0.06% per minute and reached 50% self-sorted at 2.7±0.3 h. Studies with varying ratios of NHFs and H35s show that self-sorting and self-assembly are coincident in time when the proportion of NHFs are varied over a 6-fold range (14% to 85%). This method can, thus, be used to characterize the sorting behavior of additional pairs of cells, the effect of drugs, and growth factors that may change the kinetics of the process, and bring an understanding to the cellular mechanisms which control self-sorting.

Introduction

In non-adhesive environments, cells will aggregate and form three-dimensional (3D) multi-cellular microtissues.¹ In addition to aggregating, mixtures of different cell types will often segregate (self-sort), a process relevant to embryogenesis, morphogenesis, cancer metastasis, and tissue engineering.^1–3 Self-sorting has qualitatively been observed since the 1950s, and the process has been hypothesized to be the result of differences in surface adhesion molecules; the differential adhesion hypothesis (DAH).^2,4–7 According to DAH, cells are discrete mobile units within a spheroid, and cell types have differences in cohesive forces (like-to-like) and adhesive forces (unlike binding). Self-sorting occurs due to these differences with cells of highest cohesion in the core and cells with lower cohesion on the outside.² However, recent studies from a number of labs, including our own, suggest that self-sorting is more complicated and involves the biomechanics of the cytoskeleton.^8–10 These studies showed that differences in cytoskeletal mediated tension between pairs of cells also resulted in self-sorting.

Nearly all studies of self-sorting have been qualitative in nature, and there are little quantitative data on what is clearly a dynamic process. One problem is the limitations of using spinner cultures or rotational cultures to form spheroids.^5,11,12 Although spheroids that have been clearly self-sorted are produced at the end of the spinner culture method, it is impossible to monitor in real time the kinetics of self-assembly and self-sorting. Several groups have used simulations to model the process of self-sorting.^13–16 For example, most recently, self-sorting has been quantitatively described using an order parameter, which is based on a geometrically driven argument to describe the relationship between heterotypical interface length and the system size.¹³ Additional simulations involve the analysis of cell surface tension during the different states of reorganization using either two-dimensional lattice simulations or free particle simulations.^14,16 However, missing from the self-sorting field are quantitative empirical data on the kinetics of self-sorting, the extent of self-sorting, and the quantification of various cellular systems (e.g., surface adhesion molecules versus cytoskeletal motors) in the process of self-sorting.

Using micro-molded non-adhesive hydrogels, we have qualitatively analyzed the self-sorting behavior of several cell types. In particular, we have extensively characterized the interaction and self-sorting of normal human fibroblasts (NHFs) and reuber-H35 rat hepatoma cells (H35s).¹⁷ In a heterotypic spheroid of NHFs and H35s, the NHFs will sort to the center forming a central core, and the H35s will sort to the outside to form the outer shell. Here, we describe a newly developed assay to measure and quantify the kinetics and extent of self-sorting in 3D microtissues using epifluorescent microscopy. NHFs and H35s were labeled with red and green fluorescent tracking dyes, respectively. The mixture of cells was seeded onto micro-molded non-adhesive hydrogels, and a time course of fluorescent images was taken using conventional and side-view microscopy as the cell mixture self-assembled and self-sorted in 3D. The ratio of red and green fluorescence of concentric hollow cylinders was calculated, compared with a reference spheroid of similar size and shape that had perfectly sorted, and a goodness-of-fit was used to determine sorting. We found that a 1:1 ratio (NHF:H35) self-sorted to a final extent of 88±3% at an initial rate (v_o) of 0.36±0.06% per minute, and the time to reach 50% self-sorted (t_1/2) was 2.7±0.3 h. When normalized to self-assembly, the rate of self-sorting and the rate of self-assembly were coincident in time. The method was further used to quantify how the rate and extent of self-sorting changed as the ratio of NHFs and H35s was varied in spheroids of similar size. This method provides important quantitative data on the kinetics and extent of self-sorting, is applicable to any pair of cell types, and can be used to investigate in detail the complex molecular and cellular process of self-sorting in 3D.

Materials and Methods

Design, fabrication, and casting of micro-molds

Micro-molds were produced as previously described.¹⁷ Briefly, micro-molds were designed using the computer design software SolidWorks (SolidWorks Corporation, Concord, MA). Designs used for side-view microscopy contained a single row of 21 recesses, each recess being 400 μm in diameter and 800 μm in depth. From these files, wax molds were produced with a ThermoJet^® rapid prototyping machine (3D Systems Corporation, Valencia, CA). Polyacrylamide gels used for side-view microscopy were reproduced directly from the wax molds.¹⁸ All chemicals, unless otherwise noted, were purchased from Sigma Aldrich (St. Louis, MO). A mixture of acrylamide/bis-acrylamide (29:1 ratio), ammonium persulfate, 0.5 M Tris Buffer (pH 6.8), and dulbecco's modified eagle's medium (DMEM) (Invitrogen, Carlsbad, CA) was degassed. To initiate polymerization, N, N, N′, N′-tetramethylethlyenediamine was added. The solution was mixed, pipetted into the wax mold, and a glass cover slip was placed on the mold to create a flat bottom on the gel. After 10 min, the hydrogel was removed from the mold, placed into sterile six-well plates, and washed with DMEM several times. Hydrogels were equilibrated overnight in DMEM before use.

Micro-molds used for conventional view inverted microscopy contained a 12×8 array of 96 recesses (MicroTissues, Inc., Providence, RI) and were sterilized by autoclaving. Hydrogels were cast from the micro-molds, using a 2% molten agarose solution, prepared by mixing sterile Ultrapure^™ agarose (Invitrogen) powder and 0.9% saline; agarose was melted via the microwave oven, and 0.25 mL was added to the micro-mold. After the agarose gelled (∼5 min), gels were transferred to a 24-well tissue culture plate where they were equilibrated in culture medium overnight.

Cell culture and hydrogel seeding

NHFs (passages 2–12), derived from neonatal foreskins, and reuber-H35 rat hepatoma cells (H35s) (Passages 6–14) were grown in DMEM (Invitrogen) supplemented with 10% fetal bovine serum (Thermo Fisher Scientific, Waltham, MA) and 1% penicillin/streptomycin (Sigma) at 37°C with 10% CO₂. Cells were stained by incubation in DMEM 5 μM Cell Tracker Red CMPTX, Cell Tracker Green CMFDA, or Cell Tracker Blue CMAC (Invitrogen) for 50 min; medium was changed to serum-free DMEM and incubated for 30 min. Cells were then trypsinized according to standard protocol, counted, and then mixed in the appropriate ratios of NHFs: H35s. The mixed population of cells were spun down at 800 rpm for 6 min, and re-suspended in 100 μL of DMEM. For all ratios and experimental conditions, the total number of cells was held constant. Each micro-molded hydrogel containing 96 recesses was seeded with a total of 0.15×10⁶ cells per hydrogel. Cells were allowed to settle for 30 min; then, 2 mL of fresh medium was added to each of the wells. Time-lapse microscopy was used to acquire images every 30 min for 15 h at 37°C and a 10% CO₂ atmosphere.

Microscopy and image analysis

Two forms of microscopy were used in this method. Horizontal view microscopy was used to validate the depth (z) of the spheroid. A Mitutouo FS-110 microscope altered to lie on its back was used to view samples that were placed on a translational stage. Brightfield images were taken through the eyepiece of the camera using a Nikon Coolpix 900 digital camera. For conventional inverted microscope images (x–y), a Carl Zeiss Axio Observer Z1 equipped with an AxioCam MRm camera (Carl Zeiss MicroImaging, Thornwood, NY) and Xcite 120 XL mercury lamp (Exfo Life Sciences Division, Mississauga, Ontario) were used to obtain brightfield, phase contrast, and epi-fluorescent images. ImageJ Software (Rasband, W.S., ImageJ, NIH) was used to measure the height, major axis, and minor axis of the spheroid, as well as the fluorescent intensity of 10 μm shells across the spheroid.

Generation of theoretical curves for a perfect sort

A macro was developed to calculate the theoretical core-to-shell ratio for a range of spheroid sizes and shapes that had perfectly sorted. The known ratio between the total volume of the two cells in the spheroid is given by

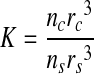(1)

,

where r_c and n_c are the radius and number of the cell type that sort to the core, and r_s and n_s are the radius and number of the cell type that sort to the shell. The depth of the shell c can be determined using the relationship

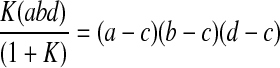(2)

,

where a is the half-width, b is the half-height, and d is the half-depth of the spheroid. The spheroid was then broken into 10 μm concentric shells (cylinders), and the volume of both cell types within each shell was determined by shell integration.

Quantification of self-sorting

To quantify self-sorting at a given location in the spheroid, we locally calculated the deviation of the experimental value from the theoretical value of a perfectly sorted spheroid of comparable size and shape. This was repeated at each point along the experimental and theoretical curves. We determined the overall percent self-sorted at each time point using a goodness-of-fit of the experimental data to the theoretical model, using the coefficient of determination, R², such that

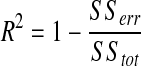(3)

,

where SS_tot is the total sum of squares (proportional to the sample variance), and SS_err is the sum of squares of residuals. R² values are bounded between 0 and 1, such that 0 signifies no fit to the theoretical data, and 1 signifies a perfect fit. R² values can be negative as well, when the model is not linear. A negative number indicates no fit between the theoretical and experimental data, and, thus, can be set to 0.

Statistical analysis

T-tests were performed to determine statistical significance with p-values <0.05 considered statistically significant.

Results and Discussion

To analyze the process of self-sorting, we seeded a cell mixture (1:1) of NHFs (labeled red) and H35s (labeled green) onto micro-molded agarose gels. The cells settled to the bottom of the recesses, and fluorescent wide-field images were obtained over 15 h as they self-assembled and self-sorted (Fig. 1). The cells assembled from a thin layer of randomly distributed mono-dispersed cells settled at the bottom of each recess into a spheroid where NHFs formed the central core and H35s formed the outer shell of the spheroid. The processes of both self-assembly and self-sorting occurred during the 15 h time frame and involved not only movement of cells in the x, y, and z dimensions, but also specific movements of the two different cell types relative to one another to achieve self-sorting.

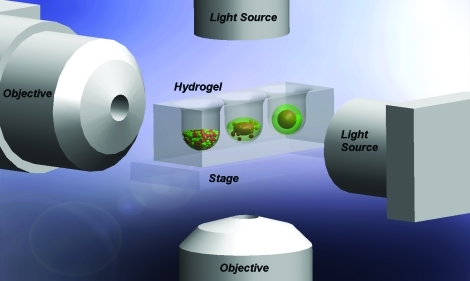
FIG. 1.

Experimental set-up of horizontal and normal view microscopy. Horizontal view (z) and normal view (inverted) (x, y) microscopy were used to capture time-lapse images of self-assembly and self-sorting. Color images available online at www.liebertonline.com/tec

To determine the uniformity of the spheroids, the size and the ratio of NHFs and H35 cells within each of the recesses at the initial (0 h) and final (15 h) time points were measured (Fig. 2). The major (x) and minor (y) axes, respectively, were 339±13 μm and 347±16 μm at 0 h, and 193±9 μm and 190±12 μm at 15 h (n=12). The sizes were uniform, and the decrease in the x and y axes over time indicated that the cells were self-assembling a 3D spheroid whose z axis was increasing. To quantify the changes in the z axis and determine whether spheroid volume remained constant over time, we also obtained side-view images of the spheroids. The computed volume at 0, 3, 6, 9, 12, and 15 h was 2.5±0.6×10⁶ μm³. These data show that cell distribution in each recess was uniform with regard to total cell number, which controls the final spheroid size. Furthermore, the ratio of red-to-green fluorescent intensity was also uniform for each recess and remained constant. At time zero, the ratio was 0.873±0.069 and after 15 h, the ratio was 0.861±0.073 (n=12). These data indicate that after 15 h, the cells formed an oblate spheroid of uniform size and volume in each recess. This verification of uniformity allows us to calculate spheroid height and volume from conventional images of the x and y axes. Moreover, we know from previous work that if spheroids have a z height less than 205 μm, there is minimal loss of the red and green fluorescent signal.

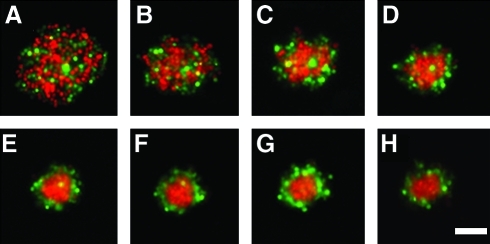
FIG. 2.

A mixture of normal human fibroblasts (NHFs) and H35s self-assembled and self-sorted within 15 h. A mixture (1:1) of NHFs (red) and H35s (green) self-assembled to form a three-dimensional spheroid and self-sorted such that NHFs formed the central core, and H35s formed the outer shell. Wide-field fluorescent images were obtained (A) immediately post seeding (0 h), (B) 1 h, (C) 2 h, (D) 3 h, (E) 6 h, (F) 9 h, (G) 12 h, and (H) 15 h after seeding. Scale bar=100 μm. Color images available online at www.liebertonline.com/tec

To quantify self-sorting, we used the elliptical tool in ImageJ to draw a circular perimeter encompassing the entire spheroid (Fig. 3), and measured total red and green fluorescence. The perimeter was then eroded radially 10 μm, and the fluorescence of each of the fluorophores was quantified for each 10 μm shell until the radius was less than 10 μm. Each 10 μm shell was, in fact, a hollow cylinder that collected the fluorescence from the x, y, and z planes of the spheroid (Fig. 3). To determine the net fluorescence, the background fluorescence was calculated as fluorescence per area, and the cylinders were corrected for this accordingly. Net fluorescence was normalized to the total fluorescence in the spheroid to account for differences in exposure time, photobleaching, and fluorescent properties of the fluorophores. To determine the extent to which a spheroid was self-sorted, the ratio of relative red and green fluorescence in each 10 μm cylinder was calculated. A core-to-shell ratio (NHF to H35) was used to ensure that the ratio was always a defined number. Randomness (unsorted) was defined by the geometry of the spheroid, as well as the size and ratio of the input cells. Since NHFs have a diameter of 20 μm and H35s, a diameter of 17 μm, a 1:1 mix of these cells has a randomness ratio of 1.63. We defined self-sorting as a change from randomness, thus a mathematical change from 1.63, which could be either an increase or a decrease from this value.

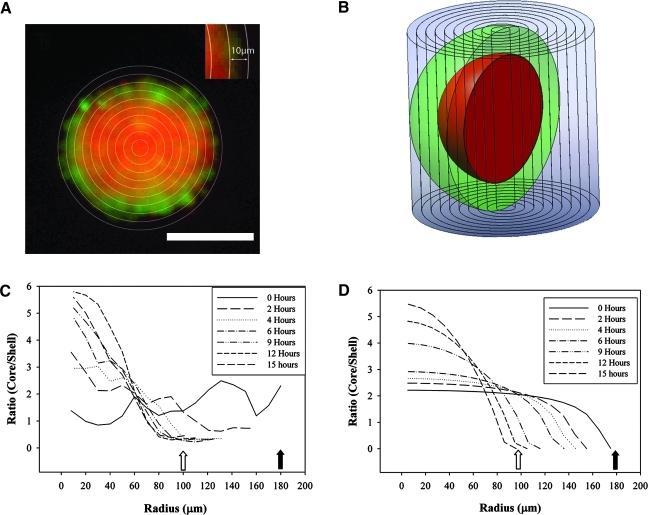
FIG. 3.

Quantification of self-sorting. For each wide-field fluorescent image, concentric 10 μm rings were drawn, and the integrated fluorescence quantified for each 10 μm shell (inset). Shown is a fluorescent image of a 1:1 mix of NHFs (red) and H35s (green) after 6 h of self-assembly (A). Each 10 μm shell is a hollow cylinder through the spheroid as diagrammed (B). The center of the spheroid is a cylinder and not a hollow cylinder. The ratio of red to green fluorescence was computed for each cylinder of a 15 h time series of fluorescent images of a 1:1 mix of NHFs and H35s. Starting x, y radii of 181 μm (filled arrow) and z radius of 30 μm changed to an x, y radii of 101 μm (open arrow) and z radius of 95 μm after 15 h. Red-to-green ratio of each cylinder is plotted as a function of radial position (x, y) in the spheroid (C). As a reference, we calculated the expected red-to-green ratios of the radial cylinders of perfectly sorted spheroids of different sizes (D). This range of sizes coincided with the changes in shape of a spheroid self-assembling from a thin layer of cells to an oblate spheroid. Using the coefficient of determination, R², self-sorting was quantified by determining a goodness-of-fit of the experimental data of a spheroid of specific shape to the theoretical perfect sort of a spheroid of identical shape. Color images available online at www.liebertonline.com/tec

The opposite state of randomness is perfect self-sorting. Although the value for randomness is the same at all locations in the spheroid and is independent of spheroid shape, the theoretical value for perfect self-sorting varies at each radial location and is dependent on spheroid shape. To calculate these values for perfect self-sorting, we designed a visual basic macro that models the theoretical volume ratios of two different cell types that have formed a perfectly self-sorted spheroid of given shape. A perfectly self-sorted spheroid has a core of one cell type (NHFs) surrounded by a shell of the other cell type (H35s). The macro calculates the total volume of the core cells and the total volume of shell cells in each 10 μm cylinder using a shell integration method, and then calculates the expected volume ratios (core cells/shell cells) for each cylinder.

During self-assembly, the shape of the spheroid undergoes significant changes. Over time, a thin layer of mono-dispersed cells settled in the bottom of each recess forms an oblate spheroid that progresses toward, but rarely reaches, a perfect sphere. We used our macro to generate theoretical curves of the perfect sort for this shape evolution over time. From our experimental measurements, the starting x, y radii of 180 μm and z height of 30 μm progresses to a final spheroid with an x, y radii of 101 μm and z height of 95 μm, which can be seen by the leftward shift of the endpoints of each curve (Fig. 3C). Corresponding experimental curves for each time point (Fig. 3D) were generated and compared with the theoretical curves. To quantify the percent sorted, we calculated the deviation of the data from the theoretical values for a perfect sort at each radial location using the coefficient of determination R², with values bounded between 0 and 1, with 1 representing a perfect sort. The R² value is significant on its own, and we convert that value into a percent sorted, or percent correlated to the theory of the perfectly sorted.

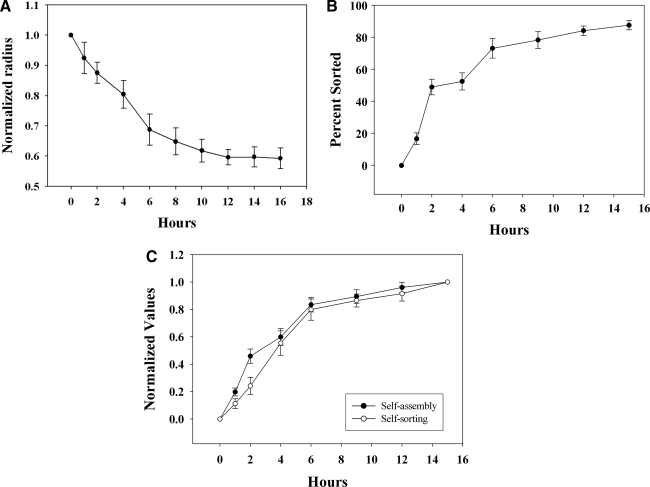
We quantified the kinetics and extent of self-sorting of a 1:1 mix of NHFs and H35s and compared them with the kinetics of self-assembly. Self-assembly was quantified by measuring the decrease in radius, which by 15 h had decreased by 0.59±0.03% of its original length (Fig. 4). At 15 h, self-sorting was 88±3%. To compare the rates of self-assembly and self-sorting, we normalized the values and calculated the initial rate (v_o), the time to reach 50% (t_1/2), and the time to reach steady state (t_ss). For self-assembly, v_o was 0.24±0.08% per minute, t_1/2 was 2.9±0.4 h, and t_ss was 8.5±0.3 h. For self-sorting, v_o was 0.36±0.06% per minute, t_1/2 was 2.7±0.3 h, and t_ss was 8.4±0.5 h. Thus, self-sorting and self-assembly in the 1:1 mix were coincident in time.

FIG. 4.

Self-assembly and self-sorting are coincident in time. Self-assembly (A) and self-sorting (B) of a 1:1 mix of NHFs and H35s were quantified. Self-assembly was quantified by measuring the change in radius (x, y plane) of the spheroid over time. Self-sorting was quantified by determining a goodness-of-fit (R²) of the experimental data of a spheroid of specific shape to the theoretical perfect sort of a spheroid of identical shape with values bounded between 0 and 1, with 1 representing a perfect sort. To directly compare their kinetics, self-assembly and self-sorting values were normalized to their starting and ending values and replotted (C). n=12 and error bars represent standard deviations.

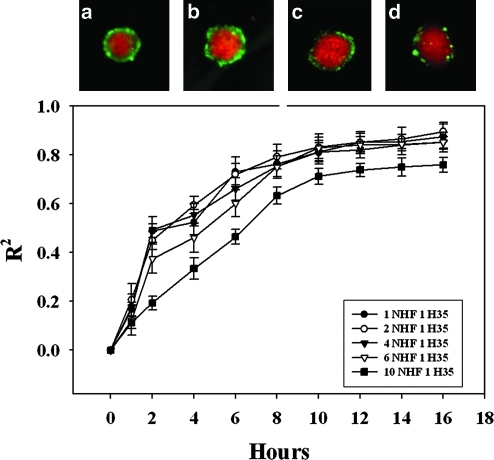
To determine whether the ratio of input cells influenced self-assembly or self-sorting, we increased the proportion of NHF (NHF: H35, 10:1, 6:1, 4:1, 2:1, 1:1) and kept the total number of cells constant. With increasing NHFs, spheroid size remained constant with a larger core of NHFs and a decreased shell of H35s (Fig. 5). As the proportion of NHFs was increased, there were no significant changes to the kinetics or extent of self-assembly (Table 1). There were no significant differences when the proportion of NHFs was reduced (1:2, 1:4), suggesting that the proportion of NHFs is not rate limiting over this range. With regards to self-sorting, as the proportion of NHFs was increased, t_ss was unaffected, but the t_1/2 was increased (6:1=3.8±0.3 h, 10:1=6.4±0.4 h), and the extent of self-sorting was decreased at the highest proportion (80±6%). The expected size of a perfectly formed H35 shell at the highest proportion of NHFs is only 4–5 μm in thickness, which may limit the accuracy of our measurement at this cell ratio.

FIG. 5.

Increasing proportions of NHFs do not change the parameters of self-sorting. Varying ratios of NHFs and H35s were seeded in agarose hydrogels, and self-assembly and self-sorting were quantified. 15 h images (a–d) of NHF:H35 (red: green) ratios of 1:1, 2:1 (a), 4:1 (b), 6:1 (c), and 10:1 (d) show that even at higher proportions of NHF:H35, self-sorting still occurred such that NHFs formed the inner core, and H35s formed the outer shell. The kinetics of self-sorting for the 10:1 spheroids was significantly different from the other ratios. The general shape of the curve is the same, but the magnitude was decreased, as seen with the initial velocities (p<0.05). All other parameters, including the final extent of self-sorting, the time to reach 50% sorted (t_1/2), and the time to reach steady state (t_ss), were not significantly different among the different ratios of NHF:H35. n=12 for all ratios, scale bar=100 μm. Color images available online at www.liebertonline.com/tec

Table 1.

Kinetics and Extent of Self-Sorting and Self-Assembly

	Self-sorting			Self-assembly
Ratio NHF:H35	vo (% min−1)	t1/2 (h)	Extent (%)	vo (% min−1)	t1/2 (h)	Extent (%)
1:10	0.4±0.5	6.5±0.5	64±6	0.1±0.2	6.4±0.4	0.71±0.04
1:06	0.4±0.3	4.5±0.7	84±4	0.1±0.3	4.1±0.4	0.65±0.05
1:04	0.4±0.2	2.9±0.2	84±4	0.3±0.4	2.9±0.3	0.63±0.07
1:02	0.4±0.1	2.7±0.3	86±3	0.4±0.2	2.3±0.4	0.59±0.05
1:01	0.4±0.1	2.7±0.3	88±3	0.3±0.1	2.9±0.4	0.59±0.03
2:01	0.4±0.3	2.5±0.4	90±4	0.4±0.2	2.5±0.4	0.57±0.03
4:01	0.4±0.3	2.7±0.2	86±5	0.5±0.3	2.6±0.3	0.57±0.04
6:01	0.4±0.5	3.8±0.3	85±5	0.5±0.3	2.9±0.5	0.54±0.03
10:01	0.4±0.3	6.4±0.6	80±6	0.4±0.3	2.7±0.5	0.55±0.04

Self sorting and self-assembly are coincident in time when spheroids are composed of between 14 and 85% normal human fibroblasts.

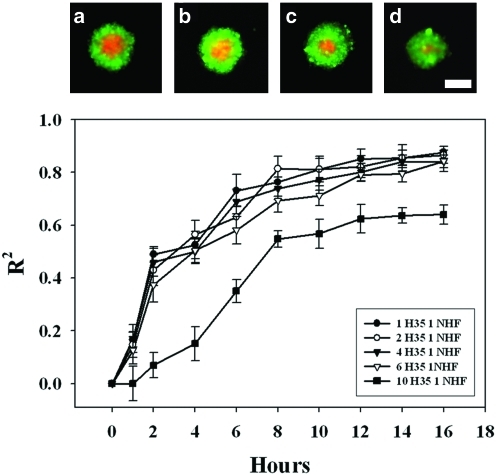
When we increased the proportion of H35s (NHF: H35, 1:2, 1:4, 1:6, and 1:10), spheroid size was constant with a decreased core of NHFs and an increased shell thickness of H35s (Fig. 6). At the highest proportions of H35s (1:6, 1:10), self-assembly was slowed and the extent of self-assembly was decreased. Likewise, self-sorting was also affected. The extent of self-sorting decreased for the highest proportion of H35s (1:10, 64±6%), and both the t_ss and the t_1/2 increased for the highest proportions of H35s (1:6, 1:10), suggesting that when self-assembly is slowed by a rate limiting number of NHFs, the extent and rate of self-sorting are also slowed. However, over a significant range of different cell ratios (NHF: H35, 1:4, 1:2, 1:1, 2:1, 4:1), the rate and extent of self-assembly and self-sorting are constant. The method in this article is the first that quantifies the kinetics and extent of self-sorting of empirical data from easy-to-obtain fluorescent images of cells as they undergo self-sorting. Previous quantitative methods have focused mainly on using mathematical models to simulate the process of self-sorting.^13–16 Our method provides a straightforward means to quantify the sorting of any pair of cell types and to obtain quantitative data useful for investigating the mechanism of self-sorting and the cellular processes that control it.

FIG. 6.

Increasing proportions of H35s reduce the rate and extent to which the cells self-sort. Images at 15 h (a–d) showed at high proportions of H35:NHF (1:10) (d), self-sorting was not as advanced as when the proportion of H35:NHF was lower. The kinetics of self-sorting for the 10:1 spheroids was significantly different from the other ratios (p<0.01), as well as for all other parameters, including the final extent of self-sorting, the initial velocity (v_o), the time to reach 50% sorted (t_1/2), and the time to reach steady state (t_ss). n=12 for all ratios, scale bar=100 μm. Color images available online at www.liebertonline.com/tec

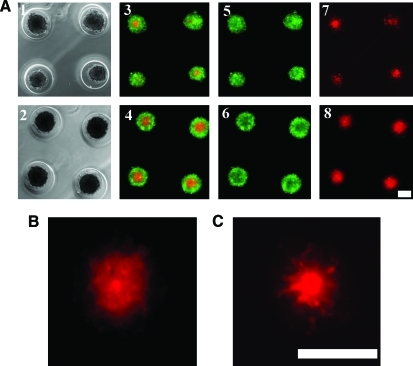
To examine more closely the situation where the proportion of NHFs is small (NHF: H35, 1:10), phase-contrast and fluorescent images were obtained and compared with the 1:4 mix (Fig. 7). There were no obvious differences in spheroid size, but the fluorescent images showed differences in the organization of the NHF core. The NHF core in the 1:4 mix was tightly packed and surrounded by an H35 shell, whereas the NHF core in the 1:10 mix was more loosely packed with extensions into the H35 shell. This suggests that when NHF numbers are high, homotypic interactions cause the formation of a tight core. However, when NHF numbers are low, there are homotypic interactions to form a core, but also increased heterotypic interactions that give rise to NHF extensions into the shell. One possible explanation is that the tension environment changes when the percentage of NHFs is low. Previous work has shown that in high-tension states, fibroblasts rely on actomyosin contraction, but in low-tension states, fibroblasts use microtubule-dependent dendritic extensions that provide mechanical structure to their environment.^19,20

FIG. 7.

Heterotypic interactions increase when the proportion of NHFs is low. Phase-contrast (A1, 2) and fluorescence images (A3–8) were obtained of NHF (red): H35 (green), 10:1 (A1, 3, 5, 7), and 4:1 (A2, 4, 6, 8) spheroids that self-assembled for 24 h. Spheroids were similar in size and the corresponding mixed red and green fluorescence, green alone, and red alone images show the spheroids have self-sorted. Higher magnification shows a tight NHF core in the 4:1 mix (B) and looser NHF core with extensions into the H35 shell for the 10:1 mix (C). Scale bars=200 μm. Color images available online at www.liebertonline.com/tec

Conclusions

In summary, we have developed an image-based method that quantifies the kinetics and extent of the self-sorting that occurs when two different cell types aggregate and self-assemble in a scaffold-free environment. The method is used with wide-field fluorescent images and can be used to quantify the initial rate (v_o), the time to reach 50% (t_1/2), and the extent of self-sorting. Studies with varying ratios of NHFs and H35s show that self-sorting proceeds with kinetics identical to self-assembly and that self-sorting proceeds with the same kinetics when the proportion of NHFs are varied over a six-fold range (14% to 85%). This method is applicable to the study of the self-sorting behavior of other pairs of cell types as well as drugs that might accelerate or inhibit self-sorting. As such, the method can help bring a quantitative understanding to the dynamics of self-sorting and the cellular mechanisms that control it. Self-sorted 3D microtissues with heterotypic cell interactions that mimic key physiological functions of native tissue and organs may have applications in drug discovery, toxicity testing, and cell therapy.

Acknowledgment

This work was funded, in part, by a grant from the Rhode Island Science and Technology Advisory Council and NIH R01EB008664-01A1.

Disclosure Statement

J.R.M. has an equity interest in MicroTissues, Inc. This relationship has been reviewed and managed by Brown University in accordance with its conflict of interest policies.