Extinction models for cancer stem cell therapy

Abstract

Cells with stem cell-like properties are now viewed as initiating and sustaining many cancers. This suggests that cancer can be cured by driving these cancer stem cells to extinction. The problem with this strategy is that ordinary stem cells are apt to be killed in the process. This paper sets bounds on the killing differential (difference between death rates of cancer stem cells and normal stem cells) that must exist for the survival of an adequate number of normal stem cells. Our main tools are birth–death Markov chains in continuous time. In this framework, we investigate the extinction times of cancer stem cells and normal stem cells. Application of extreme value theory from mathematical statistics yields an accurate asymptotic distribution and corresponding moments for both extinction times. We compare these distributions for the two cell populations as a function of the killing rates. Perhaps a more telling comparison involves the number of normal stem cells N_H at the extinction time of the cancer stem cells. Conditioning on the asymptotic time to extinction of the cancer stem cells allows us to calculate the asymptotic mean and variance of N_H. The full distribution of N_H can be retrieved by the finite Fourier transform and, in some parameter regimes, by an eigenfunction expansion. Finally, we discuss the impact of quiescence (the resting state) on stem cell dynamics. Quiescence can act as a sanctuary for cancer stem cells and imperils the proposed therapy. We approach the complication of quiescence via multitype branching process models and stochastic simulation. Improvements to the τ-leaping method of stochastic simulation make it a versatile tool in this context. We conclude that the proposed therapy must target quiescent cancer stem cells as well as actively dividing cancer stem cells. The current cancer models demonstrate the virtue of attacking the same quantitative questions from a variety of modeling, mathematical, and computational perspectives.

1. Introduction

Cancer cells with stem cell-like properties represent a novel target of therapy that may revolutionize the treatment of cancer. Mathematical models sharpen our understanding of how cancer stem cell populations evolve and suggest optimal strategies to attack them. Because they undergo repeated divisions, stem cells accumulate mutations over time. Cells derived from stem cells start down differentiation pathways that involve a limited number of cell divisions. Once they reach the end of their pathways, differentiated cells no longer accumulate the mutations caused by faulty DNA replication during cell division. Thus, many oncologists contend that only cells with stem cell-like properties can drive cancer [2,4,5,13,17,21,41,46,49,51,52,54,55,57,59,64–66,68,71]. Because normal stem cells are vital for the maintenance and repair of tissues [58], safe eradication of cancer stem cells requires selectively targeting cancer stem cells while sparing normal stem cells. In the current paper we explore in depth this hypothetical strategy and discuss its implications for the design of the next generation of cancer therapeutics. In a related paper we apply and extend some of these results to address current challenges facing medical oncologists in targeting leukemic stem cells [61].

There are controversies about what is meant by a cancer stem cell. Some of the properties we describe may hold for some malignant progenitor cells. Some authors use the term stem-like cell and tumor initiating cell when referring to cells with the above properties. We use the term stem cell in this article in that sense.

Our point of departure is the stochastic theory of linear birth–death processes. This is well trod ground mathematically [18,28,31,39,40,42,45], but the current problems raise novel issues not encountered in the standard treatments. For instance, how can one approximate the distribution of the extinction time for either population of stem cells? This brings in extreme-value theory from statistics, eigenfunction expansions, and the finite Fourier transform. We particularly fixate on three related questions: (a) What is the killing differential (difference between death rates of cancer stem cells and normal stem cells) that makes our hypothetical therapy viable? (b) What is the distribution of the number of normal stem cells at the random time of extinction of the cancer stem cells? (c) What implications does the phenomenon of quiescence have for the proposed therapy? To answer questions (a) and (b), we condition one birth–death process on the random extinction time of the other birth–death process. To answer question (c), we turn to multi-type branching processes, with stem cells of either kind divided into active and quiescent types. Because some of our answers are approximate, it helps to look at the same problem from multiple perspectives. This leads us to introduce the subject of stochastic simulation by τ-leaping [60]. Except for numerically unstable eigenfunction expansions, the different techniques discussed here reinforce one another and increase our confidence in the basic model.

Nomenclature
CSC	cancer stem cell
HSC	hematopoietic stem cell
NH	number of healthy stem cells at random time of extinc- tion of cancer stem cells
Mn	time at which n clans of stem cells go extinct
Greek symbols
β	birth rate per stem cell
δ	death rate per stem cell
ϕ	rate of quiescence per actively dividing stem cell
α	rate of awakening per quiescent stem cell
ν	death rate per quiescent stem cell
βC	birth rate per cancer stem cell
δC	death rate per cancer stem cell
βH	birth rate per healthy stem cell
δH	death rate per healthy stem cell
ϕC	rate of quiescence per actively dividing cancer stem cell
αC	rate of awakening per quiescent stem cancer cell
νC	death rate per quiescent stem cancer stem cell
ϕH	rate of quiescence per actively dividing healthy stem cell
αH	rate of awakening per quiescent healthy stem cell
νH	death rate per quiescent healthy stem cell

Before presenting an overview of the rest of the paper, let us comment on the relevance of stochastic models in general and birth–death processes in particular. In a nutshell, stochastic models are ideal for studying stem cell dynamics because key events of interest, such as extinction of a population of stem cells, are probabilistic in nature. Stem cells occupy well defined niches in the body, and it is not too hard to imagine the stem cell clans behaving independently, at least in the short run. Thus, linear birth–death processes appear to offer a good vehicle for modeling [18,28,31,39,40,42,45].

In the next section, we provide a brief overview of stem cell biology. In Section 3 we start with the distribution of the extinction time for a subcritical birth–death process starting with a single cell. This classical result is inadequate for our purposes because we typically start with many cells and must track all clans issuing from them. Using extreme-value theory, we find an accurate asymptotic distribution for the time at which all clans go extinct. This result allows us to compare probability densities for the extinction times of two coexisting populations of stem cells: normal stem cells and cancer stem cells, dying at different rates under therapy. Convergence in distribution does not imply convergence of moments, so in Section 3.2 we verify convergence of the mean and variance of the extinction times to the mean and variance of the asymptotic distribution.

In Section 3.3, we study the number of normal stem cells N_H remaining at the random time all cancer stem cells go extinct. We derive the mean and variance for N_H by conditioning on the extinction time of cancer stem cells. These quantities are heavily dependent on the selectivity of a therapy. We also compute the full distribution of N_H using eigenvalue expansions and the finite Fourier transform. In Section 3.5 we discuss the quiescent (resting) state of the stem cell, and its impact on cancer stem cell dynamics under therapies that selectively eliminate actively dividing cells. Quiescence requires new models and a different set of numerical tools. We particularly focus on simulation and τ-leaping in Section 4. Our discussion summarizes all findings and comments on the role of mathematical modeling in cancer therapy.

2. Biological background

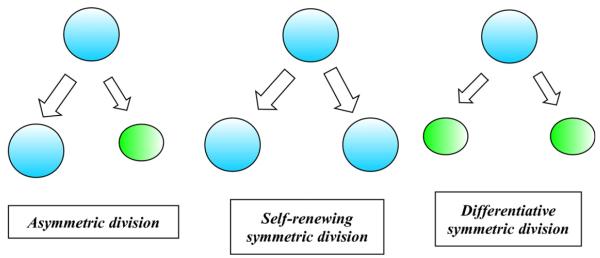
Let us begin by describing some biological features of stem cells that shape our birth–death process models. Two of the principal distinguishing features of stem cells are self-renewal and potency [48]. Self-renewal refers to the ability of a cell to indefinitely reproduce copies of itself at the same level of differentiation. In asymmetric cell division, a stem cell produces an identical daughter cell and a second more differentiated daughter cell. A stem cell can also divide symmetrically, generating two copies of itself in self-renewing symmetric division, or generating two partially differentiated daughter cells in differentiative symmetric division. Fig. 1 depicts the three modes of cell division.

Fig. 1.

Self-renewal capacity of stem cells.

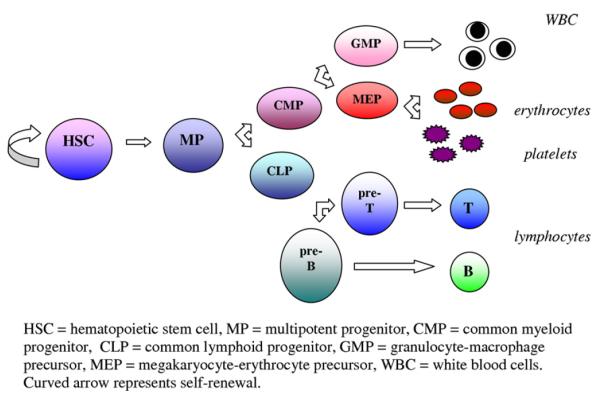
Potency is the capacity of a stem cell to replenish all of the highly specialized cells of a tissue. For instance, hematopoietic stem cells can give rise to a closely related family of cells that circulate in the blood. Fig. 2 illustrates the ability of the hematopoietic stem cell to generate multipotent progenitors, which then begin the process of differentiation, either into the myeloid lineage or the lymphoid lineage. The cells of the myeloid lineage carry oxygen to tissues (erythrocytes), help with clot formation (platelets), and fight acute infection (granulocytes), while the cells of the lymphoid lineage populate the immune system (B and T lymphocytes). It is noteworthy that progenitor cells do have the ability to self-renew, but only for a limited time. Only stem cells have the capacity for indefinite self-renewal. (see Fig. 3)

Fig. 2.

Multipotency of hematopoietic stem cells. Adapted from [7].

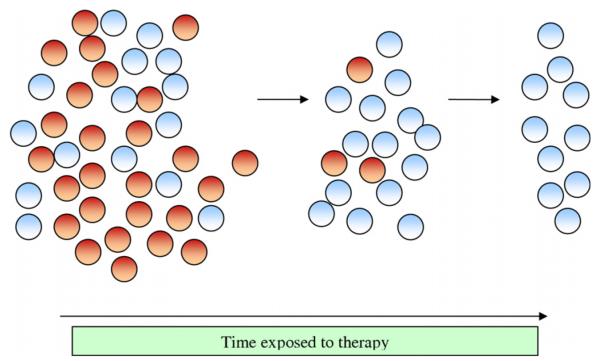
Fig. 3.

Selective destruction of cancer stem cells under targeted therapy.

Additional important features of stem cells include slow self-renewal and quiescence; these allow stem cells to maintain a long life span [48]. Different kinds of stem cells spend varying percentages of time in an actively dividing state and a quiescent (resting) state. For example, embryonic stem cells spend about 90% of the time in an actively dividing state, whereas hematopoietic stem cells are quiescent approximately 75% of the time [11]. Stem cells can enter the state of quiescence and later re-awaken.

3. Stem cell extinction times under therapy

In our simplified model of therapy, there are two populations of stem cells, normal stem cells and cancer stem cells. These coexisting populations do not interact. The cancer stem cells originate by a sequence of mutations from the normal stem cells. We take the existence of cancer stem cells as given and ignore repeated transitions to the cancer state. We model each population as a linear birth–death process X_t in continuous time t with constant birth rate β and constant death rate δ per particle. The process X_t counts the number of particles at time t.

Birth–death processes have been the subject of extensive study for many decades [18,28,31,39,40,42,45]. Some classic results that are useful to us are the mean and variance of the number of particles at time t starting with n particles at time 0 by time t

$$\mathbb{E}\left(X_t\right)=n{e}^{(\beta -\delta )t},$$ (1)

$$\mathbb{V}\mathrm{ar}\left(X_t\right)=\mathbb{V}\mathrm{ar}\left(X_0\right)e^{2(\beta -\delta )t}+\mathbb{E}\left(X_0\right)\frac{(\beta +\delta )}{(\beta -\delta )}[e^{2(\beta -\delta )t}-e^{(\beta -\delta )t}],$$ (2)

and the probability of extinction of a population starting with a single particle at time 0:

$$F\left(t\right)=\frac{\delta -\delta e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}}.$$ (3)

The major theme of this paper is the comparison of the times until extinction of the two stem cell populations. We now apply and refine the elementary results described above.

3.1. Extinction times with multiple clans

Suppose we start with n stem cells at time 0. If T_i denotes the time of extinction of the clan emanating from stem cell i, then we are interested in the time M_n = max_iT_i at which all n clans go extinct. Assuming that each clan behaves independently as a linear birth–death process with parameters β and δ, the distribution of M_n is

$$\mathrm{Pr}(M_n\le t)=F{\left(t\right)}^n,$$

where F(t) is given by Eq. (3). Fortunately, we can apply the asymptotic theory of extreme order statistics [20,36] to understand the distribution of M_n. The standard case of the theory says that there are two sequences of constants a_n and b_n such that

$$\underset{n\to \infty }{\lim }\mathrm{Pr}\left(\frac{M_n-a_n}{b_n}\le t\right)=\underset{n\to \infty }{\lim }\mathrm{Pr}(M_n\le a_n+b_{n}t)=e^{-e^{-t}}$$ (4)

for all t. The extreme value (Gumbel) distribution exp(−e^−t) has mean γ and variance π²/6, where γ ≈ 0.57722 is the Euler–Mascheroni constant. The moment generating function of the extreme value distribution can be written for argument θ as

$${\int }_{-\infty }^{\infty }{e}^{\theta x}{e}^{-x}{e}^{-e^{-x}}dx=\Gamma (1-\theta )$$ (5)

in terms of Euler’s gamma function. It is plausible that

$$\mathbb{E}\left(M_n\right)\approx a_n+\gamma b_n,\mathbb{V}\mathrm{ar}\left(M_n\right)\approx \frac{b_n^2{\pi }^2}{6},$$

and we will prove this later.

The key to finding the sequences a_n and b_n is to identify a function R(t) such that

$$\underset{t\to \infty }{\lim }\frac{1-F[t+xR(t\left)\right]}{1-F\left(t\right)}=e^{-x}$$ (6)

for all x. (See Theorem 14 of [20].) Once we have R(t) in hand, we determine a_n and b_n via the equations $1-F\left(a_n\right)=\frac{1}{n}$ and b_n = R(a_n). In the current situation, R(t) is the constant (δ — β)⁻¹. The equation

$$\frac{1}{n}=1-F\left(a_n\right)=1-\frac{\delta -\delta e^{(\beta -\delta )a_n}}{\delta -\beta e^{(\beta -\delta )a_n}}=\frac{\delta -\beta }{\delta e^{(\beta -\delta )a_n}-\beta }$$

entails

$$\frac{n(\delta -\beta )+\beta }{\delta }=e^{(\beta -\delta )a_n},$$

which in turn implies

$$a_n=\frac{1}{\delta -\beta }\left[\ln n+\ln \left(\frac{\delta -\beta +\frac{\beta }{n}}{\delta }\right)\right].$$ (7)

It follows that $\mathbb{E}\left(M_n\right)$ grows at the slow rate ln n and $\mathbb{V}\mathrm{ar}\left(M_n\right)$ tends to the constant π²/[6(δ − β)²].

These conclusions are all predicated on satisfaction of condition (6). In view of Eq. (3), we have

$$\underset{t\to \infty }{\lim }\frac{1-F[t+xR(t\left)\right]}{1-F\left(t\right)}=\underset{t\to \infty }{\lim }\frac{1-\frac{\delta e^{(\delta -\beta )t+x}-\delta }{\delta e^{(\delta -\beta )t+x}-\beta }}{1-\frac{\delta e^{(\delta -\beta )t}-\delta }{\delta e^{(\delta -\beta )t}-\beta }}=\underset{t\to \infty }{\lim }\frac{\delta e^{(\delta -\beta )t}-\beta }{\delta e^{(\delta -\beta )t+x}-\beta }=e^{-x}.$$

This proves condition (6) and validates all of the conclusions drawn from it.

We can also solve for the time t that renders the extinction probability F(t)ⁿ equal to a given number p > 0. Since

$$\underset{n\to \infty }{\lim }\frac{1-p^{\frac{1}{n}}}{\frac{1}{n}}=-\frac{d}{dx}\left(p^x\right){\mid }_{x=0}=-\ln p,$$

we have

$$\ln \left[n(1-p^{\frac{1}{n}})\right]\approx \ln (-\ln p).$$

In view of the identity (3), the solution of the equation p = F(t)ⁿ therefore satisfies

$$\begin{array}{cc}\hfill t=& -\frac{1}{\delta -\beta }\ln \left(\frac{\delta -\delta p^{1∕n}}{\delta -\beta p^{1∕n}}\right)\hfill \\ \hfill =& \frac{1}{\delta -\beta }\left\{\ln \left(\delta -\beta p^{\frac{1}{n}}\right)-\ln \delta +\ln n-\ln \left[n(1-p^{\frac{1}{n}})\right]\right\}\hfill \\ \hfill \approx & a_n-\frac{1}{\delta -\beta }\ln (-\ln p).\hfill \end{array}$$ (8)

This is precisely the approximation the extreme value theory entails.

As an illustration of our results, consider an advanced form of leukemia. We now have separate birth rates, death rates, and initial numbers of stem cells, which we subscript by the index H for healthy and C for cancerous, corresponding to the normal hematopoietic stem cell (HSC) and cancer stem cell (CSC) populations. Total initial hematopoietic stem cell population size (22,000) is based on numbers extrapolated from murine and feline data [1]. Because recent evidence suggests that HSCs divide approximately once every 42 weeks [1], we accordingly chose our birth rates β_H = β_C = 0.02 week⁻¹.

The size of the CSC compartment can be highly variable across individuals and within an individual over time. For more aggressive malignancies, such as melanoma, higher proportions of cell functionally defined as CSCs are observed [56]. We begin with a large ratio of cancer stem cells to healthy stem cells to model an advanced phase of disease.

Birth rates of CSCs, β_C, may vary for different tumors and may, in fact, vary over the course of disease [6,38]. In our models, we use the birth rate of normal hematopoietic stem cells [1] as a starting point. We make the assumption that birth rates are identical for healthy stem cells and leukemic stem cells. Although this assumption may not be realistic, we emphasize that our results are more dependent on the difference between birth and death rates than on the rates themselves.

Our death rates (δ_H and δ_C) reflect the range of rates and selectivities that might occur under a wide group of therapeutic agents. As new therapies targeting stem cells emerge, new death rates will be observed. Unfortunately, we do not have an estimate of killing rates of either healthy stem cells or cancer stem cells under therapy. These have not been observed. However, we do have an estimate of the normal death rate of healthy stem cells without therapy ~0.002 per cell per day [14,50]. This death rate was estimated for hematopoietic stem cells based on response to imatinib, which probably does not target leukemic stem cells. We hypothesize that the death rate of both CSCs and HSCs will be higher under therapy that is designed to target cancer stem cells, and our chosen death rate parameters reflect this assumption. Examples of therapies that have been shown to be effective in selectively targeting cancer stem cells in chronic leukemia include parthenolide in chronic myelogenous leukemia [37]. Antigen expression patterns, and hence susceptibility to therapy, may vary from patient to patient [19,37].

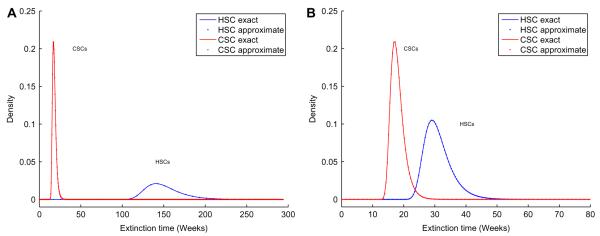
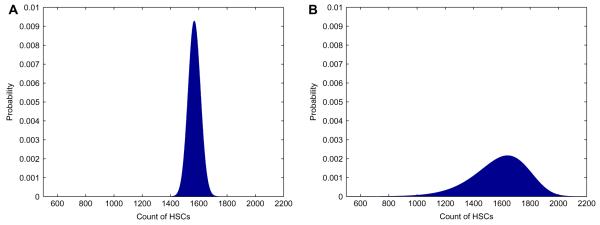
Suppose for the sake of argument, we start with n_H = 4,400 and n_C = 17,600 and take δ_H = 0.08 week⁻¹ and δ_C = 0.59 week⁻¹. Our asymptotic results allow us to examine the probability densities of the extinction times of both CSCs and HSCs. The top panel of Fig. 4 shows that the asymptotic probability density of the extinction time of CSCs has a narrow spike around 18 weeks, whereas that of HSCs has a narrow spike around 139 weeks. We observe good agreement between results obtained using the Gumbel approximation (dotted lines) and exact results (solid lines) obtained by differentiating the distribution function. There is very little overlap between the two extinction-time densities. This suggests that for the given parameter values, most likely the CSCs would be eradicated long before the HSCs become extinct. The appearance of these probability density curves confirms a wide therapeutic window of opportunity. However, when we take the death rates δ_H = 0.31 week⁻¹ and δ_C = 0.59 week⁻¹, the densities displayed in the bottom panel of Fig. 4) dangerously overlap.

Fig. 4.

Extinction time densities for CSCs and HSCs. Top: δ_C = 0.59 week⁻¹, δ_H = 0.08 week⁻¹. Bottom: δ_C = 0.59 week⁻¹, δ_C = 0.31 week⁻¹.

The weak ln n dependence of the sequence a_n on n suggests the possibility of safely eradicating CSCs even when they sharply out-number HSCs. In this regard, it is helpful to define the selectivity σ of a therapy as the ratio

$$\sigma =\frac{{\delta }_C-{\beta }_C}{{\delta }_H-{\beta }_H}$$

of the differences between death and birth rates for CSCs versus HSCs. For safe eradication one needs σ to be substantially greater than ln n_C/ln n_H.

Passing back and forth between the formulas (3) and (9) allows us to plot the extinction probability for the HSCs at the time when the extinction probability for the CSCs reaches a predetermined level p. The survival probability of the HSC population increases fairly quickly as the difference between d_H and d_C grows. For example, take δH = 0.08 week⁻¹ and β_C = β_H = 0.02 week⁻¹. To be 80% certain that at least one ordinary stem cell remains when we are 99.9% certain no CSC remains, δ_C must be 0.15 week⁻¹ or larger, corresponding to s ≥ 2.2.

3.2. Convergence of extinction time moments

The convergence in distribution displayed in Eq. (4) does not necessarily entail convergence of moments. We address this delicate question first for means. Our point of departure is the right-tail integral

$$\mathbb{E}\left(M_n\right)={\int }_0^{\infty }\mathrm{Pr}(M_n>t)dt={\int }_0^{\infty }\left\{1-{\left[\frac{\delta -\delta e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}}\right]}^n\right\}dt$$

for the mean of M_n. To gain insight into how this integral depends on n, we make the change of variables

$$s=\frac{\delta -\delta e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}},t=-\frac{1}{(\delta -\beta )}\ln \frac{\delta -\delta s}{\delta -\beta s}.$$ (9)

The change of variables implies the change in differentials

$$dt=\left[\frac{1}{(\delta -\beta )(1-s)}-\frac{\beta }{(\delta -\beta )(\delta -\beta s)}\right]ds$$ (10)

and the range of integration (0, 1) for s. Since

$$\frac{1-s^n}{1-s}=(1+s+\cdots +s^{n-1}),$$

it follows that

$$\begin{array}{cc}\hfill \mathbb{E}\left(M_n\right)=& {\int }_0^1(1-s^n)\left[\frac{1}{(\delta -\beta )(1-s)}-\frac{\beta }{(\delta -\beta )(\delta -\beta s)}\right]ds\hfill \\ \hfill =& \frac{1}{\delta -\beta }\left[1+\frac{1}{2}+\cdots +\frac{1}{n}\right]-{\int }_0^1\frac{(1-s^n)\beta }{(\delta -\beta )(\delta -\beta s)}ds\hfill \\ \hfill =& \frac{1}{\delta -\beta }[\ln n+\gamma ]+\frac{1}{\delta -\beta }\ln \left(\frac{\delta -\beta }{\delta }\right)+O\left(\frac{1}{n}\right),\hfill \end{array}$$ (11)

where γ enters the picture through the well-known expansion

$$H_n=\ln n+\gamma +\frac{1}{2n}+O\left(\frac{1}{n^2}\right)$$

of the harmonic sum $H_n=1+\frac{1}{2}+\cdots +\frac{1}{n}$ [27], and

$$\frac{\beta }{\delta -\beta }{\int }_0^1\frac{s^n}{\delta -\beta s}ds=O\left(\frac{1}{n}\right)$$

by virtue of the boundedness of 1/(δ − βs) on [0, 1]. Our formula for $\mathbb{E}\left(M_n\right)$ confirms the limit

$$\underset{n\to \infty }{\lim }\mathbb{E}\left(\frac{M_n-a_n}{b_n}\right)=\gamma .$$

We now validate a similar limit for the variance of the extinction times. Expressing the second moment as an integral of the right-tail probability and taking into account Eqs. (9) and (10) produce

$$\begin{array}{cc}\hfill \mathbb{E}\left(M_n^2\right)=& 2{\int }_0^{\infty }t\mathrm{Pr}(M_n>t)dt=-\frac{2}{{(\delta -\beta )}^2}{\int }_0^1\ln \left(\frac{1-s}{1-\frac{\beta }{\delta }s}\right)(1-s^n)\hfill \\ \hfill & \times \left[\frac{1}{(1-s)}-\frac{\beta }{(\delta -\beta s)}\right]ds.\hfill \end{array}$$ (12)

We will attack the integral (12) in piecemeal fashion. For instance,

$$\begin{array}{cc}\hfill {\int }_0^1(1-s^n)\frac{\ln (1-s)}{1-s}ds=& {\int }_0^1\ln (1-s)\sum _{k=0}^{n-1}{s}^{k}ds\hfill \\ \hfill =& -{\int }_0^1\sum _{j=1}^{\infty }\frac{s^j}{j}\sum _{k=0}^{n-1}{s}^{k}ds\hfill \\ \hfill =& -\sum _{j=1}^{\infty }\sum _{k=0}^{n-1}\frac{1}{j(j+k+1)}\hfill \\ \hfill =& -\sum _{j=1}^{\infty }\sum _{k=0}^{n-1}\left(\frac{1}{j}-\frac{1}{j+k+1}\right)\frac{1}{k+1}\hfill \\ \hfill =& -\sum _{k=0}^{n-1}\frac{1}{k+1}\left(1+\frac{1}{2}+\cdots +\frac{1}{k+1}\right)\hfill \\ \hfill =& -\sum _{k=1}^n\frac{H_k}{k}.\hfill \end{array}$$

Fortunately, the two further helpful identities

$$\sum _{k=1}^n\frac{H_k}{k}=\frac{1}{2}\left(\sum _{k=1}^n\frac{1}{k^2}+H_n^2\right),\sum _{k=1}^{\infty }\frac{1}{k^2}=\frac{{\pi }^2}{6}$$

are true [27]. It follows that

$${\int }_0^1(1-s^n)\frac{\ln (1-s)}{(1-s)}ds=-\frac{1}{2}\left[\frac{{\pi }^2}{6}+{(\ln n+\gamma )}^2\right]+O\left(\frac{\ln n}{n}\right).$$

Another piece of the integral (12) is amenable to the fundamental theorem of calculus; namely,

$$\beta {\int }_0^1\frac{\ln (1-\frac{\beta }{\delta }s)}{\delta -\beta s}ds=-\frac{1}{2}{\phantom{\mid }{\left[\ln \left(1-\frac{\beta }{\delta }s\right)\right]}^2\mid }_0^1=-\frac{1}{2}{\left[\ln \left(1-\frac{\beta }{\delta }\right)\right]}^2.$$

The integral

$${\int }_0^1\beta s^n\frac{\ln (1-\frac{\beta }{\delta }s)}{\delta -\beta s}ds=O\left(\frac{1}{n}\right)$$

because (δ − βs)⁻¹ and ln (δ − βs) are bounded on [0, 1]. Likewise,

$${\int }_0^1\beta s^n\frac{\ln (1-s)}{\delta -\beta s}ds=O\left(\frac{\ln n}{n}\right)$$

because

$$\begin{array}{cc}\hfill {\int }_0^1{s}^n\ln (1-s)ds=& -{\int }_0^1\sum _{j=1}^{\infty }\frac{1}{j}{s}^{n+j}ds=-\sum _{j=1}^{\infty }\frac{1}{j(n+j+1)}\hfill \\ \hfill =& O\left(\frac{\ln n}{n}\right).\hfill \end{array}$$

Two other parts of the integral partially cancel. The first part amounts to

$$\begin{array}{cc}\hfill -{\int }_0^1\ln \left(1-\frac{\beta }{\delta }s\right)\frac{1-s^n}{1-s}ds=& {\int }_0^1\sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{s^j}{j}\sum _{k=0}^{n-1}{s}^{k}ds\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\sum _{k=0}^{n-1}\frac{1}{j+k+1}\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}(H_{n+j}-H_j).\hfill \end{array}$$

The second part is

$$\begin{array}{cc}\hfill -{\int }_0^1\beta \ln (1-s)\frac{1}{\delta -\beta s}ds=& \frac{\beta }{\delta }{\int }_0^1\sum _{k=1}^{\infty }\frac{s^k}{k}\sum _{j=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j{s}^{j}ds\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\sum _{k=1}^{\infty }\frac{1}{k(j+k)}\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\sum _{k=1}^{\infty }\left(\frac{1}{k}-\frac{1}{j+k}\right)\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}{H}_j.\hfill \end{array}$$

The sum of these two parts is

$$\begin{array}{cc}\hfill \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}{H}_{n+j}=& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\left[\ln (n+j)+\gamma +O\left(\frac{1}{n}\right)\right]\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\ln \left(\frac{n+j}{n}\right)+\sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}(\ln n+\gamma )\hfill \\ \hfill & +O\left(\frac{1}{n}\right)\hfill \\ \hfill =& \sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\ln \left(1+\frac{j}{n}\right)-(\ln n+\gamma )\ln \left(1-\frac{\beta }{\delta }\right)\hfill \\ \hfill & O\left(\frac{1}{n}\right)\hfill \end{array}$$

Because ln (1 + x) ≤ x for x > 0, it follows that

$$\sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j\frac{1}{j}\ln \left(1+\frac{j}{n}\right)\le \frac{1}{n}\sum _{j=1}^{\infty }{\left(\frac{\beta }{\delta }\right)}^j=O\left(\frac{1}{n}\right).$$

Putting together the various parts of the integral (12) and multiplying by $-\frac{2}{{(\delta -\beta )}^2}$ give

$$\mathbb{E}\left(M_n^2\right)=\frac{1}{{(\delta -\beta )}^2}\left\{\frac{{\pi }^2}{6}+{\left[\ln n+\gamma +\ln \left(\frac{\delta -\beta }{\delta }\right)\right]}^2\right\}+O\left(\frac{\ln n}{n}\right).$$

In view of the asymptotic expression (11) for the mean, we have

$$\mathbb{V}\mathrm{ar}\left(\frac{M_n-a_n}{b_n}\right)=\frac{{\pi }^2}{6}+O\left(\frac{\ln n}{n}\right),$$

which implies the convergence of the variance of $b_n^{-1}(M_n-a_n)$ to the variance of the Gumbel distribution.

3.3. How many HSCs remain when CSCs go extinct?

The single most important measure of success in therapy is the count of HSCs when the cancer stem cells go extinct. This is a difficult issue to attack mathematically because one must take a snapshot of the HSC population at a random stopping time. Let N_H be the number of HSCs at the random time D_C when the cancer stem cells are eradicated. This notation is consistent with the convention in this section of subscripting all quantities by either H and C to indicate the HSC population and the CSC population, respectively. To make progress, we make the simplifying assumption that the random variable

$$\frac{M_{n_C}-a_{n_C}}{b_{n_C}}$$

conforms exactly to the extreme value distribution. To recover the mean and variance of N_H, we condition on D_C in the formulas

$$\mathbb{E}\left(N_H\right)=\mathbb{E}\left[\mathbb{E}\right(N_H\mid D_C\left)\right],$$ (13)

$$\mathbb{V}\mathrm{ar}\left(N_H\right)=\mathbb{E}\left[\mathbb{V}\mathrm{ar}\right(N_H\mid D_C\left)\right]+\mathbb{V}\mathrm{ar}\left[\mathbb{E}\right(N_H\mid D_C\left)\right].$$ (14)

Consider first the mean of N_H. According to Eq. (1), we have

$$\mathbb{E}(N_H\mid D_C)=n_H{e}^{({\beta }_H-{\delta }_H)D_C}.$$

Thus, Eq. (13) shows that evaluation of $\mathbb{E}\left(N_H\right)$ boils down to evaluation of the moment generating function of D_C. In view of Eq. (5), D_C has moment generating function

$$\mathbb{E}\left(e^{\theta M_{n_C}}\right)=e^{a_{n_C}\theta }\Gamma (1-\theta b_{n_C}).$$ (15)

A brief calculation now gives

$$\mathbb{E}\left(N_H\right)=n_H\Gamma \left(1+\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right){\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{-\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}.$$

To calculate the variance of N_H from the decomposition (14), we note that Eq. (2) implies

$$\mathbb{V}\mathrm{ar}(N_H\mid D_C)=n_H\frac{({\beta }_H+{\delta }_H)}{({\beta }_H-{\delta }_H)}[e^{2({\beta }_H-{\delta }_H)D_C}-e^{({\beta }_H-{\delta }_H)D_C}].$$

Invoking the generating function (15) therefore yields

$$\begin{array}{cc}\hfill \mathbb{E}\left[\mathbb{V}\mathrm{ar}\right(N_H\mid D_C\left)\right]=& n_H\frac{({\beta }_H+{\delta }_H)}{({\beta }_H-{\delta }^H)}\Gamma \left(1+2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right)\hfill \\ \hfill & \times {\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{-2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}-n_H\frac{({\beta }_H+{\delta }_H)}{({\beta }_H-{\delta }_H)}\Gamma \left(1+\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right)\hfill \\ \hfill & \times {\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}.\hfill \end{array}$$ (16)

We handle the second term on the right of Eq. (14) by first noting that $\mathbb{E}\left[\mathbb{E}\right(N_H\mid D_C\left)\right]=\mathbb{E}\left(N_H\right)$. We combine this with

$$\begin{array}{cc}\hfill \mathbb{E}\left[\mathbb{E}{(N_H\mid D_C)}^2\right]=& n_H^2\mathbb{E}\left[e^{2({\beta }_H-{\delta }_H)D_C}\right)]\hfill \\ \hfill =& n_H^2\Gamma \left(1+2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right){\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{-2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}\hfill \end{array}$$

to get

$$\begin{array}{cc}\hfill \mathbb{V}\mathrm{ar}\left[\mathbb{E}\right(N_H\mid D_C\left)\right]=& n_H^2\Gamma \left(1+2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right){\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{-2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}\hfill \\ \hfill & -n_H^2\Gamma {\left(1+\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}\right)}^2{\left[\frac{n_C({\delta }_C-{\beta }_C)+{\beta }_C}{{\delta }_C}\right]}^{-2\frac{{\delta }_H-{\beta }_H}{{\delta }_C-{\beta }_C}}.\hfill \end{array}$$ (17)

Eqs. (14), (16), and (17) fully determine $\mathbb{V}\mathrm{ar}\left(N_H\right)$.

Let us define the killing efficiency κ of a therapy as the ratio of the death rate to birth rate of CSCs, κ = δ_C/β_C. We can then formulate the mean number of HSCs present at the time when all the CSCs are eradicated as a function of the selectivity σ of a therapy and the killing efficiency, according to the formula

$$\mathbb{E}\left(N_H\right)\approx n_H\Gamma (1+{\sigma }^{-1}){\left[n_C\right(1-{\kappa }^{-1})+{\kappa }^{-1}]}^{-\frac{1}{\sigma }}.$$ (18)

The variance can also be formulated as a function of κ and σ. Fig. 5 plots the average $\mathbb{E}\left(N_H\right)$ as a function of σ and κ. A higher selectivity entails a higher average number of HSCs at the time of eradication of the CSCs. For example, starting with n_H = 4,400 and n_C = 17,600, with a killing efficiency κ = 25, and a selectivity σ = 10 or greater, we expect 1,581 HSCs to survive. It is noteworthy that the selectivity required to ensure that, on average, 1,000 HSCs remain at the time of CSC extinction (σ = 10) is much higher than the selectivity required to be 80% sure that at least one HSC survives (σ = 2.2). Values of the average $\mathbb{E}\left(N_H\right)$ are heavily dominated by σ. Examination of Eq. (18) reveals that κ is less important in determining the average $\mathbb{E}\left(N_H\right)$. In contrast, κ does play a large role in determining the average time to eradication of the CSCs. For instance with σ held constant at 10, the extinction time is approximately 4 years when κ = 3 and 18 weeks when κ = 25. The corresponding values for $\mathbb{E}\left(N_H\right)$ are 1,640 and 1,581.

Fig. 5.

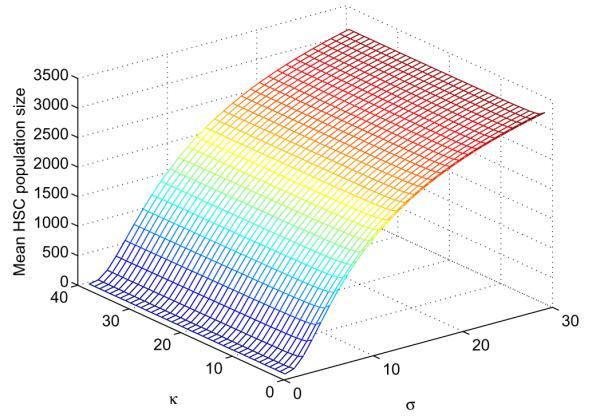
Dependence of $\mathbb{E}\left(N_H\right)$ on selectivity σ and killing efficiency κ of a therapy.

3.4. Eigenfunction expansions and finite Fourier transforms

Previous sections have dealt with means and variances. Finding the full distribution of the number of HSCs at the time of extinction of the CSCs requires new techniques. We explored two possibilities, eigenfunction expansions [39,35] and Fourier analysis [32,44,45]. Despite their elegance, eigenfunction expansions turn out to be far less reliable than approximations based on the finite Fourier transform. Indeed, the eigenfunction approximation to the distribution of N_H suffers serious roundoff errors when N_H is supported on a large number of points. The terms in the series are large and tend to alternate in sign. Fourier analysis offers a more numerically stable method of computing the distribution of N_H. The Fourier approach applies generically to any probability generating function $P\left(s\right)={\sum }_{j=0}^{\infty }{p}_j{s}^j$ [32,44]. To extract the coefficients of P(s), extend it to the boundary of the unit circle in the complex plane via the equation $P\left(e^{2\pi it}\right)={\sum }_{j=0}^{\infty }{p}_j{e}^{2\pi ijt}$, where $i=\sqrt{-1}$. This creates a periodic function in t whose kth Fourier coefficient p_k can be recovered via the finite Riemann sum

$$p_k={\int }_0^{1}P\left(e^{2\pi it}\right)e^{-2\pi ikt}dt\approx \frac{1}{m}\sum _{j=0}^{m-1}P\left(e^{2\pi ij∕m}\right)e^{-2\pi ikj∕m}.$$

In practice, one evaluates this finite Fourier transform via the fast Fourier transform algorithm for some large power m of 2. For sufficiently large m, all of the coefficients p₀, … , p_m−1 can be computed accurately. Accuracy can be checked by comparing the numerically computed mean and variance of P(s) with its theoretical mean and variance.

To apply the Fourier method to find the distribution of N_H, let G_H(s, t) and G_C(s, t) be the probability generating functions of the number of HSCs and CSCs at the fixed time t. Thus, the generating function of the number of normal stem cells at the random time when cancer stem cells are eradicated is given by

$$G_{N_H}\left(s\right)={\int }_0^{\infty }{G}_H(s,t)\frac{\partial }{\partial t}{G}_C(0,t)dt,$$

which can be numerically evaluated for any s, including s on the boundary of the unit circle. With this generating function at our disposal, we can retrieve the distribution of N_H by the fast Fourier transform as just explained.

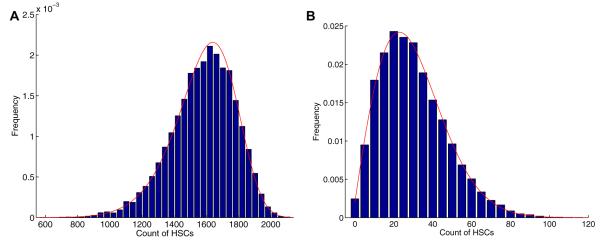
Fig. 6 shows the distribution of normal cells at the random time when cancer stem cells become extinct calculated by fast Fourier transform. The numerical means and variances from this distribution match those implied by formulas (13) and (14). The large spike at zero is caused by the amount of times the healthy population reaches extinction. Figs. 7 and 8 display the distributions of normal stem cells at fixed and random times under two typical parameter settings. As expected the distribution at a fixed time of CSC extinction is less variable than that generated with a random time. For the parameters chosen in Fig. 7, there appears to be an adequate number of HSCs at the time of CSC extinction, suggesting a safe therapy. By contrast, when we increase the death rate of HSCs (Fig. 8), we see that there is some chance that the HSCs will be wiped out by the time all CSCs have been eradicated.

Fig. 6.

The distribution of normal stem cells when cancer stem cells are eradicated based on the finite Fourier transform. The parameter setting is n_H = 4,400, β_H = 0.024 week⁻¹, δ_H = 0.03 week⁻¹, n_C = 17,600, β_C = 0.024 week⁻¹, and δ_C = 0.036 week⁻¹.

Fig. 7.

Distribution of HSCs when CSCs become extinct, assuming death rate of HSCs δ_H = 0.08 week⁻¹. Initial clan sizes are n_H = 4,400 and n_C = 17,600, birth rates are β_H = β_C = 0.024 week⁻¹, and death rate of CSCs δ_C = 0.59 week⁻¹. Top: Distribution at the (fixed) mean cancer extinction time 18 weeks. Bottom: Distribution at the (random) cancer extinction time.

Fig. 8.

Distribution of HSCs when CSCs become extinct, assuming death rate of HSCs δ_H = 0.31 week⁻¹. Initial clan sizes are n_H = 4,400 and n_C = 17,600, birth rates are β_H = β_C = 0.024 week⁻¹, and death rate of CSCs δ_C = 0.59 week⁻¹. Top: Distribution at the (fixed) mean cancer extinction time 18 weeks. Bottom: Distribution at the (random) cancer extinction time.

3.5. Therapy in the presence of quiescence

In the reversible state of quiescence, a stem cell does not divide. Here we consider therapies that target actively dividing stem cells and largely spare quiescent stem cells. In this case, we predict that the active cancer stem cell population will be eradicated first and leave behind a quiescent cancer stem cell population, which on awakening causes recurrence of the cancer. We now present a model that validates this intuition. The model therefore highlights the danger in targeting only active cancer stem cells. For the sake of simplicity, we ignore the slow flow of active stem cells into the resting state of quiescence. We will repair this defect in Section 3.6.

Let ν be the death rate per quiescent cancer stem cell, α be rate of awakening of a quiescent cancer stem cell, and G(t) be the probability that a quiescent cancer stem cell and all of its descendants have gone extinct by time t. As in the previous model, β and δ are the birth and death rates, respectively, per cell for the actively dividing cancer stem cells. We begin by deriving an expression for G(t). Considering the short time interval (0, s), it is clear that

$$G(t+s)=[1-(\alpha +\nu \left)s\right]G\left(t\right)+\nu s+\alpha sF\left(t\right)+o\left(s\right),$$

where F(t) is the extinction probability by time t starting with a single active stem cell. Sending s to 0 leads to the differential equation

$$\frac{d}{dt}G\left(t\right)=-(\alpha +\nu )G\left(t\right)+\nu +\alpha F\left(t\right).$$

with solution

$$G\left(t\right)=\frac{\nu }{\alpha +\nu }\left[1-e^{-(\alpha +\nu )t}\right]+\alpha e^{-(\alpha +\nu )t}{\int }_0^t{e}^{(\alpha +\nu )s}F\left(s\right)ds.$$

Given the identity

$$\alpha e^{-(\alpha +\nu )t}{\int }_0^t{e}^{(\alpha +\nu )s}ds=\frac{\alpha e^{-(\alpha +\nu )t}}{\alpha +\nu }\left[e^{(\alpha +\nu )t}-1\right]=\frac{\alpha }{\alpha +\nu }\left[1-e^{-(\alpha +\nu )t}\right],$$

it follows that

$$G\left(t\right)=1-e^{-(\alpha +\nu )t}+\alpha e^{-(\alpha +\nu )t}{\int }_0^t{e}^{(\alpha +\nu )s}\left[F\right(s)-1]ds.$$ (19)

In view of Eq. (3), we have

$$1-F\left(t\right)=\frac{(\delta -\beta )e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}}.$$

Substituting this in Eq. (19) produces

$$\begin{array}{cc}\hfill 1-G\left(t\right)=& e^{-(\alpha +\nu )t}+\alpha e^{-(\alpha +\nu )t}{\int }_0^t{e}^{(\alpha +\nu )s}[1-F(s\left)\right]ds\hfill \\ \hfill =& e^{-(\alpha +\nu )t}\left[1+\alpha {\int }_0^t{e}^{(\alpha +\nu )s}\frac{(\delta -\beta )e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}}ds\right].\hfill \end{array}$$

Further progress can be made by exploiting the expansion

$$\frac{1}{1-\frac{\beta }{\delta }{e}^{(\beta -\delta )s}}=\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k{e}^{k(\beta -\delta )s}$$

in the integral

$$\begin{array}{cc}\hfill {\int }_0^t{e}^{(\alpha +\nu )s}\frac{(\delta -\beta )e^{(\beta -\delta )t}}{\delta -\beta e^{(\beta -\delta )t}}ds=& \frac{(\delta -\beta )}{\delta }{\int }_0^t\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k{e}^{[\alpha +\nu +(k+1\left)\right(\beta -\delta \left)\right]s}ds\hfill \\ \hfill =& \frac{(\delta -\beta )}{\delta }\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k\frac{e^{[\alpha +\nu +(k+1\left)\right(\beta -\delta \left)\right]t}-1}{\alpha +\nu +(k+1)(\beta -\delta )}.\hfill \end{array}$$

In conclusion, we find that

$$\begin{array}{c}\hfill 1-G\left(t\right)=e^{-(\alpha +\nu )t}[1-\frac{\alpha (\delta -\beta )}{\delta }\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k\frac{1}{\alpha +\nu +(k+1)(\beta -\delta )}\phantom{]}\hfill \\ \hfill +\phantom{[}\frac{\alpha (\delta -\beta )}{\delta }\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k\frac{e^{[\alpha +\nu +(k+1\left)\right(\beta -\delta \left)\right]t}}{\alpha +\nu +(k+1)(\beta -\delta )}].\hfill \end{array}$$ (20)

The explicit expression (20) allows us to determine the fate of a population of m cancer stem cells in quiescence. Consistent with our assumption that the killing rate δ of active cancer stem cells is much higher than the killing rate ν of quiescent cancer stem cells, we take α + ν < β − δ. In this regime, formula (20) can be replaced by the approximations

$$1-G\left(t\right)=e^{-(\alpha +\nu )t}[1+c+o(1\left)\right],$$ (21)

where c is the positive constant

$$c=-\frac{\alpha (\delta -\beta )}{\delta }\sum _{k=0}^{\infty }{\left(\frac{\beta }{\delta }\right)}^k\frac{1}{\alpha +\nu +(k+1)(\beta -\delta )}.$$

Note that the error term o(1) in (21) tends to 0 exponentially fast as t tends to ∞.

The extinction time for the last surviving clan issuing from the m initial quiescent stem cells has distribution function G_m(t)= G(t)^m. The asymptotic theory of extreme order statistics also applies to G_m(t). Once again we proceed by identifying a constant R such that

$$\underset{t\to \infty }{\lim }\frac{1-G(t+xR)}{1-G\left(t\right)}=e^{-x}$$

for all x. In light of the approximation (21), we have

$$\frac{1-G(t+xR)}{1-G\left(t\right)}=\frac{e^{-(\alpha +\nu )(t+xR)}[1+c+o(1\left)\right]}{e^{-(\alpha +\nu )t}[1+c+o(1\left)\right]}=e^{-(\alpha +\nu )xR}[1+o(1\left)\right]$$

and this ratio approaches e^−x if and only if R = (α + ν)⁻¹. Therefore, the previously cited extreme value theorem implies that

$$\underset{m\to \infty }{\lim }{G}_m(a_m+b_{m}t)=e^{-e^{-t}}$$

for sequences a_m and b_m defined by

$$\frac{1}{m}=1-G\left(a_m\right)=e^{-(\alpha +\nu )a_m}[1+c+o(1\left)\right]$$

and b_m = R = (α + ν)⁻¹. Ignoring the error term o(1), we deduce that

$$a_m=\frac{1}{\alpha +\nu }[\ln m+\ln (1+c\left)\right].$$

The bottom line of this analysis is that the mean time to extinction for the m quiescent cancer stem cells is approximately

$$\frac{1}{(\alpha +\nu )}[\ln m+\ln (1+c\left)\right]+\frac{\gamma }{\alpha +\nu }.$$ (22)

On the other hand, the mean extinction time for the n active cancer stem cells is

$$\frac{1}{(\delta -\beta )}\left[\ln n+\ln \left(\frac{\delta -\beta +\frac{\beta }{n}}{\delta }\right)\right]+\frac{\gamma }{\delta -\beta }.$$ (23)

Our assumption α + ν < δ − β is equivalent to (δ − β)⁻¹ < (α + ν)⁻¹. Thus, unless n is much larger than m, the active cancer stem cells go extinct before the quiescent cancer stem cells. This is the opposite of what a viable therapy should achieve.

3.6. Distribution of HSCs in the presence of quiescence

Instead of ignoring flow into the quiescent state, one can incorporate it as part of a comprehensive branching process model [16]. We now briefly sketch this model. Consider a two-type branching process with quiescent cells as type 1 particles and active cells as type 2 particles. In addition to the notation of the previous section, let ϕ be the rate per cell of falling into quiescence. In a branching process, a particle reproduces at the time of its death. Let f_ij be the mean number of daughter particles of type j that a type i particle produces. Straightforward reasoning determines the reproduction matrix F = (f_ij) in our model as

$$F=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \frac{\alpha }{\alpha +\nu }\hfill \\ \hfill \frac{\varphi }{\varphi +\beta +\delta }\hfill & \hfill \frac{2\beta }{\varphi +\beta +\delta }\hfill \end{array}\right).$$

Other key ingredients are the death rates per particle. These can be summarized by the vector ψ with components ψ₁ = α + ν and ψ₂ = ϕ + β + δ. These constructs determine a matrix M(t) whose typical entry m_ij(t) equals the mean number of particles of type j at time t starting with a single particle of type i at time 0. Again standard arguments show that M(t)= e^tΩ, where Ω = [ψ_i(f_ij − 1_{{i = j}})]. Similar but more complicated reasoning yield the variance–covariance matrix of the particle counts starting from any initial configuration of particles [16].

To capture the full distribution of particle counts at a future time, it is convenient to introduce a bivariate generating function P_i(t, z) for the joint particle counts at time t starting from a single particle of type i at time 0. In our model, the backward differential equations for these two generating functions amount to

$$\begin{array}{cc}\hfill & \frac{\partial }{\partial t}{P}_1(t,\mathbf{z})=-(\alpha +\nu )P_1(t,\mathbf{z})+\nu +\alpha P_2(t,\mathbf{z})\hfill \\ \hfill & \frac{\partial }{\partial t}{P}_2(t,\mathbf{z})=-(\varphi +\beta +\delta )P_2(t,\mathbf{z})+\delta +\varphi P_1(t,\mathbf{z})+\beta P_2{(t,\mathbf{z})}^2\hfill \end{array}$$

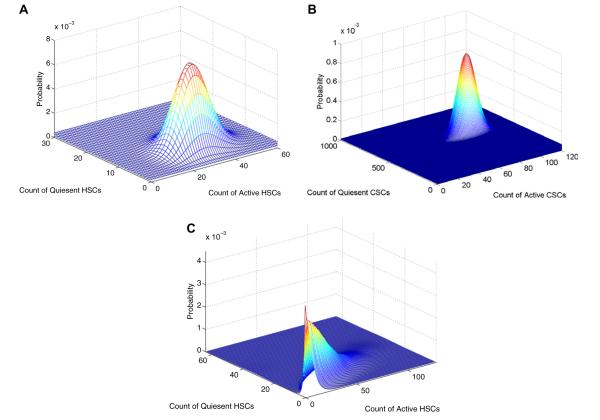
with initial condition P_i(0, z)= z_i. The probability of extinction by time t equals P₁(t, 0)^n₁ P₂(t, 0)^n₂, where n_i is the number of type i particles at time 0. Although it is impossible to solve for P₁(t, z) and P₂(t, z) analytically, it is certainly possible to solve for them numerically for any fixed value of z. This suggests retrieving the bivariate distributions via the 2D fast Fourier transform. In practice, this procedure works well and gives means and variances closely approximating the theoretical means and variances. Extension to the kind of random times we have stressed is feasible. Fig. 9 displays some typical results, for the parameter choices: β_H = β_C = 0.024 week⁻¹, δ_C = 0.59 week⁻¹, δ_H = 0.08 week⁻¹, ν_H = ν_C = 0.00024 week⁻¹, ϕ_C = ϕ_H = 0.007 week⁻¹, and α_C = α_H = 0.07 week⁻¹. Here we show the distribution of quiescent and active CSCs at the fixed mean extinction time of active CSCs, as estimated from Eq. (23), and the distribution of HSCs at the mean extinction time of quiescent CSCs, as estimated from Eq. (22). Finally, we show the distribution of HSCs at the random time of extinction of both quiescent and active CSCs.

Fig. 9.

Dynamics of quiescent and active HSCs and CSCs at fixed and random extinction times. Top: Distribution of HSCs remaining at the mean extinction time of quiescent CSCs (114 weeks). Middle: Distribution of CSCs at the mean extinction time of active CSCs (18 weeks). Bottom: Distribution of HSCs at the random time of CSC extinction.

4. Stochastic simulation

Because branching process models resist full mathematical analysis, progress depends on a variety of numerical tools. Unfortunately, as model complexity increases, all known deterministic numerical methods falter under the overwhelming computational loads. At this point simulation becomes an attractive alternative. Simulation has the further virtue of simplicity of implementation. Even when better tools are available, simulation promotes rapid testing of models and checking of approximate solutions. For these reasons, we now describe our experience with stochastic simulation in the stem cell model.

Recent advances in stochastic simulation are geared to the study of continuous-time Markov chains with a finite number of particle types, interacting via a finite number of reaction channels. While the methods first described by Gillespie [23,24] were rooted in applications to chemical reaction kinetics, particle-based stochastic simulation models have broad applications in fields as diverse as queuing theory, population dynamics, gene regulation, and biochemical networks [33,67]. The stochastic simulation algorithm (SSA) employs a wait and jump mechanism to simulate the behavior of a chain. Because it simulates every reaction, SSA can be annoyingly slow in models with large particle counts. The τ-leaping method [8,25] leaps over intermediate events by taking a fixed time step of length τ, chosen so that all reaction propensities (intensities) are relatively constant during the leap interval. At the end of the interval, each reaction channel fires a Poisson number of times with mean determined by the product of its propensity and τ. The τ-leaping method trades small losses in accuracy for much larger time steps. Our recent step anticipation leaping (SAL) method [60] generalizes τ-leaping by projecting linear and quadratic changes in reaction propensities. This promotes better accuracy without compromising speed. Here we employ the SAL method to explore stem cell dynamics in both the presence and absence of quiescence. The simulations substantiate our previous analytic and numerical results.

In a continuous-time Markov chain with a finite number of particle types, let X_t be the particle count vector at time t, r_j be the propensity of reaction j, and e^j be the increment to X_t caused by the firing of reaction j. The τ-leaping method runs an independent Poisson process for each reaction channel and sums the results over short time intervals. In ordinary τ-leaping, reaction channel j will fire r_jτ times on average during (t, t + τ). One therefore updates the particle count vector X_t = x by the sum X_t+τ = x + ∑_jN_j∊j, where N_j are independent Poisson variates with means r_jτ. In SAL, we expand each propensity to first order, replacing the constant intensity r_j of ordinary τ-leaping by the linear intensity

$$r_j\left(X_{t+s}\right)\approx r_j\left(X_t\right)+\frac{d}{dt}{r}_j\left(X_t\right)s.$$

Under this approximation, reactions of type j occur according to an inhomogeneous Poisson process during (t, t + τ), and the mean number of reactions is

$${\omega }_j(t,t+\tau )={\int }_0^{\tau }\left[r_j\left(X_t\right)+\frac{d}{dt}{r}_j\left(X_t\right)s\right]ds=r_j\left(X_t\right)\tau +\frac{d}{dt}{r}_j\left(X_t\right)\frac{1}{2}{\tau }^2.$$

This raises the question of how to calculate the derivative $\frac{d}{dt}{r}_j\left(x\right)$. The most natural route uses the chain rule

$$\frac{d}{dt}{r}_j\left(x\right)=\sum _{k=1}^d\frac{\partial }{\partial x_k}{r}_j\left(x\right)\frac{d}{dt}{x}_k$$

and sets

$$\frac{d}{dt}{x}_k=\sum _{j=1}^c{r}_j\left(x\right){∊}_k^j,$$ (24)

where ${∊}_k^j$ is the increment to species k caused by reaction j. The reaction rate Eq. (24) models the mean behavior of the system when particle counts are high and stochastic fluctuations can be ignored. The following examples employ linear SAL. Quadratic extrapolation is possible, but the improvements over linear extrapolation are rather modest [60].

4.1. Empirical distribution of HSCs when CSCs go extinct

In our basic model without quiescence, there are 2 populations of cells and 4 reaction channels. The Markov chain X_t has component X_t1 counting the CSCs and component X_t2 counting the HSCs. Table 1 lists the reaction channels, propensities, and reaction increments. Here ${∊}_j^k$ indicates the change in species k under reaction j. Any unspecified ${∊}_j^k$ is assumed to be 0.

Table 1.

Simulation of CSCs and HSCs under therapy.

Reaction	Propensity	Increment vector
CSC birth	βCx 1	${∊}_1^1=+1$
CSC death	δCx 1	${∊}_1^2=-1$
HSC birth	βHx 2	${∊}_2^3=+1$
HSC death	δHx 2	${∊}_2^4=-1$

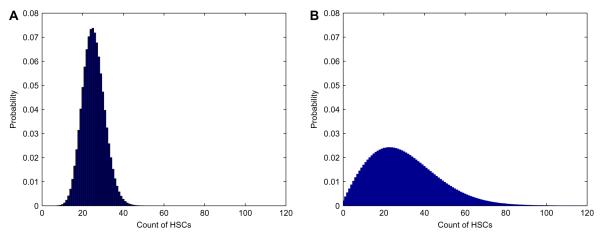
Stochastic simulation allows us to explore the distribution of the number N_H of HSCs at the random time of extinction of the CSCs; we simply record the number of HSCs when the CSC count reaches 0. Fig. 10 shows the distribution of N_H over 10,000 SAL trials for the two values δ_H = 0.08 week⁻¹ and δ_H = 0.31 week⁻¹. The other reaction rates β_C = β_H = 0.024 week⁻¹ and δ_C = 0.59 week⁻¹ match our earlier choices.

Fig. 10.

Distribution of the number of HSCs at the random time of CSC extinction. Solid bars represent results obtained using stochastic simulation, while lines represent results obtained using finite Fourier transform. Top: δ_H = 0.08 week⁻¹, σ = 10. Bottom: δ_H = 0.31 week⁻¹, σ = 2.

These results highlight the dependence of N_H on the selectivity σ of therapy. In the top panel of Fig. 10, with selectivity σ = 10, there is very little chance that the population of HSCs goes extinct before all CSCs are eradicated. By contrast, in the bottom panel of Fig. 10, with selectivity σ = 2, there is a good chance that HSCs go extinct before CSC eradication. The random variable N_H has mean ± one standard deviation of 1,580 ± 198 for σ = 10 and 30.0 ± 17.1 for σ = 2. These results agree well with our analytic formulas and numerical results based on the finite Fourier transform.

4.2. Simulations in the presence of quiescence

When we introduce quiescence into the model, we have 4 populations of cells: active CSCs (type 1) and HSCs (type 2) and quiescent CSCs (type 3 or qCSC) and HSCs (type 4 or qHSC). Table 2 lists the reactions, propensities, and increment vectors of the extended model.

Table 2.

Simulation with quiescence and awakening.

Reaction	Propensity	Increment vector
CSC birth	βCx 1	${∊}_1^1=+1$
CSC death	δCx 1	${∊}_1^2=-1$
CSC quiescence	ϕCx 1	${∊}_1^3=-1$, ${∊}_3^3=+1$
qCSC awakening	αCx 3	${∊}_1^4=+1$, ${∊}_3^4=-1$
qCSC death	νCx 3	${∊}_3^5=-1$
HSC birth	βHx 2	${∊}_2^6=+1$
HSC death	δHx 2	${∊}_2^7=-1$
HSC quiescence	ϕHx 2	${∊}_2^8=-1$, ${∊}_4^8=+1$
qHSC awakening	αHx 4	${∊}_2^9=+1$, ${∊}_4^9=-1$
qHSC death	νHx 4	${∊}_4^{10}=-1$

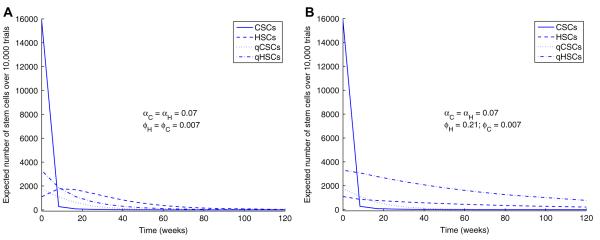
Because the deaths of quiescent cells, both qCSCs and qHSCs, are rare events, we set ν_C = ν_H = 0.00024 week⁻¹. To deduce the relative rates of awakening and falling into quiescence, consider a simple 2-state Markov chain ignoring birth and death and modeling only the passage of a single stem cell back and forth between the active and quiescent states. This chain is reversible, and the principle of detailed balance identifies π = α/(ϕ + α) as the equilibrium fraction of active stem cells. Based on observations in adult mice that approximately 75% of long-term self-renewing hematopoietic stem cells are quiescent [11], and observations in patients with chronic myelogenous leukemia that 8.7% of CD34 cells are in a quiescent state [34], we take π_H = 0.25 and π_C = 0.9. While no data are available on rates of activation and quiescence of stem cells, we start with activation rates α_H = α_C = 0.07 week⁻¹, and calculate the rates of quiescence ϕ_H = 0.21 week⁻¹ and ϕ_C = 0.007 week⁻¹ using the detailed balance condition. Given a total stem cell population size of 22,000 [1], we again start with a large proportion (80%) of CSCs: n_H = 4,400 HSCs and n_C = 17,600 CSCs. Based on the above proportions of quiescent and active HSCs and CSCs, the initial value X₀ = x has components x₁ = 15,840, x₂ = 1,100, x₃ = 1,760, and x₄ = 3,300.

We will consider two cases. The first assumes a slow backflow to quiescence (ϕ_C = ϕ_H = 0.007 week⁻¹). This scenario may be more realistic as quiescence is most likely regulated by similar mechanisms for both types of cells, and healthy stem cells might be expected to spend more time in an active state during malignancy. The second scenario is less likely and assumes that the CSCs and HSCs have reached two different equilibrium distributions. Here the backflow of quiescence is slow for CSCs (ϕ_C = 0.007 week⁻¹) and fast for HSCs (ϕ_H = 0.21 week⁻¹). We use our previous birth rates β_H = β_C = 0.024 week⁻¹ and death rates δ_C = 0.59 week⁻¹ and δ_H = 0.08 week⁻¹.

Following the trajectories of the 4 populations of stem cells over time in Fig. 11, we see it takes a much longer time for the CSCs to go extinct when quiescence is involved (t = 40 weeks). When the backflow to quiescence is much slower for CSCs (ϕ_C = 0.007 week⁻¹; ϕ_H = 0.21 week⁻¹), there is still an adequate number of HSCs at the time of extinction of the CSCs, approximately 590 (124 active and 466 quiescent), though far fewer than if therapy were to target quiescent CSCs. However, when backflow to quiescence is slow for both CSCs and HSCs, ϕ_C = ϕ_H = 0.007 week⁻¹, by the time all CSCs are finally eradicated, there are only approximately 18 HSCs (13 active and 5 quiescent). In the second scenario, quiescence serves as a sanctuary for the HSCs. The first scenario agrees with the analytic results of our modeling described in Section 3.5 and emphasizes the need for therapy to target both active and quiescent CSCs. The second scenario hints at greater subtlety and emphasizes the need for accurate measurement of all parameters.

Fig. 11.

Trajectories of active and quiescent stem cell populations. Top: Same quiescence rates for CSCs and HSCs. Bottom: Quiescence rate for HSCs ≫ quiescence rate for CSCs.

5. Conclusions

Cancer therapy based on eradicating CSCs is admittedly speculative. However, given the toll of mortality and morbidity exacted by cancer, this is a strategy worth considering in detail. Mathematical models can guide the rational design of drugs and treatments. Of course, model predictions will have to be checked by animal experiments and careful analysis of patient outcomes. Premature trials with poor outcomes can sour the prospects of even a good therapy. Our findings are cause for guarded optimism. We have shown that the relative numbers of CSCs and HSCs at the time of initiating therapy are less relevant than the selectivity of therapy. Modeling stem cell population dynamics as a birth–death process permits characterization of the extinction times for active and quiescent stem cells and calculation of the distribution of the number of HSCs at the time of eradication of CSCs. We anticipate that comparing in vitro killing rates of CSCs and HSCs will be useful in screening targeted therapies. How applicable the models will be depends on underlying parameters such as absolute quantities of stem cells, death rates of HSCs and CSCs, and relative rates of quiescence and awakening. These parameters will doubtless vary for different tumor types and stem cell populations.

Therapies proposed to target cancer stem cells operate via several different molecular mechanisms (see Table 3). For leukemic stem cells, there are small molecule targeted biologic therapies, antibody-based and immune-mediated therapies, and stem cell microenvironment targeted therapies [29,37,53,63]. DMAPT offers an example of a small molecule potentially useful in therapy; DMAPT is a parthenolide derivative that selectively eliminates leukemic stem cells and spares normal hematopoietic stem cells. The half maximal inhibitory concentration for normal stem cells under DMAPT is 10 times higher than that for leukemic stem cells. Therapies that inhibit the PI3K/PTEN/Akt pathway, which regulates growth and apoptosis of stem cells, work more efficiently in leukemic stem cells than in normal hematopoietic stem cells [30,69,70]. Dasatinib, a small molecule inhibitor of BCR-ABL, targets leukemic stem, progenitor, and differentiated cells in chronic myelogenous leukemia, but does not target the corresponding quiescent populations [12]. Antibody-based therapies inhibit the homing of the LSC to its niche (anti-CD44), activate innate immunity by targeting IL-3 (anti-CD23), and inhibit intracellular signaling. Immune-mediated cell killing is also being proposed as a mechanism to target leukemic stem cells. CD47 is an antigen expressed on leukemic stem cells which binds to a signal-regulatory protein on macrophages and stops the ingestion of the leukemic stem cells by the macrophages [47]. An antibody to CD47 is being developed to block its interaction with macrophages, facilitating activation of phagocytes. An important property of stem cells is niche-dependence [48]. Stem cell niches, distributed throughout the body, serve to regulate the total number of stem cells and whether or not stem cells maintain an undifferentiated state. Therapies that target the microenvironment are predicated on the assumptions that niche regulation is aberrant in cancer and targeting niche regulation will inhibit the abnormally activated pathways. It remains to be seen whether niche targeting will be selective for cancer stem cells. Future models should include simulation of stem cell-niche interactions.

Table 3.

Proposed therapies targeting leukemic stem cells.

Type	Example	Mechanism
Small molecule therapies	DMAPT	induces differentiation and apoptosis
	MG-132	proteasome inhibitor
	ABT-737	bcl-2 inhibitor, regulates apoptosis
	PI3K/PTEN/Akt	regulates growth and apoptosis
	inhibitor
	Dasatinib	inhibitor of BCR-ABL
Antibody-based therapies	Diphtheria- toxin-IL-3 fusion protein	inhibit intracellular signaling
	anti-CXCR4	mediates SDF-1 interaction
	anti-CD44	inhibit homing of LSC to its niche
	anti-CD23	activate innate immunity
	anti-CD47	immune-mediated cell killing
Therapies targeting the   microenvironment	γ-secretase inhibitor	inhibit self-renewal
	PI3K inhibitor anti-VEGF therapy	block prosurvival signaling target hypoxic milieu

Other proposed cancer stem cell therapies work by inducing differentiation. The tremendous potential for cure by combining differentiating agents with chemotherapy has been demonstrated in acute myelogenous leukemia with all-trans retinoic acid. In our models we consider symmetric division leading to two differentiated cells as a type of stem cell death.

We find that selectivity is an important determinant of the safety of a proposed therapy. In contrast, killing efficiency is important in determining the appropriate duration of therapy needed to drive a cancer stem cell population extinct. Both of these measures are heavily dependent on the difference between birth and death rates of a stem cell population, rather than on the birth or death rate alone. It is possible that the symmetric birth rate of cancer stem cells is much higher than that of healthy hematopoietic stem cells. For example, the regulation of asymmetric stem cell division may be disturbed during the process of carcinogenesis [10]. Because our models focus on the importance of the difference between birth and death rates, we make the simplifying assumption that the birth rates for the HSC and CSC populations are the same and simply vary death rates. If the amount of time spent by CSCs in self-renewing symmetric division were found to be substantially higher than that for HSC, the death rate of CSCs under a proposed therapy would need to be that much higher to obtain the same selectivity.

Cancer modeling is becoming more of a preoccupation for applied mathematicians. The variety of approaches is impressive. These range from continuum mechanics models of tumor growth to reaction–diffusion models of tumor vascularization and optimization of radiation doses in radiation therapy [3,9,22,62]. Branching processes and continuous-time Markov chain models have long provided quantitative insights into the dynamics of cancer initiation and proliferation [42,45]. Our stem cell models continue in this tradition. In stem cell dynamics, the population of HSCs is critically small, and their chance elimination has devastating consequences. This sober fact highlights the importance of tight control over killing differentials. Stochastic models of drug resistance of stem cells have also been explored [26,43,50]. Here modeling mutation is crucial. Further research is surely merited on the mutational pathways leading to cancer, the genetic instability of cancer stem cells, the development of resistance mutations during therapy, and the role of the stem cell niche in regulating stem cell and progenitor expansion.

We predict that stochastic simulation methods will play an increasing role in the development of more sophisticated cancer models. Stochastic simulation is ideal for studying complex systems with multiple cellular species tied together by multiple reaction channels. We have modeled sensitivity to therapy by varying death rates. To capture the role of the stem cell niche, one could assign CSCs that escape niche regulation higher birth rates or higher rates of awakening from quiescence. We have omitted progenitor cells and partially and fully differentiated cells from our models. Adding all of the complications requires flexible modeling tools. Multitype branching processes can take us only so far. As soon as the different cell types begin to interact, the branching process paradigm breaks down. This should not mean the abandonment of stochastic models, but it does put a premium on the development of faster, more accurate, and more convenient implementations of stochastic simulation. These urgent needs and the burgeoning of systems biology as a whole will drive the field of stochastic simulation.

In conclusion, mathematical modeling and the development of rational stem cell therapy will go hand in hand. The current stem cell models give us hope that attacking CSCs can cure cancer. To be successful, targeted therapies must be tuned to spare HSCs and eradicate quiescent as well as active CSCs. This second criterion rules out drugs that solely attack dividing cells. Only stochastic models can capture the extinction and small numbers phenomena connected with stem cells. These models will ultimately provide the same extraordinary insight into cancer therapy responses and resistance that they have in HIV treatment [15]. If we are fortunate, models of the two diseases will cross fertilize each other for years to come.