Local isotropic phase symmetry measure for detection of beta cells and lymphocytes

Abstract

Diabetes can be associated with a reduction in functional β cell mass, which must be restored if the disease is to be cured or progress is to be arrested. To study the cell count, it is also necessary to determine the number of nuclei within the insulin stained area. It can take a single experimentalist several months to complete a single study of this kind, results of which may still be quite subjective. In this paper, we propose a framework based on a novel measure of local symmetry for detection of cells. The local isotropic phase symmetry measure (LIPSyM) is designed to give high values at or near the cell centers. We demonstrate the effectiveness of our algorithm for detection of two types of specific cells in histology images, cells in mouse pancreatic sections and lymphocytes in human breast tissue. Experimental results for these two problems show that our algorithm performs better than human experts for the former problem, and outperforms the best reported results for the latter.

INTRODUCTION

Glucose homeostasis depends on the release of insulin and glucagon by β cells and α cells within the pancreatic islets of Langerhans, which respectively increase or reduce glucose disposal in peripheral tissues.[1] All major types of diabetes are associated with a reduction in functional β cell mass, which must be restored if the disease is to be cured or progress arrested.[2] Increasingly, drugs are being introduced into clinical practice which may be able to arrest or potentially in the future even reverse this decline at least in type 2 diabetes.[3] Not surprisingly, much research in the academic and private sectors is devoted to functional testing of genetic manipulations and therapeutic strategies aimed at interfering with loss of beta cell mass or that might restore or expand endogenous beta cell mass in animal models. Moreover, increasingly post-mortem analyses of β and islet cell mass are undertaken in patients.[4] It is not currently possible to measure changes in β cell or even islet mass during life as no sufficiently sensitive or specific imaging tools exist.[4]

Therefore, all depends on an accurate assessment of beta cell mass post-mortem. In all such cases it is necessary to estimate β cell mass by immunohistochemical (IHC) staining of pancreas tissue sections and then, for at least 5-10 levels, to measure the area of insulin immunoreactivity and divide this by the total pancreas area (mass can then be assessed by multiplying the ratio by the pancreas weight). To assess β cell count, it is necessary to also determine the number of nuclei within the insulin stained area. To obtain this data is very labor intensive and subject to observer bias. Many hours of microscopy and image capture are required followed by very time consuming analyses, so that it is not unusual for a single experimentalist to take many months to complete a single study of this kind.

A variety of methods have been proposed in the literature to address the problem of nuclei detection in histology images. Intensity-based methods such as thresholding[5] and clustering[6,7] are often employed when a high contrast is known to exist between the background and foreground (i.e., cells). Another class of methods employs active contours to segment out the boundary of cells.

The basic idea behind such techniques is that the initial contour is iteratively modified based on some criterion. Several models based upon active contours have been proposed.[6–10] However, a major drawback of methods based on active contours is that the performance is highly dependent on the seed points. Majority of these methods struggle to resolve cell boundaries for overlapping cells. Bamford et al.[8] have showed that by use of dual-active contours, it is possible to overcome such shortcomings of active contours. Another approach that is often followed is the use of watersheds. These methods treat intensity profile of an image as a topological surface. Problem with watershed segmentation is that noisy and textured images have many local minima, most of them being irrelevant for segmentation. Using the watershed on a gray image without any preparation leads to an over segmentation. The best solution to this problem consists in initially determining markers for each region of interest, including the background of the image. This makes it semiautomated with subjectivity creeping in because of the choice of markers. Other approaches include the use of a statistical model[11] for cell nuclei detection, and more recently morphological operations[12] for detection of cell nuclei.

In this paper, we present a novel method for detection of cell nuclei based on the idea of isotropic phase symmetry. We introduce a novel measure of isotropic phase symmetry which quantifies symmetry around a pixel irrespective of the direction(s) in which the symmetry is found. Since the proposed measure is calculated entirely in the frequency domain, it is invariant to both contrast and illumination variations. When applied on Hematoxlyin-positive parts of a histology image, this measure can be used for detecting cells. We demonstrate the effectiveness of the isotropic phase symmetry measure for detection of β cells using a challenging dataset consisting of 20 histology images of mouse pancreas. To the best of our knowledge, there is no existing method in the literature which addresses this problem. We further show the effectiveness of our proposed measure for detection of lymphocytes in breast histology images, which was posed as a problem in a recently held contest in pattern recognition.[13]

Experimental Data

Transgenic mouse

A transgenic plns-c-MycER^TAM mouse model[14] was employed in this study. c-MYC was switched on by daily intraperitoneal (IP) injection of 4-hydroxytamoxifen (4-OHT; Sigma-Aldrich, St. Louis, MO) at 1 mg/0.1 ml. Three-month-old female mice were killed after 8 hours of IP injection, and so were their wild-type (WT) littermates, which applied the same volume of vehicle. WT is presented in this study. Mouse pancreata were dissected and placed into 4% formaldehyde (formaldehyde-methanol free 16% w/v solution; TAAB, Berks, UK) for 2 hours at room temperature (RT). Tissues then were transferred into 30% sucrose (Sigma-Aldrich, St. Louis, MO) at 4°C overnight. After the fixation steps, pancreata were placed into a cubic mode, embedded with Tissue-Tek O.C.T. mounting medium (Sakura, Alphen aan den Rijn, The Netherlands), placed on the dry ice, and stored at -80°C. Tissues were sectioned by a cryostat (OTF 5000 Cryostat; Bright, Huntingdon, UK) at the thickness of 10 μm.

DAB and hematoxylin staining

Slides were postfixed in 4% formaldehyde for 10 minutes at 4°C, and were washed in PBS for 2 times, 3 minutes for each wash on a shaker (at 50 rpm). Hydrogen peroxide (H₂O₂) (Thermo Fisher Scientific, Pittsburgh, PA) (diluted in sterile H₂O at 1/100) was applied to each section to bleach the samples for 30 minutes at RT; then slides were washed in PBS for 5 minutes on a shaker (at 50 rpm).

A goat serum solution (150 μl goat serum (Sigma-Aldrich, St. Louis, MO) and 10 ml PBS) with triton (50 μl) (Sigma-Aldrich, St. Louis, MO) was applied to each tissue section for 30 minutes at RT to block tissues. The primary antibody (Insulin-polyclonal guinea anti-swine; Dako, Glostrup, Denmark) was applied onto the sections at 1/200 and incubated for 1 hour at RT. Then slides were washed in PBS+0.1% Tween for 3 times, and 5 minutes for each wash on a shaker (at 50 rpm). The secondary antibody (Guinea pig IgG (H and L) preabsorbed antibody (HRP); Novus Biologicals, Littleton, CO) was applied for 30 minutes onto the treatment section at 1/500 at RT. After slides were washed in PBS+0.1% Tween three times, and 5 minutes each on a shaker (50 rpm), a DAB kit (DAB substrate kit for peroxidise; Vector Laboratories, Burlingame, CA) was applied on to each section for 2 minutes, by following the protocol from the producer. Then slides were washed in sterile H₂O for 2 times, and 3 minutes for each on a shaker (50 rpm). The next step was the hematoxylin staining, which is carried out using the following steps: (1) bathed in the hematoxylin (Carl Roth, Karlsruhe, Germany) for 1.5 minutes, (2) washed under the running water for 10 minutes, (3) transferred into 70% ethanol for 1 minute, (4) transferred into 80% ethanol for 1 minute, (5) transferred into 90% ethanol for 1 minute, (6) transferred into 100% ethanol for 2 minutes, (7) immersed into xylene for 2 times in a hood, and 5 minutes for each, and (8) mounted slides with mount medium (Leica, Wetzlar, Germany) and applied coverslips. The slide images were studied by a light microscope (Axiostar plus; Carl Zeiss, Jena, Germany) with a ’40 objective, and captured by a digital camera (Powershot G5; Cannon, Tokyo, Japan).

The Proposed Algorithm for Detection of β Cells

The proposed scheme for detection of β cells is based upon the idea of phase symmetry. A schematic diagram of our detection algorithm is given in Figure 1. As a first step, the algorithm separates stains using the Ruifrok and Johnston method.[15] This is followed by the computation of local isotropic phase symmetry to identify image pixels that may be high in local symmetry. All pixel values in a local neighborhood with high values of this measure are then grouped together to form candidate cell centers. The final step ensures that the pixels surrounding detected cell centers satisfy certain criterion relating to their stain making them stain-specific cells. Figure 2 illustrates the different steps of our algorithm with the aid of an example. The remainder of this section provides a detailed description of all of these steps.

Figure 1.

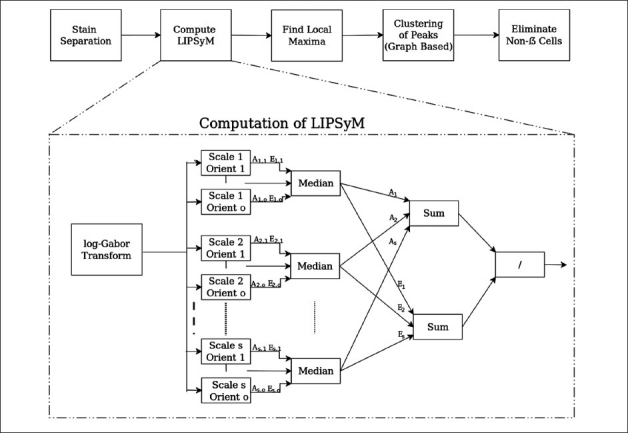
A schematic diagram of the proposed algorithm for detection of β cells

Figure 2.

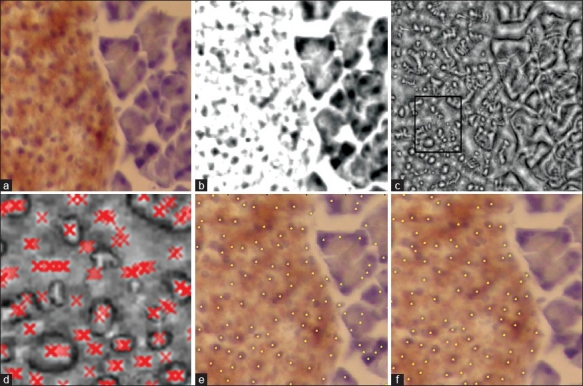
(a) Original color image; (b) H-stain; (c) Normalized median phase energy; (d) Peaks overlayed; (e) Result after clustering; (f) Final output of the algorithm

The local isotropic phase symmetry measure

If we assume cells to be elliptical blobs, one would expect centers of the cells to be at the peaks of local isotropic symmetry. Our measure is derived from Kovesi's pixel-wise symmetry measure[16] computed in the frequency domain using log-Gabor wavelets. Spatial domain approaches based on morphological properties have been surveyed as early as 1989. Xia[17] has made such a survey. A few other authors have attempted to quantify symmetry based on.[16] Xiao et al.[18] have also proposed a symmetry measure based on phase information. Loy and Zelinsky[19] have used a symmetry based approach for face detection and characterization. The log-Gabor wavelet filters have a Gaussian transfer function when viewed on the logarithmic frequency scale, and are similar to those found in the human visual system.[20] A detailed description of how The local isotropic phase symmetry measure (LIPSyM) can be computed using these filters is given below.

Computation of LIPSyM via the log-Gabor Transform

The first step in the computation of LIPSyM is to take the discrete time Fourier transform of the input image. This frequency information is filtered through a bank of log-Gabor filters. These filters are made by dividing the frequency domain into concentric circles, with each band between two consecutive circles representing different scales, and into angular strips representing different orientations. Consider there are n_s scales and n_o number of orientations, resulting in n_s × n_o different filters. Let I denote the Fourier transform of the input image, G_s,o the Gabor filter at scale s and orientation o, and V_s,o the output of the convolution of G_s,o and I.

V_s,o=I*G_s,o      (1)

Local responses of each of the Gabor filters can also be represented in terms of amplitude A_s,o(x, y) and energy E_s,o(x, y) as defined below,

A_s,o=|V_s,o (x,y)|      (2)

and

E_s,o (x,y) = |Real{V_s,o (x,y)}| – | Img {V_s,o (x,y)}|      (3)

where (x, y) denotes the 2D coordinates of a pixel, and Real and Img denote the real and imaginary parts of the filter response. Next, we define the median over all orientations for a fixed scale s for A_s,o and E_s,o as follows,

A_s (x,y) = median_{{o=1,2…,no}} A_s,o (x,y)      (4)

and

E_s (x,y) = median_{{o=1,2…,no}} E_s,o (x,y)      (5)

The use of median in the above equations plays a critical role in ensuring that our symmetry measure is isotropic, unlike the mean over all orientations used by Kovesi[16] which may return high values in the case of symmetry found only in particular directions, as shown in Figure 3. Finally, the local isotropic phase symmetry measure (LIPSyM) η(x,y) is defined as follows,

Figure 3.

Isotropic (red) vs. anisotropic (green) peaks of local phase symmetry

Grouping of the LIPSyM Peaks

The LIPSyM value η(x,y) was computed for image pixels located at (x,y), for all x, y. The peak values of η should correspond to cell centers. So we find local maxima in the LIPSyM image η(x,y). This process can potentially result in several candidate points for cell centers which are grouped into a single cell center by representing these points as a graph and using maximal cliques to partition the graph into smaller subgraphs in order to resolve any overlapping cells.

Elimination of Non-β Cells

Now that we have all the cell centers, we eliminate those cells which are not β cells. One characteristic of the β cells is that they should be stained by DAB-insulin, owing to their high insulin content. The percentage of local DAB stain was computed for each of the cell centers. This was done by creating a window around each cell center and computing the proportion of pixels found to be rich in DAB-insulin in that window, where the DAB image was obtained by using a Gaussian mixture model (GMM) with five modes. If the proportion of DAB-insulin rich pixels around a cell center is above a certain threshold, we label the cell as a β cell.

EXPERIMENTAL RESULTS

We tested the performance of the proposed approach on two case studies: first one involving detection of β cells in Hematoxylin and DAB-insulin stained histology images, and another one aimed at the detection of lymphocytes in Hematoxylin and Eosin (H and E) stained breast histology images using the ICPR contest test dataset.[13] By using these two different datasets, we intend to demonstrate the generality of our proposed framework for detection of cell nuclei of different kinds in histology images. Seven measures were used for quantitative evaluation of performance: three standard measures in sensitivity, positive predictive value (PPV), and F1-score, and four measures used in[13] and denoted as μ_d, σ_d, μ_n, σ_n. These measures evaluate the ability of the algorithm to identify centers and the total number of specialist cells (e.g., β cells and lymphocytes for our two datasets) that were identified by the algorithm: μ_d and σ_d denote the mean and standard deviation respectively of the closest distances for each of the identified cells, while μ_n and σ_n denote the mean and standard deviation respectively of absolute difference of the number of nuclei between the ground truth and the result of automatic detection. Comparative results provided below for both the datasets highlight the challenging nature of specialist nuclei detection in the presence of an often subjective ground truth.

Detection of β Cells

Our first dataset consists of 20 images of mouse pancreatic sections stained with Hematoxylin and DAB-insulin taken at 40×, with the spatial resolution of each image being 1024×768 pixels. We learnt the Hematoxylin and DAB stain vectors, as suggested in,[15] in order to identify pixels containing candidate β cell nuclei. The proposed phase symmetry measure was then used to identify β cells in a given image.

How True Is the Ground Truth?

The centers of all β cells were identified by three different experts, all with a biology or medicine background, two of them senior PhD students and a postdoctoral fellow with experience of working with such image data for several years. Due to the largely subjective nature of β cell identification, we found large differences in the markings of all pairs different experts. Therefore, we refer to the set of β cell center coordinates provided by each of the three experts as markings rather than ground truths. We conducted the following experiment to highlight the subjective nature of each of the markings. If we consider the markings provided by one of the experts to be the “ground truth” and those provided by another expert as the results of an algorithm, we can compute the aforementioned performance measures to reflect how well the two experts agree with each other. As shown in Table 1, there is low agreement found between any pair of the three experts. Such low agreement values also indicate the challenging nature of this problem.

Table 1.

Comparison of three experts’ (A, B, and C) markings against each other and against the fused ground truth (FGT)

Due to this reason, we resort to fusing the ground truth provided by three experts by first representing each cell marking as a round blob (a 2-D Gaussian with a bandwidth of eight pixels, roughly representing the size of an average cell). For each of the images in our dataset, three such images (one image per expert) containing round blobs around the marked cell centers are combined by adding them together, thresholded, resulting in a fused ground truth (FGT). The advantage of a Gaussian as opposed to just a point mark is that it makes it possible to give more confidence in a particular expert's markings by assigning weights to respective Gaussian functions.

Last three rows in Table 1 show that while the level of agreement between one of the experts and the remaining two experts increases when we fuse the ground truth from the two experts, it still remains not very high. In the remainder of this section, we present results for the algorithm's performance against the fused ground truth obtained by all three experts’ markings.

Detection Results for the Fused Ground Truth

Table 2 shows the results of our algorithm for β cell detection against the fused ground truth. As mentioned earlier, to the best of our knowledge, there is no existing method in the literature for the detection of β cells. For comparison purposes, therefore, we tested the performance of the proposed local isotropic phase symmetry measure (LIPSyM) against the standard laplacian of gaussian (LoG) filter, as proposed by Byun et al.,[21] by replacing the second building block of our scheme in Figure 1 with the LoG filter. The results show clearly that the proposed method is more sensitive and outperforms the LoG filter in terms of most of the others performance measures. The LoG filter shows slightly better performance in terms of the PPV.

Table 2.

Experimental results for the detection of β cells; best results are shown in bold

We invite fellow researchers to download this dataset from our website1 in the spirit of a healthy competition for advancement of technology to solve this basic but challenging problem.

The bane of manual marking

As already mentioned in the introduction section, it may take a few months for the marking by a human expert. Just to give the readers an idea, single experiment on beta cells may consists of about 6,000 images of the size 1024×768. Each image has about 50-300 beta cells. On average, a human expert would take about 4-5 minutes per image depending on fatigue level and other human factors. This would cost up to 500 man hours.

On the other hand, the current MATLAB implementation of our algorithm takes about 30 seconds per image on a 2.66 GHz Quad-Core workstation. This would mean for 50 computer hours, equivalent to about 2-3 days for marking without any human intervention. However, in our opinion, it would be possible to reduce the computation time further by implementation in lower level languages like C/C++. Further acceleration can be achieved by implementation on GPUs.

Thus, it can be seen that it would save valuable human expert hours from the laborious task of marking. This would allow the expert to spend their time on more fruitful activities, resulting in accelerated pace of such a research.

Detection of Lymphocytes

Our second dataset consists of 10 images which were the subject of an international competition on pattern recognition in histology images.[13] These images contain breast tissue with lymphocytic infiltration stained with Hematoxylin and Eosin (H and E) and digitized at 20×, with the spatial resolution of each image being 100×100. The centers of all lymphocytes identified by an expert were marked. We employed the standard Hematoxylin stain vector, as suggested in,[15] in order to identify pixels containing the candidate nuclei. The phase symmetry measure was then used to identify lymphocytes, without using any textural measures or any kind of supervised or unsupervised classifier, as was the case with some of the competing algorithms in that contest[22–25] Table 3 shows the results of our algorithm for lymphocyte detection as compared to four other competing methods. We quote the figures for last four of the seven aforementioned performance measures from.[13] MATLAB code for Kuse et al.'s method[22] was downloaded from their website2 and, therefore, we were able to fully compare the performance of their algorithm with ours. It is clear from these results that LIPSyM gives the best performance among all the methods, better in terms of all but one performance measures than[22] which was declared winner of the ICPR contest.[13]

Table 3.

Experimental results for the detection of lymphocytes; best results are shown in bold

CONCLUSIONS AND FUTURE WORK

In this paper, we proposed a novel measure of local isotropic phase symmetry (LIPSyM) for identifying cells. We employ LIPSyM in a systematic framework for labeling particular stain-specific cells such as insulin-rich β cells in pancreatic sections. Counting β cell mass plays a critical role in studying the development and cure of diabetes in mouse models. We studied manual detections of β cells by three experts and found very low levels of agreements between them. In fact, we found that our algorithm gives higher precision and sensitivity than any of the three experts against a fused ground truth using markings from two of the remaining experts.

We demonstrated the effectiveness of LIPSyM on another similar kind of problem, the detection of lymphocytes in breast histology images. Our results illustrate the highly subjective nature of manual detection of specific type of cells, such as β cells and lymphocytes, and consequently point to the difficulty in getting a reliable ground truth for training computer algorithms for detection of such cells. A large-scale multisite collaborative study may be a vehicle to resolve these issues by collaborative filtering and aid in the development of reliable computerized tools to objectively quantify specific cells in histology images.