Identification of Homogeneous Genetic Architecture of Multiple Genetically Correlated Traits by Block Clustering of Genome-Wide Associations

Abstract

Genome-wide association studies (GWAS) using high-density genotyping platforms offer an unbiased strategy to identify new candidate genes for osteoporosis. It is imperative to be able to clearly distinguish signal from noise by focusing on the best phenotype in a genetic study. We performed GWAS of multiple phenotypes associated with fractures [bone mineral density (BMD), bone quantitative ultrasound (QUS), bone geometry, and muscle mass] with approximately 433,000 single-nucleotide polymorphisms (SNPs) and created a database of resulting associations. We performed analysis of GWAS data from 23 phenotypes by a novel modification of a block clustering algorithm followed by gene-set enrichment analysis. A data matrix of standardized regression coefficients was partitioned along both axes—SNPs and phenotypes. Each partition represents a distinct cluster of SNPs that have similar effects over a particular set of phenotypes. Application of this method to our data shows several SNP-phenotype connections. We found a strong cluster of association coefficients of high magnitude for 10 traits (BMD at several skeletal sites, ultrasound measures, cross-sectional bone area, and section modulus of femoral neck and shaft). These clustered traits were highly genetically correlated. Gene-set enrichment analyses indicated the augmentation of genes that cluster with the 10 osteoporosis-related traits in pathways such as aldosterone signaling in epithelial cells, role of osteoblasts, osteoclasts, and chondrocytes in rheumatoid arthritis, and Parkinson signaling. In addition to several known candidate genes, we also identified PRKCH and SCNN1B as potential candidate genes for multiple bone traits. In conclusion, our mining of GWAS results revealed the similarity of association results between bone strength phenotypes that may be attributed to pleiotropic effects of genes. This knowledge may prove helpful in identifying novel genes and pathways that underlie several correlated phenotypes, as well as in deciphering genetic and phenotypic modularity underlying osteoporosis risk.

Introduction

Genome-wide association studies (GWAS) using high-density genotyping platforms offer an unbiased strategy to identify new candidate genes for different traits and diseases. A number of candidate genes have been identified for traits associated with fracture, such as bone mineral density (BMD),^(1–3) bone geometry,^(4,5) and lean mass.⁽⁶⁾ Although this is a powerful approach for disease gene discovery, many GWAS focus only on identification of candidate genes and provide no clues on gene networks that may underlie the trait variations. Genes do not work alone, especially in the genetics of complex diseases. More often, they work in an interactive network synergistically and coregulate the expression of proteins that are implicated in a trait variation. In the study of disease networks or interactomes, it has been suggested that disease genes usually are located centrally (“hub”) and are highly connected with other genes in the interactome such that perturbations of candidate genes in the same network are more likely to cause either the same or similar disease phenotypes.^(7,8) Given that many traits are correlated genetically, it is possible that common gene network(s) underlie multiple correlated trait variations. In fact, using a plethora of genetic information from high-throughput technologies such as mRNA microarray and GWAS, it is now feasible to “reverse phenotype” (whereby associations with genetic markers are used to define phenotype groupings)^(9,10) and classify multiple traits based on the similarity of their genetic organization. There is a need to develop innovative computational and informatics tools and high-throughput discovery technologies for both gene network and phenomic research⁽¹¹⁾ given the large numbers of multiple correlated traits that are common in cohorts performing GWAS.

Age-related osteoporotic fractures are common in the United States and represent a major public health threat that is likely to increase in importance as the population ages.⁽¹²⁾ Although osteoporotic fracture per se is a heritable trait, the fracture phenotype presents a challenge for a genetic study: Nontraumatic fractures typically do not occur until later in life. Therefore, quantitative risk factors for fracture [such as BMD, quantitative ultrasound (QUS), and bone geometry] are used traditionally,^(13–19) especially because these surrogate traits may be measured consistently at any age. Combinations of BMD assessments in more than one region,⁽²⁰⁾ as well as composite use of BMD with QUS⁽¹⁷⁾ or BMD with hip geometry,⁽²¹⁾ have been suggested to improve risk assessment in clinical practice. In addition, it seems worthwhile to use information on muscle mass and strength together with bone mineralization and its spatial arrangement to assess the risk of fragility because loads that are applied to the skeleton are attributable to both overall body weight and muscle contractions. These musculoskeletal anatomic structures are a conglomeration of multiple traits; some of them are phenotypically and genetically correlated. Therefore, it is important to understand how the relationship among traits is regulated⁽²²⁾ so as to gain more insights into complex disease etiologies.

In this study we present a biclustering approach for identifying common genetic architectures of different musculoskeletal traits using GWAS data. Statistical model-based clustering is useful in many applications, including gene expression analysis, but one of its drawbacks is the necessity of allocating all samples (or genes) to at least one cluster, which, owing to noise in the data, may lead to artificial clusters that have no real biologic meaning. One heuristic method that has been proposed to overcome this problem is tight clustering,⁽²³⁾ in which only samples (or variables) that are similar enough, according to some predefined criterion, are clustered together, whereas the rest are left ungrouped as outliers. However, this method works only in one dimension, considering either samples or variables, and not if both directions are to be considered simultaneously, as we wish to do here. On the other hand, biclustering or block clustering^(24–28) is an approach to simultaneously cluster row and column variables, deriving local subgroups within a data matrix. Many biclustering methods also may be adapted so that not all samples and variables need to be grouped (only ones that are “similar enough” according to some predefined measure). These approaches have been used previously in discovering local patterns in gene expression data.^(25,26) Based on a Bayesian statistical model framework proposed by Gu and Liu,⁽²⁸⁾ but with modifications to increase the robustness and efficiency of the model for dealing with the more massive GWAS data, we developed a fast and accurate algorithm to identify block clusters of single-nucleotide polymorphisms (SNP) and traits in data arising from GWAS.⁽²⁹⁾

We applied this method to results from bone and muscle traits from the Framingham Osteoporosis Study. We studied GWAS data on 23 traits and approximately 433,000 SNPs by a modification of our block-clustering algorithm.⁽²⁹⁾ The primary aim of this study was to identify homogeneous genetic architectures among different musculoskeletal traits and to classify these traits based on a reverse-phenotyping approach.⁽⁹⁾ We hypothesized that correlated musculoskeletal phenotypes would cluster together based on their SNP associations (thus representing “phenotypic moduli”⁽⁹⁾) and that the shared SNPs would indicate a gene network that contributes to the development and/or maintenance of the musculoskeletal traits (thus reflecting a “genetic modularity”⁽³⁰⁾).

Methods

Sample

The sample used for our analyses was derived from two cohorts of the population-based Framingham Heart Study. Details of the Framingham Osteoporosis Study (FOS), an ancillary study of the Framingham Heart Study, have been reported.^(31,32) In brief, the FOS original and the offspring cohorts represent members of two-generational (mostly nuclear) families recruited at different times. Descriptions of the family samples with musculoskeletal phenotypes available for analyses in the FOS are provided elsewhere,^(32,33) as well as being available publicly through the dbGaP at http://view.ncbi.nlm.nih.gov/dbgap. For this study, a sample of 2211 women and 1633 men who had phenotypic measurements and who consented to genetic analyses was available. Details on the FOS sample also are available elsewhere.^(34,35) The study was approved by the institutional review boards for human subjects research of Boston University and Hebrew SeniorLife.

Musculoskeletal phenotypes

The following measures were available in members of both cohorts of the FOS:

Bone densitometry

The participants underwent dual-energy X-ray absorptiometry (DXA) with a Lunar DPX-L device (Lunar Corp., Madison, WI, USA) between 1996 and 2001 to assess BMD at the lumbar spine (LS), femoral neck (FN), trochanter (TR), and whole body (TOT). The coefficients of variation (CVs) in normal subjects for the DPX-L have been reported previously as 0.9% for LS, 1.7% for FN, and 2.5% for TR.⁽³¹⁾

Quantitative ultrasound (QUS)

QUS of the right heel was performed to obtain calcaneal broadband ultrasound attenuation (BUA) and speed of sound (SOS) with a Sahara bone sonometer (Hologic, Inc., Waltham, MA, USA) between 1996 and 2001. Based on duplicate same-day measurements on 29 subjects, CVs for BUA and SOS were 5.3% and 0.4%, respectively.⁽³⁶⁾

Hip geometry

DXA scans were measured with an interactive computer program⁽³⁷⁾ that derived a number of proximal femoral structural variables, including gross anatomic [femoral neck length (FNL, cm) and neck-shaft angle (NSA, degrees)] and cross-sectional indices (outer, or subperiosteal, width, cm), cross-sectional bone area (CSA, cm²), and section modulus (Z, cm³) at the two femoral regions (narrow neck, NN, and femoral shaft, S). CVs were reported previously to range from 3.3% (NN outer diameter) to 9.1% (FNL).⁽³⁷⁾

Body composition

We obtained whole-body DXA scans from the study participants with the same Lunar DPX-L machine used for BMD and at the same visit. The scans were collected at medium speed for all subjects regardless of weight or body thickness. Regions of interest were analyzed using the extended analysis of the Lunar software for body composition. Lean mass was derived by subtracting regional bone mineral content from the fat-free mass of the whole body and lower extremities.

Metacarpal measurements by radiogrammetry

In the Framingham original cohort, right-hand radiographs were obtained in 1967–1969, and the subsample of the offspring cohort was radiographed using the same techniques in 1993–1995^(38,39) as part of the osteoporosis study. The digitized radiographic images of the second, third, and fourth metacarpals were measured semiautomatically (as described in detail elsewhere⁽⁴⁰⁾). CVs, calculated as root-mean-square average,⁽⁴¹⁾ ranged from 1.0% (bone length) to 7.0% (midshaft endosteal diameter). Metacarpal length and midshaft width were measured directly, whereas cortical cross-sectional indices, such as metacarpal cortical thickness (MCT, mm), cortical index (MCI, %), and section modulus (MZ, mm³), were calculated in the middle of bone diaphysis^(42–44); values of metacarpals 2, 3, and 4 were averaged.

Other measurements (covariates)

Information on age, sex, height, body mass index (BMI), and for women, menopausal status and estrogen use were obtained at the time of bone measurement. Details for these measurements are available elsewhere.^(31,45) Women were assigned to one of two estrogenic status groups: (1) premenopausal or postmenopausal on estrogen (estrogen replete) or (2) postmenopausal not on estrogen (estrogen depleted).

Genotyping, quality control, and population structure

Genotyping was conducted through the FHS SHARe (SNP Health Association Resource) project initiated in 2007 on all Framingham Study participants with DNA available using the Affymetrix 500K (250K Sty and 250K Nsp) mapping array with addition of the Affymetrix 50K MIP (gene-centric) supplemental array (Santa Clara, CA, USA). Sample-level exclusions were a participant call rate of less than 97%, a per-subject heterozygosity of ±5 SD from the mean, or a per-subject number of Mendelian errors greater than 165 (99th quantile). Genotyping from 433,510 SNPs in 8481 individuals passed these quality-control measures. Eigenstrat principal-components analysis⁽⁴⁶⁾ was applied to evaluate population structure using a subset of 425,173 SNPs (minor allele frequency [MAF] ≥0.01, Hardy–Weinberg equilibrium [HWE] p ≥10⁻⁶, and call rate ≥0.95). Ten principal components (PCs) were calculated. Since the first 4 of the 10 top PCs were significantly associated with some musculoskeletal traits ( p <.01), we consistently adjusted for PCs 1 through 4 in the SNP association analyses.

Statistical analysis

Multivariable regression analysis was performed separately in men and women from each cohort (original and offspring) to obtain normalized residual phenotypes adjusted for concurrent covariates. Cohort- and gender-specific residuals were combined in ensuing analyses. Musculoskeletal traits were adjusted for age, age², height, PC1 through PC4, and estrogenic status. Bone geometry traits additionally were adjusted for BMI.

Genome-wide association study

We performed GWAS analyses using population-based additive linear mixed-effects (LME) models⁽⁴⁷⁾ with 433,510 SNPs in men and women, separately. LME regression models adjust for within-family correlations in pedigrees of arbitrary sizes and varying degrees of relationship. Additive genetic associations were modeled using R-Kinship software (http://cran.r-project.org).

GWAS database mining

We extracted association statistics for SNPs nominally significantly associated at α level less than 10⁻⁴ with any trait from the list of 23 fracture-related phenotypes in LME analyses. There were 1109 autosomal SNPs in the initial data set. To avoid artifacts of clustering SNPs owing to patterns of linkage disequilibrium (LD), we filtered SNPs using the Tagger software (http://www.broadinstitute.org/mpg/tagger)⁽⁴⁸⁾ to exclude SNPs in higher LD (pairwise genotypic r² ≥0.5); we also used two additional thresholds: a liberal (r² ≥0.2) and a conservative, with r² ≥0.8. Since we randomly selected tag SNPs among a group of SNPs in LD at each threshold, there were several replicates for each data set. Randomly selected tag SNPs that are representative of a group at each LD threshold (r² ≥0.2, 0.5, or 0.8) were included in the biclustering procedure to reduce the effect of correlation between the markers.

Block-clustering model and fitting algorithm

We used a Bayesian model framework for our biclustering (block-clustering) algorithm. The details of the statistical model and fitting algorithm are provided in the supplementary materials. We use a modified version of the evolutionary Monte Carlo (EMC) algorithm⁽⁴⁹⁾ to fit the model. After monitoring the algorithm until it reaches convergence, we ultimately obtained the best estimate of the block clusters given the observed data. In the general case, when we can have more than one cluster in the data, we iteratively apply the algorithm repeatedly, adding block clusters one at a time after one cluster is found in the data until no more clusters can be found or at least one of the axes has been completely allocated to block clusters (no more rows or columns could be added to a cluster).

Bioinformatic analysis

Annotation

The gene annotation was done based on the UCSC table browser for all RefSeq (hg18) genes. If the SNP was located outside known genic region, the nearest RefSeq gene was assigned as the gene annotation. The distance between nongenic SNPs and the nearest gene ranged from 32 to 1757 kbp.

Identification of enriched canonical pathway in clustered genes

To determine whether any canonical pathway was enriched in the clustered SNPs, the clustered genes were imported into Ingenuity Pathways Analysis (IPA) software (Ingenuity Systems, Redwood City, CA, USA) to obtain networks for further analysis. We used IPA to identify the top enriched canonical pathways. The enriched canonical pathways were ranked by the p values of the Fisher’s exact test, which indicated the probabilities that the input genes (from the biclustered gene set) were associated with genes in the canonical pathways by chance.

Gene network inference via knowledge-based data mining

We next analyzed biologic interactions among clustered genes using the IPA tool. The gene annotations from the biclustered SNPs were entered into the IPA analysis tool to construct the biologic networks of the clustered genes. Networks are generated from the biclustered gene set by maximizing the specific connectivity of the input genes, which represents their interconnectedness with each other relative to other molecules with which they are connected in Ingenuity’s knowledge database. Networks were limited to 35 molecules each to keep them at a functional size. The p value of probability for the genes forming a network was calculated with the right-tailed Fisher’s exact test based on the hypergeometric distribution. To gain biologic insights on whether this novel gene network is associated with any known canonical pathways, we further overlaid the novel gene network with canonical pathways using IPA.

Because musculoskeletal traits are sexually dimorphic and the genetic mechanisms are likely to be sex-specific,⁽⁵⁰⁾ the analyses were performed separately in men and women. We focused on results from the 2038 women because osteoporotic fractures are more common in women, genetic regulation has been shown to differ by gender,^(50,51) and our sample size for women was greater than for men.

Results

GWAS data set

GWAS analysis by linear mixed-effects models resulted in 1109 unique SNPs associated with the 23 studied traits at the lowest p values ranging from p =1.45 ×10⁻⁵ to p =4.15 ×10⁻⁸ (Table 1). The number of SNPs associated with each trait at a p value of less than 10⁻⁴ ranged from 34 SNPs for femoral shaft width to 81 SNPs for metacarpal length. When filtered for LD, there were 668 SNPs at threshold r² ≥0.5 (at thresholds r² ≥0.8 and r² ≥0.2, there were 722 and 589 SNPs, respectively).

Table 1.

Number of Significant Associated SNPs for the Individual Phenotypes (at α <10⁻⁴)

	Trait	No. of SNPs at α <10−4	Lowest p value
1	TOT BMD	56	3.84 × 10−6
2	FN BMD	53	3.86 × 10−6
3	TR BMD	42	1.95 × 10−6
4	LS BMD	46	1.45 × 10−5
5	BUA	49	5.25 × 10−6
6	SOS	51	3.43 × 10−7
7	NSA	43	7.98 × 10−7
8	FNL	44	5.57 × 10−7
9	NN WID	58	4.15 × 10−8
10	NN CSA	55	2.73 × 10−6
11	NN BR	49	4.70 × 10−6
12	NN Z	50	8.31 × 10−8
13	S WID	34	9.71 × 10−6
14	S Z	45	1.87 × 10−7
15	S CSA	70	3.54 × 10−6
16	S BR	56	3.02 × 10−6
17	Metacarpal length	81	4.54 × 10−7
18	Metacarpal WID	53	3.14 × 10−7
19	MCI	65	2.61 × 10−7
20	MCT	50	3.47 × 10−7
21	MZ	62	1.37 × 10−6
22	WBLM	61	2.18 × 10−6
23	LLM	65	5.88 × 10−7

Block clustering of SNP data

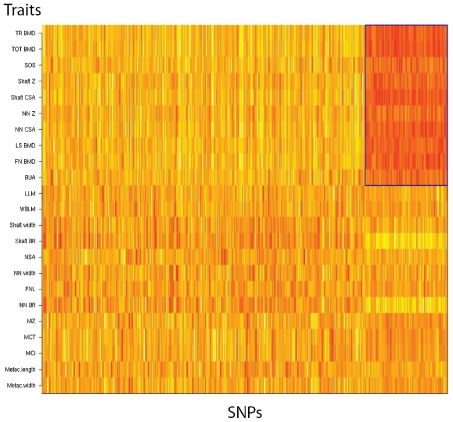
We first applied the block-clustering algorithm to the data set that consisted of regression coefficients from a single-SNP, single-trait association test with an LD cutoff at r² ≥0.5 to avoid the artifact of clustering SNPs in linkage disequilibrium. The SNPs were chosen randomly among the three replicates for the specified LD cutoff. From Fig. 1, a clear cluster of traits and SNPs is observed, the SNPs being negatively correlated with a group of 10 traits: BMD (LS, FN, TR, and TOT), both ultrasound measures, and cross-sectional area (CSA) and section moduli (Z) of the femoral neck and shaft.

Fig. 1.

Biclustering results. Heat map: yellow corresponds to the positive association; red, the negative. The resulting cluster is outlined in blue.

Next, in order to test the consistency and robustness of our algorithm to (1) initial choices of SNPs under the same LD cutoff and (2) different LD cutoffs, we applied the block-clustering algorithm to all the separate data sets under different LD cutoffs (at thresholds r² ≥0.8 and r² ≥0.2). The same 10 traits, namely, LS, FN, TR, and TOT BMD, both ultrasound measures, and CSA, and Z of femoral neck and shaft, were clustered in each data set. Similarly, the same SNPs were selected to be in the bicluster, almost irrespective of LD thresholds (Supplemental Fig. S1). There was a substantial overlap between the sets of SNPs in clusters: From 64.1% to 78.5% of SNPs were shared between the SNP clusters.

Phenomic analysis

We further carried out phenomic analyses and gene network inference procedures on the results of block clustering. Since 10 bone traits were clustered with a distinct set of SNPs, this may imply that these 10 traits share homogeneous genetic architecture to a certain extent. To evaluate this hypothesis, we performed pairwise genetic correlation analyses of all tested musculoskeletal traits and examined whether these 10 clustered traits had stronger genetic correlations than the unclustered traits (see “Supplemental Methods” for details). Pairwise genetic correlations of all traits are provided in Supplemental Table S1. Table 2 shows the mean magnitude of the genetic correlation of the analyses. As follows from the table, the mean magnitudes of the genetic correlation were significantly higher in tested clustered traits with other clustered traits (except for femoral neck Z) than with nonclustered traits. This observation confirmed that the block-clustering algorithm identified a cluster of genes that might underlie similarities between correlated traits.

Table 2.

Difference in Mean Magnitude of Genetic Correlation (ρ_g) Between (A) One Tested Clustered Trait and Other Clustered Traits (n =9) and (B) a Tested Clustered Trait and All Nonclustered Traits (n =13)

	ρg with other clustered traits (n =9)	ρg with non-clustereda traits (n =13)
Clustered trait	Mean SD	Mean SD
BUA	0.40 ± 0.25	0.17 ± 0.14
FNBMD	0.58 ± 0.24	0.31 ± 0.16
LSBMD	0.61 ± 0.16	0.18 ± 0.12
NNCSA	0.59 ± 0.22	0.17 ± 0.14
NNZ	0.37 ± 0.28	0.25 ± 0.19
SCSA	0.61 ± 0.23	0.18 ± 0.18
SOS	0.42 ± 0.26	0.20 ± 0.13
SZ	0.42 ± 0.24	0.21 ± 0.14
TOTBMD	0.61 ± 0.28	0.31 ± 0.19
TRBMD	0.55 ± 0.24	0.28 ± 0.19
Overall meanb	0.52 ± 0.10	0.23 ± 0.06c

^aNonclustered traits include NSA, FNL, NN WID, NN BR, S WID, S BR, metacarpal length, metacarpal WID, MCI, MCT, MZ, WBLM, and LLM.

^bMean was calculated using absolute value of ρ_g regardless of the direction of association.

^cPaired t test p <.001.

Canonical pathway identification and novel gene network inference

To evaluate the potential associated canonical pathway in the SNPs cluster, we annotated the clustered SNP sets using the IPA method (hereafter, we refer to the gene annotation of the clustered SNPs as clustered genes). The top three enriched canonical pathways are listed in Table 3 (the full list of the top enriched canonical pathways in clustered data sets is provided in Supplemental Table S2). The aldosterone signaling in epithelial cells; role of osteoblasts, osteoclasts, and chondrocytes in rheumatoid arthritis (RA); and Parkinson’s signaling pathways are the top three canonical pathways implicated in the analyzed data set (Fisher exact p ≤.01). Other significant pathways that associated with the data set are provided in Supplemental Table S3.

Table 3.

Top Three Enriched Canonical Pathways in Clustered Data Set 05_01

Canonical pathways	p Valuea	Ratiob	Molecules
Aldosterone signaling in epithelial cells	.003	0.04 (4/95)	PIK3R1, SCNN1B, NR3C2, PRKCH
Role of osteoblasts, osteoclasts, and chondrocytes in rheumatoid arthritis	.006	0.03 (6/228)	SFRP4, PIK3R1, WNT16, DKK2, BMP7, DKK1
Parkinson’s signaling	.008	0.12 (2/17)	GPR37, PARK2

^aFisher exact p value.

^bRatio =number of molecules in a given pathway that meet cutoff criteria/total number of molecules in that pathway (numbers shown in parentheses).

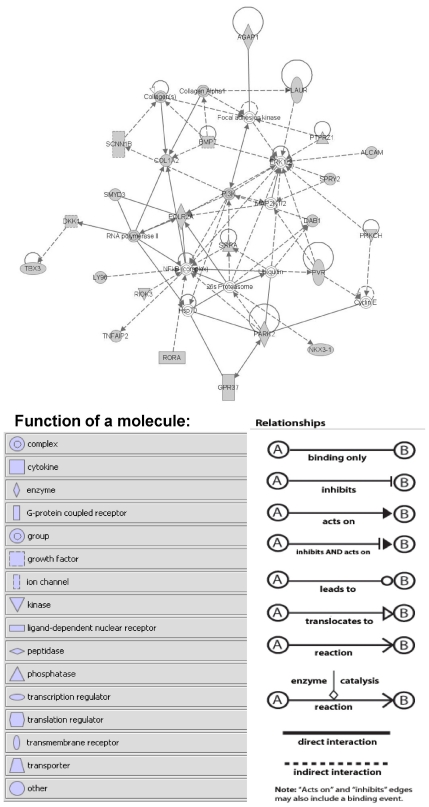
In addition to the fact that the clustered genes contained enriched canonical pathways, they also may represent a novel functional gene network. Therefore, we generated functional gene networks from the clustered genes using IPA. The most significant gene network [26S proteasome, AGAP1, ALCAM, BMP7, COL1A2, collagen α1, collagen(s), cyclin E, DAB1, DKK1, ERK1/2, focal adhesion kinase, GPR37, Hsp70, LY96, MAP2K1/2, NFkB (complex), NKX3-1, PARK2, PI3K, PLAUR, POLR2A, PRKCH, PTPRZ1, PVR, RIOK3, RNA polymerase II, RORA, SCNN1B, SIRPA, SMYD3, SPRY2, TBX3, TNFAIP2, ubiquitin) had p value of 1 × 10⁻⁴⁴ (Fig. 2). This gene network is predicted by the IPA to participate in cellular assembly and organization, embryonic development, and cellular movement functions.

Fig. 2.

Gene network predicted by the Ingenuity Pathways Analysis based on the clustered genes. Shaded genes are clustered genes identified using the biclustering algorithm.

Association of bone-related canonical pathways with the functional gene network

To gain insight on whether the functional networks were associated with any known bone-related canonical pathways, we overlaid the preceding functional network with canonical pathways and focused on the top canonical pathways that showed the greatest number of molecules within the gene network that also participated in the pathway. In the gene network presented in Supplemental Fig. S2, eight network molecules showed association with two canonical pathways. The top associated canonical pathways in this gene network are role of osteoblasts, osteoclasts, and chondrocytes in RA and molecular mechanisms of cancer.

Discussion

Osteoporosis is a complex trait with a relatively late age of onset, making it a challenging disease to study. In terms of quantitative genetics of complex traits, in the absence of a single valid endophenotype (an internal feature of a disease⁽⁵²⁾), pleiotropy among the traits is expected to assist phenotypic prioritization for a study. For example, to decide which is the best phenotype for a planned genetic study, it is imperative to be able to clearly distinguish signal from noise. This approach also results in increased power when mapping correlated phenotypes if they share pleiotropic genetic effects.⁽⁵³⁾ Our novel Bayesian block-clustering algorithm adapted the technique of evolutionary Monte Carlo⁽⁴⁹⁾ for high-dimensional SNP-phenotype data using genetic information from GWAS. Each partition represented a distinct cluster of SNPs that had similar effects over a particular set of traits. Application of this method to our data showed several SNP-trait connections. Thus we identified (1) 10 traits showing homogeneous genetic architecture and (2) the pleiotropic gene networks implicated in these clustered traits that were connected with several bone-related canonical pathways.

In this study, we analyzed many musculoskeletal phenotypes because neither is a perfect proxy for osteoporotic fracture. For example, among the hip geometry indices, in addition to Z and CSA, there were femoral neck length, neck shaft angles, and estimates of mean cortical thickness, cross-sectional moment of inertia, and an index of bone structural instability (buckling ratio) that play a role in local susceptibility to fracture.⁽⁵⁴⁾ Metacarpal bone geometry measures also had been used in epidemiologic research as well as in primary care to identify patients with osteoporosis.^(55–57) We also included the lean mass measures because the loss of muscle mass with age (“sarcopenia”) is accompanied by a decrease in muscle strength and reduced loading of the skeleton.⁽⁵⁸⁾ Using the biclustering approach, we found a strong cluster of high-magnitude coefficients and/or lower p values for some bone traits associated with a subset of SNPs. These 10 traits included BMD of several skeletal locations, heel ultrasound measures, and cross-section area (CSA) and section moduli (Z) of the femoral neck and shaft. Biologically, these 10 traits represent a functional unit of “bone strength.” Indeed, BMD and heel ultrasound measures are among best predictors of fracture risk.^(17,20) For long bones, Z is an index of bone bending strength, and CSA is an indicator of bone axial compression strength; both are important indicators of structural capacity to resist bending or compressive forces, respectively. Identification of this clustering of bone strength traits can be interpreted as a potential measure of success of our reverse-phenotyping efforts. Because high values of the coefficients were achieved for 10 traits clustering with a group of SNPs, we hypothesized that these traits should share a strong homogeneous genetic architecture. In agreement with the hypothesis, the mean magnitudes of genetic correlations among these 10 traits were higher than with the nonclustered traits, implying that the block-biclustering algorithm identified a cluster of genes that form a gene network (or genetic module) that underlies these traits.

Our clustering was independent of LD threshold and random reshuffling of the associated SNPs; indeed, to reduce the effect of correlation between the markers on the cluster analysis, we constructed data sets with three thresholds of r² ≥0.2, 0.5, and 0.8. Analyses of multiple replicates at the same LD threshold demonstrated the consistency of our algorithm and its relative robustness to LD threshold differences. The biclustering approach also highlighted some aspects of how the SNPs were selected. Although there was the expected variation in the SNPs selected to be in a given bicluster based on the different LD-based data sets, overall, the cluster was highly consistent with regard to random reshuffling. Whether the selected genes are truly associated with osteoporosis can only be shown empirically,⁽⁵⁹⁾ and it is not possible to validate our approach to selection of “pleiotropic” candidate genes without further functional investigation.

A closer investigation of the top connected networks generated by IPA provided the following interesting biologic insights: The most significant canonical pathway associated with the gene clusters was aldosterone signaling in epithelial cells. It has been well reported that aldosteronism affects bone metabolism; for instance, bone mineral and bone strength are lost in the presence of a high level of aldosterone.^(60,61) Interestingly, two (NR3C2 and PIK3R1) of four pathway genes from the cluster have been demonstrated to be involved in bone metabolism. NR3C2 encodes mineralcortical receptor (MR) that is expressed in osteocytes, osteoblasts, and osteoclasts,⁽⁶²⁾ and aldosterone activation of MR promotes osteoblastic differentiation.⁽⁶³⁾ PIK3R1 encodes a subunit of phosphatidylinositol 3 kinase, which is an important mediator in both osteoblast and osteoclast differentiation.^(64–67) Although no known function of PRKCH (protein kinase C, eta) and SCNN1B (epithelial sodium channel) is reported in any bone cell or bone diseases, gene expression of PRKCH in osteoblasts is correlated with other bone markers (ie, osteocalcin, bone sialoprotein, and alkaline phosphatase) at various differentiation and maturation stages,⁽⁶⁸⁾ suggesting that PRKCH is a potential candidate gene that affects bone metabolism.

The second most significant canonical pathway associated with the gene clusters was the pathway responsible for rheumatoid arthritis (RA). RA is a chronic inflammatory disease that leads to strucutural destruction of both bones and joints. The pathogenesis of RA in bone is an imbalance of the osteoblast-osteoclast axis driven by inflammatory processes that leads to excessive bone resorption by osteoclasts. Six genes (SFRP4, WNT16, DKK2, BMP7, DKK1, and PIK3R1) from the cluster are associated with this disease pathway. In fact, four among these six genes also belong to the Wnt/β-catenin signaling pathway,^(69–71) except BMP7. BMP-7 plays a role in calcium regulation and bone homeostasis by inducing cartilage and bone formation. It is a Food and Drug Administration–approved ectopic bone inducer for clinical use in long bone open fractures, nonunion fractures, and spine fusion. Therefore, our findings confirmed two important pathways that underlie the etiology of osteoporosis and additionally identified PRKCH and SCNN1B as the novel potential candidate genes that affect bone metabolism.

The role of the third most significant canonical pathway, the Parkinson’s signaling pathway, in bone strength is more puzzling. Recent epidemiologic studies pointed out this connection too. Thus, in community-dwelling older women with Parkinson’s disease (PD), compared with those without it, women with PD had 7.3% lower BMD.⁽⁷²⁾ Very similarly, older men with PD had a significantly greater rate of annualized total hip bone loss than those without parkinsonism.⁽⁷³⁾ Dopamine transporter (Dat)–deficient mice manifest a low-bone-mass phenotype.⁽⁷⁴⁾ We therefore believe that this tantalizing finding should be explored further, whether or not there is a dopaminergic-related connection between the diseases.

To further understand signaling cascades engaged by the most significant gene networks, we overlaid the canonical pathway genes with the gene network generated from our data set. It was shown clearly that the top canonical pathways associated with this new network are related to the skeletal system (canonical pathway role of osteoblasts, osteoclasts, and chondrocytes in rheumatoid arthritis). This observation suggested that the gene network underlying bone strength is governed by multiple signaling pathways and therefore that any perturbation of these pathways may affect the gene network and hence bone strength. Future experimentation will be required to validate these bioinformatic observations.

This study is one of the first forays into phenomics of the musculoskeletal system. Phenomics has a chance of changing how we view heritable diseases first by defining latent phenotypes that underlie genetically similar phenotype categories and second by revealing unexpected genetic links among disease entities.⁽⁷⁵⁾ The incorporation of genetic data clearly improves the quality of the predictions over those derived solely from trait correlations,⁽⁷⁶⁾ although phenotypic overlap is often a very good predictor of functional relatedness of the underlying genes.⁽⁷⁷⁾ Thus van Driel and colleagues⁽⁷⁸⁾ found that similarity between phenotypes did correlate positively with several measures of gene function, including relatedness at the level of protein sequence, protein motifs, functional annotation, and direct protein-protein interaction. We similarly hypothesized that the correlated phenotypes would share multiple associated genetic variants. Obviously, there is also an effect of the shared environmental factors or a confounding by an unmeasured—intermediate—variable.⁽⁷⁹⁾ However, we recently found that the phenotypic and genetic correlations between a pair of traits rather than environmental correlation predict how many SNPs are shared between the two traits.⁽³⁵⁾

This study has several limitations. We used SNPs rather than genes as a source of GWAS mining and later for the gene-enrichment search. In rare cases where one SNP was located on two overlapping genes, we mapped the SNP to both genes; by this, we diminished a bias toward genes that were physically close. Otherwise, genes with better annotation would be more likely to be selected, which could result in a bias toward assortment of well-investigated genes rather than novel predicted or less well-characterized genes.^(59,80) We focused on SNP-based statistics for clustering because there is not a widely agreed on and accepted theory for how to combine test statistics on multiple SNPs in a gene into one single p value (to obtain a maximum statistic to summarize association signals in that gene). When multiple distinct variants in the gene contribute to the overall association signal, the maximum statistic no longer may be the best statistic to capture such information.⁽⁸¹⁾ As noted, our model was restricted to non-overlapping clusters. We are cognizant that gene pathways overlap, as well as phenotypic modules, so that many gene networks and pathways unavoidably will share the same genes.⁽⁸¹⁾ However, the restriction of clusters to not overlap not only leads to a more rigorous model specification but also is more likely to pick out nonredundant clusters, thus overcoming one of the major drawbacks of other existing block-clustering algorithms. Because of the inclusion and exclusion criteria that, owing to redundant SNPs, might influence algorithm performance, we checked the consistency of our results by analyzing the data sets with several exclusion criteria based on LD between the SNPs. We did not apply a similar threshold to the phenotypes, whose selection was based on availability and epidemiologic evidence of their associations with fracture rather than on correlations among them. Because musculoskeletal traits are sexually dimorphic and likely to be influenced by sex-specific genetic mechanisms,⁽⁵⁰⁾ the analyses were performed separately in men and women; however, we presented results from the women because the sample size was greater, and women experience more fractures than men. Results in men appear similar; however, our study has insufficient power for a formal comparison of the clustering results between the sexes. Finally, in this study we adjusted musculoskeletal traits for age, height (bone geometry for BMI), and estrogenic status; however, some potentially important factors, such as exercise, diet, and shared household among family members, were not accounted for.

In conclusion, we used GWAS results to examine pleiotropic relationships between osteoporosis-related traits. We found a distinct SNP cluster of negative coefficients of high magnitude associated with 10 bone-strength phenotypes (mainly BMD, ultrasound, and hip strength indices). The results of biclustering can be used for finding modules within and between the genome and the phenome,^(9,30) data reduction, and choosing the best phenotypes in the pathway to fracture. Accurate understanding of disease phenotype can lead to success in identifying genetic determinants for complex disease.⁽⁵⁹⁾ Similarly, the SNP clusters pointed out the presence of potentially pleiotropic genetic pathways involved in bone strength. Targeting a gene network common for many aspects of a disease may be a favorable approach for therapeutic agent development or predicting the adverse effects of a drug. This study thus presents a novel approach to the analysis of GWAS data and provides directions for further refining of the osteoporosis phenotype and genetic pathways on which to focus in functional studies of osteoporosis.