Sparse nonnegative matrix factorization with ℓ⁰-constraints

Abstract

Although nonnegative matrix factorization (NMF) favors a sparse and part-based representation of nonnegative data, there is no guarantee for this behavior. Several authors proposed NMF methods which enforce sparseness by constraining or penalizing the ${\ell }^1\mathrm{-}\mathrm{norm}$ of the factor matrices. On the other hand, little work has been done using a more natural sparseness measure, the ${\ell }^0\mathrm{-}\mathrm{pseudo}\mathrm{-}\mathrm{norm}$. In this paper, we propose a framework for approximate NMF which constrains the ${\ell }^0\mathrm{-}\mathrm{norm}$ of the basis matrix, or the coefficient matrix, respectively. For this purpose, techniques for unconstrained NMF can be easily incorporated, such as multiplicative update rules, or the alternating nonnegative least-squares scheme. In experiments we demonstrate the benefits of our methods, which compare to, or outperform existing approaches.

1. Introduction

Nonnegative matrix factorization (NMF) aims to factorize a nonnegative matrix $\mathbf{X}$ into a product of nonnegative matrices $\mathbf{W}$ and $\mathbf{H}$. We can distinguish between exact NMF, i.e. $\mathbf{X}=\mathbf{WH}$, and approximate NMF, i.e. $\mathbf{X}\approx \mathbf{WH}$. For approximate NMF, which seems more relevant for practical applications, one needs to define a divergence measure between the data $\mathbf{X}$ and its reconstruction $\mathbf{WH}$, such as the Frobenius norm or the generalized Kullback–Leibler divergence [1]. Approaches using more generalized measures, such as Bregman divergences or the $\alpha \mathrm{-}\mathrm{divergence}$, can be found in [2,3]. In this paper, we focus on approximate NMF using the Frobenius norm as objective. Let the dimensions of $\mathbf{X}$, $\mathbf{W}$ and $\mathbf{H}$ be $D\times N$, $D\times K$, and $K\times N$, respectively. When the columns of $\mathbf{X}$ are multidimensional measurements of some process, the columns of $\mathbf{W}$ gain the interpretation of basis vectors, while $\mathbf{H}$ contains the corresponding weights. The number of basis vectors (or inner approximation rank) K is typically assumed to be $K⪡\min (D,N)$. Hence, NMF is typically used as compressive technique.

Originally proposed by Paatero and Tapper under the term positive matrix factorization [4], NMF became widely known due to the work of Lee and Seung [5,1]. One reason for its popularity is that the multiplicative update rules proposed in [1] are easy to implement. Furthermore, since these algorithms rely only on matrix multiplication and element-wise multiplication, they are fast on systems with well-tuned linear algebra methods. The main reason for its popularity, however, is that NMF tends to return a sparse and part-based representation of its input data, which makes its application interesting in areas such as computer vision [5], speech and audio processing [6–9], document clustering [10], to name but a few. This naturally occurring sparseness gives NMF a special status compared to other matrix factorization methods such as principal/independent component analysis or k-means clustering.

However, sparsity in NMF occurs as a by-product due to nonnegativity constraints, rather than being a design objective of its own. Various authors proposed modified NMF algorithms which explicitly enforce sparseness. These methods usually penalize [11,12] or constrain [13] the ${\ell }^1\mathrm{-}\mathrm{norm}$ of $\mathbf{H}$ or $\mathbf{W}$, which is known to yield a sparse representation [14,15]. An explanation for the sparseness inducing nature of the ${\ell }^1\mathrm{-}\mathrm{norm}$ is that it can be interpreted as a convex relaxation of the ${\ell }^0$-(pseudo)-norm, i.e. the number of non-zero entries in a vector. Indeed, the ${\ell }^0\mathrm{-}\mathrm{norm}$ is a more intuitive sparseness measure, which allows to specify a certain number of non-zero entries, while similar statements cannot be made via the ${\ell }^1\mathrm{-}\mathrm{norm}$. Introducing the non-convex ${\ell }^0\mathrm{-}\mathrm{norm}$ as constraint function typically renders a problem NP-hard, requiring exhaustive combinatoric search. However, Vavasis [16] has shown that NMF is NP-hard per se,¹ so we have to accept (most probably) that any algorithm for NMF is suboptimal. Hence, a heuristic method for NMF with ${\ell }^0\mathrm{-}\mathrm{constraints}$ might be just as appropriate and efficient as ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF.

Little work is concerned with ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF. The K-SVD algorithm [17] aims to find an overcomplete dictionary for sparse representation of a set of training signals $\mathbf{X}$. The algorithm minimizes the approximation error between data $\mathbf{X}$ and its reconstruction $\mathbf{WH}$, where ${\ell }^0\mathrm{-}\mathrm{constraints}$ are imposed on the columns of $\mathbf{H}$. The nonnegative version of K-SVD [18] additionally constrains all matrices to be nonnegative. Hence, nonnegative K-SVD can be interpreted as NMF with sparseness constraints on the columns of $\mathbf{H}$. Probabilistic sparse matrix factorization (PSMF) [19] is closely related to K-SVD, however, no nonnegative PSMF was proposed so far. Morup et al. [20] proposed an approximate NMF algorithm which constrains the ${\ell }^0\mathrm{-}\mathrm{norm}$ of the $\mathbf{H}$ columns, using a nonnegative version of least angle regression and selection [21]. For the $\mathbf{W}$ update, they used the normalization-invariant update rule described in [12]. In [22], a method for NMF was described, which penalizes a smoothed ${\ell }^0\mathrm{-}\mathrm{norm}$ of the matrix $\mathbf{H}$. Using this smooth approximation of the ${\ell }^0\mathrm{-}\mathrm{norm}$, they were able to derive multiplicative update rules, similar as in [1]. More details about prior art concerned with ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF can be found in Section 2.4.

In this paper, we propose two generic strategies to compute an approximate NMF with ${\ell }^0\mathrm{-}\mathrm{sparseness}$ constraints on the columns of $\mathbf{H}$ or $\mathbf{W}$, respectively. For NMF with constraints on $\mathbf{H}$, the key challenge is to find a good approximate solution for the nonnegative sparse coding problem, which is NP-hard in general [23]. For sparse coding without nonnegativity constraints, a popular approximation algorithm is orthogonal matching pursuit (OMP) [24], due to its simplicity and theoretic guarantees [25,26]. Here, we show a close relation between OMP and the active set algorithm for nonnegative least squares (NNLS) [27], which, to the best of our knowledge, was overlooked in the literature so far. As a consequence, we propose a simple modification of NNLS, called sparse NNLS (sNNLS), which represents a natural integration of nonnegativity constraints in OMP. Furthermore, we propose an algorithm called reverse sparse NNLS (rsNNLS), which uses a reversed matching pursuit principle. This algorithm shows the best performance of all sparse coders in our experiments, and competes with or outperforms nonnegative basis pursuit (NNBP). Note that basis pursuit usually delivers better results than algorithms from the matching pursuit family, while requiring more computational resources [28,25]. For the second stage in our framework, which updates $\mathbf{W}$ and the non-zero coefficients in $\mathbf{H}$, we show that the standard multiplicative update rules [1] can be used without any modification. Also, we propose a sparseness maintaining active set algorithm for NNLS, which allows to apply an alternating least squares scheme for ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF.

Furthermore, we propose an algorithm for NMF with ${\ell }^0\mathrm{-}\mathrm{constrained}$ columns in $\mathbf{W}$. As far as we know, no method exists for this problem so far. The proposed algorithm follows a similar approach as in ${\ell }^1\mathrm{-}\mathrm{constrained}$ NMF [13], projecting the columns of $\mathbf{W}$ onto the closest vectors with desired sparseness after each update step. In experiments, the algorithm runs much faster than the ${\ell }^1\mathrm{-}\mathrm{constrained}$ method. Furthermore, the results of the proposed method are significantly sparser in terms of the ${\ell }^0\mathrm{-}\mathrm{norm}$ while achieving the same reconstruction quality.

Throughout the paper, we use the following notation. Upper-case boldface letter denote matrices. For sets we use Fraktur letters, e.g. $\mathcal{P}$. A lower-case boldface letter denotes a column vector. A lower-case boldface letter with a subscript index denotes a specific column of the matrix denoted by the same upper-case letter, e.g. ${\mathbf{x}}_i$ is the ith column of matrix $\mathbf{X}$. Lower-case letters with subscripts denote specific entries of a vector or a matrix, e.g. x _i is the ith entry of $\mathbf{x}$ and $x_{i,j}$ is the entry in the ith row and the jth column of $\mathbf{X}$. A matrix symbol subscripted with a set symbol denotes the submatrix consisting of the columns which are indexed by the elements of the set, e.g. ${\mathbf{W}}_{\mathcal{P}}$ is the sub-matrix of $\mathbf{W}$ containing the columns indexed by $\mathcal{P}$. Similarly, a vector subscripted by a set symbol is the sub-vector containing the entries indexed by the set. With $\parallel ·{\parallel }_p,p\ge 1$ we denote the ${\ell }^p\mathrm{-}\mathrm{norm}$: $\parallel \mathbf{x}{\parallel }_p={({\sum }_i|x_i{|}^p)}^{1/p}$. Further, $\parallel ·{\parallel }_0$ denotes the ${\ell }^0\mathrm{-}\mathrm{pseudo}\mathrm{-}\mathrm{norm}$, i.e. the number of non-zero entries in the argument. The Frobenius norm is defined as $\parallel \mathbf{X}{\parallel }_F=\sqrt{{\sum }_{i,j}|x_{i,j}{|}^2}$.

The paper is organized as follows. In Section 2 we discuss NMF techniques related to our work. We present our framework for ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF in Section 3. Experiments are presented in Section 4 and Section 5 concludes the paper.

2. Related work

Let us formalize NMF as the following optimization problem:

$$\underset{\mathbf{W},\mathbf{H}}{\mathrm{minimize}}\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{subject}\mathrm{to}\mathbf{W}\ge 0\mathrm{,}\mathbf{H}\ge 0,$$ (1)

where $\ge$ denotes the element-wise greater-or-equal operator.

2.1. NMF via multiplicative updates

Lee and Seung [1] showed that $\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F$ is nonincreasing under the multiplicative update rules

$$\mathbf{H}\leftarrow \mathbf{H}\otimes \frac{({\mathbf{W}}^T\mathbf{X})}{({\mathbf{W}}^T\mathbf{WH})}$$ (2)

and

$$\mathbf{W}\leftarrow \mathbf{W}\otimes \frac{({\mathbf{XH}}^T)}{({\mathbf{WHH}}^T)},$$ (3)

where $\otimes$ and / denote element-wise multiplication and division, respectively. Obviously, these update rules preserve nonnegativity of $\mathbf{W}$ and $\mathbf{H}$, given that $\mathbf{X}$ is element-wise nonnegative.

2.2. NMF via alternating nonnegative least squares

Paatero and Tapper [4] originally suggested to solve (1) alternately for $\mathbf{W}$ and $\mathbf{H}$, i.e. to iterate the following two steps:

$$\mathbf{H}\leftarrow \underset{\mathbf{H}}{\arg \min }\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{s}.\mathrm{t}.\mathbf{H}\ge 0,$$

$$\mathbf{W}\leftarrow \underset{\mathbf{W}}{\arg \min }\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{s}.\mathrm{t}.\mathbf{W}\ge 0.$$

Note that $\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F$ is convex in either $\mathbf{W}$ or $\mathbf{H}$, respectively, but non-convex in $\mathbf{W}$ and $\mathbf{H}$ jointly. An optimal solution for each sub-problem is found by solving a nonnegatively constrained least-squares problem (NNLS) with multiple right hand sides (i.e. one for each column of $\mathbf{X}$). Consequently, this scheme is called alternating nonnegative least-squares (ANLS). For this purpose, we can use the well known active-set algorithm by Lawson and Hanson [27], which for convenience is shown in Algorithm 1. The symbol ${}^{†}$ denotes the pseudo-inverse.

Algorithm 1

Active-set NNLS [27].

1:	$\mathcal{Z}=\{1,\dots ,K\},\mathcal{P}=\varnothing$
2:	$\mathbf{h}=\mathbf{0}$
3:	$\mathbf{r}=\mathbf{x}-\mathbf{Wh}$
4:	$\mathbf{a}={\mathbf{W}}^T\mathbf{r}$
5:	while$\left|\mathcal{Z}\right|>0$and$\exists i\in \mathcal{Z}:a_i>0$do
6:	$i^{⁎}=\arg \max \mathbf{a}$
7:	$\mathcal{Z}\leftarrow \mathcal{Z}⧹i^{⁎}$
8:	$\mathcal{P}\leftarrow \mathcal{P}\cup i^{⁎}$
9:	${\mathbf{z}}_{\mathcal{P}}={\mathbf{W}}_{\mathcal{P}}^{†}\mathbf{x}$
10:	${\mathbf{z}}_{\mathcal{Z}}=0$
11:	while$\exists j\in \mathcal{P}:z_j<0$do
12:	$\alpha =\underset{k\in \mathcal{P}}{\min }{h}_k/(h_k-z_k)$
13:	$\mathbf{h}\leftarrow \mathbf{h}+\alpha (\mathbf{z}-\mathbf{h})$
14:	$\mathcal{Z}\leftarrow \{i|h_i=0\}$
15:	$\mathcal{P}\leftarrow \{i|h_i>0\}$
16:	${\mathbf{z}}_{\mathcal{P}}={\mathbf{W}}_{\mathcal{P}}^{†}\mathbf{x}$
17:	${\mathbf{z}}_{\mathcal{Z}}=0$
18:	end while
19:	$\mathbf{h}\leftarrow \mathbf{z}$
20:	$\mathbf{r}=\mathbf{x}-\mathbf{Wh}$
21:	$\mathbf{a}={\mathbf{W}}^T\mathbf{r}$
22:	end while

This algorithm solves NNLS for a single right hand side, i.e. it returns ${\arg \min }_{\mathbf{h}}\parallel \mathbf{x}-\mathbf{Wh}{\parallel }_2,\mathrm{s}.\mathrm{t}.\mathbf{h}\ge 0$, for an arbitrary vector $\mathbf{x}$. The active set $\mathcal{Z}$ and the in-active set $\mathcal{P}$ contain disjointly the indices of the $\mathbf{h}$ entries. Entries with indices in $\mathcal{Z}$ are held at zero (i.e. the nonnegativity constraints are active), while entries with indices in $\mathcal{P}$ have positive values. In the outer loop of Algorithm 1, indices are moved from $\mathcal{Z}$ to $\mathcal{P}$, until an optimal solution is obtained (cf. [27] for details). The inner loop (steps 11–18) corrects the tentative, possibly infeasible (i.e. negative) solution $\mathbf{z}$ to a feasible one. Note that i ^⁎ is guaranteed to be an element of $\mathcal{Z}$ in step 6, since the residual $\mathbf{x}-\mathbf{Wh}$ is orthogonal to every column in ${\mathbf{W}}_{\mathcal{P}}$, and hence ${\mathbf{a}}_{\mathcal{P}}\equiv 0$. Lawson and Hanson [27] showed that the outer loop has to terminate eventually, since the residual error strictly decreases in each iteration, which implies that no in-active set $\mathcal{P}$ is considered twice. Unfortunately, there is no polynomial runtime guarantee for NNLS. However, they report that the algorithm typically runs well-behaved.

For ANLS, one can apply Algorithm 1 to all columns of $\mathbf{X}$ independently, in order to solve for $\mathbf{H}$.² However, a more efficient variant of NNLS with multiple right hand sides was proposed in [29]. This algorithm executes Algorithm 1 quasi-parallel for all columns in $\mathbf{X}$, and solves step 16 (least-squares) jointly for all columns sharing the same in-active set $\mathcal{P}$. Kim and Park [30] applied this more efficient variant to ANLS-NMF. Alternatively, NNLS can be solved using numerical approaches, such as the projected gradient algorithm proposed in [31]. For the remainder of the paper, we use the notation $\mathbf{h}=\mathrm{NNLS}(\mathbf{x},\mathbf{W})$ to state that $\mathbf{x}$ is approximated by $\mathbf{Wh}$ in NNLS sense. Similarly, $\mathbf{H}=\mathrm{NNLS}(\mathbf{X},\mathbf{W})$ denotes the solution of an NNLS problem with multiple right hand sides.

2.3. Sparse NMF

Various extensions have been proposed in order to incorporate sparsity in NMF, where sparseness is typically measured via some function of the ${\ell }^1\mathrm{-}\mathrm{norm}$. Hoyer [11] proposed an algorithm to minimize the objective $\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F^2+\lambda {\sum }_{\mathit{ij}}\left|H_{\mathit{ij}}\right|$, which penalizes the ${\ell }^1\mathrm{-}\mathrm{norm}$ of the coefficient matrix $\mathbf{H}$. Eggert and Koerner [12] used the same objective, but proposed an alternative update which implicitly normalizes the columns of $\mathbf{W}$ to unit length. Furthermore, Hoyer [13] defined the following sparseness function for an arbitrary vector $\mathbf{x}$:

$$\mathrm{sparseness}(\mathbf{x})=\frac{\sqrt{D}-\parallel \mathbf{x}{\parallel }_1/\parallel \mathbf{x}{\parallel }_2}{\sqrt{D}-1},$$ (4)

where D is the dimensionality of $\mathbf{x}$. Indeed, $\mathrm{sparseness}(\mathbf{x})$ is 0, if all entries of $\mathbf{x}$ are non-zero and their absolute values are all equal, and 1 when only one entry is non-zero. For all other $\mathbf{x}$, the function smoothly interpolates between these extreme cases. Hoyer provided an NMF algorithm which constrains the sparseness of the columns of $\mathbf{W}$, the rows of $\mathbf{H}$, or both, to any desired sparseness value according to (4). There are further approaches which aim to achieve a part-based and sparse representation, such as local NMF [32] and non-smooth NMF [33].

2.4. Prior art for ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF

As mentioned in the Introduction, relatively few approaches exist for ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF. The K-SVD algorithm [17] aims to ${\mathrm{minimize}}_{\mathbf{W},\mathbf{H}}\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F,$ subject to $\parallel {\mathbf{h}}_i{\parallel }_0\le L,\forall i,$ where $L\in \mathbb{N}$ is the maximal number of non-zero coefficients per column of $\mathbf{H}$. Hence, the nonnegative version of K-SVD (NNK-SVD) [18] can be considered as an NMF algorithm with ${\ell }^0\mathrm{-}\mathrm{sparseness}$ constraints on the columns of $\mathbf{H}$. However, the sparse coding stage in nonnegative K-SVD is rather an ad hoc solution, using an approximate version of nonnegative basis pursuit [28]. For the $\mathbf{W}$ update stage, the K-SVD dictionary update is modified, by simply truncating negative values to zero after each iteration of an SVD approximation.

In [20], an algorithm for NMF with ${\ell }^0\mathrm{-}\mathrm{sparseness}$ constraints on the $\mathbf{H}$ columns was proposed. For the sparse coding stage, they used a nonnegative version of least angle regression and selection (LARS) [21], called NLARS. This algorithm returns a so-called solution path of the ${\ell }^1\mathrm{-}\mathrm{regularized}$ objective $\parallel \mathbf{x}-\mathbf{Wh}{\parallel }_F^2+\lambda \parallel \mathbf{h}{\parallel }_1$ using an active-set algorithm, i.e. it returns several solution vectors $\mathbf{h}$ with varying $\lambda$. For a specific column $\mathbf{x}$ out of $\mathbf{X}$, one takes the solution $\mathbf{h}$ with desired ${\ell }^0\mathrm{-}\mathrm{sparseness}$ (when there are several such vectors, one selects the solution with smallest regularization parameter $\lambda$). Repeating this for each column of $\mathbf{X}$, one obtains a nonnegative coding matrix with ${\ell }^0\mathrm{-}\mathrm{sparseness}$ on its columns. To update $\mathbf{W}$, the authors used the self-normalizing multiplicative update rule described in [12].

In [22], the objective $\parallel \mathbf{x}-\mathbf{Wh}{\parallel }_F^2+\alpha {\sum }_i{\sum }_j{f}_{\sigma }(h_{i,j})$ is considered, where $f_{\sigma }(h)=\exp (-h^2/2{\sigma }^2)$. For $\sigma \to 0$, the second term in the objective converges to $\alpha$ times the number of non-zero entries in $\mathbf{H}$. Contrary to the first two approaches, which constrain the ${\ell }^0\mathrm{-}\mathrm{norm}$, this method calculates an NMF which penalizes the smoothed ${\ell }^0\mathrm{-}\mathrm{norm}$, where penalization strength is controlled with the trade-off parameter $\alpha$. Therefore, the latter approach proceeds similar as the NMF methods which penalize the ${\ell }^1\mathrm{-}\mathrm{norm}$ [11,12]. However, note that a trade-off parameter for a penalization term is generally not easy to choose, while ${\ell }^0\mathrm{-}\mathrm{sparseness}$ constraints have an immediate meaning.

3. Sparse NMF with ${\mathbf{\ell }}^{\mathbf{0}}\mathbf{-}\mathbf{constraints}$

We now introduce our methods for NMF with ${\ell }^0\mathrm{-}\mathrm{sparseness}$ constraints on the columns of $\mathbf{W}$ and $\mathbf{H}$, respectively. Formally, we consider the problems

$$\underset{\mathbf{W},\mathbf{H}}{\mathrm{minimize}}\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{subject}\mathrm{to}\mathbf{W}\ge 0,\mathbf{H}\ge 0\mathrm{,}\parallel {\mathbf{h}}_i{\parallel }_0\le L,\forall i$$ (5)

and

$$\underset{\mathbf{W},\mathbf{H}}{\mathrm{minimize}}\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{subject}\mathrm{to}\mathbf{W}\ge 0,\mathbf{H}\ge 0\mathrm{,}\parallel {\mathbf{w}}_i{\parallel }_0\le L,\forall i.$$ (6)

We refer as $\mathrm{NMF}{\ell }^0$-H and $\mathrm{NMF}{\ell }^0$-W to problems (5) and (6), respectively. Parameter $L\in \mathbb{N}$ is the maximal allowed number of non-zero entries in ${\mathbf{w}}_i$ or ${\mathbf{h}}_i$.

For $\mathrm{NMF}{\ell }^0$-H, the sparseness constraints imply that each column in $\mathbf{X}$ is represented by a conical combination of maximal L nonnegative basis vectors. When we interpret the columns of $\mathbf{W}$ as features, this means that each data sample is represented by maximal L features, where typically $L⪡K$. Nevertheless, if the reconstruction error is small, this implies that the extracted features are important to some extend. Furthermore, as noted in the Introduction, for unconstrained NMF it is typically assumed that $K⪡\min (D,N)$. We do not have to make this restriction for $\mathrm{NMF}{\ell }^0$-H, and can even choose $K>D$, i.e. we can allow an overcomplete basis matrix $\mathbf{W}$ (however, we require $K<N$).

For $\mathrm{NMF}{\ell }^0$-W, the sparseness constraints enforce basis vectors with limited support. If for example the columns of $\mathbf{X}$ contain image data, sparseness constraints on $\mathbf{W}$ encourage a part-based representation.

NMF algorithms usually proceed in a two stage iterative manner, i.e. they alternately update $\mathbf{W}$ and $\mathbf{H}$ (cf. Section 2). We apply the same principle to $\mathrm{NMF}{\ell }^0$-H and $\mathrm{NMF}{\ell }^0$-W, where we take care that the sparseness constraints are maintained.

3.1. $\mathrm{NMF}{\ell }^0$-H

A generic alternating update scheme for $\mathrm{NMF}{\ell }^0$-H is illustrated in Algorithm 2. In the first stage, the sparse coding stage, we aim to solve the nonnegative sparse coding problem. Unfortunately, the sparse coding problem is NP-hard [23], and an approximation is required. We discuss several approaches in Section 3.1.1. In the second stage we aim to enhance the basis matrix $\mathbf{W}$. Here we allow that non-zero values in $\mathbf{H}$ are adapted during this step, but we do not allow that zero values become non-zero, i.e. we require that the sparse structure of $\mathbf{H}$ is maintained. We will see in Section 3.1.2 that all NMF techniques discussed so far can be used for this purpose. Dependent on the methods used for each stage, we can derive different algorithms from the generic scheme. Note that NNK-SVD [18] and the ${\ell }^0\mathrm{-}\mathrm{constrained}$ NMF proposed by Morup et al. [20] also follow this framework.

Algorithm 2

$\mathrm{NMF}{\ell }^0$-H.

1:	Initialize $\mathbf{W}$ randomly
2:	for$i=1:\mathrm{numIter}$do
3:	Nonnegative Sparse Coding: Sparsely encode data $\mathbf{X}$, using fixed basis matrix $\mathbf{W}$, resulting in a sparse, nonnegative matrix $\mathbf{H}$.
4:	Basis Matrix Update: Enhance basis matrix $\mathbf{W}$ and coding matrix $\mathbf{H}$, maintaining the sparse structure of $\mathbf{H}$.
5:	end for

3.1.1. Nonnegative sparse coding

The nonnegative sparse coding problem is formulated as

$$\underset{\mathbf{H}}{\mathrm{minimize}}\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F\mathrm{subject}\mathrm{to}\mathbf{H}\ge 0\mathrm{,}\parallel {\mathbf{h}}_i{\parallel }_0\le L,\forall i.$$ (7)

Without loss of generality, we assume that the columns of $\mathbf{W}$ are normalized to unit length. A well known and simple sparse coding technique without nonnegativity constraints is orthogonal matching pursuit (OMP) [24], which is shown in Algorithm 3. OMP is a popular technique, due to its simplicity, its low computational complexity, and its theoretical optimality bounds [25,26].

Algorithm 3

Orthogonal matching pursuit (OMP).

1:	$\mathbf{r}\leftarrow \mathbf{x}$
2:	$\mathbf{h}=\mathbf{0}$
3:	$\mathcal{P}=\varnothing$
4:	for l=1:Ldo
5:	$\mathbf{a}={\mathbf{W}}^T\mathbf{r}$
6:	$i^{⁎}=\arg \max \left|\mathbf{a}\right|$
7:	$\mathcal{P}\leftarrow \mathcal{P}\cup \{i^{⁎}\}$
8:	${\mathbf{h}}_{\mathcal{P}}\leftarrow {\mathbf{W}}_{\mathcal{P}}^{†}\mathbf{x}$
9:	$\mathbf{r}\leftarrow \mathbf{x}-{\mathbf{W}}_{\mathcal{P}}{\mathbf{h}}_{\mathcal{P}}$
10:	end for

In each iteration, OMP selects the basis vector which reduces the residual $\mathbf{r}$ most (steps 6 and 7). After each selection step, OMP projects the data vector into the space spanned by the basis vectors selected so far (step 8).

Several authors proposed nonnegative variants of OMP [26,34,35], where all of them replace step 6 with $i^{⁎}=\arg \max \mathbf{a}$, i.e. the absolute value function is removed in order to select a basis vector with a positive coefficient. The second point, where nonnegativity can be violated, is in step 8, the projection step. Bruckstein et al. [26] used NNLS [27] (Algorithm 1) instead of ordinary least squares, in order to maintain nonnegativity. Since this variant is very slow, we used the multiplicative NMF update rule for $\mathbf{H}$ (cf. (2)), in order to approximate NNLS [35]. Yang et al. [34] left step 8 unchanged, which violates nonnegativity in general.

However, there is a more natural approach for nonnegative OMP: Note that the body of the outer loop of the active-set algorithm for NNLS (Algorithm 1) and OMP (Algorithm 3) perform identical computations, except that OMP selects $i^{⁎}=\arg \max \left|\mathbf{a}\right|$, while NNLS selects $i^{⁎}=\arg \max \mathbf{a}$, exactly as in the nonnegative OMP variants proposed so far. NNLS additionally contains the inner loop (11–18) to correct a possibly negative solution. Hence, a straightforward modification for nonnegative sparse coding, which we call sNNLS (which equally well can be called nonnegative OMP), is simply to stop NNLS, as soon as L basis vectors have been selected (i.e. as soon as $\left|\mathcal{P}\right|=L$ in Algorithm 1). Note that NNLS can also terminate before it selects L basis vectors. In this case, however, the solution is guaranteed to be optimal [27]. Hence, sNNLS guarantees to find either a nonnegative solution with exactly L positive coefficients, or an optimal nonnegative solution with less than L positive coefficients. Note further that OMP and NNLS have been proposed in distinct communities, namely sparse representation versus nonnegatively constrained least squares. It seems that this connection has been missed so far. The computational complexity of sNNLS is upper bounded by the original NNLS algorithm [27] (see Section 2.2), since it only contains an additional stopping criterion ($\left|\mathcal{P}\right|=L$).

We further propose a variant of matching pursuit, which does not only apply to the nonnegative framework, but generally to the matching pursuit principle. We call this variant reverse matching pursuit: instead of adding basis vectors to an initially empty set, we remove basis vectors from an optimal, non-sparse solution. For nonnegative sparse coding, this method is illustrated in Algorithm 4, to which we refer as reverse sparse NNLS (rsNNLS). The algorithm starts with an optimal, non-sparse solution in step 1. While the ${\ell }^0\mathrm{-}\mathrm{norm}$ of the solution is greater than L, the smallest entry in the solution vector is set to zero and its index is moved from the in-active set $\mathcal{P}$ to the active set $\mathcal{Z}$ (steps 4–7). Subsequently, the data vector is approximated in NNLS sense by the remaining basis vectors in $\mathcal{P}$, using steps 9–19 of Algorithm 1 (inner correction loop), where possibly additional basis vectors are removed from $\mathcal{P}$. For simplicity, Algorithm 4 is shown for a single data vector $\mathbf{x}$ and corresponding output vector $\mathbf{h}$. An implementation for data matrices $\mathbf{X}$, using the fast combinatorial NNLS algorithm [29], is straightforward. Similar as for sNNLS, the computational complexity of rsNNLS is not worse than for active-set NNLS [27] (Section 2.2), since in each iteration one index is irreversibly removed from $\mathcal{P}$. The NNLS algorithm (step 1) needs at least the same number of iterations to build the non-sparse solution. Hence, rsNNLS needs at most twice as many operations as NNLS.

Algorithm 4

Reverse sparse NNLS (rsNNLS).

1:	$\mathbf{h}=\mathrm{NNLS}(\mathbf{x},\mathbf{W})$
2:	$\mathcal{Z}=\{i|h_i=0\},\mathcal{P}=\{i|h_i>0\}$
3:	while$\parallel \mathbf{h}{\parallel }_0>L$do
4:	$j=\underset{i\in \mathcal{P}}{\arg \min }{h}_i$
5:	$h_j\leftarrow 0$
6:	$\mathcal{Z}\leftarrow \mathcal{Z}\cup \{j\}$
7:	$\mathcal{P}\leftarrow \mathcal{P}⧹\{j\}$
8:	Perform steps 9–19 of Algorithm 1.
9:	end while

The second main approach for sparse coding without nonnegativity constraints is basis pursuit (BP) [28], which relaxes the ${\ell }^0\mathrm{-}\mathrm{norm}$ with the convex ${\ell }^1\mathrm{-}\mathrm{norm}$. Similar as for matching pursuit, there exist theoretical optimality guarantees and error bounds for BP [36,15]. Typically, BP produces better results than OMP [28,25]. Nonnegative BP (NNBP) can be formulated as

$$\underset{\mathbf{h}}{\mathrm{minimize}}\parallel \mathbf{x}-\mathbf{Wh}{\parallel }_2+\lambda \parallel \mathbf{h}{\parallel }_1\mathrm{subject}\mathrm{to}\mathbf{h}\ge 0,$$ (8)

where $\lambda$ controls the trade-off between reconstruction quality and sparseness. Alternatively, we can formulate NNBP as

$$\underset{\mathbf{h}}{\mathrm{minimize}}\parallel \mathbf{h}{\parallel }_1\mathrm{subject}\mathrm{to}\parallel \mathbf{x}-\mathbf{Wh}{\parallel }_2\le ϵ\mathrm{,}\mathbf{h}\ge 0,$$ (9)

where $ϵ$ is the desired maximal reconstruction error. Formulation (9) is more convenient than (8), since the parameter $ϵ$ is more intuitive and easier to choose than $\lambda$. Both (8) and (9) are convex optimization problems and can readily be solved [37]. To obtain an ${\ell }^0\mathrm{-}\mathrm{sparse}$ solution from a solution of (8) or (9), we select the L basis vectors with the largest coefficients in $\mathbf{h}$ and calculate new, optimal coefficients for these basis vectors, using NNLS. All other coefficients are set to zero. The whole procedure is repeated for each column in $\mathbf{X}$, in order to obtain a coding matrix $\mathbf{H}$ for problem (7). NNK-SVD follows this approach for nonnegative sparse coding, using the algorithm described in [11] as approximation for problem (8).

3.1.2. Enhancing the basis matrix

Once we have obtained a sparse encoding matrix $\mathbf{H}$, we aim to enhance the basis matrix $\mathbf{W}$ (step 4 in Algorithm 2). We also allow the non-zero values in $\mathbf{H}$ to vary, but require that the coding scheme is maintained, i.e. that the “zeros” in $\mathbf{H}$ have to remain zero during the enhancement stage.

For this purpose, we can use a technique for unconstrained NMF as discussed in Section 2. Note that the multiplicative update rules (2) and (3) can be applied without any modification, since they consist of element-wise multiplications of the old factors with some update term. Hence, if an entry in $\mathbf{H}$ is zero before the update, it remains zero after the update. Nevertheless, the multiplicative updates do not increase $\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F$, and typically reduce the objective. Therefore, step 4 in Algorithm 2 can be implemented by executing (2) and (3) for several iterations.

We can also perform an update according to ANLS. Since there are no constraints on the basis matrix, we can proceed exactly as in Section 2.2 in order to update $\mathbf{W}$. To update $\mathbf{H}$, we have to make some minor modifications of the fast combinatorial NNLS algorithm [29], in order to maintain the sparse structure of $\mathbf{H}$. Let $\overline{\mathcal{Z}}$ be the set of indices depicting the zero-entries in $\mathbf{H}$ after the sparse coding stage. We have to take care that these entries remain zero during the active set algorithm, i.e. we simply do not allow that an entry, whose index is in $\overline{\mathcal{Z}}$, is moved to the in-active set. The convergence criterion of the algorithm (cf. [27]) has to be evaluated considering only entries whose indices are not in $\overline{\mathcal{Z}}$. Similarly, we can modify numerical approaches for NNLS such as the projected gradient algorithm [31]. Generally, the $\mathbf{W}$ and $\mathbf{H}$ matrices of the previous iteration should be used as initial solution for each ANLS iteration, which significantly enhances the overall speed of $\mathrm{NMF}{\ell }^0$-H.

3.2. $\mathrm{NMF}{\ell }^0$-W

We now address problem $\mathrm{NMF}{\ell }^0$-W (6), where we again follow a two stage iterative approach, as illustrated in Algorithm 5. We first calculate an optimal, unconstrained solution for the basis matrix $\mathbf{W}$ (with fixed $\mathbf{H}$) in step 3. Next, we project the basis vectors onto the closest nonnegative vector in Euclidean space, satisfying the desired ${\ell }^0\mathrm{-}\mathrm{constraints}$. This step is easy, since we simply have to delete all entries except the L largest ones. Step 7 enhances $\mathbf{H}$, where also the non-zero entries of $\mathbf{W}$ can be adapted, but maintaining the sparse structure of $\mathbf{W}$. As in Section 3.1.2, we can use the multiplicative update rules due to their sparseness maintaining property. Alternatively, we can also use the ANLS scheme, similar as in Section 3.1.2. Our framework is inspired by Hoyer's ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF [13], which uses gradient descent to minimize the Frobenius norm. After each gradient step, the algorithm projects the basis vectors onto the closest vector with desired ${\ell }^1\mathrm{-}\mathrm{sparseness}$ (cf. (4)).

Algorithm 5

$\mathrm{NMF}{\ell }^0$-W.

1:	Initialize $\mathbf{H}$ randomly
2:	for$i=1:\mathrm{numIter}$do
3:	${\mathbf{W}}^T=\mathrm{NNLS}({\mathbf{X}}^T,{\mathbf{H}}^T)$
4:	for$j=1:K$do
5:	Set $D-L$ smallest values in ${\mathbf{w}}_j$ to zero
6:	end for
7:	Coding Matrix Update: Enhance the coding matrix $\mathbf{H}$ and basis matrix $\mathbf{W}$, maintaining the sparse structure of $\mathbf{W}$.
8:	end for

4. Experiments

4.1. Nonnegative sparse coding

In this section we empirically compare the nonnegative sparse coding techniques discussed in this paper. To be able to evaluate the quality of the sparse coders, we created synthetic sparse data as follows. We considered random overcomplete basis matrices with D=100 dimensions and containing $K\in \{\mathrm{200,400},800\}$ basis vectors, respectively. For each K, we generated 10 random basis matrices using isotropic Gaussian noise; then the sign was discarded and each vector was normalized to unit length. Further, for each basis matrix, we generated “true” $K\times 100$ sparse encoding matrices $\mathbf{H}$ with sparseness factors $L\in \{\mathrm{5,10},\dots ,50\}$, i.e. we varied the sparseness from L=5 (very sparse) to L=50 (rather dense). The values of the non-zero entries in $\mathbf{H}$ were the absolute value of samples from a Gaussian distribution with standard deviation 10. The sparse synthetic data $\mathbf{X}$ is generated using $\mathbf{X}=\mathbf{WH}$. We executed NMP [35], NNBP, sNNLS, rsNNLS and NLARS³ [20] on each data set. For NNBP we used formulation (9), where $ϵ$ was chosen such that an SNR of $120\mathrm{dB}$ was achieved, and we used an interior point solver [38] for optimization. All algorithms were executed on a quad-core processor (3.2 GHz, 12 GB memory).

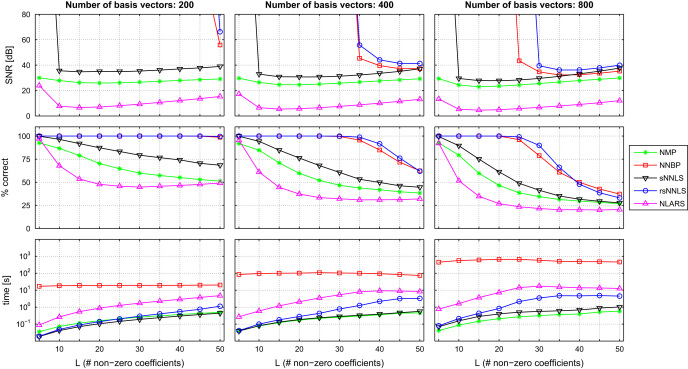
Fig. 1 shows the performance of the sparse coders in terms of reconstruction quality ($\mathit{SNR}=10{\log }_{10}\parallel \mathbf{X}{\parallel }_F^2/\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F^2\mathrm{dB}$), percentage of correctly identified basis vectors, and runtime, averaged over the 10 independent data sets per combination of K and L, where the SNR was averaged in the linear domain (i.e. arithmetic mean). Curve parts outside the plot area correspond to SNR values larger than 120 dB (which we considered as perfect reconstruction). NLARS shows clearly the worst performance, while requiring the most computational time after NNBP. sNNLS performs consistently better than NMP, while being approximately as efficient in terms of computational requirements. The proposed rsNNLS clearly shows the best performance, except that it selects slightly less correct basis vectors than NNBP for K=800 and $L>40$. Note that NNBP requires far the most computational time,⁴ and that the effort for NNBP depends heavily on the number of basis vectors K. rsNNLS is orders of magnitude faster than NNBP.

Fig. 1.

Results of sparse coders, applied to sparse synthetic data. All results are shown as a function of the number of non-zero coefficients L (sparseness factor), and are averaged over 10 independent data sets. First row: reconstruction quality in terms of SNR. Markers outside the plot area correspond to perfect reconstruction ($>120\mathrm{dB}$). Second row: percentage of correctly identified basis vectors. Third row: runtime on logarithmic scale. Abbreviations: nonnegative matching pursuit (NMP) [35], nonnegative basis pursuit (NNBP) [28,18], sparse nonnegative least squares (sNNLS) (this paper), reverse sparse nonnegative least squares (rsNNLS) (this paper), nonnegative least angle regression and selection (NLARS) [20].

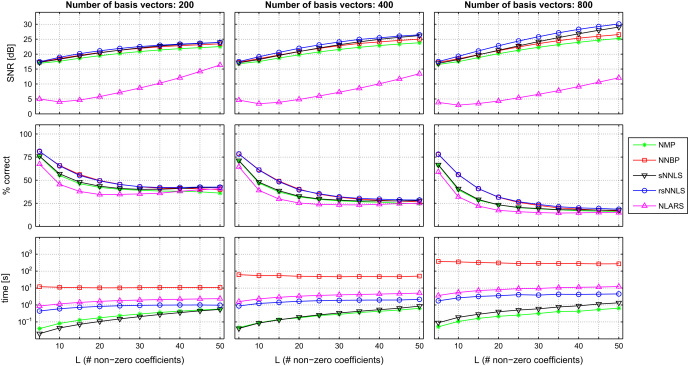
We repeated the experiment, where we added positive, uniformly distributed noise to the synthetic sparse data, such that $\mathrm{SNR}=10\mathrm{dB}$. Note that the choice of $ϵ$ for NNBP is now more difficult: A too small $ϵ$ renders problem (9) infeasible, while a too large $ϵ$ delivers poor results. Therefore, for each column in $\mathbf{X}$, we initially selected $ϵ$ according to $\mathrm{SNR}=19\mathrm{dB}$. For the case where problem (9) turned out to be infeasible, we relaxed the SNR constraint by $-3\mathrm{dB}$ until a feasible problem was obtained. The results of the experiment with noisy data is shown in Fig. 2 . As expected, all sparse coders achieve a lower reconstruction quality and identify less correct basis vectors than in the noise-free case. The proposed rsNNLS shows the best performance for noisy data.

Fig. 2.

Results of sparse coders, applied to sparse synthetic data, contaminated with noise (SNR=10 dB). All results are shown as a function of L and are averaged over 10 independent data sets. First row: reconstruction quality in terms of SNR. Second row: percentage of correctly identified basis vectors. Third row: runtime on logarithmic scale. Abbreviations: nonnegative matching pursuit (NMP) [35], nonnegative basis pursuit (NNBP) [28,18], sparse nonnegative least squares (sNNLS) (this paper), reverse sparse nonnegative least squares (rsNNLS) (this paper), nonnegative least angle regression and selection (NLARS) [20].

4.2. $\mathrm{NMF}{\ell }^0$-H applied to spectrogram data

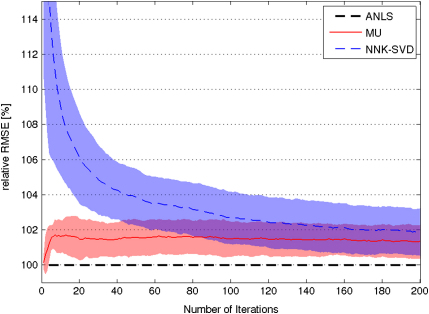
In this section, we compare methods for the update stage in $\mathrm{NMF}{\ell }^0$-H (Algorithm 2). As data we used a magnitude spectrogram of 2 min of speech from the database by Cooke et al. [39]. The speech was sampled at 8 kHz and a 512 point FFT with an overlap of 256 samples was used. The data matrix finally had dimensions 257×3749. We executed $\mathrm{NMF}{\ell }^0$-H for 200 iterations, where rsNNLS was used as sparse coder. We compared the update method from NNK-SVD [18], the multiplicative update rules [1] (Section 3.1.2), and ANLS using the sparseness maintaining active-set algorithm (Section 3.1.2). Note that these methods are difficult to compare, since one update iteration of ANLS fully optimizes first $\mathbf{W}$, then $\mathbf{H}$, while one iteration of NNK-SVD or the multiplicative rules only reduce the objective, which is significantly faster. Therefore, we proceeded as follows: we executed 10 (inner) ANLS iterations per (outer) $\mathrm{NMF}{\ell }^0$-H iteration, and recorded the required time. Then we executed the versions using NNK-SVD and the multiplicative updates, respectively, where both were allowed to update $\mathbf{W}$ and $\mathbf{H}$ for the same amount of time as ANLS in each outer iteration. Since NNK-SVD updates the columns of $\mathbf{W}$ separately [18], we let NNK-SVD update each column for a kth fraction of the ANLS time.

For the number of basis vectors K and sparseness value L, we used each combination of $K\in \{\mathrm{100,250},500\}$ and $L\in \{\mathrm{5,10},20\}$. Since the error depends strongly on K and L, we calculated the root mean square error (RMSE) of each update method relative to the error of the ANLS method, and averaged over K and L: ${\mathrm{RMSE}}_{\mathit{rel}}(i)=\frac{1}{9}{\sum }_{K,L}\parallel \mathbf{X}-\mathbf{W}(K,L,i)\mathbf{H}(K,L,i){\parallel }_F/\parallel \mathbf{X}-{\mathbf{W}}_{\mathrm{ANLS}}(K,L,i){\mathbf{H}}_{\mathrm{ANLS}}(K,L,i){\parallel }_F$, where i denotes the iteration number of $\mathrm{NMF}{\ell }^0$-H, $\mathbf{W}(K,L,i)$ and $\mathbf{H}(K,L,i)$ are the factor matrices of the method under test in iteration i, for parameters K and L. Similarly, ${\mathbf{W}}_{\mathrm{ANLS}}(K,L,i)$ and ${\mathbf{H}}_{\mathrm{ANLS}}(K,L,i)$ are the factor matrices of the ANLS update method. Fig. 3 shows the averaged relative RMSE for each update method, as a function of i. The ANLS approach shows the best performance. The multiplicative update rules are a constant factor worse than ANLS, but perform better than NNK-SVD. After 200 iterations, the multiplicative update rules and NNK-SVD achieve an average error which is approximately 1.35% and 1.9% worse than the ANLS error, respectively. NNK-SVD converges slower than the other update methods in the first 50 iterations.

Fig. 3.

Averaged relative RMSE (compared to ANLS update) of multiplicative update rules (MU) and nonnegative K-SVD (NNK-SVD) over number of $\mathrm{NMF}{\ell }^0$-H iterations. The shaded bars correspond to standard deviation.

4.3. $\mathrm{NMF}{\ell }^0$-W applied to face images

Lee and Seung [5] reported that NMF returns a part-based representation, when applied to a database of face images. However, as noted by Hoyer [13], this effect does not occur when the face images are not aligned, like in the ORL database [40]. In this case, the representation happens to be rather global and holistic. In order to enforce a part-based representation, Hoyer constrained the basis vectors to be sparse. Similarly, we applied $\mathrm{NMF}{\ell }^0$-W to the ORL database, where we constrained the basis vectors to have sparseness values L corresponding to $33\%$, $25\%$ and $10\%$ of the total pixel number per image (denoted as sparseness classes a, b and c, respectively) As in [13], we trained 25 basis vectors per sparseness value. We executed the algorithm for 30 iterations, using 10 ANLS coding matrix updates per iteration. In order to compare our results to ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF [13], we calculated the average ${\ell }^1\mathrm{-}\mathrm{sparseness}$ (using (4)) of our basis vectors. We executed ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF on the same data, where we required the basis vectors to have the same ${\ell }^1\mathrm{-}\mathrm{sparseness}$ as our $\mathrm{NMF}{\ell }^0$-W basis vectors. We executed the algorithm for 2500 iterations, which were necessary for convergence. Fig. 4 shows the resulting basis vectors returned by $\mathrm{NMF}{\ell }^0$-W and ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF, where dark pixels indicate high values and white pixels indicate low values.

Fig. 4.

Top: basis images trained by $\mathrm{NMF}{\ell }^0$-W. Bottom: basis images trained by ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF. Sparseness: 33% (a), 25% (b), 10% (c), 52.4% (d), 43% (e), 18.6% (f) of non-zero pixels.

We see that the results are qualitatively similar, and that the representation becomes a more local one, when sparseness is increased (from left to right). We repeated this experiment 10 times and calculated the ${\ell }^0\mathrm{-}\mathrm{sparseness}$ (in % of non-zero pixels), the $\mathit{SNR}=10{\log }_{10}\parallel \mathbf{X}{\parallel }_F^2/\parallel \mathbf{X}-\mathbf{WH}{\parallel }_F^2\mathrm{dB}$ and measured the runtime for both methods. The averaged results are shown in Table 1 , where the SNR was averaged in the linear domain.

Table 1.

Comparison of ${\ell }^0\mathrm{-}\mathrm{sparseness}$ (in percent of non-zero pixels), ${\ell }^1\mathrm{-}\mathrm{sparseness}$ (cf. (4)), reconstruction quality in terms of SNR, and runtime for ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF [13] and $\mathrm{NMF}{\ell }^0$-W. SNR^⁎ denotes the SNR value for ${\ell }^1\mathrm{-}\mathrm{NMF}$, when the same ${\ell }^0\mathrm{-}\mathrm{sparseness}$ as for $\mathrm{NMF}{\ell }^0$-W is enforced.

Method	${\ell }^0$ (%)	${\ell }^1$	SNR (dB)	SNR⁎ (dB)	Time (s)
${\ell }^1\mathrm{-}\mathrm{NMF}$	52.4	0.55	15.09	14.55	2440
$\mathrm{NMF}{\ell }^0$-W	33	0.55	15.07	–	186
${\ell }^1\mathrm{-}\mathrm{NMF}$	43	0.6	14.96	14.31	2495
$\mathrm{NMF}{\ell }^0$-W	25	0.6	14.94	–	164
${\ell }^1\mathrm{-}\mathrm{NMF}$	18.6	0.73	14.31	13.52	2598
$\mathrm{NMF}{\ell }^0$-W	10	0.73	14.33	–	50

We see that the two methods achieve de facto the same reconstruction quality, while $\mathrm{NMF}{\ell }^0$-W uses a significantly lower number of non-zero pixels. One might ask if the larger portion of non-zeros in ${\ell }^1\mathrm{-}\mathrm{NMF}$ basis vectors stems from over-counting entries which are extremely small, yet numerically non-zero. Therefore, Table 1 additionally contains a column showing SNR${}^{⁎}$ for ${\ell }^1\mathrm{-}\mathrm{NMF}$, which denotes the SNR value when the target ${\ell }^0\mathrm{-}\mathrm{sparseness}$ is enforced, i.e. all but the 33%, 25%, 10% of pixels with largest values are set to zero. We see that when a strict ${\ell }^0\mathrm{-}\mathrm{constraint}$ is required, $\mathrm{NMF}{\ell }^0$-W achieves a significantly better SNR (at least 0.5 dB in this example). Furthermore, $\mathrm{NMF}{\ell }^0$-W is more than an order of magnitude faster than ${\ell }^1\mathrm{-}\mathrm{sparse}$ NMF in this setup.

5. Conclusion

We proposed a generic alternating update scheme for ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF, which naturally incorporates existing approaches for unconstrained NMF, such as the classic multiplicative update rules or the ANLS scheme. For the key problem in $\mathrm{NMF}{\ell }^0$-H, the nonnegative sparse coding problem, we proposed sNNLS, whose interpretation is twofold: it can be regarded as sparse nonnegative least-squares or as nonnegative orthogonal matching pursuit. From the matching-pursuit perspective, sNNLS represents a natural implementation of nonnegativity constraints in OMP. We further proposed the simple but astonishingly well performing rsNNLS, which competes with or outperforms nonnegative basis pursuit. Generally, ${\ell }^0\mathrm{-}\mathrm{sparse}$ NMF is a powerful technique with a large number of potential applications. $\mathrm{NMF}{\ell }^0$-H aims to find a (possibly overcomplete) representation using sparsely activated basis vectors. $\mathrm{NMF}{\ell }^0$-W encourages a part-based representation, which might be particularly interesting for applications in computer vision.

Biographies

Robert Peharz received his MSc degree in 2010. He currently pursues his PhD studies at the SPSC Lab, Graz University of Technology. His research interests include nonnegative matrix factorization, sparse coding, machine learning and graphical models, with applications to signal processing, audio engineering and computer vision.

Franz Pernkopf received his PhD degree in 2002. In 2002 he received the Erwin Schrödinger Fellowship. From 2004 to 2006, he was Research Associate in the Department of Electrical Engineering at the University of Washington. He received the young investigator award of the province of Styria in 2010. Currently, he is Associate Professor at the SPSC Lab, Graz University of Technology, leading the Intelligent Systems research group. His research interests include machine learning, discriminative learning, graphical models, with applications to image- and speech processing.