Automated object-based classification of topography from SRTM data

Abstract

We introduce an object-based method to automatically classify topography from SRTM data. The new method relies on the concept of decomposing land-surface complexity into more homogeneous domains. An elevation layer is automatically segmented and classified at three scale levels that represent domains of complexity by using self-adaptive, data-driven techniques. For each domain, scales in the data are detected with the help of local variance and segmentation is performed at these appropriate scales. Objects resulting from segmentation are partitioned into sub-domains based on thresholds given by the mean values of elevation and standard deviation of elevation respectively. Results resemble reasonably patterns of existing global and regional classifications, displaying a level of detail close to manually drawn maps. Statistical evaluation indicates that most of classes satisfy the regionalization requirements of maximizing internal homogeneity while minimizing external homogeneity. Most objects have boundaries matching natural discontinuities at regional level. The method is simple and fully automated. The input data consist of only one layer, which does not need any pre-processing. Both segmentation and classification rely on only two parameters: elevation and standard deviation of elevation. The methodology is implemented as a customized process for the eCognition® software, available as online download. The results are embedded in a web application with functionalities of visualization and download.

Graphical abstract

Highlights

►First object-based classification of Earth's topography from 1 km SRTM. ► Results resemble patterns of existing global and regional classifications. ► Procedure fully automated, results exported as shapefiles. ► Results embedded in a web application for visualization and download.

1. Introduction

Landforms are ‘natural objects that partition the Earth's surface into fundamental spatial entities, which define boundary conditions for processes operative in the fields of geomorphology, hydrology, ecology, pedology and others’ (MacMillan and Shary, 2009). Therefore, the research interest in designing classification systems of landforms at various scales (MacMillan and Shary, 2009) is not surprising as the demand for subdivisions of the surface into manageable objects even grows (Evans, 2011). While early approaches relied on field surveys, manual processing of topographic maps or drawing boundaries on aerial photographs, digital classifications have greatly benefited from developments in remote sensing in terms of processing techniques and increasing quality of remotely sensed digital elevation models (DEMs). The Shuttle Radar Topography Mission (SRTM) demonstrated the power of synthetic aperture radar (SAR) interferometry to create a global DEM; it marked a milestone in the field of remote sensing (Farr et al., 2007; Shortridge and Messina, 2011) opening new avenues for applications in Earth Sciences.

SRTM DEMs offer new possibilities for landform classifications at regional and global scales, which were previously hindered by the uneven quality of the available data. Physiographic classifications at global scale are particularly important as they provide standardized datasets that enable consistent and comparative analyses of the Earth's surface. Land form information contained within global datasets has the potential of fostering new insights into the land surface analysis (Hammond, 1964), which might be helpful in improving terrain-based environmental modeling through investigations on the areal covariation of properties. However, SRTM data are still rather under-used from this perspective, though it has been released for almost one decade. Iwahashi and Pike (2007) produced the only landform classification at global scale on SRTM data. This is a data-driven approach consisting in an unsupervised nested-means algorithm and a three part geometric signature; slope gradient, local convexity, and surface texture were used as descriptors of the land-surface properties. Individual cells were allocated to classes by using the mean of each variable as the dividing threshold in nested twofold-partitioned maps. The resulting classes resemble existing maps in various regions, including Fenneman's physical divisions (Fenneman and Johnson, 1946) and Hammond's terrain types (Hammond, 1954).

Object-based image analysis (OBIA) has gained prominence in the field of remote sensing during the last decade, being credited with the potential of overcoming weaknesses associated with the per pixel analysis, as for instance neglecting geometric and contextual information (Blaschke, 2010). OBIA has proved effective in landform classification from DEMs (Drăguţ and Blaschke, 2006; van Asselen and Seijmonsbergen, 2006) as it better satisfies the object conceptual model of landforms compared to the traditional per cell methods (Drăguţ and Eisank, 2011). As part of OBIA, the multiresolution segmentation (MRS) algorithm has been found the most sensitive to morphological discontinuities in DEMs (van Niekerk, 2010). The ability of capturing morphological discontinuities is an important asset in designing natural spatial entities (landforms or topographic regions) that maximize internal homogeneity while minimizing external homogeneity. Though the number of OBIA applications in analysis of DEMs has increased in the last five years, an object-based methodology applicable at global scale is still missing.

The main objective of our research is developing an object-based method to automatically classify topography from SRTM data at broader scales into landform types (MacMillan and Shary, 2009) or topographic regions (Iwahashi and Pike, 2007). This method should have the following characteristics: 1) simplicity; 2) versatility; and 3) multi-scale character. Simplicity consists in avoiding data pre-processing, derivation of additional input layers (e.g. slope and curvature.), and parameterization, i.e. deciding which combination of input variables are suitable and how to weight their importance in classification. The method was designed to process a single layer of elevation values, which is the support for segmentation and calculation of standard deviation. Elevation and local relief are essential in classification of topography at broad scales (Hammond, 1954; Wood and Snell, 1960). We replaced local relief with standard deviation of elevation, which is a more stable measure of variation (Evans, 1998). Versatility means that this general-purpose method should be easily customizable for specific applications. Results were compared with existing classifications at global (Iwahashi and Pike, 2007) and regional levels (Fenneman and Johnson, 1946).

2. Methods

Building on our previous results (Drăguţ and Blaschke, 2006), we used an MRS algorithm (Baatz and Schäpe, 2000) to partition a digital elevation model (DEM) into homogeneous regions, which were further classified in physiographic regions with the help of the nested-means technique (Iwahashi and Pike, 2007). New algorithms were designed to automate selection of scale parameters for land-surface segmentation (Section 2.1) and to decompose the scene complexity on three levels (Section 2.2). The whole procedure was implemented as a ‘push-the-button’ solution using the eCognition Network Language (CNL) within the eCognition Developer®, version 8.64.

As input we used the global dataset (more than 600 million cells) of the SRTM DEM V4 (Reuter et al., 2007; Jarvis et al., 2008) resampled to 1 km (http://srtm.csi.cgiar.org). The algorithm was applied to the elevation layer without any prior pre-processing.

2.1. Automated optimization of the scale parameter

MRS provides a region-growing algorithm that merges individual pixels into image objects or regions based on the local homogeneity criteria (Baatz and Schäpe, 2000). The degree of local homogeneity to be used in the merging decision is set by a user-defined parameter called scale parameter (SP). Drăguţ et al. (2010) introduced a method that assist an objective decision on SP, based on the concept of local variance (LV) graphs (Woodcock and Strahler, 1987). In brief, the method consists in producing multiple segmentations of the same dataset by a constantly increasing SP, calculating LV for each scale as the average standard deviation (SD) of objects at the scene level, plotting LV against SP, and interpreting the resulting variogram-like graph. Similar to the variogram analysis, the LV graphs display ranges that approximate sizes of support units (here replacing distance) at which spatial autocorrelation between them tend to cease. Thus, ranges mark the highest spatial independence of objects in the dataset at a given scale (Drăguţ et al., 2011).

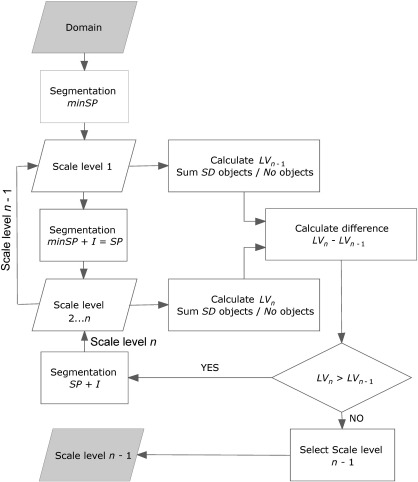
Here we replaced the interpretation of graphs with an automatic procedure for selecting SP at a range (Fig. 1). For an input domain (the first one being the whole extent of the SRTM data), segmentation of the elevation layer is performed in a bottom–up approach, starting from the minimum value of SP (minSP). At each upper scale, the SP value increases with the increment I (similar to lag). Difference in LV between each new level and the previous one is calculated in an iterative approach, until the value is equal to zero or negative. When reaching this value, the previous level is selected; this is an approximation of the equivalent of sill on the LV graph.

Fig. 1.

Workflow to automate the optimization of the scale parameter for land-surface segmentation. The domain of interest is repeatedly segmented by starting at the lowest possible value of SP (minSP) and by constantly increasing SP by an user-specified interval (I). The process stops when the local variance value of the actual level (LV_n) is equal or lower than the value of the previous level (LV_n − 1). The level n − 1 is then selected as the optimal scale for segmentation.

For processing the global dataset, the value of 10 was set as minSP; this was rather a technical constraint, as starting segmentation at an SP value of 1 would have prohibitively increased the time of processing. The value of I was different for each level as detailed in the next section. The shape criterion was weighted to zero; therefore only elevation values were considered in segmentation, without shape optimization.

2.2. Multi-scale decomposition of complexity

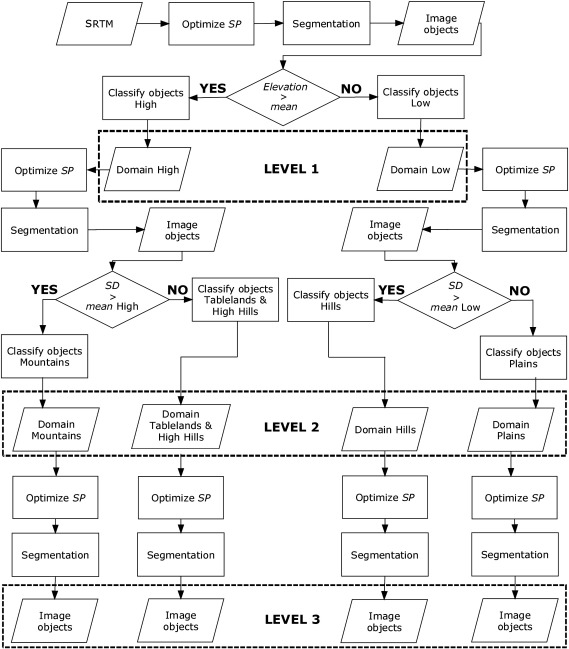
The multiresolution segmentation algorithm minimizes the average heterogeneity of image objects weighted by their size (Baatz and Schäpe, 2000). When applied to DEMs, particularly those with large extents and contrasting topography, the same SP value tends to oversegment rough areas, while under-segmenting smooth ones; the weight on objects size would not compensate the high level of heterogeneity. We addressed this issue by decomposing land-surface complexity into increasingly homogeneous domains, structured on three levels (Fig. 2), with the help of segmentation combined with the nested means approach (Iwahashi and Pike, 2007).

Fig. 2.

Multi-scale decomposition of land-surface complexity into increasingly homogeneous domains. The hierarchy of three levels is obtained by applying the nested means approach to optimized terrain segmentation scales. The whole system is self-adaptive and can easily be used on DEMs with higher resolutions.

The input SRTM was segmented with the optimum SP value (Fig. 1) and resulting objects were partitioned into two domains, ‘High’ and ‘Low’, based on a threshold given by mean elevation of objects at the level of scene. Each domain was further segmented with optimized SP values and partitioned based on a threshold given by the mean SD of elevation. The same procedure of segmentation is applied to each domain of the second level to produce the objects at the third level (Fig. 2).

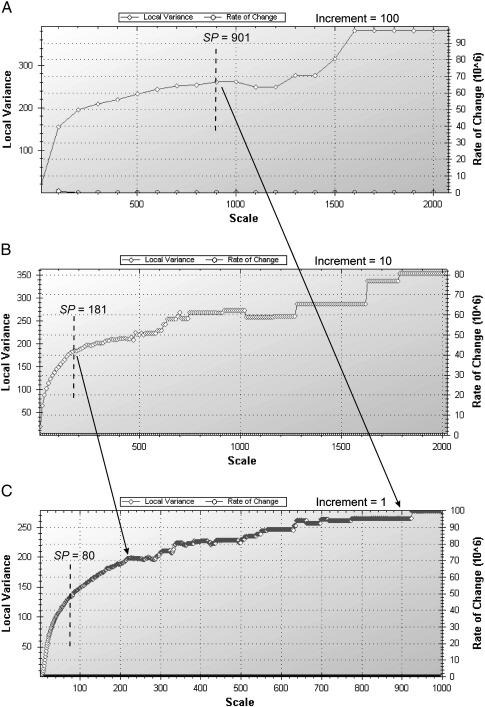
Optimization of SP was performed using different values of increment for each of the three levels to replace selection of multi-scale levels through human interpretation of the LV graphs by an automated procedure. In previous work (Drăguţ et al., 2010, 2011) we showed that prominent peaks on the LV graph indicated the scales where the data are organized in meaningful pattern. Smoothing the LV graph by increasing the increment is a solution for automation. To illustrate this procedure, we present the LV graphs resulting from segmentation of the DEM at the extent of the Austrian territory (Fig. 3). The LV graph obtained by increasing SP by an increment of 1 (Fig. 3C) depicts the smallest variations of the LV values. The first step in this graph occurred at an SP value of 80 (the LV value at SP = 81 was lower or equal to the LV value at SP = 80), which coincides with a marked change in the LV curve. Performing the same analysis with increments of 10 (Fig. 3B) and 100 (Fig. 3A) leads to the smoothing of details so that two prominent peaks in Fig. 3C are approximated by equivalents of sill at SP values of 181 (Fig. 3B) and 901 (Fig. 3A), respectively. These equivalents of sill can be identified automatically as explained in Section 2.1.

Fig. 3.

Smoothing the LV graph by increasing the increment in the iterative bottom–up segmentation from 1 (C), to 10 (B) and 100 (A). As small variations on the graphs are successively smoothed from C to A, the equivalents of sill (shown by dashed vertical lines) occur at increasing values of SP (80 in C, 181 in B, and 901 in A). The equivalents of sill in smoothed graphs (B and A) approximate prominent peaks on the graph obtained with an increment of 1 (C), as indicated by the two arrows.

Scale is intimately related to the complexity of scene so that small and large objects can coexist in the same level. Segmentation with a single SP value would over-segment larger objects or under-segment the smaller ones. To account for this issue, domains at each level as in Fig. 2 were segmented twice, with consecutively smaller increments. Objects produced with SP values detected using larger increments (therefore larger sized) were separated into two groups: those with both mean and maximum elevations lower than the mean elevation of the domain or with both mean and minimum elevations higher than the mean elevation of the domain were retained, while all others were exported to separate maps and further segmented with smaller increments. The former category includes ‘pure’ objects that do not include any cell lower or higher than the characteristic elevation of the class, while the latter one includes large objects spanning across heterogeneous areas. Thus, the global DEM was segmented with increments of 100 and 10 respectively to produce the two domains in Level 1; the same increments were used to segment each of these two domains; the four domains in Level 2 were segmented with increments of 10 and 1 respectively to produce the image objects in Level 3.

To avoid the ‘island effect’ in segmentation, i.e. biasing the size of objects towards numerous small islands, areas smaller than the minimum mapping unit (MMU) relative to each level were not considered in segmentation. The MMU values were selected as a function of the DEM resolution (1 km) (FAO, 2003) as follows: 400 km² for Level 1 (estimating scales in range 1:10,000,000 to 1:20,000,000), 100 km² for Level 2 (1:3,000,000 to 1:10,000,000), and 4 km² for Level 3 (1:1,000,000 to 1:3,000,000).

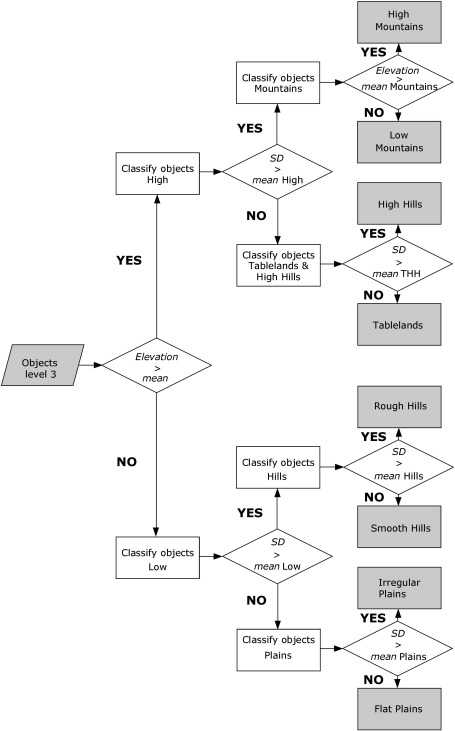
2.3. Classification scheme

Classification is structured on three levels (Fig. 4). At each level, thresholds are automatically set up as means of elevation and its SD (Fig. 4). Mean values at scene levels are computed based on object values, which represent averages of cell values within each object. Although this is an unsupervised classification, classes were labeled according to a simplified version of Hammond's (1954) scheme. An alternative would be using purely morphometric descriptors as in Iwahashi and Pike (2007). We preferred labeling the outputs following a simplified version of Hammond's scheme to increase comprehensibility of the classification.

Fig. 4.

Classification scheme for partitioning the global dataset into eight classes, according to a simplified version of Hammond (1954). Mean values of elevation and standard deviation (SD) define thresholds to split subsequent domains into two, and finally to assign eight physiographic classes to L3 objects.

The objects at the first level were divided into classes ‘High’ and ‘Low’ by the mean elevation of objects. At the second level, classes ‘Mountains’, ‘Tablelands and High Hills’, ‘Low Hills’, and ‘Plains’ were separated by the mean SD value of objects corresponding to each domain in Level 1. The objects of the third level were classified into eight classes using mean elevations as thresholds (classes ‘High Mountains’, ‘Low Mountains’, ‘High Plains’, and ‘Low Plains’) and the mean SD value of elevation (classes ‘High Hills’, ‘Tablelands’, ‘Rough Low Hills’, and ‘Smooth Low Hills’).

2.4. Evaluation

As classification was designed for general purposes, standard methods of assessment (e.g. confusion matrix) would have not been appropriate for evaluating the results. For the present study we followed an evaluation strategy that was twofold. On the one hand a quantitative assessment was performed based on a recently introduced innovative approach. On the other hand an online evaluation system was set up to acquire qualitative feedback from potential users.

2.4.1. Statistical assessment

In the field of OBIA it is common to assess segmentations in terms of region uniformity and region contrast. Optimal results should basically fulfill the two conditions of (1) maximizing intra-object homogeneity and (2) maximizing inter-object heterogeneity. To some degree the same principles also apply to class regions, where each region is considered a merge of adjacent objects belonging to the same class.

Two standard statistical indices, the intra-object variance (ν) and the Moran's I spatial autocorrelation index (I), were calculated. Global Moran's I value gives an indication of the overall external separability of spatial objects, whereas mean variance measures the degree of internal homogeneity of spatial objects. Espindola et al. (2006) successfully utilized a combination of those measures to identify optimal region-growing segmentations in a multi-scale analysis. Recently, it has been shown that classification accuracies are highest for optimal segmentations (Gao et al., 2011).

The mean intra-object variance was calculated using the following equation:

$$\nu =\frac{{\sum }_{i=1}^n{a}_i{\nu }_i}{{\sum }_{i=1}^n{a}_i}$$ (1)

where ν_i is the variance of the cell values within object i, and a_i is the area of object i. The mean intra-object variance ν is calculated as area weighted average, where more weight is put on larger objects, thus reducing the effects of possible instabilities induced by small objects. Interpretation of ν is straightforward: the higher the value, the greater is the overall objects' heterogeneity; the lower the value, the more homogeneous objects are in terms of the measured property. Commonly, a direct relationship between the mean size of objects and the intra-object variance exists: if objects are large, ν is high and vice versa.

Moran's I is formulated as:

$$I=\frac{n{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{\mathit{ij}}\left(y_i-\overline{y}\right)\left(y_j-\overline{y}\right)}{\left({\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2\right)\left({\sum }_{i\ne j}\sum w_{\mathit{ij}}\right)}$$ (2)

where n is the total number of objects, y_i is the mean value of object i, $\overline{y}$ is the mean value of the scene, and w_ij is weight that measures the spatial adjacency of objects i and j. The value of w_ij is 1 if objects i and j are adjacent; otherwise w_ij = 0. Values of Moran's I range from − 1 to + 1. Indices close to zero and negative values indicate that differences in the mean values of neighboring objects are generally high. Thus, the overall spatial heterogeneity is high (dispersed pattern), which is desirable in OBIA. High positive values are obtained if object values are spatially homogeneous (clustered pattern).

Statistics were derived for the following three domains:

• –Objects per level: All objects of an optimal segmentation level were considered for the statistics. Thus, we obtained level-specific measures for inter- and intra-object heterogeneity. Optimal segmentation should be a compromise between the two.
• –Objects per class: Only objects of the same class were assessed. Results provided an indication of inter- and intra-object heterogeneity per class. Ideally, spatial autocorrelation should be positive and variance is relatively low.
• –Class regions per level: Initially, neighboring objects of the same class were merged. Then, level-specific statistics were calculated for the obtained class regions in order to measure inter-class separability, which preferably should be high (negative Moran's I or values close to zero).

Moran's I values were derived with the open-source software tool GeoDa (Anselin, 2005) for the two object properties: mean elevation (I_ME) and mean standard deviation of elevation (I_MSD). Variance indices were only calculated for I_ME. A general size constraint was set to exclude objects smaller than four pixels from analysis. In addition, isolated objects, i.e. objects without direct neighbors, were not taken into account.

2.4.2. Qualitative assessment

In addition to the quantitative evaluation an online system was implemented consisting of two components: a web application, where we put the preliminary results of the finest-level classification, and a questionnaire for acquiring feedback from potential users. A request for participation along with a concise description of the method and web service was distributed among known experts and relevant user groups on the internet (e.g. Geomorphometry Society and Yahoo GMorph Group). With the help of the web application, interested users could visually explore and evaluate results, and provide their personal views via the online survey. Users were kindly asked to evaluate results with respect to (1) thematic and spatial accuracy, (2) versatility and fruitfulness, and (3) general usefulness. The survey was open for four months.

3. Results

The global dataset was processed in more than 138 h on a personal computer with a 2.66 GHz quad-core processor and 8 GB RAM. Results were embedded within a web application that offers services for exploring and downloading the data, available at the following address: (http://zgis202.plus.sbg.ac.at/LandformClassification/default.aspx).

3.1. Classification results

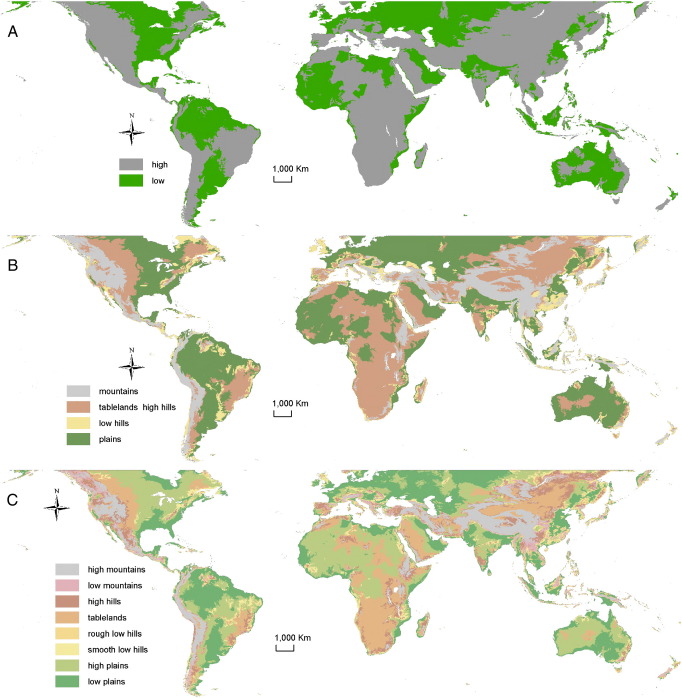
Maps in Fig. 5 show the results of global classification at Level 1 (L1, A), Level 2 (L2, B), and Level 3 (L3, C). The three scale levels reflect the correspondence between the size of objects, as controlled by SP, and thematic resolution, which increases from L1 to L3. Classes match recognizable topographic regions according to the three levels of generalization and most of boundaries appear to follow major natural discontinuities at regional level. For a detailed visualization of the results, the reader is encouraged to use either the web application or the file in Appendix 1 (supplementary on-line material) for visualization in Google Earth.

Fig. 5.

Global classification of topography at Level 1 (A), Level 2 (B), and Level 3 (C).

Summary statistics of variables used in classification are provided in Table 1 (elevation) and Table 2 (standard deviation of elevation). For each variable, Mean, SD, Min and Max values of objects are calculated and grouped by scale levels and classes. Spatial frequency of topographic classes and the percentage of objects per class were added to Table 1. Although slope gradient was not used in classification, its summary statistics were calculated within each class, as this variable is an important indicator of land-surface ruggedness. Slope was calculated for each grid cell within a standard 3 × 3 moving window, and values were summarized within each topographic class using zonal statistics.

Table 1.

Spatial frequency of topographic classes (% Area) and number of objects (% No of objects), and summary statistics of elevation, grouped by scale levels. Statistics (Mean, SD, Min, and Max) are calculated at scene levels based on the average values of objects.

Level/class	% Area	% No of objects	Mean	SD	Min	Max
Level 1	100	100	321.72	453.85	− 218.04	5796.46
High	58.35	28.37	863.27	542.58	321.89	5796.46
Low	41.65	71.63	107.23	93.95	− 218.04	321.50
Level 2	100	100	424.55	614.66	− 181.81	5545.89
Mountains	16.49	13.68	1416.05	989.16	426.88	5545.89
Tablelands and High Hills	31.52	16.92	745.25	418.25	424.78	5017.19
Low Hills	9.54	26.55	244.19	92.73	− 181.81	423.61
Plains	42.45	42.85	93.14	103.54	− 43.27	422.67
Level 3	100	100	566.78	603.19	− 223.09	6093.79
High Mountains	9.21	5.79	2193.03	885.88	1440.45	6093.79
Low Mountains	4.36	9.68	989.41	244.53	567.11	1439.27
High Hills	7.85	10.24	988.93	450.85	566.87	5230.50
Tablelands	16.71	9.61	881.00	335.75	566.80	5137.78
Rough Low Hills	2.66	10.45	372.89	115.50	− 223.09	566.47
Smooth Low Hills	6.52	14.91	290.68	136.60	− 90.60	566.56
High Plains	27.52	17.33	336.90	91.89	193.14	566.77
Low Plains	25.17	22.00	79.75	57.89	− 81.09	193.02

Table 2.

Summary statistics of standard deviation, grouped by scale levels and topographic classes. Statistics (Mean, SD, Min, and Max) are calculated at scene levels based on the average values of objects.

Level/class	Mean	SD	Min	Max
Level 1	99.11	112.70	0.00	1482.64
High	215.44	132.05	0.00	1482.64
Low	53.03	57.82	0.00	328.73
Level 2	104.96	111.00	0.00	811.45
Mountains	320.01	101.52	199.14	811.45
Tablelands and High Hills	101.39	53.41	0.00	199.12
Low Hills	132.10	52.41	63.45	366.05
Plains	20.89	18.49	0.00	63.34
Level 3	95.83	88.19	0.00	826.87
High Mountains	289.03	96.14	162.02	826.87
Low Mountains	226.95	55.99	161.64	588.23
High Hills	126.37	19.63	92.64	161.49
Tablelands	56.67	23.27	0.00	92.53
Rough Low Hills	159.56	38.23	116.13	402.97
Smooth Low Hills	85.63	15.92	59.92	116.07
High Plains	28.08	15.81	0.00	59.91
Low Plains	20.27	15.95	0.00	59.92

Objects classified as ‘High’ make almost 60% of the Earth's surface, while counting only about one third of the total number of 4977 objects in L1 (Table 1). This imbalance is due to the large number of small, low-elevation islands. Although islands smaller than 400 km² were not considered in segmentation, they were taken into account in classification as features on the Earth's surface; these islands represent 70.44% of the total number of objects in this level. As a result, mean elevation of objects at L1 dropped to 321 m. This value separates objects into two domains well differentiated in terms of elevation (Table 1). The ‘Low’ and ‘High’ classes visually correspond to human perception on higher and lower areas at planetary level (Fig. 5A). Moreover, they characterize surfaces of different roughness as indicated by the statistics of standard deviation (Table 2) and slope gradient (Table 3).

Table 3.

Summary statistics of slope gradient, grouped by scale levels and topographic classes. Mean, SD, Min, and Max are calculated based on cells within each class (zonal statistics).

Level/class	Mean	SD	Min	Max
Level 1
High	2.71	3.87	0.00	59.95
Low	0.56	1.14	0.00	35.43
Level 2
Mountains	6.17	5.29	0.00	59.95
Tablelands and High Hills	1.38	1.90	0.00	36.27
Low Hills	2.07	2.40	0.00	35.43
Plains	0.42	0.59	0.00	27.83
Level 3
High Mountains	6.75	5.73	0.00	59.95
Low Mountains	6.93	4.87	0.00	50.25
High Hills	2.96	2.71	0.00	36.27
Tablelands	0.93	1.19	0.00	27.47
Rough Low Hills	4.66	3.59	0.00	39.34
Smooth Low Hills	2.17	2.05	0.00	31.58
High Plains	0.56	0.72	0.00	32.55
Low Plains	0.40	0.63	0.00	31.66

As the degree of generalization decreases, the spatial frequency of low-elevation classes (e.g. ‘Low Hills’ and ‘Plains’) increases by approximately 10% at L2 as compared to L1 (Table 1). The basins of Congo and Chad, the Upper Nile plains, and the hilly region in southeastern China are the most obvious areas that changed from ‘High’ at L1 to ‘Low Hills’ and ‘Plains’ at L2 (Fig. 5B). The class ‘Low Hills’ shows the highest discrepancy between the spatial frequency and the share in the number of objects, which indicates that many small islands fall into this category (Table 1). Statistics of elevation illustrate a logical vertical distribution of the four classes (Table 1). The class ‘Plains’ presents a large variability of elevation values, which is explained by inclusion of isolated hills, as for instance the hills in southeastern Colombia. This is a reasonable generalization of small-sized features, in line with the common regionalization, i.e. in the given example hills are not considered separately, but included within the Amazon region, one of the five natural regions of Colombia. The minimum elevation occurs in the class ‘Low Hills’, not as expected in ‘Plains’. However, this minimum is obtained for the object that delineates the Dead Sea region, which is rougher than plains at global level. Statistics of standard deviation (Table 2) and slope gradient (Table 3) show that the four classes partition the land surface variability properly.

Classification is further detailed at the third level (Fig. 5C). Spatial frequencies are generally balanced with shares of objects, except for the two categories of mountains and the two categories of hills (Table 1). The class ‘High Mountains’ shares a large area compared to the number of objects, while ‘Low Mountains’ shows a reverse case. This is due to the normal spatial configuration, as ‘Low Mountains’ appear scattered around more compact areas of ‘High Mountains’. The two classes of hills present low spatial frequencies despite relatively high shares in the number of objects due to larger presence of islands. Statistics of elevation show a logical vertical distribution of the eight classes, except for ‘High Plains’ with higher mean elevation than ‘Smooth Low Hills’ (Table 1). This means that smooth surfaces at comparatively higher altitudes are classified as plains (Fig. 5C). The Kazakh Uplands represent such an example. We consider such situations to be consistent with the rationales of the classification system, given that separation between hills and plains was done based on land-surface variability.

3.2. Evaluation based on Moran's I and variability

The summary statistics of Moran's I and variability are shown in Table 4.

Table 4.

Results of the statistical evaluation.

Domain		Class	Object count	IME	IMSD	Intra-object variance
Objects per level	Level 1 (L1)	All	1253	0.387	0.295	219,926.82
Level 2 (L2)	All	3202	0.759	0.581	22,893.24
Level 3 (L3)	All	21,807	0.795	0.647	14,573.10
Class regions per Level	L1	All	330	− 0.608	− 0.404	527,403.77
L2	All	974	0.235	− 0.163	213,453.96
L3	All	8459	0.585	0.283	96,184.95
Objects per class	L1	High	967	0.271	0.258	366,075.34
Low	286	− 0.647	− 0.493	14,619.09
L2	Mountains	849	0.671	0.298	108,608.36
Tablelands and High Hills	1091	0.807	0.496	9826.49
Low hills	529	− 0.517	− 0.109	14,214.26
Plains	733	0.736	0.062	1254.06
L3	High Mountains	1472	0.658	0.321	98,280.41
Low Mountains	2433	− 0.437	0.339	52,494.00
Tablelands	2433	0.897	0.385	3229.25
High Hills	2597	0.791	0.081	15,474.42
Rough Low Hills	1953	− 0.507	0.061	24,446.25
Smooth Low Hills	3137	0.043	− 0.067	7100.63
High Plains	4299	0.55	0.629	865.77
Low Plains	3483	0.447	0.362	511.47

3.2.1. Objects per level

Indices of spatial autocorrelation are all valued positive, indicating that the spatial separability between adjacent objects is relatively low. In general results show increasing spatial autocorrelation for both properties Mean and SD from L1 to L3 while intra-object variance decreases. Logically, as the number of objects per level increases, objects become smaller in size, which leads to reduced object variability and differences in values of adjacent objects.

What is striking is that Moran's I values of L3 are only slightly higher than those of L2. Although the number of objects is seven times higher at L3, the degree of spatial separability between objects at those two levels is nearly the same. At least variance reduces significantly from L2 to L3. However, the results suggest that segmentation of L3 is too fine in some areas.

3.2.2. Class regions per level

Statistics calculated for the domain of class regions give an indication of between-class separability and within-class variance. Basically, statistical measures follow the same trends as observed for object levels. Nevertheless, due to the fusion of objects to class regions, the number of objects is lower. For instance, originally L1 consisted of 1253 objects which have been reduced to 330 class regions after merging. Due to the reduced number of objects, values of spatial autocorrelation are low and those of variances are high. Individual classes are well separated if values of spatial autocorrelation are negative or around zero. This is the case for class regions of L1 and L2. At L3 the spatial contrast of adjacent class regions seems to be relatively low, which is supported by positive Moran's I values. Nevertheless it is likely that statistics for this domain are heavily impacted by the thematic resolution, i.e. the number of classes which changes from two (L1) to eight (L3).

3.2.3. Objects per class

The results of class-specific statistics depend on both thematic resolution and class characteristics. Obviously, a lower number of classes lead to a lower intra-class spatial homogeneity and a higher variance. At L1, where objects are categorized into only two classes, I_ME and I_MSD actually show minimum values relative to the according set of class-specific measures. Indices are slightly positive for ‘High’ and strongly negative for ‘Low’. This suggests that segmentation of class ‘Low’ is not ideal as objects are too large in average resulting in high within-class heterogeneity. In contrast, class ‘High’ exhibits a similar degree of spatial uniformity as L1 (I_ME of 0.271 and 0.387 respectively). Negative spatial autocorrelation is likewise observed for some of the sub-classes of ‘Low’: ‘Low Hills’ at L2, and ‘Rough Low Hills’ and ‘Smooth Low Hills’ at L3. Apparently, if a class is under-segmented at the coarser scale, it is probable that some of the sub-classes at finer levels are not optimally segmented as well. Contrarily, significantly high values of Moran's I may be a sign of over-segmentation, especially if both calculated indices show very high values. The highest I_ME and I_MSD are observed for the L3 class ‘Tablelands’ (0.897 and 0.385) and for ‘Tablelands and High Hills’ at L2 (0.807 and 0.496).

Segmentations of remaining classes of the two finer levels L2 and L3 appear to be a good compromise between class homogeneity and intra-class object variability. Except for the under- and over-segmented categories as discussed above, spatial homogeneity of classes is high as indicated by positive values of Moran's I. Variance corresponds well with the ruggedness idea of specific classes. Values are highest for rough terrain classes such as ‘Mountains’ at L2 or ‘High Mountains’ at L3 and lowest for smooth physiographic classes such as ‘Plains’ at L2 or ‘Low Plains’ at L3.

3.3. Evaluation based on the online survey

Within the evaluation period 33 people out of 143 interested completed the questionnaire, i.e. a completion rate of 23%. Major outcomes of the survey are as follows.

3.3.1. Accuracy

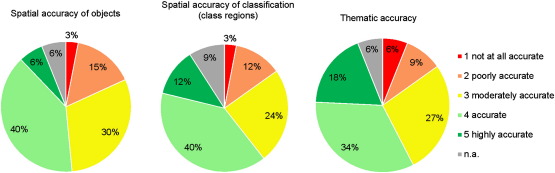
The results of the visual accuracy assessment made by the users are illustrated in Fig. 6. People were asked to evaluate the spatial accuracy of objects and of class regions as well as the thematic accuracy. Basically, the three individual diagrams show a similar picture. In each case about half of the evaluators are of the opinion that results are accurate or highly accurate (grades of 4 and 5 respectively) with the lowest percentage (42%) for the spatial accuracy of class regions. The proportion of people not satisfied with the accuracy (rating of 1 or 2) varies between 15% and 18%, where the highest percentage is observed for the spatial precision of object boundaries.

Fig. 6.

Evaluation of accuracies of the physiographic dataset at Level 3. User perspectives on the spatial accuracy of objects (left) and class regions (middle) as well as on the thematic accuracy (right). Results were obtained through an online survey.

3.3.2. Versatility and fruitfulness

Feedback in this category mainly included users' perspectives on potential application fields and adaptation issues. Outcomes are graphically summarized in Fig. 7. All in all the evaluators identified ten scientific fields to which the physiographic classes and objects are potentially applicable. Answers were categorized into eight classes. The two most selected disciplines are geomorphology and landscape ecology (22 and 21 votes respectively), followed by geology and soil science (both 14). Interestingly, agricultural science got the same number of selections as hydrology and ecology (13). Concerning adaptation the majority of users (31%) believe that manipulation of the results is neither easy nor difficult. At least 40% indicate that adaptation is very simple or simple, against 9% saying that it is difficult to adapt the results. Obviously, the question created some uncertainty amongst evaluators, since one fifth did not provide a valid rating.

Fig. 7.

Evaluation of versatility and fruitfulness of the physiographic dataset at Level 3. User perspectives on potential application fields (left) and on adaptation (right). Results were obtained through an online survey.

3.3.3. General usefulness

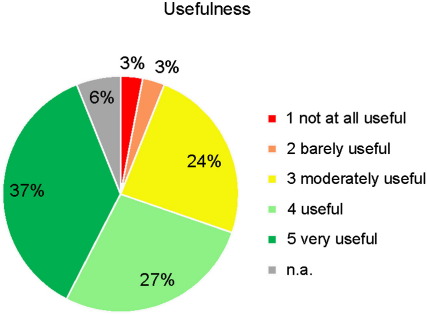
More than one third of experts find the provided dataset very useful (Fig. 8). Another 27% still indicate that it is useful. Only two people (6%) really doubt that the physiographic classification can be of any use. The rest 24% expressed a neutral opinion (grade of 3).

Fig. 8.

User perspectives on the general usefulness of the physiographic dataset at Level 3. Results were obtained through an online survey.

4. Discussion

Our classification produced patterns visually comparable to the existing per cell classifications at global level (Meybeck et al., 2001; Iwahashi and Pike, 2007), although it appears more generalized. More in depth comparisons were made at the level of the conterminous United States, where the classification of Fenneman and Johnson (1946) is available in geospatial format (http://water.usgs.gov/GIS/metadata/usgswrd/XML/physio.xml) (Fig. 9). When compared to Fenneman and Johnson (1946), the object-based classification appears quite successful in depicting well individualized areas, bounded by major regional discontinuities, such as the Olympic Mountains, the Oregon Coast Range, the Klamath Mountains, the California Coast Ranges, the Salton Trough, the California Trough, the Puget Trough, the Northern Cascade Mountains, the Black Hills, the subunits of the Interior Highlands, and those of the Appalachian Highlands. However, it seems less successful in delineating highly heterogeneous areas such as the Intermountain Plateaus and highly homogeneous areas such as the Interior Plains or the Atlantic Plain; these areas look too generalized. Iwahashi and Pike's (2007) classification (in the following abbreviated as IP) does a better job in these areas, probably as a consequence of a higher number of classes.

Fig. 9.

Comparison between Iwahashi and Pike (A) and the object-based classification (B). Both classifications are compared with the polygons delineating Fenneman and Johnson's (1946) sections for the conterminous United States. The legend of (A) represents the 16 topographic classes of Iwahashi and Pike (2007) symbolized according to their degree of slope steepness (gentler from 1 to 16). The red square in (B) shows the extent of Fig. 10.

IP was also statistically compared with the classification at L3 presented in this study. Since IP was only available in digital raster format, the classification was transformed into a feature dataset. Due to the huge number of IP objects, statistics of spatial autocorrelation and object variance were not calculated on a global basis, as originally planned, but only for the conterminous USA (Table 5). IP for the USA still consists of 373,644 objects resulting in considerably high Moran's I indices (I_ME = 0.993 and I_MSD = 1). Hence, the spatial contrast of adjacent IP objects is low, which is not optimal at all. The 436 extracted class regions at L3 are also positively correlated, implying that the spatial contrast is relatively low, though higher than for IP. Surprisingly, the intra-object variance of 53,000 for the class regions seems to be acceptable, since it is only about twice the object variance of IP. We would have expected a much higher internal variability of class regions, because of the low number of objects. These results suggest that the object-based classification performs better than IP in partitioning the land surface, particularly in terms of roughness, according to the basic principle of regionalization (maximizing internal homogeneity and external difference).

Table 5.

Statistical comparison of the object-based class regions at L3 with the classification of Iwahashi and Pike (2007) for the conterminous USA.

Domain	Object count	IME	IMSD	Intra-object variance
Class regions L3	436	0.611	0.399	53,000
Objects IP	373,644	0.993	1	24,186

As Bittner (2011) has demonstrated, a trade-off is required between delineation of geographic regions (which relies on local qualities) and their classification (which relies on global qualities). Such trade-off is possible with OBIA, since object delineation is clearly separated from classification of objects. The methodology presented here puts more emphasis on capturing topographic discontinuities based on local contrasts and leaves the classification of objects at a generic level. The eight classes might not coincide with some geomorphic categories, as for instance piedmont or footslopes. As this classification is unsupervised, the resulting categories represent geomorphometric entities that should be interpreted as representations of different land surfaces in terms of roughness and altitudinal position, relevant to a given extent (in this work the whole Earth surface). These entities can be further interpreted by incorporating expert knowledge and (possibly) other data to extract geomorphologically relevant categories (Eisank et al., 2011). For a comprehensive discussion on differences between geomorphometric classification and geomorphological mapping, see Evans (2011). The classification scheme has been designed for general purposes, i.e. to offer a synopsis of the Earth surface in respect to the two variables. Nevertheless, the classification can be tuned for specific goals by manipulating the objects and their attributes (see Appendix 2 in supplementary on-line material for a list of available attributes) through basic GIS operations. For instance, even though the alluvial plain of the Mississippi River was smoothed out within a large flat plain (Fig. 9B), its boundaries are captured as parts of distinct objects (Fig. 10), which can easily be reclassified to depict the alluvial plain distinctly. This is only one of many examples proving the high versatility of results.

Fig. 10.

Polygons (in black) classified as ‘Low Plains’ corresponding to regional topographic discontinuities such as the contacts of the alluvial plain of the Mississippi River. Location of the area is shown in Fig. 9B. For comparison, red lines represent a section from the Mississippi Alluvial Plain as delineated by Fenneman and Johnson (1946).

Land-surface classifications have usually been implemented based on combinations of land-surface variables that make up a geometric signature (Pike, 1988). Selection of the optimal number of variables as input data (aka parameterization) depends on spatial scales (Iwahashi and Pike, 2007) and might involve subjective decisions. We demonstrated that using a single variable as input data, namely elevation, can lead to reasonable results as shown by visual inspection, statistical assessment and the survey. This was possible as the method of LV graphs, when applied to DEMs, shares the rationales of the topographic grain concept (Wood and Snell, 1960). Pike et al. (1989) defined topographic grain as a threshold phenomenon of spatial autocorrelation that measures the areal dominance of terrain by its characteristic local relief. Topographic grain therefore evaluates the characteristic horizontal spacing of major topographic features by integrating measures of distance, local relief (aka elevation range) and scale. For the present study we replaced the unit-cell size by the object size, and local relief by standard deviation of elevation, which is a more stable measure of variation (Evans, 1998) and enhances the graph (Pike et al., 1989). Thus, two of the three components of Iwahashi and Pike's (2007) geometric signature, namely slope gradient and surface texture, were approximated in our methodology from a single input data. Indeed, Table 3 shows a logical distribution of summary statistics of slope gradient among classes even though this variable was not used in classification. Accounting indirectly for the two land-surface variables via the LV with topographic grain approach makes this methodology much less sensitive to DEM resolution and accuracy, two main issues acknowledged by Iwahashi and Pike (2007). Our tests on various extends (not presented here) showed similarly satisfying results when using the 90 m SRTM DEM as input. Accuracy, on the other hand, becomes a less important issue in an OBIA approach, as local variation is smoothed out by objects.

Application of the LV method did not necessarily result in ‘perfect’ segmentation of the entire scene. Naturally, the more complex a scene is, the more challenging scale optimization becomes. The results of the statistical assessment demonstrated that over- and under-segmentation could not be fully avoided — not even when applying an optimization strategy that works regionally. Though considered in this work, scene complexity is an issue that deserves more research. For the present study we used a rather crude criterion of selecting highly variable objects to be re-processed at each level, namely mean and min/max elevations not belonging to an elevation domain. An iterative procedure based on internal variability and external difference of each object could be a better solution to cope with scene complexity.

5. Conclusions

The global SRTM DEM at 1 km is automatically classified into eight topographic classes using an OBIA approach. Global complexity is decomposed on three levels by an iterative algorithm that identifies appropriate scales in the data, produces scale-relevant objects, and partitions these objects into domains of similar land-surface properties.

The results reasonably resemble patterns of existing global and regional classifications, and the statistical evaluation indicates that most of classes satisfy the regionalization requirements of maximizing internal homogeneity while minimizing external homogeneity. Exceptions are given by ‘Tablelands’, which are over-segmented, and the two categories of low hills, which are under-segmented. Most of volunteers participating in an online survey are satisfied with the accuracy, versatility and usefulness of the results.

The present study introduces the first OBIA classification of landforms at global level. Compared to existing per cell classifications, the object-based approach appears to produce more generalized results and a better partition of the land surface from a regionalization perspective, particularly regarding surface roughness. The results are delivered in a vector format, thus ready for GIS analyses and customizing.

The methodology is implemented as a customized process for the eCognition^® software, available online at http://www.scala-project.at. The results are embedded in a web application with functionalities of visualization and download, available at http://zgis202.plus.sbg.ac.at/LandformClassification/default.aspx.

Supplementary data associated with this article can be found in the online version, at doi:10.1016/j.geomorph.2011.12.001. These data include Google maps of the most important areas described in this article.

The following ZIP file contains the Google maps of the most important areas described in this article.

Map

ZIP file containing the Google maps of the most important areas described in this article.