Two-Axis Acceleration of Functional Connectivity Magnetic Resonance Imaging by Parallel Excitation of Phase-Tagged Slices and Half k-Space Acceleration

Abstract

Whole brain functional connectivity magnetic resonance imaging requires acquisition of a time course of gradient-recalled (GR) volumetric images. A method is developed to accelerate this acquisition using GR echo-planar imaging and radio frequency (RF) slice phase tagging. For N-fold acceleration, a tailored RF pulse excites N slices using a uniform-field transmit coil. This pulse is the Fourier transform of the profile for the N slices with a predetermined RF phase tag on each slice. A multichannel RF receive coil is used for detection. For n slices, there are n/N groups of slices. Signal-averaged reference images are created for each slice within each slice group for each member of the coil array and used to separate overlapping images that are simultaneously received. The time-overhead for collection of reference images is small relative to the acquisition time of a complete volumetric time course. A least-squares singular value decomposition method allows image separation on a pixel-by-pixel basis. Twofold slice acceleration is demonstrated using an eight-channel RF receive coil, with application to resting-state functional magnetic resonance imaging in the human brain. Data from six subjects at 3 T are reported. The method has been extended to half k-space acquisition, which not only provides additional acceleration, but also facilitates slice separation because of increased signal intensity of the central lines of k-space coupled with reduced susceptibility effects.

Introduction

This work was carried out in a context of functional connectivity magnetic resonance imaging (fcMRI), which is also called resting-state MRI (Biswal et al., 1995). The specific purpose of this work was to reduce the time needed for acquisition of a single volumetric gradient-recalled echo-planar imaging (GR-EPI) data set. For whole-brain connectomics (Sporns et al., 2005), a time course of these data sets is required. A familiar methodology in fcMRI image analysis involves the cross correlation of a seed voxel resting-state time course with other voxel time courses (Biswal et al., 1995). In principle, every possible correlation coefficient that can be formed between pairs of voxel time courses arising from gray matter can be of interest. Ideally, one would acquire all voxel time courses simultaneously to preserve coherencies of resting-state fluctuations across the entire brain. This “ideal” constraint can be relaxed somewhat because of the sluggishness of the neurovascular coupling. A challenging but realistic goal is to achieve a whole-brain data set in a time <2 sec.

In addition, it is desirable to minimize intravoxel dephasing and loss of signal intensity in regions of high susceptibility gradients, including the frontal and temporal lobes. An EPI sequence with thin slices minimizes signal dropout from intravoxel dephasing. The requirement of thin slice acquisition to avoid intravoxel dephasing places a further constraint on the acquisition of a single volumetric GR-EPI data set: the resolution should be high. A value of 1 to 2 mm cubic may be sufficient (Muller, 1988).

Acquisition can be accelerated by the use of partial k-space EPI (Jesmanowicz et al., 1998). Not only is the number of k-space lines that must be acquired in a single image reduced, but also the echo-time (TE) can be relatively shorter, which minimizes signal dropout. The time required to cover k-space can be further reduced by the use of in-plane sensitivity encoding (SENSE) or one of its derivatives (King and Angelos, 2000). Both partial k-space and SENSE cause a reduction of the ratio of signal to thermal noise because less time is used to collect the data in an image. When the signal arises from physiological fluctuations that are of interest and the noise arises both thermally and from physiological fluctuations that are not of interest, the situation becomes more complex. In the judgment of the authors, use of partial k-space in fcMRI is almost always desirable because of the freedom it provides in setting the TE value. Partial k-space, in-plane SENSE, and use of thin slices in concert are expected to reduce intravoxel dephasing that causes signal dropout.

Multislice acquisition of two-dimensional MR images to cover a volume of tissue—the brain, for example—most commonly proceeds one slice at a time. The acquisition time can be reduced by simultaneously acquiring two or more slices. To achieve this goal, we designed tailored multislice excitation pulses with distinct phase tagging of each slice, and developed a strategy to disentangle the overlapping slices in the acquired data. We specifically consider here parallel multislice acquisition in a context of GR-EPI and fcMRI. Slice excitation and acquisition occur in parallel rather than in series. The acquired signal is increased and the degradation of the signal-to-noise ratio (SNR) is minimized when using multislice acquisition.

The literature of simultaneous excitation of more than one slice in an MRI multislice volumetric acquisition has primarily been concerned with development of strategies to disentangle the overlapped data. Early articles (Muller, 1988; Souza et al., 1988) are defined as those written before the development of receive-only coil arrays. Slices were labeled either in-phase or 180 degrees out-of-phase, and separated by additions and subtractions. In this method, there is no acceleration of the rate at which images are acquired, although the image quality is improved for a fixed acquisition time.

Larkman et al. (2001) introduced the use of coil sensitivity profiles to separate overlapping signals from simultaneously excited slices. A subsequent advance was the use of coil-sensitivity profiles to provide both acceleration in the coverage of k-space and in the separation of overlapping signals from simultaneously excited slices (Breuer et al., 2005, 2006; Kyriakos et al., 2006). The field had advanced sufficiently by 2006 that Kyriakos et al. were able to write a review article on generalized encoding (Kyriakos et al., 2006).

The most common method for achieving selective excitation of two or more slices has been to modulate the normal five-lobe slice-selection profile (Moeller et al., 2008) with a cosine or a sine wave. Lee et al. (2006) introduced another method using Shinnar-Le Roux pulse design of slice-multiplexed RF pulses. Although multislice excitation was introduced >20 years ago (Muller, 1988) and refined in the intervening years, the method is not in common use.

These articles (Breuer et al., 2005, 2006; Kyriakos et al., 2006) were concerned with acceleration of the acquisition of high-quality anatomic images in reduced overall acquisition time to achieve greater efficiency in use of the MRI scanner. The problem posed in this article is somewhat different. We are willing to use time to optimize the acquisition of fcMRI information from each subject that can aid in slice separation. However, the actual acquisition of each whole brain data set has to be done below the hemodynamic response time, which is on the order of 2 sec.

Three recent abstracts consider acceleration in the slice-selection direction in a context of fMRI (Moeller et al., 2008, Moeller et al., 2009; Jesmanowicz et al., 2009) using GR-EPI. Abstracts by Moeller were carried out at 7 T using a 16-channel excite/receive head coil. This was extended to a full article (Moeller et al., 2010). These authors did not consider functional connectivity. A recent communication has also appeared with further technological advances and applications (Feinberg et al., 2010). The work described in the present article, as well as in an abstract (Jesmanowicz et al., 2009), was carried out at 3 T using a whole body excitation coil and an axially symmetric eight-channel receive-only head coil.

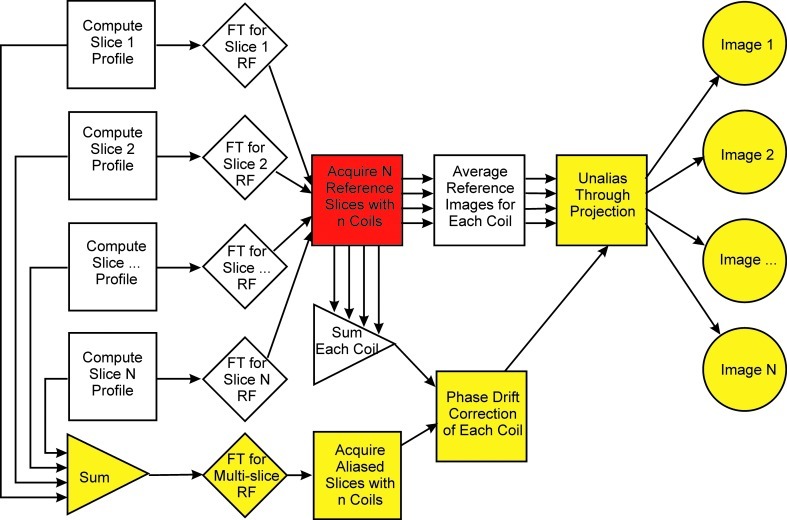
An overview of the multislice acceleration method that is developed in this article is shown in Figure 1. The image formation pathway for full NEX acquisition is indicated by the yellow steps along the lower and right-hand sides of the figure. There are three events along this pathway: (i) excitation by a multislice RF pulse, (ii) phase drift correction, and (iii) unaliasing through projection. When partial NEX acquisition acceleration is used, the reconstruction is performed after slice separation, which is not shown in this figure.

FIG. 1.

Flow chart of data acquisition and reconstruction when using parallel slice excitation with phase-tagging.

The columns of connected squares and diamonds on the left concern RF pulse formation. The position and RF phase of each of the N individual slices are determined, and the Fourier transform (FT) is calculated assuming a single excitation frequency for the slice group. For reference slices these pulses are used independently. For aliased slices, the FT of the composite pulse is calculated by summing the N slice profiles and calculating the FT of the sum.

The penultimate block is shown in red. Short time courses of reference images are obtained for each slice for each of the n-member RF coil arrays. The first few are discarded to avoid T1 relaxation effects, and the remaining images are averaged to improve the SNR. Thus, there are N×n reference images of good SNR available, n for each of the N slices. These are complex-valued images. It is noted that, to some degree, physiological fluctuations are averaged in this process.

RF phase drift that we associated with B₀ drift was encountered. It usually arises from a bulk susceptibility effect as the body of the subject relaxes toward a stable prone position, or from a heating effect during image acquisition. A facsimile of an aliased multicoil image data set was created by summing the reference images in the complex domain and was used to correct each aliased image in the multicoil time course for phase drift.

Finally, we arrive at the block labeled “unalias through projection.” For each aliased voxel, a complex valued number exists from each of the n channels; in addition, the reference images provide unaliased data from the N slices and n channels for that voxel. Singular value decomposition is used to solve the system of linear equations on a voxel-by-voxel basis. Data are combined across channels in this process yielding N unaliased slices. This process is similar to traditional SENSE unaliasing except that the excitation magnitude and phase are used for spatial encoding.

Materials and Methods

Excitation using tailored pulses

This study was performed on a GE Signa EXCITE 3 T MR scanner. Pulses were formed without the need for hardware modifications. User-defined control variables permitted the scanner operator to define the location, width, and phase of each slice to be excited. The software formed the inverse FT of the required slice profiles, including not only positions but also relative phases (Jesmanowicz and Hyde, 2003). The pulse duration was 6.4 ms with a 2 μs update time. This pulse duration is twice that of the default mode of the normal GE scanner. Each complex-valued composite RF pulse was formed from a single transmit frequency. With this method, reference slices needed for multislice separation can be acquired with exactly the same phase as the combined image by masking the unneeded part of the composite profile. For two slices, a 90-degree phase difference between slices is an obvious choice. In the ideal case of a uniform phase profile in each slice and absolute phase aligned with the I acquisition channel, the first slice would be in the I channel and the second in the Q. In such a case, it is apparent that twofold acceleration is attainable with a single RF coil, although that is not the thrust of this article.

Generalized reconstruction

Reference images are acquired in each of the channels of the coil array by excitation of each slice. In fact, 20 reference images are acquired for each 100-image time course, and the last 15 of these reference images are averaged for improved SNR. A reference image time course is collected for every acquisition, although once per study session may be sufficient. Thus, for the TR value of 2 sec, the duration of the complete reference image time course is 40 sec multiplied by N for N-fold acceleration. Sensitivity profiles of each coil are not explicitly formed. Images are formed pixel-wise by complex-valued projection of the overlapping signals detected in each channel onto the corresponding single-channel reference vectors. Extension to more than two slices is straightforward with more than one receiver coil.

Offsets in phase because of drifts of B₀, as well as noise on the x and y gradients, are corrected in the following steps:

Step 1: Let the entries in an image time course be designated by 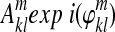, where m counts images and k, l enumerates pixels x and y. From the I, Q sum of the reference slices in the group: .

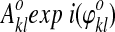Step 2: Make phase differences (neglecting considerations about amplitude):

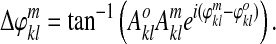(1)

Step 3: Fit polynomials 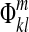to :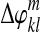

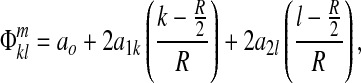(2)

where R=image resolution.

Step 4: Subtract phase 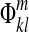from all images in the image time course to correct image phases:

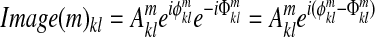(3)

Phase drifts a₀ arise, at least in part, from the transfer of heat produced in gradient coils. Phase gradients drifts a_1k and a_2l are made by bulk susceptibility effects and subject settling. These drifts cause cross-talk unless corrected.

The reconstruction method for parallel slice phase-tagging can allow for the reconstruction of complex-valued or amplitude separated images. Complex-valued images preserve phase variation from the reference images. Such phase variation is only necessary when using statistical methods that require the use of complex-valued data (Calhoun et al., 2002; Menon, 2002; Rowe and Logan, 2004), and complex data are also needed for half Fourier reconstruction (Jesmanowicz et al., 1998).

The decision to reconstruct only amplitude images in the slice-separation algorithm yields an improvement in the unaliasing. By solving for only the amplitude component of the deviation from the reference images, the algorithm halves the number of unknowns in the unaliasing problem. Thus, the separation problem is more overdetermined when only amplitude solutions are desired, yielding an improvement in the least squares fitting of the separated slices. Interestingly, this methodology of reconstructing amplitude images from the complex-valued data can be taken to an extreme, allowing a reduction factor of two times the number of coils—a twofold improvement over previously published parallel imaging techniques (Pruessmann et al., 1999; Sodickson and Manning, 1997).

The method of parallel slice acquisition with phase-tagging utilizes reference images that are acquired serially with the same pulse sequence. These reference images contain spatially varying magnitude sensitivity from coil profiles and spatially varying phase from the combined effects of the vector reception field for each specific RF receive channel, local magnetic field properties, and the RF excitation phase. Both the magnitude and phase are utilized to separate the aliased images, as shown in Equation 4, which can be solved through singular value decomposition (Press et al., 1994):

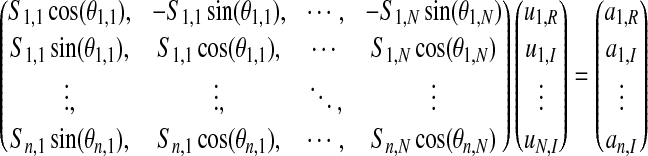(4)

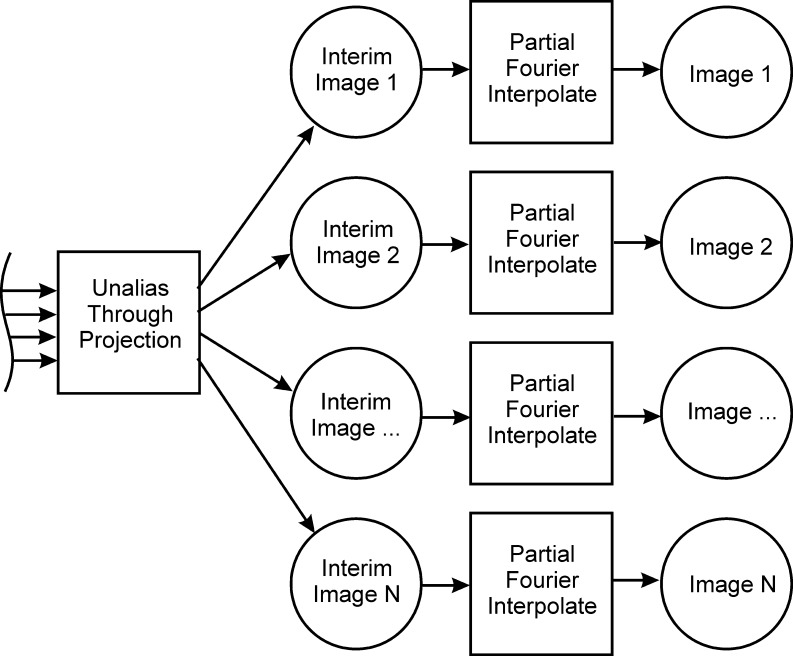
Here, the real and imaginary aliased signal, a_n,R/I, of N aliased voxels in n coils is the unaliased real and imaginary signal, u_N,R/I, encoded by the coil magnitude sensitivity profile of coil n at the aliased voxel N, S_n,N, and observed magnetization phase, θ_n,N. The reference image magnitude and phase are used to determine S and θ, respectively. This yields unaliased images that have near unity value, which can be scaled by a combination of the reference images to yield the expected spatial contrast. This real-valued isomorphism of the complex-valued modified SENSE equation includes 2n equations with 2N unknowns. Thus, as long as n is greater than or equal to N, solutions to this parameterization exist. The result is the deviation of the magnetization vector from the reference image. Standard partial Fourier interpolation can then be performed on the separated images, as shown in Figure 2. In the process for partial Fourier imaging, reference data and acquired data are zero filled and unaliased before performing partial Fourier interpolation.

FIG. 2.

Expansion of Figure 1 including partial Fourier reconstruction. Acquired data and reference data are zero filled and reconstructed as in Figure 1, with partial Fourier processing performed after slice separation.

However, when phase is not of interest, unaliased amplitude-only images are reconstructed and the even columns of the encoding matrix and the even rows of the unknown vector in the above equation are eliminated. Thus, the ratio of the number of equations to the number of solutions is increased by a factor of two, allowing the determination of a higher quality solution. This parameterization allows higher accelerations than previously described for parallel imaging (Jesmanowicz et al., 2011).

From the original work by Pruessmann (Pruessmann et al., 1999), the ratio of the SNRs of the separately acquired slices and unaliased slices yields the product of the unaliasing g-factor, g, and the square root of the reduction factor, R:

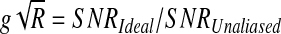(5)

In this work, the SNR is considered the temporal SNR, or the temporal mean of a voxel divided by its temporal standard deviation. As described by Moeller et al. (2010), the reduction factor is 1 because the number of k-space lines is not reduced with the simultaneous reception of multiple slices. Thus, the g-factor is the ratio of SNRs of separately acquired to unaliased image time series.

The g-factor was initially described as a measure of only coil covariance. With the addition of RF phase-tagging, it is expanded here to include the magnetization phase from RF excitation and magnetic field shimming. Further, the g-factor can be reduced by increasing the overdetermined nature of the unaliasing problem by solving for only amplitude values.

Imaging protocol

A gradient EPI sequence of our own design was used (Jesmanowicz et al., 1998), and acquisition was done off-line using a computer equipped with three Mercury (Chelmsford, MA) ECDR-GC316 cards (Jesmanowicz and Hyde, 2006) running Linux OS. The high dynamic range of these receivers is well suited for the increased signal associated with multiple excited slices. Acquisition parameters of the coronal slices included TR=2 sec, BW=208 kHz, FOV=24 cm, slice thickness-3 mm, slice separation-0 mm, 28 slices. At 1 NEX and at 96×96 resolution, a minimal possible TE at this BW was 40.5 ms due to slew rate limitations. At ½ NEX and at 96×96 resolution with 12 overscan lines, the minimal possible TE was 11.2 ms. Pairs of aliased slices were separated by 14 slices, and therefore the 28-slice volume was acquired over 14 shots. Although the method is capable of acquiring 56 parallel slices in a 2 sec TR, we reduced it by a factor of two to achieve the same T₁ contrast between reference and parallel slice acquisitions. Tailored transmit pulses lasted 6.4 ms and were loaded with 2 μs update steps. Twenty image time courses were acquired as reference slices. Time courses of 135 images for fMRI data and time courses of 100 images for fcMRI data were acquired. At the time, the only available multichannel coil was a radially symmetric eight-channel, GE receive-only brain array (GE model number 102869). The magnet was shimmed for each subject using the standard GE automatic shimming protocol followed by manual shimming using a tagging grid (Jesmanowicz and Hyde, 1994). Individual slices were phase-tagged, with phases lying in the first quadrant. Studies were carried out across six subjects under a protocol approved by the Medical College of Wisconsin's Institutional Review Board.

Data analysis protocol

Data were reconstructed as described above using locally developed software. Functional activations were computed by correlating a time shifted ideal boxcar function with the unaliased fMRI data. The voxel in the left motor cortex exhibiting the maximal correlation was selected as a seed voxel for the fcMRI study.

The reconstructed resting-state time series was spatially registered with a 6 degree of freedom registration algorithm, spatially smoothed with a 3 mm full width at half maximum Gaussian kernel, Fourier filtered with an ideal temporal notch filter with a pass band of 0.01 to 0.10 Hz, and correlated with the seed voxel, utilizing the InstaCorr routine of AFNI (Cox, 1996). The maps were thresholded at the level of 0.70 to illustrate the motor network and overlaid on the first image of the unaliased time series. At much lower thresolds, some low-level negative correlations between some voxels of unaliased slices are observed at levels that do not affect the functional connectivity results.

The g-factors from the unaliasing method were computed by taking the ratio of the temporal SNR of the reference images to the temporal SNR of the unaliased resting-state data. Only data masked to the brain were utilized in computing a histogram of g-factors.

Results

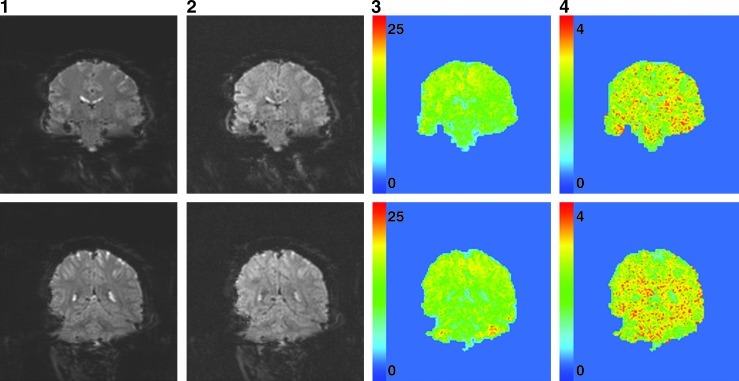
Figures 3 and 4 show images obtained with twofold acceleration in the slice-encoding direction. Figure 3 includes aliased images from two slices in each of the 8 coils of the receiver array. Phase cancelation occurs in some locations, but coil sensitivities suffice in image separation, as seen in the unaliased images in the final column. In Figure 4, visual differences between the reference images in the first column and unaliased images in the second column are not apparent. Maps of temporal standard deviations from the unaliased images are shown in the third column, and yield the usual high temporal standard deviations in cerebral spinal fluid and gray matter. Further, the fourth column illustrates the spatial structure of the computed g-factors. Such geometry-factors are lower in voxels with high signal because slight errors in the observed real and imaginary data yield smaller errors in the observed phase.

FIG. 3.

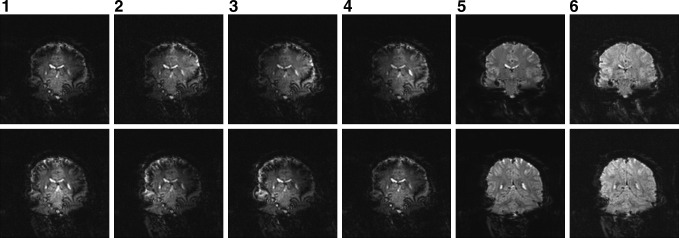
Individual coil aliased images (columns 1 through 4), reference images (column 5), and unaliased images (column 6).

FIG. 4.

Mean reference (column 1), mean unaliased (column 2), unalaised temporal standard deviation (column 3), and g-factor (column 4) for two aliased slices.

It is noted that this acceleration is greater than twofold acceleration in the phase encoding direction with EPI because the overhead for fat presaturation, slice selection, and pausing to attain an appropriate echo time are shared among the simultaneously excited pulses. This advantage is shown in Table 1. Images shown were obtained with the eight-channel head coil, and similar images with greater variance were reconstructed utilizing subsets of the eight channels (data not shown). As expected, more channels are desirable for greater acceleration and reduced noise in the reconstructed image.

Table 1.

Slices Available in a 2 Sec Repetition Time with Various Acceleration Methods

	Standard	Partial Fourier	Standard SENSE	Parallel slice standard	Parallel slice partial Fourier
96×96 slices in a 2 sec TR	28	38	44	56	76

The technique was combined with partial k-space acceleration, yielding both further acceleration and the signal benefits associated with shorter echo times and readouts (Hyde et al., 2001). We found best results by performing the partial NEX algorithm after slice separation with zero filling. By using reference images with zero filling, slice separation removes all phase variation from receiver coil profiles and shimming, thereby improving the conjugate symmetry of k-space. We observed an improvement in image quality with the combined technique over a threefold multislice acceleration in spite of similar final levels of acceleration. With the acceleration provided by partial NEX acquisition, the echo time can be shortened considerably. The number of overscan lines is selected to yield acceptable blood oxygen level dependent (BOLD) contrast.

In other experiments (not presented here), fourfold multislice acceleration was demonstrated, with increased artifacts from the poorly conditioned system of equations. Receiver coils with more spatial variation in their sensitivity profiles and more coils are expected to enable further acceleration.

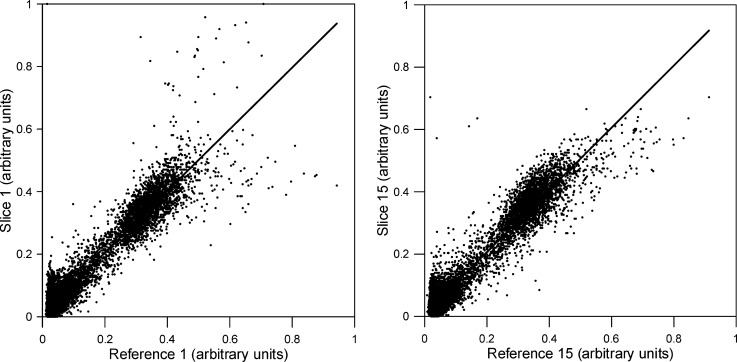
Scatter plots were made comparing the unaliased voxel intensities with the corresponding voxel intensities in the reference images. Figure 5 shows slices 1 and 15, which were aliased together. The unaliased voxels from slice 1 are highly correlated with the voxels from the reference image of slice 1 (R²=0.92, Fig. 5a), and are poorly correlated with voxels from the reference image of slice 15 (R²=0.65, not shown). Likewise, unaliased voxels from slice 15 are highly correlated with voxels from the reference image of slice 15 (R²=0.94, Fig. 5b), and are poorly correlated with voxels from the reference image of slice 1 (R²=0.62, not shown).

FIG. 5.

Scatter plots of corresponding voxel signal intensities for two corresponding unaliased slices. After unaliasing, each slice shows good agreement with the corresponding reference slice, while exhibiting random correlation with the other aliased reference slice.

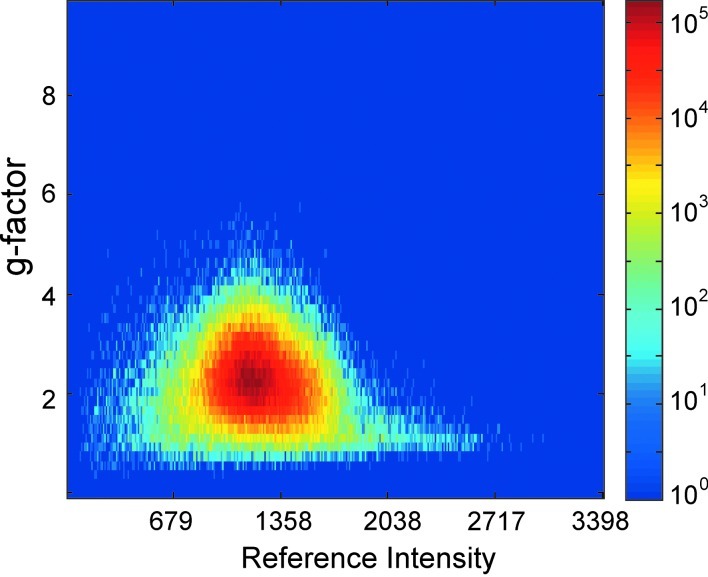
The g-factor of this method is not constant and varies across the reconstructed images as seen in Figure 6. Because the phase variance is inversely proportional to the magnitude of signal (Haacke et al., 1999), it influences slice separation. The g-factors in the brain tend toward unity when reference images have higher signal intensities. Further, in regions where signal intensities are reduced by destructive interference, the g-factor tends toward higher numbers. A modest average g-factor within the brain of 2.49 was observed.

FIG. 6.

Logarithmic histogram of g-factors computed for each voxel in the brain of the acquired volume. Median g-factor 2.49. Geometry factors tend toward unity with greater reference image intensity because of the method's dependence on phase.

Resting-state functional connectivity

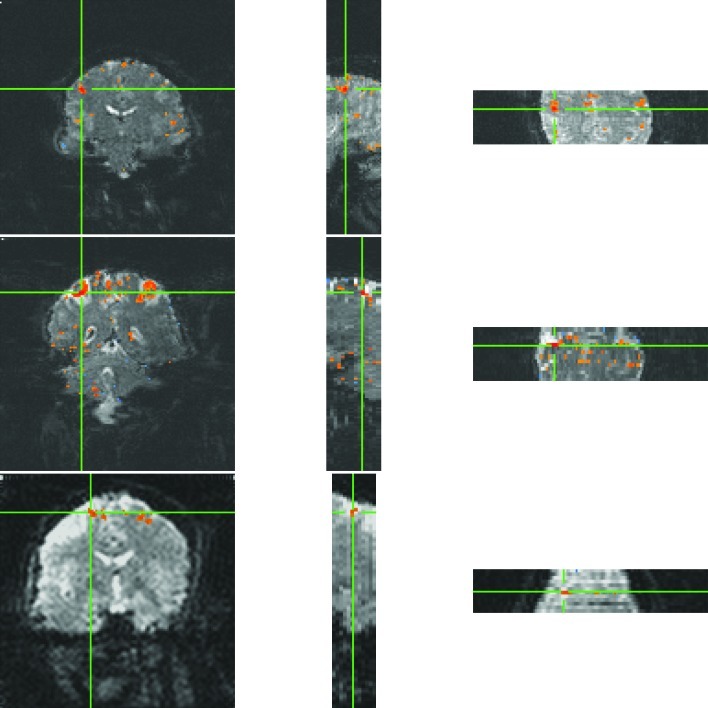
An important motivation for increased echo planar image acceleration lies in application to whole brain connectomics. Resting-state functional connectivity data were acquired in each subject, and connectivity maps from a seed region in the left motor cortex from three subjects are shown in Figure 7. With a correlation coefficient threshold of 0.7 (p≤5.8×10^–6), correlation is apparent with the contralateral motor cortex, as well as the supplementary motor area. Only individual subjects are shown, as the goal of this article is to present a proof of concept of phase tagging exitation pulses and its applicability to parallel imaging.

FIG. 7.

Individual subject resting state correlation maps from unaliased coronal slices, with a seed taken from the left motor cortex, thresholded at a correlation coefficient of 0.70 (p≤5.8×10^–6). Unaliased voxels, separated by 14 coronal slices, do not exhibit aliased resting state correlations.

These data sets are indicative of the quality of separation of the slices. Any imperfection in the separation process causes the time series from one voxel to leak into the time series of the aliased voxel. The effect of such leaking is smaller than intuition suggests because resting-state functional connectivity relies on small correlation amplitudes of 5% to 10%. Thus, a leakage of even 10% would lead to a fraction of a percent of false contrast. Aliased slices (in this case, coronal slices that are 14 slices apart) exhibit small negative levels of correlation and do not influence the observed final results. As seen in Figure 7, patterns of mirrored regions of anticorrelation are not apparent in the slice encoding direction. Without nuisance regression of physiologic parameters or anatomical regions of interest (Margulies et al., 2010), all gray matter was found to be highly correlated.

Discussion

This work has introduced the concept of phase tagging simultaneously excited slices to increase the number of linearly independent equations in the unalising process. Although many physical processes contribute to the observed phase of a given voxel, including the excitation phase, magnetic field homogeneity, and receive coil phase, experimentally controlling the excitation phase of simultaneously excited slices enhances the separation of slices acquired in parallel. Unaccelerated reference images, empirically including phase from all confounding sources, are used for aliased slice separation. Further, low order spatial phase drift is corrected in the unaliasing algorithm. We tested the limits of differentiating between two or more excited slices based on the difference(s) in slice excitation phase(s).

The relative excitation phases across each of the n/N groups of slices are coherent. Explicit formation of receive-coil profiles was tested. The best results were obtained when directly using the reference slices for unaliasing. Coil profiles coupled with exact reference slice phases gave poorer results, and worse results were obtained when using profiles without phase information.

From a theoretical perspective, it is interesting that two slices can be detected simultaneously and independently from a single-mode transmit/receive whole-volume coil, and, presumably, four slices from a two-channel quadrature excite/receive coil. It is notable that for twofold acceleration, any plane-of-section can be used, since spatially varying coil sensitivities are not needed for image unaliasing. In work not shown here, the principle was established that the number of possible slices is twice the number of coils in a multicoil array. However, this usage is not recommended. A receive coil with as many channels as possible seems preferable. The use of multiple channels increases the SNR relative to a single-mode coil. In addition, the acceleration increases linearly with the number of simultaneously excited slices that are acquired in parallel without substantial degradation of SNR from data subsampling with respect to single-slice acquisition.

The method was evaluated for an eight-channel head coil for two 3 mm slices. A method for multislice reconstruction using the slice profiles of this coil was developed. Axial symmetry of the eight coils in this head coil restricted the plane-of-section for slice acceleration to coronal or sagittal. For acceleration of the coverage of k-space, this coil is restricted to axial slices.

In our hands, present technology for twofold acceleration of GR-EPI acquisition yields images using 3 mm cubic voxels that cannot be distinguished by visual inspection from single slice images. Extension to thinner slices and fourfold acceleration seems well within reach using a 32-channel receive-only head coil. Slice tagging permits several strategies for volumetric coverage of the slice-encoding direction, including (i) equally spaced slices in each group as far apart as possible, (ii) different numbers of slices in the various groups depending on the sensitivity profiles of the various coils, and (iii) using a distribution of slice spacings and thicknesses in each group.

Cross-talk between slices occurs because of imperfect phase registration of complex-valued reference images with actual complex-valued excited slices. It can occur because of motion or B₀ drift. Fluctuations in image phase from temporal fluctuations in shim coil currents and noise in the gradient system are likely to cause difficulties in unaliasing. Because of the final scaling by the reference image, imperfect magnitude registration has proven to be less problematic. The artifact from cross-talk is the induction of negative correlation between a voxel and its unaliased counterpart, because signal from one voxel is displaced into the other. For fcMRI, which is based on weak signals, a small amount of cross-talk is acceptable. Nevertheless, because fcMRI is based on correlations of low-frequency physiological fluctuations across space, careful attention to the possibility of cross-talk is appropriate. The present results show that such cross-talk does not impact the fcMRI analysis in the motor system.

The algorithm presented here is dependent on reference slices that have unchanging locations in brain tissue throughout the acquisition. However, we found that the method is robust to small motion because of the smoothly varying coil profiles. Further, because data are simultaneously acquired in multiple slices, more information about brain motion is present in the data set than with single-slice acquisition, which has a potential for being useful. Data were successfully reconstructed in cases where a subject moved on the order of the pixel dimension between the acquisition of reference and aliased images.

The literature establishes that coil profiles can be used simultaneously for acceleration of acquisition of multiple slices and for coverage of k-space (Breuer et al., 2005, 2006; Kyriakos et al., 2006), and simulations have indicated that similar two-axis acceleration can be achieved using the methods of this communication. Further, the unaliasing performed in this work was found to be more robust using reference images than when using derived coil profiles, and similar improvements are observed in simulations when using reference images in place of coil profiles with two axis acceleration.

The slice selection implemented in this work relies on the assumption that the FT of the desired slice profile is the necessary RF pulse profile. However, nonlinearities in the Bloch equations are present. The RF phase difference between simultaneously acquired slices must be selected such that spins in intermediate slices do not experience nutation. It is expected that the excited multislice profiles can be improved by utilizing a numerical solution to the Bloch equations for the determination of the RF waveform.

Time is required to obtain the reference images, which is an overhead on the method. However, it is small in the circumstance of collecting 100 or more volumetric GR-EPI data sets, as is in most fMRI or R-fMRI studies. Most importantly, the acquisition of slices during experimental resting state runs is accelerated by a factor equal to the number of slices being simultaneously excited. This acceleration translates into an increase in the number of slices that can be acquired in a repetition time that is sufficiently short that resting state coherences are preserved.

Acknowledgment

This work was supported by grant R01 EB007827 from the National Institutes of Health.

Author Disclosure Statement

The authors have no commercial associations that might create a conflict of interest in connection with this article.