Disparity-Specific Spatial Interactions: Evidence from EEG Source Imaging

Abstract

Using cortical source estimation techniques based on high-density EEG and fMRI measurements in humans, we measured how a disparity-defined surround influenced the responses to the changing disparity of a central disk within five visual ROIs: V1, V4, lateral occipital complex (LOC), hMT+, and V3A. The responses in the V1 ROI were not consistently affected either by changes in the characteristics of the surround (correlated or uncorrelated) or by its disparity value, consistent with V1 being responsive only to absolute, not relative, disparity. Correlation in the surround increased the responses in the V4, LOC, and hMT+ ROIs over those measured with the uncorrelated surround. Thus, these extrastriate areas contain neurons that are sensitive to disparity differences. However, their evoked responses did not vary systematically with the surround disparity. Responses in the V3A ROI, in contrast, were increased by correlation in the surround and varied with its disparity. We modeled these V3A responses as attributable to a gain modulation of the absolute disparity response, where the gain amplitude is proportional to the center–surround disparity difference. An additional experiment identified a nonlinear center–surround interaction in V3A that facilitates the responses when center and surround are misaligned but suppresses it when they share the same disparity plane.

Introduction

In the geometry of binocular vision, absolute disparity is defined as the difference in the two retinal coordinates of a given feature, whereas relative disparity refers to the difference between the absolute disparities of a pair of features. Absolute disparity changes with every change in convergence, but relative disparity, the disparity difference, is a fixed property of any pair of features and is unaffected by convergence, except for a change in sign.

Twenty-five years ago, Erkelens and Collewijn (1985a,b) proposed a dichotomy between absolute disparity as a stimulus for convergence and relative disparity as a stimulus for depth perception. Following their idea, Neri (2005) suggested that the ventral pathway, because of its role in object perception, would be significantly involved in processing relative disparity, whereas the dorsal pathway, important in providing sensory input for movements, would contribute more to the processing of absolute disparity (see also Anzai and DeAngelis, 2010).

This functional division between relative and absolute disparity is not quite so simple. For one thing, changes in the absolute disparity of small features (isolated dots or lines) can be perceived, albeit poorly. Psychophysical thresholds for detecting changes in absolute disparity are many times higher than thresholds for detecting changes in relative disparity (Westheimer, 1979; Regan et al., 1986; McKee et al., 1990a; Read et al., 2010), but absolute disparity modulation is not invisible. Of more importance, relative disparity plays a critical role in guiding actions, in addition to its role in the perception of object shape and figure–ground relationships. For example, it is well established that relative disparity contributes to the planning and guidance of grasp movements (Morgan, 1989; Watt and Bradshaw, 2003; Melmoth and Grant, 2006; Melmoth et al., 2009). Based on these considerations, the response to relative disparity in visual cortex should be pervasive, rather than confined to a single visual pathway (Orban et al., 2006).

The main objective of this study is to determine how the properties of a second disparity in the image, i.e., a correlated surround, alter the population response to disparity modulation of a central disk. In our previous study (Cottereau et al., 2011a), we had observed that correlation in the surround altered the responses in four extrastriate areas: V4, lateral occipital complex (LOC), hMT+, and V3A. Here, we focus on how varying the surround disparity affects these responses. From our analysis, we found that V3A is the only ROI where the responses are systematically modified by the surround disparity. We modeled the V3A responses as a modulation of its absolute disparity responses, whose amplitude is proportional to the center–surround disparity difference. A final experiment testing nonlinear interactions between the center and surround confirms the model and shows that the responses are facilitated when center and surround are misaligned and suppressed when they share the same disparity plane (iso-disparity suppression).

Materials and Methods

Subjects

Twenty-seven subjects participated in the electroencephalogram (EEG) experiments (18 males, 9 females; age range, 20–69 years). All subjects participating in the recording sessions were volunteers, with normal stereopsis and normal or corrected-to-normal visual acuity. The three subjects in the psychophysical study had much prior training in stereoacuity studies before the measurements of their disparity modulation thresholds. All subjects were given instructions and detailed information about the experiments. They provided written informed consent before participating in the study in accordance with the Helsinki Declaration; the human subjects review committee of Smith-Kettlewell Eye Research Institute approved the study.

Stimulus

The basic stimulus (Fig. 1) consisted of a central disk, surrounded by a large annulus; both were composed of dynamic random dots that changed positions every 47 ms (21.25 Hz). The diameter of the surround annulus was 7.48° in the fifth EEG study and 12° in the other studies. The diameter of the central disk was 5° (EEG experiments 1 and 6), 6° (EEG experiments 2–4, and 7), or 4° (EEG experiment 5). The disparity of the central disk was shifted either 12.4 or 16 arcmin every 472 ms (2.12 Hz) in a steady-state EEG paradigm. We chose this temporal frequency because it was above the frequency where vergence could follow the disparity modulation (Rashbass and Westheimer, 1961; Erkelens and Collewijn, 1985b), meaning that vergence could not cancel the changes in stimulus disparity. The dot density (in number of dots by square degree of visual field) was 30 in experiments 1, 5, 6, and 7 and 20 in experiments 2–4. For all studies, the EEG recording trial for each stimulus presentation lasted 11 s; the first second of the data record was discarded to avoid start-up transients. Trials for all conditions were run interspersed in random order in 10 min blocks. The blocks were repeated four times, producing altogether a total of 20 trials (100 s) per condition.

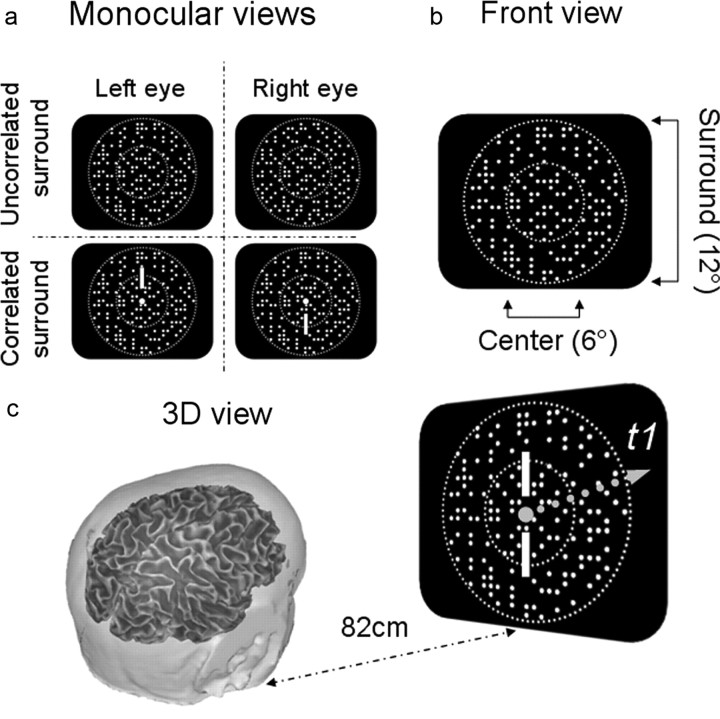
Figure 1.

Diagram of stimulus configuration of dynamic random dots (update rate, 21.2 Hz); central 5 or 6° disk modulated at 2.12 Hz from 0–12 or 0–16 arcmin uncrossed disparity; a 12° annulus consisted of either uncorrelated disparity noise or binocularly correlated dots presented at fixed disparity. Viewing distance was either 77 or 82 cm depending on experimental setup. a, Two monocular images for the correlated and uncorrelated conditions. b, Front view. c, A 3D view.

We used two different types of stereoscopes for these studies: a mirror stereoscope and a beamsplitter-based system. In the mirror stereoscope, the stimuli were presented on a pair of matched Sony monitors (Multiscan GS 220) viewed at a distance of 77 cm. At this viewing distance, the outer dimensions of the screens were 23° high × 18° wide. The monitors and mirrors were angled for natural convergence at this viewing distance. The contrast of the bright dots was 90%. In the interval between trials, the screen was filled with bright static dots at zero disparity to prevent changes in light adaptation. In the beamsplitter system, orthogonally polarized images from two matched Sony Trinitron monitors (model 110GS), were combined via a beamsplitter and viewed through appropriately oriented polarized filters placed immediately in front of the eyes. Each eye could see the image on only one screen; the viewing distance was 82 cm, and the contrast of the bright dots was 90%. Each separate experiment described below was, of course, conducted on a single stereoscope; experiments 2, 4, 6, and 7 were performed in the mirror stereoscope, and experiments 1, 3, and 5 were performed in the beamsplitter system. We checked whether the difference in stereoscopes affected our most sensitive measure, namely psychophysical stereoacuity thresholds. We found that the thresholds were not significantly different for the two types of stereoscopes. As will be apparent in the results below, the general pattern of EEG responses for comparable conditions was also unaffected by the change in stereoscopes.

Main experiments

Absolute and relative disparity modulation (11 subjects: 6 males, 5 females).

In four interspersed conditions, we measured the response to either crossed or uncrossed disparity modulation of a central disk with two types of surrounds: (1) absolute disparity condition: surround consists of uncorrelated disparity noise, similar to a stimulus used by Prince et al. (2000); the central disk shifted at 2.12 Hz either between a crossed disparity of 12.4 arcmin and zero or between an uncrossed disparity of 12.4 arcmin and zero; (2) relative disparity condition: surround consists of binocularly correlated dots presented in the fixation plane; the central disk shifted at 2.12 Hz either between a crossed disparity of 12.4 arcmin and zero or between an uncrossed disparity of 12.4 arcmin and zero.

For the correlated surround conditions, we presented a pair of nonius lines and a binocularly visible fixation point superimposed on the center of the disk-annulus stimulus. Subjects were asked to keep the nonius lines aligned during a recording trial. We eliminated the nonius lines and the fixation point for the uncorrelated surround conditions to remove all immediate reference stimuli. Because this study was partly conducted for comparison with Cottereau et al. (2011a), the central disk was 5° in diameter.

Varying the absolute disparity of the surround (14 subjects: 10 males, 4 females).

To determine how the disparity of the surround influenced the relative disparity response, we measured the response to uncrossed disparity modulation of a 6° disk for three different surround conditions: (1) uncorrelated surround: surround consists of uncorrelated disparity noise; the central disk shifted between an uncrossed disparity of 12.4 arcmin and zero at 2.12 Hz; (2) correlated surround in fixation plane: central disk shifted between an uncrossed disparity of 12.4 arcmin and 0 (fixation plane) at a temporal frequency of 2.12 Hz; correlated surround presented in a fixation plane; (3) correlated surround in non-zero plane: correlated surround presented at an uncrossed disparity of 14 arcmin; the central disk shifted between an uncrossed disparity of 1.6 arcmin and an uncrossed disparity of 14 arcmin at 2.12 Hz.

Note that the first two conditions in this experiment are almost the same as the conditions for experiment 1. We repeated these conditions so that we could compare them to the third condition in the same subjects and in the same recording sessions.

Systematic shift in disparity of the correlated surround (10 subjects: 8 males, 2 females).

In this experiment, we parametrically varied the absolute disparity of the correlated surround from 0 to 16 arcmin. For this EEG study, the 6° disk jumped from an uncrossed disparity of 16 arcmin to zero disparity during each period. In interspersed conditions, the correlated surround was presented at 0, 4, 8, 12, and 16 arcmin of uncrossed disparity.

Attention control (9 subjects: 5 males, 4 females).

We measured the effect of attention on the EEG response to disparity modulation, using a paradigm in which subjects (1) viewed the center–surround configurations passively as in experiments 1–3 described above, (2) attended to intermittent random changes in the magnitude of the disparity modulation and pressed a button when they detected a change (directed attention), and (3) attended to five letters superimposed on the center of the display and pressed a button whenever one of them was different from the other four (divided attention). The letters were Fs of random orientation that intermittently turned either into all Ls or four Ls and one T for a brief period; the subject pressed one of two buttons to indicate that the letters were either all Ls or included a T at one of the five locations. Both the disparity task and letter task were very difficult, set so that the incremental change in disparity or the duration of the letter test were detected only about 80% of trials.

Testing the nonlinear interactions (11 subjects: 8 males, 3 females).

In this experiment, we isolated and quantified nonlinear interactions between center and surround. The diameters of the center and surround were 4 and 7.48°, respectively. We recorded four different interspersed conditions. In the first, the center was moving between 12.4 arcmin during the first-half cycle and 0 arcmin during the second one (frequency, 2.12 Hz) while the surround was composed of uncorrelated dots (see also experiments 1 and 2). In the second, the center was composed of uncorrelated dots while the surround moved at 2.12 Hz between 12.4 and 0 arcmin. In conditions 3 and 4, both the center and surround moved in depth. They were either always aligned (i.e., moving in phase) in condition 3 or always misaligned (i.e., moving in antiphase) in condition 4. The linear prediction for condition 3 was obtained by adding the responses to conditions 1 and 2. For condition 4, the linear prediction was obtained by summing condition 1 to condition 2 shifted by 180° (i.e., changing the two half cycles so that the responses correspond first to the surround in the fixation plan and then at 12.4 arcmin).

Fixation bias estimation.

To determine whether the absence of a fixation point produced a fixation bias in the uncorrelated surround conditions, we performed a psychophysical nonius alignment test (McKee and Mitchison, 1988; Ukwade et al., 2003) for one uncorrelated surround condition (12.4 arcmin uncrossed disparity). The subject viewed the disparity-modulated disk surrounded by the uncorrelated noise for 11 s, an arrangement identical to the one used for the EEG recording (corresponding to condition 2a). After each 11 s trial, we briefly presented a nonius stimulus consisting of three vertical lines in the upper visual field of the left eye and a single vertical line in the lower visual field of the right eye. The observer judged which of three upper vertical lines was most closely aligned with the single lower vertical line; these measurements were repeated for two different distances separating the upper lines: 5.6 and 12 arcmin. On most trials, observers matched the lower line with an upper line corresponding to zero disparity, but on some trials, they chose the line at 5.6 arcmin corresponding to an uncrossed disparity. Based on these measurements, we concluded that during the uncorrelated surround conditions, there might be a small bias of ≤3 arcmin in the direction of the disparity modulation of the disk.

In addition to this psychophysical measurement of bias, we also included a control condition to measure fixation effects on the uncorrelated surround condition in the EEG study on the effect of surround disparity (experiment 2 described above). In the control, a fixation point and nonius lines were superimposed on the modulating disk (0–12.4 arcmin uncrossed disparity) when surrounded by the uncorrelated disparity noise. The presence of the fixation point increased the response amplitude to the uncorrelated surround condition slightly. This increase may have been attributable to a reduction in fixation bias or to the presence of a “reference” target, i.e., the fixation point, in the central fovea. We repeated the statistical analysis that compared correlated and uncorrelated surround conditions, substituting the uncorrelated surround condition with the fixation point for the condition without the fixation point. The pattern of results was essentially the same as those shown in Figure 6 for the uncorrelated surround without the fixation point.

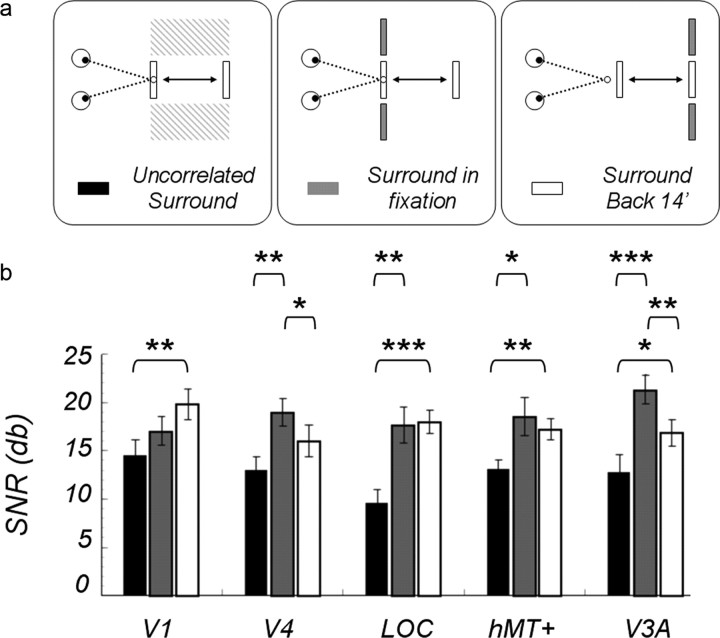
Figure 6.

a, Diagram of the stimulus configurations. b, SNRs of the odd harmonic responses averaged over 14 subjects; a central disk modulated by 12.4 arcmin uncrossed disparity with a surround composed of uncorrelated disparity noise (black bars), a correlated surround in a fixation plane (gray bars), or a correlated surround presented with a fixed uncrossed disparity of 14 arcmin (white bars) are shown. Asterisked brackets show the significant post hoc comparisons: *0.05 level; **0.01 level; ***< .001 level.

Psychophysical thresholds.

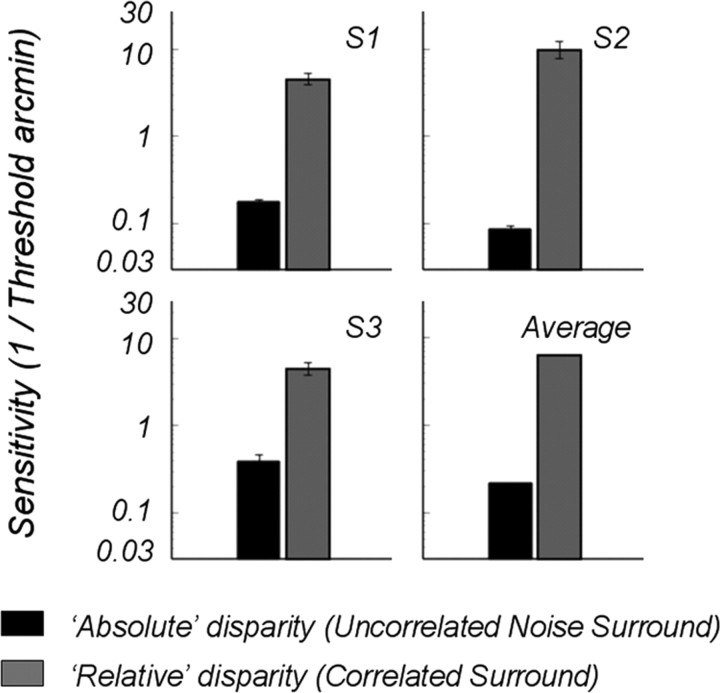
We also measured disparity modulation thresholds psychophysically for the two surround conditions. Observers judged, in which of two intervals, the disparity of a 6° central disk was modulated by a tiny amount in an uncrossed direction. The stimuli were presented for 472 ms, equal to one period of our EEG presentations. The stimuli were presented in a mirror stereoscope and viewed at a distance of 86 cm. Four different modulation values were presented interspersed in a random sequence in a 100-trial block. We fitted a Weibull function to the percentages correct for these four values and estimated threshold as the disparity modulation corresponding to 81.6% correct. We measured thresholds for each subject and condition in three separate blocks (300 trials total); the thresholds were averaged from the three blocks and are plotted as sensitivities (1/threshold) in Figure 4.

Figure 4.

Psychophysical sensitivity (1/threshold) to disparity modulation of the center when surrounded by correlated surround (black bars) or surrounded by uncorrelated disparity noise (gray bars). The duration of stimulus was one period (472 ms).

EEG signal acquisition and source imaging procedure

The EEG data were collected with 128-sensor HydroCell Sensor Nets (Electrical Geodesics) and bandpass filtered from 0.1 to 200 Hz. After each experimental session, the 3D locations of all electrodes and three major fiducials (nasion, left, and right periauricular points) were digitized using a 3Space Fastrack 3-D digitizer (Polhemus). For all observers, the 3D digitized locations were used to coregister the electrodes to their T1-weighted anatomical MRI scans. Raw data were evaluated off-line according to a sample-by-sample thresholding procedure to remove noisy sensors that were replaced by the average of the six nearest spatial neighbors. Once noisy sensors were substituted, the EEG was rereferenced to the common average of all the sensors. Additionally, EEG epochs that contained a large percentage of data samples exceeding threshold (25–50 μV) were excluded on a sensor-by-sensor basis.

Structural and functional magnetic resonance imaging

Structural and functional magnetic resonance imaging (fMRI) scanning was conducted at 3T (Siemens Tim Trio) using a 12-channel head coil. We acquired a T1-weighted MRI dataset (3D MP-RAGE sequence; 0.8 × 0.8 × 0.8 mm³) and a 3D T2-weighted dataset (spin echo sequence at 1 × 1 × 1 mm³ resolution) for tissue segmentation and registration with the functional scans. For fMRI, we used a single-shot, gradient-echo EPI sequence (TR/TE, 2000/28 ms; flip angle, 80; 126 volumes per run) with a voxel size of 1.7 × 1.7 × 2 mm³ (128 × 128 acquisition matrix; 220 mm FOV; bandwidth, 1860 Hz/pixel; echo spacing, 0.71 ms). We acquired 30 slices without gaps, positioned in the transverse-to-coronal plane approximately parallel to the corpus callosum and covering the whole cerebrum. Once per session, a 2D spin echo T1-weighted volume was acquired with the same slice specifications as the functional series to facilitate registration of the fMRI data to the anatomical scan. The general procedures for these scans (head stabilization, visual display system, etc.) are standard and have been described in detail previously (Brewer et al., 2005).

The FreeSurfer software package (http://surfer.nmr.mgh.harvard.edu) was used to perform gray and white matter segmentation and a midgray cortical surface extraction. This cortical surface had 20,484 isotropically spaced vertices and was used both as a source constraint and for defining the visual areas. The FreeSurfer package extracts both gray/white and gray/CSF boundaries, but these surfaces can have different surface orientations. In particular, the gray/white boundary has sharp gyri (the curvature changes rapidly) and smooth sulci (slowly changing surface curvature), whereas the gray/CSF boundary is the inverse, with smooth gyri and sharp sulci. To avoid these discontinuities, we generated a surface partway between these two boundaries that has gyri and sulci with approximately equal curvature.

Individual boundary element method (BEM) conductivity models were derived from the T1- and T2-weighted MRI scans of each observer. The FSL toolbox (http://www.fmrib.ox.ac.uk/fsl/) was also used to segment contiguous volume regions for the scalp, outer skull, and inner skull and to convert these MRI volumes into inner skull, outer skull, and scalp surfaces (Smith, 2002; Smith et al., 2004). The MNESuite software package was used to calculate the BEM model of the expected scalp potential for any given cortical source (Hämäläinen and Sarvas 1989).

Visual area definition

Retinotopic field mapping using rotating wedges and expanding/contracting rings produced regions of interest (ROIs) defined by the visual cortical areas V1, V2v, V2d, V3v, V3d, V3A, and V4 in each hemisphere (Tootell and Hadjikhani, 2001; Wade et al., 2002). ROIs corresponding to hMT+ were identified using low-contrast motion stimuli similar to those described by Huk and Heeger (2002).

The LOC was defined using a block-design fMRI localizer scan. During this scan, the observers viewed blocks of images depicting common objects (12 s per block) alternating with blocks containing scrambled versions of the same objects. The stimuli were those used in a previous study (Kourtzi and Kanwisher, 2000). The regions activated by these scans included an area lying between the V1/V2/V3 foveal confluence and hMT+ that we identified as LOC. This definition covers almost all regions (e.g., V4d, LOC, LOp) that have previously been identified as lying within object-responsive lateral occipital cortex (Kourtzi and Kanwisher, 2000; Tootell and Hadjikhani, 2001).

Cortically constrained inverse

An L2 minimum norm inverse was computed with sources constrained to the location and orientation of the cortical surface (Hämäläinen et al., 1993). In addition, we modified the source covariance matrix in two ways to decrease the tendency of the minimum norm procedure to place sources outside of the visual areas. These constraints involved (1) increasing the variance allowed within the visual areas by a factor of 2 relative to other vertices and (2) enforcing a local smoothness constraint within an area, using the first- and second-order neighborhoods on the mesh with a weighting function equal to 0.5 for the first order and 0.25 for the second order (Cottereau et al., 2011c). The smoothness constraint therefore respects areal boundaries unlike other smoothing methods, such as LORETA, that apply the same smoothing rule throughout cortex (Pascual-Marqui et al., 1994).

ROI-based analysis of the steady-state visual-evoked potential

A discrete Fourier transform was used to estimate the average response magnitude associated within each functionally defined ROI for the odd components (first and third harmonics) of the steady-state frequency (2.12 Hz) (Cottereau et al., 2011a). To take into account the difference of noise levels between the recordings from each of our subjects (Vialatte et al., 2010), we computed the signal-to-noise ratio (SNR) and divided these values by the root mean square of the associated noise that is defined for a given frequency f by the average amplitude of the two neighbor frequencies (i.e., f − δf and f + δf, where δf gives the frequency resolution of the Fourier analysis). The corresponding SNRs are presented in decibels (20 × log₁₀).

Cross talk

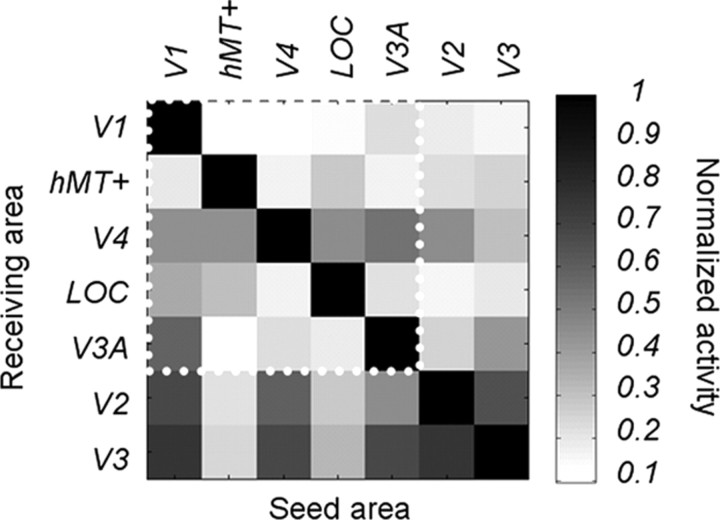
In a previous study (Cottereau et al., 2011a), we described how we estimated the theoretical cross talk among visual areas for a specific EEG study. Cross talk refers to the neural activity generated in other areas that is attributed to a particular ROI, caused by the smoothing of the electric field by the head volume. In brief, for each subject, we simulated the cross talk by placing sources in one ROI and estimating their contribution to other ROIs, using the same forward and inverse methods described above. The global cross talk matrix (i.e., averaged across all the subjects who participated in our EEG experiments) is shown in Figure 2 for seven ROIs (V1, V2, V3, V4, LOC, V3A, and hMT+); the cross talk magnitude shown in the matrix is proportional to activity originating in the ROI where the cross talk is being estimated. From our simulations, it was apparent that there was significant cross talk in areas V2 and V3 (the last two rows of the matrix). For this reason, we excluded these two ROIs from our analysis and focused on V1, V3A, V4, hMT+, and the LOC. These areas are more widely separated, and their estimated activities are therefore more reliable. Within this subset of ROIs, the biggest cross talk comes from a V1 contribution to V3A (55%) and a V3A contribution to V4 (50%). We discuss below the influence of cross talk coming from other regions that were not defined using fMRI (see Results, Absolute versus relative disparity).

Figure 2.

Theoretical estimates of cross talk between source-imaged EEG signals in retinotopically defined visual areas. Grayscale values at rows i and column j represent the relative contribution area j to the cortical current density estimate in area i. Individual definitions from seven different areas (V1, hMT+, V4, LOC, V3A, V2, and V3) are included. The ROIs used in the study are grouped together within the white dotted line region. Areas V2 and V3, which were excluded from the main analyses, are also presented here for comparison.

Statistical analysis

In the frequency domain, pairwise t tests or repeated-measure ANOVAs were performed on the SNRs at the odd harmonics. For the ANOVA, we specifically tested effects of conditions, of ROIs, and their interaction. Significant effects were followed up by post hoc pairwise t tests. The validity of the t tests (normal hypothesis) and ANOVAs (equal variance hypothesis) were controlled using Lillliefors and Mauchly's sphericity tests, respectively. No significant effects were obtained from these tests, and, consequently, we did not correct the p values.

In the time domain, statistical differences between the evoked potential of two conditions were calculated at each time point using permutation tests based on the work of Blair and Karniski (1993). Given a null hypothesis of no effect attributable to the response category, the waveforms for any two categories from a given subject are exchangeable. Response waveforms were randomly exchanged for each individual in the pool of subjects. For this permutation sample, we calculated the mean difference potential and the T value of this difference for each time point in the response waveform. Repeatedly rerandomizing the permutation of category exchanges for each subject allowed us to accumulate a reference distribution of T values. From each permutation sample, we noted the maximum number of consecutive T values passing the 0.05 threshold over all time points in the response waveforms and accumulated these run lengths into a second reference distribution. The difference potential at a given time point in the experimentally measured waveform was deemed significant if the number of consecutive T values passing the 0.05 threshold exceeded 95% of those in the run length reference distribution. This procedure is a temporal equivalent of clusterwise correction.

Results

Absolute versus relative disparity

In our first experiment, we measured the EEG response to disparity modulation of a central disk (Fig. 1), surrounded by an annulus of uncorrelated disparity noise, our “absolute” disparity condition, and compared this response with that obtained when the same modulated disk was surrounded by an annulus composed of correlated dots presented at zero disparity, our relative disparity condition. Dynamic random dots contain no monocular cues, so the monocular images were indistinguishable between conditions. The correlated surround dots created a surface, defined solely by disparity, which served as a reference plane. This experiment was a replication of our previous study, but with a different stimulus configuration. In the study by Cottereau et al. (2011a), the central disk changed from a crossed to an uncrossed disparity symmetrically, straddling the fixation plane. Here, the central disk moved from the fixation plane to 12 arcmin crossed or to 12 arcmin uncrossed disparity in separate conditions. The main effect of this change in stimulus configuration was a large increase in the odd harmonic responses, for reasons that will be clear subsequently.

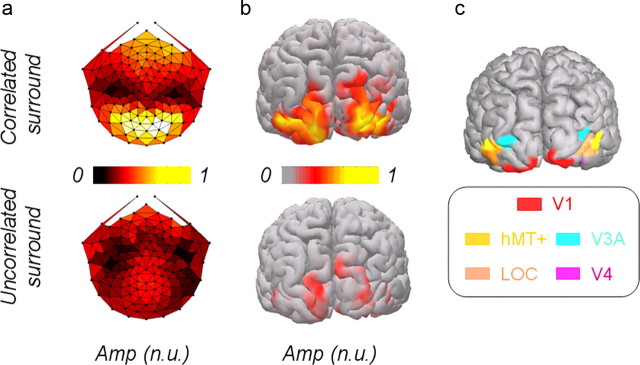
To demonstrate the effect of the two types of surround on the cortical response to changing disparity, we first show topographic maps of the first harmonic and the corresponding source activity, recorded from all the subjects and mapped on one subject's cortex (Fig. 3a,b). Clearly, the disparity modulation response was strongly affected by the correlated surround. These cortical images are shown here only for visualization purposes; our analysis will be conducted in the five ROIs defined by fMRI retinotopy and standard localizers (Fig. 3c). The enhanced first harmonic response produced by the correlated surround across so much of the visual cortex presumably reflects the importance of relative disparity information, or at least disparity interactions, in both human perception and motor guidance.

Figure 3.

a, Topological map of the first harmonic scalp activity [normalized units (n.u.), averaged across subjects] in response to 12.4 arcmin disparity modulation of central disk surrounded by disparity noise (left) or surrounded by a correlated surface presented in a fixation plane (right). b, SNR activity of cortical sources (normalized units) of the first harmonic, mapped from all the subjects on one subject's cortex. c, Five regions of interest labels. Amp, Amplitude.

Were we really measuring an absolute disparity response in our uncorrelated surround condition? In our display, it was impossible to remove all possible reference stimuli. The edges of the display screens and distant objects imaged in the far periphery could, in principle, have served as a reference framework for the disparity modulation of the disk, but the noise probably obscured these weak references. The strongest proof that this condition contained no significant relative disparity information comes from our psychophysical threshold measurements for detecting disparity modulation using the same stimulus configurations used for the EEG measurements.

Thresholds for the correlated surround averaged about 11 arcsec, whereas thresholds for the uncorrelated surround averaged over 6 arcmin, more than a factor of 30 higher. Three other highly trained subjects (data not shown) were unable to detect any change in the central disk when surrounded by the uncorrelated noise, even for very large disparity changes. The difference in these thresholds is comparable to similar psychophysical measurements made by Regan et al. (1986) for a single isolated dot moving in depth, presented with and without a reference. In Figure 4, we have plotted our results as sensitivity (reciprocal of threshold) for easier comparison with the EEG SNRs.

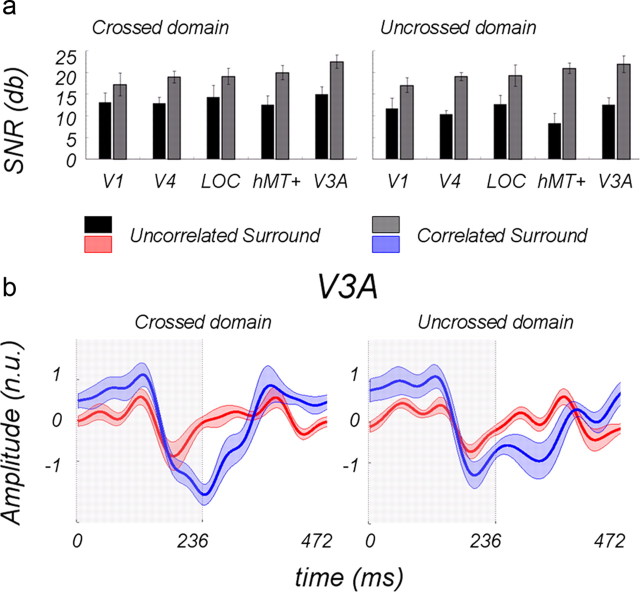
Figure 5 shows the SNRs for the odd (first and third) harmonics in the five ROIs averaged over subjects for the two surround conditions; the left side of the figure shows the crossed disparity responses, and the right side shows the uncrossed responses. Note first that the disparity modulation with an uncorrelated surround condition (Fig. 5, black bars) produces a sizeable response in all ROIs. The average SNR was >12 dB, indicating that the average amplitude at the odd harmonics was about 4 times the noise level in their neighborhood of the Fourier spectrum. The crossed response to “absolute disparity” seems to be somewhat higher than the uncrossed response, consistent with our previous EEG findings (Cottereau et al., 2011a) and fMRI measurements (Preston et al., 2008).

Figure 5.

a, SNRs of odd harmonic responses averaged over 11 subjects for central disk modulated by 12.4 arcmin disparity, surrounded either by uncorrelated disparity noise (black bars) or by a binocularly correlated surface presented at fixed zero disparity (gray bars). b, Temporal waveforms in normalized units (n.u.) for the ROI V3A; the disk was at ±12.4 arcmin disparity for the first half of the period (shaded areas) and at zero disparity for the second half. The red curve shows a response with uncorrelated surround; the blue curve shows a response with binocularly correlated surround in fixation plane.

As was discussed by Cottereau et al. (2011a), electromagnetic imaging gives a blurry representation of the sources responsible for the measured scalp activity; the spatial resolution of this technique is poorer than fMRI measurements [but see Cottereau et al. (2011b) for a good match between the retinotopic reconstructions obtained from the technique used in the present study but applied to MEG imaging and fMRI estimates]. Thus, the ROIs should be treated as a cortical region surrounding the designed label. For example, the SNR labeled “V3A” in Figure 5 certainly represents source activity from V3A, but it may also include additional activity from adjacent areas, such as V3, V3B, or V7. We have estimated the cross talk among the five ROIs (see Materials and Methods) using simulations, but we did not attempt to estimate cross talk from other adjacent anatomical regions, e.g., V3B or V7, since we had no rigorous way of defining them. It is interesting that our simulations show that the V3A receives the largest amount of cross talk from V1, but as our results will show, the response patterns in the V3A ROI do not resemble those attributed to the V1 ROI.

The correlated surround (gray bars) produced a significant increase in the SNR of the odd harmonics overall. This was confirmed by a pairwise t test (p = 4.2.e⁻²³). The smallest effect was in area V1, and the largest effect was in dorsal area hMT+. The increase in the odd harmonic response produced by the surround was ∼6 dB (factor of 2) in the ventral areas and ∼9 dB in the dorsal areas (factor of 3). These effects seem smaller than the effect of the surround on the psychophysical thresholds, but the EEG responses come from the entire population within an ROI, whereas the thresholds undoubtedly depend on a select group of fine-scale neurons where the enhancement might be stronger than at coarser scales. Generally, the results in Figure 5 suggest that the ventral pathway is no more responsive to relative disparity than the dorsal pathway.

To further illustrate the effect of the surround on the response to changing disparity, we show the normalized waveforms for the two conditions for the area with the biggest SNRs when the surround is correlated: V3A. The waveforms are displayed in Figure 5b. If we had simply averaged the individual waveforms across subjects, the subjects with the largest response amplitudes would have dominated the resulting waveforms, so we first normalized the responses from individual subjects (by dividing by the SD of the response amplitudes across all conditions and ROIs) and then averaged the normalized responses. To make effect of the disparity modulation, per se, easier to see, the curves also have been filtered to remove frequencies above 15 Hz, thereby removing the response at 21.2 Hz associated with dot update rate. The red curve shows the waveform for the uncorrelated surround, and the blue curve shows the waveform for the correlated surround.

By examining the red curve, one can see that the response amplitude is larger in the first-half period (Fig. 5, shaded area), when the disk is 12.4 arcmin behind the fixation plane, than during the second half, when the disk is in the fixation plane (zero disparity). This asymmetry in response amplitude is responsible for the odd harmonics plotted by the black bars (Fig. 5a); note that the units are very different, so a direct comparison of the waveforms with the bars is not possible. We previously have shown that the disparity response of all these ROIs peaks between 4–16 arcmin declining at smaller and larger disparities (Cottereau et al., 2011a), so the odd harmonic response is a direct consequence of the disparity tuning of these areas. The main reason why this stimulus configuration produces larger odd harmonics (asymmetrical responses) than the symmetrical configuration used in our previous study is because the central disk moves up and down the disparity tuning function, i.e., from 0–12 arcmin.

This asymmetry is amplified by the presence of the correlated surround, as shown by the increase in the odd harmonics (Fig. 5, gray bars). From the blue curve, it is apparent that the response is enhanced when the disk is behind or in front of the surround, during the first half of the period. The enhanced response may be attributable to the presence of two different disparities in close spatial proximity, perhaps a preliminary calculation of relative disparity, but there is another possible explanation. The large increase in the response could reflect a change in surface structure. As the central disk shifts back and forth between the two disparities, it “makes and breaks” a continuous surface formed with the surround in the fixation plane (Fig. 6a, middle). If many disparity-sensitive neurons in these extrastriate ROIs were responsive to an abrupt “break” in an implicit surface, their activity could have greatly increased the odd harmonic response.

Is surface segmentation the basis of the surround effect?

To test whether surface segmentation is the basis of the surround effect, we repeated the comparison between the uncorrelated and correlated surrounds, but we added a third condition. The three conditions are diagrammed in Figure 6a in bird's-eye view. The first two pictures are diagrams of the uncorrelated surround condition and the correlated surround condition used in the first experiment described above. In the third condition (Fig. 6, right), the correlated surround was shifted back from the fixation plane to an uncrossed disparity of 14 arcmin; the disparity modulation of the disk remained 12.4 arcmin, but now it moved from 14 to 1.6 arcmin. This manipulation meant that the disk and surround formed a continuous surface at 14 arcmin, which was repeatedly broken, similar to the make-and-break of the surface in the fixation plane. Note that the disk forms a continuous surface with the surround in both the middle and right pictures (Fig. 6). The basic comparison between the two types of surrounds (uncorrelated and correlated) was repeated within the same recording session with new subjects, so that we could compare all three conditions directly.

In Figure 6, we plotted the odd harmonic SNRs for these three conditions: uncorrelated surround (black bars), correlated surround in fixation plane (gray bars), and correlated surround at 14 arcmin uncrossed disparity (white bars). Shifting the surround back 14 arcmin produced a variety of effects in the different ROIs. If changes in surface structure accounted for a portion of the odd harmonic response, its contribution varied from ROI to ROI. A repeated-measures (three surround conditions) × (five ROIs) ANOVA led to a main effect of surround condition (p = 5.9⁻⁶) and a significant interaction (p = 0.004). Post hoc paired t tests were performed to complete the analysis. Significant comparisons are displayed in Figure 6 (*p < 0.05, **p < 0.01, and ***p < 0.001). Curiously, the backward shift produced a significant increase in the V1 ROI, although as we shall show subsequently, this ROI is not consistently affected by the presence or location of the surround. Based on our previous findings and monkey single-cell studies (Cumming and Parker, 1999), we had not expected any relative disparity effects in V1, so the observed increase caused by the surround could arise from cross talk from all the areas surrounding V1, but particularly the V3A ROI (Fig. 2).

Neurons in the LOC and hMT+ ROIs may be particularly responsive to surface segmentation cues, since the odd harmonic SNRs at these locations were nearly the same whether the surround was presented at fixation or back 14 arcmin. In contrast, moving the surround back 14 arcmin produced a significant decline in the odd harmonics for the V4 and V3A ROIs; this effect was particularly strong in the V3A ROI. It seemed as though there was something special about the fixation plane. One possible explanation for this result was that these two ROIs were affected by attention-driven increases in neural activity. Our subjects were asked to maintain fixation on a small fixation target and to keep nonius lines aligned during recording sessions, no matter where the stimulus appeared, a task that may have focused attention on the fixation plane. Thus, responses to breaks in a surface at fixation could have received an extra boost from attention.

To determine whether attention accounted for the fixation plane response in V3A and, to a lesser extent, in V4, we repeated the EEG measurements for the two surround conditions, while manipulating attention. Subjects were asked to view the displays passively, to attend to changes in the disparity modulation of the central disk (directed attention), or to attend to changes in a set of letters superimposed on the center of the disk (divided attention). These manipulations of attention had no significant effect on the SNRs in any ROI, no matter whether the surround was presented in the fixation plane or 14 arcmin behind the plane. In their fMRI study, Tsao et al. (2003) also found that attention had no consistent effect on disparity-driven BOLD signals in early visual areas.

Our initial experiment comparing the uncorrelated and correlated surrounds tested whether a particular ROI was predominately encoding absolute or relative disparity. When we shifted the correlated surround 14 arcmin behind the plane, the relative disparities in the image remained the same as they were when the surround was at zero disparity. Two of the extrastriate areas, LOC and hMT+, gave statistically equivalent responses to the two correlated surround conditions, a result that was consistent with either an invariant response to relative disparity or a response driven by surface segmentation cues. The decline in the V4 ROI, while significant, was small, but the decline in the V3A ROI was large and highly significant.

The V3A ROI was clearly affected by the combined presence of the disk and annulus disparities, but it did not give an invariant response to the difference between them. Responses in this area therefore cannot be explained by the only existing model of relative disparity processing (Thomas et al., 2002), because that model computes an invariant relative disparity signal on the basis of combinations of absolute disparity. Thus, we developed and tested two alternative models to explain our results in the V3A ROI. Understanding disparity processing in this region of cortex is important, beyond the present results, because many other studies of population responses have shown V3A to be extremely responsive to disparity (Backus et al., 2001; Tsao et al., 2003; Preston et al., 2008; Cottereau et al., 2011a). In the next section, we used the temporal waveforms associated with the three conditions in Figure 6 to model the V3A responses, instead of the Fourier magnitudes, so that we could analyze the responses after each disparity transition in the stimulus separately. Using these data, we compared two simple models of surround interaction in the disparity domain, one a multiplicative model and the other an additive model.

Modeling the odd harmonics in V3A

We will first discuss the multiplicative model, because it best explains our results. This model has two components, (1) the disparity tuning curve (Fig. 7a) for the V3A ROI and (2) a multiplicative gain that amplifies or suppresses the disparity response to the central disk in the presence of the surround. In the multiplicative model, the surround exerts a multiplicative modulatory effect on the response to the center. Surround gain increases the underlying disparity response when the disk and surround are in different planes and reduces the underlying disparity response when they are in the same plane (Bradley and Anderson, 1998). Furthermore, we speculate that this gain is proportional to the disparity separating the disk and the surround. The multiplicative model thus implements center–surround antagonism in the disparity domain. The additive model is described in detail after a discussion of the multiplicative model.

Figure 7.

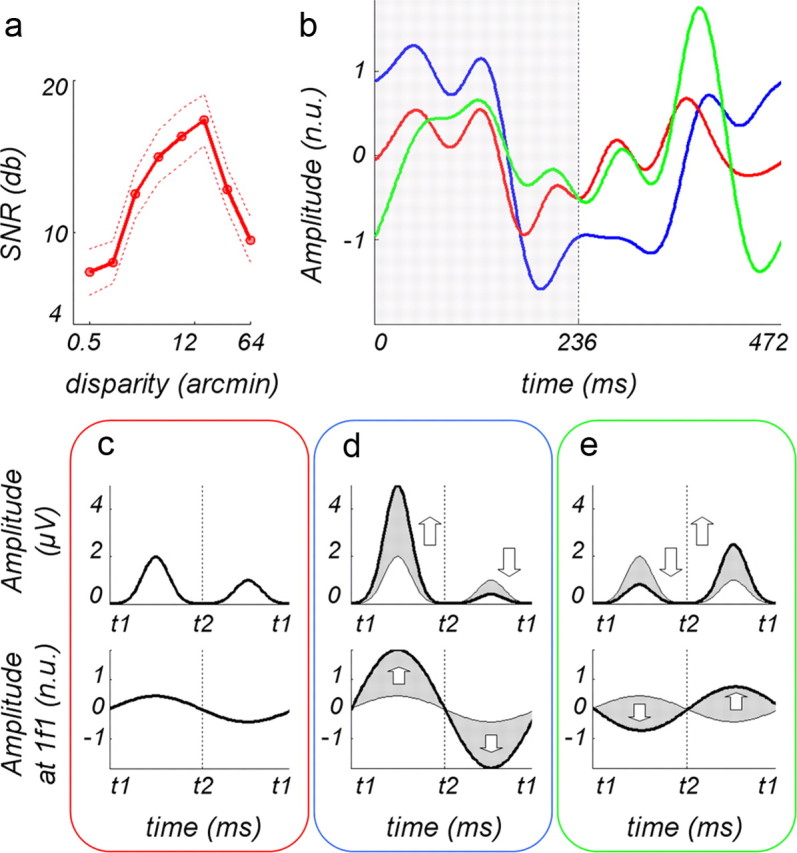
Multiplicative model of odd harmonic responses in ROI V3A. a, Disparity tuning for V3A ROI (Cottereau et al., 2011a). The tuning function is shown here for tutorial purposes. It is based on the average of crossed and uncrossed disparity responses, whereas the responses shown in b are only from uncrossed disparities. Because the crossed response is slightly higher than the uncrossed, this function is a bit higher than the true tuning function for uncrossed disparity, but the shape is approximately correct. b, Average normalized waveforms for uncorrelated surround (red curve), correlated surround at fixation (blue curve), and correlated surround at 14 arcmin uncrossed disparity (green curve); the shaded region shows time period when the surface is broken for blue curves; for green curves, the surface is broken during the second time period (236–472 ms). Curves have been filtered to remove frequencies above 15 Hz. c, Model amplitudes to 12 arcmin at t1 and 0 at t2 (top row) and resulting first harmonic (bottom row) for uncorrelated surround condition. d, Amplitudes to 12 arcmin at t1 and 0 at t2 (top row) and resulting first harmonic (bottom row) for correlated surround in fixation plane. e, Model amplitudes to 14 arcmin at t1 and 1.6 at t2 (top row) and first harmonic (bottom row) for correlated surround at 14 arcmin. The up arrows indicate that the gain is positive, whereas the down arrows indicate that the gain is negative. The abbreviation n.u. refers to normalized units.

The temporal waveforms associated with the three conditions plotted in Figure 6 are shown in Figure 7b. The red curve shows the waveform for the uncorrelated surround, the blue curve for the correlated surround at fixation, and the green curve for the correlated surround presented back at 14 arcmin disparity (Fig. 6a). For the stimulus conditions associated with the red and blue curves, the central disk appeared at an uncrossed disparity of 12.4 arcmin during the first half of the stimulus period (Fig. 6a, shaded area) and returned to the fixation plane for the second half. For the green curve, the disk began at an uncrossed disparity of 14 arcmin (the same plane as the surround) for the first-half period and shifted to 1.6 arcmin near the fixation plane for the second half.

The red curve (uncorrelated surround) shows that the amplitude of the response was larger during the first half of the period than during the second half, producing the asymmetry associated with the first harmonic. As we noted above, this asymmetry arises from the disparity tuning of this ROI, which shows that the response to 12.4 arcmin is greater than the response near zero. In the model, we have diagrammed this difference in amplitude in the top row of Fig. 7c (red box) and the resulting effect on the first harmonic in the bottom row of 7c.

The correlated surround increased the odd harmonic responses, compared with the responses with the uncorrelated surround. Indeed, the blue curve shows that the asymmetry in the temporal waveform had increased; the response was smaller when the disk was at zero, forming a continuous surface with the surround, then when the disk was behind the surround at 12.4 arcmin disparity. We have modeled this response pattern as representing an increased gain in the underlying disparity response to 12.4 arcmin, given by the tuning function, and a reduced gain in the underlying response at zero disparity. The arrows in the top row of blue box show the changes in gain. These paired increases and decreases in the gain together produce a large increase in the first harmonic (bottom row of blue box). When the correlated surround was presented at 14 arcmin uncrossed disparity, the central disk appeared in front of the surround during the second-half period. Thus, as shown by the green curve, the increased gain at 1.6 arcmin disparity appears between 236 and 472 ms. Because the segmentation occurred at different times, the blue and green curves appear to be out of phase by ∼180°. Our model predicts increased gain when the disk is at a different disparity from the surround (second half) and decreased gain when the disk is in the same plane as the surround (first half). Thus, the gain amplifies the small disparity response at 1.6 arcmin and suppresses the larger disparity response at 14 arcmin, based on the tuning function. The net result is that, when the surround was shifted back to 14 arcmin, the responses in both halves of the period were more similar, producing smaller odd harmonics than those observed when the surround was in the fixation plane. To visualize this process, look at the top row of the green box in Fig. 7e. As shown by the arrows, the gain at 14 arcmin, when the surface was continuous, decreased, and the gain at 1.6 arcmin increased. The bottom row of the green box shows the resulting first harmonic, which is smaller than the first harmonic in the bottom row of the blue box. The first harmonic shown in the bottom row of the three boxes match the pattern of results in Figure 6 for the V3A ROI.

We also considered an additive model in which the response in the V3A ROI increased because additional neurons were activated by the presence of a correlated surround. In this model, we assumed that this ROI contained neurons that were tuned to both absolute and relative disparity. The surround stimulated neurons sensitive to relative disparity, neurons that did not respond, or did not respond optimally, to the changing disparity of the central disk when the surround was uncorrelated. This approach predicted an overall increase in the response, but it did not explain why the odd harmonics, in particular, were increased by the correlated surround (the enhanced asymmetry in the blue and green curves in Fig. 7b). To explain the increase in the odd harmonics, we also assumed that neurons tuned to large relative disparities were more numerous or more responsive than neurons tuned to small relative disparities. If so, neurons tuned to a relative disparity of 12 arcmin would have produced a greater response than neurons tuned to a relative disparity of zero, an asymmetrical increase when the disk is separated from the surround. There is some neurophysiological evidence for this speculation; Umeda et al. (2007) noted that in V4, neurons coding a relative disparity of zero (“disparity continuity neurons”) were rare. Thus, the tuning function for relative disparity might look similar to the tuning function for absolute disparity (Fig. 7a). Cottereau et al. (2011a) found that the shape of the disparity tuning function was not altered much by the addition of the correlated surround.

The simple version of the additive model predicted that the blue and green curves should have been mirror images of one another, because in both cases, neurons tuned to a relative disparity of 12 arcmin added to the population response. Thus, the odd harmonics for the two surround conditions were predicted to be the same, contrary to our results (Fig. 6). However, we had also assumed that the V3A ROI had a large population of neurons tuned to absolute disparity. The overall response to the stimulus is the sum of the responses from neurons tuned to both relative and absolute disparity. The response of this absolute disparity population is given by the tuning function shown above, so when the disk moved back to 12 arcmin, the response from neurons tuned to absolute disparity was greater than when the disk moved forward to 1.6 arcmin, thereby producing a larger odd harmonic response to the surround at fixation than the odd harmonic response to the surround at 14 arcmin.

Effects of varying the surround disparity

At this point, the two models (multiplicative and additive) of disparity interactions in area V3A are ad hoc, merely qualitative formulations inferred from the data. In the next sections, we describe two other experiments designed to test (1) whether center–surround disparity interactions are driven by the center–surround disparity difference and (2) whether disparity interactions are multiplicative or additive.

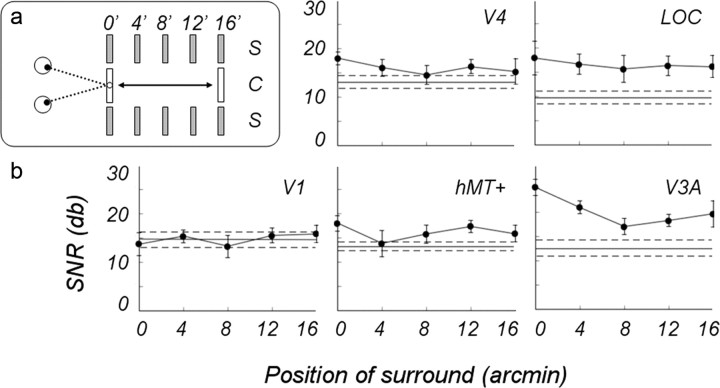
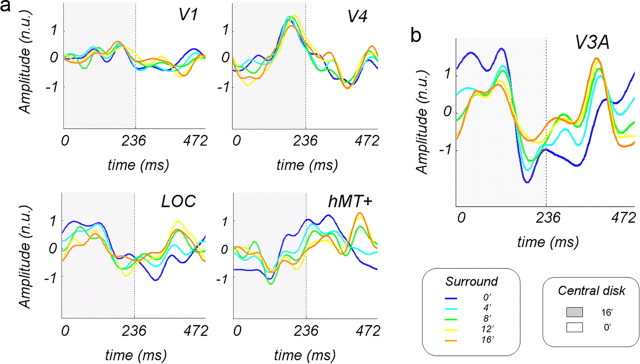
Do center–surround interactions depend on the center–surround disparity difference? We parametrically varied the disparity of the correlated surround to determine how its location altered the response to the disparity modulation of the central disk. The disk modulation was increased to 16 arcmin uncrossed disparity, and the fixed surround was presented at one of five uncrossed disparities (0, 4, 8, 12, and 16 arcmin) in interspersed conditions (see diagram in Fig. 8a). Note that when the surround is presented at the intermediate position, e.g., 8 arcmin, the surface was “broken” in both halves of the temporal period. This experiment also allowed us to test the generality of the surround effects in all five ROIs and compare the relative strength and consistency of these effects across ROIs. The results of this experiment are shown in Figure 8. The horizontal lines show the SNR of these ROIs in the uncorrelated surround condition, taken from the data shown in Figure 6.

Figure 8.

a, Diagram of the stimulus configurations. b, SNRs of the odd harmonic responses in five ROIs averaged over 10 subjects; a central disk modulated by 16 arcmin uncrossed disparity is shown. Correlated surround shifted in separate conditions from a fixation plane to 16 arcmin behind the fixation plane in 4 arcmin increments. Horizontal lines show responses to an modulated disk with an uncorrelated surround, taken from data in Figure 6; dotted lines show ±1 SE.

A repeated-measures (five surround positions) × (five ROIs) ANOVA led to a main effect of the surround position (p = 0.025) and significant interaction between surround position and ROI (p = 0.025). It was apparent that the V1 ROI was little affected by the surround, no matter what its position. Therefore, we concluded that most of the neurons in the V1 ROI respond to absolute disparity, as we also concluded in our previous study (Cottereau et al., 2011a). The SNRs in all four extrastriate areas changed as the surround was moved back from the fixation plane, but clearly the pattern varied somewhat from ROI to ROI. The function in area hMT+ was noisy, particularly at 4 arcmin, but averaged across the five positions, the increase in the SNR was ∼3.5 dB (50%) higher with the correlated than with the uncorrelated surround. Similarly, in the V4 ROI, the correlated surround increased the SNR by ∼3 dB (40%), on average, so we concluded that both hMT+ and V4 were affected by the presence of the surround. The SNR in the LOC ROI was almost constant across the five positions, on average almost 7 dB (approximate factor of 2) over the baseline, which demonstrated a significant effect of the surround on the response of this ROI at all positions. In the V3A ROI, the average increase was more than a factor of 2, also indicating a significant surround effect, especially when the surround was in the fixation plane, as was shown in the previous experiment.

In all the extrastriate ROIs, the responses to the surround middle positions (4, 8, and 12 arcmin), where the modulating disk straddles the surround, mainly hover over the baseline. This result meant that it was not the break in the surface per se that increased the odd harmonic response to the disk modulation. Rather, it was the presence of two different disparities in close spatial proximity that created this interaction. When the surround was positioned at zero and 16 arcmin, the relative disparity separating the center from the surround was the same but inverted in time, with the break occurring during the first-half period for the zero surround and during the second-half period for the 16 arcmin surround. For areas LOC and hMT+, the SNR for these two conditions were not significantly different statistically, a replication of the results shown in Figure 6 for a different combination of center modulation and surround positions. Did this result mean that the populations of these two areas were actually encoding relative disparity? In the hMT+ ROI, the temporal waveform corresponding to the surround at zero was definitely not the mirror image of the waveform corresponding to the surround at 16 arcmin (see Fig. 10a), a result that seemed inconsistent with an invariant response to a fixed relative disparity. The reversed match between the waveforms for 0 and 16 arcmin surrounds was better for the LOC ROI but remained imperfect.

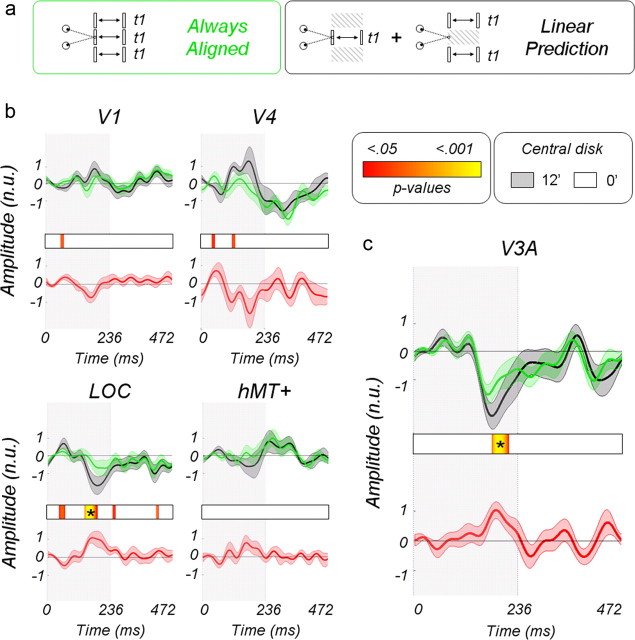
Figure 10.

Nonlinear interaction associated with an alignment of center and surround. a, Diagram of the different conditions. The simultaneous manipulation of center and surround is emphasized in green, whereas the associated linear prediction (center moving alone plus surround moving alone) is emphasized in black. b, Corresponding average normalized waveforms estimated from areas V1, V4, LOC, and hMT+. The red curves give the differences. The color bar provides associated p values. c, Responses in area V3A. Asterisks emphasize a significant time window after correction for multiple comparisons. The abbreviation n.u. refers to normalized units.

We were particularly interested in the V3A temporal waveforms because of the strong effects of surround disparity seen in this ROI (Fig. 9b). How well did our multiplicative model capture the changes in the waveforms as we shifted the surround backward?

Figure 9.

Average normalized waveforms corresponding to the five disparities of the surround. Curves have been filtered to remove frequencies above 15 Hz. The shaded area corresponds to the first half of the period when the central modulating disk was in the fixation plane. During the second-half period, the disk was at 16 arcmin disparity. a, Waveforms in V1, V4, LOC, and hMT+. b, Waveform in V3A. The abbreviation n.u. refers to normalized units.

During the first-half period of the stimulation cycle (between t = 0 and t = 236 ms), the center is displayed at a disparity of 16 arcmin, and the disparity difference between center and surround is therefore varying from 16 arcmin when the surround is at 0 arcmin in condition 1 to 0 arcmin when the surround is presented at 16 arcmin in condition 5 (the intermediate values being 4, 8, and 12 arcmin for conditions 2–4). Our model predicts that gain is proportional to the center–surround difference, so the response amplitudes should diminish with the condition during the first-half period. This effect is clearly observed in the corresponding time courses (from the blue curve to the orange one). During the second-half period (between t = 236 and t = 472 ms), the center shifts to the fixation plane, and the center–surround difference varies between 0 arcmin in condition 1 and 16 arcmin in condition 5. In this case, the model predicts that the response amplitudes should increase with the condition number. Once again, this effect is observed.

The waveforms shown in Figure 9 are in agreement with the odd harmonic responses shown in Figure 8; the SNR is smaller for condition 3 (smaller difference between center and surround with ±8 arcmin) and bigger in conditions 1 and 5 (16 arcmin of difference). As in the previous experiment, the absolute disparity tuning function gives rise to a larger SNR in condition 1 when compared with condition 5, because in this condition, the increase attributable to the center–surround difference is built on a response to 16 arcmin that is intrinsically larger than the responses to 0 arcmin (see Fig. 7, d and e, for a schematic illustration). The larger SNR in condition 2 when compared with condition 4 has the same explanation, the underlying shape of the disparity tuning function.

In a last experiment, we test whether these interactions are caused by a multiplicative or an additive mechanism.

Nonlinear interactions between center and surround

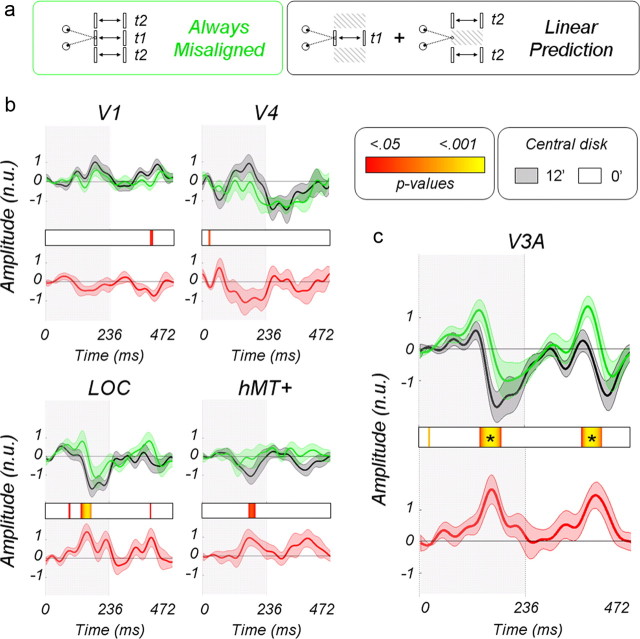
In this experiment, we directly tested the additive and multiplicative models by making linear predictions based on isolated center and surround responses and observing how they failed to fit with responses obtained from simultaneous stimulation of center and surround. The linear predictions are obtained by summing the responses to the center moving in depth alone with an uncorrelated surround plus the responses to the surround moving in depth with an uncorrelated center (see Materials and Methods, Main experiments). We were particularly interested in two specific interactions: those obtained when both center and surround are always aligned (i.e., moving in phase) and those when they are always misaligned (i.e., out of phase). Figure 10 describes the effect when center and surround are always aligned (see Fig. 10a for a schematic description of the stimuli). The multiplicative model predicts suppression for stimuli with continuously aligned planar disparities and facilitation for segmented stimuli, whereas the additive model predicts facilitation for segmented stimuli and no effect for continuous planes.

The normalized time courses in Figure 10b correspond to the linear predictions (in black), and the true responses to center and surround moving in phase are shown in green for the V1, V4, LOC, and hMT+ ROIs. The average values have been baseline corrected to 0 over the first 50 ms time window. The red curves are the differences and therefore provide a measure of the nonlinear interaction. No significant interactions are observed in the V1, V4, and hMT ROIs. In the LOC ROI, we observe that the signals are suppressed when compared with the linear prediction around 180 ms after center and surround have both moved to 12.4 arcmin. This suppression is significant after correction for multiple comparisons (see Materials and Methods, Statistical analysis). Responses in V3A are shown in Fig. 10c. As in the LOC, a suppression can be observed around 180 ms when center and surround are aligned at 12.4 arcmin.

Figure 11 describes the interaction when center and surround are always misaligned (see Fig 11a for a schematic description of the stimuli). In V1, V4, hMT+, and LOC, no significant differences are observed between the real measurements and their linear predictions (Fig. 11b). Low p value trends are, however, present in the LOC ROI when the center is at 12.4 arcmin and the surround in the fixation plane. In V3A, however (Fig. 11c), significant differences are observed both in the first-half (center at 12.4 arcmin and surround at 0 arcmin) and in the second-half cycles (center in the fixation plan and surround at 12.4 arcmin). The responses in the real recordings are larger than the linear predictions around 165 and 380 ms, beginning with a relative increase of the early positivity around 135 and 340 ms. Interestingly, the falling phase of the positivity is lagged in time, suggesting that additional processing occurs when center and surround interact. Together, our results suggest that facilitation by the surround acts more quickly than suppression.

Figure 11.

Nonlinear interaction associated with a misalignment of center and surround. a, Diagram of the different conditions. b, Corresponding average normalized waveforms estimated from areas V1, V4, LOC, and hMT+. c, Responses in area V3A. See Figure 10 for the details of the legend. The abbreviation n.u. refers to normalized units.

This experiment clearly shows the gain mechanism in V3A suppresses the disparity responses when center and surround are aligned (coplanar) and facilitates it when they are misaligned/segmented in depth. The additive model would not have led to these differences and must therefore be discarded.

Discussion

In the Introduction, we described a simple dichotomy between absolute and relative disparity, based on binocular geometry. To test whether the neural populations in five human visual ROIs were sensitive to relative disparity, we compared the response of these areas with disparity modulation of a central disk when surrounded by uncorrelated disparity noise, or by a correlated surround at a fixed depth. Although the V1 ROI population response was mainly unaffected by the surround, the V3A, LOC, V4, and hMT+ ROIs were sensitive to disparity differences. However, we have no compelling evidence that the bulk of the neurons in these four ROIs give an invariant response to a fixed difference in disparity to relative disparity in the geometric sense.

In humans, area V3A has been shown to be extremely responsive to disparity (Backus et al., 2001; Preston et al., 2008; Cottereau et al., 2011a). Despite the lack of tight homology of this area between humans and monkeys, disparity responses in macaque V3A have very similar properties (Tsao et al., 2003). Maximal effects of surround disparity were observed in the V3A ROI in the present experiment, and because of this, we focused our modeling on data from this ROI. According to the model, when surrounded by uncorrelated noise, disparity modulation between 0 arcmin and 12 arcmin produces an odd harmonic response in V3A because of the underlying disparity tuning; the population response at zero is smaller than the response at 12 arcmin. By examining the temporal waveforms, we found that the surround enhanced the response when the surround and the center were at different disparities and suppressed the response when the surround and the center shared the same disparity. To explain this pattern, we proposed a multiplicative “gain” model in which the surround modulates the center response in an antagonistic fashion and contrasted it with an additive model in which relative disparity response was added to absolute disparity responses. Only the multiplicative model is consistent with the pattern of nonlinear interactions found in our last experiment.

A previous model of disparity processing in monkeys (Thomas et al., 2002) proposed a “relative disparity” energy model to explain how a single neuron might encode an invariant disparity difference. Their model involves summing and squaring a pair of absolute disparities to extract a constant disparity difference. This model computes an invariant relative disparity signal from combinations of absolute disparity responses. We did not observe invariant response in our data. Moreover, the Thomas model cannot generate the suppressive interaction that we have observed. We found that even if we incorporated the underlying disparity tuning function, a population version of the relative disparity model did not handle the observed dependence of the response on the surround disparity.

A more promising physiological model was suggested by Bradley and Anderson (1998). They measured changes in the neural response to optimal targets stimulating the classical receptive field, when other targets were placed far outside the receptive field in the so-called suppressive surround. When these distant targets had the same disparity as the optimal target, the response was suppressed. When the distant targets had a different disparity from the optimal stimulus, the response increased over the baseline response. These effects of surround disparity seem to be similar to other surround effects that have been observed with surround motion or orientation cues (Allman et al., 1985; Sillito et al., 1995). Most single-unit studies in LGN and V1 have focused on the suppression of firing rates produced by stimuli falling outside the classical receptive field (Cavanaugh et al., 2002; Bonin et al., 2005), but enhanced firing produced by a surround has also been reported (Sillito et al., 1995; Polat et al., 1998; Ichida et al., 2007). Antagonistic surround interactions in the disparity domain may contribute to perceptual induction effects in which motion in depth in one part of the visual field induces the perception of motion in depth in another part of the visual field (Gogel and Griffin, 1982; Likova and Tyler, 2003). Induced effects on perceived surface slant by a remote disparity surround have also been reported (Kumar and Glaser, 1991).

Why does V3A show such a strong population response to disparity stimuli? It may be that V3A is uniquely sensitive to disparity. Disparity is particularly important in planning and generating grasp movements (Melmoth et al., 2009). This visual area projects either directly or indirectly to the anterior intraparietal area (AIP) (Anderson et al., 1990; Baizer et al., 1991; Sakata et al., 1997; Nakamura et al., 2001; Orban et al., 2006). AIP is known to be selective for grasp in monkeys (Murata et al., 2000; Durand et al., 2007) and humans (Culham et al., 2003; Tunik et al., 2005; Durand et al., 2009). In their study using C-deoxyglucose to map activity in macaque cortex, Kilintari et al. (2011) found that grasp movements activated V3d and V3A even when the movements were made in the dark, which shows the close link between V3A and neural areas controlling grasp movements.

A neural process that enhances disparity differences may be valuable in guiding grasp movements. One can make the case that absolute disparity determines the positions of the fingers in grasp, since we are usually looking at the object we plan to grasp. These absolute disparities could be encoded separately for each part of the hand in a framework tied to fixation. The different absolute disparities that control the z-axis separation between the fingers and the object to be grasped could be “compared” by some mechanism that gives a graded response to their separation, such as the surround effect that we have described here. Note that our results showed that the surround enhanced the absolute disparity response of the modulating disk in a graded way that depended on the depth separation between disk and surround. Parietal areas could use this graded response to a disparity difference from V3A to guide changes in the positions of the fingers to complete the grasp movement. Thus, we are speculating that the disparity information in V3A is both absolute for the guidance of hand movements in a fixation-based framework and “relative,” in the sense that the population response shows sensitivity to disparity differences but does not encode “invariant relative disparity.” This idea is consistent with the findings of Neri et al. (2004). In their fMRI adaptation paradigm, they presented a pair of transparent planes separated by a fixed difference in disparity at many different absolute disparities to adapt areas sensitive to relative disparity independent of absolute disparity. V3A and other dorsal areas were not affected by relative disparity adaptation. A recent study by Anzai et al. (2011) confirmed this result in monkeys by showing that disparity tuning in macaque area V3A did not shift with the surround disparity. Interestingly, this study also found that the surround significantly modulated the gain of the responses, in agreement with our findings.

Our psychophysical experiment confirmed the observation that human observers are very insensitive to unreferenced changes in disparity (Erkelens and Collewijn, 1985a). Prince et al. (2000) found that few neurons in V1 had neural thresholds that were comparable to the monkey's referenced behavioral thresholds. Without a reference, the monkey's thresholds were far worse than these neural thresholds. Prince et al. (2000) concluded that the monkey needed the reference to distinguish between the disparity changes produced by convergence and those produced by changes in the stimulus, as both would drive V1 neurons. Relative disparity neurons in extrastriate areas combine inputs from pairs of neurons tuned to absolute disparity (Thomas et al., 2002; Umeda et al., 2007; Parker, 2007) and respond to the difference independent of changes in convergence. The particular relative disparity neurons that extract the highly precise signals emerging from the fine-scale V1 neurons could provide the neural basis for referenced stereoacuity in primates.

Do our EEG results have anything to do with human stereoacuity? We found that, in all the extrastriate areas, the population response was enhanced by the presence of the correlated reference surround, particularly for disparity differences occurring with the fixation plane surround, where stereoacuity thresholds are most precise (Ogle, l953; Blakemore, 1970; McKee et al., 1990b). Our proposed gain model for V3A, an increased gain to disparity differences coupled to suppression of similarities, could certainly boost sensitivity to small differences. Possibly gain mechanisms operate in some visual areas to enhance sensitivity, whereas other visual areas depend on relative disparity neurons. Or perhaps all areas contain both gain mechanisms and relative disparity neurons, with each serving different functions within the population.