Isolating the Contributions of Familiarity and Source Information to Item Recognition: A Time Course Analysis

Abstract

Recognition memory may be mediated by the retrieval of distinct types of information, notably, a general assessment of familiarity and the recovery of specific source information. A response-signal speed–accuracy trade-off variant of an exclusion procedure was used to isolate the retrieval time course for familiarity and source information. In 2 experiments, participants studied spoken and read lists (with various numbers of presentations) and then performed an exclusion task, judging an item as old only if it was in the heard list. Dual-process fits of the time course data indicated that familiarity information typically is retrieved before source information. The implications that these data have for models of recognition, including dual-process and global memory models, are discussed.

Recognition memory may be based at times on a simple assessment of familiarity and at other times on the retrieval of a structured set of associative information that includes the source of the memory. Dual-process models make this argument explicit, positing that recognition can be mediated by a general assessment of familiarity and by recollection processes that recover specific source information (e.g., Atkinson & Juola, 1973; Jacoby & Dallas, 1981; Mandler, 1980). For example, Atkinson and Juola used response time data from well-learned lists to argue that items with high or low familiarity values are associated with a fast old or a fast new response, respectively, whereas items with intermediate familiarity values engage a slower search process to identify the presence of the item within a particular context (list). Mandler proposed a dual-process model in which one process quickly evaluates an item’s familiarity while another (independent) process performs a search of memory. More recently, Jacoby and colleagues (e.g., Jacoby, 1991; Yonelinas & Jacoby, 1994) argued that recognition is mediated by independent contributions from an automatic assessment of familiarity and a consciously controlled recollection operation. The process dissociation procedure has been used to derive estimates for the contribution of each process to various recognition tasks (Jacoby, 1991; see also Jacoby, Toth, & Yonelinas, 1993, and Yonelinas, 1994, for arguments based on receiver-operating characteristics [ROC] analyses).

The distinction between recollection and familiarity has been related to differences in subjective experience (e.g., Gardiner & Java, 1993; Gardiner, Ramponi, & Richardson-Klavehn, 1998) and has been used to delineate different anatomical bases for memory in an attempt to explain why recognition memory performance is sometimes relatively preserved in persons with amnesia (e.g., Aggleton & Shaw, 1996). The distinction is also useful for explaining why aging and some forms of brain damage result in an increase in false recognition, the mistaken claim that one has encountered an item in a particular circumstance (Jacoby, 1999; Schacter, Norman, & Koutstrall, 1998; Ste.-Marie, Jennings, & Finlayson, 1996). However, these recent developments have been largely separate from a literature aimed at devising formal models of recognition. Our goals in this study are to help bridge that gap and to provide nearly unquestionable evidence that recognition can rely on different forms or uses of memory.

Global memory models (e.g., Gillund & Shiffrin, 1984; Hintzman, 1988; Murdock, 1982; for an overview, see Clark & Gronlund, 1996) primarily treat item recognition as an assessment of familiarity or strength, conceptualized as the degree of match between cues at retrieval time and all items in memory. Although these models propose distinct recall operations for overt recall, recognition is usually modeled as a direct-access process that yields a unidimensional familiarity or strength value. The familiarity or strength metric can be contextualized to various degrees by integrating contextual cues with the recognition probe at test. In an influential study, Gillund and Shiffrin argued that a global assessment of familiarity was sufficient to account for standard recognition data. They rejected the notion that a (search-based) recall operation supplements a global comparison because they failed to find interactions of key variables (e.g., list length and orienting tasks) across short and long response deadlines (under 900 ms versus after 1.5 s). The assumption was that a long deadline provided more time for recall, so that variables that differentially affect recall should have shown a greater effect at long than at short deadlines.

We report two studies that demonstrate crossover effects in recognition false-alarm rates as a function of retrieval time. These crossover interactions directly implicate the retrieval of two distinct types of information with different underlying time courses. From the perspective of dual-process models of recognition (e.g., Atkinson & Juola, 1973; Jacoby, 1991; Mandler, 1980; see also Gillund & Shiffrin, 1984), the data provide strong support for a quickly accruing, source-invariant assessment of familiarity and a slower recollection process that recovers specific source information. We explore how these effects can be accommodated by global memory models, arguing that they require postulating two distinct retrieval operations, analogous to dual-process models or, alternatively, different decision rules for the recovery of familiarity (uncontextualized) and source (contextualized) information.

We begin by reviewing evidence for the role of source information in recognition. We first briefly consider evidence from the source-monitoring paradigm, a popular experimental procedure for addressing issues of the recovery of source information. We note that this paradigm has been important for focusing research on the recovery of source information; however, studies within this framework have not cleanly isolated and specified the relationship between familiarity information and source information. We argue that a better means of isolating and contrasting the two types of information is to place them in opposition to one another. We briefly review several time course studies that have adopted a similar logic.

Source Monitoring

Source-monitoring paradigms attempt to assess the retrieval of source information by examining overt source attributions (Johnson, Hashtroudi, & Lindsay, 1993). Participants respond to test items by choosing one of n alternatives to denote whether and in what context the test item was studied. This paradigm has been applied to several issues, including eyewitness memory, amnesia, and age-related differences in memory (for a review, see Johnson et al., 1993), often with the intention of demonstrating selective impairments in certain types of source discriminations (e.g., Foley & Johnson, 1985; Harvey, 1985) or the dissociation of source attributions and old–new discriminations (e.g., Hashtroudi, Johnson, & Chrosniak, 1989; Mitchell, Hunt, & Schmitt, 1988).

Early attempts to assess the accuracy of various source attributions and to disentangle source attributions from (old–new) detection were hampered by the lack of a set of consistent and well-motivated measurement procedures. Batchelder and Riefer (1990) and Riefer and Batchelder (1988) demonstrated that a major limitation of early measures was their inability to estimate the probability of detection and source discriminations uncontaminated by response biases. As a solution to this problem, they proposed that multinomial models should be applied to source-monitoring data, under the assumption that the psychological processes underlying source monitoring can be parameterized in terms of discrete probability states (e.g., high-threshold approximation to signal detection theory; see Batchelder & Riefer, 1990; Batchelder, Riefer, & Hu, 1994; Kinchla, 1994).

Johnson, Kounios, and Reeder (1994) capitalized on and extended the potential of multinomial models by applying these decomposition procedures to time course data. Their particular application examined differences between pictures that were either perceived or imagined. The response-signal speed–accuracy trade-off (SAT) procedure (Reed, 1973, 1976; Wickelgren, 1977) was used to measure how the probabilities of perceived, imagined, and new responses varied over retrieval time. This procedure (see Experiment 1) required participants to respond at various intervals following the onset of the test probe, thereby generating a time course function that measures the growth of retrieval as a function of processing time. Johnson et al.’s (1994) study was targeted at the questions of whether old–new detection was associated with an earlier time course than source discriminations (perceived versus imagined) and whether there were time course differences between the two types of source discriminations.

Unfortunately, the data reported by Johnson et al. (1994) do not enable one to draw clear conclusions concerning whether old–new detection is associated with an earlier time course than the retrieval of source information. The data do demonstrate that old–new detection is associated with a higher overall level of accuracy than the two source discriminations. However, if one accepts the multinomial model adopted by Johnson et al. (1994) as a veridical model of the relationship between old–new detection and the recovery of source information, then one is forced to conclude that source information for imagined items is available before items can be detected as either old or new and that the opposite pattern is true for perceived items. A detail discussion of the limitations of Johnson et al.’s (1994) study is presented in Appendix A.

The combination of SAT and multinomial modeling represents an important advancement in source-monitoring research. The blending of these procedures addresses issues of the underlying retrieval processes that mediate source attributions and, in doing so, provides a basis on which to integrate source-monitoring work with a large body of research on specific memory processes (see below). As outlined in Appendix A, we believe that the mixed patterns in Johnson et al.’s (1994) study are attributable to methodological shortcomings (viz., too few data points, a low number of response lags, and insufficient degrees of freedom to eliminate potential response biases). Although these limitations can be overcome by a more extensive design, an alternative procedure provides a more optimal means of isolating and contrasting component processes because it enables the contributions of component processes to be observed directly.

Opposition Logic

Familiarity information and source information are often highly correlated, so that factors (e.g., repetition) that lead to high familiarity values also lead to salient source information. As a result, the two types of information often work in concert, providing mutually supportive evidence. Intuitively, for example, one can recognize a person by a sense of familiarity and by recovering the specific context in which one met the person. When both types of information act in concert, as in a typical recognition or source-monitoring task, it is difficult to isolate the contribution of each type of information. However, the two forms of information can be isolated by placing them in opposition to one another, such that one provides evidence antithetical to the evidence provided by the other. Beyond methodological concerns, the opposition procedure provides a plausible experimental implementation of frequently encountered situations in which familiarity information and source information are negatively correlated. These situations can be particularly difficult for persons suffering from memory disorders, including age-related memory deficits (Jacoby, 1999).

For the studies reported here, we used an exclusion task to place familiarity information and source information in opposition. We built on a paradigm used by Jacoby (1999) in which participants first read a list of words and then listened to a different list of words. In Jacoby’s study, words were presented from one to five times in the read list and once only in the spoken list. Exclusion instructions at test were used to place the two processes in opposition to one another. Participants were instructed to respond “yes” to an item only if it was from the heard list and were explicitly told that they could be assured that an item was not in the heard list if they recalled it as having been read. The crucial variable of interest was the impact of repetition on read (lure) items. Repetition should increase both familiarity and recollection; however, given the exclusion instructions, increased familiarity should induce participants to false alarm (mistake a read item as heard), whereas better recollection of an item as being read should decrease the tendency for a false alarm.

Jacoby (1999) used response deadlines that required participants to respond within either 0.75 or 2 s after the onset of the recognition probe. With a short deadline, repetition produced progressively higher false-alarm rates. With a longer deadline, repetition produced progressively lower false-alarm rates. Jacoby argued that responses were based primarily on familiarity at the short deadline, which led to higher false-alarm rates the more often an item was read. With additional retrieval time, recollection could be used to assess whether an item was read, heard, or new. As the probability of recollecting an item as having been read was greater the more often it was read, the false-alarm rate was correspondingly attenuated at the longer deadline.

The differential impact of repetition at the short and long deadlines is consistent with a two-process model of recognition composed of a fast assessment of familiarity and a slower recollection process. Deadline procedures are, however, less than optimal for contrasting the time course of component cognitive processes (Wickelgren, 1977). Trials must be blocked by deadlines, so participants can adopt different study and response strategies across blocks (for an example, see Ratcliff, 1978). Additionally, the use of only two deadlines does not allow one to precisely track the relative contributions of the two processes over the full time course of recognition. The response-signal SAT procedure provides an alternative means of assessing the contributions of two-component processes.

SAT

SAT procedures have been effectively used in several domains to isolate the contributions of component processes with different underlying time courses (e.g., Dosher, 1984; Dosher & Rosedale, 1989; Dosher, McElree, Hood, & Rosedale, 1989; Gronlund & Ratcliff, 1989; Hintzman & Curran, 1994; McElree & Dosher, 1989; McElree & Griffith, 1995; Ratcliff & McKoon, 1982, 1989). The general research strategy has been similar to that of the Jacoby (1999) study in that differences in false-alarm rates have been used to track the time course of component processes. We briefly describe a subset of these studies both to highlight relevant findings and to illustrate how this type of analysis can serve to isolate underlying processes.

Relational Information

Ratcliff and McKoon (1982) used opposition logic in combination with SAT procedures in a study that examined processes underlying the semantic verification of simple propositions. Statements such as A robin is a bird were contrasted with anomalous statements such as A problem is a swallow and, crucially, statements with reversed category dominance relationships, such as A bird is a robin. Statements with reversed dominance relationships produced nonmonotonic time course functions with high false-alarm rates (relative to anomalous statements) early in retrieval (less than 700 ms) that were attenuated with further retrieval time. Ratcliff and McKoon (1982) argued that these biphasic functions indicate that semantic analysis involves the processing of two types of information: a fast assessment of semantic similarity, which leads to an early acceptance of statements with reversed dominance relationships, and a slower assessment of relational information, which attenuates the initial misanalysis.

Similar effects have been found in the episodic domain. In a sentence recognition task, Ratcliff and McKoon (1989) found that test sentences with rearranged subjects and objects produced high false-alarm rates early in retrieval that subsided with additional processing time. Likewise, Gronlund and Ratcliff (1989) found that rearranged pairs produced biphasic false-alarm functions when the task required associative recognition. Notably, the false-alarm rate for rearranged pairs was monotonic when the task required a positive response to studied items (whether or not the members of a test pair were studied together), indicating that the biphasic functions were directly linked to associative recognition processes. Both studies indicated that associative or relational information accrues later than item information. One interpretation of these results is that familiarity is made available early in retrieval from a global matching operation but that associative or relational information requires a slower recall operation (Clark, 1992; Clark & Gronlund, 1996; however, see Gronlund & Ratcliff, 1989). Indeed, Dosher (1984) and Dosher and Rosedale (1989) used mismatched pairs to estimate the point at which a recall operation was initiated and found that the point was substantially longer than the estimated point at which familiarity information was available.

Item Information

It is perhaps not entirely surprising to find time course differences between the retrieval of familiarity (or similarity) information and the retrieval of more complex forms of information, such as associative and relational information (see also McElree & Dosher, 1993, and Gronlund, Edwards, & Ohrt, 1997, for comparisons of the time course for retrieving item and temporal- or spatial-order information). However, nonmonotonic retrieval functions also have been documented in nominal item recognition tasks. These studies are more pertinent to our primary interest in the relationship between familiarity and the retrieval of source information, although the retrieval of associative information may have much in common with the retrieval of source information or may indeed be identical to it (Hockley & Cristi, 1996).

McElree and Dosher (1989) manipulated how recently a lure was studied in an SAT variant of the Sternberg (1975) item recognition task. Relative to temporally distant lures (negative probes drawn from three or more trials back), lures that were members of the previous study list induced a high false-alarm rate early in retrieval (interruption times < 900 ms), consistent with a higher familiarity or strength value. With additional retrieval time (interruption times > 900 ms), the false-alarm rate for recent lures decreased, approaching the rate for distant lures. These biphasic false-alarm functions were argued to result from an early assessment of familiarity that was later attenuated by the retrieval of list-specific information.

McElree (1998) extended these results by showing that both episodic familiarity and semantic similarity intruded early in the course of recognizing items from categorized lists. Recently studied lures and lures from the semantic categories in a study list both produced high false-alarm rates early in retrieval when compared with a baseline false-alarm rate for less recently studied, semantically unrelated lures. Here, too, the false-alarm rate decreased with additional retrieval time, suggesting that more specific information attenuates a rapidly accruing assessment of familiarity. Intrusions based on semantic similarity are analogous to the associative relatedness effects found in the Deese (1959) paradigm, recently revived by Roediger and McDermott (1995) (for reviews, see Roediger, 1996, and Schacter et al., 1998). The time course data are consistent with the contention that “false memories” may be produced when familiarity information is not opposed by the recovery of more detailed source information.

Intrusions based on semantic similarity also can be induced by the test context or environment. Dosher et al. (1989) found that, when a studied test item was preceded by a semantically related word, hit rates were higher than when the test item was preceded by an unrelated prime. The difference in hit rates, however, was completely offset by a corresponding increase in the false-alarm rates for lures preceded by a semantically related prime. Because the advantage in hit rates was cancelled by the increase in false-alarm rates, Dosher et al. argued that priming acted as a form of bias (see also Dosher, 1991; Jacoby, McElree, & Trainham, 1999; Ratcliff & McKoon, 1997; Ratcliff, McKoon, & Verwoerd, 1989). As with the false-alarm rates for lures with high familiarity, a nonmonotonic bias effect was observed, with a peak early in retrieval that subsided with additional retrieval time. The time course of the bias effect is consistent with the notion that a related prime increased the subjective familiarity of both studied and unstudied items by a constant amount. As in other studies, high initial familiarity values were countered later in retrieval by the recovery of list-specific information.

Finally, Hintzman and Curran (1994) reported a similar pattern of high false-alarm rates in two SAT studies that examined difficult item discriminations (Experiments 2 and 3). Highly similar lures (e.g., a plural of a singular study word) produced high early false-alarm rates that were likewise attenuated later in retrieval. On the basis of these results, Hintzman and Curran argued that recognition is mediated largely by a general assessment of familiarity information but that familiarity is supplemented by a recall operation when recognition is difficult. In this interpretation, familiarity information accrues earlier than source information, and the latter is used to discount items with inappropriately high familiarity values. The tendency here is to relegate the recovery of source information to a secondary role, which Clark and Gronlund (1996) characterize as a recall-to-reject component.

Current Study

These time course studies are consistent with the notion that recognition is mediated by a mixture of responses based on an early assessment of familiarity and the later retrieval of specific source information. The recovery of source information in later phases of retrieval is, however, only indirectly motivated by this type of data. The attenuation of a high initial false-alarm rate could result from changes in criteria across retrieval time. Dosher et al. (1989), for example, noted that the decrease in false-alarm rate later in retrieval could result from strategic attempts to correct for high initial familiarity values.

The SAT studies reported here were modeled on the Jacoby (1999) read–heard exclusion paradigm. The two-list design, in which the lists differ in a salient source property (read or heard), provides an ideal situation with which to contrast responses based on an assessment of familiarity and responses based on the recovery of specific source information. By manipulation of the number of times an item is read, both familiarity and the probability of recovering source information are jointly varied. The exclusion instructions place the two types of information in opposition to one another, so that respective false-alarm rates can be used to pinpoint when both forms of information begin to accrue. Deriving false-alarm functions for items with different numbers of repetitions and, hence, different degrees of learning enables one to examine whether simple changes in criteria are sufficient to explain nonmonotonic false-alarm rates. Whereas some forms of a nonmonotonic function are compatible with simple criterion shifts, others are not; in particular, crossover functions for items that differ in degree of learning cannot be explained by criterion shifts (see Ratcliff, Van Zandt, & McKoon, 1995).

Experiment 1

Participants first read a list of 28 words, half of which were presented once and half of which were presented three times. After studying the read list, participants next listened to a list of 28 spoken words, none of which had been presented in the read list. The study phase was followed by a recognition test consisting of a mixture of heard, (once- and thrice-) read, and new items. The exclusion instructions required participants to respond positively to an item only if it was presented in the heard list. Moreover, participants were told that they could be certain that an item was not in the heard list if they recalled it as having been in the read list. Our primary interest was in the respective false-alarm rates for the read, thrice-read, and new items when the exclusion instructions placed the hypothesized familiarity information and source information in opposition to one another. The SAT procedure was used to derive measures of how these two types of information unfolded across the time course of recognition.

Method

Participants

Nine participants from New York University took part in this experiment. Each participated in four 1-hr sessions plus an additional 1-hr practice session that served as training for the SAT procedure. All sessions were completed within a 2-week period. All participants were native speakers of English and had normal or corrected vision.

Materials

A total of 1,584 three- to nine-letter words were selected from Paivio, Yuille, and Madigan’s (1968) norms and the Toronto word pool (Friendly, Franklin, Hoffman, & Rubin, 1982). A total of 560 words were used as stimuli for the read lists, and 560 words were used for the heard lists. The number of words ensured that each study phase contained novel words. A SoundBlaster 16 audio card was used to digitally record and present the words in the spoken lists. A female voice read each word at an approximately 2-s rate.

Design and procedure

Stimulus presentation, response collection, and feedback were controlled by an IBM-compatible computer running Micro Experimental Laboratory software (Schneider, 1988). Each of the four experimental sessions consisted of five study–test phases. Each study phase consisted of visual presentation of a list of words to be read; this step was followed by a list of spoken words. Read lists were 56 items long and composed of 14 words presented once and 14 words presented three times. The order of presentation was random but with the constraint that 10 to 25 intervening words were presented before a word was repeated, and once- and thrice-presented items were equally distributed throughout the study list. Read items were presented for 1,500 ms, with 500-ms blank intervals between words. Each spoken list consisted of 28 words presented at a 2-s rate.

The study phase was followed by 70 recognition tests consisting of a random mixture of 28 heard words, 14 once-read items, 14 thrice-read items and 14 new items. The sequence and timing of each test trial were as follows. (a) Two centered fixation points (plus signs) were presented for 350 ms. (b) Test words were presented on a clear screen. (c) The test item remained on the screen for 100, 300, 500, 750, 1,000, 2,000, or 3,000 ms, at which time the screen cleared and a tone sounded to cue a participant to respond. Participants responded by pressing one of two designated keys (the C key = “no,” and the M key = “yes”). (d) Following a response, the latency to respond to the tone was displayed for 400 ms; the step was followed by a 750-ms intertrial interval. Participants were instructed to respond to the tone within 270 ms. They were told that responses over 270 ms were too long and that responses under 100 ms were anticipations. A “Too quick!” warning was displayed if a participant’s response was under 100 ms.

Following the 70-item test, a second test consisting of eight new items, four once-read items and four thrice-read items. For this test, participants were instructed to respond positively to an item if it was in the read list. This second test was used to encourage participants to attend to the read list.

Results and Discussion

The latency to respond to the interruption cue and proportion correct for tests of the heard, read, and new items for each of the 9 participants are presented in Appendix B.

Standard d′ scaling

The false-alarm rates for once-read, thrice-read, and new items were our primary interest. These conditions were first contrasted by scaling the z score for the hit rate for heard items against the false-alarm rate for new items, the false-alarm rate for items once read, and the false-alarm rate for thrice-read items. The top panel in Figure 1 shows these d′ scalings for the average (over participants) data as a function of retrieval time (the lag of the interruption tone plus the latency to respond to the tone).

Figure 1.

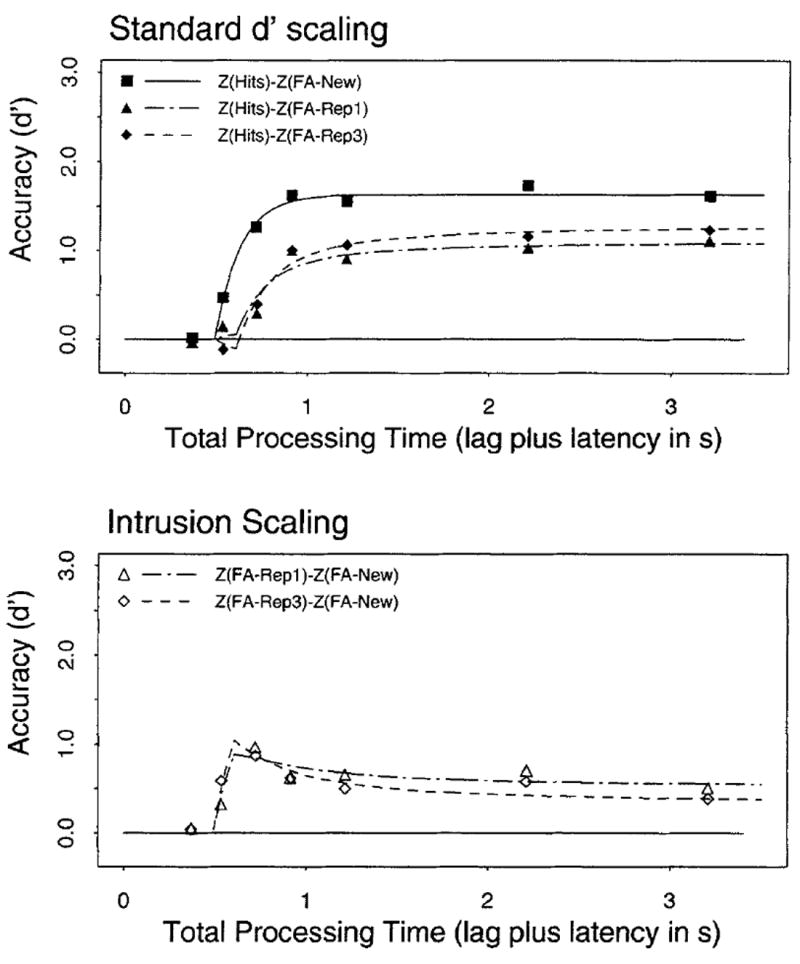
Average d′ accuracy as a function of processing time (lag of the response cue plus latency to respond to the cue) from Experiment 1. (Top panel) Standard d′ scalings of the hit rate for heard items against the false-alarm rates for new items (solid squares), once-read (solid triangles), and thrice-read (solid diamonds) items. (Bottom panel) Intrusion scalings of the false-alarm rate for new items against the false alarm rates for once-read (open triangles) and thrice-read (open diamonds) items. Smooth curves in each panel show the fits of the dual-process model (Equation 3) with the (average) parameters listed in Table 1. FA = false-alarm rate; Rep1 = items read once; Rep3 = items read three times.

Two salient properties are apparent from Figure 1. First, at the latest interruption point (times >3 s), there were large differences in the d′ index of performance, F(2, 16) = 15.395, MSE = 0.0382. These d′ differences were engendered by differences in the false-alarm rates for the three types of lures. False-alarm rates were significantly lower for new items than for once read, t(8) = 6.67, p < .05, and thrice read items, t(8) = 3.42, p < .05. The false-alarm rate with maximal retrieval time was higher for once-read items than for thrice-read items (corresponding d′ values were 1.11 and 1.29, respectively), although this difference was not significant, t(8) = 1.75.

In addition to these asymptotic differences, the functions were also associated with different underlying time courses. The two functions scaled against the false-alarm rate from the read items were substantially depressed at early interruption times relative to the function scaled against the false-alarm rate from new items. This depression indicates that the differences in false-alarm rate early in retrieval are not proportional to the differences in asymptote. If such were the case, the functions would display proportional rise times in which all functions would reach a set proportion (e.g., 2/3) of their respective asymptote at the same time. The disproportional rise times evident in the top panel of Figure 1 suggest that the false-alarm rates vary in a nonmonotonic fashion across retrieval time. We first provide evidence that these functions are indeed associated with time course differences beyond simple asymptotic variation. We then isolate the respective false-alarm rates and model how these differences can arise from the recovery of familiarity and source information.

To quantify differences in time course, it is necessary to fit empirical data with a time course function. Full time course SAT functions can be modeled as an exponential approach to a limit:

$$d^{\prime }(t)=\mathrm{\lambda }(1-e^{-\mathrm{\beta }(t-\mathrm{\delta })}),\mathrm{for}t>\mathrm{\delta },\mathrm{else}0.$$ (1)

Equation 1 describes the growth of accuracy over retrieval time with three parameters: (a) λ, an asymptotic parameter reflecting the overall probability of recognition; (b) δ, an intercept parameter reflecting the discrete point in time when accuracy departs from chance (d′ = 0); and (c) β, a rate-of-rise parameter that describes the rate at which accuracy grows from chance to asymptote. Differences in retrieval speed or dynamics are reflected in either the intercept (δ) or the rate of rise to asymptote (β) or both. The intercept and rate of an SAT function reflect either the rate of continuous information accrual or the distribution of finishing times of a discrete or quantal process (Dosher, 1976, 1979, 1981, 1982, 1984; Meyer, Irwin, Osman, & Kounios, 1988; Ratcliff, 1988; see also Ratcliff, 1978, for an alternative three-parameter equation derived from the random-walk (diffusion) model and McElree & Dosher, 1989, for a comparison of the two equations in the short-term memory domain).

The analyses reported here were performed on individual participant data. The average (over participants) data were used to summarize consistent patterns across participants. Equation 1 was fit to the data with an iterative hill-climbing algorithm (Reed, 1976), similar to STEPIT (Chandler, 1969), that minimized the squared deviations of predicted values from observed data. Goodness of fit was assessed with three criteria. The first criterion is the value of an R² statistic,

$$R^2=1-\frac{\sum _{i=1}^n{(d_i-{\widehat{d}}_i)}^2/(n-k)}{\sum _{i=1}^n{(d_i-\overline{d})}^2/(n-1)},$$ (2)

where d_i represents the observed values, d̂_i indicates the predicted values, d̄ is the mean, n is the number of data points, and k is the number of free parameters (Reed, 1973). This R² statistic is the proportion of variance accounted for by the fit, adjusted by the number of free (k) parameters (Judd & McClelland, 1989). The second criterion is evaluation of the consistency of the parameter estimates across the participants. The third criterion is evaluation of whether the fit yielded systematic (residual) deviations that could be accommodated by allocating more (i.e., separate) parameters to various conditions.

A hierarchical model testing scheme was used to determine the best fitting exponential model. The three functions were fit with sets of nested models that systematically varied the three parameters of Equation 1. These models ranged from a null model, in which all functions were fit with a single asymptote (λ), rate (β), and intercept (δ), to a fully saturated (nine-parameter) model, in which each function was fit with a unique asymptote, rate, and intercept.

Given the significant differences in performance at the latest interruption time (3 s), exponential models with a single asymptotic parameter (λ) produced extremely poor fits of the average data and the data from each of the 9 participants. For example, a 1λ-1β-1δ model had an R² of .775 for fits of the average data. Allotting a separate asymptote to each condition, namely, a 3λ-1β-1δ model, substantially improved the fit, resulting in an R² of .898. Comparable differences were observed in the fits for all the individual participants. Subsequent model fits, however, demonstrated that differences in asymptotic level only could not adequately capture the pattern illustrated in Figure 1.

A 3λ-1β-2δ model was found to produce the best fit to the average, data and to the data from 7 of the 9 participants (R² = .980 for the average data, ranging from .694 to .908 across participants). This model allotted a separate asymptotic parameter (λ), a common rate parameter (β), and one intercept (δ) to the function scaled against new lures and another intercept to the two functions scaled against read items. For 7 participants, this model produced the highest adjusted R² of all possible models. For one participant (viz., 9), a better fit was produced by a simpler, 3λ-1β-1δ, model (R² = .778), which assumed only asymptotic differences. Another participant performed poorly on the task, with asymptotic d′s close to or below chance (0.716, 0.173, and −0.271 for functions scaled with new, once-read, and thrice-read, respectively). For this participant, all models produced an extremely low adjusted R² (<.493), and it was not possible to discriminate among different models. For the average data, the estimated intercept for the function scaled against new items was 490 ms; this value was 669 ms for the two functions scaled against read items. These estimates were similarly ordered for all participants’ data when fit with the 3λ-1β-2δ model, and the results of a t test of the intercept parameters were significant, t(8) = 4.277, p < .05.

This difference in intercept indicates that, early in retrieval (490 to 669 ms), read items produced a false-alarm rate high enough to completely offset the increases in the hit rate associated with heard items, thereby producing d′s at or near chance. In contrast, during the same period, the false-alarm rate for new items was substantially lower than the false-alarm rate for both read items and the hit rate for heard items, leading to above-chance performance. These data suggest that prior exposure to an item leads to high familiarity values and that responses early in retrieval are based on a general assessment of familiarity without regard to the source of the familiarity. With additional retrieval time (>669 ms), the false-alarm rate for read items diminished relative to both the false-alarm rate for new items and the hit rate for heard items. Additional retrieval time enables the assessment of source information, which disproportionally reduces the false-alarm rate for read items relative to that for new items. An alternative d′ scaling provides a more precise means of isolating the differences in false-alarm rates for the new and read conditions.

Intrusion scaling

As described by Dosher et al. (1989) and McElree and Dosher (1989), the z score for the false-alarm rate for once- and thrice-read items was scaled against the false-alarm rate for the new items. This type of scaling, which we refer to as d′_INT scaling, directly assesses the degree to which the false-alarm rate for once- and thrice-read items exceeds that for new items, that is, the degree to which a read item intrudes into judgments of heard items over and above the baseline rate for new items. Higher d′_INT values denote poorer performance because of a higher false-alarm rate in the read conditions. (If the rate for the read items equaled the rate for the new items, d′_INT values would equal zero. If the rate for read items was lower than that for new items, d′_INT scores would take on negative values.)

The bottom panel of Figure 1 shows the d′_INT scaling for the average data. Inspection of the observed d′_INT values shows that the functions reach a peak value at times under 1 s and then diminish with further retrieval time. This pattern is consistent with the notion that responses are based on a source-invariant assessment of familiarity at early retrieval times. With additional retrieval time, source information is recovered, leading to an attenuation of the false-alarm rate.

Dual-process model

The claim that two types of information underlie exclusion judgments can be formalized and tested with a dual-process retrieval model. Ratcliff (1980) derived a two-process SAT model from the diffusion model (see Dosher et al., 1989, for an application to a priming paradigm), and McElree and Dosher (1989) adapted this approach to the exponential form:

$$d\prime (t)=\{\begin{array}{ll}{\mathrm{\lambda }}_1(1-e^{-\mathrm{\beta }(t-{\mathrm{\delta }}_1)}),& \mathrm{for}{\mathrm{\delta }}_1<t<{\mathrm{\delta }}_2\\ {\mathrm{\lambda }}_2+\frac{({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2)({\mathrm{\delta }}_2-{\mathrm{\delta }}_1)}{(t-{\mathrm{\delta }}_1)}\times (1-e^{-\mathrm{\beta }(t-{\mathrm{\delta }}_1)}),& \mathrm{for}t\ge {\mathrm{\delta }}_2.\end{array}$$ (3)

Equation 3 states that during an initial time slice (δ₁ < t < δ₂), response accuracy is controlled by the accrual of one type of information, in this application, the accrual of familiarity. Accuracy during this period is modeled by the top part of the equation, a simple exponential approach to the asymptote λ₁. At time δ₂, source information begins to accrue, possibly from a recollection process (see below). The net effect is to shift response accuracy from the asymptote λ₁ operative during the first period (δ₁ < t < δ₂) to a new asymptote, λ₂. The bottom part of the equation estimates this new asymptote and when the shift in processing begins (δ₂).

Our primary interest is in the parameters λ₁ and λ₂ for both the once-read and thrice-read items. To the degree to which both d′_INT functions are nonmonotonic, with early high false-alarm rates that are attenuated with further retrieval time, λ₁ estimates should be higher than λ₂ estimates. Crucially, if repetition of the read items increases familiarity, thereby inducing a higher false-alarm rate, then λ₁ should be higher for thrice-read items than for once-read items. The opposite ordering is expected for the λ₂ parameter. That is, if repetition increases the probability of recovering an item’s source, then the false-alarm rate and the corresponding d′_INT values should be lower for thrice-read items than for once-read items. In the model fit, we therefore expect that λ₂ will be lower for thrice-read items than for once-read. Finally, δ₂ should be later than δ₁ if the recovery of source information has a slower time course than does an assessment of familiarity.

The dual-process model was simultaneously fit to all five functions shown in Figure 1 to derive stable and internally consistent parameter estimates. Allotting separate λ₁ and λ₂ parameters to the once-read and thrice-read items yielded a higher adjusted R² than models that assumed a common λ₁ or a common λ₂ or both. (R² = .964 in the average data, ranging from .606 to .904 across the 6 participants with acceptable data.) Table 1 presents the parameter estimates for fits of the average data and individual participant data. The smooth functions in Figure 1 show the fits of the dual-process model to the average data by use of the average parameters listed in Table 1.

Table 1.

Parameter Estimates From Experiment 1 for the Dual-Process Model

Parameter	Average	Participant
		1	2	3	4	5	6	7	8	9
λ1: familiarity for items read one time (d′ units)	1.55	4.30	2.17	2.59	3.15	1.20	1.04	3.75	−.43	0.01
λ1: familiarity for items read three times (d′ units)	1.82	8.00	1.85	4.57	7.67	1.56	1.21	3.55	1.35	0.71
λ2: recollection for items read one time (d′ units)	0.51	1.23	0.76	0.59	0.84	0.11	0.11	0.14	0.44	0.29
λ2: recollection for items read three times (d′ units)	0.31	0.89	0.39	0.01	0.84	0.02	0.47	0.14	0.55	−0.29
λN: asymptotic accuracy for new items (d′ units)	1.64	2.71	1.77	1.68	1.09	1.27	1.07	2.28	1.52	1.81
β: common rate parameter	7.27	4.82	1.97	4.78	9.99	9.22	5.99	6.73	2.18	2.48
δ1: familiarity intercept (ms)	490	422	321	498	482	500	493	304	370	350
δ2: recollection intercept (ms)	608	459	751	523	488	701	677	418	313	528
Adjusted R2	.964	.798	.839	.838	.555	.606	.817	.904	.599	.851

In the average data, once-read items had a λ₁ estimate of 1.55 d′ units and a λ₂ estimate of 0.51 d′ units. For the thrice-read items, λ₁ was estimated to be 1.82 d′ units and λ₂ was estimated to be 0.32 d′ units. Thus, for both types of read items, λ₁ was estimated to be substantially higher than λ₂. Results of paired t tests contrasting the λ₁ and λ₂ estimates for both the once-read and thrice-read items were significant, t(8) = 3.03, p < .05, and t(8) = 3.57, p < .05, respectively. These parameter values support the notion of the opposition of familiarity information and source information, resulting in nonmonotonic false-alarm rates.

Additionally, repetition had the predicted effect on the false-alarm rate for read items. The λ₁ parameter was higher for thrice-read items than for once-read items by 0.27 d′ units, and the λ₂ parameter was lower for thrice-read items than for once-read items by 0.19 d′ units. With just a few exceptions (see Table 1), this pattern was seen in the fits of each participant’s data. Results of a paired t test contrasting the λ₁ estimate for once- versus thrice-read items was significant, t(8) = 2.44, p < .05. However, a comparable comparison of the λ₂ estimate failed to reach significance, although the trend toward a higher λ₂ estimate for once-read items was apparent across individual participant data. These differences indicate that repetition significantly increased familiarity and induced a trend toward increased recovery of source information. We carried out Experiment 2 to explore this latter trend further.

Finally, the estimates of the time at which familiarity and source information began to be recovered, namely, δ₁ and δ₂, respectively, also showed the anticipated pattern. The intercept for the familiarity process (δ₁) was estimated to be 490 ms for the average data. The point at which source information began to exert an influence (δ₂) was estimated to be 608 ms, 118 ms later. Results of a paired t test contrasting the two intercept estimates were significant, t(8) = 2.55, p < .05.

Experiment 2

One limitation of Experiment 1 was that although there was clear evidence to support the notion that repetition increases initial familiarity values, the evidence for an impact of repetition on the recovery of source information was weak. Although at late retrieval times thrice-read items yielded lower false-alarm rates than once-read items, the difference was not significant with standard d′ scaling. Similarly, the difference in the parameter estimates for the contribution of source information (λ₂) showed the appropriate trend but also was not significant. A second experiment was done to replicate the pattern of results seen here and to further examine whether repetition can induce opposite but reliable effects on the recovery of both familiarity information and source information. To provide a more sensitive test of the potential effects of repetition, we simply increased the number of times a read item was repeated from three to five times.

Method

Participants

Eight participants from New York University took part in this experiment; none had participated in Experiment 1.

Materials, design, and procedure

The experiment was identical to Experiment 1, except that the read list consisted of 28 items, half of which were presented once and half of which were repeated five rather than three times. Three to 50 words intervened between repetitions of a word.

Results and Discussion

The latency to respond to the interruption cue and proportion correct for tests of the heard, read, and new items for each of the 8 participants are presented in Appendix C.

Standard d’ scaling

As in Experiment 1, we first scaled the z score for the hit rate for heard items against the false-alarm rate for new items, the false-alarm rate for items read once, and the false-alarm rate for items read five times. The top panel in Figure 2 shows these d′ scalings for the average (over participants) data as a function of retrieval time.

Figure 2.

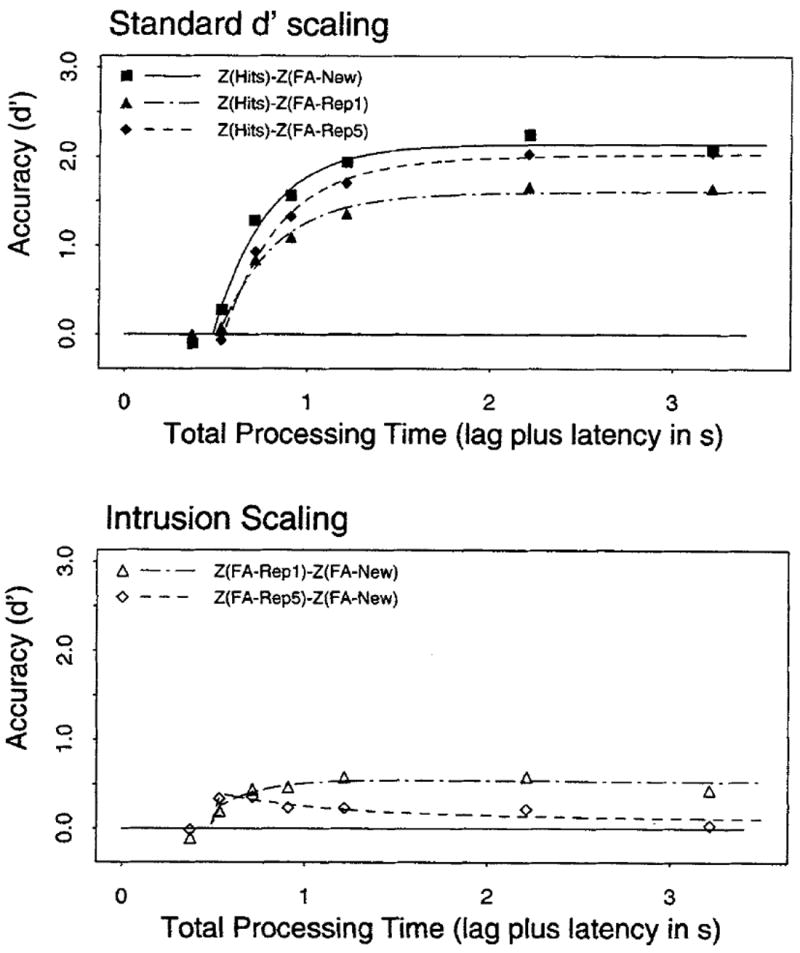
Average d′ accuracy as a function of processing time (lag of the response cue plus latency to respond to the cue) from Experiment 2. (Top panel) Standard d′ scalings of the hit rate for heard items against the false-alarm rates for new items (solid squares), items read once (solid triangles), and items read five times (solid diamonds). (Bottom panel) Intrusion scalings of the false-alarm rate for new items against the false-alarm rate for items read once (open triangles) and items read five times (open diamonds). Smooth curves in each panel show the fits of the dual-process model (Equation 3) with the (average) parameters listed in Table 2. FA = false-alarm rate; Rep1 = items read once; Rep5 = items read five items.

As in Experiment 1, there were clear differences in performance at the latest interruption point (times >3 s), F(2, 14) = 4.82, MSE = 0.0970. As documented more fully below, these d′ differences were primarily attributable to the high false-alarm rate for once-read items early in retrieval, which was only slightly corrected with further retrieval time. The asymptotic false-alarm rates for once-read items were significantly higher than those for new items, t(7) = 3.23, p < .05, and items repeated five times, t (7) = 3.39, p < .05. The false-alarm rates with maximal retrieval times for new items and items read five times did not significantly differ, t(7) = 0.18. However, inspection of Figure 2 shows that there were substantial differences between new and repeatedly read items early in retrieval.

Fits of Equation 1 to the three functions revealed clear evidence for differences in the dynamics portions of the functions, although the exact form of the differences varied across participants. For all participants, there was a large dynamics difference between the function scaled with new items and the two functions scaled with read items. There was also evidence of a smaller difference between once-read and repeatedly read items for 4 of the 7 participants. The average data were best fit with a 3λ-1β-3δ model in which a separate intercept was allotted to each condition (R² = .989). As in Experiment 1, this model improved the fit from a (null) 1λ-1β-1δ model (R² = .931) and a 3λ-1β-1δ model that assumed asymptotic differences only (R² = .959). This fit yielded a fast intercept associated with new items (474 ms), an intermediate intercept associated with once-read items (509 ms), and a slightly longer intercept associated with repeatedly read items (529 ms). Results for 2 participants (viz., 2 and 5) were similarly best fit with this type of model (R² = .928 and .865, respectively). Results for participants 6 and 8 were best fit with a 3λ-3β-1δ model, in which the dynamics differences were better captured by the rate than by the intercept (R²s = .928 and .808, respectively). The three remaining participants did not show substantial improvements in R² when a separate dynamics parameter was allocated to each condition. For these participants, two dynamics parameters sufficed, one for the function with new items and another for the function involving read items. Results for participant 7 were best fit by a 3λ-1β-2δ model (R² = .991), whereas results for participants 1 and 4 were best fit by a 3λ-2β-1δ model (R²s = .941 and .816, respectively).

The results of a pairwise comparison of the δ parameter estimates for once-read and repeatedly read items derived from a 3λ-1β-3δ model were significant, t(7) = 3.41, p < .05. However, as before, the crucial differences concerned the relative false-alarm rates across retrieval time, and those differences were more directly observable with the d′_1NT scaling.

Intrusion scaling and dual-process model fits

The bottom panel of Figure 2 shows the d′_INT scaling of the false-alarm rates for the once-read and the repeatedly read items. For repeatedly read items, there was a clear nonmonotonic form with a high intrusion rate early in retrieval that was substantially attenuated with further retrieval time. For the once-read items the evidence for nonmonotonicity was less apparent. However, fits of a dual-process model provide a better basis on which to assess variations in false-alarm rates across the time course of recognition. As in Experiment 1, we used Equation 3 to estimate the strength of familiarity (λ₁), the corrective influence of recovering source information (λ₂), and the time at which familiarity information and source information begin to accrue (δ₁ and δ₂, respectively).

Table 2 shows the parameter estimates for the dual-process model applied to the average data and individual participant data. The smooth functions in Figure 2 show the fits of the dual-process model to the average data by use of the relevant parameters listed in Table 2. As in Experiment 1, the λ₁ estimates were higher than the λ₂ estimates for both read-once and repeatedly read items. For once-read items, λ₁ was estimated to be 1.54 d′ units in fits of the average data, and λ₂ was estimated to be 0.51 d′ unit. For repeatedly read items, λ₁ was estimated to be 2.36 d′ units, and λ₂ was estimated to be 0.07 d′ units. Results of paired t tests on the parameter estimates showed that λ₁ estimates were significantly higher than λ₂ estimates for both once-read items t(7) = 3.98, p < .05, and repeatedly read items, t(7) = 6.94, p < .05. Additionally, familiarity was estimated to be operative at δ₁ = 484 ms in the average data, whereas source information was estimated to be operative later, at δ₂ = 537 ms, t(7) = 2.85, p < .05. Hence, as in Experiment 1, the time course data showed evidence of a high initial false-alarm rate that was attenuated with further retrieval time.

Table 2.

Parameter Estimates From Experiment 2 for the Dual-Process Model

Parameter	Average	Participant
		1	2	3	4	5	6	7	8
λ1: familiarity for items read one time (d′ units)	1.54	2.00	0.84	1.37	1.33	1.39	2.86	3.37	0.93
λ1: familiarity for items read five times (d′ units)	2.36	2.30	3.90	1.60	1.80	3.35	4.81	3.06	1.31
λ2: recollection for items read one time (d′ units)	0.51	0.21	0.48	0.53	−0.11	0.49	1.00	0.49	0.81
λ2: recollection for items read five times (d′ units)	0.07	−0.37	−0.26	−0.20	−0.63	0.31	0.77	−0.19	0.54
λN: asymptotic accuracy for new items (d′ units)	2.14	2.47	2.14	1.39	1.09	1.82	2.33	4.16	1.64
β: common rate parameter	3.42	4.96	2.74	2.76	2.92	3.19	3.64	3.31	3.64
δ1: familiarity intercept (ms)	484	509	491	453	334	365	492	466	500
δ2: recollection intercept (ms)	537	526	551	476	420	474	564	523	802
Adjusted R2	.991	.929	.925	.844	.853	.736	.890	.990	.741

Estimates for the dual-process model for this experiment provided clear evidence for the differential impact of repetition on the two phases of retrieval. As in Experiment 1, λ₁ was lower for once-read items than for repeatedly read items (1.54 vs. 2.36 in the average data, t[7] = 2.44, p < .05), indicating that repetition leads to high familiarity values that engender high false-alarm rates early in retrieval. Likewise, as in Experiment 1, the opposite ordering was observed for the λ₂ parameter, the measure of source information: λ₂ was higher for once-read items than for repeatedly read items. However, here the differences in the λ₂ parameter were significant (0.51 vs. 0.07 in the average data, t[7] = 5.98, p < .05). These model fits suggest that despite being associated with high familiarity values early in retrieval, repeatedly read items have a high probability for the recovery of source information later in retrieval. In the average data, the recovery of source information almost perfectly compensates for the high false-alarm rate produced by an assessment of familiarity (λ₂ = 0.07). Inspection of Table 2 shows that for 5 of the 8 participants, λ₂ estimates were negative, indicating that source information led to a lower false-alarm rate for repeatedly read items than for (baseline) new items.

General Discussion

Empirical Summary

The coupling of the SAT and opposition procedures provided strong evidence that recognition can be mediated by a mixture of two types of information, specifically, an assessment of familiarity and the recovery of source information. The key data that support this contention are the differential false-alarm rates across retrieval time for the different types of lures. At early retrieval times, repeatedly read items produced higher false-alarm rates than once-read items which in turn produced higher false-alarm rates than unstudied (new) items. This ordering suggests that initial responses are based on the strength or familiarity of the recognition probe. At later retrieval times, however, these initial false-alarm rates were attenuated as a direct function of how often an item was read. Items that were read five times had asymptotic false-alarm rates that were, on average, close to the baseline level for new items (see Figure 2). Items that were read once or three times had asymptotic false-alarm rates approximately 0.5 to 0.7 d′ units higher than those for new items. This pattern indicates that, with additional time, recovered source information is available to correct misattributions stemming from high initial familiarity values.

The dual-process model provided a means of estimating the contribution of each type of information. Fits of this model to the time course data yielded a consistent set of parameters across experiments, despite the fact that different participants took part in each experiment and each experiment had only a few participants. For the average data, once-read items in Experiments 1 and 2 had nearly identical λ₁ estimates of 1.55 and 1.54 d′ units, respectively, indicating comparable familiarity values. In contrast, items read three times in Experiment 1 yielded a λ₁ of 1.82 d′ units, and items read five times in Experiment 2 yielded a higher value of 2.36 d′ units. The pattern of the λ₂ estimates was opposite. For once-read items the λ₂ estimate was 0.51 d′ units in both experiments. The λ₂ estimate was lower for items read three times in Experiment 1, 0.32 d′ units, and lower still for items read five times in Experiment 2, 0.07 d′ units. The λ₂ parameter reflects the corrective influence that results from recovering source information (viz., determining that an item was read and hence should be excluded). The estimates for items read five times suggest that salient source information almost perfectly corrected for the misleading effects of high familiarity.

Generality of the Results

The crossover effects documented here were induced by placing familiarity information and source information in opposition through exclusion instructions. These instructions emphasized source information, enabling us to directly contrast the recovery of familiarity information and source information. We suspect that most types of recognition judgments involve mixtures of the two types of information isolated here, even when the two forms of information act in concert. The exclusion instructions simply provided an effective experimental paradigm with which to isolate the contribution of each type of information. One may question, however, whether the important pattern of data reported here is crucially linked to the exclusion instructions. Consider, by way of illustration, associative recognition. Gronlund and Ratcliff (1989) found a nonmonotonic function for rearranged pairs only when the task required participants to judge whether items in a pair had been studied together. A monotonic function was observed when participants were simply asked to judge whether both items had been studied, although not necessarily together. Slower associative information was apparently not used when the task could be performed on the basis of item information alone. For our task, one may argue that the exclusion instructions induced participants to use a form of information that would not have been used otherwise.

However, similar nonmonotonic false-alarm functions have been observed in item recognition tasks with standard rather than exclusion instructions (e.g., Dosher et al., 1989; McElree, 1998; McEIree & Dosher, 1989). This finding indicates that the nonmonotonic form is not restricted to exclusion instructions. Moreover, it is important to point out that most recognition tasks are in fact tacit exclusion tasks, in that recognition judgments typically are restricted to some context. (The judgment that typically is requested is not “Have you experienced this item before?” but rather “Did you experience this item in the study session?”) Our procedure simply makes explicit the tacit instructions to exclude all but one context.

Additionally, two recent studies reported by Hintzman and colleagues (Hintzman & Caulton, 1997; Hintzman, Caulton, & Levitin, 1998) provide convergent evidence for the results reported here. They directly compared tasks requiring old–new recognition with tasks requiring the retrieval of source information, either (visual or auditory) modality or list discrimination judgments. The old–new recognition tasks were found to have intercepts 94 to 119 ms earlier than the two tasks requiring the retrieval of source information. Although caution should be exercised in drawing conclusions across different tasks—time course differences can reflect different criteria induced by different instructions and can be contaminated by unknown mixtures of different processes¹—these estimates compare favorably to the 115-ms (Experiment 1) and 50-ms (Experiment 2) differences in δ₁ and δ₂ estimates obtained here with dual-model fits.

Implications for Recognition Models

The crossover false-alarm rates for items with different exposures are the key feature of the data that directly motivate the distinction between familiarity information and source information. Although other item recognition studies have found high initial false-alarm rates for variables that affect familiarity (e.g., Dosher et al., 1989; Hintzman et al., 1998; Hintzman & Curran, 1994; McElree, 1998; McElree & Dosher, 1989), the crossover effects reported here extend prior work by providing a pattern of results that cannot be explained by simple changes in decision criteria across retrieval time. If one adopted a signal detection analysis by assuming, for example, an ordered distribution of familiarity values corresponding to the number of presentations, namely, new items < once-read items < repeatedly read items, no placement of response criteria could simultaneously produce the response orders FA (read repeatedly) > FA (read once) > FA (new) at early retrieval times and FA (read repeatedly) < FA (read once) < FA (new) at later retrieval times (where FA is false-alarm rate). To produce this pattern, the familiarity distributions would need to be reordered, and that would be tantamount to a claim that additional information was recovered at later retrieval times.

The biphasic time course functions require postulating (a) that two types of retrieval processes are differentially applied across retrieval or, alternatively, (b) that two forms of information are retrieved with different time courses. The former is the approach explicitly adopted in dual-process theories of recognition (e.g., Atkinson & Juola, 1973; Jacoby & Dallas, 1981; Mandler, 1980). The dual-process (SAT) model fits illustrate the feasibility of this type of theory for predicting the full time course functions. The early asymptote (λ₁) reflects the assessment of familiarity that emerged at time δ₁ (490 ms in Experiment 1 and 484 ms in Experiment 2), and the late asymptote (λ₂) reflects the contribution of recollection that emerged at time δ₂ (608 ms in Experiment 1 and 537 ms in Experiment 2). Within this framework, our data suggest that recollection is operative 50 to 100 ms later than an assessment of familiarity. This difference is consistent with the notion that recollection operations are more computationally intensive than an assessment of familiarity (see below) and is also consistent with the claim in dual-process models of recognition that familiarity is mediated by an automatic process whereas recollection is mediated by a consciously controlled process (Jacoby, 1991; Mandler, 1980).

Global memory models (e.g., MINVERA2, Hintzman, 1988; SAM, Gillund & Shiffrin, 1984; TODAM2, Murdock, 1982, 1993, 1997) typically assume that recognition is mediated by a unidimensional familiarity or strength statistic. These approaches adopt a (unidimensional) signal detection analysis which, as illustrated above, cannot accommodate crossover effects without additional assumptions. Global models do, however, propose alternative retrieval operations for overt recall. For example, although SAM treats recognition as an assessment of the degree of match between retrieval cues and all representations in memory (see below), recall is accomplished by a sequence of sampling and recovery operations (Gillund & Shiffrin). Similarly, recognition in TODAM2 (Murdock, 1982, 1993) is mediated by the dot product of a retrieval vector and a composite memory vector, whereas recall is accomplished by correlational or autoassociation operations. Given these separate recognition and recall operations, one approach to modeling our biphasic functions is to assume, as in dual-processing models, that a recall operation is used in tandem with a global assessment of familiarity. Indeed, Ratcliff et al. (1995) have used a variant of SAM with this form to fit data from Jacoby (1991) that, like the data here, show opposing effects of a single variable.

Biphasic retrieval functions do not, however, necessitate postulating distinct recognition and recall operations. An alternative approach is to assume that familiarity information and source information are retrieved by a common retrieval mechanism through differential cuing of memory and that different decision rules are applied to each type of retrieved information. We illustrate this approach with SAM. This model assumes local memory representations in which items are represented as memory images. An image contains three types of information: (a) item information, such as the name and identity of the study element; (b) interitem or associative information; and (c) context elements that localize the image to a particular study context. For recognition, each type of information is assumed to be associated with cues at a retrieval time with some strength S. Familiarity (F) for a recognition probe (I_j) given a retrieval context (C) is determined by a (global) operation that sums over all images in memory (I):

$$F(C,I_j)=\sum _{k=1}^{n}S{\left(C,I_k\right)}^{\mathit{Wc}}S{\left(I_j,I_k\right)}^{\mathit{Wj}}.$$ (4)

In Equation 4, familiarity is a multiplicative function of the strength of context information for the item in memory [S(C, I_j)], the strength of the probe to its representation in memory [S (I_j, I_j)], and the associative strength of the probe to other items in memory [S(I_j, I_k)]. Context, item, and associative information are given weights (W), which are typically assumed to sum to 1 (Gillund & Shiffrin, 1984). The multiplicative rule in Equation 4 makes explicit the notion that different familiarity values can be derived from otherwise identical memory representations if different retrieval cues (and/or weights) are used to query memory.

Biphasic functions for read items can result from the use of different retrieval cues coupled with different decision rules early and late in retrieval. The particular pattern that needs to be explained is the ordering of false-alarm rates early in retrieval that reverses later in retrieval. Assume, for expository purposes, that the primary difference between read and heard items lies in contextual coding implicit in the S(C, I_j) term in Equation 4 and that item information in the S(I_j, I_j) term is amodal. High initial familiarity values will result from an initial memory query that largely ignores contextual information, effectively placing heavy weight on the S(I_j, I_j) term. If amodal item information dominates the initial query, then read items will produce higher familiarity values than new items, with higher values the more an item is repeated. If familiarity is used as a basis for responding positively, the false-alarm rates will show the appropriate pattern [viz., FA (new) < FA (read once) < FA (read repeatedly)]. With further retrieval time, appropriate contextual cues can be integrated with the retrieval probe and the S(C, I_j) term can be given greater weight than the S(I_j I_j) term in the memory query. Consistent with the instructions of the exclusion task, contextual cues that effectively query whether an item is presented in a read format need to be incorporated into the retrieval operation. Once again, read items will yield higher familiarity values than new items, with higher values the more an item is repeated. Now, however, the contextualized familiarity values can be used as a basis for excluding the item. This alternative decision rule will reverse the pattern seen at early retrieval times, producing the observed FA (read repeatedly) < FA (read once) < FA (new) order. This scenario effectively preserves the assumption that a global retrieval operation underlies the task by assuming that two different types of familiarity values are computed, one relatively context free and another context sensitive, and that different decision rules are applied to each derived measure.

A similar approach is possible in any global model that allows the memory representation to be queried with a variable set of retrieval cues. For example, TODAM2 argues that context is modeled as a set of contextual features appended to feature-based item vectors (Murdock, 1993). Recently, Shiffrin and Steyvers (1997) proposed a model that uses contextual features to limit the class of representations over which familiarity is calculated. As with SAM, one can argue that early in retrieval the memory representation is probed with a representation of the test item that is largely amodal. With additional retrieval time, the probe can be combined with contextual cues appropriate to the exclusion instructions and an alternative decision rule can be adopted.

A recent model by Dennis and Humphreys (1998), the bind cue decide model of episodic memory, proposes a somewhat different framework well suited to this general approach. Memory storage in this model is viewed as a binding operation in which features of the study item are bound to contextual features. Key to Dennis and Humphreys’ approach is the notion that a study item can be bound to several types of context (e.g., associative, list-wide, experiment-wide, encoding, and environmental contexts). Recognition consists of using the test item as a cue to reactivate a contextually bound representation. The recognition decision rule uses a Bayesian procedure to assess the likelihood (odds ratio) for the retrieved memory vector given a (reinstated) context vector. High false-alarm rates early in retrieval could be accounted for by assuming that early comparisons assess the retrieved memory vector against an experiment-wide context vector. Later in retrieval, the memory vector might be compared to a list-wide context vector. Attenuation of the high initial false-alarm rates could result from comparing the memory vector to a “read” context. Here, too, one must also assume that this later comparison is used as a basis on which to reject or discount items with high matches (see Dennis & Humphreys).

These alternatives recast what can be described as a difference in retrieval operations into a difference in retrieval cues at test coupled with alternative decision rules. A difference in processing can often be recast in terms of a difference in information content alone, and similar ambiguities have been noted in other domains, for example, the associative recognition (Clark & Gronlund, 1996; Gronlund & Ratcliff, 1989), semantic verification (Ratcliff & McKoon, 1982), categorization (Nosofsky, 1988), and mental imagery (Anderson, 1978; Pylyshyn, 1973) domains. Our data do not enable one to reject one or another of these alternatives but rather serve to place constraints on the framework provided by various global memory models (Clark & Gronlund). The time course data from both experiments indicate that source information accrues later than does familiarity information and that extant frameworks must assume that additional time is needed to either initiate a recollection operation or establish retrieval cues (and a decision rule) that query for the source-specific information. Discriminating between these alternatives is important for the development and assessment of quantitative memory models. Perhaps further experiments will provide a better basis on which to determine how best to model data such as ours. However, for other purposes, such as isolating memory deficits in special populations (e.g., Foley & Johnson, 1985; Harvey, 1985; Hastroudi et al., 1989; Jacoby, 1999; Mitchell et al., 1988), discrimination at this level of description may be unnecessary.

Relationship Between Familiarity and Source Information

Our contention that recognition involves a mixture of source information and familiarity information does not preclude the possibility that one form of information sometimes may be dominant, so that in some circumstances, recognition may be mediated by a relatively pure assessment of either familiarity or source information. The claim that recognition may be based on a relatively pure assessment of familiarity is not controversial; this has been the dominant approach to modeling recognition. However, that recognition may sometimes be based on source information alone—recollection rather than familiarity in dual-process models—is a nonstandard if not controversial claim.

Hintzman and Curran (1994), for example, contend that familiarity is the primary basis for recognition and that recollection (source information) is used to supplement familiarity under difficult circumstances. Although recollection may indeed play a key role in difficult discriminations, the implication of the view advocated by Hintzman and Curran is that recall of source information should be viewed as a late selection mechanism, in which participants recall to reject items of high familiarity (see Clark & Gronlund, 1996). Similar notions have been suggested for associative recognition (Clark, 1992; Gronlund & Ratcliff, 1989) and to explain memory illusions and memory confabulations (Schacter et al., 1998).

A recall-to-reject view is justified to the degree to which there are intrinsic and unalterable time course differences between the recovery of familiarity information and the recovery of source information. If familiarity information is available earlier than source information, the latter can have only the restricted function of filtering evidence provided by the former. Although current time course data certainly are consistent with a recall-to-reject view, no studies have rigorously tested the principal role assigned to familiarity by many current memory models. It is possible that salient and easily accessible source information circumvents the appeal to familiarity rather than just attenuating a potentially misleading sense of familiarity (Jacoby, Kelly, & McElree, in press).

Appendix A

Reevaluating Johnson et al. (1994)

To separately assess (old–new) detection and source discrimination for perceived and imagined items, Johnson et al. (1994) applied Batchelder and Riefer’s (1990) multinomial model 5b to response deadlines probabilities. This model represents one of a class of multinomial models for source monitoring. Model 5b assumes that source discrimination is contingent on successfully detecting an item as old (a redundancy assumption; e.g., Joordens & Merikle, 1993), and the two sources (perceived and imagined) differ in probability of discrimination. Figure A1 represents the parameter estimates of interest from Johnson et al.’s (1994) Experiment 2.

SAT time-course data—be they observed data or derived parameters, as in Figure A1—enable one to separately assess the asymptotic probability of detection or discrimination and the dynamics or speed with which this information becomes available. That is, although various conditions may differ in their respective asymptotic level, the intercept and rate of the SAT accuracy functions provide a basis on which to test the speed with which this information accrues over time. To do so, however, one must fit the derived functions with an explicit time-course equation. Because Johnson et al. (1994) did not perform such a fit, we reanalyzed their data by reapplying model 5b and fitting the parameter estimates for D (the probability of old–new detection), d1 (the probability of successfully discriminating the source of an imagined item given that it was detected as old), and d2 (the probability of successfully discriminating the source of a perceived item given that it was detected as old). Equation 1, rewritten here in probability rather than d′ units, was used to quantify the time course of each multinomial parameter:

$$p(t)=\mathrm{\lambda }(1-e^{-\mathrm{\beta }(t-\mathrm{\delta })}),\mathrm{for}t>\mathrm{\delta },\mathrm{else}0,$$ (A1)

where λ is the asymptotic parameter reflecting the overall probability of detection or discrimination, δ is the intercept reflecting the discrete point in time when accuracy departs from chance, and β is the rate-of-rise parameter that describes the rate at which accuracy grows from chance to asymptote.

The parameter estimate for (source-invariant) detection (D) was asymptotically higher than the estimates of discrimination for either imagined (d1) or perceived (d2) items, indicating that, as Johnson et al. (1994) concluded, old–new detection was more accurate than either source attribution. However, with respect to time course, reflected in both the δ and the β measures, the data do not indicate that old–new detection is available before the discrimination of source. Although (old–new) detection is associated with an earlier time course than the discrimination of perceived items, as illustrated by the substantial shifts in intercepts in Figure A1 (δ_D = 88 ms; δ_d2 = 297 ms), exactly the opposite relationship is found for imagined items (δ_d1 = 10 ms) (overall time course estimates, δ + β⁻¹, for D, d1, and d2 were 456, 287, and 544 ms, respectively).

Johnson et al.’s (1994) data are inconclusive with respect to whether old−new detection occurs before source discrimination: The mean parameter estimates indicate that source information was available for perceived items before the items could be detected as old but that source information for imagined items was available after the items were detected as old. Although such a pattern is possible, the time-course estimates are highly suspect. Consider, for example, the d1 parameter. The fast-dynamics estimates (δ and β) are largely attributable to the high values at the first two interruption points (300 and 500 ms). However, the confidence intervals for these estimates are very large (0.56±21 at 300 ms and 0.67±21 at 500 ms). Given this range, it is possible that source information for perceived items could have the same or a slower time course than old–new detection.

The uncertainties in Johnson et al.’s (1994) model fits are attributable to noisy data (each data point is based on 10 trials per participant) and a low number of response lags (typical SAT experiments use from 6–8 points to map out the full time course of processing). Compounding these problems further is the fact that three response categories do not provide sufficient degrees of freedom for the application of multinomial models that take into account differences in response biases for the two source discriminations (models 6 and 7 in Batchelder & Riefer, 1990). Thus, the discrimination estimates in Figure A1 are not free of potential differences in the bias to respond “perceived” or “imagined.”

The limitations of Johnson et al.’s (1994) experiment can be overcome by a more extensive design, one that increases the number of trials per participant, increases the number of (preasymptotic) interruption points, and uses four or more response categories (to factor out response biases; see Batchelder & Riefer, 1990). However, it is questionable whether the source monitoring paradigm provides the most optimal means of isolating and contrasting component processes. The contributions of component processes cannot be directly observed but rather only inferred from specific model decomposition, and it is by no means certain what sort of multinomial model provides a veridical characterization of the processes that underlie source monitoring (e.g., Buchner, Erdfelder, Steffens, & Martensen, 1997). We believe that stronger evidence for the contribution and temporal properties of various processes can be acquired by placing them in opposition to one another and measuring the effect on performance.

Figure A1.

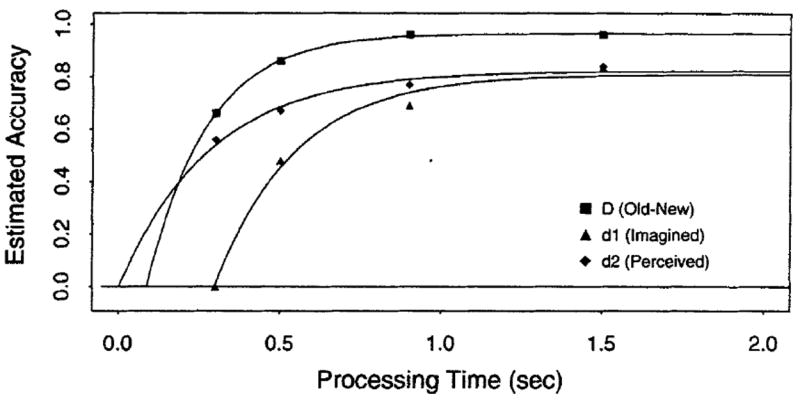
Model 5b source monitoring parameter estimates as a function of processing time (lag of the response cue) for Johnson et al.’s (1994, Experiment 2) data (parameter D is the probability of old–new detection, d1 is the probability of detecting the source of an imagined item, and d2 is the probability of detecting the source of a perceived item). The smooth functions show fits of an exponential approach to a limit (Equation A1) to the three-parameter estimates.

Appendix B

Latency and Proportion Correct in Experiment 1

Item	Measure	Value at interruption point (s)
		0.1	0.3	0.5	0.7	1.0	2.0	3.0
Participant 1
Heard	Latency	.341	.290	.240	.224	.235	.221	.224
	Proportion correct	.263	.475	.738	.797	.720	.804	.712
Read one time	Latency	.368	.278	.264	.236	.244	.240	.227
	Proportion correct	.600	.527	.694	.846	.682	.695	.710
Read three times	Latency	.343	.282	.270	.251	.239	.225	.232
	Proportion correct	.512	.450	.589	.777	.825	.742	.850
New	Latency	.340	.277	.237	.229	.234	.228	.235
	Proportion correct	.789	.842	.951	.975	1.000	.973	.926
Participant 2
Heard	Latency	.254	.258	.235	.230	.234	.225	.223
	Proportion correct	.625	.594	.675	.675	.575	.769	.746
Read one time	Latency	.260	.247	.251	.234	.231	.227	.221
	Proportion correct	.410	.256	.333	.410	.375	.512	.575
Read three times	Latency	.245	.0255	.253	.240	.238	.226	.225
	Proportion correct	.350	.410	.300	.425	.692	.575	.700
New	Latency	.260	.259	.248	.226	.232	.226	.222
	Proportion correct	.450	.564	.794	.769	.897	.897	.800
Participant 3
Heard	Latency	.281	.242	.223	.224	.219	.215	.203
	Proportion correct	.437	.392	.675	.721	.787	.794	.787
Read one time	Latency	.285	.246	.228	.228	.227	.228	.209
	Proportion correct	.692	.641	.435	.692	.525	.634	.600
Read three times	Latency	.285	.253	.239	.224	.230	.212	.214
	Proportion correct	.450	.525	.692	.717	.717	.775	.825
New	Latency	.288	.246	.235	.237	.225	.224	.209
	Proportion correct	.400	.692	.750	.820	.871	.736	.800
Participant 4
Heard	Latency	.221	.194	.184	.188	.182	.182	.180
	Proportion correct	.375	.325	.557	.645	.750	.725	.519
Read one time	Latency	.222	.192	.205	.189	.193	.191	.178
	Proportion correct	.736	.589	.421	.394	.650	.225	.550
Read three times	Latency	.231	.203	.188	.194	.186	.185	.179
	Proportion correct	.675	.475	.435	.425	.461	.435	.375
New	Latency	.229	.196	.182	.188	.183	.178	.199
	Proportion correct	.650	.564	.842	.743	.675	.794	.743
Participant 5
Heard	Latency	.244	.209	.205	.198	.203	.194	.195
	Proportion correct	.600	.468	.475	.658	.687	.662	.696
Read one time	Latency	.244	.218	.204	.206	.198	.196	.193
	Proportion correct	.350	.750	.410	.692	.650	.634	.775
Read three times	Latency	.241	.215	.220	.209	.206	.206	.198
	Proportion correct	.575	.500	.368	.575	.675	.775	.675
New	Latency	.247	.223	.197	.202	.204	.196	.189
	Proportion correct	.500	.625	.850	.800	.650	.794	.900
Participant 6
Heard	Latency	.284	.241	.217	.215	.216	.219	.220
	Proportion correct	.487	.525	.575	.687	.625	.662	.637
Read one time	Latency	.302	.228	.217	.220	.210	.221	.218
	Proportion correct	.525	.500	.425	.538	.743	.561	.725
Read three times	Latency	.290	.241	.231	.215	.219	.222	.212
	Proportion correct	.550	.425	.425	.500	.400	.525	.650
New	Latency	.287	.239	.210	.210	.210	.221	.216
	Proportion correct	.525	.575	.700	.725	.775	.717	.775
Participant 7
Heard	Latency	.218	.202	.184	.180	.185	.184	.182
	Proportion correct	.050	.350	.625	.737	.650	.625	.696
Read one time	Latency	.219	.203	.183	.180	.183	.178	.183
	Proportion correct	.850	.650	.675	.871	.875	.951	.925
Read three times	Latency	.215	.207	.192	.185	.180	.183	.175
	Proportion correct	.875	.600	.800	.900	.900	.875	.950
New	Latency	.217	.188	.181	.174	.189	.177	.177
	Proportion correct	.925	.975	.950	.974	.950	.974	.975
Participant 8
Heard	Latency	.270	.227	.234	.227	.232	.220	.217
	Proportion correct	.387	.379	.550	.600	.562	.662	.737
Read one time	Latency	.270	.232	.227	.235	.228	.224	.214
	Proportion correct	.575	.625	.600	.871	.625	.707	.675
Read three times	Latency	.276	.239	.238	.225	.223	.225	.215
	Proportion correct	.775	.575	.578	.750	.825	.631	.700
New	Latency	.271	.235	.226	.220	.226	.222	.214
	Proportion correct	.589	.725	.800	.875	.750	.871	.825
Participant 9
Heard	Latency	.263	.248	.223	.213	.223	.225	.219
	Proportion correct	.125	.325	.512	.762	.750	.875	.775
Read one time	Latency	.263	.242	.228	.213	.218	.225	.214
	Proportion correct	.900	.950	.625	.641	.775	.756	.775
Read three times	Latency	.267	.239	.227	.228	.231	.227	.210
	Proportion correct	.900	.775	.750	.875	.825	.825	.850
New	Latency	.280	.231	.217	.215	.226	.227	.218
	Proportion correct	.900	.850	.800	.850	.800	.769	.825

Appendix C

Latency and Proportion Correct in Experiment 2

Item	Measure	Value at interruption point (s)
		0.1	0.3	0.5	0.7	1.0	2.0	3.0
Participant 1
Heard	Latency	.272	.221	.197	.200	.202	.209	.214
	Proportion correct	.700	.712	.887	.924	.887	.950	.937
Read one time	Latency	.268	.229	.205	.202	.211	.205	.208
	Proportion correct	.250	.256	.675	.666	.666	.829	.775
Read five times	Latency	.281	.218	.193	.188	.195	.198	.214
	Proportion correct	.350	.250	.769	.878	.871	.900	.900
New	Latency	.283	.236	.199	.198	.204	.206	.200
	Proportion correct	.150	.425	.575	.775	.846	.850	.850
Participant 2
Heard	Latency	.254	.233	.215	.217	.217	.222	.225
	Proportion correct	.687	.650	.825	.800	.912	.887	.949
Read one time	Latency	.253	.228	.223	.215	.227	.228	.225
	Proportion correct	.275	.500	.400	.536	.512	.625	.600
Read five times	Latency	.254	.229	.223	.220	.220	.217	.212
	Proportion correct	.225	.250	.450	.625	.650	.800	.800
New	Latency	.264	.219	.206	.217	.212	.225	.221
	Proportion correct	.350	.350	.650	.666	.700	.731	.775
Participant 3
Heard	Latency	.320	.256	.231	.220	.218	.211	.206
	Proportion correct	.425	.632	.737	.762	.750	.810	.712
Read one time	Latency	.311	.264	.258	.225	.230	.214	.218
	Proportion correct	.475	.500	.575	.400	.425	.650	.600
Read five times	Latency	.306	.261	.244	.217	.226	.216	.211
	Proportion correct	.550	.500	.625	.666	.675	.853	.825
New	Latency	.327	.272	.225	.241	.239	.221	.222
	Proportion correct	.475	.425	.650	.536	.743	.775	.700
Participant 4
Heard	Latency	.270	.240	.228	.221	.221	.227	.231
	Proportion correct	.620	.640	.610	.630	.650	.710	.620
Read one time	Latency	.278	.224	.224	.225	.224	.226	.236
	Proportion correct	.440	.460	.580	.612	.760	.843	.700
Read five times	Latency	.266	.231	.227	.219	.221	.228	.232
	Proportion correct	.300	.520	.660	.760	.918	.803	.900
New	Latency	.280	.237	.224	.227	.230	.233	.231
	Proportion correct	.420	.500	.760	.686	.755	.760	.700
Participant 5
Heard	Latency	.307	.243	.213	.204	.201	.214	.208
	Proportion correct	.225	.325	.437	.562	.645	.569	.600
Read one time	Latency	.319	.263	.225	.205	.195	.217	.201
	Proportion correct	.820	.717	.820	.804	.820	.846	.825
Read five times	Latency	.308	.260	.234	.203	.207	.213	.213
	Proportion correct	.657	.605	.700	.794	.750	.800	.900
New	Latency	.319	.254	.207	.204	.222	.203	.218
	Proportion correct	.825	.923	.925	.805	.925	.975	.925
Participant 6
Heard	Latency	.238	.209	.200	.203	.195	.196	.197
	Proportion correct	.350	.400	.537	.487	.550	.550	.544
Read one time	Latency	.246	.207	.204	.202	.211	.204	.193
	Proportion correct	.600	.525	.625	.743	.871	.878	.850
Read five times	Latency	.235	.214	.220	.209	.220	.196	.202
	Proportion correct	.625	.425	.625	.634	.820	.925	.900
New	Latency	.234	.208	.203	.202	.204	.211	.198
	Proportion correct	.550	.550	.900	.975	.950	1.000	1.000
Participant 7
Heard	Latency	.261	.221	.189	.195	.202	.208	.208
	Proportion correct	.575	.662	.900	.925	.975	1.000	.962
Read one time	Latency	.263	.228	.215	.210	.214	.215	.217
	Proportion correct	.450	.425	.600	.825	.925	.850	.975
Read five times	Latency	.260	.225	.225	.187	.206	.213	.214
	Proportion correct	.425	.375	.800	.923	.975	.975	1.000
New	Latency	.269	.233	.200	.199	.219	.221	.226
	Proportion correct	.450	.650	.850	.926	.974	.975	1.000
Participant 8
Heard	Latency	.214	.198	.186	.188	.200	.200	.197
	Proportion correct	.550	.433	.583	.678	.650	.650	.661
Read one time	Latency	.226	.196	.195	.194	.196	.201	.198
	Proportion correct	.566	.400	.566	.655	.466	.548	.800
Read five times	Latency	.213	.190	.190	.196	.205	.203	.203
	Proportion correct	.500	.433	.466	.516	.586	.733	.700
New	Latency	.228	.221	.184	.192	.216	.203	.201
	Proportion correct	.366	.433	.633	.866	.862	.900	.866