The Temporal Dynamics of Visual Search: Evidence for Parallel Processing in Feature and Conjunction Searches

Abstract

Feature and conjunction searches have been argued to delineate parallel and serial operations in visual processing. The authors evaluated this claim by examining the temporal dynamics of the detection of features and conjunctions. The 1st experiment used a reaction time (RT) task to replicate standard mean RT patterns and to examine the shapes of the RT distributions. The 2nd experiment used the response-signal speed–accuracy trade-off (SAT) procedure to measure discrimination (asymptotic detection accuracy) and detection speed (processing dynamics). Set size affected discrimination in both feature and conjunction searches but affected detection speed only in the latter. Fits of models to the SAT data that included a serial component overpredicted the magnitude of the observed dynamics differences. The authors concluded that both features and conjunctions are detected in parallel. Implications for the role of attention in visual processing are discussed.

One of the major tools for investigating primitives of the visual system and the role of attention in visual object recognition has been the visual search task, in which an observer searches for a prespecified target among an array of distractors. A key finding to emerge from this paradigm is that search time and accuracy systematically vary with the type of target and the number of distractor elements (set size). Searching for a target that differs from distractors by a simple feature (e.g., searching for a tilted line among vertical lines) yields fast reaction times (RTs) and low errors that are largely unaffected by set size (Treisman, 1993; Treisman & Gormican, 1988; Treisman & Souther, 1985). In contrast, searching for a target that represents a conjunction of features present in the distractor set (e.g., searching for a red vertical line among blue vertical and red horizontal lines) typically yields slower RTs and higher error rates that systematically vary with set size (Treisman, 1993; Wolfe, 1994). Several types of conjunction searches produce approximately linear RT set-size functions, with slopes that typically range from 20–30 ms for target-present trials and 40–60 ms for target-absent trials (e.g., Wolfe, 1996).

Following the rationale that was originally proposed by Sternberg (1966, 1975), these RT patterns have led to claims that different mechanisms underlie the detection of features and conjunctions (e.g., Enns & Rensink, 1990a, 1990b; Treisman & Gelade, 1980; Treisman & Gormican, 1988; Treisman & Sato, 1990; Wolfe, 1994; Wolfe, Cave, & Franzel, 1989). The shallow RT slopes observed in feature searches have been interpreted as evidence for a parallel mechanism, in part because it has been deemed physiologically infeasible to have serial processes with slopes of less than 10 ms/item (Crick, 1984). Treisman and Gormican (1988), for example, argued that features like orientation are primitives of the early visual system, which are preattentively registered in parallel by independent feature modules. Such features can be detected by monitoring in parallel the output of any number of feature modules.

Conjunction search, in contrast, requires detecting the co-occurrence of two or more features at one spatial location. Feature integration theory (FIT; Treisman & Gelade, 1980) contends that the detection of a conjunction requires attention to integrate information across feature modules, which introduces a bottleneck in processing. According to this view, particular locations, defined by either items or groups of items (Treisman, 1991, 1993; Treisman & Gelade, 1980; Treisman & Gormican, 1988), must be serially inspected in order to detect the co-occurrence of the prespecified features. The serial deployment of attention leads to linear effects of set size on mean RT with slope greater than 10 ms/item. The serial search is also thought to be self-terminating as the slopes for target-present functions are typically half the slopes for target-absent functions. That is, if observers terminate a search when a target is found, then on average only half the items need to be examined in target-present trials, whereas all items must be examined in target-absent trials (Sternberg, 1966).

The serial–parallel dichotomy proposed in FIT has guided the interpretation of several search studies (e.g., Enns & Rensink, 1990a, 1990b) and has been incorporated into other search models. For instance, the guided search model (GSM; Cave & Wolfe, 1990; Wolfe, 1994, 1996; Wolfe et al., 1989; Wolfe, Yu, Stewart, Shorter, & Cave, 1990) adopts a two-stage architecture proposed by Hoffman (1978, 1979). The first stage detects all simple features in parallel and guides a second stage that is serial and that takes place in limited areas of the visual field. During the first stage, the information activated by simple features is added and registered in a global map of activation in which each location represents the probability of containing a target. In the second stage, attention is directed at the location with the highest activation level. The search stops if the target is detected at this location; otherwise, attention is directed at the next highest location until a target is found or until no remaining location has sufficient activation.

Unfortunately, the elegant RT logic that motivates models such as FIT and GSM provides less than satisfactory grounds for drawing a sharp dichotomy between parallel and serial processing and the related distinction between preattentive and attentive processing. This logic is predicted on the basis of a set of strong assumptions concerning the arrangement of serial-processing stages and their mapping to observable RT data—assumptions that have been repeatedly challenged since the logic was first proposed in the mid-1960s (see Luce, 1986; Sternberg, 1975; Townsend & Ashby, 1983). As a consequence, other search models have been proposed to account for the differential impact of set size on mean RT. As outlined below, these models contend that the detection of both features and conjunctions is mediated by a parallel mechanism (e.g., Duncan & Humphreys, 1989; Eckstein, 1998; Humphreys & Müller, 1993; Kinchla, 1992; Mordkoff, Yantis, & Egeth, 1990; Palmer, 1994, 1995; Palmer, Ames, & Lindsey, 1993; Pavel, 1990; Verghese & Nakayama, 1994).

We report two experiments that jointly examine the parallel (preattentive) and serial (attentive) dichotomy as an explanation for differences between feature and conjunction searches. The primary purpose of the first experiment was to replicate with conventional RT procedures the standard patterns of mean RT and error rate for feature and conjunction searches. The second, crucial experiment used the speed–accuracy trade-off (SAT) procedure to examine the full time course of feature and conjunction searches. Time-course data provide conjoint measures of processing speed and accuracy that provide a much stronger basis on which to contrast serial- and parallel-processing architectures than RT data alone. The reported data undermine the serial (conjunction) and parallel (feature) search dichotomy proposed in models such as FIT and GSM. We conclude that both feature and conjunction searches are best described as parallel processes. We discuss the implications of these findings for the role of attention in visual processing.

Problems Associated With Interpreting RT Patterns

The patterns of mean RT that are often interpreted as evidence for a serial architecture can unfortunately arise from various types of parallel architectures. Townsend (1972, 1990) and Townsend and Ashby (1983) have argued that, at most, linear RT functions indicate limited processing capacity. Strictly speaking, capacity limits are orthogonal to the issue of serial versus parallel processing because both types of operations may have either limited or unlimited capacities. In this vein, several limited-capacity parallel search models have been proposed in which linear RT functions result from decreases in rate of information accrual as additional comparisons are concurrently performed (Murdock, 1971; Rumelhart, 1970; Shaw, 1982; Townsend & Ashby, 1983). Other parallel architectures have also been put forward. Humphreys and Müller (1993) have demonstrated that both linear and nonlinear, steep and shallow search slopes are compatible with a model in which conjunctions are detected by monitoring the output of a network that registers features and conjunctions with a parallel, hierarchical coding scheme. Empirically, parallel architectures have received support from studies examining the effects of target redundancy (e.g., Mordkoff, Yantis, & Egeth, 1990) and differences between sequential versus simultaneous display presentations (e.g., Kinchla, Chen, & Evert, 1995).

Central to the claim that linear functions entail serial processing is an assumption that differences in RT uniquely reflect underlying differences in processing dynamics or speed. However, differences in RT can arise from a confluence of factors other than processing speed resulting from a serial architecture. Increasing the number of elements in a display increases the complexity of the decision process and potentially reduces the sensory quality of each element (e.g., Kinchla, 1980, 1992; Palmer, 1994, 1995; Pavel, 1990; Shaw, 1982; Verghese & Nakayama, 1994; see Sperling & Dosher, 1986, for a general exposition of this position). Both factors may affect discriminability, which in turn may be the key determinant of set-size effects (Duncan & Humphreys, 1989).

As set size increases, the amount of information that must be integrated to form a decision increases, and, crucially, so does the probability of errors in target detection. Confusability theories attribute set-size effects to the noisy quality of the sensory impressions, which increases the risk of confusing the target with a distractor as the number of distractors increases (e.g., Carrasco, Evert, Chang, & Katz, 1995; Kinchla, 1974; Kinchla et al., 1995; Palmer, 1994, 1995; Palmer et al., 1993; Pavel, 1990; Shaw, 1982; Verghese & Nakayama, 1994). Principles from signal detection theory are often used to account for how set size affects discriminability. Within such a framework, set size is predicted to have a greater impact on discriminability in conjunction searches because of the multidimensional nature of the required decision process (e.g., Eckstein, 1998; Pavel, 1990). Most models of this type focus on untimed accuracy rather than on RT data. However, generic RT models, like Ratcliff’s (1978) diffusion (continuous random-walk) model, provide an explicit framework for specifying how differences in discriminability translate into differences in RT (see also Palmer, 1998; Verghese & Nakayama, 1994).

Differences in discriminability can also be linked to sensory rather than decision factors. In typical search tasks, increasing set size also increases the (average) retinal eccentricity of the target. Target eccentricity has a pronounced and persistent effect on search. Targets appearing at peripheral locations are detected (Carrasco et al., 1995; Carrasco, McLean, Katz, & Frieder, 1998), localized, and identified (Carrasco & Chang, 1995; Carrasco & Theofanou, 1997) more slowly and less accurately than those appearing near the central fixation point. Neither overt (with eye movements) nor covert (without eye movements) attentional shifts can explain the eccentricity effect. This effect is equally pronounced when eye movements are prevented as when they are not, and a highly similar eccentricity effect emerges in tasks that are considered to require varying degrees of attentional involvement (e.g., feature vs. conjunction searches or display durations that afford different numbers of covert attentional shifts). Carrasco and colleagues (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, et al., 1998) proposed that these performance similarities reflect fundamental sensory factors such as spatial resolution and lateral inhibition common to all types of search.

Carrasco and Frieder (1997) eliminated eccentricity effects by magnifying the size of peripheral stimuli so as to compensate for retinal inhomogeneity. Under these conditions, the set-size effect was eliminated for feature searches and substantially attenuated for conjunction searches. Furthermore, Carrasco and Yeshurun (1998) peripherally precued target locations and found that both the set-size and the eccentricity effects were attenuated but not eliminated for both feature and conjunction searches. Given that set-size effects were not eliminated by precuing, these effects must reflect factors other than the serial deployment of attention.

Studies have also demonstrated the importance of other sensory factors. For instance, stimulus information content and spatial resolution predict search time in multiple-fixation searches of both feature and conjunction searches (Geisler & Chou, 1995). Search performance for orientation, spatial frequency, or color is closely related to discrimination thresholds for orientation, spatial frequency, or opponent color mechanisms, suggesting that search performance is determined by early visual processes (Verghese & Nakayama, 1994). Likewise, Carrasco, McLean, et al. (1998) demonstrated that stimulus size, orientation, and spatial frequency influence the extent of the eccentricity effect and the efficiency of search performance.

Explanations that are based on sensory and decision factors share the common assumption that differences in RT cannot be uniquely interpreted as differences in the underlying processing dynamics (speed). RT can vary with differences in discriminability alone, whether these differences are sensory in nature or are due to the complexity of the decision process. Given that RT varies with discriminability, the RT patterns for various search conditions cannot uniquely identify serial or parallel architectures.

SAT Analysis of Visual Search

Discriminating among alternative search models requires data that enable one to cleanly isolate how set size affects target discriminability and processing speed in both feature and conjunction searches. The response-signal SAT procedure provides conjoint assessments of discrimination (accuracy) and processing dynamics (speed) by deriving time-course functions that measure the growth of accuracy over processing time (e.g., Dosher, 1976, 1979, 1981, 1982, 1984; McElree, 1993, 1996, 1998; McElree & Dosher, 1989, 1993; Ratcliff, 1979, 1981; Ratcliff & McKoon, 1989; Reed, 1973, 1976; Wickelgren, 1977).

The SAT study reported here (Experiment 2) required observers to respond (“target present” or “target absent”) when a response cue (a tone) was presented at one of seven points from 0.2 to 2.0 s after the onset of a search array. Accuracy was thereby measured at times when performance was near chance and was measured up through times when accuracy reached an asymptotic level. The asymptote of the SAT function provides a measure of the overall discriminability of a target among a set of distractors when maximal processing time is allowed. The preasymptotic portion of the time-course function measures processing speed or dynamics, which is jointly specified by (a) the intercept of the SAT function, (b) the point in time when accuracy departs from a chance level, and (c) the rate at which accuracy grows from intercept to asymptote.

The curves in Figure 1 present two hypothetical patterns of time-course functions derived from the SAT procedure. Figure 1A depicts two conditions that differ in asymptotic accuracy alone. Explanations of search performance that are based on claims that larger set sizes lower discriminability—either by reducing the sensory quality of the stimuli or by increasing noise in the decision process—predict that the asymptote of the SAT functions will decrease with larger set sizes. Asymptotic differences are predicted to be present in both feature and conjunction searches, although the effect may be more pronounced in the latter (e.g., Duncan & Humphreys, 1989; Eckstein, 1998; Pavel, 1990).

Figure 1.

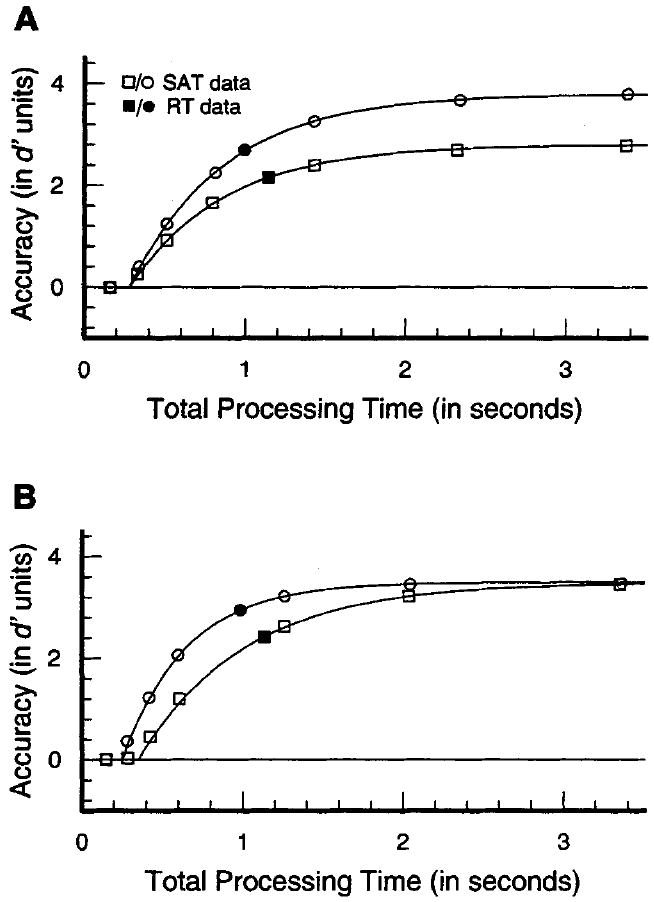
Hypothetical speed–accuracy trade-off (SAT) functions illustrating two conditions that differ by SAT asymptote only (Figure 1A) or SAT intercept and rate (Figure 1B). The filled symbols show (hypothetical) reaction time (RT) points plotted in SAT coordinates (see text), illustrating that approximately the same difference in mean RT and RT accuracy is consistent with either differences in SAT asymptote (Figure 1A) or SAT dynamics (Figure 1B).

Crucially, if set size affects the speed of the search process, then the preasymptotic portion of the functions will be differentially affected by set size. Such a situation is depicted in Figure 1B, in which the functions are associated with different intercepts and rates of rise to asymptote. (For expository purposes, the functions are shown rising to a common asymptote.) Dynamics differences, either SAT intercept or rate differences, reflect either the rate of continuous information accrual if processing is continuous or the distribution of finishing times if processing is discrete (Dosher, 1976, 1979, 1981, 1982, 1984; Meyer, Irwin, Osman, & Kounois, 1988; Ratcliff, 1988). The dynamics portion of the time-course functions provides a strong test of serial and parallel models of search performance. McElree and Dosher (1989, 1993) exploited this property of the SAT function to test serial retrieval models proposed to account for linear RT functions that were induced by increasing the size of a memory set rather than a search set (e.g., Sternberg, 1975; Theios, 1973). (For other applications of the SAT procedure to serial- and parallel-processing issues, see Dosher, 1982; McElree, 1993, 1998; McElree & Griffith, 1995; Ratcliff, 1979; and Reed, 1976.) As illustrated below, a key prediction of a serial-processing architecture is that the SAT intercept will increase and/or that the SAT rate will slow with larger search sets.

The inability of RT data to uniquely isolate temporal differences in processing is graphically illustrated by the filled symbols in Figure 1, which show (hypothetical) data from an RT task plotted in speed–accuracy coordinates. Figure 1A illustrates that a difference in mean RT (distance on the abscissa) and RT accuracy (distance on the ordinate) can arise if the corresponding SAT time-course functions differ in asymptotic accuracy alone. Figure 1B illustrates that a nearly identical difference in mean RT and RT accuracy can arise from underlying differences in the dynamics of processing.¹ Empirically, differences in RT have been found to reflect differences in asymptotic accuracy alone (e.g., Corbett & Wickelgren, 1978; Dosher, 1984; McElree, 1993; McElree & Dosher, 1989), differences in dynamics alone (Dosher, 1981; Dosher & Rosedale, 1989; McElree & Griffith, 1995), or mixtures of asymptotic and dynamics differences (McElree, 1996, 1998; McElree & Dosher, 1993; McElree & Griffith, 1998). McElree and Dosher (1989) found that linear RT functions in memory search tasks arose solely from asymptotic differences in discriminability as a function of set size.

Predictions From a Serial Architecture

Dynamics differences, expressed as either differences in SAT intercept and/or differences in SAT rate, are the signature pattern of any model that has a serial-processing component (McElree, 1993; McElree & Dosher, 1989, 1993; McElree & Griffith, 1995). To understand this point, assume that the probability of a single comparison finishing by time t is exponentially distributed with a rate of information accrual equal to β. A serial model assumes that the search is accomplished by performing a sequence of these comparison operations. The probability that a series of exponentially distributed comparisons complete by time t is gamma distributed, with an order α equal to the number of implicit comparison processes:

$$P(T\le t)=\frac{{\mathrm{\beta }}^{\mathrm{\alpha }}}{(\mathrm{\alpha }-1)!}{\int }_0^{t-\mathrm{\delta }}{e}^{-\mathrm{\beta }{t}^{\prime }}{t^{\prime }}^{\mathrm{\alpha }-1}{\mathit{dt}}^{\prime },t>\mathrm{\delta },\mathrm{else}0.$$ (1)

Equation 1 is a cumulative gamma function, representing the convolution of α independently and identically distributed exponential distributions, each of which describes the completion time for a single comparison in a serial operation. The overall function is offset by a base time δ to reflect encoding and response time. To compute the probability of a correct response as a function of processing time, gammas of various orders must be combined in a manner that reflects the number of underlying serial comparison processes in the search.

We illustrate serial predictions for set sizes of 4, 10, and 16 items, which were the set sizes used in the SAT experiment. For target-absent conditions, a serial search mechanism follows an exhaustive decision rule, that is, a “no” response is made after all distractors have been compared. Hence, target-absent performance reflects “pure” gammas with orders (α) equal to the number of distractor elements. The proportion correct as a function of processing time is determined by the probability that gammas of order α have completed by time t. This proportion is incremented by a guessing factor (with a probability of .5) for cases in which the search has not been completed by the time a response is required.² For target-present trials, the decision rule inferred on the basis of RT slope functions is self-terminating, that is, a “yes” response is made as soon as one of the elements matches the search criteria. In modeling mean RT, one simply assumes that the average search time will reflect one half the number of elements in the display. When modeling SAT data, however, one models the complete distribution of finishing times in a cumulative form. In a set size of 4, for example, a target may be found on the first, second, third, or fourth comparison. Assuming a random search order, there is an equal probability of finding a match on each comparison. Therefore, performance reflects a probabilistic mixture of gammas with orders (α) of 1, 2, 3, and 4, each weighted by a probability of .25, plus a correction for guessing. Likewise, performance in a set size of 10 represents 10% mixtures of gammas with a equal to 1–10, whereas performance in a set size of 16 represents 6.25% mixtures of gammas with α equal to 1–16.

Figure 2 shows predicted accuracy as a function of processing time for the three set sizes. Accuracy is represented here in (equal-variance, Gaussian) d′ units, derived by scaling the hit rate for target-present performance against the corresponding false-alarm rate for the target-absent condition. Because in most cases performance is less than perfect, we assumed that the overall error rate for each judgment was 5% and that each implicit comparison process had an additional 1% chance of error. This assumption produced lower asymptotic performance as set size increased, consistent with claims that the complexity of the search processes induces lower performance (Kinchla, 1980; Palmer, 1994, 1995; Pavel, 1990; Sperling & Dosher, 1986).

Figure 2.

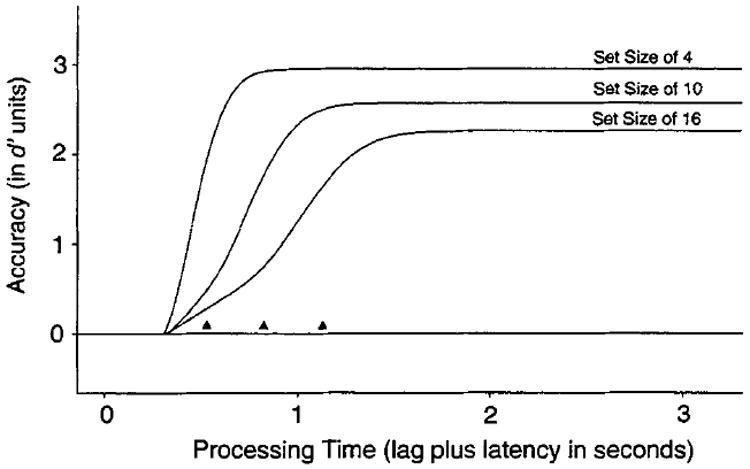
Predicted speed–accuracy trade-off (SAT) functions (d′ accuracy as a function of processing time) for set sizes of 4, 10, and 16 items, assuming a serial self-terminating search.

The key point illustrated in Figure 2 is that, independent of asymptotic differences, a serial search assumption predicts large differences in the dynamics across set size. This point is illustrated by the solid triangles, which indicate when each function reaches two thirds of its asymptote. These two-thirds marks shift toward longer times as set size increases, reflecting the fact that information accrual is progressively slowed by adding serial comparison processes. The shape of the functions in Figure 2 (i.e., the progressive “S-ing” of the functions as set size increases) is a specific consequence of having used a gamma function. Of course, an exponential (hence gamma) distribution is not the only distribution that might be used to model a serial process, although it is frequently chosen for its tractability (e.g., McClelland, 1979; McElree & Dosher, 1993; Townsend & Ashby, 1983). However, the disproportionality in the rate of information accrual will be a general property of any distribution that reflects the convolution of several underlying distributions, each of which reflects a serial comparison process.

Disproportional dynamics are predicted by any search model that includes a serial-processing component. For example, although GSM (Cave & Wolfe, 1990; Wolfe, 1994, 1996) following Hoffman (1978, 1979), proposes that parallel preprocessing limits the number of locations to which attention is directed, dynamics differences of the form just illustrated are predicted by the claim that attention can only be directed to one location at a time. Parallel preprocessing only attenuates the predicted dynamics differences if the number of items with activation levels sufficient to warrant a serial search disproportionately decrease with larger set sizes. (Of course, in this case, GSM also does not predict linear RT functions.) This may be the case if distractors are heterogeneous, with some distractors lacking the features that are relevant to the search. In the conjunction search task reported here, however, all distractors shared one feature in common with the target, so no set-size-specific attenuation of the search set is predicted by GSM. Evaluation of SAT dynamics provides a strong test of the basic serial architecture assumed in models such as GSM, as well as in less elaborated models such as FIT. The failure to find large dynamics differences provides grounds on which to reject serial architectures.

Predictions From Parallel Architectures

In contrast to conjunction searches, the consensus is that feature searches are mediated by a parallel mechanism. Parallel models are inherently more flexible than serial models (Townsend & Ashby, 1983) and, consequently, so are the corresponding SAT predictions. Whether disproportional dynamics are evidenced in feature or in conjunction searches depends on the underlying nature of the parallel mechanism.

A defining property of parallel models is that more than one comparison process is initiated at a time. Unlimited-capacity parallel models typically assume that all comparisons are initiated at the same time and proceed at the same processing rate. The term unlimited capacity refers here to the contention that an unlimited number of comparisons can be concurrently processed without decrements in the rate of information accrual. The term does not imply error-free performance; to the contrary, viable versions of this type of model typically predict substantial decrements in accuracy as the number of comparisons increases (e.g., Kinchla, 1992; Palmer, 1995). This class of models can be compatible with proportional SAT dynamics (equal rates and intercepts), independent of differences in SAT asymptotes (e.g., Figure 1A). McElree and Dosher (1989) proposed a variant of this type of model for memory search. However, disproportional dynamics—although more modest than those illustrated in Figure 2—can arise from decision factors. For example, disproportional dynamics can result from an increased tendency in larger set sizes to false alarm early in processing (McElree & Dosher, 1989; Ratcliff, 1978; see Experiment 2 of present study).

Disproportional dynamics can also result from capacity-limited parallel models. One possibility is that although all comparison processes are initiated at the same time, the rate of information accrual for each process depends on the number of comparisons performed concurrently (e.g., Murdock, 1971; Townsend & Ashby, 1983). In this case, the SAT functions are associated with the same intercept, but rates are controlled by the number of comparisons (McElree & Dosher, 1989). A more elaborate version of this type of model was proposed by Shaw and Shaw (1977). They assumed that several, but not necessarily all, comparisons are initiated at the start of a search. A fixed capacity, which determines processing rate, is divided among concurrent comparisons either equally or according to differential prior probabilities. As failure rate increases (no evidence for a target), resources are increasingly allocated to other ongoing comparisons and to new comparisons. This type of model also predicts disproportional dynamics in the form of differential rates of rise to asymptote.

Experimental Logic

Given the fact that some variants of a parallel model are compatible with disproportional dynamics, the logic of applying SAT procedures to the search task is as follows. Failure to find disproportional dynamics provides grounds to reject serial models and capacity-limited parallel models, and this, by default, provides evidence in favor of an unlimited-capacity parallel model. Disproportional dynamics provide grounds on which to reject certain variants of unlimited-capacity parallel models, providing evidence that supports either serial-processing models or a restricted class of parallel models. Discriminating among the latter requires fitting the form and magnitude of the dynamics differences.³ In this study, by contrasting both feature and conjunction searches, we gained further constraints by comparing across tasks.

To test these classes of models, we examined the effect of set size on both feature (a vertical blue line among tilted blue lines) and conjunction (a vertical blue line among tilted blue and red vertical lines) searches. Prior to reporting the crucial SAT results, we report a conventional RT task, using the same observers and same essential experimental parameters as the SAT study. We do so to demonstrate standard RT results and the convergence between RT and SAT methods.

Experiment 1: RT Task

Two fundamental and interrelated conditions must be met to properly examine the effect of set size on search. The first condition is that observers should not be able to benefit from eye movements (Carrasco et al., 1995; Carrasco, McLean, et al., 1998; Klein & Farrell, 1989). Questions concerning the interaction of overt attention through eye and head movements and search are important issues for research, but if observers are able to execute eye movements, then these movements may impose a serial pattern on an otherwise parallel architecture. This concern is particularly crucial when contrasting feature and conjunction searches, as observers are more likely to move their eyes with more complex stimuli to bring particular regions of the display into foveal processing (e.g., Carrasco et al., 1995; Kinchla, 1992). The interesting claim of Treisman and colleagues (Treisman & Gelade, 1980; Treisman & Gormican, 1988; Treisman & Sato, 1990) is that shifts of covert attention have the same inherent serial property as do overt movements.

To prevent eye and head movements, we limited the display duration to 150 ms (fixed-viewing condition), a time that was too brief to allow observers to fixate on more than one location in the display (Mayfrank, Kimmig, & Fischer, 1987). As a point of comparison, we also used a free-viewing condition, in which the display was available until observers responded. We anticipated that observers would make fewer errors in the latter case (Carrasco et al., 1995; Carrasco, McLean, et al., 1998). For conjunction searches, the slope of the RT function should be steeper under free- as compared with fixed-viewing conditions if overt eye movements are contributing to estimates of search time.

The second criterion is that one should take steps to unconfound set size and stimulus discriminability. If larger set sizes increase the probability of a target occurring in more peripheral regions, targets will be less discriminable in larger arrays, increasing mean RT and associated error rates (Carrasco et al., 1995; Carrasco, McLean, et al., 1998). Processing is inherently better near the fovea because its spatial resolution is greater than in the periphery (DeValois & DeValois, 1988). In the current studies, the target and distractors subtending 0.4° were placed on an imaginary circumference at 7.1° eccentricity, separated by at least 2.2°. These display characteristics decreased the potential for lateral masking and ensured that stimulus eccentricity would be constant for all set sizes.

Method

Observers

Six observers, whose ages ranged from 17 to 25 years old, participated in four 1-hr sessions. Observers were each paid $32 for their participation. All but 1 observer (CW) were naive as to the purposes and method of the experiment. All had normal or corrected-to-normal vision.

Apparatus and stimuli

The stimuli were presented on a Power PC Macintosh microcomputer with a high-resolution color monitor. Each observer performed one session of each of four experimental tasks: two feature and two conjunction searches. Observers searched for a blue vertical target among blue tilted (feature search) or blue tilted and red vertical (conjunction search) distractors. Each search type was divided into two experimental conditions, as defined by display durations; the display appeared either for 150 ms (fixed-viewing condition) or until the observer responded (free-viewing condition). Each display consisted of 4, 7, 10, 13, or 16 tilted (24° clockwise) and vertical blue or red lines [(x, y) = (.175, .108) or (.632, .350) in standard Commission Internationale de l’Eclairage color space] presented against a white background. The items were scattered among 16 positions on an invisible circle (polar grid) that had a radius of 9.25 cm. On the basis of a viewing distance of 73 cm, fixed by a chin rest, this subtended a 7.1° visual angle at 7.1° of eccentricity. Bars subtended 0.4° × 0.03° of visual angle; the target was vertical, and the distractors were rotated 24° clockwise. The positions occupied by the target and the distractors were chosen randomly, with a constraint that in each experimental session, for each set size, the target appeared in all 16 locations at least six times.

Design

A four-way factorial design was used (task: feature vs. conjunction; display duration: fixed-viewing vs. free-viewing; target: absent vs. present; and set size: 4, 7, 10, 13, or 16 elements). Each of 10 experimental blocks consisted of 100 randomized trials, for a total of 1,000 experimental observations per observer in each of four experimental sessions: fixed-viewing feature search, fixed-viewing conjunction search, free-viewing feature search, and free-viewing conjunction search. Thus, for each observer, there were 200 trials for each of the five set sizes in the four Search Type × Viewing conditions.

Procedure

Observers were asked to search for a single orientation-feature target (a vertical blue line) that appeared among homogeneous distractors (blue tilted lines for the feature search or blue tilted and red vertical lines for the conjunction search). Observers were told that half of the displays would contain the target and that the task was to press a “yes” key, using the index or middle finger of their dominant hand when the target appeared or a “no” key if no target appeared. Half the observers used their index finger for a “yes” response, and the other observers used their middle finger.

Observers were instructed to respond as rapidly and as accurately as possible, because both speed and accuracy were to be recorded. Feedback appeared at the center of the screen at the location of the permanent fixation point to indicate whether observers responded within the allotted time (3 s; a plus sign or a minus sign was used to indicate correct and incorrect responses, respectively) or to indicate that time had run out (indicated by a circle). Observers’ error rate was displayed on the screen after each block. Observers performed one practice block before each experimental session. The sequence of the four experimental tasks was randomized across observers.

Results

Figure 3 shows the mean RT and error rate for the two searches under both viewing conditions.

Figure 3.

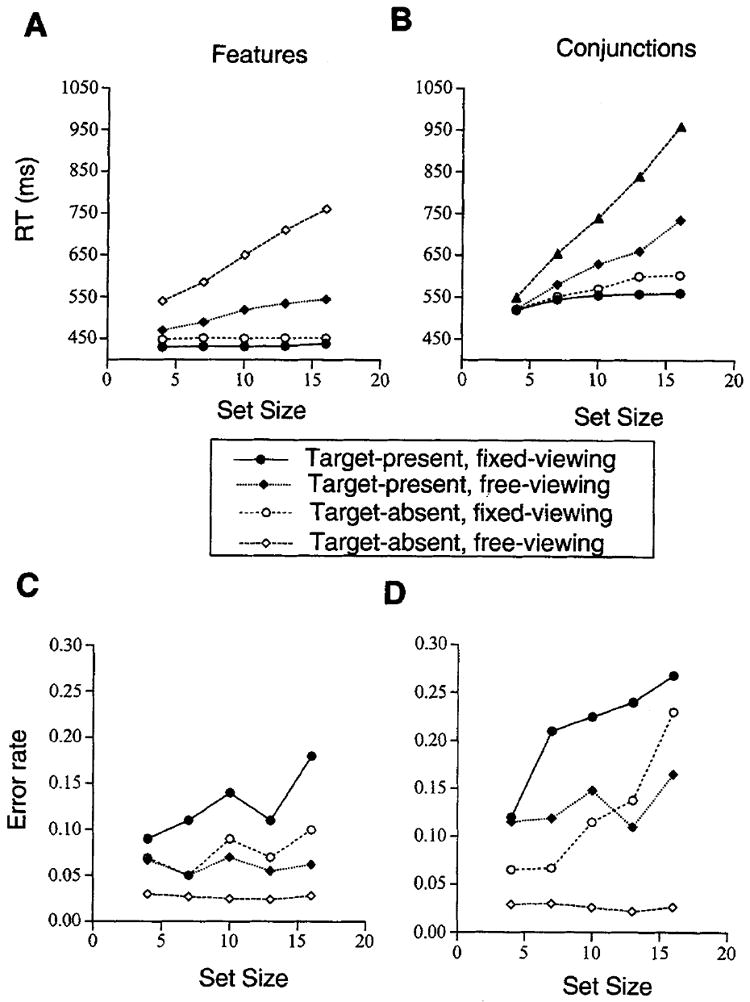
Observers’ mean correct reaction times (RTs; in milliseconds; Figures 3A and 3B) and error rates (proportion; Figures 3C and 3D) for present and absent vertical targets as a function of set size for feature (Figures 3A and 3C) and conjunction (Figures 3B and 3D) searches under the fixed-viewing conditions (150-ms stimulus duration) and the free-viewing conditions of Experiment 1.

Fixed-viewing condition

A three-way analysis of variance (ANOVA) was performed on the observers’ correct mean RT and error rate for feature and conjunction searches under the fixed-viewing condition, with search type (feature vs. conjunction), set size (4, 7, 10, 13, or 16 elements), and target (present or absent) as fixed variables. All results reported here were significant (at least p < .05). Observers were faster at correctly detecting features than conjunctions, detecting target-present than target-absent trials, and searching smaller than larger set sizes. However, an interaction of set size with search type and with target indicated that the effect of set size was more pronounced for conjunctions than for features, as well as for target-absent than for target-present trials. Moreover, a three-way interaction showed that the RT difference between target-present and target-absent trials was greater for the conjunction than for the feature searches as set size increased. An ANOVA performed on the proportion of errors showed that there were more errors for target-present than for target-absent trials and for larger than for smaller set size and that the effect of set size was more pronounced for conjunction than for feature searches.

On the basis of observers’ mean RT for each set size, least square slope estimates for target-absent and for target-present trials were obtained. The average slopes for the linear fits were 1.3 ms/item for both target-present and target-absent trials in feature searches and 4.4 ms/item for target-present and 7.8 ms/item for target-absent trials in conjunction searches. Following conventional criteria, the slope estimates here would be interpreted as evidence for a parallel search process because they are less than 10 ms/item (cf. Cave & Wolfe, 1990; Duncan & Humphreys, 1989; Egeth, Folk, & Mullin, 1989; Enns & Rensink, 1990a, 1990b; Treisman & Gelade, 1980; Treisman & Gormican, 1988; Wolfe et al., 1989). However, the conjunction slope estimates approximate the 2:1 absent:present ratio that is typically taken as indicative of a serial self-terminating search (e.g., Pashler, 1987a; Treisman & Gelade, 1980; Wolfe, 1994; but see Humphreys & Müller, 1993, and van Zandt & Townsend, 1993).

We view these heuristic interpretations of slope estimates with caution because mean RT can dramatically vary with decision factors, sensory factors, and other factors. Here, the absolute slope estimates cannot be directly interpreted as indicators of processing time, given that error rates also systematically increased with set size. For feature search, the error slopes were 0.006/item and 0.003/item for target-present and target-absent trials, respectively, and for conjunction search the slopes were 0.012/item for target-present trials and 0.013/item for target-absent trials.

We note also that RTs were faster for target-present than for target-absent trials but that the error rates were higher for target-present than for target-absent trials in both search types. This pattern has often been found for both feature and conjunction searches. Some authors have analyzed the error rates (e.g., Carrasco et al., 1995; Carrasco, McLean, et al., 1998; Enns & Rensink, 1990a, 1990b; Humphreys, Quinlan, & Riddoch, 1989; Pashler, 1987b; Wolfe et al., 1989), whereas others have just mentioned them (e.g., Cavanagh, Arguin, & Treisman, 1990; Egeth, Virzi, & Garbart, 1984; Pashler, 1987a; Treisman, 1982, 1991) or have collapsed them across the two types of trials (Treisman & Gormican, 1988; Treisman & Sato, 1990; Wolfe et al., 1990). Zenger and Fahle (1997) argued that the higher proportion of misses as compared with false alarms may reflect an optimized decision strategy for an imperfect search process. However, this pattern may also be indicative of a speed-accuracy tradeoff; this is an additional reason to interpret slope estimates with caution.

Free-viewing condition

As with the fixed-viewing conditions, observers were marginally faster at correctly detecting features than conjunctions (p < .10), detecting target-present than target-absent trials, and searching smaller than larger set sizes. Significant interactions indicated that the effect of set size was more pronounced for conjunctions than for features as well as for target-absent than for target-present trials (Figure 3). The error rate ANOVA revealed that task and target interacted: There were more errors for conjunction- than for feature-present targets, but the error rates did not differ for the target-absent trials. The effect of target was only significant for the conjunction search.

For the feature searches, the RT slope was 6.5 ms/item for the target-present trials and 20 ms/item for the target-absent trials. In this condition, the slopes of the error functions were zero. Although the RT slope for target-present trials was below the typical range for a serial process (10 ms/item), the RT slope for target-absent trials was not. Moreover, these slopes approximated the 2:1 absent:present ratio. Accordingly, it could be argued that performance is best explained by a parallel search mechanism in the fixed-viewing condition and by a serial self-terminating mechanism in the free-viewing condition. It is possible that overt eye movements imposed a serial structure on an otherwise parallel process in this case. The low, flat error rates in this condition lend credence to the notion that participants may have used eye movements to enhance performance. The Appendix presents an analysis of the RT distributions from both the free- and fixed-viewing conditions. Consistent with an eye-movement interpretation, free-viewing conditions show large shifts in the leading edge of the RT distributions for features and conjunction searches.

For conjunction searches, the slopes for target-present and target-absent trials were 15.5 and 34.3 ms/item, which were within the range usually considered plausible for a serial process. Additionally, these slopes approximated the 2:1 absent:present ratio as in the fixed-viewing condition. The slopes of the error functions were lower in the free- than in the fixed-viewing condition, namely, −0.001/item and 0.004/item for the target-present and target-absent trials, respectively.

Discussion

The present results highlight the fact that the criteria thought to reveal the nature of the search do not yield consistent conclusions. The RT and error slopes are similar to previous findings on feature and conjunction searches for a vertical target under fixed-viewing and free-viewing conditions (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, et al., 1998). In agreement with previous visual search studies, the effects of set size and target were more pronounced for conjunction than for feature searches in both of our viewing conditions (e.g., Carrasco & Frieder, 1997; Duncan & Humphreys, 1989; Treisman & Gelade, 1980; Treisman & Gormican, 1988; Treisman & Sato, 1990; Wolfe, 1994; Wolfe et al., 1989).

In both feature and conjunction searches, the RT range was greater for the free- than for the fixed-viewing condition, whereas the opposite was true for errors. The pattern of data is consistent with the notion that the time-limited viewing conditions induced observers to adopt a more liberal response criterion and to opt for faster responses at the expense of higher error rates. Beyond simple criterion differences, the overall differences in speed and accuracy between the fixed- and free-viewing conditions are likely to be due to the fact that eye movements are rendered ineffectual in the fixed-viewing condition, leaving covert attentional shifts as the only attentional mechanism to operate on the representation of the briefly presented display (e.g., Bergen & Julesz, 1983; Saarinen & Julesz, 1991). The fact that the search for the vertical target was somewhat hampered in the fixed-viewing condition is in agreement with this notion, as well as with other studies (Carrasco et al., 1995; Carrasco, McLean, et al., 1998; Klein & Farrell, 1989). The error rates for the fixed-viewing condition were comparable to those obtained in similar tasks under free-viewing (e.g., Enns & Rensink, 1990a; Klein & Farrell, 1989; Treisman, 1982) and fixed-viewing (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, et al., 1998) conditions. The error rates did not increase to the extent observed by Treisman and Gormican (1988) and to the extent anticipated by Klein and Farrell (1989). We conclude that using a brief duration was an effective way to preclude eye movements and control target eccentricity. The Appendix presents a more extensive analysis of the RT task. An analysis of the shapes of the RT distributions is used to further examine the evidence for serial processing and to highlight the potential effects of eye movements in the free-viewing conditions.

Experiment 2: SAT Measures

The data from the RT task displayed a typical pattern for feature and conjunction searches, aside from some inconsistencies, which were likely a consequence of speed-accuracy trade-offs. The SAT variant of the search paradigm provides an alternative means of testing whether conjunction searches differ from feature searches in requiring a serial attentional mechanism. The response-signal SAT procedure effectively controls speed accuracy trade-offs, which, as evidenced in Experiment 1, can confound the interpretation of RT results. Importantly, this procedure provides estimates of processing speed independent of potential differences in discriminability, decision processes, or both.

Method

Observers

The 6 observers who participated in the RT task participated in nine 1-hr sessions (eight experimental sessions and one practice session) and were each paid $72 for their participation.

Apparatus, stimuli, and procedure

The apparatus, stimuli, and procedure were the same as in Experiment 1, with three exceptions. First, because the SAT procedure required substantially more trials than an RT task, only three set sizes of 4, 10, and 16 elements were used. For each observer, 1,000 trials were run, with 333 trials for two sets and 334 trials for a randomly chosen third set size. This resulted in at least 47 trials for each observer at each of the seven response lags (see below) for each set size. Second, in the fixed-viewing feature task, the orientation of the distractors was reduced from 24° to 12°, so that accuracy rates were comparable to those of the conjunction search. Third, observers were required to respond within 300 ms of a tone presented at one of seven response lags, either 210, 300, 450, 600, 750, 900, or 2,000 ms after the onset of the display. The response lag was randomly varied across trials. Observers were instructed and trained to respond within 300 ms of the tone. After a response, feedback appeared at the center of the screen indicating observers had responded within the allotted time (indicated by a plus sign) or that time to respond had run out (indicated by a circle). This feedback appeared at the location of the permanent fixation point. Each observer had one practice session to become acquainted with the procedure before participating in the eight experimental sessions: two sessions for each of the four experimental tasks (one feature and one conjunction search task with both fixed- and free-viewing conditions).

Data analysis

To derive time-course measures that were not influenced by particular response biases, we computed d′ values using the z score for the hit rate for target-present trials and the z score for the false-alarm rate for target-absent trials at each response lag for each set size. Perfect performance at any lag was adjusted by a minimum-error correction (Macmillan & Creelman, 1991).

To estimate asymptotic accuracy and processing dynamics (speed) as a function of set size, the empirical SAT functions were fit with an exponential approach to a limit:

$$d^{\prime }(t)=\mathrm{\lambda }(1-e^{-\mathrm{\beta }(t-\mathrm{\delta })}),\mathrm{for}t>\mathrm{\delta },\mathrm{else}0.$$ (2)

Equation 2 describes the growth of accuracy over processing time using three parameters: (a) λ, an asymptotic parameter reflecting the overall accuracy with maximal processing time; (b) δ, an intercept parameter reflecting the discrete point in time when accuracy departs from chance (d′ = 0); and (c) β, a rate of rise parameter that describes the rate at which accuracy grows from chance to asymptote. Numerous studies have found that Equation 2 provides a precise quantitative summary of the shape of a full time-course SAT function (e.g., Dosher, 1976, 1979, 1981, 1982, 1984; McElree, 1993, 1996; McElree & Dosher, 1989, 1993; Reed, 1973, 1976; Wickelgren, 1977).

All analyses were performed on the individual observers’ data. Consistent patterns across observers were summarized with the average (over observers) data. Differences among the SAT functions were quantified by fitting Equation 2 to the data with an iterative hill-climbing algorithm (Reed, 1976), similar to STEPIT (Chandler, 1969), which minimized the squared deviations of predicted values from observed data. A hierarchical model testing scheme was used. The SAT data were fit with sets of nested models that systematically varied the three parameters of Equation 2. These models ranged from a null model in which all functions were fit with a single asymptote (λ), rate (β), and intercept (δ) to a fully saturated model in which each function was fit with a unique set of parameters. The quality of the fit was assessed by using three criteria. The first criterion was value of an R² statistic,

$$R^2=1-\frac{\mathbf{\sum }_{i=1}^n{(d_i-{\widehat{d}}_i)}^2/(n-k)}{\mathbf{\sum }_{i=1}^n{(d_i-\overline{d})}^2/(n-1)},$$ (3)

where d_i represents the observed data values, d̂_i indicates the predicted values, d̂ is the mean, n is the number of data points, and k is the number of free parameters (Reed, 1973). This R² statistic is the proportion of variance accounted for by the fit, adjusted by the number of (k) free parameters (Judd & McClelland, 1989). The second criterion was an evaluation of the consistency of the parameter estimates across the observers, and the third criterion was an evaluation of whether the fit yielded systematic (residual) deviations that could be accommodated by allocating more (i.e., separate) parameters to various conditions.

Results

Free-viewing conditions

Figure 4 presents the empirical SAT data for the free-viewing conditions for feature (Figure 4A) and conjunction (Figure 4B) searches. In both cases, for almost all observers, the functions reached perfect performance at the longest lag. Measures of processing speed estimated from the preasymptotic portions of the SAT function are valid only if performance is not artificially constrained by limits on the performance scale. As processing dynamics could not be veridically estimated, the free-viewing conditions were not analyzed.

Figure 4.

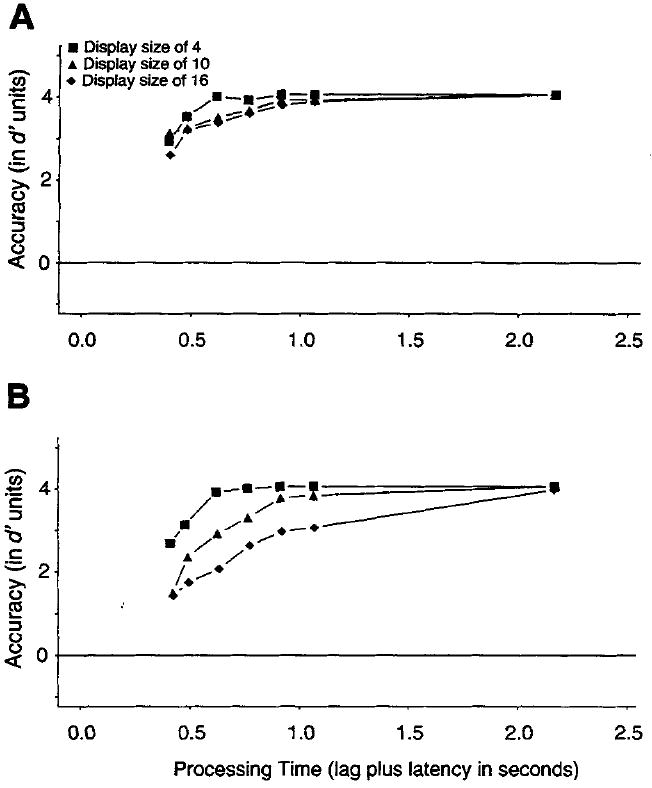
Average d′ accuracy (symbols) as a function of processing time (lag of the response cue plus latency to respond to the cue) for different set sizes for feature (Figure 4A) and conjunction (Figure 4B) searches under the free-viewing conditions of Experiment 2.

Fixed-viewing feature searches

Figure 5A presents the average (over observers) empirical SAT data for feature searches under the fixed-viewing condition. Asymptotic performance decreased with larger set sizes. The average d′ values were 2.57, 2.08, and 1.95 for set sizes of 4, 10, and 16 elements, respectively, when we used performance at the two longest interruption lags as an empirical measure of asymptotic accuracy. This difference was significant across observers, F(2, 10) = 5.91, p < .02. Correspondingly, all viable fits of Equation 2 to the full time-course data required allotting a separate asymptotic parameter (λ) to each set-size function. When the average d′ data were fit with a simple 1λ–1β–1δ model, in which the three set-size functions were fit with a common set of parameters, the adjusted R² value was .329 (ranging from .163 to .781 across the 6 observers). A 3λ–1β–1δ model increased the adjusted R² value to .834 (ranging from .492 to .963 across observers). The λ estimates were 2.7, 2.2, and 1.9 d′ units for set sizes of 4, 10, and 16, respectively. Most importantly, the λ parameter estimates were identically ordered in all 6 observers.

Figure 5.

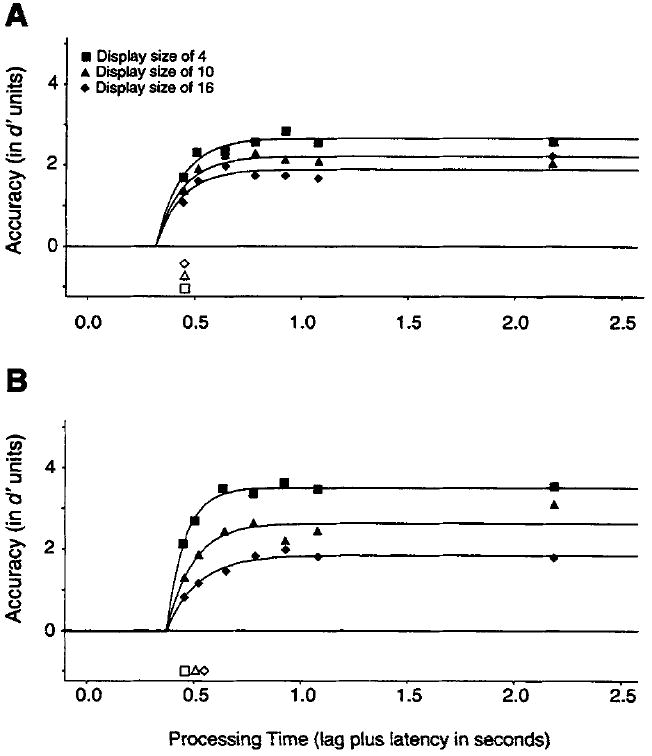
Average d′ accuracy (symbols) as a function of processing time (lag of the response cue plus latency to respond to the cue) for different set sizes for feature (Figure 5A) and conjunction (Figure 5B) searches under the fixed-viewing conditions (150-ms stimulus duration) of Experiment 2. Smooth curves show the best fits of Equation 3 with the (average) parameters listed in Table 1. Open symbols show the point in time when the corresponding functions reach two thirds of their asymptote.

To test for differences in processing dynamics, which were reflected in either the rate (β) or intercept (δ) parameters of Equation 2, we applied to the data models with all possible allocations of the three exponential parameters.⁴ In the average data, as with 5 of the 6 observers, all models that varied dynamics parameters substantially reduced the adjusted R² values obtained with the 3λ–1β–1δ model. For example, a 3λ–3β–1δ model, which assumed rate differences in addition to asymptotic differences, yielded an average adjusted R² value of .824, and the estimated rate parameters were near identical for set sizes 4, 10, and 16 (107, 103, and 113 in β⁻¹ ms units, respectively). A 3λ–1β–3δ model, which assumed intercept rather than rate differences, yielded an average adjusted R² value of .810, and here too the intercept estimates were within a few milliseconds of one another (309, 307, and 316 ms). For some observers, the reduction in adjusted R² value was more extreme than what was observed in the average data. Across participants, no consistent ordering of dynamics parameters was observed with the 3λ–3β–1δ model, the 3λ–lβ–3δ model, or the fully saturated 3λ–3β–3δ model. The reduction of adjusted R² values and the lack of consistent parameter estimates indicates that models with additional dynamics parameters were not accounting for systematic variance in the data sets.

There was, consequently, no evidence in our data to indicate that set size affected the speed of detecting a simple feature. The smooth lines in Figure 5A show the best fitting 3λ–lβ–1δ exponential model of the average data, on the basis of the parameter estimates listed in Table 1. The open symbols below the chance level show the times when each detection function reaches two thirds of its asymptote. These symbols graphically illustrate the fact that the functions are associated with proportional dynamics. The parameters for individual observers’ data are also listed in Table 1.

Table 1.

Exponential Parameter Estimates

Parameter	Average	CC	CW	MD	ML	MP	YSa
Feature search
Set size
4 λ	2.67	1.99	3.16	1.84	1.95	2.89	4.12
10 λ	2.23	1.64	2.88	1.04	1.55	2.74	3.42
16 λ	1.91	1.45	2.34	0.99	1.49	2.29	2.86
Common
β	8.28	7.68	5.24	11.99	11.13	13.47	9.58
δ	0.316	0.273	0.235	0.437	0.370	0.354	0.255
Adjusted R2	.834	.962	.670	.559	.491	.629	.804
Conjunction search
Set size
4 λ	3.53	3.19	3.61	2.79	4.01	3.87	4.08
10 λ	2.66	1.94	2.98	2.37	3.74	3.38	3.35
16 λ	1.86	1.39	2.58	1.29	2.90	2.02	2.41
4 β	11.95	14.9	8.47	4.16	8.22	10.07	7.82
10 β	8.23	14.9	5.87	1.41	3.97	4.39	5.06
16 β	7.08	14.9	6.48	0.52	3.62	3.66	3.62
Common δ	0.373	0.317	0.334	0.310	0.336	0.399	0.209
Adjusted R2	.946	.682	.684	.877	.911	.879	.823

Note. CC, CW, MD, ML, MP, and YS = participants’ initials.

^aParticipant YS’s data for conjunction fits were marginally better fit by 3λ–1β–3 δ model (adjusted R² = .858) rather than the 3 λ–3 β–1 δ model reported here.

Fixed-viewing conjunction searches

Figure 5B illustrates that asymptotic performance also decreased with larger set sizes in conjunction searches, F(2, 10) = 33.1, p < .0001. The average d′ values were 3.51, 2.79, and 1.81 for set sizes of 4, 10, and 16 elements, respectively, at the two longest interruption lags. Consequently, fitting the full time-course functions here also required allotting separate λs to each set size. A 3λ–1β–1δ model yielded a consistently ordered set of λ parameters across observers and substantially improved the adjusted R² value over a simple (null) 1λ–1β–1δ model (.932 vs. .189 in the average data, with improvements that ranged from .355 to .750 R² units across the 6 observers).

However, asymptotic differences alone were not sufficient to capture all regularities in the data. Further varying of the dynamics parameters substantially improved the adjusted R² value over the 3λ–1β–1δ model. In the average data and in 4 of the 6 observers, a 3λ–3β–1δ model, in which a separate rate was allotted to each set size, was found to give the best fit to the time-course data. The adjusted R² value for average data was .946, ranging from .684 to .911 across the 4 observers. One observer (YS) was better fit by a model in which the dynamics difference was captured in intercept (a 3λ–1β–3δ model) rather than rate (a 3λ–3β–1δ model; .858 vs. .823). The remaining observer (CC) showed a decrease in adjusted R² value for either a 3λ–3β–1δ model or a 3λ–1β–3δ model when compared with the simpler 3λ–1β–1δ model (.634 or .639 vs. .681). For unknown reasons, however, this observer showed nonmonotonic d′ values across lags for two of the three conditions, and, as a result, all fits were highly unstable.

In the average data, the estimated rate (β) was 11.9, 8.23, and 7.07 for a set size of 4, 10, and 16, respectively (84, 121, and 141 in [β⁻¹] millisecond units). With just one (small) reversal for set sizes of 10 and 16 for 1 observer, the parameters were similarly ordered across the 5 observers with stable data, and an ANOVA on the parameter estimates was significant, F(2, 8) = 24.02, p < .0001. In contrast to feature searches, the time-course data for conjunction searches indicate that set size affects both target discriminability and processing dynamics. The smooth curves in Figure 5B show the best fitting 3λ–3β–1δ model, on the basis of the average parameter estimates in Table 1. The open symbols below the chance level indicate the points in time when the functions reach two thirds of their respective asymptotes. The shift toward longer times with larger set sizes illustrates the disproportionality in processing dynamics induced by set size. Table 1 lists the parameter estimates for the individual observers.

Target-present versus target-absent conditions

The d′ scaling ensures that estimates of detection speed and accuracy are not unduly affected by response biases but does not enable one to directly examine target-present and target-absent trials. To do so, we separately analyzed these trials using proportion-correct data.

For feature searches, there was no evidence to indicate that dynamics (intercept or rate) varied with set size for target-present and target-absent trials, despite the fact that for both types of trials proportion correct at asymptote declined as set size increased (average estimates of .88, .86, and .81 for target-present trials and .89, .82, and .79 for target-absent trials for set sizes of 4, 10, and 16 items, respectively). For conjunction searches, the proportion correct also systematically declined with increasing set sizes for both target-present and target-absent trials (average estimates of .96, .94, and .84 for target-present and .96, .84, and .76 for target-absent trials for set sizes of 4, 10, and 16 items, respectively). However, dynamics differences were clearly evident in both target-present and target-absent trials. Average adjusted R² values increased from .883 to .935 for the target-present conditions and from .882 to .914 for the target-absent conditions for a 3λ–3β–1δ as compared with a 3λ–1β–1δ model. Parameter estimates indicated that the rate of information accrual slowed as set size increased from 4 to 16 items for both types of trials. For set sizes of 4, 10, and 16, the average rates were 8.57, 7.89, and 6.34 for target-present trials and 6.99, 4.68, and 5.34 for target-absent trials, respectively. In the latter case, the ordering is slightly at odds with the target-present and d′ analysis in that a set size of 10 is associated with slower rate than a set size of 16. This pattern in the average data reflects the fact that, for unknown reasons, 2 of 6 observers showed this aberrant ordering.

Discussion

Asymptotic accuracy systematically decreased with larger set sizes in both feature and conjunction searches. Our finding of lower discriminability values for larger set sizes is consistent with claims that increasing the number of elements increases noise in the decision process (Kinchla, 1980; Palmer, 1994, 1995; Pavel, 1990; Sperling & Dosher, 1986). It is also possible that sensory factors gave rise to lower performance with larger set sizes (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, et al., 1998; Geisler & Chou, 1995). However, because we controlled for known confounds, such as eccentricity and the potential for lateral masking, we believe that asymptotic differences within the search tasks were largely determined by decision factors.

Although not significant, F(2, 5) = 3.16, p = .14, asymptotic levels were somewhat higher in conjunction than in feature searches. However, this difference was likely due to the fact that the orientation difference between targets and distractors was less in the feature search (12° vs. 24°). Despite this fact, set size had a greater impact on conjunction searches, F(2, 10) = 7.4, p = .011. This interaction is consistent with the assumption that conjunction searches use more complex stimuli and require a more complex decision process than feature searches (Eckstein, 1998; Pavel, 1990).

The crucial result concerns processing dynamics. Set size had no effect on processing speed (intercept or rate) in feature searches, but SAT rates systematically decreased with larger set sizes in conjunction searches. Additionally, the overall dynamics for conjunction searches were slower than feature searches. Although the (average) rate parameter (β) for feature searches was in the middle of the range of the rate parameters for the conjunction searches (i.e., 8.27 vs. 11.9, 8.23, and 7.07), the intercept (δ) for feature searches was substantially earlier than the intercept for conjunction searches (316 vs. 373 ms). Combining intercept and rate into a composite measure of processing speed (δ + β⁻¹) shows that the (average) processing speed was 432 ms for feature searches as compared with 457, 495, and 513 ms for conjunction searches of 4, 10, and 16 elements, respectively.

The absence of an effect of set size on processing dynamics for feature searches is consistent with claims that features can be detected in parallel without observable capacity limits. In contrast, the systematic effect of set size on conjunction search dynamics indicates that detecting a conjunction imposes a limit on processing that is not typically observed in simple feature detection. The crucial question concerns whether this dynamics effect is due to a serial process, as proposed in models such as FIT and GSM.

Fits of the serial assumption

A serial mechanism for conjunction searches does predict a slowing of SAT dynamics (Figure 2). However, comparison of Figure 2 and the empirical data in Figure 5B suggests that the magnitude of the dynamics differences predicted by a serial-processing component exceeds the range of observed differences. We formalized this impression by fitting to the average data the serial search model outlined in the introduction.

Asymptotic accuracy levels for each of the three set sizes were first fixed by setting them to the empirical d′ values at the two longest SAT lags (0.9 and 2 s). The d′ values as a function of processing time were fit by combining mixtures of the cumulative gamma function (Equation 1) in a manner that reflected the implicit number of comparison processes in both target-present and target-absent trials in each of the set-size conditions (see the introduction). The least square fitting procedure was used to estimate the values of the (mean) comparison rate and the intercept (β and δ in Equation 1) so as to best accommodate the observed dynamics differences across set sizes of 4 to 16.

Fits of this model to the time-course data clearly demonstrated that observed dynamics differences are not compatible with a serial-processing assumption. The serial model vastly overpredicted the spread in the functions at all points below the asymptote. We modified the serial model in several ways but still found that a serial process could not adequately fit the data. For example, initially we assumed that the nominal set size equaled the de facto set size of the search process.⁵ As an alternative, we used the observed asymptotic hit and false-alarm rates for target-present and target-absent trials as an estimate of the number of elements in the search set, under the (questionable) assumption that errors in performance reflect the unavailability of elements in the observers’ visual representation of the display. This effectively reduced the differences in the number of comparisons across set sizes of 4 to 16 because error rates were higher for larger set sizes. Additionally, the comparison rates were allowed to vary between matches (hits) and mismatches (correct rejections) because the exhaustive processing rule on target-absent trials was largely contributing to the misfits of the rise portions of the functions. With these enhancements, the fit to the data was better but was far from adequate.

Figure 6 shows fits of the modified serial model. (Dashed lines show the exponential model fits as a point of comparison.) As is readily apparent from examination of the early portions of the function (times less than 1 s), the serial model grossly overpredicts the range of the dynamics differences. The model overestimates performance when set size was 4, rising 200–300 ms earlier than the data, and vastly underestimates performance when set size was 16, missing all but the last data point. This is an intrinsic failure of a serial-processing assumption, which is not linked to the particulars of our modeling assumptions. Whereas one could certainly adopt other distributions to model a serial process, plausible distributions will, we believe, fail in exactly the same manner as the gamma. The failure of the model is not due to the fact that the exponential processes rise too slowly or too quickly—rate of rise is a free parameter—but rather it is due to the core assumption that individual comparisons are sequentially ordered. Mathematically, that assumption requires that overall performance is determined by convolving the finishing-time distributions for each comparison process. The inability of a serial model to capture the observed range of differences is due to the convolution requirement and not to the particulars of the comparison distribution.

Figure 6.

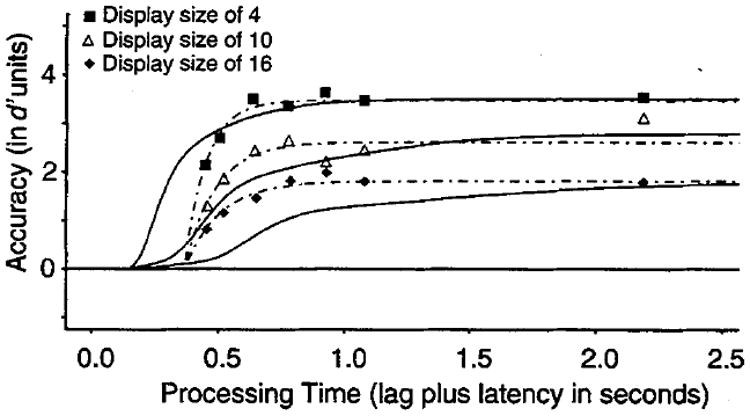
Best fitting serial self-terminating model (smooth functions) of the average speed–accuracy trade-off (SAT) data for conjunction searches under the fixed-viewing conditions (150-ms stimulus duration) of Experiment 2. Dashed lines show the best fitting exponential model on the basis of the parameters listed in Table 1.

Additionally, one may wonder whether grouping prior to serial processing improves the quality of fit. For example, in revised versions of FIT, groups of items rather than single items are able to serve as the comparison unit in a serial search (Treisman, 1991, 1993; Treisman & Gormican, 1988; see also Duncan & Humphreys, 1989). The fundamental problem with the serial model is, however, the tendency to overpredict the range of dynamics differences across set sizes of 4 to 16. Pooling regions of the display into a single comparison group simply scales the overall number of comparisons across the three set sizes and does not appreciably improve the quality of fit.

Similarly, an appeal to an initial stage of parallel preprocessing, as proposed in GSM, will not salvage a serial-processing assumption. To accommodate approximately linearly increasing RT functions (e.g., Experiment 1), GSM must assume that the number of elements receiving activation sufficient to attract a serial search is proportional to the number of elements in the array. This assumption simply functions like a grouping principle; it reduces the absolute number of items in the serial search sets but has no effect on the inability of the model to capture the range of observed dynamics differences. To attenuate the range of predicted differences, the proportion of items activated must differentially decrease with larger set sizes. However, that assumption is theoretically unmotivated, as our conjunction search conditions provide no basis on which the parallel process could differentially segment smaller versus larger displays. Moreover, such an assumption would be incompatible with the observed RT data and with the SAT asymptotic profiles. If fewer items are activated with larger set sizes, then mean RT, RT error rates, and SAT asymptotes for conjunction searches should all show a nonlinear, negatively accelerating trend with increasing set size. If there is any suggestion of a departure from linearity in all three types of data, it is in exactly the opposite direction. GSM, like FIT, cannot accommodate the time-course profiles.

Finally, we note that an attentionally controlled task may become automatic with practice. One view of automaticity argues that a serial process is replaced by a parallel process with extensive practice (Schneider & Shiffrin, 1977). Accordingly, the failure of the serial model could stem from the fact that our conjunction search data represent a mixture of these two types of processes. We empirically addressed this issue by a split-half analysis. Two average data sets were constructed by averaging d′ scores across observers from the first and second sessions of the fixed-viewing conjunction searches. The range of dynamics differences across set size should be larger in the first half if practice modified the search.

Figure 7 presents the observed d′ performance for the first (Figure 7A) and second (Figure 7B) halves, along with the best fitting exponential functions. The model fits yielded clear evidence that practice improved search performance. Observers were more accurate during the second than the first half, evidenced by higher asymptotic d′ levels (3.6 vs. 3.5, 2.9 vs. 2.7, and 2.2 vs. 1.8 for set sizes of 4, 10, and 16 items, respectively), and the estimates of search speed (rate parameters) were faster for the second as compared with the first half (8.1 vs. 6.0, 6.0 vs. 4.8, and 4.7 vs. 3.8 for set sizes of 4, 10, and 16 items, respectively). Crucially, however, the range of differences across the three set sizes were nearly identical, namely, 91 versus 94 in (β⁻¹) millisecond units. There is, consequently, no support for the notion that the conjunction search data represent a mixture of two search operations or that practice modified the nature of the search operation.

Figure 7.

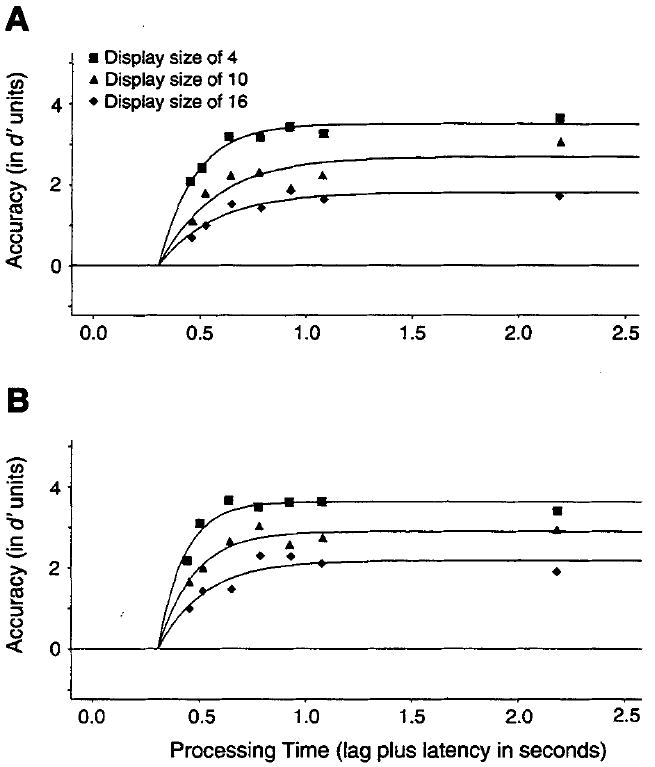
Average d′ accuracy (symbols) as a function of processing time (lag of the response cue plus latency to respond to the cue) for different set sizes for the first (Figure 7A) and second (Figure 7B) sessions of the conjunction searches under the fixed-viewing conditions (150-ms stimulus duration) of Experiment 2. Smooth curves show the best fits of Equation 3.

The inability of a serial model to accommodate the SAT data accords with the fact that not all properties of the RT data were fully consistent with a serial interpretation. We found in Experiment 1 that the RT slope as a function of set size was lower than what is expected from a serial search. The Appendix shows that whereas some properties of the RT distributions were consistent with a serial model of conjunction searches, others were not. In particular, the pattern of RT variance for target-present and target-absent trials predicted by a serial self-terminating model was not found (see also Ward & McClelland, 1989).

Parallel models

The proportional dynamics observed in feature searches are compatible with an unlimited-capacity parallel search model (e.g., Palmer, 1994; Palmer et al., 1993; see McElree & Dosher, 1989). However, we believe that although this type of model is consistent with the feature search data, an unlimited-capacity parallel model cannot fully accommodate the dynamics differences observed in conjunction searches.

The core property of an unlimited-capacity parallel model is that any number of comparisons can be performed concurrently without decrements in processing speed for the individual comparisons. This property is what enables such a model to be compatible with proportional dynamics. Nevertheless, dynamics differences can arise from decision factors. In particular, dynamics differences can result from an increased tendency to false alarm early in processing as the number of distractors increases (McElree & Dosher, 1989; Ratcliff, 1978). For an illustration of this principle, consider Ratcliff’s (1978) diffusion (random-walk) model. The general framework assumes that a positive response occurs when one of the comparisons yields a match (a self-terminating rule) and that a negative response occurs when all comparisons yield a mismatch (an exhaustive rule). For modeling RT data, matches and mismatches occur when a comparison process (the walk) that starts at position z exceeds either a positive or a negative evidence boundary, respectively. In modeling SAT data, the boundaries are set to infinity, and a positive response is selected if, at the time of the SAT response signal, at least one of the comparisons is greater than z (i.e., has moved toward the positive evidence boundary); otherwise, a “no” response is selected (Ratcliff, 1978). With a larger number of distractors, there is a greater probability that one of the comparisons will stray into the positive response region, thereby leading to a false alarm. The effect is largest at early times when little evidence has accumulated (i.e., the walks are close to the starting value z), and this introduces disproportional growth rates across different set sizes (McElree & Dosher, 1989).

Note, however, such a model predicts that dynamics will slow for target-absent trials only. For target-present trials, the increased tendency of comparison processes associated with distractors to stray into the positive response region will increase, rather than decrease, the probability of a hit. Thus, if set size is predicted to have any effect on target-present trials, it would be to increase growth rate as the number of distractors increases.⁶ Crucially, dynamics slow as set size increases in both target-present and target-absent trials in our data. This pattern suggests that the dynamics differences are not simply due to decision factors in an unlimited-capacity parallel model. Our data indicate that the number of concurrent comparisons affects the speed of processing of both targets and distractors.

These data are more consistent with capacity-limited parallel search models, in which the rate of informational accrual is determined by the number of concurrent comparisons (e.g., Murdock, 1971; Shaw & Shaw, 1977; Townsend & Ashby, 1983). According to this type of model, the decrement in SAT rate reflects a slowing of search speed as a fixed (processing) capacity is spread more diffusely over the items in the array. The exponential model fits of the proportion correct data give expression to this type of model, in that the exponential dynamics parameters (intercept, δ, and rate, β, in Equation 2) can be interpreted as the distribution of finishing times to complete the search process. Under this construal, fits of the target-present and target-absent conditions provide direct estimates of how the rates of individual comparisons decrease with the number of concurrent comparisons.

It is possible that other formulations of a parallel model may also prove to be compatible with the data. Humphreys and Müller (1993) have proposed a parallel model that produces linear RT functions for conjunction targets among heterogeneous distractors (an inverted T among upright Ts) but flat RT functions for conjunctions among homogeneous distractors (an inverted T among right- or left-oriented Ts). Linear functions are produced by a recursive rejection rule in which distractors are grouped (by excitatory connections between similar stimuli) and in which the group with the highest activation level is rejected on each iteration of the model. Flat functions are produced in homogeneous arrays because distractors in all set sizes are grouped into a single group and rejected en masse. It is difficult to definitively state whether this model is compatible with our data without first extending the architecture to feature detection and to the conjunction dimensions examined here (color and orientation) and, crucially, developing a set of decision rules to simulate time-course predictions.⁷ Without these developments, one cannot be certain that the model can accommodate the data that suggest a capacity-limited parallel search.

Relation to RT data

The Appendix presents an analyses of the shape of the RT distributions derived from Experiment 1. The primary purpose of this analysis was to further test predictions of a serial model. However, the results of this analysis provide strong convergent evidence for the SAT results.

For feature searches, the only change in the RT distributions was that the positive skew, or rightward tail, of the distributions increased with larger set sizes. In conjunction searches, however, set size also engendered shifts in the leading edge and mode of the RT distributions. As Ratcliff and Murdock (1976) noted, a change in skew suggests that only a few trials or items are affected by the manipulation. This type of effect is consistent with the notion that set size affects the discriminability of a proportion of elements in the array. Shifts in the leading edge, in contrast, indicate that set size slows the processing of all elements in the array.

When comparing SAT functions, we found that set size affected dynamics (the measure of processing speed) in conjunction searches only. Other explicit comparisons of SAT functions and the shapes of the RT distributions have shown a similar linkage between SAT dynamics (rate or intercept) and shifts in the RT distribution. For example, in a memory search paradigm, McElree and Dosher (1993) and McElree (1998) found that conditions that produce SAT dynamics differences also produced concomitant shifts in the leading edge and mode of the respective RT distributions. B. A. Dosher (personal communication, 1989) found that visually embedding test items in (masking) characters induced a slowing of the SAT rate parameter that was also mirrored by changes in the leading edge and mode of the RT distribution.

Conversely, experimental factors that affect only the asymptote of the SAT function (nontemporal aspects of processing) do not shift the leading edge and mode of the RT distributions but rather simply increase the positive skew, or rightward tail, of the RT distribution. In a memory scanning paradigm, McElree and Dosher (1989) found that set size affected asymptotic accuracy rather than inducing changes in the retrieval dynamics. Hockley (1984) and Hockley and Corballis (1982) found that the size of the memory set affected only the skew of distribution, with larger set sizes shifting the tail toward longer times.

This correspondence between SAT results and the analysis of the shape of an RT distribution is impressive, because there are several differences between the tasks that could undermine a direct relationship. Decision processes in an RT task are more complex than those for an SAT task. In a random-walk model, as we have noted, RT tasks require setting an upper and lower boundary on the random walk to establish response criteria, whereas responses in an SAT task are simply determined by the position of the walks at the experimenter-controlled response time. One behavioral consequence of this difference is that the shape of an RT distribution may be strongly dependent on the particular speed–accuracy criterion used in the RT task (Luce, 1986; see McElree & Dosher, 1993; and Ratcliff, 1978, for specific illustrations). From a modeling perspective, factors that control one of the SAT parameters may induce changes in all three parameters of the RT distribution. In the random-walk model, changes in the resonance parameter (discriminability in a search task) affect the asymptote of the SAT function. Although this parameter strongly impacts the tail of the RT distribution, large differences in resonance also induce small changes in the leading edge and mode of the distribution (Ratcliff, 1978). Given these facts, a tight coupling of results across the two tasks may not always be observed.

General Discussion

Although the effects of set size on mean RT have been central to theorizing about the interaction of attention and visual processing, there has been little consensus on how these effects should be interpreted. Three classes of models have been proposed to account for set-size effects. Models such as FIT (Treisman, 1991, 1993; Treisman & Gelade, 1980; Treisman & Gormican, 1988) and GSM (Cave & Wolfe, 1990; Wolfe, 1994, 1996; Wolfe et al., 1989) contend that these effects reflect differences in processing speed that arise from the necessity of serially deploying covert attention to particular locations in the visual representation. Another class of models shares the assumption that set-size effects reflect underlying differences in processing speed but contends that multielement displays can be processed in parallel (e.g., Shaw & Shaw, 1977; Townsend & Ashby, 1983). Set-size effects are thought to arise from capacity limits on parallel processing. A third class of models differs from the first two in suggesting that set size affects the discriminability of elements in the array rather than processing speed per se. Larger set sizes reduce discriminability by lowering sensory quality or increasing noise in the decision process (e.g., Carrasco et al., 1995; Carrasco & Frieder, 1997; Kinchla, 1992; Kinchla et al., 1995; Palmer, 1994; Palmer et al., 1993; Pavel, 1990; Shaw, 1982).

As discussed earlier, RT data are of limited value in discriminating between these alternatives because RT can vary with either differences in discriminability, differences in processing speed, or unknown mixtures of the two effects. The SAT procedure provides a means of deriving separate estimates of discriminability (accuracy) and processing speed. Two important results emerged from the application of the SAT procedure to the visual search paradigm.

Discriminability

The SAT data reported in Experiment 2 clearly demonstrated that set size does indeed affect the discriminability of targets in both feature and conjunction searches. We found that asymptotic detection accuracy systematically decreased with larger set sizes for both feature and conjunction searches. These systematic differences in accuracy follow from confusability accounts (e.g., Kinchla, 1974, 1992; Palmer, 1994; Palmer et al., 1993; Sperling & Dosher, 1986). If there is noise in each comparison process, increasing the number of elements in the search will increase the probability of an error in the decision process. Asymptotic differences may also result from sensory rather than decision factors (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, et al., 1998; Geisler & Chou, 1995; Verghese & Nakayama, 1994). However, we suspect that sensory factors contributed little to the discriminability effects reported here as we attempted to minimize factors that are often confounded with set size (eccentricity and lateral masking).

Signal-detection theory gives expression to confusability accounts. Following the research of Green and Swets (1966), Kinchla (1974, 1992; see also Palmer, 1994, 1995; Pavel, 1990) noted, that discriminability is expected to decrease as the square root of n, the number of elements in the set:

$$d^{\prime }=1/{(n{\sigma }^2)}^{1/2}.$$ (4)

In Equation 4, the internal representation of each element in the set is assumed to be Gaussian distributed with variance σ², centered on 1 if it is a target and 0 otherwise. Fits of this model to the asymptotic d′ values from Experiment 2 are shown in Figure 8. The model fits the average data well, yielding an R² value of .945 for feature searches and .837 for conjunction searches with variance terms of 0.1697 and 0.1335, respectively. The larger variance for feature as compared with conjunction searches is consistent with the fact that the orientation differences were less in the former (12° vs. 24°). The model expressed in Equation 4 undoubtedly represents a simplification of complexities of the decision processes in search, most notably, for conjunction searches, in which the decision process must be responsive to the multidimensional nature of the stimuli. Nevertheless, the model serves to illustrate that decision factors alone predict differences in discriminability. The observed differences in asymptote reinforce the formal argument that RT data cannot be used to unambiguously measure processing time.

Figure 8.

Fits (dashed lines and filled symbols) of a simple signal-detection model (Equation 4) to the asymptotic discrimination level (solid lines and open symbols) observed in Experiment 2.

Search Speed

Whereas the asymptotic patterns demonstrate that discriminability is a key factor in explaining search performance, the time-course profiles indicate that confusability alone does not provide a sufficient explanation of intrinsic differences between feature and conjunction searches. For feature searches, SAT dynamics were proportional (equal intercepts and rate) across set size. For conjunction searches, in contrast, set size engendered disproportional dynamics (rate slowing). This result indicates that detecting a conjunction of features is capacity limited.

The application of an explicit serial model to the time-course data indicates that the observed dynamics differences were not of a form that would support the claim that detecting a conjunction of simple visual features requires serial processing. These fits indicate that arguments that attention must be directed to one location at a time in order to detect the co-occurrence of two features are incorrect (e.g., Treisman & Gelade, 1980; Treisman & Gormican, 1988; Treisman & Sato, 1990; Wolfe, 1994; Wolfe et al., 1989). The range of dynamics differences indicates that several items can be processed concurrently or in parallel. The form of the dynamics differences is consistent with claims that the rate of information accrual for individual comparisons is inversely related to the number of concurrent comparisons (e.g., Shaw & Shaw, 1977; Townsend & Ashby, 1983). Although decision factors can engender disproportional dynamics, the systematic effect of set size on dynamics for both target-present and target-absent trials suggests that the number of concurrent comparisons affects the speed of processing of both target and distractors, as predicted by capacity-limited parallel models.

Features and Conjunctions: The Role of Attention

The SAT time-course profiles mirror the dichotomy between feature and conjunction searches often observed in RT data. Hence, our data require one to draw a distinction between feature and conjunction searches, at least at an empirical level. An often cited difference between feature and conjunction searches is that distractors are typically more heterogenous in the latter (Duncan & Humphreys, 1989). In our experiments, for example, distractors consisted of blue tilted lines in feature searches and blue tilted and red vertical lines in conjunction searches. Because distractor heterogeneity can affect the form of the RT function (e.g., Duncan & Humphreys, 1989; Humphreys & Müller, 1993), a reasonable hypothesis is that the more heterogenous distractors in conjunction searches induced differences in dynamics.

However, that hypothesis is not supported by a recent finding. Dosher, Han, and Lu (1998) contrasted the impact of homogeneous and heterogenous distractors on SAT time-course profiles for feature searches (line orientation). Homogeneous distractors were associated with faster rates than were heterogenous distractors, but, like our feature searches, proportional dynamics were observed across set size for both types of distractors. Because distractor heterogeneity does not appear to engender dynamics differences across set size, it is unlikely that this factor was responsible for the differences we found in feature and conjunction searches.

Similar to the notions presented in FIT and GSM, we believe that the primary difference between tasks rests crucially with the processing demands required to monitor a conjunction of features rather than a single feature. In contrast to the notions presented in FIT and GSM, however, we do not believe that this requires positing a sharp dichotomy between preattentive and attentive processes. Although the SAT data could motivate an amended version of this distinction—one in which attentive processing was not equated with serial processing—we note that our failure to observe systematic effects of set size on feature detection dynamics may reflect limits on the temporal resolution of the SAT task or reflect that the processing demands across the range of set sizes tested here did not sufficiently tax the limits of feature detection.

The view that feature and conjunction searches lie on a continuum has received support from at least two lines of research. Carrasco and Yeshurun (1998) found that an explicit attentional manipulation, namely, precuing target locations, lowered mean RT and error rates for both feature and conjunction searches and did not eliminate the set-size effect. Similar results have been reported for other types of feature discriminations (Cheal & Lyon, 1992) for texture segmentation tasks (Yeshurun & Carrasco, 1998), and for acuity tasks (Yeshurun & Carrasco, 1999). An account that argues that features are detected preattentively does not provide a ready explanation for why restricting attention to a limited region of the display should improve performance.

Joseph, Chun, and Nakayama (1997) reported that feature detection (an oddly oriented Gabor patch) was hampered by a concurrent task (detecting a white letter in a stream of dark letters). Dual-task paradigms are complex, and it is difficult to isolate the source of an observed processing deficit (see Pashler, 1998; Sperling & Dosher, 1986). Nevertheless, the decrements in feature detection under conditions of high processing demands induced by a secondary task are consistent with the contention that feature detection, like the detection of a conjunction of features, requires attentional resources.

Neither the Carrasco and Yeshurun (1998) nor the Joseph et al. (1997) studies provided direct evidence of the type of capacity limitation that was documented here. Our results indicate that the key distinction between feature and conjunction searches is whether set size affects processing speed. The enhancement in performance reported in Carrasco and Yeshurun and the decrement in performance reported by Joseph et al. may reflect different levels of discriminability induced by the respective manipulations rather than changes in processing dynamics.⁸ Showing direct evidence for a continuum requires demonstrating that attentional manipulations affect the dynamics of feature detection. For example, with reference to the Joseph et al. study, evidence for the role of attention in feature detection would take the form of a demonstration that high processing loads induced a slowing of dynamics with larger set size. We, like the authors of these studies, question a sharp dichotomy that assumes the existence of a separate, privileged category of preattentive processing. However, we stress that compelling evidence for this case requires procedures that separately assess processing accuracy and processing speed.

Finally, whereas our data support a parallel model of both feature and conjunction searches, we do not assume that all types of visual discriminations can be accomplished in parallel. We suspect that processing demands at some point could exceed the limits of parallel processing. Our data indicate that models such as FIT and GSM have incorrectly drawn the boundary between serial and parallel processing. In our view it remains to be determined at what point processing demands force a serial mode of operation. The visual search paradigm seems well suited to addressing these types of issues, but only when coupled with more rigorous experimental and modeling techniques.

Appendix

RT Distributions

We examined the shapes of the RT distributions for feature and conjunction searches in both fixed- and free-viewing conditions to further assess the evidence for serial processing and to further explore differences between the two viewing conditions.

Stemberg (1973, 1975) pointed out that higher moments of the RT data can provide additional and potentially stronger evidence for a serial mechanism than can (mean) slope estimates. A crucial prediction of a serial self-terminating search is that the minima of the (correct) RT distributions remain invariant across set size (Sternberg, 1973; see also Townsend & Ashby, 1983). This invariance results from the fact that there is some probability in all set sizes that the first comparison will produce a match. A serial exhaustive processing mechanism, however, predicts that the minimum RT will shift toward longer times with larger set sizes. This results from the fact that a response is executed only after the final comparison and, consequently, the minimum of the finishing time distribution is determined by the size of the search set. For conjunction searches, models such as FIT and GSM assume a self-terminating rule for target-present trials and an exhaustive processing rule for target-absent trials. Hence, these models predict invariance and shifting of the leading edge of the RT distribution for target-present and target-absent trials (respectively).

Parallel models are more flexible with respect to the shape of the RT distribution. For example, Ratcliff’s (1978) exposition of a diffusion, or continuous random-walk, model of RTs demonstrated that invariance of the leading edge of the RT distributions for various set sizes can be a property of a fully parallel model. However, shifts in the leading edge can result from large differences in the resonance parameter of the diffusion model, namely, the parameter that reflects the discriminability of the target. It is important to point out, then, that these RT distributional properties provide a strong test of a serial model but do not provide unequivocal evidence.

Forty RT distributions were constructed for each of the 6 observers; 1 for each of the target-present and target-absent trials in each of the five set sizes (4, 7, 10, 13, and 16 elements) for both feature and conjunction searches under both the fixed- and the free-viewing conditions. Each of the 240 distributions were constructed by defining 15 equal-probability bins and adjusting the (time) width of the respective bins. This procedure yields more stable estimates than does the alternative method of defining equal (time) intervals and calculating response frequency within each interval (see Ratcliff, 1979). Group (average) distributions were constructed by vincentized averaging over the observers (Ratcliff, 1979).

Although several functions have been proposed for RT distributions (see Luce, 1986), we used an Ex-Gaussian function, proposed by Ratcliff and Murdock (1976), because it has been found to provide a precise summary of the shape of RT distributions from several RT tasks (e.g., Hockley, 1984; Hockley & Corballis, 1982; McElree, 1998; McElree & Dosher, 1993; Ratcliff, 1978; Ratcliff & Murdock, 1976):

$$f(t)=\frac{e^{-[(t-\mathrm{\mu }/\tau )]+{\mathrm{\sigma }}^2/{\mathrm{\tau }}^2}}{\mathrm{\tau }\sqrt{(2\mathrm{\pi })}}{\int }_{-\infty }^{[(t-\mathrm{\mu })/\mathrm{\sigma }]-\mathrm{\sigma }/\mathrm{\tau }}{e}^{-y^2/2}\mathit{dy}.$$ (A1)

Equation A1 is the convolution of a Gaussian and an exponential distribution. The two parameters of the Gaussian, namely the mean μ and the variance σ², describe the leading edge and mode of the RT distribution. These parameters provide the important summary statistics for evaluating serial models. The parameter τ of the exponential distribution describes the rightward tail or skew of the distribution.

The distributions from all observers were individually fit, but we restrict our discussion to the general patterns evident in the group distributions. (See Ratcliff, 1979, for a demonstration that the vincentizing method ensures that properties of the individual distributions are not distorted in group distributions.) Figure A1 presents the estimates for three Ex-Gaussian parameters for feature (squares) and conjunction (triangles) searches under fixed-viewing (filled symbols) and free-viewing (open symbols) conditions.

Fixed-Viewing Distributions

The consensus that feature searches are mediated by a parallel mechanism was supported by the lack of an effect of set size on the leading edge or mode of the distributions (μ and σ parameters) for both target-present and target-absent trials. The distributions for target-absent trials were shifted toward longer times than were the corresponding distributions for target-present trials, evidenced by larger μ values (415, 415, 422, 420, and 421 ms as compared with 381, 387, 386, 383, and 387 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively) and correspondingly larger σ values (34, 32, 25, 27, and 27 ms as compared with 26, 27, 22, 18, and 21 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively). However, both parameters were fairly stable across set size. The only change that set size induced was a small (and not completely consistent) increase in the skew or rightward tails of the distribution, reflected in the τ parameter (50, 48, 55, 69, and 78 ms in target-present trials and 55, 55, 65, 77, and 59 ms in target-absent trials for set sizes of 4, 7, 10, 13, and 16 items, respectively). Changes in the skew of a distribution reflect the fact that only a proportion of the trials were affected by set size and that they are consistent with changes in discriminability (cf. Experiment 2 of present study; McElree & Dosher, 1989, 1993; Ratcliff, 1978; Ratcliff & Murdock, 1976).

For conjunction searches, as with feature searches, the distributions for target-absent trials were shifted toward longer times than the corresponding distributions for target-present trials, as evidenced by larger μ values (476, 484, 516, 532, and 533 ms as compared with 451, 457, 464, 463, and 460 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively) and slightly larger σ values (35, 40, 39, 42, and 56 ms as compared with 39, 43, 35, 45, and 38 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively). However, there was a distinct shift in the leading edge and mode with increasing set size for target-absent trials: μ increased by 57 ms and σ by 21 ms from the set size of 4 to the set size of 16. For target-present trials there was at best only a slight trend in the comparable parameters: μ differed at most by 13 ms and σ by 6 ms across set sizes of 4–16. As with feature searches, the skew of the distribution tended to increase with set size (44, 60, 67, 62, and 85 ms in target-present trials and 49, 70, 60, 68, and 74 ms in target-absent trials for set sizes of 4, 7, 10, 13, and 16 items, respectively).

Figure A1.

Estimated mu, sigma, and tau parameters from fits of the Ex-Gaussian model to the average (vincentized) reaction-time distributions for feature and conjunction searches under fixed- and free-viewing conditions.

This pattern approximates what is expected from a serial search mechanism with a self-terminating rule on target-present trials and an exhaustive rule on target-absent trials. However, we note that other properties of the distributions are not fully compatible with a serial interpretation. A serial self-terminating model also predicts that RT variability should increase more for target-present than target-absent trials as a function of set size (Schneider & Shiffrin, 1977; Sternberg, 1975). Our results showed the opposite pattern; RT variability increased more for the target-absent than the target-present trials. (This property is self-evident in the parameter estimates in Figure A1. The changes in τ are comparable across both types of trials, but μ and σ substantially shift for target-absent trials, thereby reducing the overall variance relative to target-present trials.)

Free-Viewing Distributions

The open symbols in Figure A1 show the free-viewing conditions. For feature searches, as with the fixed-viewing condition, the distributions for target-absent trials were shifted toward longer times than the corresponding distributions for target-present trials, evidenced by the larger μ values (454, 475, 558, 573, and 620 ms as compared with 412, 415, 428, 441, and 439 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively) and somewhat larger σ values (33, 39, 65, 92, and 77 ms as compared with 46, 39, 46, 49, and 45 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively). Unlike the fixed-viewing condition, however, there was a substantial shift in μ and σ as set size increased for target-absent trials. This shift was large, with μ ranging from 454 to 620 ms and σ ranging from 33 to 77 ms. In fact, the magnitude of the shift far exceeded what was observed in conjunction searches in the fixed-viewing condition. For target-present trials, σ was fairly constant, whereas μ ranged from 412 to 439 ms as set size increased from 4 to 16 items. As with the fixed-viewing condition, the skew of the distribution tended to increase with set size (39, 56, 56, 56, and 83 ms in target-present trials and 71, 66, 67, 80, and 114 ms in target-absent trials for set sizes of 4, 7, 10, 13, and 16 items, respectively).

Because there was no effect of set size on the leading edge or mode for either target-absent or target-present trials under free-viewing conditions, we believe that this shift in the RT distributions reflects a (serial) search strategy that involved eye movements. One interpretation of this pattern is that observers delayed in responding “no” in target-absent trials on a proportion of trials until they fixated on another region of the display. The difference in minima across set sizes of 4 to 16 would have enabled observers to make an additional eye movement after the onset of the display.

For conjunction searches, the distributions for target-absent trials were again shifted toward longer times than the corresponding distributions for target-present trials, with larger μ values (498, 565, 629, 721, and 759 ms as compared with 443, 484, 499, 508, and 512 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively) and larger σ values (54, 72, 71, 96, and 129 ms as compared with 41, 61, 83, 58, and 99 ms for set sizes of 4, 7, 10, 13, and 16 items, respectively). For conjunction searches, set size also had a large effect on the leading edge and mode of distributions in both target-present and target-absent trials: μ ranged from 443 to 512 ms and σ ranged from 41 to 99 ms for target-present trials, whereas μ ranged from 498 to 759 ms and σ ranged from 54 to 129 ms for target-absent trials. The skew of the distribution also tended to increase with set size (44, 57, 54, 71, and 72 ms in target-present trials and 33, 59, 71, 68, and 131 ms in target-absent trials for set sizes of 4, 7, 10, 13, and 16 items, respectively). The larger impact of set size across all three parameters in the free- as compared with fixed-viewing conjunction searches is likewise consistent with the notion that observers delayed responding on a proportion of trials until they were able to fixate on another region of the screen. For target-absent trials, the minima of the RT distributions shifted substantially, extending over 250 ms from small (4) to large (16) set sizes. These large changes in minima are certainly within the range that plausibly implicates eye movements.

The potential for eye movements is not the only difference between the fixed- and free-viewing conditions. Another salient difference is that a fixed-viewing condition imposes a limit on information availability. Although research on iconic memory (e.g., Gegenfurtner & Sperling, 1993; Sperling, 1960) indicates that information availability is not simply restricted to the physical stimulus duration (e.g., 150 ms), the fast decaying properties of visual representations suggest that less information would be available in our fixed-viewing conditions than in our free-viewing conditions (Carrasco et al., 1995; Carrasco, McLean, et al., 1998; Klein & Farrell, 1989). Indeed, performance was less accurate for fixed- versus free-viewing conditions in the RT task and in the SAT task reported in Experiment 2. It seems unlikely, however, that a principled explanation for the shapes of the RT distribution for the fixed- versus free-viewing conditions can be formulated in terms of differences in information availability alone. Note first that these differences in the shape of the RT distributions concern correct trials only. Moreover, one would expect that lower levels of information availability would slow rather than speed RTs. We believe, therefore, that the differences between fixed- and free-viewing conditions reflect strategic differences in processing and that these differences are most plausibly related to the potential for overt eye movements in the latter case. To the degree that researchers are interested in characterizing properties of covert attentional shifts, these data indicate that short display durations provide a more veridical means of examining the role of covert attention.