Integrin Clustering in Two and Three Dimensions

Abstract

Integrins are transmembrane proteins that allow cells to bind to their external environment. They are the primary regulators of cell-matrix interactions, with direct roles in cell motility and signaling, which in turn regulate numerous physiological processes. Under common experimental conditions, integrins tend to cluster for sturdy and effective binding to extra-cellular matrix molecules. These clusters often evolve into focal adhesions, which regulate downstream signaling. However, integrin clusters are more pronounced and have longer lifetimes in two-dimensional assays than in more realistic three-dimensional environments. While a number of models and theoretical approaches have focused on integrin binding and diffusion, the reasons for the differences between two- and three-dimensional clustering have remained elusive. In this study, we model an individual cluster attached to a two-dimensional collagen film and attached to collagen fibers of various sizes in three-dimensional matrices. We then discuss how our results explain differences in size and lifetime, and how they hint at reasons for other differences between the two environments. Further, we make predictions regarding the stability of clusters based on different overall intracellular conditions. Our results show good agreement with experiments and provide a quantitative basis for understanding how matrix dimensionality and structure regulate integrin behavior in environments that mimic in vivo conditions.

Introduction

Integrins are transmembrane proteins vital to cell-substrate adhesion.^1,2 They are the primary molecules that directly attach the cell membrane to the extracellular matrix or other substrate, and as such they have been intently studied for decades. Additionally, they are involved in cell signaling, and both directly and indirectly in cell motility. Integrins are important to differentiation of cells, apoptosis, and cancer at multiple stages including metastasis. It is certain that their behavior is dependent on mechanical forces, clustering, and a long list of cellular signals.

Functional integrin units are actually protein heterodimers, with subunits α and β.¹ Each subunit has a structure that, as with all transmembrane proteins, contains hydrophilic domains (for the intracellular and extracellular regions of the protein) and at least one hydrophobic domain between them (for interaction with the membrane). In the extracellular portion of the integrin is a structure which attaches preferentially to certain other proteins with a particular polypeptide sequence.³ In many of the most-studied integrins, this sequence is RGD.

The primary source of these RGD sequences available to an integrin in vivo is the extracellular matrix, a three-dimensional scaffolding based in many cases on collagen fibers. Collagen fibers range in size from tens of nanometers to microns in diameter (see, e.g.,^4,5). While in recent years three-dimensional matrices have been used in vitro, experiments have traditionally been done on flat plates, often covered in collagen film. From a chemical perspective, this film is almost exactly the same as the fiber, but it has distinct effects on cells.^6,7

On two-dimensional substrates, integrins often gather in very large clusters known as focal adhesions. These are defined to be clusters larger than 1 μm in diameter, with certain signaling effects and associated intracellular processes.^8,9 Focal adhesions are generally chemically and physically attached inside the cell to actin stress fibers, though that attachment is indirect through a number of non-integrin proteins. These actin stress fibers are part of the cytoskeleton that provide the cell with both force-inducing and force-sensing capabilities.

In the three-dimensional matrix, though, these features are generally not seen. Integrin clusters in three dimensions have smaller size (often hundreds of nm), shorter lifetimes (sometimes minutes or less), and sparser if any connections to actin stress fibers.^6,10–12 (These are not necessarily universal traits, but the collection of traits has been observed in multiple cell lines and cell types,¹² most notably the favorite object of adhesion study, the fibroblast.) They also have a more varied chemical composition in at least some situations.⁶ Such differences are known to have effects on overall cell adhesion and motility. It is reasonable that they may additionally have significant effects on cell division and differentiation, though many other complicating factors exist for these processes.

The distinction in integrin clustering behavior between the two environments has vexed researchers since they were first noticed, as the chemical compositions of a two-dimensional substrate and a three-dimensional matrix can be made identical through chemical or physical means. A large number of studies have examined those differences and attempted to account for them. We suggest here an explanation for the differences in the size and other aspects of three-dimensional adhesions. For verification, we perform a few calculations which are related to our suggestion.

Collagen fibers are thin when compared to animal cell length. This gives the cell environment in a three-dimensional matrix a complicated geometry. To a point, the cell is likely to conform to the local available space’s geometry, but it will not do so as a bag of water would; even without stress fibers, the cell’s shape is somewhat maintained by its cortical cytoskeleton. This is important because viable integrin-mediated contact between membrane and collagen requires that the part of the membrane occupied by the integrin is no farther from the collagen than the maximum height of the integrin’s extracellular domain. A collagen fiber curving away from a cell membrane can only be expected to have a limited amount of contact with the cell, as pictured in Figure 1. We note that this picture is an oversimplification; the membrane is expected to curve somewhat. However, as we explain later, this effect should if anything increase the effects of fiber radius on cluster size.

Figure 1.

Collagen fiber (gray and curved) in contact with cell membrane (blue). Though the fiber is in contact with the cell where they are close, the shape of the fiber makes additional contact impractical given the limited size of the integrins (green). Some integrins are depicted unattached, and therefore free to diffuse.

Depending on the number of collagen fibers with which a cell is in contact, the total viable collagen contact experienced by the cell could be quite limited. We began with the hypothesis that such an effect could considerably alter integrin clustering dynamics in a three-dimensional matrix as opposed to on a two-dimensional substrate, and implemented a simulation to give a picture of how much and in what ways the clustering could change in the local microenvironment of a single cell-fiber interface.

Methods

To simulate the environment in which integrins bind to collagen, we reproduced Monte Carlo simulation work by Lin and Brown representing membrane fluctuations.¹³ This treated out-of-plane fluctuations as bending of an essentially elastic sheet with pinned corners, using a stiff cortical cytoskeleton as the basis of the pinning. While Lin and Brown originally intended their work to be representative of a purely spectrin cortical cytoskeleton, it is applicable to primarily actin-based networks because their cytoskeleton was assumed to be stiff, and actin is stiffer than spectrin. The geometry of the cortical cytoskeleton was assumed to be square for the sake of simplicity, 112 nm on a side as justified with a small sampling of calculations of cytoskeletal corral size in various cells. Time steps were 0.3 ns. The membrane bending modulus was 2 × 10⁻²⁰ J, as in Lin and Brown. The other parameters, such as pinning spring constants, were taken from the same article.

We simulated the collagen as a semi-infinite cylinder running parallel to the resting position (flat, zero-energy conformation) of the membrane. The two-dimensional substrate was modeled as a cylinder of diameter 10¹⁵ m, effectively infinite for the purposes of this simulation, which essentially amounted to a flat plane at a specific height above the membrane.

To the forces listed in Lin and Brown, we added a pinning force treating integrins as springs in the z direction with a spring constant of 98 pN/nm, a set distance above the membrane, with fixed x and y positions, and which detached stochastically according to bond dynamics equations.¹⁴ Specifically, the detachment probability was given by $P_{\text{detach}}=e^{f/f_{\beta }}\mathrm{\Delta }t/t_{\text{off}}^{\circ }$, where f was the force applied, f_β was the thermal energy barrier level k_BT/x_β dependent on the barrier width x_β, Δt was the time step, and $t_{\text{off}}^{\circ }$ was the unstressed lifetime of the integrin-collagen bond. The specific integrin modeled was the α₂β₁, which is known to attach to collagen and have appropriate time-scale dynamics for a short-lived adhesion. The barrier width was taken to be 2.3 and the unstressed lifetime to be 0.8 s, based on work by Taubenberger and colleagues in Chinese hamster ovary cells.¹⁵ (The primary integrin found in work by Cukierman et al in their three-dimensional adhesions was the α₅β₁; unfortunately, work on this integrin lacks barrier width information, while the mean rupture force is similar.¹⁶)

Integrin barrier width and membrane stiffness are particularly variable in real systems, and the stiffness of the membrane (or that of the adjacent glycocalyx) is known to have an effect on integrin clustering.¹⁷ Therefore, we performed simulations with altered values of both. Barrier width was increased by a factor of 5, and membrane stiffness was increased and decreased by factors of 10, for sensitivity analysis.

Because of the large difference between membrane fluctuation lifetimes and integrin bond lifetimes, we scaled the membrane fluctuation time-step by a factor of 10⁵, still an order of magnitude below even the fastest detachment we observed in the simulation. To ensure that this did not introduce artificial behavior, we divided the scaling factor by 10 without any noticeable changes (data not shown).

In addition, we ensured that integrins were spaced in a physically relevant way: they were not allowed to overlap in grid spaces, which were 7 nm apart from each other. Estimates of integrin diameter range from 5 to 10 nm. While a different grid spacing (and integrin diameter) may change precise numerical results, we do not expect that they would change the qualitative trends we see.

We simulated only the space and membrane in the immediate neighborhood of a single collagen fiber. This is not intended to suggest that only a single fiber is present; in general, at least several (and usually many) fibers are necessary for proper adhesion and motility behavior. In general, though, we suggest that the relevant physics dictates that our definition of word “cluster” should be a group of integrins which are close enough together that they can have an effect on each other through stabilization of the membrane, which seems to be at most tens of nanometers away from each other both via our simulations and via experiment.¹⁸ Geometric factors prevent a single integrin cluster defined in this way from attaching a cell to more than an individual fiber, or at most an individual branching fiber. A realistic simulation of a whole cell would involve multiple separate individual cluster simulations, likely affecting each other through intracellular signaling.

It is not clear how heterogeneous the fiber diameters in a whole-cell simulation should be to accurately reflect a cell’s environment. Also, fiber diameter obviously has a strong effect on the ratio between collagen density and the number of fibers in a cell’s immediate environment. Both of these factors would be important for a whole-cell simulation. For a single-cluster simulation, though, these considerations can be put aside.

Our Monte Carlo simulations began with all possible grid points occupied with integrins attached to the collagen. This is not in itself realistic, but the simulation quickly forced the detachment of unrealistically-attached integrins. It does imply that the cluster sizes we see are the maximum possible, as opposed to average values. We did not include the necessary dynamics for the initial cluster formation, which would likely be quite complex. However, the “potentially-binding fraction” f_bind (the fraction of area on the membrane which contains activated integrins and will bind in a given amount of time, defined in detail below) is not unrelated to this matter, and could in theory be used to estimate the process.

All cluster sizes given are in number of bound integrins per 112 nm length of collagen fiber; precise realistic lengths for these fibers in contact with cells depend on higher-order geometries of collagen fibers in a given environment. From Figure 8 on, most of the collagen radii simulated required multiple 112 nm squares in the width dimension; for these, the maximum possible number of integrins (and the maximum possible distance away from the center of the collagen) was simulated, one 112 nm square at a time. We assumed that conditions on one side of the collagen, at equal distances from the center of the collagen, mirrored those on the other. The exception was the effectively-infinite radius representing the 2D substrate; as this had no other reasonable size constraint, we assumed duplicated conditions over a span of 10 μm to replicate a small cell’s width.

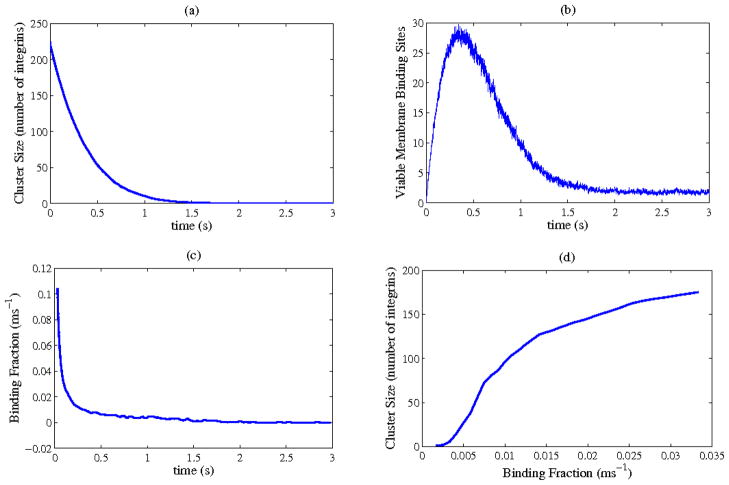
Figure 8.

Sample calculation of viable cluster size. (a): number of integrins still attached to the collagen at time t. (b): number of places on the membrane within 2 of the ideal binding position with respect to collagen at time t. (c): fraction of the spaces shown in (b) which would need to bind to collagen, per ms, to stabilize the loss of integrins shown in (a). (d): size of cluster stabilized by a given potentially-binding fraction, as defined in (c).

Rather than separately modeling integrin concentration, integrin activation, integrin redistribution, and integrin binding, we realized that these combined together have a single effect on the system. Thus, a system with a concentration of 500 integrins/μm², 30% of which are activated, will bind to a collagen fiber in almost exactly the same way as a system with a concentration of 1000 integrins/μm², 15% of which are activated. A system with a concentration of 100 activated integrins/μm², each binding at a rate of $k_{\text{b}}^1$, will bind to the collagen in the same way as a system with a concentration of 200 activated integrins/μm² and an individual binding rate of $k_{\text{b}}^2=k_{\text{b}}^1/2$.

Our model did not include intracellular signaling, direct binding kinetics, or integrin concentration (or locations) separately. This was intentional. The signaling processes involved are highly complex, generally involving multiple kinds of non-integrin proteins interacting, and should not occur in large amounts on the time scales examined. Further, precise reaction rates for these signaling cascades have generally not been established, so including effects on that level would have added a significant amount of guesswork. Instead, we simply mention that integrin attachment and the forces on them cause intracellular signals on long time scales, and it is not unreasonable to believe that the feedback from those signals to integrin re-binding would take longer than the relatively quick lifetimes of a typical three-dimensional cluster. Further still, there are additional factors like a possible increase in local integrin concentration in the immediate neighborhood of fibers which are difficult to model explicitly; these can be more easily expressed in the single binding fraction. Additionally, factors like matrix stiffness and ligand affinity, which can affect the binding rate, are quite complex even in a two-dimensional case.¹⁷ In the three-dimensional case, a proper treatment of stiffness would need to take into account the difference between the stiffness of the fiber material and the stiffness of the overall fiber structure. We therefore abstracted its effects.

To include all these effects in a reasonable way, we define the “potentially-binding fraction”, f_bind, in terms of the other quantities mentioned. We call [I] the local concentration of integrins, in slightly unconventional units (fraction of membrane which is occupied by integrins, estimated as 4.9 × 10⁻⁵ times the number of integrins per μm²). The fraction of integrins which are activated is p_act. The binding rate for an integrin-collagen distance within 2 (the experimentally-determined barrier width) of its ideal binding distance is k_b. (The “ideal binding distance” in this case was set arbitrarily to 3 nm. It is simply a subtractive factor from the collagen-membrane distance and has no other effect on the simulation.) In this language, f_bind = p_actk_b[I]. It is an overall measure of cell binding on the smallest possible relevant level. It is not a common description of the system in question; however, we suggest that it is the description most important to the effects of the intracellular environment on integrin activity.

Fundamentally, this approach means that we assume a fairly uniform integrin concentration in the immediate neighborhood of the collagen fiber, and do not keep track of individual integrin positions, or details regarding their diffusion or redistribution. It would, in theory, be possible to keep track of these items via simulation. However, such simulations would have been far more computation-intensive and would have involved a great deal of inventive work regarding almost entirely unknown kinetics. As there is no experimental data regarding sufficiently-detailed kinetics or local differences in concentrations between areas separated by tens to hundreds of nanometers on the cell surface near collagen fibers, it is unclear that such a simulation would be more accurate or useful than the simplified version we used.

While we did model a few values of f_bind starting with no bound integrins at all, our general approach was different. Rather than modeling each possible value of f_bind separately, we found the value of f_bind necessary to stabilize the cluster at a given size. We did this by finding the rate of cluster decay at each time t (the negative derivative with respect to time of the cluster size c(t)), d(t). Next, we found at each time t the number of grid points on the membrane without a currently-bound integrin which were within 2 of the ideal binding distance, and called this number s(t). If a fraction f of these contained activated integrins, the rate of integrin binding at time t would be k_bfs = f_binds. So, to have a stable cluster in which the rate of binding is equal to the rate of unbinding/decay, d = f_binds, or f_bind = s/d at a given time t. As the most important aspect of the system at a given time t is the cluster size at that time (which gives rise to all other behavior), each time uniquely corresponds to the cluster size which the system exhibited at the time. Hence, the value of f_bind which would make the system stable at time t is the value of f_bind which would make the system stable at the size c(t). We note that this gives the maximum possible (as opposed to average) viable cluster size, in number of integrins per 112 nm of collagen fiber length, at a given potentially-binding fraction. Alternatively, one could see it as giving the minimum possible value of f_bind for a given cluster size. From our individual f_bind calculations starting with no integrins, the main difference seems to be a slight shift in f_bind.

As mentioned in the introduction, we made one major simplification regarding overall cell membrane shape. While we modeled fluctuations on the nanometer scale, the overall shape of the cytoskeletal support mechanism for the membrane was assumed to be flat on the scale of a few hundred nanometers. This is not strictly accurate; the cell membrane and cortical cytoskeleton do curve around objects in its environment, to a point. However, the amount of curvature necessary to make more contact with a collagen fiber is greater for a small fiber than for a large one. This curvature is limited by both the membrane and the cytoskeleton; especially curved shapes are energetically disfavored. Also, the total amount of additional space available on a fiber that membrane curvature can make available, even with infinite possible curvature, is smaller for smaller fibers. (An absolute upper bound for a fiber of radius r would be 2πrL per length L of fiber, and this would be unrealistically high since it would require the fiber to be entirely engulfed by the cell.) In short, membrane curvature should increase the effective radius of a fiber, but should do so in a way that grows with the increase of the actual fiber radius. Consequently, we expect the overall results regarding fiber size to be even more pronounced than those in our simulation.

All coding for this work was done in C and run on individual desktop and laptop computers. Any data analysis not performed using C was in MATLAB.

Results and Discussion

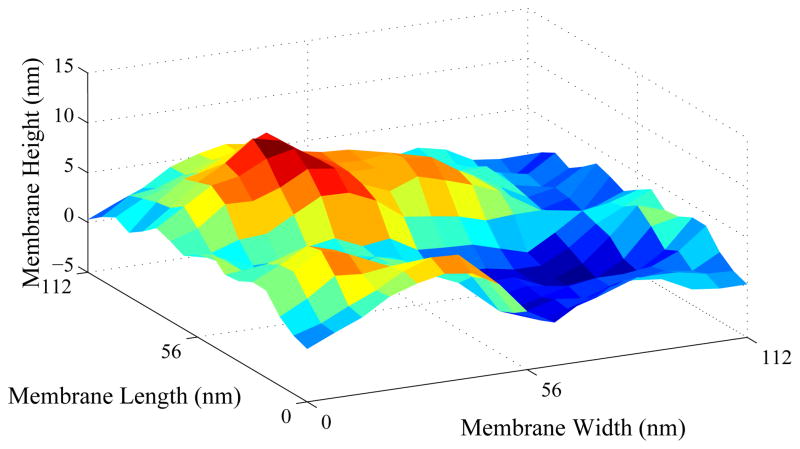
Our modeled collagen was placed above the membrane’s ground state. Since our model relied on forces to which integrins would be subjected, we needed to realistically represent the pressure and thermal fluctuations associated with a physically undulating membrane. Without membrane-collagen interaction, simple thermal fluctuations cause the membrane to behave as shown in Figure 2, in agreement with simulation data shown in,¹³ which agreed in turn with previous experiments.

Figure 2.

Simulation of a pinned section of membrane without integrin or collagen effects.

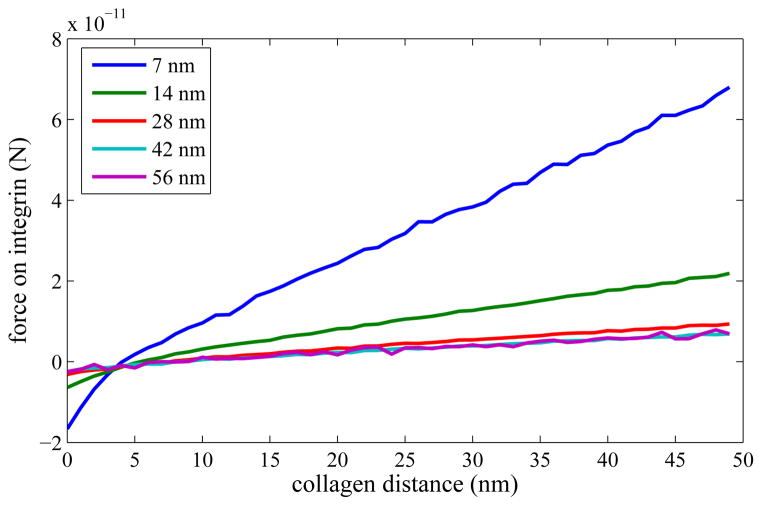
Our first simulation involving collagen examined the relationship between the z-position of the collagen and the mean directional force it exerts on the membrane through an integrin. (This is directly applicable to pressure on the membrane.) The relationship is essentially linear when detachment is not allowed, though the slope of the line depends on the distance on the xy plane of the integrin from the cortical cytoskeleton filaments (Figure 3). We observe that in this case the membrane essentially acts as a spring (according to the traditional F = −kx, where k here depends on the amount of membrane that stretches), which is unsurprising since it is modeled as mostly elastic. It is also reasonable since on the nanosecond time scale elasticity corresponds to real cell membrane out-of-plane fluctuations.

Figure 3.

Directional force on an integrin as a function of the smallest distance between the collagen and the cell membrane’s ground state, without detachment. The fairly simple relationship is due purely to the elasticity of the membrane and the amount of membrane available for stretching. The separate lines are for various distances between the integrin and the membrane pinning position (in both x and y coordinates); 56 nm is the precise center of the fluctuating membrane. This force is in the extracellular direction (towards the fiber), so very close fibers which actually push the membrane away show negative forces.

When stochastic detachment is allowed, higher z-positions cause the integrins to detach faster (Figure 4). As the detachment algorithm is explicitly force-dependent and collagen-membrane distance is directly related to force, this should be expected. Nonetheless, it is an important piece of information for properly interpreting later results, when collagen geometry creates a varying minimum collagen-membrane distance for various places on the membrane. (The difference in detachment may seem slight at first glance. This is partially because there is relatively little difference between 2 nm and 14 nm from the perspective of an integrin on most of the membrane, where natural thermal fluctuations would normally cause undulations almost that large anyway; on the other hand, this means that the distance is not artificial or unreasonable, as it might be if we were to increase it by another order of magnitude.)

Figure 4.

Cluster size in time for two different collagen heights. The larger distance between membrane and collagen (and, hence, higher force) causes a slight but certain increase in the detachment rate. This graph is representative of those at other collagen radii and heights (not shown).

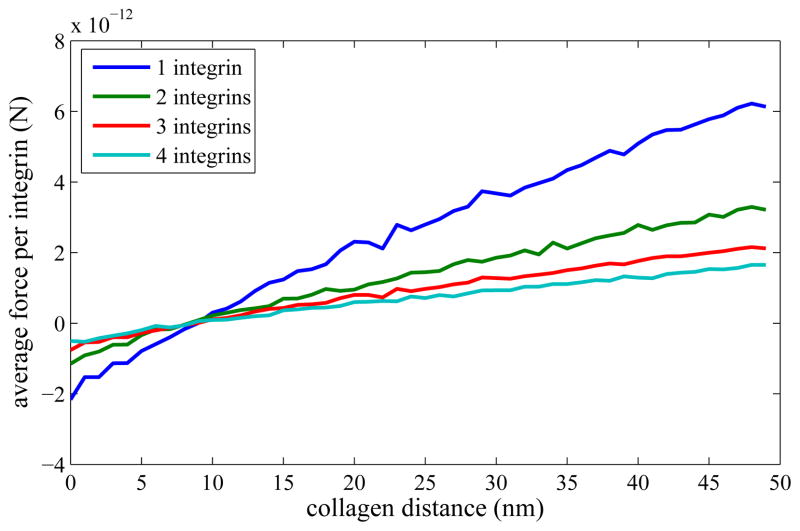
Second, we examined the effects of clustering on the forces involved. Figure 5 demonstrates that, without detachment, the average directional force on a cluster of n integrins, per integrin, is roughly 1/n times the force on a single integrin in approximately the same position. This is because the integrins can share the load between them, though they do not always do so evenly. It shows how a large cluster could make an individual integrin-collagen bond more stable by spreading the load and thus decreasing the force on that integrin. When we explicitly include detachment, we find a more complex relationship in general, which is most easily described in terms of the third set of calculations.

Figure 5.

Mean force in the extracellular direction per integrin as a function of clustering. The total force is spread over the total number of integrins, and so the mean force is inversely proportional to that number.

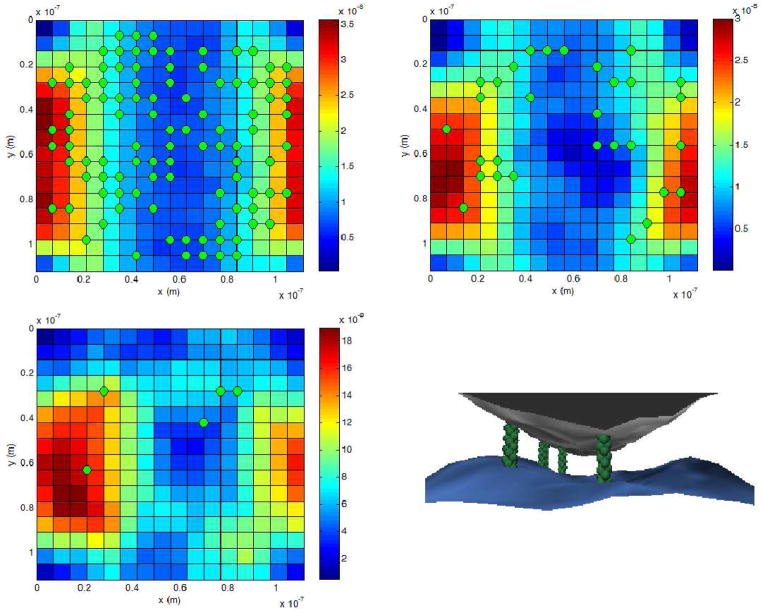
Third, we examined the effect of finite collagen size on maximum viable integrin cluster size. “Viable” in this case was considered to be a cluster size which could be stable, given some probability of integrin reattachment if the membrane was appropriately placed. One sample of such a simulation is shown in Figure 6. Three separate points in time are graphed, and the third point in time is shown from two different viewpoints to highlight the geometry of the system.

Figure 6.

Example simulation with a collagen fiber of radius 60 nm. Top left: contour plot of membrane height with 100 labeled integrin-collagen bonds (green dots) intact. Top right: 30 integrin-collagen bonds intact. Bottom left: 5 integrin-collagen bonds intact. Bottom right: 5 integrin-collagen bonds intact, as seen from one side. (One integrin is directly behind another, so only four are easily visible.) In all cases, the membrane excitation geometry roughly follows the collagen.

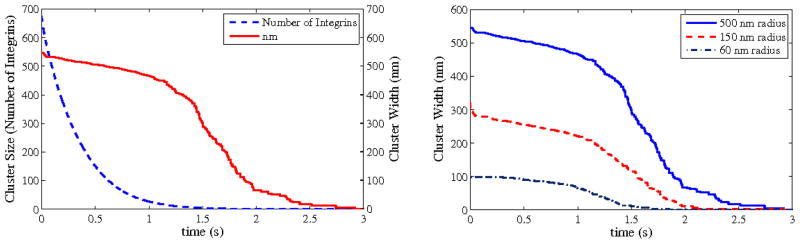
The cluster size measurement we use, number of bound integrins, is arguably the most useful metric for determining cell behavior (see our Conclusions for our reasoning on this), but this does make them somewhat difficult to compare to previous experimental results. Therefore, we have included a comparison between the number of integrins and the width of the cluster in Figure 7. The left graph shows the averaged evolution over time of a cluster bound to a 500 nm radius fiber, in number of integrins and width of cluster. The right graph shows cluster width for fiber radii of 60, 150, and 500 nm.

Figure 7.

Width of cluster over time. Left: Cluster size, both in width and in number of bound integrins, over time for a collagen fiber radius of 500 nm. Right: Cluster width in time for three different diameters of fiber. It is clear that width and number of integrins do not share a direct correlation, as there is an issue of density. However, overall trends are the same, and while width is easier to compare to experiment, number of bound integrins is an extremely important quantity.

Our full results come from a slightly more complex calculation based on results such as those in Figure 6. We give an example in Figure 8 with a collagen radius of 500 nm and height of 3 nm. Figure 8a shows the number of integrins attached to the collagen at a given point in time; the number decreases because of stochastic detachment. In Figure 8b, we see the number of grid points on the membrane which are appropriately positioned for integrin-collagen reattachment at a given point in time. Figure 8c shows the fraction of those places, f_bind, where an integrin would need to bind per unit time in order to counteract the loss in size shown in Figure 8a. By then matching each time from Figure 8c to a cluster size with Figure 8a (see Methods), we can then find the maximum stable cluster size for a given f_bind, shown in Figure 8d.

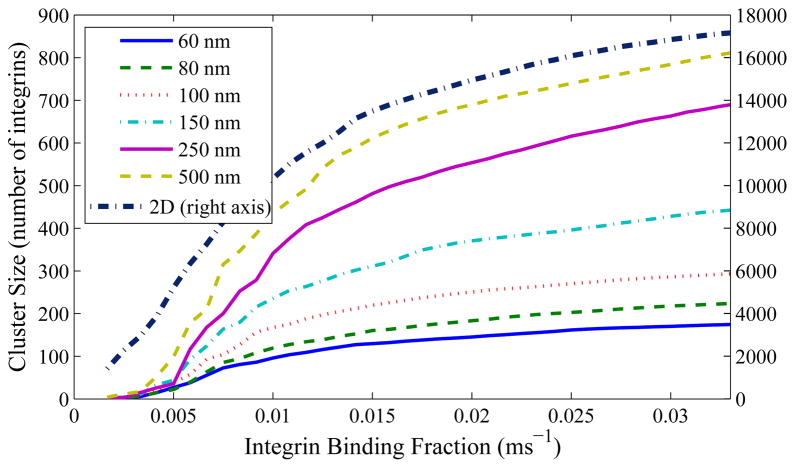
Graphing several of these for different collagen radii, we arrive at Figure 9. This clearly shows that a smaller collagen fiber is incapable of supporting as large an integrin cluster as a larger fiber. We also performed a calculation for an effectively infinite collagen fiber radius (10¹⁵ m), which would correspond to a 2D collagen film surface. The relevant size was over an order of magnitude larger than that for a three-dimensional fiber for any given f_bind. Additionally, stable clusters appear on a 2D film at less than half the minimum possible value of f_bind seen in any of the three-dimensional fiber simulations. Larger and more stable clusters should therefore be easier for cells to form on 2D substrates.

Figure 9.

Maximum viable cluster size for a given potentially-binding fraction f_bind, over several collagen radii. Smaller collagen radii lead to smaller viable clusters for a given f_bind. Results for a 2D substrate were simulated but were over an order of magnitude larger in width and are graphed on the secondary vertical axis. Note that the minimum f_bind for a cluster size of 50 with a 60 nm fiber is approximately 0.006/ms, whereas for a 2D substrate it can be extrapolated to roughly an order of magnitude less.

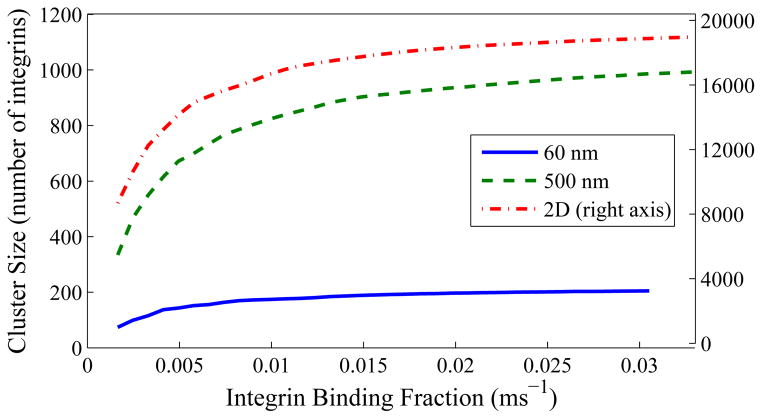
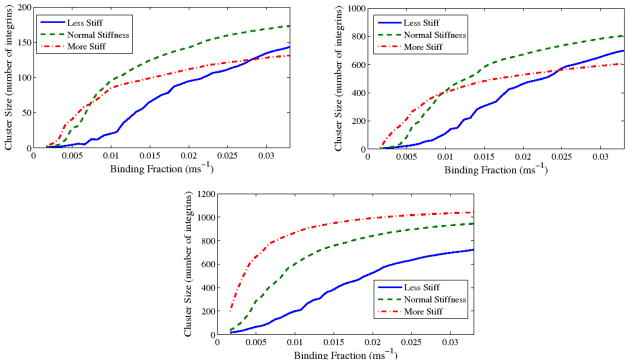
To examine the sensitivity of these results on an important parameter which changes from integrin to integrin, we examined the effects of a greatly increased barrier width. Increasing this width by a factor of 5 gives similar, though not identical, results, as shown in Figure 10. To show effects of another parameter which changes based on cell type and health, we varied membrane stiffness (to account for stiffness of the lipid bilayer itself or the attached glycocalyx) by a factor of 10 in either direction. Results of these simulations are shown in Figure 11. They are easily explained by the fact that this stiffness helps integrins stabilize the membrane around them (see, e.g.,¹⁷), but also keeps the membrane from conforming to the geometry of a three-dimensional fiber.

Figure 10.

Maximum viable cluster size as in Figure 9, but with integrin barrier width increased by a factor of 5. Similar, though not identical, behavior can be seen, meaning that while the results can be carried from one integrin type to another, detailed quantitative predictions will depend on integrin type.

Figure 11.

Maximum viable cluster size for radius 60 nm (top left), 500 nm (top right), and 2D surface (bottom). “More stiff” has a membrane stiffness increased by a factor of 10; “Less stiff” has it decreased by a factor of 10.

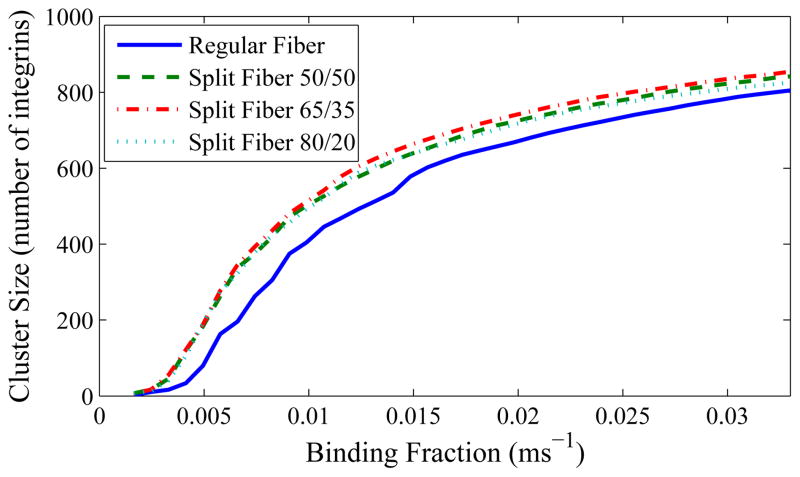
Last, we account for the possibility of a different fiber geometry, a branching fiber. As previously mentioned, multiple fibers would have difficulties in physically affecting the membrane adjacent to each other, but a single fiber branching out into two could theoretically get around that problem. We have therefore simulated a group of branching fibers, and compared them to non-branching fibers. Before the branch, all fibers have a radius of 500 nm. Their cross-sectional area is then divided into two pieces. It is divided evenly in one instance, into 65%/35% pieces in another, and into 80%/20% pieces in another. The two branches diverge 30 degrees in opposite directions from the original fiber direction, and remain in contact with the cell membrane as much as possible (rather than remaining coaxial with the pre-branching fiber). This gives rise to Figure 12.

Figure 12.

Branched fibers with various branching ratios compared to non-branched fibers. All branching seems to slightly increase cluster size in the ideal case; however, the difference is small compared to most other factors that affect cluster size.

The relationship between position and force demonstrated in Figure 3 is simple, but important. Integrins are known to be force-sensitive. They are also, by necessity, distance-dependent, since they cannot stretch past a certain point without beginning to unfold and losing their functionality. Our results demonstrate that the force and distance dependences are also highly interrelated because of the attachment to the effectively elastic membrane.

More importantly, the effect of finite collagen size is quite significant. This effect is a strong geometric constraint on integrin clusters in three-dimensional matrices. Two-dimensional collagen films, used to line the environments for two-dimensional cell adhesion and motility studies, are very smooth, with their surface heights varying generally at most tens of nanometers over spans of microns.¹⁹ Realistic three-dimensional environments have collagen fibers that vary considerably more, even if we ignore the added effects of multiple fibers touching or being intertwined.

We also observe that the pressure and distance conditions change at the point where the collagen curvature makes integrin binding difficult. This could have significant effects on which kinds of integrins bind at these points. It could also significantly change the results of the force-dependent signaling processes that the integrins perform. Given the high level of interdependency in the system, such changes could alter overall cluster lifetimes if the clusters last long enough for these signaling processes to feed back.

Further, the pressures involved in two- and three-dimensional environments are different, causing more changes to the forces and distances involved. On a two-dimensional substrate, the main overall pressure would presumably be from gravity, an extremely small one especially when spread out over the entire portion of the cell in contact with the substrate. In contrast, a cell in a three-dimensional environment would likely have significant pressure due to steric constraints, squeezing through areas that it fits into snugly. It could also have some local pressure due to gravity in places where it is in contact with collagen below it; though mostly insignificant, this would be larger than the two-dimensional pressure because there would be fewer points of support in three-dimensions. We suggest, therefore, that in general a three-dimensional environment should impose more inward-directed force on a given attached integrin than a similar two-dimensional environment. This may have effects on which kinds of integrins are useful to cells in that environment, especially when combined with the inherent force-distance relationship demonstrated above.

Experimental verification of this model’s conclusions may be slightly more complex than it would seem at first, though it is certainly not impossible. This is because in part of the scale of the model, which does not include explicit details on biochemical feedback mechanisms. It may be possible to mimic some aspects of 3D-like behavior on a 2D plate by laying a single layer of semi-sparse, thin fibers on a non-adhesive plate, but we suggest that a lack of more complex geometries would mean clusters would likely be very long. (As our cluster sizes for both 2D and 3D clusters were given per 112 nm of fiber length, the size is limited by how much of the length of the fiber is in contact with the cell.) This could be corrected via nanopatterning (e.g.,,²⁰ in which smaller clusters were observed but other behaviors were not mentioned and may not have been observed). If nanopatterning were used, though, one would still expect some differences in behavior because of the high degree of feedback involved in the system and the lack of biochemical signals coming from the non-attached side of the cell; in model terms, this lack of signaling would result in a different value of f_bind. It would therefore only be possible to verify a single model result, the size, via this method. However, verification of the model itself could be performed using individual fibers of different diameters in otherwise-uniform and repeated microenvironments.

Conclusions

Our results show that there is a simple relationship between collagen geometry/fiber size, local pressure, and the maximum size of viable integrin clusters. (This relationship is simplest in terms of the number of bound integrins, which is the most relevant size in respect to both strength of binding and amount of biochemical response. Biochemical responses should have power-law, often linear, patterns with respect to protein number, and adhesion strength should be at least close to linear. The relationship between fiber size and cluster width does obviously exist as well.) We can, then, explain the difference in cluster size between two- and three-dimensional microenvironments, found in experimental work.^6,10,11

While potentially important and not previously highlighted in the literature, this result may not by itself seem especially powerful. However, there are more subtle conclusions from our simulations. Our results show that the potentially-binding fraction required for a viable cluster on a two-dimensional film is considerably smaller than any of those on realistic collagen fibers. The difference shown in Figure 9 implies that two-dimensional cluster adhesions should be more stable than their three-dimensional cousins because it is easier for the system to keep them at a significant size. This means the lifetime of a three-dimensional cluster should be shorter than that of its two-dimensional counterpart, something else seen in experiment.¹⁰ Therefore, we can explain the difference in the lifetimes of two- and three-dimensional clusters using our model. For that matter, comparison with experiment does not end with these studies; implications that small-radius fibers should have unstable adhesions have been shown in a non-collagenous experimental environment, specifically with carbon fibers.²¹

Finally, we predict that, while higher membrane/glycocalyx stiffness promotes clustering to a point, a sufficiently stiff membrane (or glycocalyx) will interfere with integrin clustering in three dimensions in cases where binding is frequent. This may seem to be in disagreement with the literature on two-dimensional clustering-stiffness results, but in reality it comes from the addition of a geometric factor which is in conflict with the kind of stability that membrane stiffness can provide.

Because of general agreement with experiments, we submit that our model is a good beginning to a realistic representation of the effects of the physical three-dimensional environment on integrin clustering (specifically the non-uniform and semi-sparse nature of the collagen fiber matrix from the point of view of the cell membrane). It demonstrates why clusters in three dimensions are smaller and have smaller lifetimes than those in two dimensions, and provides some explanation of differences in composition. These effects are a very significant contribution to the differences between cell adhesions found in two-dimensional environments as opposed to those in three-dimensional environments.^6,10,12