Correcting for Population Stratification in Genomewide Association Studies

Abstract

Genomewide association studies have become the primary tool for discovering the genetic basis of complex human diseases. Such studies are susceptible to the confounding effects of population stratification, in that the combination of allele-frequency heterogeneity with disease-risk heterogeneity among different ancestral subpopulations can induce spurious associations between genetic variants and disease. This article provides a statistically rigorous and computationally feasible solution to this challenging problem of unmeasured confounders. We show that the odds ratio of disease with a genetic variant is identifiable if and only if the genotype is independent of the unknown population substructure conditional on a set of observed ancestry-informative markers in the disease-free population. Under this condition, the odds ratio of interest can be estimated by fitting a semiparametric logistic regression model with an arbitrary function of a propensity score relating the genotype probability to ancestry-informative markers. Approximating the unknown function of the propensity score by B-splines, we derive a consistent and asymptotically normal estimator for the odds ratio of interest with a consistent variance estimator. Simulation studies demonstrate that the proposed inference procedures perform well in realistic settings. An application to the well-known Wellcome Trust Case-Control Study is presented. Supplemental materials are available online.

1. INTRODUCTION

One and a half decades ago, Risch and Merikangas (1996) showed that genomewide association (GWA) studies interrogating hundreds of thousands or more genetic variants have far greater power than traditional linkage studies in detecting the genetic factors for complex human diseases (e.g., cancer, diabetes, cardiovascular diseases, mental disorders). The catalog of single nucleotide polymorphisms (SNPs) (International HapMap Consortium 2005) and the advances in genotyping technology have made GWA studies a reality. Indeed, the number of these studies has grown exponentially in recent years, and their success in identifying genetic basis of complex human diseases was declared “breakthrough of the year” by the journal Science in 2007. Most GWA studies use a case-control design, which compares the allele frequencies between disease subjects (i.e., cases) and disease-free subjects (i.e., controls). Because of the need to adjust for multiple testing, large samples are required to attain sufficient power in detecting the modest genetic effects expected for complex human diseases.

It is widely recognized that unobserved population substructure or stratification can generate spurious associations, that is, associations between disease and genetic variants that are not linked to any causative loci (Lander and Schork 1994). This problem of unmeasured confounders arises when the population under study is composed of several latent ancestral subpopulations that have different allele frequencies and also different risks of disease. The effects of stratification increase with sample size, so that even subtle population substructure can yield grossly inflated type I error for large GWA studies. Case-control studies are particularly prone to population stratification, especially when cases and controls are obtained from different sources. Indeed, the concern over population stratification led many to advocate family-based studies, which are more costly and less powerful than case-control studies.

Delvin and Roeder (1999) proposed a simple approach, known as “genomic control,” to correcting for population stratification in case-control studies. In this approach, the chi-squared statistics are calculated at a set of null markers across the genome, and their empirical median is divided by the median of the chi-squared distribution to produce an inflation factor, which is then used to adjust the test statistics at all candidate SNPs. This adjustment is crude, especially when the degrees of stratification vary substantially among the SNPs.

Pritchard et al. (2000) developed the so-called “structured association,” which assigns subjects to discrete subpopulations (with possibly fractional memberships) based on a set of unlinked genetic markers and tests for associations within sub-populations. This approach is computationally intractable for large numbers of markers. It is difficult to correctly estimate the population substructure or to correctly assign individuals to subpopulations, especially when the population under study is a continuous mixture of ancestral subpopulations.

The prevailing approach to adjusting for population stratification is principal components analysis, which infers continuous axes of genetic variation from genomic markers and includes those axes as covariates in the association analysis (Chen et al. 2003; Zhang, Zhu, and Zhao 2003; Price et al. 2006). It is unclear how many axes should be used or how their effects on disease should be modeled. Price et al. (2006) suggested including the 10 axes with the highest eigenvalues as covariates with linear effects, and their method, EIGENSTRAT, has been used in virtually all recent GWA studies. The assumption of linear effects is likely violated in practice. Zhang, Zhu, and Zhao (2003) and Chen et al. (2003) modeled the effects semiparametrically thorough a kernel function, which can be computationally unstable when the dimension is greater than two.

Epstein, Allen, and Satten (2007) calculated a stratification score, which is the individual’s estimated odds of disease as a function of his or her ancestry-informative markers, and tested for association within strata defined by the stratification score. The use of the stratification score tends to attenuate the estimates of the genetic effects at candidate SNPs and thus reduce statistical power, especially when the set of ancestry-informative markers is large (Lee et al. 2008). Recently, Zhao, Rebbeck, and Mitra (2009) calculated a propensity score (Rosenbaum and Rubin 1983) by regressing the genotype of each candidate SNP on ancestry-informative markers, and used the resulting propensity score as a linear term in the logistic regression model for the disease association; they did not theoretically justify their method.

This article provides a rigorous statistical treatment of the problem of population stratification. We formulate the confounding due to population stratification through appropriate statistical models, identify necessary and sufficient conditions for the use of genomic markers to correct for this confounding, and develop inference procedures that properly correct for the confounding. Our methods avoid the aforementioned limitations of the existing methods. Indeed, our theory yields valuable insights into the behavior of the existing methods. We demonstrate the advantages of the new methods through simulated and real data.

2. THEORY AND METHODS

2.1 Statistical Framework

We consider case-control GWA studies. Let D indicate, by the values 1 versus 0, whether or not the subject has the disease of interest, and let G denote the genotype at a candidate locus, which is defined as simply the number of minor alleles. We are interested in making inference about the effect of G on D in the presence of population stratification. We represent the unknown population substructure by an unobserved, possibly vector-valued variable U. We collect data on a set of potentially correlated genomic markers, denoted by Z, which is informative about the latent population substructure U.

It is natural to assume the following odds model:

$$\frac{Pr(D=1\mid G=g,\mathbf{U}=\mathbf{u},\mathbf{Z}=\mathbf{z})}{Pr(D=0\mid G=g,\mathbf{U}=\mathbf{u},\mathbf{Z}=\mathbf{z})}=e^{\beta (g)+\gamma (\mathbf{u},\mathbf{z})},$$ (1)

where β is a parametric function, and γ is a completely unknown function. (The usual intercept term is absorbed in the arbitrary function γ.) Under the additive mode of inheritance, β(g) = βg; under the dominant or recessive mode of inheritance, β (g) = β I(g ≥ 1) or β I(g = 2); under the co-dominant mode of inheritance, β (g) = β₁I(g = 1) + β₂I(g = 2). The additive mode of inheritance is used almost exclusively in practice.

Remark I

Because of the arbitrariness of the function γ, model (1) is semiparametric. Indeed, model (1) is completely nonparametric under the null hypothesis that β (g) = 0. This feature is important because proper control of type I error is a prominent task in GWA studies.

Remark 2

Model (1) allows certain ancestry-informative markers to be associated with disease (even after conditioning on the true ancestry) and includes the special case where ancestry-informative markers are independent of disease conditional on the true ancestry such that

$$\begin{array}{l}\frac{Pr(D=1\mid G=g,\mathbf{U}=\mathbf{u},\mathbf{Z}=\mathbf{z})}{Pr(D=0\mid G=g,\mathbf{U}=\mathbf{u},\mathbf{Z}=\mathbf{z})}=\frac{Pr(D=1\mid G=g,\mathbf{U}=\mathbf{u})}{Pr(D=0\mid G=g,\mathbf{U}=\mathbf{u})}\\ =e^{\beta (g)+\gamma (\mathbf{u})}.\end{array}$$

We normally set γ (u, z) in (1) to γ (u) so as to estimate the marginal effect of G, although the general formulation allows estimation of the effect of G conditional on some other SNPs.

2.2 Identifiability

It is well known that odds ratios are identifiable from case-control data (Prentice and Pyke 1979). In our setting, however the odds ratio parameter β might not be identifiable, because U is never observed. To be able to estimate β, we require that Z be sufficiently informative about U such that β can be correctly identified by stratifying on Z instead of on U. In other words, the following model must hold:

$$\frac{Pr(D=1\mid G=g,\mathbf{Z}=\mathbf{z})}{Pr(D=0\mid G=g,\mathbf{Z}=\mathbf{z})}=e^{\beta (g)+\xi (\mathbf{z})},$$ (2)

where ξ is some unknown function different from γ. Theorem 1 and Proposition 1 provide necessary and sufficient conditions under which model (1) indeed implies model (2).

Theorem 1

A necessary and sufficient condition for model (2) to hold is that U is independent of G conditional on Z in the control population, that is,

$$Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=0)=Pr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=0).$$ (3)

Proposition 1

1. Condition (3) is equivalent to that U is independent of G conditional on Z in the case population, that is,

   $$Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=1)=Pr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=1).$$ (4)

2. If β = 0, then both (3) and (4) are equivalent to that U and G are independent given Z in the study sample, that is, Pr(U = u|G = g, Z = z) = Pr(U = u|Z = z).

Remark 3

The foregoing results imply that it is possible to correct for the confounding effects of U if Z dissolves the link between U and G such that U is independent of G for each stratum of Z in the control population (or, equivalently, in the case population). Note that the conditional independence does not hold in the whole population or in the combined sample of cases and controls if there is population stratification and β is nonzero.

Remark 4

Conditions (3) and (4) are reasonable in that they require the aspect of the unknown population substructure U, which needs to be controlled for when estimating the effect of G to be fully contained in the observed marker data Z. These conditions hold trivially if U is completely determined by Z. They also hold even if U is not completely determined by Z but the part of U not captured by Z is unrelated to G.

The proofs of Theorem 1 and Proposition 1 are given in the Appendix. Hereinafter, we assume that condition (3) or, equivalently, (4) holds. Our goal is to make inference on β.

2.3 Inference Procedures

The observed data consist of (D_i, G_i, Z_i), i = 1, …, n, where n is the total number of study subjects. Under model (2), the likelihood takes the form

$$\prod _{i=1}^n\frac{e^{D_i\{\beta (G_i)+\xi ({\mathbf{Z}}_i)\}}}{1+e^{\beta (G_i)+\xi ({\mathbf{Z}}_i)}}.$$

In general, it is difficult to maximize this likelihood, because the function ξ (·) is unknown and can be highly nonlinear. If Z is discrete with a small number of values, then ξ (Z) can be easily parameterized. If Z is continuous but very low-dimensional, we may apply a nonparametric smoothing method. If Z is discrete with many values or continuous with dimension higher than three, then it is desirable to find a low-dimensional representation of Z, say ψ(Z), such that ψ (Z) can replace Z in model (2). Such a ψ(Z) exists and is given in the following theorem.

Theorem 2

If

$$Pr(G=g\mid \mathbf{Z}=\mathbf{z},D=0)=Pr(G=g\mid \mathit{\psi }(\mathbf{Z})=\mathit{\psi }(\mathbf{z}),D=0),$$

then

$$\frac{Pr(D=1\mid G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x})}{Pr(D=0\mid G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x})}=e^{\beta (g)+\xi (\mathbf{x})}$$

for some function ξ.

The proof is given in the Appendix. This result shows that we can simply identify a low-dimensional function ψ (Z) such that G and Z are independent given ψ (Z) in the control population. Clearly, ψ (Z) can be chosen to be Pr(G = g|Z = z, D = 0), which is at most two-dimensional. We refer to this function as the genotype-associated propensity score (GAPS) because it pertains to the propensity of having genotype g for a subject with markers Z.

There is an important difference between GAPS and the traditional propensity score of Rosenbaum and Rubin (1983). The latter is used to mitigate the nonrandomness of treatment assignment such that within each score stratum, the treatment assignment is independent of the potential outcome under the assumption of no unmeasured confounders. In contrast, our propensity score is used to remove the confounding of latent population substructure such that within each score stratum, the genotype of the candidate SNP is independent of the unmeasured confounders U. Under the odds ratio model, our propensity scores are based on the relationship between G and Z in the control population rather than in the entire population.

We may determine Pr(G = g|Z = z, D = 0) by supervised learning methods, such as discriminant analysis, classification trees, and support vector machines. It is computationally simpler to adopt a parametric model. For example, we may assume the proportional odds model acknowledging the ordinal nature of G. It is biologically more sensible and numerically more stable to formulate the effects of Z on G at the nucleotide level. Let G⁽¹⁾ (or G⁽²⁾) indicate, by the values 1 versus 0, whether the nucleotide inherited from the father (or the mother) is the minor allele, such that G = G⁽¹⁾ + G⁽²⁾. It is natural to specify the following logistic model:

$$\frac{Pr(G^{(k)}=1\mid \mathbf{Z},D=0)}{Pr(G^{(k)}=0\mid \mathbf{Z},D=0)}=e^{{\mathit{\eta }}^{\text{T}}\mathbf{Z}},k=1,2.$$ (5)

(We have expanded Z to include the unit component and absorbed the intercept term in η.) We set ψ (Z) = η^TZ, which is only one-dimensional. Without loss of generality, we focus on the additive mode of inheritance such that β (G) = β G. Then model (2) becomes

$$Pr(D=1\mid G,\mathbf{Z})=\frac{e^{\beta G_i+\xi ({\mathit{\eta }}^{\text{T}}\mathbf{Z})}}{1+e^{\beta G+\xi ({\mathit{\eta }}^{\text{T}}\mathbf{Z})}}.$$ (6)

The likelihood for η based on the observed data (D_i, G_i, Z_i), i = 1, …, n, is

$$\sum _{i=1}^n(1-D_i)\frac{e^{G_i{\mathit{\eta }}^{\text{T}}{\mathbf{Z}}_i}}{{(1+e^{{\mathit{\eta }}^{\text{T}}{\mathbf{Z}}_i})}^2}.$$

The resulting maximum likelihood estimator is denoted by η̂. Given η̂, we estimate β by maximizing the following pseudo-likelihood function:

$$\prod _{i=1}^n\frac{e^{D_i\{\beta G_i+\xi ({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\}}}{1+e^{\beta G_i+\xi ({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}}.$$

Because ξ (·) is an unknown function, adopting a nonparametric approach is desirable. The simplest approach is to stratify the subjects into K strata based on the (estimated) propensity scores {η̂^TZ_i; i = 1, …, n}. Then β can be estimated by the standard logistic regression of D on G and (K – 1) dummy variables. The discontinuity of the stratification makes it difficult to account for the variation in estimating η. (Unlike the traditional propensity score, our propensity score is conditional on the disease status, so its influence function is not orthogonal to that of β; thus the variation in estimating the propensity score cannot be ignored.)

We propose to use B-splines to approximate ξ. Specifically, let B₁(·), …, B_Kn (·) be the B-spline basis functions of order m (m ≥ 3) with the interior knots being the k/(K_n – 2m) (k = 0, 1, …, K_n – 2m) quantiles of {η̂^TZi; i = 1, …, n}. Then ξ (x) can be approximated by ${\sum }_{k=1}^{K_n}{\theta }_k{B}_k(x)$, where θ₁, …, θ_Kn are unknown coefficients. We estimate β and θ ≡ (θ₁, …, θ_Kn)^T by maximizing the following approximate log-likelihood function:

$$\sum _{i=1}^n\left[D_i\left\{\beta G_i+\sum _{k=1}^{K_n}{\theta }_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\right\}-log\left\{1+e^{\beta G_i+{\sum }_{k=1}^{K_n}{\theta }_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}\right\}\right].$$

This maximization can be done using the standard Newton–Raphson algorithm. The resulting estimators are denoted by β̂ and θ̂.

The asymptotic properties of β̂ are stated in the following theorem. In this theorem and in its proof, given in the Appendix, ζ₀ denotes the true value of any parameter or function ζ.

Theorem 3

Assume that the following regularity conditions hold:

• (C.1)If c^TZ = 0 with probability 1 for some constant vector c, then c = 0. In addition, $var(G\mid {\mathit{\eta }}_0^{\text{T}}\mathbf{Z})>0$ with positive probability.
• (C.2)The support of Z is bounded, and ${\mathit{\eta }}_0^{\text{T}}\mathbf{Z}$ has a bounded continuous support.
• (C.3)The function γ₀(u, z) and the joint density of (U, Z) have bounded fourth derivatives and are bounded away from 0 in the support of (U, Z).
• (C.4)The number of the B-spline basis functions K_n → ∞, $n^{-1/2}{K}_n^6\to 0$, and $n^{-1/2}{K}_n^7\to \infty$.

Then n^1/2(β̂ − β₀) converges in distribution to a mean-0 normal random variable.

Remark 5

The first part of condition (C.1) is equivalent to the linear independence of Z, and the second part ensures that G is not completely determined by ${\mathit{\eta }}_0^{\text{T}}\mathbf{Z}$. This condition is required for the consistency of the parameter estimators. Conditions (C.2) and (C.3) impose some smoothness on the distribution of (U, Z). Condition (C.4) is satisfied by any K_n = n^ν with ν ∈ (1/14, 1/12).

Remark 6

The number of basis functions K_n plays the role of the smoothing parameter in B-splines. The value of K_n should be large enough so that the B-spline basis is flexible, but not too large, to avoid overfitting. We typically set K_n to be between 2 and 10. If the effects of populations stratification are fully accounted for, then the genomic control λ (Delvin and Roeder 1999), which is the ratio of the median of the observed chi-squared test statistics to the theoretical median of the chi-squared distribution, will be equal to 1. Thus we may choose a value of K_n such that the resulting λ is close to 1.

The proof of Theorem 3 is given in the Appendix. The main challenge is that the dimension of the parameter vector θ increases with increasing sample size. In the proof, we show that the asymptotic variance of β̂ can be consistently estimated by treating model (6) as a parametric model with parameters β, θ, and η. A sandwich variance estimator is used to account for the variation due to the plug-in estimation of η.

It follows from Proposition 1(a) that the conclusion of Theorem 2 also holds if Pr(G = g|Z = z, D = 1) = Pr(G = g|ψ(Z) = ψ(z), D = 1). Thus Theorem 3 continues to hold if we replace D = 0 in model (5) by D = 1. We refer to our methods as GAPS(C) if η is estimated from the control sample and GAPS(D) if η is estimated from the disease (i.e., case) sample. Estimating η from the combined sample of cases and controls is generally invalid.

Although both are theoretically valid, GAPS(C) and GAPS(D) may yield different results in actual data analysis. In our approach, the propensity scores are first calculated from the control or case sample and then matched into the other sample. The scores calculated from the sample with a finer latent substructure might not be well matched in the sample with a coarser latent substructure, and the resulting GAPS method might not be fully effective. For this reason, we suggest using both GAPS(C) and GAPS(D) in practice. If the latent substructures are balanced between the case and control samples, then the two methods will yield similar results; otherwise, the mismatch of the two samples may warrant further investigation.

2.4 Dimension Reduction

GWA studies survey the entire genome with high-density genotyping platforms containing approximately 1 million SNPs. It is customary to infer ancestry from the dense SNP data themselves rather than collect additional data on ancestry informative markers. For such high-dimensional markers, however, estimating ψ(Z) of Section 2.3 directly is a challenge. We suggest reducing the dimension of Z before applying the methods described in Section 2.3. Particularly, we find a low-dimensional representation of Z by performing principal components analysis on a distance matrix among study subjects.

Define the n × p matrix X, whose ith row is the 1 × p vector of genotypes for the ith subject. We standardize each column of X to have mean 0 and variance 1. The resulting matrix is still denoted by X. We define an n × n distance matrix whose (i, j)th element is a distance measure between the ith and jth subjects (i.e., the ith and jth rows of X). The choice of the correlation of genotypes as the distance yields EIGENSTRAT, whereas setting the distance to the square root of the maximum of the correlation of genotypes and 0 yields Laplacian eigenmaps (Zhang, Niyogi, and McPeek 2009; Lee et al. 2010). The latter distance is less sensitive to outliers (i.e., subjects with markedly different ancestry) than the former. We perform an eigenvalue decomposition of the distance matrix. The first few principal components (PCs) are the low-dimension representation of X and will replace Z in the inference procedures of Section 2.3. According to the multidimensional scaling theory, the space spanned by the first few PCs is the optimal low-dimensional embedding, which tends to preserve the original pairwise distances.

Remark 7

By replacing the original set of markers Z with the PCs, we now require that condition (3) or equivalent condition (4) hold, with Z being the PCs. Note that the original Z might contain certain information that is not part of the PCs as long as that information is not associated with U or G. Although a larger number of PCs yields a more accurate low-dimensional representation, including a very large number of PCs in association analysis may cause numerical instability. For most studies, population substructures are well captured by the first few (e.g., 10) PCs.

2.5 Comparisons With Other Approaches

Our approach is in the same vein as EIGENSTRAT, the stratification score of Epstein et al. (EAS), and the propensity score of Zhao et al. (ZRM), in that all four approaches adjust for population stratification by including ancestry-related covariates in the logistic regression model for the SNP–disease association. For EIGENSTRAT, the covariates are the top 10 PCs. For EAS, the covariate pertains to the probability of disease given ancestry-informative markers. ZRM uses the propensity score based on the entire sample, whereas our approach uses the propensity score based on the control sample or case sample, in this section we examine the differences between our approach and EIGENSTRAT, EAS, and ZRM.

Both our approach and EIGENSTRAT use principal components analysis for dimension reduction. In our approach, the ancestry-related covariate used in the SNP-disease association model is a scalar function of the PCs, and its effect on the disease status is modeled nonparametrically. In EIGENSTRAT, the PCs enter into the SNP–disease association model as linear terms. As shown in the proof of Theorem 2,

$$\xi (\mathbf{z})=log{\int }_{\mathbf{u}}{e}^{\gamma (\mathbf{u},\mathbf{z})}dPr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=0),$$

so the effects of PCs on the odds ratio of disease can be highly nonlinear. For example, if U is dichotomous with Pr(U = u|Z = z, D = 0) = e^uαz/(1 + e^αz) and γ(u, z) = γu, then ξ(z) = log{(1 + e^γ+αz)/(1 + e^αz)}. Thus, EIGENSTRAT can yield biased estimation of the SNP–disease association, although it is optimal when the assumption of linear effects holds. If there is only a single PC, then the kernel method of Chen et al. (2003) is essentially equivalent to our spline method. If there are more than two PCs, then this kernel method is unstable, whereas our method is unaffected, because the propensity score is one-dimensional.

The stratification score of EAS is an estimate of ξ in model (2) with β = 0, and thus removes the bias due to population stratification under β = 0. To effectively remove the bias, the stratification score must be calculated correctly. EAS calculates the stratification score as a linear combination of ancestry-informative markers, even though ξ may be a highly nonlinear function. Because the stratification score of EAS involves the disease status, the variation due to estimation of the score may not be ignored in the association testing. When β ≠ 0, the stratification score is not an appropriate estimate of ξ, so the resulting estimator of β may be biased. Originally, EAS selected ancestry-informative markers via partial least squares regression, which can result in substantial overfitting and loss of power when there are a large number of markers (Lee et al. 2008). Recently, Sarasua et al. (2009) suggested calculating the stratification score based on the top 10 PCs instead of on individual markers.

Both our approach and ZRM rely on propensity scores. However, our propensity scores are first calculated from the control or case sample and then matched to the other sample, whereas those of ZRM are calculated from the combined sample of cases and controls. As shown in Proposition 1(b), the propensity scores based on the entire sample are inappropriate when β ≠ 0, and thus ZRM does not yield consistent estimators of nonzero β. Even under the null hypothesis that β = 0, ZRM still may produce biased estimation of β because it enters the propensity score into the SNP–disease association model as a linear term, which is likely a faulty functional form. ZRM does not account for variation due to estimation of the propensity scores, and thus may underestimate the variance of the estimated genetic effect. ZRM has some other limitations, including requiring an arbitrary dichotomization of G and accommodating only low-dimensional markers.

3. SIMULATION STUDIES

We conducted a series of simulation studies to assess the Performance of the proposed methods in realistic settings. We used a case-control design with 1000 cases and 1000 controls. We generated data for controls as follows. We first simulated 1 million markers in the same manner as done by Price et al. (2006). We then calculated the PCs for these markers and set Z = (1, Z₁, …, Z₁₀)^T, where Z₁, …, Z₁₀ are the top PCs. Given Z, we generated G from model (5) with ${\mathit{\eta }}^{\text{T}}\mathbf{Z}=-0.3+0.6{\sum }_{j=1}^{10}{Z}_j$. We generated data for cases under model (1) with β(g) = βg and γ(u, z) = γu using acceptance–rejection sampling. Specifically, we generated Z and G as before and generated U from the logistic probability function

$$U+{\left\{1+e^{0.7{\sum }_{j=1}^{10}{Z}_j+\epsilon }\right\}}^{-1},$$

where ε is an independent normal variable with mean 0 and variance σ². (Note that U ranges between 0 and 1 and can be understood as an ancestry proportion, such as the fraction of European ancestry. If σ² = 0, then U is determined by Z without error; if σ² ≠ 0, then U is not fully captured by Z.) We accepted the observation (G, Z) if a uniform [0, 1] random variable was less than M⁻¹e^βG+γU, where M is an upper bound for e^βG+γU, γ = −1.2, and β = −0.4, 0 or 0.4.

We used B-splines of order 3 on the 10 quantiles of the propensity scores. For comparisons, we included the logistic regression of D on G and Z, as well as the logistic regression of D on G and U. The former pertains to EIGENSTRAT with Z being the PCs, and the latter pertains to the ideal situation of known population substructure. We also included EAS and ZRM. Table 1 summarizes the results of the simulation studies for making inference on β.

Table 1.

Summary statistics for the simulation studies

Method		σ2=0			σ2 =0.25
		β = −0.4	β = 0	β = 0.4	β = −0.4	β = 0	β =0.4
Known structure	Bias	−0.0034	−0.0008	0.0023	−0.0029	−0.0002	0.0023
	SE	0.0807	0.0800	0.0846	0.0791	0.0788	0.0828
	SEE	0.0804	0.0802	0.0832	0.0794	0.0791	0.0820
	Power	0.9609	0.00098	0.9356	0.9667	0.00093	0.9443
GAPS	Bias	0.0008	0.0041	0.0069	0.0005	0.0039	0.0067
	SE	0.0814	0.0803	0.0844	0.0812	0.0802	0.0841
	SEE	0.0813	0.0805	0.0835	0.0813	0.0804	0.0834
	Power	0.9471	0.00098	0.9399	0.9481	0.00093	0.9387
EIGENSTRAT	Bias	0.0389	0.0403	0.0431	0.0345	0.0374	0.0404
	SE	0.0767	0.0762	0.0808	0.0766	0.0761	0.0805
	SEE	0.0776	0.0777	0.0810	0.0777	0.0777	0.0809
	Power	0.9220	0.0023	0.9863	0.9267	0.0020	0.9857
EAS	Bias	0.1085	0.0302	0.0236	0.1109	0.0297	0.0230
	SE	0.0688	0.0747	0.0799	0.0682	0.0745	0.0797
	SEE	0.0705	0.0771	0.0805	0.0700	0.0770	0.0804
	Power	0.8258	0.0014	0.9773	0.8270	0.0014	0.9766
ZRM	Bias	0.0479	0.0381	0.0352	0.0446	0.0352	0.0326
	SE	0.0759	0.0733	0.0807	0.0758	0.0731	0.0804
	SEE	0.0774	0.0775	0.0807	0.0774	0.0775	0.0806
	Power	0.9036	0.0018	0.9822	0.9106	0.0016	0.9816

NOTE: Bias is the mean of the estimator of β minus the true value. SE is the standard error of the parameter estimator. SEE is the mean of the standard error estimator. Power is the empirical type I error (under β = 0) or power (under β = −0.4 or 0.4) for testing the null hypothesis H₀ : β = 0 at the 10⁻³ nominal significance level. Each entry is based on 1 million replicates. The results for GAPS pertain to GAPS(C); those of GAPS(D) are nearly identical.

For GAPS, the parameter estimator is virtually unbiased, the standard error estimator is accurate, and the type I error is close to the nominal significance level. Indeed, GAPS does nearly as well as the logistic regression with known substructure in terms of bias, standard error, type I error, and power. EIGENSTRAT, EAS and ZRM all yield biased parameter estimation and inflated type I error. Because the biases are positive whether the true β is positive or negative, these three methods are more powerful than GAPS under β = 0.4 and less powerful than GAPS under β = −0.4.

We also assessed the performance of GAPS under misspecified models. For example, we generated G from model (5) with ${\mathit{\eta }}^{\text{T}}\mathbf{Z}=-0.3+0.6{\sum }_{j=1}^{10}{Z}_j+0.3Z_1{Z}_2$, but ignored the interaction in calculating the propensity scores. Under β = 0, the bias of β̂ was approximately 0.004 with standard error 0.08, and the type I error was approximately 0.0008 at the 10⁻³ nominal significance level, whether σ² = 0 or 0.25. In addition, when the propensity scores were generated from the proportional odds model but estimated under model (5), the simulation results remained virtually the same.

Finally, we considered the simulation setting of Price et al. (2006), for which EIGENSTRAT is optimal. We found that GAPS had accurate control of the type I error and was nearly as powerful as EIGENSTRAT. For discrete subpopulations with moderate ancestry differences between cases and controls, the power to detect the causal SNPs was approximately 0.460 for GAPS and 0.483 for EIGENSTRAT; for admixed population with ancestry differences between cases and controls based on ancestry risk r = 2, the power to detect the causal SNPs was approximately 0.468 for GAPS and 0.485 for EIGENSTRAT.

4. REAL EXAMPLE

The Wellcome Trust Case Control Consortium (WTCCC) (2007) conducted a landmark GWA study in the British population using the Affymetrix GeneChip 500K Mapping Array Set. The study examined approximately 2000 individuals for each of seven major diseases—bipolar disorder (BD), coronary artery disease (CAD), Crohn’s disease (CD), hypertension (HT), rheumatoid arthritis (RA), type 1 diabetes (T1D), and type 2 diabetes (T2D)—and a shared set of approximately 3000 controls. The seven conditions are all common familial diseases of major public health significance. The control individuals came from two sources: 1500 individuals from the 1958 British Birth Cohort and 1500 individuals from blood donors. Even after exclusion of individuals with evidence of recent non-European ancestry, the British population is heterogeneous, having been shaped by several waves of immigration from southern and northern Europe. The case and control samples might differ in the distribution of ancestry, due either to bias in ascertaining controls or to overrepresentation of sub-populations with higher disease risk in cases.

We wished to compare the effectiveness of the proposed and existing methods in correcting for population stratification in the WTCCC data. After downloading the data from the WTCCC Web site, we excluded the SNPs and subjects on the WTCCC’s exclusion lists. In addition, we removed SNPs on the sex chromosomes, as well as any SNP with missing rate > 5%, minor allele frequency < 1%, or Hardy–Weinberg p-value < 0.001. The resulting data contain approximately 395,000 SNPs with slightly less than 5000 subjects for each case-control comparison; see Table 2 for details. For principal components analysis, we removed two small regions of known extensive local LD, namely the MHC region on chromosome 6 (25–35 Mb) and the chromosome 8 inversion region (7–13 Mb), excluded SNPs with minor allele frequencies < 5%, and generated a pruned subset of SNPs with pairwise correlations r² < 0.25 through two iterations of the PLINK (Purcell et al. 2007) command “indep-pairwise 200 100 0.25.” For each disease, the pruned subset contains approximately 81,000 SNPs. We performed principal components analysis on the pruned data sets by iteratively deleting any SNPs that are strongly associated with the top 10 PCs (p-values < 10⁻⁸). We used the top 10 PCs for all methods. Nonparametric estimation showed evidence of nonlinear effects of the PCs on the odds ratios of disease. For GAPS, we used B-splines of order 3 on the 10 quantiles of the propensity scores.

Table 2.

Analysis of the WTCCC data

	BD	CAD	CD	HT	RA	T1D	T2D
# subjects	4806	4864	4686	4890	4798	4901	4862
# analyzed SNPs	394,661	394,668	394,849	394,749	394,703	394,677	394,641
# SNPs used in PCs	81,348	81,246	80,971	81,256	81,281	81,289	81,309
	Genomic control λ
Unadjusted	1.118	1.072	1.111	1.068	1.039	1.058	1.083
EIGENSTRAT	1.080	1.067	1.078	1.070	1.038	1.057	1.066
EAS	1.080	1.062	1.088	1.069	1.036	1.053	1.061
ZRM	1.048	1.064	1.072	1.074	1.040	1.061	1.059
GAPS(C)	1.057	1.012	1.013	1.005	0.980	0.998	1.014
GAPS(D)	1.036	0.999	1.005	0.997	0.970	0.989	1.004

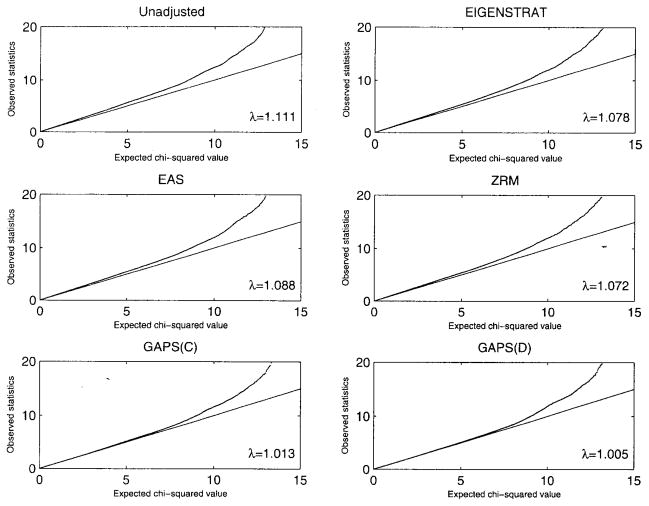
Figure 1 provides quantile–quantile plots for Crohn’s disease. Without adjustment of population stratification, the observed test statistics are noticeably higher than the expected values, even in the left tail, and λ is approximately 1.11. EIGENSTRAT, EAS, and ZRM change the results only slightly, with values of λ of 1.08, 1.09, and 1.07, respectively. For both GAPS(C) and GAPS(D), the observed statistics agree well with the expected values except in the extreme right tail, which corresponds to significant association signals, and the values of λ are approximately 1.01.

Figure 1.

Quantile–quantile plots for analysis of the WTCCC data on Crohn’s disease with or without correction for population stratification. The straight line pertains to the null distribution.

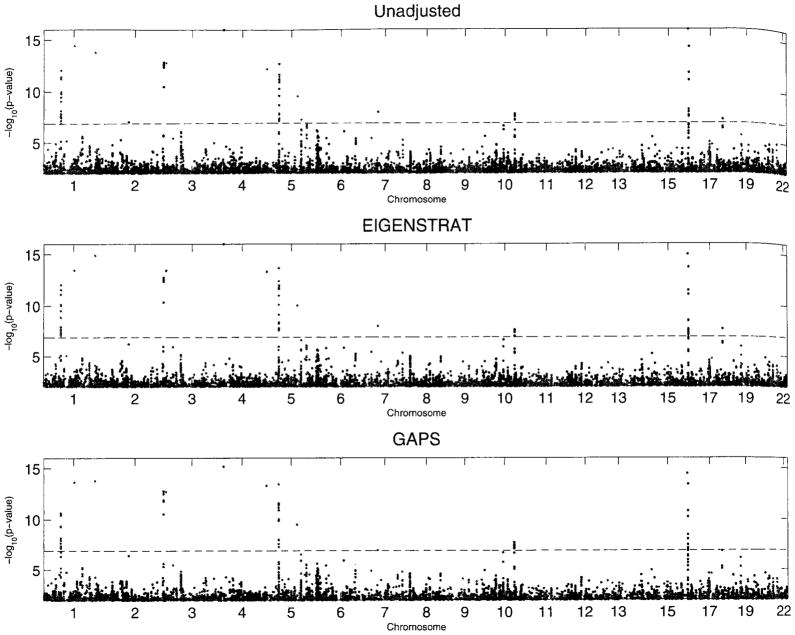
Figure 2 compares the unadjusted analysis, EIGENSTRAT, and GAPS(C) for Crohn’s disease. The first two methods yield highly similar results, whereas GAPS(C) reduces the number of significant SNPs considerably and yields quite different rankings of the top SNPs. The numbers of SNPs reaching the Bonferroni threshold of genomewide significance are 70, 72, 68, 70, 58, and 63 for the unadjusted analysis, EIGENSTRAT, EAS, ZRM, GAPS(C), and GAPS(D), respectively. For the top 100SNPs picked by the unadjusted analysis, the Pearson’s correlation coefficients of the unadjusted analysis with EIGENSTRAT, EAS, ZRM, GAPS(C), and GAPS(D) are 0.967, 0.981, 0.985, 0.935, and 0.918, respectively, and the corresponding Spearman’s rank correlation coefficients are 0.966, 0.986, 0.968, 0.915, and 0.938.

Figure 2.

The p-values (< 10⁻²) for the analysis of the WTCCC data on Crohn’s disease with or without correcting for population stratification. The dashed line pertains to the Bonferroni threshold for genomewide significance.

The results for the other six diseases are similar to those for Crohn’s disease. As shown in Table 2, the λ values of GAPS(C) and GAPS(D) are very close to 1, except for BD and RA. For all seven diseases, the λ values produced by GAPS(C) and GAPS(D) are closer to 1 than those of EIGENSTRAT, EAS, and ZRM, the only exception being GAPS(C) for BD. When we increased the number of knots from 10 to 12 for BD, the λ values for GAPS(C) and GAPS(D) became 1.015 and 0.993. Incidentally, replacing the standard PCs with those of Laplacian eigenmaps did not produce markedly different results; the details are omitted.

5. DISCUSSION

We have developed a theoretically justifiable and computationally feasible approach to correcting for population stratification in GWA studies. Our methods maintain proper control of type I error and provide consistent estimators of odds ratios with proper variance estimators. The computing time for GAPS is longer than that for EIGENSTRAT, but by less than one-fold. The relevant software will be posted on our Web site soon.

In the WTCCC example, we used the top 10 PCs for all methods. This approach, originally suggested by Price et al. (2006), seems to work well empirically in terms of controlling λ. It is possible to pick the PCs based on the Tracy–Widom (1994) test; however, that strategy tends to identify a very large number of PCs, causing numerical instability in downstream association analysis. We can determine which PCs to use by a variable selection procedure, at the cost of additional computation time.

The estimation of the odds ratio of disease with a candidate SNP requires that condition (3) or, equivalently, condition (4) holds. The validity of this condition, which is required not only by our methods but also by all others, is not directly testable. Violation of this assumption would be a potential source of the deviation of the observed test statistics from the theoretical values in the quantile-quantile plot. In the Supplemental Materials, we describe a method for conducting sensitivity analysis.

The only other possible reason for our methods to lose control of type I error would be miscalculation of the propensity scores. To reduce the computational burden, we adopt a parametric approach to calculating the propensity scores. Our experience shows that GAPS is insensitive to this modeling assumption. In our simulation studies, GAPS continued to have correct type I error under various misspecified models for propensity scores. In the analysis of the WTCCC data, the results were virtually unchanged when we replaced model (5) by the proportional odds model. The robustness of GAPS to the model misspecification for the propensity score is attributable to the fact that the effect of the propensity score on the risk of disease is modeled nonparametrically. It is possible to avoid parametric modeling as well as dimension reduction by relating the genotype of a candidate SNP directly to genomic markers through a supervised learning technique (e.g., random forest, support vector machine). Then the selected markers will be specific and predictive for that particular SNP. It would be computationally intensive to do this for every candidate SNP in a GWA study. One compromise might be to use parametric modeling for the initial screening and then apply supervised learning to a small set of top SNPs.

In some studies, population stratification is due to cryptic relatedness or family structure. The identifiability conditions presented in Section 2.2 still apply to such situations, because eqs. (1)–(4) pertain to the marginal distribution of (D, G, U, Z). The proposed estimator of β continues to be valid, but the variance estimation should account for the within-cluster dependence through the generalized estimating equation approach.

We have focused on case-control studies. However, our theoretical development does not rely on the case-control design, so our methods can be readily applied to cross-sectional studies with binary traits. Similar methods can be developed for continuous traits in cross-sectional studies and potentially censored age-at-onset data from cohort studies. Furthermore, it is possible to expand our methods to make likelihood-based inference on haplotype–disease associations along the lines of Lin and Zeng (2006).

APPENDIX: PROOFS OF THEORETICAL RESULTS

Proof of Theorem 1

For notational simplicity, we assume that all variables are discrete. Clearly,

$$Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=1)=\sum _{\mathbf{u}}\frac{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=1)}{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0)}\times Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0).$$

Under model (1),

$$\begin{array}{l}\frac{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=1)}{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0)}=\frac{Pr(D=1\mid \mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z})}{Pr(D=0\mid \mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z})}\frac{{\pi }_0}{{\pi }_1}\\ =e^{\beta (g)+\gamma (\mathbf{u},\mathbf{z})}\frac{{\pi }_0}{{\pi }_1},\end{array}$$ (A.1)

where π₀= Pr(D = 0) and π₁= 1 − π₀. Thus,

$$\begin{array}{l}Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=1)=\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}\sum _{\mathbf{u}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=0)\times Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=0)\\ =\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=0)\times \sum _{\mathbf{u}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=0).\end{array}$$

As a result,

$$\frac{Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=1)}{Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=0)}=\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}\sum _{\mathbf{u}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=0).$$

Because γ is arbitrary, we conclude that

$$\frac{Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=1)}{Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=0)}=e^{\beta (g)+\xi (\mathbf{z})}$$

if and only if pr(U = u|G = g, Z = z, D = 0) does not depend on g. The theorem is proved.

Proof of Proposition 1

1. It follows from (A.1) that

   $$\begin{array}{l}Pr(\mathbf{U}=\mathbf{u},G=g\mid \mathbf{Z}=\mathbf{z},D=1)=Pr(\mathbf{U}=\mathbf{u},G=g\mid \mathbf{Z}=\mathbf{z},D=0)\times e^{\beta (g)+\gamma (\mathbf{u},\mathbf{z})}\frac{{\pi }_0}{{\pi }_1}\frac{Pr(\mathbf{Z}=\mathbf{z}\mid D=0)}{Pr(\mathbf{Z}=\mathbf{z}\mid D=1)}.\end{array}$$ (A.2)

   If U and G are independent conditional on Z in the control population, then Pr(U = u, G = g|Z = z, D = 0) can be factorized into a product of two functions, one involving (u, z) and one involving (g, z). Thus, the right side of (A.2) is also a product of a function of (u, z) and a function of (g, z), which implies that U and G are independent conditional on Z in the case population. The other direction can be argued in a similar manner.

2. Clearly,

   $$Pr(\mathbf{U}=\mathbf{u},G=g\mid \mathbf{Z}=\mathbf{z})=(p_{0}Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0)+p_{1}Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=1))/(p_{0}Pr(\mathbf{Z}=\mathbf{z}\mid D=0)+p_{1}Pr(\mathbf{Z}=\mathbf{z}\mid D=1)),$$
   where p₀ is the sample proportion of controls, and p₁ = 1 − p₀. It follows from (A.1) that

   $$Pr(\mathbf{U}=\mathbf{u},G=g\mid \mathbf{Z}=\mathbf{z})=Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0)\times \frac{p_0+p_1{e}^{\beta (g)+\gamma (\mathbf{u},\mathbf{z})}{\pi }_0/{\pi }_1}{p_{0}Pr(\mathbf{Z}=\mathbf{z}\mid D=0)+p_{1}Pr(\mathbf{Z}=\mathbf{z}\mid D=1)}.$$

   If β(g) = 0, then Pr(U = u, G = g|Z = z) = Pr(U = u, G = g, Z = z|D = 0)ζ (u, z) for some function ζ (u, z). Using the arguments of the previous paragraph, we obtain the equivalence between the two conditional independence conditions. Note that the equivalence does not hold if β(g) ≠ 0 and γ (u, z) depends on u.

Proof of Theorem 2

Note that

$$Pr(G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x}\mid D=1)=\sum _{\mathbf{u},\mathbf{z}:\mathit{\psi }(\mathbf{z})=\mathbf{x}}\frac{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=1)}{Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0)}\times Pr(\mathbf{U}=\mathbf{u},G=g,\mathbf{Z}=\mathbf{z}\mid D=0).$$

Under model (1) and condition (3),

$$\begin{array}{l}Pr(G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x}\mid D=1)=\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}\sum _{\mathbf{u},\mathbf{z}:\mathit{\psi }(\mathbf{z})=\mathbf{x}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid G=g,\mathbf{Z}=\mathbf{z},D=0)\times Pr(G=g,\mathbf{Z}=\mathbf{z}\mid D=0)\\ =\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}\sum _{\mathbf{u},\mathbf{z}:\mathit{\psi }(\mathbf{z})=\mathbf{x}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=0)\times Pr(G=g\mid \mathbf{Z}=\mathbf{z},D=0)Pr(\mathbf{Z}=\mathbf{z}\mid D=0).\end{array}$$

By the assumption of the theorem, Pr(G = g|Z = z, D = 0) = Pr(G = g|ψ (Z) = x, D = 0) for z satisfying ψ (z) = x. Thus,

$$\begin{array}{l}Pr(G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x}\mid D=1)=\frac{{\pi }_0}{{\pi }_1}{e}^{\beta (g)}Pr(G=g\mid \mathit{\psi }(\mathbf{Z})=\mathbf{x},D=0)\times \sum _{\mathbf{u},\mathbf{z}:\mathit{\psi }(\mathbf{z})=\mathbf{x}}{e}^{\gamma (\mathbf{u},\mathbf{z})}Pr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=0)Pr(\mathbf{Z}=\mathbf{z}\mid D=0)\\ =\frac{{\pi }_0}{{\pi }_1}Pr(G=g,\mathit{\psi }(\mathbf{Z})=\mathbf{x}\mid D=0)e^{\beta (g)+\xi (\mathbf{x})},\end{array}$$

where

$$\xi (\mathbf{x})=log\left\{\sum _{\mathbf{u},\mathbf{z}:\mathit{\psi }(\mathbf{z})=\mathbf{x}}{e}^{\gamma (\mathbf{u},\mathbf{z})}\times Pr(\mathbf{U}=\mathbf{u}\mid \mathbf{Z}=\mathbf{z},D=0)Pr(\mathbf{Z}=\mathbf{z}\mid D=0)/Pr(\mathit{\psi }(\mathbf{Z})=\mathbf{x}\mid D=0)\right\}.$$

The conclusion holds.

Proof of Theorem 3

The proof of this theorem pertains to three major results: consistency, asymptotic normality, and variance estimation.

Consistency

Let 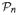and 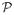denote the empirical and true probability measures, respectively. By the classical likelihood theory for parametric models (e.g., Lehmann and Casella 1998, chap. 6), η̂ converges to η₀ in probability, and

$$\widehat{\mathit{\eta }}-{\mathit{\eta }}_0=({\mathcal{P}}_n-\mathcal{P}){\stackrel{\sim }{\mathbf{l}}}_{\mathit{\eta }}(D,G,\mathbf{Z};{\mathit{\eta }}_0)+o_p\left(n^{-1/2}\right),$$ (A.3)

where

$${\stackrel{\sim }{\mathbf{l}}}_{\mathit{\eta }}(D,G,\mathbf{Z};\mathit{\eta })=E{\left[(1-D)\frac{2e^{\mathit{\eta }\text{T}\mathbf{Z}}{\mathbf{Z}}^{\otimes 2}}{{(1+e^{{\mathit{\eta }}^{\text{T}}\mathbf{Z}})}^2}\right]}^{-1}(1-D)\left(G-\frac{2e^{{\mathit{\eta }}^{\text{T}}\mathbf{Z}}}{1+e^{{\mathit{\eta }}^{\text{T}}\mathbf{Z}}}\right)\mathbf{Z},$$

and a^⊗2 = aa^T for any column vector a. It follows from the proof of Theorem 2 and condition (C.3) that ξ₀(·) has a bounded fourth derivative. By theorem 6.25 of Schumaker (2007), we can find a B-spline approximation to ξ₀(x), denoted by $\stackrel{\sim }{\xi }(x)={\sum }_{k=1}^{K_n}{\stackrel{\sim }{\theta }}_k{B}_k(x)$, such that ${\left|\right|\stackrel{\sim }{\xi }-{\xi }_0\left|\right|}_{W^{1,\infty }(\mathcal{R})}\le O(K_n^{-2})$ and ${\left|\right|\stackrel{\sim }{\xi }-{\xi }_0\left|\right|}_{L^2(\mathcal{R})}\le O(K_n^{-7/2})$, where denotes the real line and ||f||_{W^1,∞( )} = ||f||_{L^∞( )} + ||f′||_{L^∞( )} for any differentiable function f with derivative f′.

Define l(β, ξ; η) = D{βG + ξ(η^TZ)} − log{1 + e^{βG+ ξ(ηTz)}}. Also, write $\stackrel{\sim }{\xi }(x)={\sum }_{k=1}^{K_n}{\stackrel{\sim }{\theta }}_k{B}_k(x)$. Because 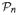l(β, ξ; η̂) is maximized at (β̂, ξ̂), we have 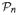l(β̂, ξ̂; η̂) ≥ 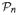l(β₀, ξ̃; η̂). Let ${\epsilon }_n=1/(1+\mid \widehat{\beta }-{\beta }_0\mid +{\sum }_{k=1}^{K_n}\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid )$. The concavity of l(β, ξ; η) for fixed η yields

$${\mathcal{P}}_{n}l\left({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };\widehat{\mathit{\eta }}\right)\ge {\mathcal{P}}_{n}l({\beta }_0,\stackrel{\sim }{\xi };\widehat{\mathit{\eta }}).$$

As a result,

$$({\mathcal{P}}_n-\mathcal{P})\left[l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };\widehat{\mathit{\eta }})-l({\beta }_0,\stackrel{\sim }{\xi };\widehat{\mathit{\eta }})\right]\ge \mathcal{P}\left[l({\beta }_0,\stackrel{\sim }{\xi };\widehat{\mathit{\eta }}-l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\stackrel{\sim }{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };\widehat{\mathit{\eta }})\right].$$ (A.4)

Note that

$$\begin{array}{l}|l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };\widehat{\mathit{\eta }})-l({\beta }_0,\stackrel{\sim }{\xi };\widehat{\mathit{\eta }})\\ -\left\{l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\stackrel{\sim }{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };{\mathit{\eta }}_0)-l({\beta }_0,\stackrel{\sim }{\xi };{\mathit{\eta }}_0)\right\}|\\ \le O_p(\mid \widehat{\mathit{\eta }}-{\mathit{\eta }}_0\mid )\underset{k}{max}{\left|\right|B_k^{\prime }(x)\left|\right|}_{l^{\infty }}\le K_n{O}_p(n^{-1/2})\end{array}$$

uniformly in G and Z, where $B_k^{\prime }(x)={dB}_k(x)/dx$. Thus, (A.4) yields

$$({\mathcal{P}}_n-\mathcal{P})\left[l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };{\mathit{\eta }}_0)-l({\beta }_0,\stackrel{\sim }{\xi };{\mathit{\eta }}_0)\right]+O_p(K_n{n}^{-1/2})\ge \mathcal{P}\left[l({\beta }_0,\stackrel{\sim }{\xi };{\mathit{\eta }}_0)-l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };{\mathit{\eta }}_0)\right].$$ (A.5)

By lemma 2.6.15 of van der Vaart and Wellner (1996), the function

$$l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };{\mathit{\eta }}_0)-l({\beta }_0,\stackrel{\sim }{\xi };{\mathit{\eta }}_0)$$

belongs to a bounded Vapnik–Červonenkis class with index (K_n + 3) and has a bounded covering function. Thus, the left side of (A.4) can be further bounded by O_p(K_nn^−1/2). The second-order Taylor expansion of the right side of (A.5) at (β₀, ξ₀) yields

$$\mathcal{P}[l({\beta }_0,\stackrel{\sim }{\xi };{\mathit{\eta }}_0)]=\mathcal{P}[l({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)]-O_p(K_n^{-7}).$$

By similar arguments, there exists some positive constant c₀ such that

$$\mathcal{P}[l({\epsilon }_n\widehat{\beta }+(1-{\epsilon }_n){\beta }_0,{\epsilon }_n\widehat{\xi }+(1-{\epsilon }_n)\stackrel{\sim }{\xi };{\mathit{\eta }}_0)]=\mathcal{P}[l({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)]-c_{0}E\left[{\left\{{\epsilon }_n(\widehat{\beta }-{\beta }_0)G+{\epsilon }_n(\widehat{\xi }({\mathit{\eta }}_0^{\text{T}}\mathbf{Z})-\stackrel{\sim }{\xi }({\mathit{\eta }}_0^{\text{T}}\mathbf{Z}))+(\stackrel{\sim }{\xi }({\mathit{\eta }}_0^{\text{T}}\mathbf{Z})-{\xi }_0({\mathit{\eta }}_0^{\text{T}}\mathbf{Z}))\right\}}^2\right].$$

It then follows from (A.5) and condition (C.1) that

$$O_p(K_n{n}^{-1/2})+O_p(K_n^{-7})\ge c_0{\epsilon }_n^2\{{\mid \widehat{\beta }-{\beta }_0\mid }^2+{\left|\right|\widehat{\xi }-\stackrel{\sim }{\xi }\left|\right|}_{L_2(\mathcal{Z})}^2\},$$

where 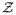denotes the support of ${\mathit{\eta }}_0^{\text{T}}\mathbf{Z}$. Because ${\left|\right|\widehat{\xi }-\stackrel{\sim }{\xi }\left|\right|}_{L_2(\mathcal{Z})}^2\ge c_1{\sum }_k{\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid }^2$ for some constant c₁ (de Boor 1978, p. 155), we have

$${\left\{1+\mid \widehat{\beta }-{\beta }_0\mid +\sum _k\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid \right\}}^2\{O_p(K_n{n}^{-1/2})+O_p(K_n^{-7})\}\ge \left\{{\mid \widehat{\beta }-{\beta }_0\mid }^2+\sum _k{\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid }^2\right\}.$$

Thus,

$$\left\{1+{\mid \widehat{\beta }-{\beta }_0\mid }^2+\sum _k{\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid }^2\right\}{K}_n^2\{O_p(K_n{n}^{-1/2})+O_p(K_n^{-7})\}\ge \left\{{\mid \widehat{\beta }-{\beta }_0\mid }^2+\sum _k{\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid }^2\right\}.$$ (A.6)

Condition (C.4) implies that $O_p(K_n^3{n}^{-1/2})+O_p(K_n^{-5})<1/2$ for sufficiently large n. It then follows from (A.6) that

$$O_p(K_n^3{n}^{-1/2})+O_p(K_n^{-5})\ge \left\{{\mid \widehat{\beta }-{\beta }_0\mid }^2+\sum _k{\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid }^2\right\}.$$

Thus,

$${\mid \widehat{\beta }-{\beta }_0\mid }^2+{\left|\right|\widehat{\xi }-\stackrel{\sim }{\xi }\left|\right|}_{L_2(\mathcal{R})}^2=O_p(K_n^3{n}^{-1/2})+O_p(K_n^{-5}),$$

which implies that

$${\left|\right|\widehat{\xi }-\stackrel{\sim }{\xi }\left|\right|}_{W^{1,\infty }(\mathcal{R})}\le O_p\left(\sum _{k=1}^{K_n}\mid {\widehat{\theta }}_k-{\stackrel{\sim }{\theta }}_k\mid \right)K_n+O_p(K_n^3/n^{1/4}+1/K_n).$$

By the choice of K_n in condition (C.4), we obtain |β̂ − β₀| → 0 and ||ξ̂ − ξ₀||_{W^1,∞( 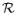)} → 0 in probability. This proves the consistency.

To determine the convergence rate, we reexamine the inequality given in (A.4) by setting ε_n to 1. Because ξ̂ converges to ξ₀ in W^1,∞-norm, the left side of (A.4) is o_p(n^−1/2), whereas the right side is bounded from below by $c_2({\mid \widehat{\beta }-{\beta }_0\mid }^2+{\left|\right|\widehat{\xi }-{\xi }_0\left|\right|}_{L_2(\mathcal{Z})}^2)-O_p(K_n^{-7})$ for some positive constant c₂. Thus,

$${\mid \widehat{\beta }-{\beta }_0\mid }^2+{\left|\right|\widehat{\xi }-{\xi }_0\left|\right|}_{L_2(\mathcal{Z})}^2=O_p(K_n^{-7})+o_p(n^{-1/2}).$$

Asymptotic normality

We first derive the least favorable direction for β₀; that is, we obtain a function h₀(·) such that

$$E[l_{\xi }^{\ast }{l}_{\beta }]=E[l_{\xi }^{\ast }{l}_{\xi }[h_0]],$$

where l_β is the score for β₀, l_ξ[h₀] is the score function for ξ₀ along the submodel ξ₀ + εh₀, and $l_{\xi }^{\ast }$ is the dual operator of l_ξ. By the semi-parametric efficiency theory (Bickel et al. 1993),

$$h_0(x)=\frac{E[q(G,\mathbf{Z})G\mid {\mathit{\eta }}_0^{\text{T}}\mathbf{Z}=x]}{E[q(G,\mathbf{Z})G\mid {\mathit{\eta }}_0^{\text{T}}\mathbf{Z}=x]},$$

where $q(G,\mathbf{Z})=e^{{\beta }_{0}G+{\xi }_0({\mathit{\eta }}_0^{\text{T}}\mathbf{Z})}/{(1+e^{{\beta }_{0}G+{\xi }_0({\mathit{\eta }}_0^{\text{T}}\mathbf{Z})})}^2$. Clearly, h₀(·) has a bounded fourth derivative. We approximate h₀ by the B-spline sequence h̃ and show that ${\left|\right|h_0-\stackrel{\sim }{h}\left|\right|}_{W^{1.\infty }(\mathcal{R})}=O_p(K_n^{-2})$ and ${\left|\right|h_0-\stackrel{\sim }{h}\left|\right|}_{L_2(\mathcal{R})}=O_p(K_n^{-7/2})$. Because β̂ solves the equation

$${{\mathcal{P}}_n\frac{\partial }{\partial \beta }l(\widehat{\beta }+\epsilon ,\widehat{\xi }+\epsilon \stackrel{\sim }{h};\widehat{\mathit{\eta }})|}_{\epsilon =0}=0,$$

we obtain 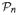l_β (β̂, ξ̂; η̂) + 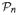l_ξ(β̂, ξ̂; η̂) [h̃] = 0. Thus,

$$({\mathcal{P}}_n-\mathcal{P})\{l_{\beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})+l_{\xi }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})[\stackrel{\sim }{h}]\}=-\mathcal{P}\{l_{\beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})+l_{\xi }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})[\stackrel{\sim }{h}]\}.$$ (A.7)

Because ξ̂ and h̃ have bounded first derivatives and l_β and l_ξ are differentiable, the Donsker theorem (van der Vaart and Wellner 1996, thm. 2.5.2) implies that the left side of (A.7) is equal to

$$({\mathcal{P}}_n-\mathcal{P})\{l_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\}+o_p(n^{-1/2}).$$

Given the consistency of (β̂, ξ̂, η̂), the Taylor expansion of the right side of (A.7) yields

$$\begin{array}{l}-(1+o_p(1))\mathcal{P}\{l_{\beta \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\}(\widehat{\beta }-{\beta }_0)\\ -(1+o_p(1))\mathcal{P}\{l_{\beta \xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[\widehat{\xi }-{\xi }_0]\\ +l_{\xi \xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0,\widehat{\xi }-{\xi }_0]\}-(1+o_p(1))\\ \times \mathcal{P}\left\{\frac{\partial }{\partial \mathit{\eta }}{l}_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+\frac{\partial }{\partial \mathit{\eta }}{l}_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\right\}(\widehat{\mathit{\eta }}-{\mathit{\eta }}_0)\\ +O_p({\mid \widehat{\beta }-{\beta }_0\mid }^2+{\left|\right|\widehat{\xi }-{\xi }_0\left|\right|}_{L_2(\mathcal{Z})}^2+{\mid \widehat{\mathit{\eta }}-{\mathit{\eta }}_0\mid }^2),\end{array}$$ (A.8)

where l_ββ (β, ξ; η) denotes the second derivative of l(β, ξ; η) with respect to β, l_βξ (β, ξ; η)[h] denotes the further derivative of l_ξ(β, ξ; η) [h] with respect to β, and l_ξξ (β, ξ, η)[h, h̃] denotes the further derivative of l_ξ [h] along the submodel ξ + εh̃.

The choice of h₀ implies that the second term of (A.8) is 0. The convergence rate of (β̂, ξ̂), together with condition (C.4), implies that the last term of (A.8) is o_p(n^−1/2). Thus,

$$\begin{array}{l}-(1+o_p(1))\mathcal{P}\{l_{\beta \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\}(\widehat{\beta }-{\beta }_0)\\ =({\mathcal{P}}_n-\mathcal{P})\{l_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\}\\ +\mathcal{P}\left\{\frac{\partial }{\partial \mathit{\eta }}{l}_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+\frac{\partial }{\partial \mathit{\eta }}{l}_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\right\}(\widehat{\mathit{\eta }}-{\mathit{\eta }}_0)\\ +o_p(n^{-1/2}).\end{array}$$ (A.9)

We claim that that 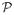{l_ββ (β₀, ξ₀; η₀) + l_ξβ(β₀, ξ₀, η₀)[h₀]} is nonzero. If this claim does not hold, then l_β (β₀, ξ₀; η₀) + l_ξ(β₀, ξ₀; η₀)[h₀] has zero variance and thus must be equal to 0 with probability 1. That is, $G+h_0({\mathit{\eta }}_0^{\text{T}}\mathbf{Z})=0$ or $var(G\mid {\mathit{\eta }}_0^{\mathbf{T}}\mathbf{Z})=0$ with probability 1, which contradicts condition (C.1). The asymptotic normality of β̂ then follows from (A.9) and (A.3).

Variance estimation

From the proof of asymptotic normality, the influence function for β̂ is

$$\begin{array}{l}-\mathcal{P}{\{l_{\beta \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi \beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\}}^{-1}\\ \times [l_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+l_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\\ +\mathcal{P}\left\{\frac{\partial }{\partial \mathit{\eta }}{l}_{\beta }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)+\frac{\partial }{\partial \mathit{\eta }}{l}_{\xi }({\beta }_0,{\xi }_0;{\mathit{\eta }}_0)[h_0]\right\}{\stackrel{\sim }{\mathbf{l}}}_{\mathit{\eta }}(D,G,\mathbf{Z};{\mathit{\eta }}_0)].\end{array}$$

If we can find a consistent estimator of h₀ in the L₂(P) space, denoted by ĥ, then a consistent estimator of the limiting variance of n^1/2(β̂ − β₀) is

$$\begin{array}{l}{\mathcal{P}}_n{\{l_{\beta \beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})+l_{\xi \beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})[\widehat{h}]\}}^{-2}\\ \times {\mathcal{P}}_n[l_{\beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})+l_{\xi }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})[\widehat{h}]\\ {+{\mathcal{P}}_n\left\{\frac{\partial }{\partial \mathit{\eta }}{l}_{\beta }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})+\frac{\partial }{\partial \mathit{\eta }}{l}_{\xi }(\widehat{\beta },\widehat{\xi };\widehat{\mathit{\eta }})[\widehat{h}]\right\}{\widehat{\mathbf{l}}}_{\mathit{\eta }}(D,G,\mathbf{Z})]}^2,\end{array}$$ (A.10)

where

$${\widehat{\mathbf{l}}}_{\mathit{\eta }}(D,G,\mathbf{Z})={\mathcal{P}}_n{\left[(1-D)\frac{2e^{{\widehat{\mathit{\eta }}}^{\text{T}}\mathbf{Z}}{\mathbf{Z}}^{\otimes 2}}{{(1+e^{{\widehat{\mathit{\eta }}}^{\text{T}}\mathbf{Z}})}^2}\right]}^{-1}\times (1-D)\left(G-\frac{2e^{{\widehat{\mathit{\eta }}}^{\text{T}}\mathbf{Z}}}{1+e^{{\widehat{\mathit{\eta }}}^{\text{T}}\mathbf{Z}}}\right)\mathbf{Z}.$$

To find a consistent estimator for h₀, we solve the following equation:

$${\mathcal{P}}_n[l_{\xi }^{\ast }{l}_{\xi }[h]]={\mathcal{P}}_n[l_{\xi }^{\ast }{l}_{\beta }],$$ (A.11)

where the parameters (β, ξ, η) are evaluated at (β̂, ξ̂, η̂), and h is on the tangent space of the sieve space, that is, $h(x)={\sum }_{k=1}^{K_n}{\theta }_k{B}_k(x)$. As a linear operator, the left side of (A.11) converges to $E[l_{\xi }^{\ast }{l}_{\xi }[h]]$ with the parameters taking the true values. Because the information operator $E[l_{\xi }^{\ast }{l}_{\xi }[h]]$ is invertible, so is ${\mathcal{P}}_n[l_{\xi }^{\ast }{l}_{\xi }[h]]$. In addition, the inverse of the latter converges to the inverse of the former. If then follows from the continuity of linear operators that the solution to (A.11), denoted by ĥ, converges to h₀.

Note that eq. (A.11) is essentially a system of linear equations. Algebraically, the calculation of (A.10) is equivalent to the variance estimation by treating model (6) as a parametric model with parameters β, θ, and η. Thus, the limiting covariance matrix of n^1/2(β̂ − β₀, (θ̂ − θ₀)^T)^T can be consistently estimated by the sandwich estimator H⁻¹VH⁻¹, where

$$\begin{array}{l}\mathbf{H}=-n^{-1}\sum _{i=1}^n\frac{e^{\widehat{\beta }{G}_i+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}}{{\{1+e^{\widehat{\beta }{G}_i+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}\}}^2}{\left[\begin{array}{c}{G}_i\\ B_1({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\\ ⋮\\ B_{K_n}({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\end{array}\right]}^{\otimes 2},\\ \mathbf{V}=n^{-1}\sum _{i=1}^n{\mathbf{W}}_i^{\otimes 2},\\ {\mathbf{W}}_i=\left\{D_i-\frac{e^{\widehat{\beta }{G}_i+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}}{1+e^{\widehat{\beta }{G}_i+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)}}\right\}\left[\begin{array}{c}{G}_i\\ B_1({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\\ ⋮\\ B_{K_n}({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_i)\end{array}\right]\\ -(n^{-1}\sum _{j=1}^n\frac{e^{\widehat{\beta }{G}_j+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_j)}{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k^{\prime }({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_j)}{{\{1+e^{\widehat{\beta }{G}_j+{\sum }_{k=1}^{K_n}{\widehat{\theta }}_k{B}_k({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_j)}\}}^2}\\ \times \left[\begin{array}{c}{G}_j\\ B_1({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_j)\\ ⋮\\ B_{K_n}({\widehat{\mathit{\eta }}}^{\text{T}}{\mathbf{Z}}_j)\end{array}\right]{\mathbf{Z}}_j^{\text{T}}){\widehat{\mathbf{l}}}_{\mathit{\eta }}(D_i,G_i,{\mathbf{Z}}_i).\end{array}$$