Nonrigid Registration and Classification of the Kidneys in 3D Dynamic Contrast Enhanced (DCE) MR Images

Abstract

We have applied image analysis methods in the assessment of human kidney perfusion based on 3D dynamic contrast-enhanced (DCE) MRI data. This approach consists of 3D non-rigid image registration of the kidneys and fuzzy C-mean classification of kidney tissues. The proposed registration method reduced motion artifacts in the dynamic images and improved the analysis of kidney compartments (cortex, medulla, and cavities). The dynamic intensity curves show the successive transition of the contrast agent through kidney compartments. The proposed method for motion correction and kidney compartment classification may be used to improve the validity and usefulness of further model-based pharmacokinetic analysis of kidney function.

1. INTRODUCTION

The kidneys maintain normal homeostasis by filtering and excreting metabolic waste products, by regulating acid base balance, and by moderating blood pressure and fluid volume [1]. Renal diseases can lead to kidney failure that requires life-long dialysis or renal transplantation. Early detection and treatment can prevent this progression towards end stage renal disease. Therefore, it is important to monitor renal function precisely for the assessment of disease progression and follow-up of therapy. Dynamic contrast enhanced (DCE) magnetic resonance imaging (DCE-MRI) provides a promising non-invasive technique for the assessment of physiological parameters such as renal blood flow or glomerular filtration rate without the need of ionizing radiation [2]. In DCE-MRI, contrast agent Gd-DTPA is injected into the bloodstream. As the agent perfuse into the organ, the kidneys are imaged rapidly and repeatedly. During the perfusion, Gd- DTPA causes a change in the relaxation time of the tissue and creates a contrast change in the images [3]. As a result, the patterns of the contrast change provide functional information, while MRI provides good anatomical information which helps in distinguishing the diseases that affect different regions of the kidneys [4]. One of the major advantages of DCE-MRI lies in the separable assessment of perfusion and filtration parameters for each kidney while blood tests just deliver global data [5].

A major problem in abdominal imaging is motion artifacts due to respiration [2, 6–9]. Various methods have been proposed to reduce the motion artifacts [6]. Various image registration methods have been applied to the abdominal images [10–15]. The goal of this study is to evaluate non-rigid registration and classification methods to improve DCE-MRI image quantification.

2. METHODS

DCE-MRI assesses the signal dynamics caused by contrast material transit through the renal cortex, medulla and the collecting system [16]. This technique implies the administration of gadolinium containing contrast agents, which enter the capillaries, are partly filtered in the glomeruli, then pass through the renal tubules or are evacuated by the veins. By analyzing the contrast enhancement as a function of time, several clinically relevant parameters such as blood flow, blood volume, mean transit times and glomerular filtration can be derived [17–19]. Our assessment method consists of four major steps: (1) Preprocess and select one 3D volume as the reference, and then register other volumes to this reference; (2) Manually segment left and right kidneys in the reference volume; (3) Classify segmented kidneys into three classes (cortex, medulla, and cavities). (4) Apply the three-class object maps to all registered volumes and perform assessment of time courses. Figure 1 shows typical DCE-MRI images at different time courses. The image intensity of the kidneys increase and then reduce along capturing time. The variety indicates perfusion and filtration function of the kidney.

Figure 1.

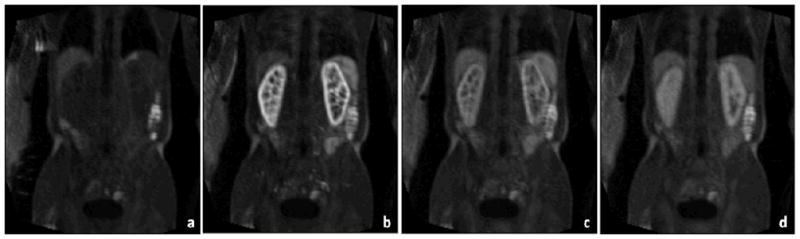
DCE-MRI images at different time points.

Motion correction of abdominal DCE-MRI time series is a challenge. Two types of motion and deformation present and are visible in the images. The first type is the motion and deformation of tissue as a result of respiration, while the second is the motion of the contrast agent. To correct motion resulting from breathing, the registration method needs to be unaffected by intensity changes caused by the accumulation and excretion of the contrast agent.

The demons algorithm is an automatic non-rigid image registration algorithm, accounting for non-rigid deformation of the subject by means of a diffusion model [20, 21]. Demons forces are estimated using the optical flow formula. An improved demon algorithm [22] with a much better efficiency was exploited in our study and it has an adaptive force strength adjustment during the iterative process. A slight adaptation of the algorithm makes the registration edge-emphasized by using the edge strength of the image to control the optical flow in different regions. By emphasizing the edges, the smoothing/noise-removing effect caused by the dataset estimation will minimize the effects of texture distortion in the registered images. A normalization factor proposed by [23] allows the force strength to be adjusted adaptively over different iterations to determine the scale of deformation.

For each voxel, The energy function to minimize in the case of the demons registration algorithm, between a registered image f (floating image) and a truth image r (reference image), is described as follows:

$$E(u)={(I_r-I_f+u\nabla I_f)}^2+{\beta }^2{(I_r-I_f)}^2·u^2$$ (1)

where I_r and I_f are the intensities of the same voxel in the respective images r and f, ∇ is the gradient operator and u is the estimated displacement (update velocity). β is the normalization factor. It is noted that the demons registration algorithm is a local approximation, thus it is performed for a certain number of iterations until the solution converges; the displacement vector u is updated in each iteration so that any deformation in the image are accounted for progressively. In our experiments, the number of iterations is set to be 100 to ensure convergence, but if the energy function falls below a certain threshold in any iteration, the algorithm is terminated immediately since an optimized solution is found. The similarity measure used here is the squared pixel distance, with squared gradient of the transformation field being set as the smoothness regularization.

The optical flow equation for finding small deformations is used as the basis for demons registration [24]. The optical flow equation defines how the registration forces act on the image to account for deformation. The estimated displacement u required for a point in the reference image r to match a point in the floating image f is given by:

$$u=\frac{(I_r-I_f)\nabla I_f}{{\mid \nabla I_f\mid }^2+{\beta }^2{(I_r-I_f)}^2}+\frac{(I_r-I_f)\nabla I_r}{{\mid \nabla I_r\mid }^2+{\beta }^2{(I_r-I_f)}^2}$$ (2)

The first term in (2) is derived directly from (1) given that the error gradient is zero where the error is at a minimum. In [25], the velocity formula contained only the first term in (2) without the constant, which uses only edges in the reference image as the passive internal force. It is based on pixel velocities caused by edge based forces. The term in the denominator serves to make the velocity equation more stable in image registration. To regularize the deformation field, Gaussian smoothing is performed on the velocity field since the estimated displacement obtained is local. The second term in (2) is then introduced in [22] to improve registration convergence efficiency and robustness. The resulting pixel velocity transformation field is filtered by a Gaussian kernel for global registration. The demons are responsible for applying force vectors on the deformable grid in moving images. Based on the location of the grid point in moving images with respect to the contours in fixed images, the demons decide the direction of the force vectors. Iteratively, the force created by the demons cause motion that is applied to the model. As the model draws closer to the contours, the forces applied decreases gradually after each iteration. At convergence, the determined deformation field in moving images is applied to warp into fixed images.

For the DCE-MRI images, each of the epochs provides a 3D volume which is registered to a pre-determined base 3D volume. For the fixed volume we first segment cavities manually and then use fuzzy C-mean classification methods [26–29] to class cortex and medulla. Finally we apply three classes object maps to all registered volumes and perform assessment of time courses. The conventional FCM algorithm is an iterative method that produces an optimal c partition for the image ${\{x_i\}}_{i=1}^N$ by minimizing the weighted intergroup sum of squared error objective function FCM

$$\mathit{FCM}=\sum _{k=1}^c\sum _{i=1}^N{u}_{ik}{\left|\right|x_i-v_k\left|\right|}^2$$ (3)

where ${\{v_k\}}_{k=1}^c$ is the characterized intensity center of the class k, and c is the number of underlying tissue types in the image which is given before classification. The u_ik represents the possibility of the voxel i belonging to the class k and it is required that u_ik ∈ [0,1] and ${\displaystyle \sum _{k=1}^c}{u}_{ik=1}$ for any voxel i.

3. RESULTS

Highly accelerated renal perfusion imaging was developed allowing high frequency imaging during the first-pass of 0.05 mmol/kg ProHance using a 3D spoiled gradient echo technique with fat saturation and centric-radial k-space acquisition using a 430 mm² FOV, TR=3.7ms, TE=1.7ms, flip=30°, 30 slices at 2.8 mm slice thickness, TFE factor = 120, 0.9 second per dynamic scan volume, and iPAT factor=2. A phased array 4-element surface flexible body wrap coil is used. The Gd is infused at a constant rate over 20s.

Figure 2 illustrates the visual assessment of the registration results at different time course. There is motion before registration, and if not corrected, the motion will introduce errors for the analysis of DCE-MR images. Figure 3 shows evaluation of the registration algorithm based on the comparison between the mean intensity time courses within a ROI before registration and after registration. Figure 4 indicates evaluation of the registration algorithm based on the comparison of the mean intensity time courses of cortex, medulla and cavities of the left kidney before and after registration. However, the curve is still not as smooth as we would expect. We first thought that registration may not be able to correct the motion. In order to explain this phenomenon we performed a phantom experiment without motion. We filled syringes and a bottle with Gd-DTPA and used them as phantoms. We used the same protocol to scan the phantoms. Figure 5 shows the intensity curves of two ROIs in two phantoms. There is still fluctuation in the time intensity curves even the phantoms did not have any motion. In MRI, signal-to-noise ratio (SNR) is trade-off with other image enhancements, such as higher resolution, shorter scan times [30, 31]. In our DCE-MRI, a 3D volume can be captured within one second and SNR in the images can be affected. MR intensity inhomogeneity affects the mean intensity in kidneys [24] [28]. Our phantom data show that motion may be one of the major factors but may not be the only factor that affect the quantification of DCE-MRI data.

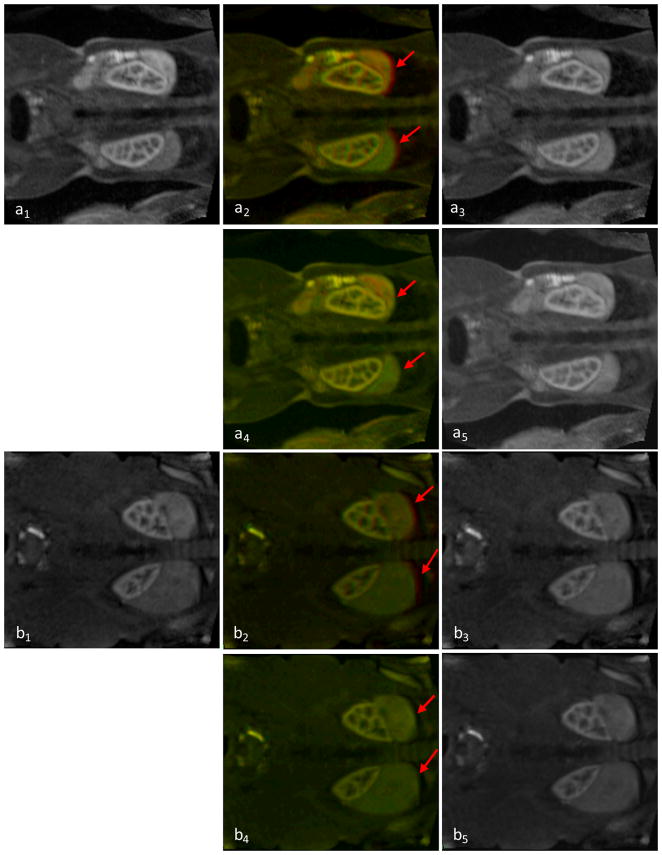
Figure 2.

Visual assessment of DCE-MR images before and after registration. a₁ and b₁ are a slice of the original reference images from two patients. a₂ and b₂ are the fusion image before registration, a₃ and b₃ are the floating image before registration. a₄ and b₄ are the fusion image after registration, a₅ and b₅ are the registered image. Red arrows show that the motion before registration and the improvement after registration.

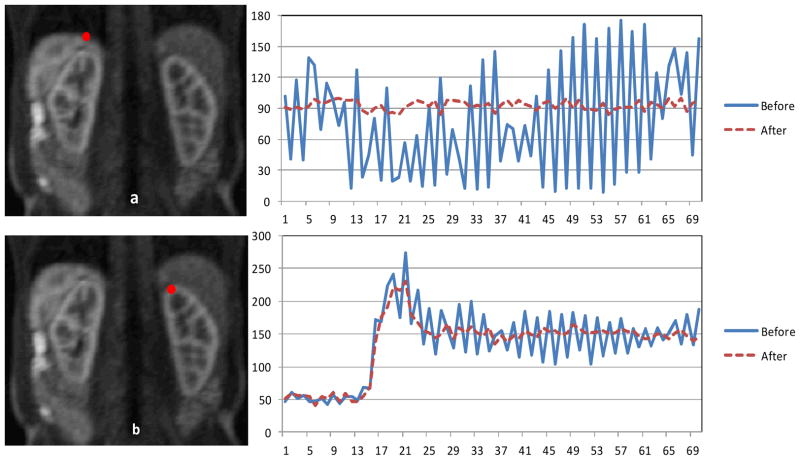
Figure 3.

Evaluation of the registration algorithm based on the comparison between the mean intensity time courses within a ROI before registration and after registration. ROI selection is depicted to the left of the time courses. The Y is the intensity and X is the time frame.

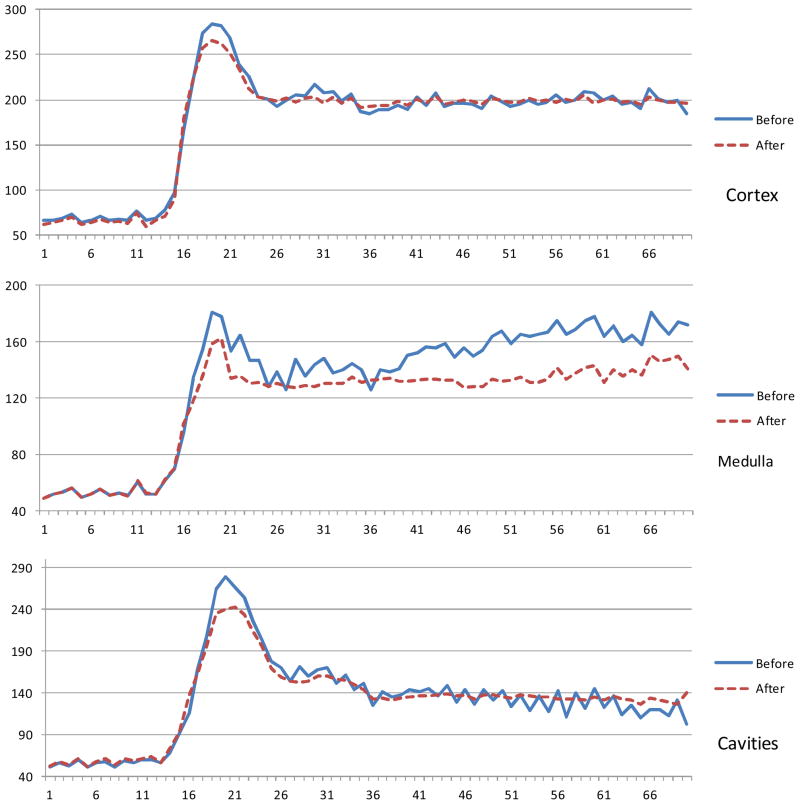
Figure 4.

Time intensity curves of the three classes () before and after registration. The curves become smooth because of registration. The Y is the intensity and X is the time frame.

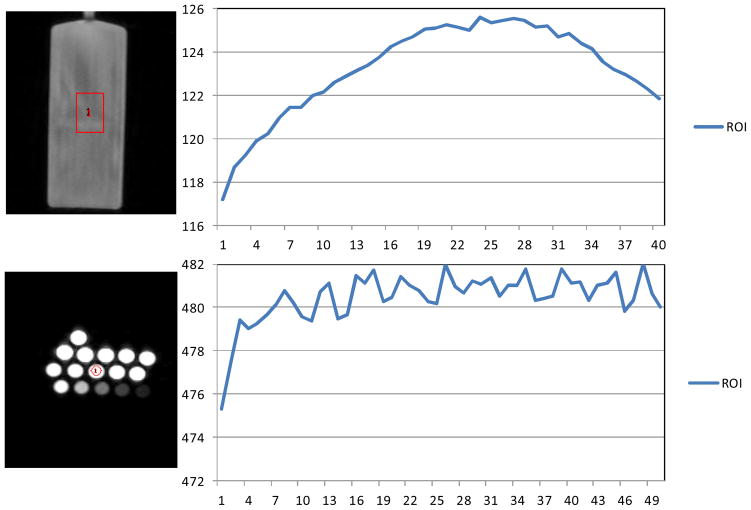
Figure 5.

The time intensity curves (right) of the regions of interest (ROIs) in the phantoms without motion. The intensity curves are not as smooth as we would expect, indicating that motion may not be the only factor that affects the DEC-MRI data quantification. The Y is the intensity and X is the time frame.

4. DISCUSSION AND CONCLUSION

We applied a non-rigid image registration method to reduce motion artifacts in DCE-MRI data. We also applied a fuzzy C-mean classification to classify the kidney into three classes i.e. cortex, medulla, and cavities. The proposed image analysis approach can be used as a processing tool for kidney DCE-MRI quantification.