Proportional hazards model for competing risks data with missing cause of failure

Abstract

We consider the semiparametric proportional hazards model for the cause-specific hazard function in analysis of competing risks data with missing cause of failure. The inverse probability weighted equation and augmented inverse probability weighted equation are proposed for estimating the regression parameters in the model, and their theoretical properties are established for inference. Simulation studies demonstrate that the augmented inverse probability weighted estimator is doubly robust and the proposed method is appropriate for practical use. The simulations also compare the proposed estimators with the multiple imputation estimator of Lu and Tsiatis (2001). The application of the proposed method is illustrated using data from a bone marrow transplant study.

1. Introduction

Competing risks data are commonly encountered in medical studies. Typically the responses to a treatment can be classified in terms of failure from disease of interest or from non-disease-related causes. Hence, in the competing risks framework, each individual is exposed to K distinct types of risks and the eventual failure can be attributed to precisely one of the risks. Let T^* denote the time to failure, Δ^* the cause of failure, and Z a p-dimensional vector of possibly time-dependent covariates. Then a principal estimable quantity in competing risks data is the cause-specific hazard function of cause k, defined, in the absence of censoring, by

$${\lambda }_k^{\ast }(t\mid Z)=\underset{h\to 0}{lim}{h}^{-1}P(t\le T^{\ast }<t+h,{\mathrm{\Delta }}^{\ast }=k\mid T^{\ast }\ge t,Z),$$

which is the instantaneous rate of experiencing the event of type k at time t, having not experienced any of the K competing events until time t. Without loss of generality in our study, we consider only two causes of failure, the cause of interest as cause 1 and the other as cause 2 (i.e. Δ^* = 1 or 2). In many applications involving follow-up studies, however, individuals may be subject to censoring. Let C be a censoring time and $T^{\ast }=min(T_1^{\ast },T_2^{\ast })$, where $T_1^{\ast }$ and $T_2^{\ast }$ denote the latent failure times from causes 1 and 2, respectively. Then the observed data consist of observations of (T, Δ, Z), where T = min(T^*, C) and Δ = Δ^*I(T^* ≤ C). If the failure time T^* is observed, Δ is the cause of failure and Δ = 0 otherwise. The observable cause-specific hazard function of cause k in the presence of censoring is given by

$${\lambda }_k(t\mid Z)=\underset{h\to 0}{lim}{h}^{-1}P(t\le T<t+h,\mathrm{\Delta }=k\mid T\ge t,Z),k=1,2.$$

Throughout the paper, we assume that Z is an external covariate process (Kalbfleish and Prentice, 2002) and the censoring time C is conditionally independent of (T^*, Δ^*) given Z (Lu and Tsiatis, 2001; Gao and Tsiatis, 2005; Lu and Liang, 2008). Under this assumption, it can be shown that ${\lambda }_k^{\ast }(t\mid Z)={\lambda }_k(t\mid Z)$ if the distribution of C is continuous at t. A number of statistical models for the relationship between the cause-specific hazard function of interest and regression covariates have been studied, among others, by Benichou and Gail (1990); Prentice et al. (1978); Cheng et al. (1998); Shen and Cheng (1999); Scheike and Zhang (2003). In this article we study the proportional hazards model for describing the relationship,

$${\lambda }_1^{\ast }(t\mid Z)={\lambda }_0(t)e^{{\beta }_0^{\top }Z(t)},$$ (1)

where λ₀(·) is a nonnegative, but otherwise unspecified baseline hazard function and β₀ is a p-dimensional vector of regression parameters. The parameter β₀ can be consistently estimated by treating all the failure times with Δ ≠ 1 as censored observations and using the partial likelihood score equation proposed by Cox (1972, 1975). The estimator will be called the full-case estimator, denoted by β̂_F in the paper.

In practice, however, the information needed for the cause of failure may be lost, or it may be difficult to determine the cause of disease or death for some individuals (Andersen et al., 1996). When we have missing causes in data, a naive method for estimating the regression parameter β₀ is to simply ignore the missing data and use the partial likelihood score equation to the complete data only. The so-called complete-case estimator, denoted by β̂_C, is clearly inefficient and can lead to serious bias. Thus, analysis of competing risks data with missing cause of failure has received considerable attention and a number of models have been proposed. Dinse (1982, 1986) considered nonparametric estimation for incomplete cause of death data with no covariate. Goetghebeur and Ryan (1990) proposed a modified log-rank test to compare survival in two groups, Dewanji (1992) suggested a modification of that approach, and Goetghebeur and Ryan (1995) extended the results of Goetghebeur and Ryan (1990) to proportional hazards regression model. More recently, Lu and Tsiatis (2001) proposed a parametric model to model the probability that the missing cause is the cause of interest while allowing the inclusion of additional auxiliary covariates and then estimated the regression parameters by using a multiple imputation method (Rubin, 1987, 1996). Gao and Tsiatis (2005) considered linear transformation models and Lu and Liang (2008) considered the additive hazards model for analysis of competing risks data with missing cause of failure.

For right-censored survival data in which the censoring indicator is missing, Lo (1991) considered the problem of nonparametric maximum likelihood estimation of a survival function in the absence of covariates, McKeague and Subramanian (1998) developed a survival function estimator assuming that the censoring indicators are missing completely at random. Subramanian (2000) considered further development of efficient estimation of the regression parameters under proportionality assumptions of the conditional hazards, and Gijbels et al. (2007) proposed a class of estimating functions for the regression parameters of the Cox proportional hazard model, among others.

In this study of analysis of competing risks data with missing cause of failure, we derive two different estimators for the regression parameters in model (1), namely the inverse probability weighted estimator and augmented inverse probability weighted estimator, and establish their theoretical properties. The first approach, following the idea of Horvitz and Thompson (1952), uses the inverse probability weighted complete-case technique to estimate the regression parameter. This approach uses only the complete cases and relies on correct modeling for the probability of missing causes. It has been shown that the inverse probability weighted estimator is inconsistent when the respective parametric model is misspecified, and is inefficient (Gao and Tsiatis, 2005; Lu and Liang, 2008; Scharfstein et al., 1999). It would be desirable, therefore, to obtain improved efficiency over the inverse probability weighted estimator. The second approach, adapting the idea of Robins et al. (1994), augments the inverse probability weighted complete-case estimating equation with a consistent estimator of the conditional distribution of the cause of interest that incorporates information available for individuals whose cause of failure is missing. See Subramanian and Bandyopadhyay (2010) for homogeneous right censored data with missing censoring indicators.

The paper is structured as follows. In Section 2, the inverse probability weighted estimator and augmented inverse probability weighted estimator are developed. The asymptotic properties of the corresponding estimators are established in Section 3. In Section 4, we investigate the finite sample properties of the proposed estimators through simulations, including comparisons with the multiple imputations estimator proposed by Lu and Tsiatis (2001). A bone marrow transplant data set is analyzed in Section 4. Some conclusions and discussions are given in Section 5. Technical derivations are detailed in Appendix.

2. Estimating equations

Since the cause of failure may not be observed for some individuals, we define the missingness indicator R as follows. If an individual’s death is observed, then R = 1 when the cause of failure information Δ^* is observed and R = 0 otherwise. If an individual is censored, we always define R = 1. We also introduce auxiliary covariates A which are not of interest for modelling the cause-specific hazard function but may be used to describe the missingness mechanism. The utilization of auxiliary information has been considered by Lu and Tsiatis (2001), Gao and Tsiatis (2005), Lu and Liang (2008), Gilbert, McKeague, and Sun (2008), among others. Then the observed data will consist of

$$O_i=\{T_i,Z_i,A_i,R_i,I({\mathrm{\Delta }}_i=0),R_{i}I({\mathrm{\Delta }}_i=1),R_{i}I({\mathrm{\Delta }}_i=2)\}$$

for i = 1, …, n. We assume that {O_i, i = 1, …, n} are independent identically distributed. The possible choices are {T_i, Z_i, A_i, 1, 0, 1, 0} for the individual who died from the cause 1, {T_i, Z_i, A_i, 1, 0, 0, 1} for the individual who died from the cause 2, {T_i, Z_i, A_i, 0, 0, 0, 0} for the individual who died with missing cause, and {T_i, Z_i, A_i, 1, 1, 0, 0} for the censored individual.

We also assume that the cause of failure is missing at random (MAR) (Rubin, 1976); that is, the probability that the cause of failure is missing given Δ > 0 and W = (T, Z, A) depends only on the observed W, but not on the unobserved Δ,

$$P(R=1\mid \mathrm{\Delta },\mathrm{\Delta }>0,W)=P(R=1\mid \mathrm{\Delta }>0,W).$$ (2)

The assumption implies that

$$\begin{array}{l}P(R=1\mid \mathrm{\Delta }>0,W)=P(R=1,\mathrm{\Delta }=1\mid \mathrm{\Delta }>0,W)+P(R=1,\mathrm{\Delta }=2\mid \mathrm{\Delta }>0,W)\\ =P(R=1\mid \mathrm{\Delta }=1,\mathrm{\Delta }>0,W)P(\mathrm{\Delta }=1\mid \mathrm{\Delta }>0,W)+P(R=1\mid \mathrm{\Delta }=2,\mathrm{\Delta }>0,W)P(\mathrm{\Delta }=2\mid \mathrm{\Delta }>0,W)\\ =P(R=1\mid \mathrm{\Delta }=1,\mathrm{\Delta }>0,W)[P(\mathrm{\Delta }=1\mid \mathrm{\Delta }>0,W)+P(\mathrm{\Delta }=2\mid \mathrm{\Delta }>0,W)]\\ =P(R=1\mid \mathrm{\Delta }=1,\mathrm{\Delta }>0,W),\end{array}$$

and likewise for the case involving Δ = 2. See also Lu and Tsiatis (2001), Gao and Tsiatis (2005), and Lu and Liang (2008).

2.1. Inverse probability weighted estimator

Following the inverse selection probability idea of Horvitz and Thompson (1952), the method of inversely weighting the probability of complete-case has been commonly used in missing data problems. To do that, we need to estimate the probability of a complete case, π(Q) ≡ P (R = 1|Q), where Q = (W, Δ). By the MAR assumption and R = 1 when Δ = 0, we have

$$\begin{array}{l}\pi (Q)=P(R=1\mid W,\mathrm{\Delta })\\ =P(R=1\mid W,\mathrm{\Delta },\mathrm{\Delta }>0)·I(\mathrm{\Delta }>0)+P(R=1\mid W,\mathrm{\Delta },\mathrm{\Delta }=0)·I(\mathrm{\Delta }=0)\\ =P(R=1\mid W,\mathrm{\Delta },\mathrm{\Delta }>0)·I(\mathrm{\Delta }>0)+1·I(\mathrm{\Delta }=0)\\ =P(R=1\mid W,\mathrm{\Delta }>0)·I(\mathrm{\Delta }>0)+I(\mathrm{\Delta }=0)\\ =r(W)·I(\mathrm{\Delta }>0)+I(\mathrm{\Delta }=0),\end{array}$$ (3)

where r(W) = P (R = 1|W, Δ > 0). We consider that the probability of complete-case r(W_i) may be specified as a parametric model r(W_i, ψ₀), in terms of a few unknown parameters ψ₀. Accordingly, let π(Q_i, ψ₀) = r(W_i, ψ₀)I(Δ > 0) + I(Δ = 0). Since R is binary, one can posit the logistic model $\text{logit}\{r(W_i,\psi )\}=W_i^{\top }\psi$, though other parametric models can also be used. By (2) and (3), the likelihood L regarding to π(Q, ψ₀) is

$$\begin{array}{l}L(\pi )=\prod \pi {(Q_i)}^{I(R_i=1)}{(1-\pi (Q_i))}^{I(R_i=0)}\\ =\prod \pi {(Q_i)}^{I(R_i=1)I({\mathrm{\Delta }}_i>0)}·\pi {(Q_i)}^{I(R_i=1)I({\mathrm{\Delta }}_i=0)}·{(1-\pi (Q_i))}^{I(R_i=0)I({\mathrm{\Delta }}_i>0)}\\ =\prod r{(W_i)}^{I(R_i=1)I({\mathrm{\Delta }}_i>0)}·1·{(1-r(W_i))}^{I(R_i=0)I({\mathrm{\Delta }}_i>0)},\\ \text{because}\pi (Q_i)=r(W_i)\text{when}{\mathrm{\Delta }}_i>0,\text{and}\pi (Q_i)=1\text{when}{\mathrm{\Delta }}_i=0\\ =\prod r{(W_i)}^{I(R_i=1)I({\mathrm{\Delta }}_i>0)}·{(1-r(W_i))}^{(1-R_i)I({\mathrm{\Delta }}_i>0)}.\end{array}$$

This implies that the maximum likelihood estimator ψ̂ of ψ can be estimated by maximizing the likelihood based on uncensored data

$$\prod _{i=1}^n{\{r(W_i,\psi )\}}^{R_{i}I({\mathrm{\Delta }}_i>0)}{\{1-r(W_i,\psi )\}}^{(1-R_i)I({\mathrm{\Delta }}_i>0)}.$$

It is known that for a correctly specified model r(W_i, ψ), ψ̂ consistently estimates ψ₀, the true value of the parametric component of r(W_i, ψ) (Haberman, 1974, 1977; Gourieroux and Monfort, 1981).

We define the counting process N_i(t) = I(Δ_i = 1)I(T_i ≤ t) and at-risk process Y_i(t) = I(T_i ≥ t). Let a^⊗0 = 1, a^⊗1 = a, and a^⊗2 = aa^⊤ for a vector a. Let

$$\begin{array}{c}{\stackrel{\sim }{S}}^{(m)}(t,\beta ,\psi )=\frac{1}{n}\sum _{i=1}^n\frac{R_i}{\pi (Q_i,\psi )}{Y}_i(t)e^{{\beta }^{\top }{Z}_i(t)}{Z}_i{(t)}^{\otimes m},\\ \stackrel{\sim }{Z}(t,\beta ,\psi )={\stackrel{\sim }{S}}^{(1)}(t,\beta ,\psi )/{\stackrel{\sim }{S}}^{(0)}(t,\beta ,\psi ),\\ \stackrel{\sim }{V}(t,\beta ,\psi )=\frac{{\stackrel{\sim }{S}}^{(2)}(t,\beta ,\psi )}{{\stackrel{\sim }{S}}^{(0)}(t,\beta ,\psi )}-\stackrel{\sim }{Z}{(t,\beta ,\psi )}^{\otimes 2}\end{array}$$

for m = 0, 1, 2. Then we consider the following inverse probability weighted estimating equation for β₀:

$$U_I(\beta ,\widehat{\psi })=\sum _{i=1}^n{\int }_0^{\tau }\frac{R_i}{\pi (Q_i,\widehat{\psi })}\left(Z_i(t)-\stackrel{\sim }{Z}(t,\beta ,\widehat{\psi })\right){dN}_i(t),$$ (4)

where τ > 0 is the end of follow-up time. The inverse probability weighted estimator (IPW) of β solves the above equation and is denoted by β̂_I. When there is no missing cause, the equation (4) consequently becomes the partial likelihood score equation proposed by Cox (1972, 1975). The cumulative baseline hazard function ${\mathrm{\Lambda }}_0(t)={\int }_0^t{\lambda }_0(u)du$ can be estimated by

$${\widehat{\mathrm{\Lambda }}}_{I0}(t)=\sum _{i=1}^n{\int }_0^t\frac{R_i}{\pi (Q_i,\widehat{\psi })}\frac{{dN}_i(u)}{n{\stackrel{\sim }{S}}^{(0)}(u,{\widehat{\beta }}_I,\widehat{\psi })}.$$

2.2. Augmented inverse probability weighted estimator

The inverse probability weighted estimator β̂_I uses only complete cases. Thus, it is inefficient. In addition, its consistency relies on correct modelling of the probability r(W_i, ψ₀). To improve the robustness and efficiency over β̂_I, we adapt the idea of Robins et al. (1994) and propose to augment the inverse probability weighted estimating equation with a consistent estimator of the conditional distribution of the cause of interest that utilizes available information for individuals with missing cause of failure.

Consequently, we estimate the probability that the cause of failure is the cause of interest ρ(W) ≡ P (Δ = 1| Δ > 0, W). Let f(t, Δ = 1| Δ > 0, z, a) be the conditional joint density of T and Δ = 1 given (Δ > 0, Z = z, A = a). Then for w = (t, z, a),

$$\begin{array}{l}\rho (w)=\frac{f(t,\mathrm{\Delta }=1\mid \mathrm{\Delta }>0,z,a)}{f(t\mid \mathrm{\Delta }>0,z,a)}\\ =\frac{f(t,\mathrm{\Delta }=1\mid z,a)}{f(t,\mathrm{\Delta }=1\mid z,a)+f(t,\mathrm{\Delta }=2\mid z,a)}\\ =\frac{{\stackrel{\sim }{\lambda }}_1(t\mid z,a)}{{\stackrel{\sim }{\lambda }}_1(t\mid z,a)+{\stackrel{\sim }{\lambda }}_2(t\mid z,a)},\end{array}$$

where λ̃_k(t|z, a) is the conditional cause-specific hazard function of T at t due to cause Δ = k given (Z, A) = (z, a) for k = 1, 2. Here, instead of directly estimating ρ(W_i) which requires the estimation of two unknown cause-specific hazard functions, we posit a parametric model ρ(W_i, γ₀) for ρ(W_i) in terms of a few unknown parameters γ₀. It is natural to use a logistic regression model $\text{logit}\{\rho (W_i,\gamma )\}=W_i^{\top }\gamma$, but other parametric models can also be accommodated.

There is, however, an issue with obtaining estimates for γ in the presence of missingness. The MAR assumption implies that given Δ > 0 and W, R is independent of Δ; that is,

$$P(\mathrm{\Delta }=1\mid \mathrm{\Delta }>0,W)=P(\mathrm{\Delta }=1\mid R,\mathrm{\Delta }>0,W).$$ (5)

By (5), ρ(W_i) can be deduced from the complete cases with R_i = 1 and Δ_i > 0. This suggests that the maximum likelihood estimator γ̂ of γ can be obtained by maximizing the likelihood based on complete-case data

$$\prod _{i=1}^n{\{\rho (W_i,\gamma )\}}^{R_{i}I({\mathrm{\Delta }}_i=1)}{\{1-\rho (W_i,\gamma )\}}^{R_{i}I({\mathrm{\Delta }}_i=2)}.$$

Since γ̂ is the maximum likelihood estimator, then for a correctly specified model ρ(W_i, γ), γ̂ consistently estimates γ₀, the true value of the parametric component model ρ(W_i, γ) (Haberman, 1974, 1977; Gourieroux and Monfort, 1981).

Now, we define the counting process $N_i^{\ast }(t)=I({\mathrm{\Delta }}_i>0)I(T_i\le t)$. Let

$$\begin{array}{c}{S}^{(m)}(t,\beta )=\frac{1}{n}\sum _{i=1}^n{Y}_i(t)e^{{\beta }^{\top }{Z}_i(t)}{Z}_i{(t)}^{\otimes m},\\ \overline{Z}(t,\beta )=S^{(1)}(t,\beta )/S^{(0)}(t,\beta ),\\ V(t,\beta )=\frac{S^{(2)}(t,\beta )}{S^{(0)}(t,\beta )}-\overline{Z}{(t,\beta )}^{\otimes 2}.\end{array}$$

Then we propose the following augmented inverse probability weighted estimating equation

$$U_A(\beta ,\widehat{\psi },\widehat{\gamma })=\sum _{i=1}^n{\int }_0^{\tau }(Z_i(t)-\overline{Z}(t,\beta ))\left[\frac{R_i}{r(W_i,\widehat{\psi })}{dN}_i(t)-\frac{R_i-r(W_i,\widehat{\psi })}{r(W_i,\widehat{\psi })}\rho (W_i,\widehat{\gamma }){dN}_i^{\ast }(t)\right],$$ (6)

where ψ̂ and γ̂ are the maximum likelihood estimators defined earlier. The augmented inverse probability weighted estimator (AIPW) of β solves the above equation (6) and is denoted by β̂_A. The cumulative baseline hazard function can be estimated by

$${\widehat{\mathrm{\Lambda }}}_{A0}(t)=\sum _{i=1}^n{\int }_0^t\frac{1}{{nS}^{(0)}(u,{\widehat{\beta }}_A)}\left[\frac{R_i}{r(W_i,\widehat{\psi })}{dN}_i(u)-\frac{R_i-r(W_i,\widehat{\psi })}{r(W_i,\widehat{\psi })}\rho (W_i,\widehat{\gamma }){dN}_i^{\ast }(u)\right].$$

3. Asymptotic results

When the model for r(W_i) is correctly specified, we let ψ₀ be the true value of ψ such that r(W_i) = r(W_i, ψ₀). Under Condition (A.4) stated in the Appendix, $\widehat{\psi }\stackrel{P}{\to }{\psi }_0$. When the model for ρ(W_i) is correctly specified, we let γ₀ be the true value of γ such that ρ(W_i) = ρ(W_i, γ₀). In this case, $\widehat{\gamma }\stackrel{P}{\to }{\gamma }_0$. In general, under Condition (A.4), there exist ψ^* and γ^* such that $\widehat{\psi }\stackrel{P}{\to }{\psi }^{\ast }$ and $\widehat{\gamma }\stackrel{P}{\to }{\gamma }^{\ast }$ (White, 1982). We have ψ^* = ψ₀ if r(W_i) is correctly specified, and γ^* = γ₀ if ρ(W_i) is correctly specified.

Let s^(m)(t, β) = E[Y₁(t)e^β⊤Z₁(t) Z₁(t)^⊗m], z̄(t, β) = s⁽¹⁾(t, β)/s⁽⁰⁾(t, β), and v(t, β) = s⁽²⁾(t, β)/s⁽⁰⁾(t, β) − z̄(t, β)^⊗2.

Theorem 1

Assume Condition A given in the Appendix. If r(W_i, ψ₀) is correctly specified for r(W_i), then ${\widehat{\beta }}_I\stackrel{P}{\to }{\beta }_0$ and $\sqrt{n}\left({\widehat{\beta }}_I-{\beta }_0\right)$ converges in distribution to a zero-mean Gaussian random vector with covariance matrix ${\mathrm{\sum }}^{-1}E[{\omega }_i{\omega }_i^T]{\mathrm{\sum }}^{-1}$, where

$$\begin{array}{c}\mathrm{\sum }={\int }_0^{\tau }v(t,{\beta }_0){\lambda }_0(t)s^{(0)}(t,{\beta }_0)dt,\\ {\omega }_i={\int }_0^{\tau }\{Z_i(t)-\overline{z}(t,{\beta }_0)\}\frac{R_i}{\pi (Q_i,{\psi }_0)}{dM}_i(t)-V_{\psi }{I}_{\psi }^{-1}{S}_{\psi i},\end{array}$$

$M_i(t)=N_i(t)-{\int }_0^t{Y}_i(u)e^{{\beta }_0^{\top }{Z}_i(u)}d{\mathrm{\Lambda }}_0(u)$, V_ψ is given in (8), I_ψ and S_ψi are given in (11) in the Appendix.

The asymptotic covariance matrix ${\mathrm{\sum }}^{-1}E({\omega }_i{\omega }_i^T){\mathrm{\sum }}^{-1}$ can be consistently estimated by

$${\widehat{\mathrm{\sum }}}_I^{-1}\left(n^{-1}\sum _{i=1}^n{\widehat{\omega }}_i{\widehat{\omega }}_i^{\top }\right){\widehat{\mathrm{\sum }}}_I^{-1},$$

where

$$\begin{array}{c}{\widehat{\mathrm{\sum }}}_i=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }\frac{R_i}{\pi (Q_i,\widehat{\psi })}\stackrel{\sim }{V}(t,{\widehat{\beta }}_I,\widehat{\psi }){dN}_i(t),\\ {\widehat{\omega }}_i={\int }_0^{\tau }\frac{R_i}{\pi (Q_i,\widehat{\psi })}\{Z_i(t)-\stackrel{\sim }{Z}(t,{\widehat{\beta }}_I,\widehat{\psi })\}d{\widehat{M}}_i(t)-{\widehat{V}}_{\psi }{\widehat{I}}_{\psi }^{-1}{\widehat{S}}_{\psi i},\end{array}$$

and ${\widehat{M}}_i(t)=N_i(t)-{\int }_0^t{Y}_i(u)e^{{\widehat{\beta }}_I^{\top }{Z}_i(u)}d{\widehat{\mathrm{\Lambda }}}_{I0}(u)$. Here V̂_ψ, Î_ψ and Ŝ_ψi are obtained by replacing with their respective sample estimators and substituting (β̂_I, ψ̂) for (β₀, ψ₀) in V_ψ, I_ψ, and S_ψi.

The following establishes the asymptotic properties of β̂_A.

Theorem 2

Assume Condition A given in the Appendix. If at least one of r(W_i, ψ₀) and ρ(W_i, γ₀) is correctly specified for r(W_i) and ρ(W_i), then ${\widehat{\beta }}_A\stackrel{P}{\to }{\beta }_0$ and $\sqrt{n}\left({\widehat{\beta }}_A-{\beta }_0\right)$ converges in distribution to a zero-mean Gaussian random vector with covariance matrix ${\mathrm{\sum }}^{-1}E[{\phi }_i{\phi }_i^T]{\mathrm{\sum }}^{-1}$, where

$$\mathrm{\sum }={\int }_0^{\tau }v(t,{\beta }_0){\lambda }_0(t)s^{(0)}(t,{\beta }_0)dt,$$

and

$${\phi }_i={\int }_0^{\tau }\{Z_i(t)-\overline{z}(t,{\beta }_0)\}{dM}_i^{\ast }(t)-P_{\psi }{(I_{\psi }^{\ast })}^{-1}{S}_{\psi i}^{\ast }-P_{\gamma }{(I_{\gamma }^{\ast })}^{-1}{S}_{\gamma i}^{\ast }.$$

Here M^*(t) is defined in (17), and P_ψ, $I_{\psi }^{\ast },S_{\psi i}^{\ast }$, P_γ, $I_{\gamma }^{\ast }$ and $S_{\gamma i}^{\ast }$ are given in (15) and (19) in the Appendix.

It is interesting to notice that if r(W_i, ψ₀) = r(W_i), then P_γ = 0, and if ρ(W_i, γ₀) = ρ(W_i), then P_ψ = 0. When both the models for r(W_i) and ρ(W_i) are correctly specified, we have P_ψ = 0 and P_γ = 0 and hence, ${\phi }_i={\int }_0^{\tau }\{Z_i(t)-\overline{z}(t,{\beta }_0)\}{dM}_i^{\ast }(t)$.

The asymptotic covariance matrix ${\mathrm{\sum }}^{-1}E({\phi }_i{\phi }_i^T){\mathrm{\sum }}^{-1}$ can be consistently estimated by

$${\widehat{\mathrm{\sum }}}_A^{-1}\left(n^{-1}\sum _{i=1}^n{\widehat{\phi }}_i{\widehat{\phi }}_i^{\top }\right){\widehat{\mathrm{\sum }}}_A^{-1},$$

where

$$\begin{array}{c}{\widehat{\mathrm{\sum }}}_A=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }V(t,{\widehat{\beta }}_A)\left[\frac{R_i}{r(W_i,\widehat{\psi })}{dN}_i(t)-\frac{R_i-r(W_i,\widehat{\psi })}{r(W_i,\widehat{\psi })}\rho (W_i,\widehat{\gamma }){dN}_i^{\ast }(t)\right],\\ {\widehat{\phi }}_i={\int }_0^{\tau }\{Z_i(t)-\overline{Z}(t,{\widehat{\beta }}_A)\}d{\widehat{M}}_i^{\ast }(t)-{\widehat{P}}_{\psi }{({\widehat{I}}_{\psi }^{\ast })}^{-1}{\widehat{S}}_{\psi i}^{\ast }-{\widehat{P}}_{\gamma }{({\widehat{I}}_{\gamma }^{\ast })}^{-1}{\widehat{S}}_{\gamma i}^{\ast },\end{array}$$

and

$${\widehat{M}}_i^{\ast }(t)=\frac{R_i}{r(W_i,\widehat{\psi })}{N}_i(t)-\frac{R_i-r(w_i,\widehat{\psi })}{r(W_i,\widehat{\psi })}\rho (W_i,\widehat{\gamma })N_i^{\ast }(t)-{\int }_0^t{Y}_i(u)e^{{\widehat{\beta }}_A^{\top }{Z}_i(u)}d{\widehat{\mathrm{\Lambda }}}_{A0}(u).$$

Here P̂_ψ, ${\widehat{I}}_{\psi }^{\ast },{\widehat{S}}_{\psi i}^{\ast }$, P̂_γ, ${\widehat{I}}_{\gamma }^{\ast }$ and ${\widehat{S}}_{\gamma i}^{\ast }$ are the empirical counterparts of P_ψ, $I_{\psi }^{\ast },S_{\psi i}^{\ast }$, P_γ, $I_{\gamma }^{\ast }$ and $S_{\gamma i}^{\ast }$ given in (15) and (19) in the Appendix, obtained by replacing with their respective sample estimators and substituting (β̂_A, ρ̂, γ̂) for (β₀, ψ^*, γ^*).

4. Numerical results

4.1. Simulation studies

We present simulation studies conducted to evaluate the performance of our proposed methods. We set τ = 2.0 and consider a univariate covariate Z, where Z follows a uniform distribution on [0, 1]. Given Z, the latent failure time $T_1^{\ast }$ of interest is generated from the proportional hazards model ${\lambda }_1^{\ast }(t\mid Z)=\lambda e^{\beta Z}$, where λ = 1 and β = −0.5. The other latent failure time $T_2^{\ast }$ is generated from a Gompertz distribution with a hazard function ${\lambda }_2^{\ast }(t\mid Z)=e^{\theta +\nu t}$, where θ = −0.5 and ν = 0.2. The censoring time C is generated from an exponential distribution which yields about 20% censoring level. We consider a single auxiliary covariate A which follows a Bernoulli distribution with success probability of 0.5. We also consider a logistic regression model logit{r(W, ψ)} = ψ₁ + ψ₂T + ψ₃Z + ψ₄A for missing cause of failure. We have about 20% missingness with ψ = (0.7, 1, −1, 1) and about 45% missingness with ψ = (−0.8, 1, −1, 1). In the settings we consider here, the true model ρ(W) is given by a logistic regression model logit{ρ(W)} = −θ − νT +βZ. To study the performance of the estimators when r(W) is misspecified, we posit two different parametric models of r(W, ψ), where one is a correctly specified logistic model and the other is a misspecified constant model r₀ ∈ (0, 1) independent of W. To study the behavior when ρ(W) is misspecified, we consider various model specifications. We posit a correctly specified logistic model logit{ρ(W, γ)} = γ₁ + γ₂T + γ₃Z (Model 1), a misspecified logistic model logit{ρ(W, γ)} = γ₁ + γ₂Z (Model 2), a misspecified logistic model logit{ρ(W, γ)} = γ₁ + γ₂T (Model 3) and a misspecified constant model ρ₀ ∈ (0, 1) independent of W (Model 4). The simulation studies consist of 1000 runs with the sample size n = 200 and n = 400. We also conduct comparison with the multiple imputation estimators, studied by Lu and Tsiatis (2001), with the number of imputation m = 1 and m = 5.

The results from Table 1 and Table 2 show that the complete-case estimator β̂_C shows large biases in all the settings. When the parametric model for r(W) is correctly specified, both the IPW estimator β̂_I and AIPW estimator β̂_A show small biases, but the AIPW estimator has smaller standard errors than the corresponding IPW estimator. When the parametric model for ρ(W) is correctly specified, the multiple imputation estimator has small biases, but the multiple imputation estimator tends to have larger biases when ρ(W) is misspecified. As expected, the AIPW estimator is clearly not sensitive to the misspecification if one of the parametric models for r(W) and ρ(W) is misspecified. In fact, the AIPW estimator performs quite well even when both the parametric models r(W) and ρ(W) are misspecified. The standard errors of the multiple imputation estimator decrease as the number of imputation increases. The standard errors of the multiple imputation estimator and the AIPW estimator are comparable when ρ(W) is correctly specified. However, the multiple imputation estimator seems to have small standard errors than the AIPW estimator under misspecified ρ(W). The estimated standard errors of the AIPW estimator are close to the sample standard errors, and the 95% confidence intervals have reasonable coverage probabilities.

Table 1.

Summary statistics of simulation results with 20% missingness under various model specifications of ρ(·).

Estimator	n = 200				n = 400
	Bias	SSE	MSE	CP	Bias	SSE	MSE	CP
β̂C	−0.136	0.442	0.447	96.0	−0.129	0.322	0.313	92.6
β̂Ic	−0.007	0.422	0.426	96.4	−0.002	0.313	0.299	93.9
β̂Im	−0.107	0.430	0.430	96.1	−0.182	0.392	0.385	92.2
	(Model 1)				(Model 1)
β̂Ac	−0.005	0.406	0.416	96.2	0.002	0.301	0.292	94.4
β̂Am	−0.003	0.403	0.411	96.5	0.003	0.351	0.345	95.1
β̂M1	−0.003	0.427	0.437	96.3	0.003	0.313	0.306	94.3
β̂M5	−0.005	0.406	0.419	96.6	0.005	0.302	0.294	94.4
	(Model 2)				(Model 2)
β̂Ac	−0.005	0.406	0.416	96.1	0.002	0.301	0.292	94.4
β̂Am	−0.007	0.403	0.412	96.4	0.001	0.297	0.290	94.3
β̂M1	−0.012	0.428	0.438	96.2	−0.003	0.314	0.307	94.3
β̂M5	−0.011	0.408	0.420	96.6	−0.001	0.303	0.295	94.0
	(Model 3)				(Model 3)
β̂Ac	−0.004	0.406	0.416	96.2	0.002	0.300	0.292	94.5
β̂Am	0.005	0.395	0.405	96.7	0.010	0.292	0.286	94.5
β̂M1	0.061	0.370	0.383	96.3	0.066	0.273	0.269	93.8
β̂M5	0.057	0.347	0.364	96.2	0.067	0.260	0.255	93.8
	(Model 4)				(Model 4)
β̂Ac	−0.005	0.406	0.416	96.2	0.002	0.301	0.292	94.5
β̂Am	−0.001	0.397	0.406	96.7	0.009	0.341	0.336	95.2
β̂M1	0.056	0.367	0.383	96.5	0.062	0.273	0.269	94.1
β̂M5	0.054	0.348	0.364	96.5	0.064	0.261	0.256	93.5

Bias, the mean of the estimates of β; SSE, the sample standard error of the estimates of β; MSE, the mean of the standard error estimates; CP, the empirical coverage probability of the corresponding 95% confidence intervals; β̂_C, the complete-case estimator; β̂_Ic and β̂_Im, the IPW estimators; β̂_Ac and β̂_Am, the AIPW estimators; β̂_M¹ and β̂_M⁵, the multiple imputation estimators with m = 1 and m = 5 imputations. Here c denotes the correctly specified model and m the misspecified model for r(·), respectively.

Table 2.

Summary statistics of simulation results with 45% missingness under various model specifications of ρ(·).

Estimator	n = 200				n = 400
	Bias	SSE	MSE	CP	Bias	SSE	MSE	CP
β̂C	−0.322	0.595	0.599	94.0	−0.305	0.420	0.416	88.1
β̂Ic	−0.014	0.583	0.554	93.7	0.002	0.411	0.394	94.7
β̂Im	−0.194	0.561	0.552	94.6	−0.182	0.392	0.385	92.2
	(Model 1)				(Model 1)
β̂Ac	−0.022	0.540	0.523	94.3	0.001	0.380	0.365	93.4
β̂Am	−0.011	0.493	0.494	95.8	0.003	0.351	0.345	95.1
β̂M1	−0.007	0.534	0.539	96.2	−0.006	0.377	0.376	95.2
β̂M5	−0.012	0.502	0.509	96.6	0.001	0.356	0.354	95.1
	(Model 2)				(Model 2)
β̂Ac	−0.021	0.539	0.523	94.0	0.001	0.379	0.365	93.6
β̂Am	−0.017	0.495	0.496	95.9	−0.003	0.352	0.347	94.8
β̂M1	−0.022	0.538	0.541	96.5	−0.017	0.377	0.377	95.2
β̂M5	−0.025	0.506	0.510	96.7	−0.010	0.356	0.355	94.8
	(Model 3)				(Model 3)
β̂Ac	−0.020	0.538	0.524	94.9	0.002	0.379	0.365	94.0
β̂Am	0.011	0.463	0.471	96.0	0.017	0.338	0.333	95.1
β̂M1	0.137	0.368	0.383	94.6	0.133	0.266	0.268	92.3
β̂M5	0.130	0.325	0.340	94.6	0.139	0.237	0.238	91.1
	(Model 4)				(Model 4)
β̂Ac	−0.020	0.536	0.525	94.6	0.002	0.379	0.365	94.2
β̂Am	0.004	0.469	0.476	96.2	0.009	0.341	0.336	95.2
β̂M1	0.131	0.371	0.384	95.2	0.127	0.268	0.269	92.5
β̂M5	0.126	0.327	0.340	94.7	0.134	0.239	0.239	91.5

Bias, the mean of the estimates of β; SSE, the sample standard error of the estimates of β; MSE, the mean of the standard error estimates; CP, the empirical coverage probability of the corresponding 95% confidence intervals; β̂_C, the complete-case estimator; β̂_Ic and β̂_Im, the IPW estimators; β̂_Ac and β̂_Am, the AIPW estimators; β̂_M¹ and β̂_M⁵, the multiple imputation estimators with m = 1 and m = 5 imputations. Here c denotes the correctly specified model and m the misspecified model for r(·), respectively.

To further study robustness of parameter estimates against misspecification of the parametric models for r(W) and ρ(W), we consider the same model for $T_1^{\ast }$ as described above, but here instead we generate $T_2^{\ast }$ from a Weibull distribution, log logistic distribution, exponential power distribution and gamma distribution. None of these distributions will induce a simple linear logistic regression model for ρ(W). For example, when $T_2^{\ast }$ is generated from a log logistic distribution with a hazard function ${\lambda }_2^{\ast }(t\mid Z)=\alpha \lambda t^{\alpha -1}/(1+\lambda t^{\alpha })$, the true logistic model for ρ(W) is logit{ρ(W)} = −log(α) − log(λ) + βZ + log ((1 + λT^α)/T^α−1). In all cases we misspecify ρ(W) by Model 1 to Model 4 described above. Although not presented here, the findings from these simulations are similar to those from Table 1 and Table 2.

In conclusion, the multiple imputation estimator of Lu and Tsiatis (2001) and the AIPW estimator have similar performance when the parametric models for r(W) and ρ(W) are correctly specified. The AIPW estimator has the advantage of double robustness such that the biases of the AIPW estimator remain small when the parametric model for r(W) or ρ(W) is misspecified. The bias of the multiple imputation estimator can be larger under misspecified ρ(W).

4.2. Bone marrow transplant data

Sierra et al. (2002) described the characteristics and outcomes of 452 patients with primary myelodysplasia (MDS) who received transplants from HLA-identical siblings and were registered with the International Bone Marrow Transplant Registry (IBMTR). The study has two competing risks; treatment related death defined as death in complete remission and relapse defined as recurrence of myelodysplasia. In this example, we consider 408 patients with complete covariate information obtained from the timereg package for R. Among these 408 patients, 161 patients died in complete remission, 87 patients relapsed, and 160 patients were censored. The covariates considered in our study are age of patient standardized at mean of 35 years old and platelet before transplantation (1 for more than 100 × 10⁹ per L, or 0 for less). In the data set, the causes of failure are all known. For illustration purposes, we delete some failure causes by the three following missing mechanisms; missing completely at random (MCAR), missing at random (MAR), and not missing at random (NMAR).

For the MCAR, the causes of failure are randomly selected for missing with probability 23%. For the MAR, the logistic model is chosen as logit{r(W)} = 0.5 + 1.0 * T − 1.0 * age which yields about 23% missing causes, where T is the failure time. For the NMAR, the logistic model is chosen as logit{r(W)} = 0.5+1.0*T −1.0*age−0.5*I(Δ = 1) which yields about 26% missing causes, where Δ = 1 corresponds to the death in complete remission and Δ = 2 does to relapse. We posit the logistic models for both r(W) and ρ(W) with logit{r(W, ψ)} = ψ₁ + ψ₂ * T + ψ₃ * age + ψ₄ * platelet and logit{ρ(W, γ)} = γ₁ + γ₂ * log T + γ₃ * age + γ₄ * platelet.

The results of the estimation of β based on the AIPW estimator, the complete-case estimator and the multiple imputation estimator with the number of imputation m = 5 are summarized in Table 3. For comparison, Table 3 also includes the estimation of β based on the original data without artificial missing, namely, the full-case estimator. The results from the AIPW estimator and the multiple imputation estimator are very close under all the missingness mechanisms and they are closer to the full-case estimator than the complete-case estimator. The analyses using the AIPW estimator and the multiple imputation estimator are consistent with the findings from the earlier study; that is, patients with high platelet counts have a lower risk of treatment related mortality than those with low platelet counts, and a higher risk rate is seen among the older patients.

Table 3.

Estimation of the effects of platelet and age for the bone marrow transplant data.

Missing	Estimator	Platelet			Age
		Est.	SEE	p-value	Est.	SEE	p-value
None	β̂F	−0.586	0.186	0.002	0.367	0.087	<0.001
MCAR	β̂C	−0.491	0.236	0.037	0.397	0.112	<0.001
	β̂A	−0.520	0.203	0.010	0.387	0.091	<0.001
	β̂M5	−0.530	0.205	0.010	0.380	0.096	<0.001
MAR	β̂C	−0.504	0.238	0.034	0.241	0.107	0.024
	β̂A	−0.566	0.204	0.006	0.380	0.090	<0.001
	β̂M5	−0.614	0.205	0.003	0.380	0.093	<0.001
NMAR	β̂C	−0.390	0.253	0.123	0.156	0.114	0.171
	β̂A	−0.529	0.220	0.016	0.350	0.098	<0.001
	β̂M5	−0.567	0.219	0.010	0.344	0.099	<0.001

Est., the estimate; SEE, the standard error estimate; p-value pertaining to testing no covariate effect; β̂_F, the full-case estimator with no missing causes; β̂_C, the complete-case estimator; β̂_A, the AIPW estimator; β̂_M⁵, the multiple imputation estimator with m = 5 imputations.

5. Conclusion

We propose the inverse probability weighted estimator and augmented inverse probability weighted estimator for analysis of competing risks data with missing cause of failure, where the Cox proportional hazard model is utilized to examine the covariate effects on the cause-specific hazard function for the failure type of interest. The augmented inverse probability weighted estimator posses the double robust property such that it is unbiased as long as one of the parametric models for r(W) and ρ(W) is correctly specified. The inverse probability weighted estimator is unbiased only when the parametric model for r(W) is correctly specified. Under the correctly specified models for r(W) and ρ(W), the augmented inverse probability weighted estimator is more efficient than the inverse probability weighted estimator.

The proposed estimators are compared with the multiple imputation estimator of Lu and Tsiatis (2001) through simulations. The multiple imputation estimator and augmented inverse probability weighted estimator have similar performance when the parametric models for r(W) and ρ(W) are correctly specified. The augmented inverse probability weighted estimator has the advantage of the double robustness over the multiple imputation estimator.

In the competing risks problem, another useful quantity is the cumulative incidence function which is the probability of occurrence by time t for a particular type of failure in the presence of other risks. It is known that the covariate effect on the cause-specific hazard for a particular type of failure can be quite different from its effect on the cumulative incidence function of that type of failure (Gray, 1988; Gaynor et al., 1993). Fine and Gray (1999) developed a direct Cox regression approach for the cumulative incidence curve based on earlier work by Gray (1988) and Pepe (1991). Recently, Andersen et al. (2003) and Klein and Andersen (2005) suggested pseudo-observation approach for direct modeling for cumulative incidence probabilities. It would be interesting to study models that relate the covariates directly to the cumulative incidence function for the failure type of interest in competing risks data with missing cause of failure.

Appendix

Condition A

• (A.1)λ₀(t) is continuous on [0, τ]. The distribution of C is continuous on [0, τ] and P (C > τ) > 0. The covariate processes Z_i(t) have paths that are left continuous and of bounded variation, and satisfy the moment condition E[||Z_i(t)||⁴ exp(2M||Z_i(t)||)] < ∞, where M is a constant such that β ∈ [−M, M]^p and ||A|| = max_k,l |a_kl| for a matrix A = (a_kl).
• (A.2)Each component of s^(j)(t, β) is continuous on [0, τ] × [−M, M]^p for M > 0, j = 0, 1, 2 and s⁽⁰⁾(t, β) > 0 on [0, τ] × [−M, M]^p. sup_{t∈[0,τ],β∈[−M,M]^p} ||S^(j)(t, β) − s^(j)(t, β)|| = O_p(n^−1/2), and sup_{ψ∈[−L,L]^q} sup_{t∈[0, τ],β∈[−M,M]^p} ||S̃^(j)(t, β, ψ) − s^(j)(t, β)|| = O_p(n^−1/2) for j = 0, 1, 2.
• (A.3)The matrix $\mathrm{\sum }={\int }_0^{\tau }v(t,{\beta }_0){\lambda }_0(t)s^{(0)}(t,{\beta }_0)dt$ is positive definite.
• (A.4)There is a σ > 0 such that r(W_i) ≥ σ for all i with Δ_i > 0. Both r(W_i, ψ) and ρ(W_i, γ) are twice continuously differentiable with respect to ψ and γ, respectively. There exist ψ^* and γ^* satisfying the equations ${ES}_{\psi i}^{\ast }=0$ and ${ES}_{\gamma i}^{\ast }=0$, respectively, where $S_{\psi i}^{\ast }$ and $S_{\gamma i}^{\ast }$ are the corresponding score functions for r(W_i, ψ) and ρ(W_i, γ) given in (19). The information matrices $I_{\psi }^{\ast }$ and $I_{\gamma }^{\ast }$ also given in (19) are positive definite.

Proof of Theorem 1

Consistency of β̂_I

Let ψ₀ be the true value of ψ such that r(W_i) = r(W_i, ψ₀) under the correctly specified model for r(W_i). Then $\widehat{\psi }\stackrel{P}{\to }{\psi }_0$. Let

$${\xi }_n(\beta ,{\psi }_0)=n^{-1}\sum _{i=1}^n{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)\frac{R_i}{\pi (Q_i,{\psi }_0)}{N}_i(dt).$$

When r(W_i, ψ₀) is the correct model for r(W_i), z̃(t, β, ψ₀) = z̄(t, β), where z̃(t, β, ψ₀) is the limit of Z̃(t, β, ψ₀). Under the conditions of Theorem 1, n⁻¹ U_I (β, ψ̂) = ξ_n(β, ψ₀) + O_p(n^−1/2) uniformly in β ∈ [−M, M]^p for M > 0.

By application of the Glivenko–Cantelli and Donsker theorems, ξ_n(β, ψ₀) = ξ(β, ψ₀) + O_p(n^−1/2) uniformly in β ∈ [−M, M]^p, where

$$\xi (\beta ,{\psi }_0)=E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)\frac{R_i}{\pi (Q_i,{\psi }_0)}{N}_i(dt)\right].$$

When r(W_i, ψ₀) is the correct model for $r(W_i),\xi (\beta ,{\psi }_0)=E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)N_i(dt)\right]$ by the double expectation formula E[·] = E{E[·|W_i, Δ_i, Δ_i > 0]} and the missing at random assumption (2). Hence

$$n^{-1}{U}_I(\beta ,\widehat{\psi })\stackrel{P}{\to }E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)N_i(dt)\right]$$

uniformly in β ∈ [−M, M]^p for M > 0.

Let 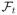= σ{N_i(s), Y_i(s), Z_i(s), 0 ≤ s ≤ t, i = 1, …, n} be the σ-field generated by the observed information on the failure/censoring times and covariates up to time t. Then the intensity of the counting process N_i(t) is given by E{N_i(dt)| 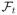} = λ₁(t|Z_i(t))Y_i(t)dt. Under the independent censoring assumption stated in the introduction, ${\lambda }_1(t\mid Z_i(t))={\lambda }_1^{\ast }(t\mid Z_i(t))$. Hence $M_i(t)=N_i(t)-{\int }_0^t{Y}_i(u){\lambda }_1(u\mid Z_i(u))du=N_i(t)-{\int }_0^t{Y}_i(u)e^{{\beta }_0^{\top }{Z}_i(u)}{\lambda }_0(u)du$ is a martin-gale with respect to 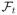. Since $E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,{\beta }_0)\right)Y_i(t)e^{{\beta }_0^{\top }{Z}_i(t)}{\lambda }_0(t)dt\right]=0$, it follows that $\xi ({\beta }_0,{\psi }_0)=E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,{\beta }_0)\right)M_i(dt)\right]=0$. By Condition (A.3), β₀ is the unique solution to ξ(β, ψ₀) = 0. We have ${\widehat{\beta }}_I\stackrel{P}{\to }{\beta }_0$ by Theorem 5.9 of van der Vaart (1998).

Asymptotic Normality of β̂_I

Since U_I (β̂_I, ψ̂) = 0, $U_I({\widehat{\beta }}_I,\widehat{\psi })=0,U_I({\beta }_0,\widehat{\psi })={-\frac{1}{n}\frac{\partial U_I(\beta ,\widehat{\psi })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}({\widehat{\beta }}_I-{\beta }_0)$, where β̃ is on the line segment between β̂_I and β₀. We have

$$\sqrt{n}\left({\widehat{\beta }}_I-{\beta }_0\right)={\left({-\frac{1}{n}\frac{\partial U_I(\beta ,\widehat{\psi })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}\right)}^{-1}\frac{1}{\sqrt{n}}{U}_I({\beta }_0,\widehat{\psi }).$$

By (A.4), $\widehat{\psi }\stackrel{P}{\to }{\psi }_0$ under correctly specified model for r(W_i). By Condition (A.2) and the consistency of β̂_I, $\stackrel{\sim }{V}(t,\stackrel{\sim }{\beta },\widehat{\psi })\stackrel{P}{\to }v(t,{\beta }_0)$ uniformly in t ∈ (0, τ]. We have

$$\begin{array}{l}{-\frac{1}{n}\frac{\partial U_I(\beta ,\widehat{\psi })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }\stackrel{\sim }{V}(t,\stackrel{\sim }{\beta },\widehat{\psi })\frac{R_i}{r(W_i,\widehat{\psi })}{dN}_i(t)\stackrel{P}{\to }E\left[{\int }_0^{\tau }v(t,{\beta }_0)\frac{R_1}{r(W_1,{\psi }_0)}{dN}_1(t)\right]\\ =\mathrm{\sum }.\end{array}$$

Thus

$$\sqrt{n}\left({\widehat{\beta }}_I-{\beta }_0\right)={(\mathrm{\sum }+o_p(1))}^{-1}{n}^{-1/2}{U}_I({\beta }_0,\widehat{\psi }).$$ (7)

Let π̇(·, ψ) = ∂π(·, ψ)/∂ψ, ṙ(·, ψ) = ∂r(·,ψ)/∂ψ, r̈(·,ψ) = ∂ṙ(·, ψ)/∂ψ^⊤, and

$$\begin{array}{c}{H}^{(1)}(t,\beta ,\psi )=\frac{1}{n}\sum _{i=1}^n{Y}_i(t)e^{{\beta }^{\top }{Z}_i(t)}\frac{R_i{\stackrel{.}{\pi }}^{\top }(Q_i,\psi )}{{\pi }^2(Q_i,\psi )},\\ H^{(2)}(t,\beta ,\psi )=\frac{1}{n}\sum _{i=1}^n{Y}_i(t)e^{{\beta }^{\top }{Z}_i(t)}{Z}_i(t)\frac{R_i{\stackrel{.}{\pi }}^{\top }(Q_i,\psi )}{{\pi }^2(Q_i,\psi )},\\ h^{(1)}(t,\beta ,\psi )=E\left[Y_1(t)e^{{\beta }^{\top }{Z}_1(t)}\frac{R_1{\stackrel{.}{\pi }}^{\top }(Q_1,\psi )}{{\pi }^2(Q_1,\psi )}\right],\\ h^{(2)}(t,\beta ,\psi )=E\left[Y_1(t)e^{{\beta }^{\top }{Z}_1(t)}{Z}_1(t)\frac{R_1{\stackrel{.}{\pi }}^{\top }(Q_1,\psi )}{{\pi }^2(Q_1,\psi )}\right].\end{array}$$

By the Taylor expansion of U_I (β₀, ψ̂) around ψ₀,

$$n^{-1/2}\sqrt{n}{U}_I({\beta }_0,\widehat{\psi })=n^{-1/2}{U}_I({\beta }_0,{\psi }_0)+{n^{-1}\frac{\partial U_I({\beta }_0,\psi )}{\partial \psi }|}_{\psi ={\psi }_0}\sqrt{n}(\widehat{\psi }-{\psi }_0)+o_p(1).$$

Note that

$${n^{-1}\frac{\partial U_I({\beta }_0,\psi )}{\partial \psi }|}_{\psi ={\psi }_0}=V_{\psi }+o_p(1),$$

where

$$V_{\psi }=E\left[\begin{array}{l}{\int }_0^{\tau }\left(Z_1(t)-\overline{z}(t,{\beta }_0)\right)\frac{R_1{\stackrel{.}{\pi }}^{\top }(Q_1,{\psi }_0)}{{\pi }^2(Q_1,{\psi }_0)}{dN}_1(t)-\left(\frac{h^{(2)}(t,{\beta }_0,{\psi }_0)}{{\stackrel{\sim }{S}}^{(0)}(t,{\beta }_0,{\psi }_0)}-\frac{{\stackrel{\sim }{S}}^{(1)}(t,{\beta }_0,{\psi }_0)h^{(1)}(t,{\beta }_0,{\psi }_0)}{{({\stackrel{\sim }{S}}^{(0)}(t,{\beta }_0,{\psi }_0))}^2}\right)\frac{R_1}{\pi (Q_1,{\psi }_0)}{dN}_1(t)\end{array}\right].$$ (8)

It follows that

$$n^{-1/2}{U}_I({\beta }_0,\widehat{\psi })=n^{-1/2}{U}_I({\beta }_0,{\psi }_0)+V_{\psi }\sqrt{n}(\widehat{\psi }-{\psi }_0)+o_p(1).$$ (9)

Since

$$\sum _{i=1}^n{\int }_0^{\tau }\frac{R_i}{\pi (Q_i,{\psi }_0)}\left(Z_i(t)-\stackrel{\sim }{Z}(t,{\beta }_0,{\psi }_0)\right)Y_i(t)e^{{\beta }_0^T{Z}_i(t)}d{\mathrm{\Lambda }}_0(t)=0,$$

we have

$$n^{-1/2}{U}_I({\beta }_0,{\psi }_0)=n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\frac{R_i}{\pi (Q_i,{\psi }_0)}\left(Z_i(t)-\stackrel{\sim }{Z}(t,{\beta }_0,{\psi }_0)\right){dM}_i(t).$$

Under correctly specified r(W_i), E[R_i{π(Q_i, ψ₀)}⁻¹M_i(t)] = 0. By Glivenko–Cantelli and Donsker theorems, $n^{-1/2}{\sum }_{i=1}^n{R}_i{\{\pi (Q_i,{\psi }_0)\}}^{-1}{M}_i(t)$ converges weakly to a mean zero Gaussian process and $\stackrel{\sim }{Z}(t,{\beta }_0,{\psi }_0)\stackrel{P}{\to }\overline{z}(t,{\beta }_0)$ uniformly in t under the correctly specified model for r(W_i). Applying Lemma 2 of Gilbert et al. (2008), we have

$${\int }_0^{\tau }\{\stackrel{\sim }{Z}(t,{\beta }_0,{\psi }_0)-\overline{z}(t,{\beta }_0)\}d\{n^{-1/2}\sum _{i=1}^n\frac{R_i}{\pi (Q_i,{\psi }_0)}{M}_i(t)\}\stackrel{P}{\to }0.$$

Hence

$$n^{-1/2}{U}_I({\beta }_0,{\psi }_0)=\sum _{i=1}^n{\int }_0^{\tau }\frac{R_i}{\pi (Q_i,{\psi }_0)}(Z_i(t)-\overline{z}(t,{\beta }_0)){dM}_i(t)+o_p(1).$$ (10)

Let S_ψi and I_ψ be the score vector and the information matrix under the parametric model r(W_i, ψ), respectively. Specifically,

$$\begin{array}{l}{S}_{\psi i}=\frac{I({\mathrm{\Delta }}_i>0)\{R_i-r(W_i,{\psi }_0)\}\stackrel{.}{r}(W_i,{\psi }_0)}{r(W_i,{\psi }_0)\{1-r(W_i,{\psi }_0)\}},\\ I_{\psi }=E\left[S_{\psi 1}{S}_{\psi 1}^{\top }-\frac{I({\mathrm{\Delta }}_1>0)\{R_1-r(W_1,{\psi }_0)\}\ddot{r}(W_1,{\psi }_0)}{r(W_1,{\psi }_0)\{1-r(W_1,{\psi }_0)\}}\right],\end{array}$$ (11)

Under (A.4),

$$\widehat{\psi }-{\psi }_0=n^{-1}\sum _{i=1}^n{I}_{\psi }^{-1}{S}_{\psi i}+o_p(n^{-1/2}).$$ (12)

By (9), (10) and (12), we have

$$n^{-1/2}{U}_I({\beta }_0,\widehat{\psi })=n^{-1/2}\sum _{i=1}^n{\omega }_i+o_p(1),$$ (13)

where

$${\omega }_i={\int }_0^{\tau }\{Z_i(t)-\overline{z}(t,{\beta }_0)\}\frac{R_i}{\pi (Q_i,{\psi }_0)}{dM}_i(t)-V_{\psi }{I}_{\psi }^{-1}{S}_{\psi i}.$$

By the central limit theorem, n^−1/2U_I (β₀, ψ̂) converges in distribution to a normal random vector with zero-mean and covariance matrix $E[{\omega }_1{\omega }_1^T]$.

It follows by (7) and (13) that $\sqrt{n}\left({\widehat{\beta }}_I-{\beta }_0\right)$ converges in distribution to a zero-mean Gaussian random vector with covariance matrix ${\mathrm{\sum }}^{-1}E[{\omega }_1{\omega }_1^T]{\mathrm{\sum }}^{-1}$.

Proof of Theorem 2

Consistency of β̂_A

Under (A.4), there exist ψ^* and γ^* such that $\widehat{\psi }\stackrel{P}{\to }{\psi }^{\ast }$ and $\widehat{\gamma }\stackrel{P}{\to }{\gamma }^{\ast }$. Let

$${\eta }_n(\beta ,{\psi }^{\ast },{\gamma }^{\ast })=n^{-1}\sum _{i=1}^n{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)\left[\frac{R_i}{r(W_i,{\psi }^{\ast })}{dN}_i(t)-\frac{R_i-r(W_i,{\psi }^{\ast })}{r(W_i,{\psi }^{\ast })}\rho (W_i,{\gamma }^{\ast }){dN}_i^{\ast }(t)\right].$$

Under Condition A, n⁻¹U_A(β, ψ̂, γ̂) = η_n(β, ψ^*, γ^*) + O_p(n^−1/2) uniformly in β ∈ [−M, M]^p for M > 0.

By application of the Glivenko–Cantelli and Donsker theorems, η_n(β, ψ^*, γ^*) = η(β, ψ^*, γ^*) + O_p(n^−1/2) uniformly in β ∈ [−M, M]^p, where

$${\eta }_n(\beta ,{\psi }^{\ast },{\gamma }^{\ast })=E\left\{{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)\left[\frac{R_i}{r(W_i,{\psi }^{\ast })}{dN}_i(t)-\frac{R_i-r(W_i,{\psi }^{\ast })}{r(W_i,{\psi }^{\ast })}\rho (W_i,{\gamma }^{\ast }){dN}_i^{\ast }(t)\right]\right\}.$$

If at least one of r(W_i, ψ₀) and ρ(W_i, γ₀) is correctly specified for r(W_i) and ρ(W_i), then $\eta (\beta ,{\psi }^{\ast },{\gamma }^{\ast })=E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)N_i(dt)\right]$ by the missing at random assumption (2) and by using the double expectation formula E[·] = E{E[·|W_i, Δ_i, Δ_i > 0]} if r(W_i) is correctly specified and using E[·] = E{E[·|W_i, R_i, Δ_i > 0]} if ρ(W_i) is correctly specified. Hence

$$n^{-1}{U}_A(\beta ,\widehat{\psi },\widehat{\gamma })\stackrel{P}{\to }E\left[{\int }_0^{\tau }\left(Z_i(t)-\overline{z}(t,\beta )\right)N_i(dt)\right]$$

uniformly in β ∈ [−M, M] if at least one of r(W_i, ψ₀) and ρ(W_i, γ₀) is correctly specified for r(W_i) and ρ(W_i). Since η(β₀, ψ^*, γ^*) = 0 and β₀ is the unique solution to η(β₀, ψ^*, γ^*) = 0 by Condition (A.3), we have ${\widehat{\beta }}_A\stackrel{P}{\to }{\beta }_0$ by Theorem 5.9 of van der Vaart (1998).

Asymptotic Normality of β̂_A

Since U_A(β, ψ̂, γ̂) = 0, $U_A({\beta }_0,\widehat{\psi },\widehat{\gamma })={-\frac{1}{n}\frac{\partial U_A(\beta ,\widehat{\psi },\widehat{\gamma })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}({\widehat{\beta }}_A-{\beta }_0)$, where β̃ is on the line segment between β̂_A and β₀. We have

$$\sqrt{n}\left({\widehat{\beta }}_A-{\beta }_0\right)={\left({-\frac{1}{n}\frac{\partial U_A(\beta ,\widehat{\psi },\widehat{\gamma })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}\right)}^{-1}\frac{1}{\sqrt{n}}{U}_A({\beta }_0,\widehat{\psi },\widehat{\gamma }).$$

By Condition (A.2) and the consistency of β̂_A, $V(t,\stackrel{\sim }{\beta })\stackrel{P}{\to }v(t,{\beta }_0)$ uniformly in t. Furthermore, by (A.4), $\widehat{\psi }\stackrel{P}{\to }{\psi }^{\ast }$ and $\widehat{\gamma }\stackrel{P}{\to }{\gamma }^{\ast }$, we have

$${-\frac{1}{n}\frac{\partial U_A(\beta ,\widehat{\psi },\widehat{\gamma })}{\partial \beta }|}_{\beta =\stackrel{\sim }{\beta }}=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }V(t,\stackrel{\sim }{\beta })\left[\frac{R_i}{r(W_i,\widehat{\psi })}{dN}_i(t)-\frac{R_i-r(W_i,\widehat{\psi })}{r(W_i,\widehat{\psi })}\rho (W_i,\widehat{\gamma }){dN}_i^{\ast }(t)\right]$$

converges in probability to

$${\mathrm{\sum }}_A=E\left[{\int }_0^{\tau }V(t,{\beta }_0)\left(\frac{R_1}{r(W_1,{\psi }^{\ast })}{dN}_1(t)-\frac{R_1-r(W_1,{\psi }^{\ast })}{r(W_1,{\psi }^{\ast })}\rho (W_1,{\gamma }^{\ast }){dN}_1^{\ast }(t)\right)\right],$$

which equals to $\mathrm{\sum }={\int }_0^{\tau }v(t,{\beta }_0){\lambda }_0(t)s^{(0)}(t,{\beta }_0)dt$ if at least one of r(W) and ρ(W) is correctly specified. Thus

$$\sqrt{n}\left({\widehat{\beta }}_A-{\beta }_0\right)={(\mathrm{\sum }+o_p(1))}^{-1}{n}^{-1/2}{U}_A({\beta }_0,\widehat{\psi },\widehat{\gamma }).$$ (14)

Let ṙ(·, ψ) = ∂r(·,ψ)/∂ψ, r̈(·, ψ) = ∂ṙ(·, ψ)/∂ψ^⊤, ρ̇(·, γ) = ∂ρ(·, γ)/∂γ, and r̈(·, γ) = ∂ρ̇(·, γ)/∂γ^⊤. By the Taylor expansion of U_A(β₀, ψ̂, γ̂) around ψ^* and γ^*,

$$\begin{array}{l}{n}^{-1/2}{U}_A({\beta }_0,\widehat{\psi },\widehat{\gamma })\\ =n^{-1/2}{U}_A({\beta }_0,{\psi }^{\ast },{\gamma }^{\ast })+{n^{-1}\frac{\partial U_A({\beta }_0,\psi ,\gamma )}{\partial \psi }|}_{(\psi ,\gamma )=({\psi }^{\ast },{\gamma }^{\ast })}\sqrt{n}(\widehat{\psi }-{\psi }^{\ast })\\ +{n^{-1}\frac{\partial U_A({\beta }_0,\psi ,\gamma )}{\partial \gamma }|}_{(\psi ,\gamma )=({\psi }^{\ast },{\gamma }^{\ast })}\sqrt{n}(\widehat{\gamma }-{\gamma }^{\ast })+o_p(1).\end{array}$$

Note that

$$\begin{array}{l}{n^{-1}\frac{\partial U_A({\beta }_0,\psi ,\gamma )}{\partial \gamma }|}_{(\psi ,\gamma )=({\psi }^{\ast },{\gamma }^{\ast })}=P_{\psi }+o_p(1),\\ {n^{-1}\frac{\partial U_A({\beta }_0,\psi ,\gamma )}{\partial \gamma }|}_{(\psi ,\gamma )=({\psi }^{\ast },{\gamma }^{\ast })}=P_{\gamma }+o_p(1),\end{array}$$

where

$$\begin{array}{l}{P}_{\psi }=E\left[{\int }_0^{\tau }\{Z_1(t)-\overline{z}(t,{\beta }_0)\}\frac{R_1{\stackrel{.}{r}}^{\top }(W_1,{\psi }^{\ast })}{r^2(W_1,{\psi }^{\ast })}\{{dN}_1(t)-\rho (W_1,{\gamma }^{\ast }){dN}_1^{\ast }(t)\}\right],\\ P_{\gamma }=E\left[{\int }_0^{\tau }\{Z_1(t)-\overline{z}(t,{\beta }_0)\}\frac{R_1-r(W_1,{\psi }^{\ast })}{r(W_1,{\psi }^{\ast })}{\stackrel{.}{\rho }}^{\top }(W_1,{\gamma }^{\ast }){dN}_1^{\ast }(t)\right].\end{array}$$ (15)

It follows that

$$n^{-1/2}{U}_A({\beta }_0,\widehat{\psi },\widehat{\gamma })=n^{-1/2}{U}_A({\beta }_0,{\psi }^{\ast },{\gamma }^{\ast })+P_{\psi }\sqrt{n}(\widehat{\psi }-{\psi }^{\ast })+P_{\gamma }\sqrt{n}(\widehat{\gamma }-{\gamma }^{\ast })+o_p(1).$$ (16)

Let $M_i(t)=N_i(t)-{\int }_0^t{Y}_i(u)e^{{\beta }_0^{\top }{Z}_i(u)}d{\mathrm{\Lambda }}_0(u)$, and

$$M_i^{\ast }(t)=\frac{R_i}{r(W_i,{\psi }^{\ast })}{N}_i(t)-\frac{R_i-r(W_i,{\psi }^{\ast })}{r(W_i,{\psi }^{\ast })}\rho (W_i,{\gamma }^{\ast })N_i^{\ast }(t)-{\int }_0^t{Y}_i(u)e^{{\beta }_0^{\top }{Z}_i(u)}d{\mathrm{\Lambda }}_0(u).$$ (17)

Since ${\sum }_{i=1}^n{\int }_0^{\tau }\left(Z_i(t)-\overline{Z}(t,{\beta }_0)\right)Y_i(t)e^{{\beta }_0^T{Z}_i(t)}d{\mathrm{\Lambda }}_0(t)=0$, it follows that

$$n^{-1/2}{U}_A({\beta }_0,{\psi }^{\ast },{\gamma }^{\ast })=n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\left(Z_i(t)-\overline{Z}(t,{\beta }_0)\right){dM}_i^{\ast }(t).$$

Similar to the arguments given above, $E[M_i^{\ast }(t)]=0$ if at least one of r(W_i) and ρ(W_i) is correctly specified. By application of the Glivenko-Cantelli and Donsker theorems, $n^{-1/2}{M}_i^{\ast }(t)$ converges weakly to a zero-mean Gaussian process and $\overline{Z}(t,{\beta }_0)\stackrel{P}{\to }\overline{z}(t,{\beta }_0)$ uniformly in t. Applying Lemma 2 of Gilbert et al. (2008), we have

$${\int }_0^{\tau }\{\overline{Z}(t,{\beta }_0)-\overline{z}(t,{\beta }_0)\}d\{n^{-1/2}\sum _{i=1}^n{M}_i^{\ast }(t)\}\stackrel{P}{\to }0.$$

Hence

$$U_A({\beta }_0,{\psi }^{\ast },{\gamma }^{\ast })=\sum _{i-1}^n{\int }_0^{\tau }(Z_i(t)-\overline{z}(t,{\beta }_0)){dM}_i^{\ast }(t)+o_p(1).$$ (18)

Let $S_{\psi i}^{\ast }$ and $I_{\psi }^{\ast }$ be the score vector and the information matrix under the parametric model r(W_i, ψ), respectively, and $S_{\gamma i}^{\ast }$ and $I_{\gamma }^{\ast }$ the score vector and the information matrix under the parametric model ρ(W_i, γ). Specifically,

$$\begin{array}{l}{S}_{\psi i}^{\ast }=\frac{I({\mathrm{\Delta }}_i>0)\{R_i-r(W_i,{\psi }^{\ast })\}\stackrel{.}{r}(W_i,{\psi }^{\ast })}{r(W_i,{\psi }^{\ast })\{1-r(W_i,{\psi }^{\ast })\}},\\ S_{\gamma i}^{\ast }=\frac{R_{i}I({\mathrm{\Delta }}_i>0)\{I({\mathrm{\Delta }}_i=1)-\rho (W_i,{\gamma }^{\ast })\}\stackrel{.}{\rho }(W_i,{\gamma }^{\ast })}{\rho (W_i,{\gamma }^{\ast })\{1-\rho (W_i,{\gamma }^{\ast })\}},\\ I_{\psi }^{\ast }=E\left[S_{\psi 1}{S}_{\psi 1}^{\top }-\frac{I({\mathrm{\Delta }}_1>0)\{R_1-r(W_1,{\psi }^{\ast })\}\ddot{r}(W_1,{\psi }^{\ast })}{r(W_1,{\psi }^{\ast })\{1-r(W_1,{\psi }^{\ast })\}}\right],\\ I_{\gamma }^{\ast }=E\left[S_{\gamma 1}{S}_{\gamma 1}^{\top }-\frac{R_{1}I({\mathrm{\Delta }}_1>0)\{I({\mathrm{\Delta }}_1=1)-\rho (W_1,{\gamma }^{\ast })\}\ddot{\rho }(W_1,{\gamma }^{\ast })}{\rho (W_1,{\gamma }^{\ast })\{1-\rho (W_1,{\gamma }^{\ast })\}}\right].\end{array}$$ (19)

Under (A.4),

$$\widehat{\psi }-{\psi }^{\ast }=n^{-1}\sum _{i=1}^n{(I_{\psi }^{\ast })}^{-1}{S}_{\psi i}^{\ast }+o_p(n^{-1/2})$$ (20)

and

$$\widehat{\gamma }-{\gamma }^{\ast }=n^{-1}\sum _{i=1}^n{(I_{\gamma }^{\ast })}^{-1}{S}_{\gamma i}^{\ast }+o_p(n^{-1/2}).$$ (21)

By (16), (18), (20), and (21), we have

$$n^{-1/2}{U}_A({\beta }_0,\widehat{\psi },\widehat{\gamma })=n^{-1/2}\sum _{i=1}^n{\phi }_i+o_p(1),$$ (22)

where

$${\phi }_i={\int }_0^{\tau }\{Z_i(t)-\overline{z}(t,{\beta }_0)\}{dM}_i^{\ast }(t)-P_{\psi }{(I_{\psi }^{\ast })}^{-1}{S}_{\psi i}^{\ast }-P_{\gamma }{(I_{\gamma }^{\ast })}^{-1}{S}_{\gamma i}^{\ast }.$$

By the central limit theorem, n^−1/2U_A(β₀, ψ̂, γ̂) converges in distribution to a normal random vector with zero-mean and covariance matrix $E[{\phi }_1{\phi }_1^T]$.

It follows by (14) and (22) that $\sqrt{n}\left({\widehat{\beta }}_A-{\beta }_0\right)$ converges in distribution to a zero-mean Gaussian random vector with covariance matrix ${\mathrm{\sum }}^{-1}E[{\phi }_1{\phi }_1^T]{\mathrm{\sum }}^{-1}$.