The allele-frequency spectrum in a decoupled Moran model with mutation, drift, and directional selection, assuming small mutation rates

Abstract

We analyze a decoupled Moran model with haploid population size $N$, a biallelic locus under mutation and drift with scaled forward and backward mutation rates ${\theta }_1={\mu }_{1}N$ and ${\theta }_0={\mu }_{0}N$, and directional selection with scaled strength $\gamma =sN$. With small scaled mutation rates ${\theta }_0$ and ${\theta }_1$, which is appropriate for single nucleotide polymorphism data in highly recombining regions, we derive a simple approximate equilibrium distribution for polymorphic alleles with a constant of proportionality. We also put forth an even simpler model, where all mutations originate from monomorphic states. Using this model we derive the sojourn times, conditional on the ancestral and fixed allele, and under equilibrium the distributions of fixed and polymorphic alleles and fixation rates. Furthermore, we also derive the distribution of small samples in the diffusion limit and provide convenient recurrence relations for calculating this distribution. This enables us to give formulas analogous to the Ewens–Watterson estimator of $\theta$ for biased mutation rates and selection. We apply this theory to a polymorphism dataset of fourfold degenerate sites in Drosophila melanogaster.

1. Introduction

In the limit of relatively high recombination and small mutation rates, each polymorphic site can be considered independent from the rest of the genome. The distribution of allele frequencies at a large number of such loci has been called the “allele-frequency spectrum” or “site-frequency spectrum”. In a classical manuscript, Wright (1931) introduced a bi-allelic equilibrium model and derived the equilibrium allele frequency distribution, up to a constant of proportionality. Most recent treatments of similar models, however, assume irreversible mutations (e.g., Sawyer and Hartl, 1992; Hartl et al., 1994; Bustamante et al., 2001; Griffiths, 2003; Ewens, 2004; Evans et al., 2007). If mutation rates are low and an outgroup is available to infer the ancestral state, i.e., if states can be polarized, theory assuming irreversibility allows inference of selection coefficients for polymorphic sites. The quality of polarization and thus the quality of inference under this model depends on the relative age of outgroups: if outgroups are too closely related, polymorphism shared among species is problematic; if outgroups are too distantly related, double mutations may obscure patterns. Thus, for real data analysis, a model allowing for back mutations may be better suited. Furthermore, if mutation parameters are to be estimated in addition to the selection coefficient, an approach using reversible mutations is necessary. Relatively recently, McVean and Charlesworth (1999) reconnect to earlier work to derive some statistics for the allele-frequency spectrum and provide such an approach. Zeng and Charlesworth (2009, 2010) use the Wright–Fisher model and forward simulations to infer parameters using sequence data with a reversible mutation model (Shapiro et al., 2007).

In population genetics theory, the Wright–Fisher model (Fisher, 1930; Wright, 1931) and later the Moran model (Moran, 1958) have received the most attention among the explicit models moving forwards in time. Many classic results were derived using diffusion theory (Fisher, 1930; Wright, 1931; Kimura, 1955a,b). A key parameter in population genetics is the population size $N$. In the limit of large $N$ (usually a reasonable assumption), results from different models and approaches converge. Diffusion theory can be seen either as a model in its own right or as an approximation to the explicit models in the limit of large $N$. Since we are mostly interested in this limit, the mathematically most tractable approach has been used, usually diffusion theory (Ewens, 2004). The models and approaches discussed so far move forward in time. Since the 1980’s, the coalescent (Kingman, 1982), an approach that looks backward in time, has been used to derive insights into the distribution of small samples and into the genealogic tree behind allelic distributions.

Using a Moran model, Muirhead and Wakeley (2009) showed that exact equilibrium solutions (up to a constant of proportionality) can be obtained relatively easily for population genetic models with mutation, drift, and frequency-dependent selection, both for infinitely many and a finite number of $K$-alleles. Some of their results go beyond those readily available by diffusion theory. Baake and Bialowons (2008) and Etheridge and Griffiths (2009) use a Moran model where mutation, selection, and drift are decoupled. With this model, Etheridge and Griffiths (2009) derive formulas for mutation, drift, and genic selection and show that they converge to the usual diffusion derived formulas in the limit of large $N$. Furthermore, boundary conditions are rather difficult to incorporate into diffusion theory (e.g., Evans et al., 2007). This argues for multiple approaches to population genetics problems, challenging the nearly exclusive focus on diffusion theory in forward models.

Starting from a decoupled Moran model (Baake and Bialowons, 2008; Etheridge and Griffiths, 2009), we concentrate particularly on small scaled mutation rates (${\theta }_0\ll 1$ and ${\theta }_1\ll 1$) with directional selection. We derive theory analogous to a model without selection and apply it to a dataset of Drosophila melanogasterintrons and fourfold degenerate sites (Shapiro et al., 2007).

2. Small $\theta$ without selection

In this section, we re-derive known results for the case without selection, i.e., the mutation-drift model. We show how results derived for the infinite sites model follow from the general case for small scaled mutation rates, i.e., with ${\theta }_0$ and ${\theta }_1$ small and of order $\theta \ll 1$.

Without selection, the mutation-drift equilibrium distribution of a locus with two alleles is known to be beta-binomially distributed in the diffusion limit and also in the decoupled Moran model (Baake and Bialowons, 2008; Etheridge and Griffiths, 2009), which we will introduce in more detail below. The probability of finding $y=i$ copies of allele one in a small sample of size $n$, with $0<i<n$, is:

$$\mathrm{Pr}(y=i\mid n,{\theta }_0,{\theta }_1)=\frac{n!}{{({\theta }_0+{\theta }_1)}_n}\frac{{\left({\theta }_0\right)}_{n-i}}{(n-i)!}\frac{{\left({\theta }_1\right)}_i}{i!}\text{,}$$ (1)

where ${\left(a\right)}_i$ is the rising factorial or Pochhammer function: ${\left(a\right)}_i=a(a+1)(a+2)\cdots (a+i-1)$ and ${\left(a\right)}_0=1$. For small $\theta$, we have ${\left(\theta \right)}_i=\theta (i-1)!+O\left({\theta }^2\right)$. Therefore, formula (1) becomes for $0<i<n$:

$$\mathrm{Pr}(y=i\mid n,{\theta }_0,{\theta }_1)=\frac{{\theta }_0{\theta }_1}{{\theta }_0+{\theta }_1}\frac{n}{i(n-i)}+O\left({\theta }^2\right)=\frac{{\theta }_0{\theta }_1}{{\theta }_0+{\theta }_1}(\frac{1}{i}+\frac{1}{n-i})+O\left({\theta }^2\right)\text{.}$$ (2)

Here, ${\theta }_0{\theta }_1/({\theta }_0+{\theta }_1)$ serves as an approximate constant of proportionality. For $y=0$ and $y=n$, we have $\mathrm{Pr}(y=0\mid n,{\theta }_0,{\theta }_1)={\theta }_0/({\theta }_0+{\theta }_1)+O\left({\theta }^2\right)$ and $\mathrm{Pr}(y=n\mid n,{\theta }_0,{\theta }_1)\approx {\theta }_1/({\theta }_0+{\theta }_1)+O\left({\theta }^2\right)$, respectively. For a sample of $L$ loci, the expectation of the sum of all polymorphic loci then is to first order in $\theta$:

$$L\sum _{i=1}^{n-1}\frac{{\theta }_0{\theta }_1}{{\theta }_0+{\theta }_1}(\frac{1}{i}+\frac{1}{n-i})=L\frac{2{\theta }_0{\theta }_1}{{\theta }_0+{\theta }_1}\sum _{i=1}^{n-1}\frac{1}{i}\text{.}$$ (3)

This recapitulates formula (17) in RoyChoudhury and Wakeley (2010). It can be rearranged to give a method of moments estimator of polymorphism in a sample that extends the Ewens–Watterson estimator of molecular variation ${\hat{\theta }}_w$ (Ewens, 1974; Watterson, 1975) to biased mutation rates. If the mutation rates are balanced, i.e., ${\theta }_0={\theta }_1=\theta$, formula (3) reduces to $L\theta {\sum }_{y=1}^{n-1}1/y$. This estimator has been derived with the infinite-sites model that assumes negligible scaled mutation rates $\theta$.

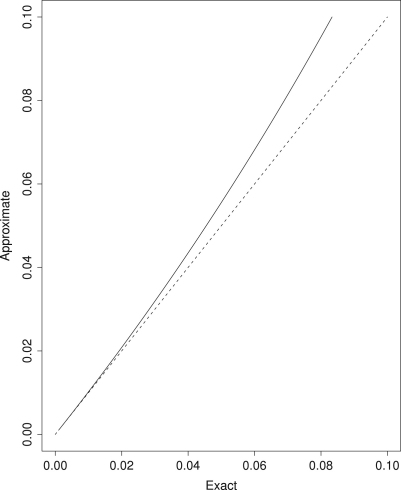
Obviously, the quality of the approximation depends on the amount of polymorphism: according to our simulations, $2{\theta }_0{\theta }_1/({\theta }_0+{\theta }_1)$ should be below 0.05, or better 0.02 (compare also: Desai and Plotkin, 2008). In Fig. 1, we plot the exact versus the approximate probability of polymorphism in a sample of $n=2$.

Fig. 1.

Comparison of the exact versus the approximate probability of polymorphism in a sample of size $n=2$ (solid line). The dashed line shows equality.

We note that in the case without selection, the same formulas also hold for $n=N$, i.e., for the equilibrium distribution of the whole population with $N$ haploid individuals. With selection, the case of small ${\theta }_0$ and ${\theta }_1$ has not been explored extensively. It is not known yet, if formulas similar to (1)–(3) can also be derived.

3. The decoupled Moran model with mutation, selection, and drift

In this section, we re-derive the equilibrium distribution of the decoupled Moran model, up to a constant, by showing that this distribution satisfies detailed balance. Baake and Bialowons (2008) and Etheridge and Griffiths (2009) use the same modified Moran model for their derivations. For the case of small mutation rates $\theta$, we will derive a simple constant of proportionality and the allele-frequency spectrum, sojourn times, and divergence rates conditional on the ancestral and fixed allele.

3.1. Basic model

With the Moran model, generations overlap. It moves from step $t$ to step $t+1$; between steps, exponentially distributed waiting times may be introduced. In the pure-drift case, a constant population of $N$ haploid individuals is assumed. In a birth/death event, a random individual $j$ dies and is replaced by the offspring of a randomly chosen individual $i$. The process repeats indefinitely. The lifespan of an individual is geometrically distributed with a mean time of $N$. It may thus be useful to re-scale time in units of $N$, i.e., to set $\tau =t/N$, to reflect the average lifespan of an individual, or to set ${\tau }^{\ast }=t/N^2$, to reflect the usual diffusion theory scaling.

With the original Moran model, mutation and selection are tied to a birth/death event, such that the replacing gamete is assumed to mutate at a rate $\mu$. Recently, Baake and Bialowons (2008) and Etheridge and Griffiths (2009) used a mathematically more convenient decoupled version, where all events are independent from each other. In this decoupled model, assume a mutation rate of ${\mu }_1$, independent of the allele’s original state, towards the first allele and set ${\theta }_1=N{\mu }_1$ (and ${\mu }_0$ and ${\theta }_0=N{\mu }_0$, respectively). Assume that allele “1” is favored over allele “0” by selection with an advantage $s=\gamma /N$. The favored allele reproduces at a rate $1+s$, the disfavored only at unit rate.

With a biallelic locus, a transition from one step to the next involves just three possibilities for any interior state, either the number of the favored allele $x$ increases or decreases by one or it remains the same. Eq. (4) in Box I, we list the probabilities of events depending on the three forces, drift, mutation, and selection.

Box I.

$$\begin{array}{cccc}\text{Transition}\hfill & \text{Drift}\hfill & \text{Mutation}\hfill & \text{Selection}\hfill \\ x_{t+1}=i+1\text{ given }{x}_t=i\text{:}\hfill & i(N-i)/N^2\hfill & {\theta }_1(N-i)/N^2\hfill & si(N-i)/N^2\hfill \\ x_{t+1}=i\text{ given }{x}_t=i+1\text{:}\hfill & (i+1)(N-i-1)/N^2\hfill & {\theta }_0(i+1)/N^2\hfill & 0\hfill \end{array}$$ (4)

The transition probabilities between neighboring states are thus:

$$\mathrm{Pr}(x_{t+1}=i+1\mid x_t=i,\theta ,s,N)=(N-i)((1+s)i+{\theta }_1)/N^2$$ (5)

and

$$\mathrm{Pr}(x_{t+1}=i\mid x_t=i+1,\theta ,s,N)=(i+1)(N-i-1+{\theta }_0)/N^2\text{.}$$ (6)

Under detailed balance, we have:

$$\mathrm{Pr}(x_{t+1}=i\mid x_t=i+1,\theta ,s,N)\mathrm{Pr}(x_t=i+1\mid N,\theta ,s)=\mathrm{Pr}(x_{t+1}=i+1\mid x_t=i,\theta ,s,N)\mathrm{Pr}(x_t=i\mid N,\theta ,s)\text{.}$$ (7)

We obtain the stationary distribution of the Moran model, up to a constant of proportionality, by substituting the following function:

$$\mathrm{Pr}(x=i\mid N,{\theta }_0,{\theta }_1,s)\propto {(1+s)}^i\frac{{\left(\frac{{\theta }_1}{1+s}\right)}_i{\left({\theta }_0\right)}_{N-i}}{i!(N-i)!}\text{.}$$ (8)

The model can easily be extended from a biallelic to a $K$-allelic locus with parent independent mutation (Etheridge and Griffiths, 2009).

Limit of large $N$. Set $p=x/N$, and let $s\to 0$ and $N\to \infty$ while $sN=\gamma$, such that ${\theta }_1/(1+s)\approx {\theta }_1$ and, by a Taylor series expansion, $(1+s)\approx e^s$. We then obtain, using Stirling’s approximation:

$$\underset{N\to \infty ,s\to 0}{lim}\mathrm{Pr}(p\mid N,\theta ,\gamma )\propto e^{\gamma p}{p}^{{\theta }_1-1}{(1-p)}^{{\theta }_0-1}\text{.}$$ (9)

This result is identical to that from diffusion theory (Wright, 1931, 1949; Kimura, 1955b; Etheridge and Griffiths, 2009). The constant of proportionality can be obtained with the confluent hypergeometric or Kummer’s function (Moran, 1962).

3.2. Allele frequencies with selection; small scaled mutation rates

For small scaled mutation rates, i.e., ${\theta }_0$ and ${\theta }_1$ small and of order $\theta \ll 1$, the probability of polymorphic states, i.e., $i=(1,\dots ,N-1)$ in Eq. (8) converges to:

$$\mathrm{Pr}(x=i\mid N,{\theta }_0,{\theta }_1,s)\propto {(1+s)}^i\frac{{\left(\frac{{\theta }_1}{1+s}\right)}_i{\left({\theta }_0\right)}_{N-i}}{i!(N-i)!}={(1+s)}^i\frac{(i-1)!\left(\frac{{\theta }_1}{1+s}\right)(N-i-1)!\left({\theta }_0\right)}{i!(N-i)!}+O\left({\theta }^2\right)={(1+s)}^{i-1}{\theta }_1{\theta }_0\frac{N}{i(N-i)}+O\left({\theta }^2\right)\text{.}$$ (10)

Similarly, we have for the monomorphic states:

$$\{\begin{array}{c}\mathrm{Pr}(x=0\mid N,{\theta }_0,{\theta }_1,\gamma )\propto {\theta }_0+O\left({\theta }^2\right)\hfill \\ \mathrm{Pr}(x=N\mid N,{\theta }_0,{\theta }_1\gamma )\propto {(1+\gamma /N)}^{N-1}{\theta }_1+O\left({\theta }^2\right)\hfill \\ \mathrm{Pr}(x=i\mid N,{\theta }_0,{\theta }_1,\gamma )\propto \frac{{\theta }_0{\theta }_1{(1+\gamma /N)}^{i-1}N}{i(N-i)}+O\left({\theta }^2\right)\text{,}i=1,\dots ,N-1\text{.}\hfill \end{array}$$ (11)

As can be seen from this equation, with small mutation rates only the boundary states $x=0$ and $x=N$ have probabilities of order one and in proportion

$$\mathrm{Pr}(x=0\mid N,\theta ,\gamma ):\mathrm{Pr}(x=N\mid n,\theta ,\gamma )={(1+\gamma /N)}^{N-1}{\theta }_1:{\theta }_0\approx e^{\gamma }{\theta }_1:{\theta }_0\text{.}$$ (12)

The ratio of the fixed, i.e., non-polymorphic allelic frequencies has been derived before in the diffusion limit, e.g., by Bulmer (1991) using arguments similar to ours.

The constant of proportionality is the inverse of the sum $S$ of all the states:

$$S={\theta }_0+{(1+s)}^{N-1}{\theta }_1+{\theta }_0{\theta }_1\sum _{i=1}^{N-1}\frac{{(1+s)}^{i-1}N}{i(N-i)}+O\left({\theta }^2\right)={\theta }_0+{(1+s)}^{N-1}{\theta }_1+{\theta }_0{\theta }_1\sum _{i=1}^{N-1}\left({(1+s)}^{i-1}(\frac{1}{i}+\frac{1}{N-i})\right)+O\left({\theta }^2\right)<{\theta }_0+{(1+s)}^{N-1}{\theta }_1+2{\theta }_0{\theta }_1{(1+s)}^{N-1}\sum _{i=1}^{N-1}\left(\frac{1}{i}\right)+O\left({\theta }^2\right)={\theta }_0+{(1+s)}^{N-1}{\theta }_1+O\left({\theta }^2\right)\approx {\theta }_0+e^{\gamma }{\theta }_1+O\left({\theta }^2\right)\text{;}$$ (13)

it can thus be approximated by $1/({\theta }_0+{(1+s)}^{N-1}{\theta }_1)$ (or $1/({\theta }_0+e^{\gamma }{\theta }_1)$ for large $N$ and small $s$), for any finite $N$ and $s$, as long as the mutation rates ${\mu }_0$ and ${\mu }_1$ and thus ${\theta }_0$ and ${\theta }_1$ are small enough. We note that there are actually two approximations involved, the first leading to formula (11) and the second to the constant, both depending on $\theta$ being small, such that only first order terms in $\theta$ may be retained. We note that, in the case without selection, the second approximation is not necessary, because there the constant of proportionality of the beta-binomial is available. Obviously, substituting $s=0$ into formula (13) provides the same result as formula (2) above.

For relatively large $N$ and small $s$, the constant of proportionality can furthermore be approximated by $1/({\theta }_0+e^{\gamma }{\theta }_1)$ using a Taylor series approximation. In the formulas below, it will become convenient to define the following constant: $C={\theta }_0{\theta }_1/({\theta }_0+{\theta }_1{(1+s)}^{N-1})$, or the form for relatively large $N$ and small $s$: $C^{\prime }={\theta }_0{\theta }_1/({\theta }_0+{\theta }_1{e}^{\gamma })$.

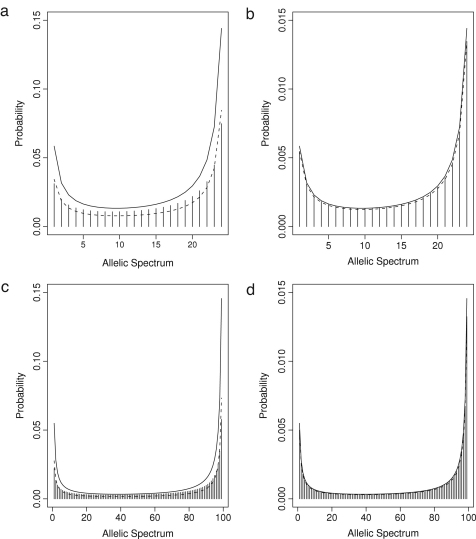
In Fig. 2, we show that for $C=0.05({\theta }_0=0.2,{\theta }_1=0.2,\gamma =1.0)$ the approximation fits only moderately well, while it fits very well for scaled mutation rates that are an order of magnitude less (${\theta }_0=0.02,{\theta }_1=0.02,\gamma =1.0$). This is similar to the results without selection in the previous section. In Fig. 2, the stippled line corresponds to only the first approximation, i.e., the constant was obtained by summing over formula (11) and the solid line to the first and second approximation, i.e., the constant was approximated by summing only the monomorphic states.

Fig. 2.

The exact probability (bars) and approximate probabilities (solid and stippled lines) for ${\theta }_0=0.2,{\theta }_1=0.2,\gamma =1.0$, (A) and (C) and ${\theta }_0=0.02,{\theta }_1=0.02,\gamma =1.0$, (B) and (D), respectively, for $N=25$, (A) and (B), and $N=100$, (C) and (D), respectively. For the stippled line, the constant was obtained by summing over formula (11); for the solid line the constant was approximated from only the monomorphic states (see the text for details).

3.2.1. A simplified equilibrium process with small $\theta$

For small ${\theta }_0$ and ${\theta }_1$, the proportion of mutations occurring in monomorphic states is of order one and of those in polymorphic states is only of order $\theta$. By ignoring the latter, we can construct a simplified process, where mutations only occur from the monomorphic states. With this equilibrium process, there is a flow of new mutations from the non-polymorphic states at a rate of $C{(1+s)}^{N-1}+O\left({\theta }^2\right)$ from $x=N$ to $x=N-1$ and $C+O\left({\theta }^2\right)$ from $x=0$ to $x=1$, respectively.

The transition probabilities are, from any interior state $i$ to state $i-1$: $i(N-i)/N^2$, and from $i$ to $i+1$: $(1+s)i(N-i)/N^2$. These transition probabilities are the same as those for the Moran model in Eq. (8), when flow that in equilibrium occurs with probability of order ${\theta }^2$ is ignored. Observing the amount of flow from 0 and $N$, we can determine the constant of proportionality to obtain the following formula for $x=i,i=(1,\dots ,N-1)$:

$$\mathrm{Pr}(x=i\mid N,\theta ,\gamma )=\frac{{\theta }_0{\theta }_1}{{\theta }_0+{(1+\gamma /N)}^{N-1}{\theta }_1}{(1+\gamma /N)}^{i-1}(\frac{1}{i}+\frac{1}{N-i})+O\left({\theta }^2\right)\text{.}$$ (14)

This is the same equilibrium distribution as derived in the previous section up to order ${\theta }^2$, when both the first and second approximation are used for the constant of proportionality (formulas (11) and (13)) and corresponds to the stippled line in Fig. 2. It can be seen that, with small $\theta$, the allele-frequency spectrum is only influenced by $\gamma$ but not by the scaled mutation rates ${\theta }_1$ and ${\theta }_0$.

For large $N$ and small $s$, using the Taylor series approximation, and setting $p=x/N$, we obtain:

$$\mathrm{Pr}(p\mid \theta ,\gamma )\approx \frac{{\theta }_0{\theta }_1}{{\theta }_0+e^{\gamma }{\theta }_1}{e}^{\gamma p}\frac{1}{Np(1-p)}+O\left({\theta }^2\right)\text{.}$$ (15)

As far as we know, Eq. (15) has only been derived up to a constant of proportionality before, although it could be derived easily from the ratio of the fixed sites and the polarized flows below, which are both well known using the diffusion approach.

3.3. Polarizing the flow

Another motivation for constructing this simplified process, is that if an outgroup is available, it is possible to “polarize” the sample into ancestral alleles, i.e., alleles that are identified as already present in the ancestral sample by their existence in the outgroup, and derived alleles. The number of derived alleles in a polymorphic sample is usually called the “derived allele-frequency spectrum”. The information on the ancestral state only makes sense if the mutation rates ${\theta }_1$ and ${\theta }_0$ are small.

In equilibrium, the flow between the monomorphic states must balance. We can think of $f_0$ as quasi-stationary distribution for alleles originating from $x=0$ of the reduced process, in which $x=0$ and $x=N$ are made boundary conditions, and similarly for $f_1$ originating from $x=N$. For $f_0$, the boundary conditions are that the flow away from state 0 must be equal to that back into state 0 plus that into state $N$ on the other side:

$$\mathrm{Pr}(x=1\mid x=0,\theta ,N)f_0(x=0\mid \theta ,N)=\mathrm{Pr}(x=0\mid x=1,\theta ,N)f_0(x=1\mid \theta ,N)+\mathrm{Pr}(x=N\mid x=N-1,\theta ,N)f_0(x=N-1\mid \theta ,N)\text{.}$$ (16)

The net flow in the interior must also balance:

$$\mathrm{Pr}(x=i\mid x=i-1,\theta ,N)f_0(x=i-1\mid \theta ,N)+\mathrm{Pr}(x=i\mid x=i+1,\theta ,N)f_0(x=i+1\mid \theta ,N)=\mathrm{Pr}(x=i-1\mid x=i,\theta ,N)f_0(x=i\mid \theta ,N)+\mathrm{Pr}(x=i+1\mid x=i,\theta ,N)f_0(x=i\mid \theta ,N)\text{.}$$ (17)

The following corresponds to the equilibrium values (as can be seen by substituting into the formulas (16) and (17)):

$$f_0(x\mid N,\theta ,s)=C{(1+s)}^{x-1}\frac{{(1+s)}^{N-x}-1}{{(1+s)}^N-1}\frac{N}{x(N-x)}+O\left({\theta }^2\right)\text{,}$$ (18)

or, if we again assume large $N$ and small $s$ such that ${(1+s)}^N\approx e^{\gamma }$, and set $p=x/N$:

$$f_0(p\mid \theta ,s)\approx C^{\prime }{e}^{\gamma p}\frac{e^{\gamma (1-p)}-1}{e^{\gamma }-1}\frac{1}{Np(1-p)}+O\left({\theta }^2\right)\text{.}$$ (19)

For the reverse direction, away from state $x=N$, we have analogously:

$$f_1(x\mid N,\theta ,s)=C{(1+s)}^{x-1}\frac{{(1+s)}^N-{(1+s)}^{N-x}}{{(1+s)}^N-1}\frac{N}{x(N-x)}+O\left({\theta }^2\right)$$ (20)

or the continuous version:

$$f_1(p\mid \theta ,s)\approx C^{\prime }{e}^{\gamma p}\frac{e^{\gamma }-e^{\gamma (1-p)}}{e^{\gamma }-1}\frac{1}{Np(1-p)}+O\left({\theta }^2\right)\text{.}$$ (21)

The discrete versions of these equations are solutions to Eq. (2.143) in Ewens (2004) and seem new. The continuous version formulas are well-known and have been derived in the context of the infinite-sites model before, e.g., formula (9.23) in Ewens (2004) and formula (31) in Evans et al. (2007), although there the constant has a different interpretation as a model with irreversible mutations is considered. From these equations, we can get the conditional probabilities of mutations entering the process. The probability of origin and fixation at the unfavored state is:

$${\mathrm{Pr}}_{00}=\frac{{(1+s)}^{N-1}-1}{({(1+s)}^{N-1}+1)({(1+s)}^N-1)}+O\left({\theta }^2\right)\approx \frac{e^{\gamma }-1}{(e^{\gamma }+1)(e^{\gamma }-1)}+O\left({\theta }^2\right)\text{;}$$ (22)

those of entering and exiting at opposite states are:

$${\mathrm{Pr}}_{01}={\mathrm{Pr}}_{10}=\frac{s{(1+s)}^{N-1}}{({(1+s)}^{N-1}+1)({(1+s)}^N-1)}+O\left({\theta }^2\right)\approx \frac{\gamma /N}{(1-e^{-\gamma })}+O\left({\theta }^2\right)\text{;}$$ (23)

and that of entering and exiting at the favored state is:

$${\mathrm{Pr}}_{11}=\frac{{(1+s)}^N({(1+s)}^{N-1}-1)}{({(1+s)}^{N-1}+1)({(1+s)}^N-1)}+O\left({\theta }^2\right)\approx \frac{e^{\gamma }(e^{\gamma }-1)}{(e^{\gamma }+1)(e^{\gamma }-1)}+O\left({\theta }^2\right)\text{.}$$ (24)

We note that for small scaled selection coefficients $\gamma$, already the first order terms differ from the model without selection for two of these probabilities: ${\mathrm{Pr}}_{00}=(N-1)/2N-(N-1)\gamma /\left(4N\right)+O\left({\gamma }^2\right)$ and ${\mathrm{Pr}}_{11}=(N-1)/2N+(N-1)\gamma /\left(4N\right)+O\left({\gamma }^2\right)$, while the others only change with the second order terms: ${\mathrm{Pr}}_{01}=1/N+O\left({\gamma }^2\right)$ and ${\mathrm{Pr}}_{10}=1/N+O\left({\gamma }^2\right)$. Summing all directions, we obtain for $0<i<N$:

$$\mathrm{Pr}(x=i\mid N,\theta ,s)=C{(1+s)}^{i-1}(\frac{1}{i}+\frac{1}{N-i})+O\left({\theta }^2\right)\text{.}$$ (25)

This is identical to Eq. (14).

Conditional flow. For determining the equilibrium distributions conditional on both origin and fixation, we need for each state $j$ the probability of fixation at the favored and unfavored states, respectively. By similar considerations to those above, we can determine that if the flow starts at $x=j$ (instead of $x=1$ or $x=N-1$ if the flow starts by mutation away from $x=0$ or $x=N$, respectively), while the end states are still $x=0$ and $x=N$, and we enter there at a rate $C/N$ per Moran time unit, the equilibrium probabilities of finding the population in state $i$, with $0<i<N$ are:

$$f_j(x=i\mid N,\theta ,s)=\{\begin{array}{c}\text{for }i\le j\text{:}C\frac{({(1+s)}^i-1)({(1+s)}^{N-j}-1)}{s({(1+s)}^N-1)}\frac{N}{i(N-i)}\hfill \\ \text{for }i\ge j\text{:}C{(1+s)}^{i-j}\frac{({(1+s)}^{N-i}-1)({(1+s)}^j-1)}{s({(1+s)}^N-1)}\frac{N}{i(N-i)}\text{.}\hfill \end{array}$$ (26)

Observing the flow out towards states 0 and $N$, it follows that the probability of fixation of the favored allele, if the process started at frequency $j$ is:

$${\pi }_j=\frac{{(1+s)}^{N-j}({(1+s)}^j-1)}{{(1+s)}^N-1}\text{.}$$ (27)

Multiplying ${\pi }_j$ with the probabilities conditional on the starting values, $f_0$ and $f_1$, respectively, results in the probabilities conditional on both starting and fixation states, e.g., for $f_{01}$:

$$f_{01}(x=i\mid N,\theta ,s)={\pi }_i\cdot f_0=C\frac{{(1+s)}^{N-i}({(1+s)}^i-1)}{{(1+s)}^N-1}{(1+s)}^{i-1}\frac{{(1+s)}^{N-i}-1}{{(1+s)}^N-1}\frac{N}{i(N-i)}+O\left({\theta }^2\right)=C{(1+s)}^{N-1}\frac{({(1+s)}^{N-i}-1)({(1+s)}^i-1)}{{({(1+s)}^N-1)}^2}\frac{N}{i(N-i)}+O\left({\theta }^2\right)\text{.}$$ (28)

For $f_{00}$, we have:

$$f_{00}(x=i\mid N,\theta ,s)=(1-{\pi }_i)\cdot f_0=C{(1+s)}^{i-1}\frac{{({(1+s)}^{N-i}-1)}^2}{{({(1+s)}^N-1)}^2}\frac{N}{i(N-i)}+O\left({\theta }^2\right)\text{.}$$ (29)

And finally for $f_{11}$, we have:

$$f_{11}(x=i\mid N,\theta ,s)={\pi }_i\cdot f_1=C{(1+s)}^{i-1}\frac{{({(1+s)}^N-{(1+s)}^{N-i})}^2}{{({(1+s)}^N-1)}^2}\frac{N}{i(N-i)}+O\left({\theta }^2\right)\text{.}$$ (30)

Again these discrete equations seem new. The continuous versions could be determined easily from the average times spent in the different states multiplied by the rate of mutations. This seems to have been done only in the context of irreversible mutation models, e.g., Eq. (9.23) in Ewens (2004) and Eq. (31) in Evans et al. (2007), where the interpretation of the constant is different. In any case, earlier derivations of these equations are quite different from ours in here.

Alternatively, the conditional transition probabilities can be determined (Ewens, 2004, Chapter 2.12), e.g.,

$$p_{x,x+1}^{\ast }=p_{x,x+1}{\pi }_x/{\pi }_{x+1}=\frac{x(N-x)}{N^2}\frac{{(1+s)}^{x+1}-1}{{(1+s)}^x-1}\text{,}$$ (31)

where we used the notation in Ewens’ book. Other conditional transition probabilities follow analogously. It can then be shown that the conditional probabilities in Eqs. (28)–(30) are the equilibrium solutions to this equation given the boundary conditions and the conditional transition probabilities.

3.4. Average sojourn times

From Eq. (28), the conditional times in each state can be determined by dividing by the corresponding rate and summing, e.g., for the flow from unpreferred to preferred:

$$E\left(t_{01}\right)=E\left(t_{10}\right)=\sum _{i=1}^{N-1}{f}_{01}(x=i\mid N,\theta ,s){\left(\frac{C}{N}\frac{s{(1+s)}^{N-1}}{({(1+s)}^N-1)}\right)}^{-1}=\sum _{i=1}^{N-1}\frac{({(1+s)}^{N-i}-1)({(1+s)}^i-1)}{s({(1+s)}^N-1)}\frac{N^2}{i(N-i)}\approx {\int }_{1/N}^{1-1/N}\frac{(e^{\gamma (1-p)}-1)(e^{\gamma p}-1)}{\gamma (e^{\gamma }-1)}\frac{N^2}{p(1-p)}dp\text{.}$$ (32)

The last line follows for large $N$, i.e., in the diffusion limit, and corresponds to earlier results (Kimura and Ohta, 1969), if time is not measured in Moran time-steps but in the usual diffusion scaling of $N$ generations. The conditional expected time to fixation from preferred to unpreferred is identical to the above equations. The two remaining times are:

$$E\left(t_{00}\right)=\sum _{i=1}^{N-1}{f}_{00}(x=i\mid N,\theta ,s){\left(\frac{C}{N}\frac{{(1+s)}^{N-1}-1}{({(1+s)}^N-1)}\right)}^{-1}=\sum _{i=1}^{N-1}\frac{{(1+s)}^{i-1}{({(1+s)}^{N-i}-1)}^2}{({(1+s)}^N-1)({(1+s)}^{N-1}-1)}\frac{N^2}{i(N-i)}\approx {\int }_{1/N}^{1-1/N}\frac{e^{\gamma p}{(e^{\gamma (1-p)}-1)}^2}{{(e^{\gamma }-1)}^2}\frac{N}{p(1-p)}dp$$ (33)

and

$$E\left(t_{11}\right)=\sum _{i=1}^{N-1}{f}_{11}(x=i\mid N,\theta ,s){\left(\frac{C}{N}\frac{{(1+s)}^{N-1}({(1+s)}^{N-1}-1-s)}{{(1+s)}^{N-1}({(1+s)}^N-1)}\right)}^{-1}=\sum _{i=1}^{N-1}\frac{{(1+s)}^{i-1}{({(1+s)}^N-{(1+s)}^{N-i})}^2}{{(1+s)}^N({(1+s)}^N-1)({(1+s)}^{N-1}-1)}\frac{N^2}{i(N-i)}\approx {\int }_{1/N}^{1-1/N}\frac{(e^{\gamma p}-1)(e^{\gamma }-e^{\gamma (1-p)})}{{(e^{\gamma }-1)}^2}\frac{N}{p(1-p)}dp\text{.}$$ (34)

In the diffusion limit, i.e., in the last line of the above equations, the conditional mean times do not change to first order in $\gamma$.

The average sojourn time can be obtained directly or by summing all times weighted by their proportions:

$$E\left(t\right)=\frac{1}{{(1+s)}^N+1}\sum _{i=1}^{N-1}{(1+s)}^{i-1}\frac{N^2}{i(N-i)}\approx \frac{N}{e^{\gamma }+1}{\int }_{1/N}^{1-1/N}\frac{e^{\gamma p}}{p(1-p)}dp\text{.}$$ (35)

To first order in $\gamma$, this is not different from the case without selection. But we can use the convexity of the exponential function to show that this is faster than the average time without selection by noting that, in the interval $]0,1[$ and for $\gamma >0,exp\left(\gamma p\right)<1+p(exp\left(\gamma \right)-1)$, such that we have, for the continuous case:

$$E\left(t\right)=\frac{N}{e^{\gamma }+1}{\int }_{1/N}^{1-1/N}\frac{e^{\gamma p}}{p(1-p)}dp<\frac{N}{e^{\gamma }+1}{\int }_{1/N}^{1-1/N}\frac{1+p(e^{\gamma }-1)}{p(1-p)}dp=\frac{N}{e^{\gamma }+1}(2log(N-1)+(e^{\gamma }-1)log(N-1))=Nlog(N-1)\text{.}$$ (36)

Here we used the equality sign in the first line, because the result is exact for the diffusion approach. The last line corresponds to the result without selection. This result seems to be new.

3.5. The rate of divergence

In empirical population genetics, fixed differences between divergent populations or species are often used for inference. The rate of accumulation of such fixed differences, also called the rate of fixation of derived variants or divergence, per unit time in equilibrium is equal to the flow from the unfavored to the favored state and vice versa, i.e., the probability of being in state $x=N-1$ conditional on starting from state 0 ($f_{01}(x=N-1\mid N,\theta ,s)$) times the transition probability of fixation of the favored allele in the next Moran event conditional on being in state $x_t=N-1$, i.e., $\mathrm{Pr}(x_{t+1}=N\mid x_t=N-1,N,\theta ,s)$ and the same in the other direction:

$$r_D=f_{01}(x=N-1\mid N,\theta ,s)\mathrm{Pr}(x_t=N\mid x_t=N-1,N,\theta ,s)+f_{10}(x=1\mid N,\theta ,s)\mathrm{Pr}(x_t=0\mid x_t=1,N,\theta ,s)=C{(1+s)}^{N-1}\frac{(1+s-1)({(1+s)}^{N-1}-1)}{{({(1+s)}^N-1)}^2}\frac{N}{N-1}\frac{N-1}{N^2}+O\left({\theta }^2\right)+C{(1+s)}^{N-1}\frac{({(1+s)}^{N-1}-1)(1+s-1)}{{({(1+s)}^N-1)}^2}\frac{N}{N-1}\frac{N-1}{N^2}+O\left({\theta }^2\right)=\frac{C}{N}\frac{2s{(1+s)}^{N-1}({(1+s)}^{N-1}-1)}{{({(1+s)}^N-1)}^2}\approx \frac{C}{N^2}\frac{2\gamma e^{\gamma }}{e^{\gamma }-1}+O\left({\theta }^2\right)=\frac{C}{N^2}\frac{2\gamma }{1-e^{-\gamma }}+O\left({\theta }^2\right)\text{.}$$ (37)

If time is scaled per generation or per $N$ generations, this rate needs to be multiplied by $N$ or $N^2$, respectively. Kimura (1962, 1969) derived the diffusion limit version of this equation.

4. Small sample properties

In this section, we derive the small sample properties, using the decoupled Moran model and the diffusion approximation. Usually in analyses of single nucleotide polymorphism data, we have a situation where a large number $L$ of loci are assumed to evolve independently according to the same model. A finite sample of size $n$ haplotypes is available from the population. In the first subsection, we will briefly describe the general results while, for the rest, we will consider the case of small scaled mutation rates.

4.1. A sample from the stationary distribution, $\theta$ not small

In population genetics, a population size of $N\ge 100$ usually approximates results for $N\to \infty$ reasonably well. Formula (8) with a population size $N$ of about 1000 may thus be taken as an approximation to the continuous distribution in formula (9). After sampling a number of $x$ alleles from the population from this distribution, a small sample of size $n$ may be obtained by sampling without replacement using the hypergeometric distribution, conditional on $x$ and $N$ with $0\le i\le n$:

$$\mathrm{Pr}(y=i\mid n,x,N)=\frac{\left(\genfrac{}{}{0ex}{}{n}{i}\right)\left(\genfrac{}{}{0ex}{}{N-n}{x-i}\right)}{\left(\genfrac{}{}{0ex}{}{N}{x}\right)}\text{.}$$ (38)

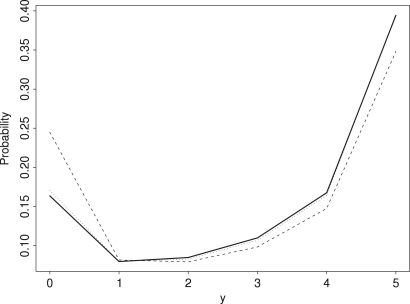
In the case without selection, setting the sample size $N$ to $n$ actually gives the identical results as this subsampling scheme. This is not true with selection, as there is obviously no selection if $N=1$ and selection is generally inefficient for extremely small $N$. For $n>4$, however, results from subsampling and results using $N=n$ are similar even for relatively large $\gamma$. As can be seen in Fig. 3, an even better approximation that fits well down to very small sample sizes is:

$$\mathrm{Pr}(y=i\mid n,N\to \infty ,{\theta }_0,{\theta }_1,s)\propto e^{\gamma /ni}\frac{{\left({\theta }_1\right)}_i{\left({\theta }_0\right)}_{n-i}}{i!(n-i)!}\text{.}$$ (39)

This formula was guessed at and then evaluated by simulations.

Fig. 3.

Likelihood of obtaining $y=(0,1,\dots ,5)$ individuals of the favored type in a sample without replacement of size $n=5$ from a population of size $N=500$ (thick line), $N=5$ (thin line) and the approximation in formula (39) (stippled line) with ${\theta }_0=0.5,{\theta }_1=0.3,\gamma =2$. Note that the sample from $N=5$ is slightly less affected by selection and thus more symmetric.

The exact marginal distribution of $y$ given $n$ and $N$ can also be obtained as in the case without selection, but the resulting equation does not simplify as easily:

$$\mathrm{Pr}(y=i\mid \theta ,s,N,n)\propto \sum _{x=i}^{N-(n-i)}\frac{\left(\genfrac{}{}{0ex}{}{n}{i}\right)\left(\genfrac{}{}{0ex}{}{N-n}{x-i}\right)}{\left(\genfrac{}{}{0ex}{}{N}{i}\right)}\left(\genfrac{}{}{0ex}{}{N}{i}\right){(1+s)}^x{\left(\frac{{\theta }_1}{1+s}\right)}_x{\left({\theta }_0\right)}_{N-x}=\left(\genfrac{}{}{0ex}{}{n}{y}\right){(1+s)}^i{({\theta }_1/(1+s))}_i{\left({\theta }_0\right)}_{n-i}\sum _{x=0}^{N-n}\left(\genfrac{}{}{0ex}{}{N-n}{x}\right){(1+s)}^x{(i+{\theta }_1/(1+s))}_x{(n-i+{\theta }_0)}_{N-n-x}\text{.}$$ (40)

The conditional distribution of $x$ in a population of size $N$ given the results $y$ from a small sample of size $n$ is for $0\le i\le N$:

$$\mathrm{Pr}(x=i\mid \theta ,N,y,n)\propto \left(\genfrac{}{}{0ex}{}{N-n}{i}\right){(1+s)}^y{(y+{\theta }_1/(1+s))}_i{(n-y+{\theta }_0)}_{N-i}\text{.}$$ (41)

This is distribution (8) with different parameters ${\theta }_0$ and ${\theta }_1$.

4.2. A sample from the stationary distribution, small scaled mutation rates $\theta$

With small scaled mutation rates, only a small proportion of sites is actually polymorphic; the rest are monomorphic. This situation is also considered in the Poisson-random-field (PRF) approach (Sawyer and Hartl, 1992; Hartl et al., 1994; Bustamante et al., 2001).

We note that the distributions of $y$ alleles of the favored type in an ordered sample of size $n$ are easier to derive than those of the practically more useful unordered samples. Furthermore, we will need the results for the ordered samples below for calculating the probability of polymorphic samples. Multiplication of the probabilities for ordered samples with $\left(\genfrac{}{}{0ex}{}{n}{y}\right)$ gives those for the unordered sample. We will indicate the probabilities of ordered samples by an asterisk.

With small scaled mutation rates $\theta$ and for large population sizes $N$, the probability of a monomorphic sample is of order one and ${lim}_{N\to \infty }\mathrm{Pr}(y=n\mid n,\gamma ,\theta )={lim}_{N\to \infty }{\mathrm{Pr}}^{\ast }(y=n\mid n,\gamma ,\theta )=e^{\gamma }C/{\theta }_0+O\left({\theta }^2\right)$ and ${lim}_{N\to \infty }\mathrm{Pr}(y=0\mid n,\gamma ,\theta )={lim}_{N\to \infty }{\mathrm{Pr}}^{\ast }(y=0\mid n,\gamma ,\theta )=C/{\theta }_1+O\left({\theta }^2\right)$, respectively. For small mutation rates and in the diffusion limit, the probability of polymorphic samples is (for $1\le i<n$):

$$\underset{N\to \infty }{lim}{\mathrm{Pr}}^{\ast }(y=i\mid n,\theta ,\gamma )=C\underset{N\to \infty }{lim}{\int }_{1/N}^{1-1/N}{e}^{\gamma p}{p}^{i-1}{(1-p)}^{n-i-1}dp+O\left({\theta }^2\right)\text{.}$$ (42)

A solution to this integral is Kummer’s function (Abramowitz and Stegun, 1970): $M(y,n,\gamma )$:

$${\int }_0^1{e}^{\gamma p}{p}^{i-1}{(1-p)}^{n-i-1}dp=\frac{(n-1)!}{(i-1)!(n-i-1)!}M(i,n,\gamma )=\frac{(n-1)!}{(i-1)!(n-i-1)!}(1+\frac{i\gamma }{n}+\frac{{\left(i\right)}_2{\gamma }^2}{{\left(n\right)}_{2}2!}+\frac{{\left(i\right)}_3{\gamma }^3}{{\left(n\right)}_{3}3!}+\cdots +\frac{{\left(i\right)}_m{\gamma }^m}{{\left(n\right)}_{m}m!}\dots )\text{.}$$ (43)

Kummer’s function is a solution to the confluent hypergeometric equation and also denoted with ${}_1{F}_1(y,n,\gamma )$ (Abramowitz and Stegun, 1970). For small and moderate $\gamma$, this series converges relatively quickly. Below we will, however, provide recurrence relations that allow for quick calculation of all terms up to the sample size $n$, since this is usually required when analyzing empirical frequency spectra.

4.3. Recurrence relations

From applying the rules of integration by parts, we get:

$${\int }_0^1{e}^{\gamma p}{p}^{y-1}{(1-p)}^{n-y-1}dp={\left[\frac{e^{\gamma p}}{a}{p}^{y-1}{(1-p)}^{n-y-1}\right]}_0^1-{\int }_0^1\frac{e^{\gamma p}}{\gamma }(y-1)p^{y-2}{(1-p)}^{n-y-1}dp+{\int }_0^1\frac{e^{\gamma p}}{\gamma }{p}^{y-1}(n-y-1){(1-p)}^{n-y-2}dp\text{.}$$ (44)

We can use formula (44) to work out the following four cases by using Eq. (42). For the remainder of the section, we will always take the limit $N\to \infty$ and assume small $\theta$ but, for the sake of brevity, leave away the limit notation and the symbol for the order in $\theta$.

4.3.1. Case: $y=1,n=2$

$${\mathrm{Pr}}^{\ast }(y=1\mid 2,\gamma ,\theta )=C{\int }_0^1{e}^{\gamma p}dp=C{\left[\frac{e^{\gamma p}}{\gamma }\right]}_0^1=C\frac{e^{\gamma }-1}{\gamma }\text{.}$$ (45)

4.3.2. Case: $y=i;2\le i\le (n-2);n>3$

$${\mathrm{Pr}}^{\ast }(y=i\mid n,\gamma ,\theta )\approx -C\frac{y-1}{\gamma }{\int }_0^1{e}^{\gamma p}{p}^{i-2}{(1-p)}^{n-i-1}dp+C\frac{n-i-1}{\gamma }{\int }_0^1{e}^{\gamma p}{p}^{y-1}{(1-p)}^{n-i-2}dp=-\frac{i-1}{\gamma }{\mathrm{Pr}}^{\ast }(y=i-1\mid n-1,\gamma ,\theta )+\frac{n-i-1}{\gamma }{\mathrm{Pr}}^{\ast }(y=i\mid n-1,\gamma ,\theta )\text{.}$$ (46)

4.3.3. Case: $y=n-1,n>2$

$${\mathrm{Pr}}^{\ast }(y=n-1\mid n,\gamma ,\theta )=C\frac{e^{\gamma }}{\gamma }-\frac{n-2}{\gamma }C{\int }_0^1{e}^{\gamma p}{p}^{n-2}dp=C\frac{e^{\gamma }}{\gamma }-\frac{n-2}{\gamma }{\mathrm{Pr}}^{\ast }(y=n-2\mid n-1,\gamma ,\theta )\text{.}$$ (47)

4.3.4. Case: $y=1,n>2$

$${\mathrm{Pr}}^{\ast }(y=1\mid n,\gamma ,\theta )=-\frac{C}{\gamma }+C\frac{n-2}{\gamma }{\int }_0^1{e}^{\gamma p}{(1-p)}^{n-3}dp=-\frac{C}{\gamma }+\frac{n-2}{\gamma }{\mathrm{Pr}}^{\ast }(y=1\mid n-1,\gamma ,\theta )\text{.}$$ (48)

We note furthermore:

$${\int }_0^1(1-p)e^{\gamma p}{p}^{y-1}{(1-p)}^{n-y-1}dp={\int }_0^1{e}^{\gamma p}{p}^{y-1}{(1-p)}^{y-1}dp-{\int }_0^1{e}^{\gamma p}{p}^y{(1-p)}^{n-y-1}dp\text{,}$$ (49)

such that:

$${\mathrm{Pr}}^{\ast }(y=i\mid n+1,\gamma ,\theta )={\mathrm{Pr}}^{\ast }(y=i\mid n,\gamma ,\theta )-{\mathrm{Pr}}^{\ast }(y=i+1\mid n+1,\gamma ,\theta )\text{.}$$ (50)

The recurrence relationships (44) and (50) are well known and correspond to formulas (13.4.4) and (13.4.3) in Abramowitz and Stegun (1970), respectively.

For the unordered case, formula (45) becomes: $\mathrm{Pr}(y=1\mid 2,\gamma ,\theta )\approx 2C(e^{\gamma }-1)/\gamma$. The formulas corresponding to (46)–(50) can be obtained easily. For later use, we will provide the formula corresponding to (50):

$$\frac{i!(n-i+1)!}{(n+1)!}\mathrm{Pr}(y=i\mid n+1,\gamma ,\theta )=\frac{i!(n-i)!}{n!}\mathrm{Pr}(y=i\mid n,\gamma ,\theta )-\frac{(i+1)!(n-i)!}{(n+1)!}\mathrm{Pr}(y=i+1\mid n+1,\gamma ,\theta )$$$$(n-i+1)\mathrm{Pr}(y=i\mid n+1,\gamma ,\theta )=(n+1)\mathrm{Pr}(y=i\mid n,\gamma ,\theta )-(i+1)\mathrm{Pr}(y=i+1\mid n+1,\gamma ,\theta )\text{.}$$ (51)

4.4. Small $\gamma$

For small $\gamma$, the recursion relationships (46)–(48) are useless, as very small and very large quantities delicately cancel out. Even with a relatively large $\gamma =0.1$ and a relatively small $n=10$numerical instabilities are too large to tolerate with double precision calculations. We therefore provide an alternative way of calculating approximations to ${\mathrm{Pr}}^{\ast }(y=n-1\mid n,\gamma ,\theta )$ that do not suffer from these deficiencies (and analogously also to the unordered probabilities $\mathrm{Pr}(y=n-1\mid n,\gamma ,\theta )$).

4.4.1. Case: $y=n-1$

We note that, in the limit of large $N,{\mathrm{Pr}}^{\ast }(y=N-1\mid N,\gamma ,\theta )$ converges to $C{e}^{\gamma }/(N-1)$. We can substitute that into the recursion (47) and run it backwards. The recursion then becomes:

$${\mathrm{Pr}}^{\ast }(y=n-1\mid n,N,\gamma ,\theta )=C\frac{e^{\gamma }}{\gamma }-\frac{n-2}{\gamma }{\mathrm{Pr}}^{\ast }(y=n-2\mid n-1,N,\gamma ,\theta )$$$${\mathrm{Pr}}^{\ast }(y=n-2\mid n-1,N,\gamma ,\theta )=\frac{C{e}^{\gamma }-\gamma {\mathrm{Pr}}^{\ast }(y=n-1\mid n,N,\gamma ,\theta )}{n-2}\text{,}$$ (52)

and we get for $N-1$:

$${\mathrm{Pr}}^{\ast }(y=N-2\mid n=N-1,N,\gamma ,\theta )\approx \frac{C{e}^{\gamma }}{N-2}-\frac{C\gamma e^{\gamma }}{(N-2)(N-1)}\text{.}$$ (53)

Carrying on, we get:

$${\mathrm{Pr}}^{\ast }(y=n-1\mid n,N,\gamma ,\theta )\approx \frac{C{e}^{\gamma }}{n-1}-\frac{C\gamma e^{\gamma }}{(n-1)n}+\frac{C{\gamma }^2{e}^{\gamma }}{(n-1)n(n+1)}-\cdots +\frac{C{(-\gamma )}^{N-n}{e}^{\gamma }}{(n-1)n(n+1)\cdots (N-2)(N-1)}=\frac{C{e}^{\gamma }}{n-1}\sum _{i=0}^{N-n}\frac{{(-\gamma )}^i}{{\left(n\right)}_i}\approx \frac{C{e}^{\gamma }}{n-1}\sum _{i=0}^{\infty }\frac{{(-\gamma )}^i}{{\left(n\right)}_i}\text{,}$$ (54)

where ${\left(n\right)}_i$ is again the ascending factorial or Pochhammer function. The last line is the limit ${\mathrm{Pr}}^{\ast }(y=n-1\mid n,N\to \infty ,\gamma ,\theta )$, i.e., the diffusion limit, and equivalent to $C{e}^{\gamma }/(n-1)M(1,n,-\gamma )=C/(n-1)M(n-1,n,\gamma )$, where $M\left(\right)$ is Kummer’s function. For $y=1$ and $n=2$, we get:

$${\mathrm{Pr}}^{\ast }(y=1\mid 2,N,\gamma ,\theta )\approx C{e}^{\gamma }\left(\sum _{i=0}^{\infty }\frac{{(-\gamma )}^i}{{\left(2\right)}_i}\right)=C\frac{e^{\gamma }-1}{\gamma }\text{,}$$ (55)

which is identical with formula (45).

Formula (54) is much more useful in the limit of small $\gamma$ and results are identical to the case without selection for $\gamma \to 0$. We suggest to use this equation to calculate ${\mathrm{Pr}}^{\ast }(y=n-1\mid n,\gamma ,\theta )$ for the locus with the largest sample size, and then to use formulas (50) or (51), respectively, for calculating all other values for sample sizes down to $n=2$.

4.4.2. Case: $y=1$

For later use, we will also derive the equivalent formulas for $y=1$. By the same reasoning, we obtain the recursion:

$${\mathrm{Pr}}^{\ast }(y=1\mid n-1,N,\gamma ,\theta )=\frac{C+\gamma {\mathrm{Pr}}^{\ast }(y=1\mid n,N,\gamma ,\theta )}{n-2}\text{.}$$ (56)

We thus have:

$${\mathrm{Pr}}^{\ast }(y=1\mid n,N,\gamma ,\theta )=\frac{C}{n-1}+\frac{C\gamma }{(n-1)n}+\frac{C{\gamma }^2}{(n-1)n(n+1)}+\cdots +\frac{C{\gamma }^{N-n}}{(n-1)n\cdots (N-2)(N-1)}=\frac{C}{n-1}\left(\sum _{i=0}^{N-n}\frac{{\gamma }^i}{{\left(n\right)}_i}\right)\approx \frac{C}{n-1}\left(\sum _{i=0}^{\infty }\frac{{\gamma }^i}{{\left(n\right)}_i}\right)\text{.}$$ (57)

The last line is the diffusion limit and equivalent to Kummer’s function $M(1,n,\gamma )$ times $C/(n-1)$. For $n=2$, we get:

$${\mathrm{Pr}}^{\ast }(y=1\mid 2,N,\gamma ,\theta )=C\left(\sum _{i=0}^{\infty }\frac{{\gamma }^i}{{\left(2\right)}_n}\right)=C\frac{e^{\gamma }-1}{\gamma }\text{.}$$ (58)

This last formula is identical to (55), as it should be.

4.4.3. Sum of all polymorphic states

We now give the results for the sum over the polymorphic states $0<i<n$ (i.e., excluding the monomorphic states) for $N\to \infty$, again using recursion. We note that for $n=2$, the probability of a polymorphic sample is:

$$\mathrm{Pr}(y=1\mid 2,\gamma ,\theta )=2{\mathrm{Pr}}^{\ast }(y=1\mid 2,\gamma ,\theta )=2(e^{\gamma }-1)/\gamma \text{.}$$ (59)

We note from formula (51) that:

$$\sum _{i=1}^{n-1}\mathrm{Pr}(y=i\mid n,\gamma ,\theta )=\sum _{i=1}^{n-2}\mathrm{Pr}(y=i\mid n-1,\gamma ,\theta )+\frac{1}{n}\mathrm{Pr}(y=1\mid n,\gamma ,\theta )+\frac{1}{n}\mathrm{Pr}(y=n-1\mid n,\gamma ,\theta )=\sum _{i=1}^{n-2}\mathrm{Pr}(y=i\mid n-1,\gamma ,\theta )+{\mathrm{Pr}}^{\ast }(y=1\mid n,\gamma ,\theta )+{\mathrm{Pr}}^{\ast }(y=n-1\mid n,\gamma ,\theta )\text{.}$$ (60)

Therefore, we have:

$$\sum _{i=1}^{n-1}\mathrm{Pr}(y=i\mid n,\gamma ,\theta )=\sum _{i=2}^n({\mathrm{Pr}}^{\ast }(y=1\mid i,\gamma ,\theta )+{\mathrm{Pr}}^{\ast }(y=i-1\mid i,\gamma ,\theta ))=C((1+e^{\gamma })\sum _{i=1}^{n-1}\frac{1}{i}+(1-e^{\gamma })\sum _{i=1}^{n-1}\frac{\gamma }{i(i+1)}+(1+e^{\gamma })\sum _{i=1}^{n-1}\frac{{\gamma }^2}{i(i+1)(i+2)}+\cdots )=C\sum _{u=0}^{\infty }(1+{(-1)}^u{e}^{\gamma })\sum _{i=1}^{n-1}\frac{{\gamma }^u}{{\left(i\right)}_{u+1}}\text{.}$$ (61)

This means that the probability of a polymorphic sample of size $n$ is the sum of the probabilities of ordered samples of the edges, ${\mathrm{Pr}}^{\ast }(y=1\mid i,\gamma ,\theta )$ and ${\mathrm{Pr}}^{\ast }(y=i-1\mid i,\gamma ,\theta )$, from the sample size $i=2$ to $n$.

We note that for small $\gamma$:

$$\sum _{i=1}^{n-1}\mathrm{Pr}(y=i\mid n,\gamma ,\theta )=\frac{{\theta }_0{\theta }_1}{{\theta }_0+e^{\gamma }{\theta }_1}(1+e^{\gamma })\sum _{i=1}^{n-1}\frac{1}{i}+O\left({\gamma }^2\right)\text{.}$$ (62)

If we compare this result with the equivalent result without selection, we see that, if forward and backward mutation rates are equal and small and selection is also small, selection does not affect polymorphism on average. This is no longer true for unequal mutation rates (Eq. (3)), has been derived earlier by RoyChoudhury and Wakeley (2010). If mutation and selection act in opposing directions, selection may actually increase polymorphism (Lawrie et al., 2011). If in a sample of $L$ loci, we observe $S$ polymorphic ones, we can solve Eq. (62) for the constant to obtain:

$$L(1+e^{\gamma })\frac{{\theta }_0{\theta }_1}{{\theta }_0+e^{\gamma }{\theta }_1}=E\left(S\right)\frac{1}{\sum _{i=1}^{n-1}\frac{1}{i}}+O\left({\gamma }^2\right)\text{.}$$ (63)

If mutation rates are equal and $\gamma =0$, this formula corresponds to the Ewens–Watterson estimator of per site scaled mutation rate $\hat{\theta }$ (Ewens, 1974; Watterson, 1975). We believe that formulas (61)–(63) are new.

4.5. Estimating parameters from a sample of $L$ loci

Assume given data from a sample of $L$ loci with $y_l$ alleles of the first type in a sample of size $n$ for each locus $l(1\le l\le L)$. Each locus is assumed to have evolved independently to mutation-selection-drift equilibrium according to the process we described in this manuscript. We want to infer three parameters from this dataset. The parametrization we have considered so far is: the scaled mutation parameters ${\theta }_0$ and ${\theta }_1$ and the scaled selection parameter $\gamma$. With small $\theta$, however, inference becomes more convenient through reparametrization. This has also been done with a slightly different model by Bustamante et al. (2001). We can estimate parameters from a sample of $L$ loci by separating three classes: the fixed alleles of the unpreferred type, the polymorphic alleles, and the fixed alleles of the preferred type. With small mutation rates, the number of polymorphic samples will be small, such that they correspond to the assumptions of a Poisson random field (PRF) (Sawyer and Hartl, 1992).

Without considering any other parameters concurrently, we can obtain a maximum likelihood estimate of the scaled selection rate $\hat{\gamma }$ from the polymorphic loci by a direct search or by more sophisticated numerical methods using the recurrence formulas or the closed form solutions in the previous subsection. From the proportion of polymorphic loci in the sample, we define $\widehat{{\beta }_1}$ as an estimate of $(1+e^{\gamma }){\theta }_0{\theta }_1/({\theta }_0+e^{\gamma }{\theta }_1)$ via formula (63) conditional on an estimate of $\hat{\gamma }$. This procedure corresponds to the Ewens–Watterson estimator of $\theta$ in the case of symmetric mutation rates and without selection. Let us parametrize the remaining parameter as ${\hat{\beta }}_2$ that estimates ${\theta }_0/({\theta }_0+e^{\gamma }{\theta }_1)$, from the proportion of disfavored alleles among the fixed sites in the sample, again conditional on $\gamma$. We note that inference of $\widehat{{\beta }_1}$ and $\widehat{{\beta }_2}$ is independent conditional on $\hat{\gamma }$. One can return to the original parameters by observing that ${\hat{\theta }}_1={\hat{\beta }}_1/\left((1+e^{\gamma }){\hat{\beta }}_2\right)$ and ${\hat{\theta }}_0={\hat{\beta }}_1{\hat{\theta }}_1{e}^{\gamma }/((1+e^{\gamma }){\hat{\theta }}_1-{\hat{\beta }}_1)$.

If we had a sample from another part of the genome that we believe to not be selected, more sophisticated inference methods would be possible.

We note that Zeng and Charlesworth (2009) use a Wright–Fisher model that they iterate to convergence to estimate the same parameters. Their way of inference is more cumbersome than ours, but should lead to nearly the same results in the limit of large $N$. Furthermore, these authors extend the model to changes in effective population size. Our reduced model allows for efficient forward simulations and could thus also be used for similar simulation based methods. Zeng (2010) extends this biallelic model to a codon model. Extension of our analytical results of the biallelic model to higher dimensions is only possible for parent independent mutations. But if mutations are rare enough, the small scaled mutation rate approximation will be useful nevertheless.

Analysis of a Drosophila melanogaster dataset.

Fourfold degenerate sites in Drosophila have been shown to be under selection (e.g. Parsch et al., 2010; Zeng and Charlesworth, 2010). In most Drosophila species including D. melanogaster, alleles with the nucleotides G and C seem to be preferred over those with A and T (Shields et al., 1988; Akashi, 1994; Carlini and Stephan, 2003), although a high fixation rate for AT in D. melanogaster suggests that this codon usage bias has been relaxed in this species (Akashi, 1996; Begun et al., 2007; Singh et al., 2009). Previous models for analysis of fourfold degenerate site data in D. melanogaster have included directional selection, mutation, and drift in equilibrium and also modeled a change in effective population size (e.g., Zeng and Charlesworth, 2010). A force towards GC creates asymmetry in the folded allele-frequency spectrum with more AT low frequency variants than expected under neutrality. The polarized allele-frequency spectra show, for alleles that mutate from GC to AT, an increase in AT low-frequency and a decrease in AT high frequency alleles, and the reverse in the other direction. Scaled mutation rates $\theta$ are below 0.02 in Drosophila and thus our model may be used. However, in D. melanogaster fourfold degenerate sites are not in equilibrium as indicated by the excess of fixed derived AT over GC alleles. Hence, application of our equilibrium theory to fourfold degenerate sites is problematic. On the other hand, short introns seem to be close to equilibrium but there also a weak directional force towards GC can be detected (see Table 1).

Table 1.

GC site-frequencies in a sample of $n=15$ sequences from D. melanogaster; columns 1–14 are the site-frequencies (absolute numbers) for polymorphic sites, columns 0 and 15 are the numbers of fixed AT and fixed GC sites, respectively. Mutations were polarized with respect to the conservative outgroup of D. simulans, D. sechelia, D. mauritiana, D. erecta and D. yakuba. For the unpolarized spectrum, the state of the outgroups was ignored.

	GC-frequencies
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
4-fold deg. sites
Unpolarized	7464	29	20	14	9	6	10	12	14	20	14	27	49	53	157	15 518
AT $\to$ GC	4810	15	6	3	2	1	1	0	2	1	1	1	1	4	3	106
GC $\to$ AT	464	4	6	7	6	3	7	10	8	11	8	19	36	40	127	12 608
Short introns
Unpolarized	3147	18	3	4	4	3	5	6	3	8	3	2	3	9	27	1602
AT $\to$ GC	2263															44
GC $\to$ AT	53															960

4.6. Materials and methods

We applied our theory to a large polymorphism dataset of D. melanogaster (Shapiro et al., 2007). The data consist of 419 autosomal loci; we only consider a sample of 15 African inbred isogenic lines. We extended the existing outgroups D. simulans, D. sechellia and D. mauritiana by sequence data from D. erecta and D. yakuba which were downloaded from www.flybase.org and aligned with ClustalW version 2.0.12. From the data, we extracted fourfold degenerate sites and short introns (position 8–30 of introns less than 66 basepairs long, which are shown to be least selectively constrained Halligan and Keightley, 2006; Parsch et al., 2010). We furthermore required that all states are known in all lines and species considered for the analyses. For polarization, we used only sites that were monomorphic in all outgroups. This may introduce a bias, but prevents errors. We present the results for the unpolarized, i.e., folded allele frequency spectra for both the fourfold degenerate and intron sites. Because only relatively few sites are available for introns, we present the analysis of the unfolded, i.e., polarized data only for the fourfold degenerate sites.

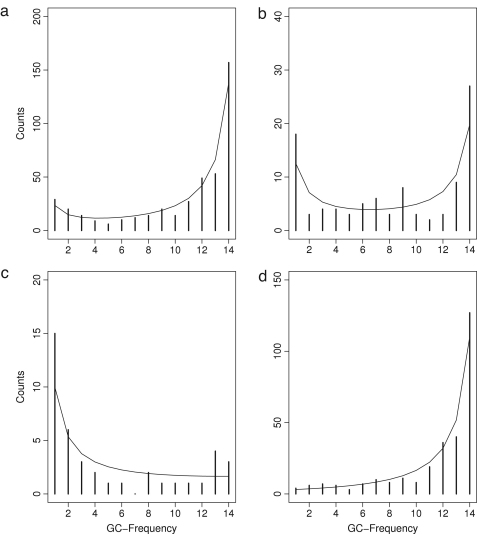
For both the unpolarized and polarized site-frequency spectra we estimated the scaled selection coefficient $\gamma$ via Eq. (14), and ${\beta }_1$ and ${\beta }_2$. We performed a likelihood ratio test to determine if the maximum likelihood estimate of $\gamma$ is significantly different from the null hypothesis of $\gamma =0$. Applying Eq. (63) and substituting an estimate for $\gamma$, we could then estimate absolute values for ${\theta }_0$ and ${\theta }_1$ (see Fig. 4).

Fig. 4.

Observed (bars) and inferred (lines) allele frequency spectra showing the GC-frequencies. A: unpolarized GC-frequencies at fourfold degenerate sites ($\gamma =2.05$). B: unpolarized GC-frequencies in introns ($\gamma =0.53$). C: polarized (AT to GC) spectrum of GC-frequencies at fourfold degenerate sites ($\gamma =2.58$). D: polarized (GC to AT) spectrum of GC-frequencies at fourfold degenerate sites ($\gamma =1.99$).

4.7. Results

Our model assumes selection–mutation-drift equilibrium. One of the equilibrium predictions is a balance of AT to GC fixed derived sites. At fourfold degenerate sites, the ratio for fixed derived sites is (AT to GC)/(GC to AT) = 106/464. The excess of GC to AT substitutions is highly significant, indicating non-equilibrium ($p<2.2\times 10^{-16}$). In introns, on the other hand, the ratio for fixed derived sites is (AT to GC)/(GC to AT) = 44/53. Thus, the numbers of substitutions are almost balancing and close to the expectation of an equilibrium ($p=0.36$).

We estimated the scaled selection coefficient $\gamma$ for short introns and fourfold degenerate sites from the site-frequency spectrum (see Fig. 4). The unpolarized spectrum of introns led to an estimate of $\gamma =0.53$, which was not significant ($p=0.086$). Since the number of fourfold degenerate sites was higher than that of introns, we could estimate $\gamma$ from the unpolarized and polarized site-frequencies. From the unpolarized, folded spectrum, $\gamma$ was found to be 2.05 and highly significant ($p=0$). Considering mutations from AT to GC and GC to AT, $\gamma$ was estimated to be 2.58 (not significant, $p=0.178$) and 1.99 (significant, $p=2.56\times 10^{-05}$), respectively. Note that the numbers differed between the two directions, which explains the significance of the smaller absolute value of $\gamma$.

Biased gene conversion might contribute to the inferred selection in introns. In that case, we would expect a similar amount of biased gene conversion at fourfold degenerate sites as well. The estimates of $\gamma$ at fourfold degenerate sites are higher, indicating selection towards GC over that observed in the introns.

We used the estimate of $\hat{\gamma }=2.0$ and the base composition at fourfold degenerate sites to estimate the scaled mutation rates ${\theta }_0$ and ${\theta }_1$. The proportion of AT-sites at fourfold degenerate sites is ${\hat{\beta }}_2=4810/17418=0.28$. From the proportion of polymorphic sites, we calculated ${\hat{\beta }}_1=0.014$, which provides an estimate for $(1+e^{\gamma }){\theta }_0{\theta }_1/({\theta }_0+{\theta }_1{e}^{\gamma })$. From this, we get ${\hat{\theta }}_0=0.017$ and ${\hat{\theta }}_1=0.006$, respectively.

4.8. Comparison with earlier results

Qualitatively, our results are consistent with the findings of Zeng and Charlesworth (2010), who used the same dataset to disentangle the genetic forces on fourfold degenerate sites and introns. Their model uses unpolarized polymorphism to estimate directional selection, mutation bias and demographic parameters. Although their model allows for a change in effective population size, they found that an equilibrium model with directional selection towards GC ($\gamma =1.29$) and constant population size fits autosomal synonymous polymorphism well. Crucially, these authors ignore outgroup information. Including this information, we must exclude an equilibrium model for fourfold degenerate sites, as the ratio of fixed diverged sites from GC to AT and vice versa deviates strongly from 1 : 1. As we find deviation from equilibrium for fourfold degenerate sites, neither their model nor our equilibrium model might be accurate. On the other hand, our analysis suggests that short introns are close to equilibrium and, thus, are more appropriate for our model. Interestingly, Zeng and Charlesworth (2010) had to assume a complex form of selection or non-equilibrium to explain the pattern of introns. This difference to our results may be ascribed to the inclusion of different length-classes of introns in their analysis. The length of introns has been found to negatively correlate with divergence, indicating selective constraints (Halligan and Keightley, 2006).

5. Discussion

We analyze a decoupled Moran model with haploid population size $N$, a biallelic locus under mutation and drift with scaled forward and backward mutation rates ${\theta }_1={\mu }_{1}N$ and ${\theta }_0={\mu }_{0}N$ and directional selection with scaled strength $\gamma =sN$. Small scaled mutation rates, ${\theta }_0\ll 1$ and ${\theta }_1\ll 1$ are appropriate for single nucleotide polymorphism data in highly recombining regions of higher organisms. For microbes and viruses, however, this approximation may not be useful Desai and Plotkin (2008). Without selection, the equilibrium distribution of a sample is beta-binomial. The infinite sites approximation corresponds to the limit of small scaled mutation rates, where each polymorphic sites is assumed to be hit by a single mutation only. Many results using the infinite sites model are available for the case without selection (e.g., Ewens, 1974; Watterson, 1975; Ewens, 2004).

With selection, the general process, without the restriction to small scaled mutation rates, has been introduced by Wright (1931) and has been studied in more detail later (e.g., Moran, 1958, 1962; McVean and Charlesworth, 1999). The limiting case of small scaled mutation rates with selection has been studied mainly in the context of Poisson random field (PRF) models (e.g., Sawyer and Hartl, 1992; Hartl et al., 1994; Bustamante et al., 2001; Griffiths, 2003; Ewens, 2004; Evans et al., 2007). The PRF model, like the infinite sites model, assumes a single mutation per polymorphic site. In its present version, it considers only irreversible mutations, nevertheless the source of mutations is not diminishing since the number of sites is assumed infinite. In finite samples, however, such a unidirectional process must lead to depletion, even if whole genomes are considered. Hence applications of the PRF model to realistic data-sets would conform to a quasi-equilibrium process.

Starting from a decoupled Moran model, we use the same approximations as in the case without selection to derive an approximation with small scaled mutation rates. In particular, we derive a simple approximation to the equilibrium distribution, with the constant of proportionality ${\theta }_0{\theta }_1/({\theta }_0+{\theta }_1{e}^{\gamma })$, for the distribution of polymorphic alleles in the population (formula (14)).

We then introduce another simplified process obtained by dropping all transitions that occur with a probability of order ${\theta }^2$ from the Moran process. Then only monomorphic states will mutate. In effect, this process consists of two quasi-equilibrium processes that are joined to balance. This simplified process is similar to those considered in Section 2.12 of Ewens (2004) and especially in Section 2 of Evans et al. (2007) in the PRF context. To first order in $\theta$, this simplified process produces the same results as the biallelic mutation, drift, and selection Moran model. This coincidence is due to the fact that in both cases the proportion of polymorphism in the population is only of order $\theta$, while that of the monomorphic states is of order one, such that the probability of a mutation occurring in an already polymorphic state is approaching zero. Zeng and Charlesworth (2009) seem to have had the same idea to join the two processes in a model, but did not further investigate the possibilities of this model. In fact, they use a Wright–Fisher model for their data analyses.

Using this simpler model we derive the sojourn times, the equilibrium proportions of fixed alleles, and fixation rates conditional on origin and fixation. These formulas are discrete analogs to those derived earlier using diffusion theory (Kimura and Ohta, 1969; Bulmer, 1991; Ewens, 2004) and converge to those results for large $N$. For practical applications, theory assuming an equilibrium distribution in a large population where small samples are taken seems most useful. Since these results hold for population sizes of $N=500$ according to our simulations, we assume that they will generally hold for all models in the diffusion limit, in particular for the Wright–Fisher model. For calculating this distribution, we provide convenient recurrence relations. This enables us to give formulas analogous to the Ewens–Watterson estimator of $\theta$ (Ewens, 1974; Watterson, 1975) for biased mutation rates and directional selection (formulas (61)–(63)) under equilibrium assumptions.

We apply this theory to a polymorphism dataset of fourfold degenerate sites in Drosophila melanogaster. Our results are qualitatively similar to those of Zeng and Charlesworth (2010), with the major quantitative differences arising not from different model choices, but from the use of polarized vs. non-polarized polymorphism, inclusion of all introns vs. only short introns, and inclusion vs. exclusion of outgroup information. While Zeng and Charlesworth (2010) used forward simulations with a Wright–Fisher model, we could more economically apply our analytical results.