Lateral suppression of mesopic rod and cone flicker detection

Abstract

This study investigated the mechanisms of flicker detection suppression by measuring mesopic rod and cone critical flicker frequencies (CFFs) at different center and surround illuminance levels. Stimuli were generated with a four-primary photostimulator that provided independent control of rod and cone excitations. The results showed that dim surrounds ≤0.2 Td suppressed cone-mediated CFFs at ≥20 Td but not rod-mediated CFFs. These results can be understood in terms of peak amplitudes of photoreceptor impulse response functions under different stimulation conditions.

1. INTRODUCTION

Anatomical and single-unit electrophysiological studies have shown that rods and cones share neural pathways and have joint inputs to retinal ganglion cells [1,2]. Rod signals are conveyed to the brain by two primary pathways that are dependent on the illumination level. One pathway is via ON rod bipolars, AII amacrine cells, and ON and OFF cone bipolars. This rod bipolar pathway [3] is slow in temporal processing and is hypothesized to mediate rod vision at scotopic light levels. The second pathway transmits rod information via rod–cone gap junctions and ON and OFF cone bipolars. This rod–cone gap junction pathway [3] is faster than the rod bipolar pathway and is hypothesized to mediate rod vision at high scotopic and mesopic light levels. A third insensitive rod pathway between rods and OFF cone bipolars has been identified but so far has been evident only in rodents [4].

The sharing of rod and cone pathways provides the basis for interactions between rod and cone signals [5]. One form of rod–cone interaction is lateral suppressive rod–cone interaction in flicker detection, in which dark-adapted rods suppress cone-mediated flicker detection at high temporal test-field frequencies [6–9]. It has been shown that this lateral suppressive rod effect on cone flicker detection occurs strongly in the inferred magnocellular (MC-) pathway [10] by reducing the amplitude and elongating the timing of cone pathway temporal impulse response functions [11]. However, for cone flicker detection with low temporal frequencies, suppression is not present [6]. Further, it is unclear whether dark-adapted rods suppress rod flicker detection. If, at mesopic light levels, rod signals are transmitted via the rod–cone gap junction pathway, then dark-adapted rods should suppress rod flicker detection because once rod signals pass the rod–cone gap junctions, rod signals become equivalent to cone signals for subsequent postreceptoral processing. To test this, rod and cone critical fusion frequencies (CFFs) were measured for three mesopic light levels in the presence of various surround illuminances covering a range of scotopic to mesopic illuminance levels. The aim of this study was to investigate the factors that determine the presence of lateral suppression in flicker detection.

2. METHODS

A. Observers

Three observers, J. S. (male, age 30 years), Y. L. (female, age 24 years), and I. V. (male, age 24 years), participated in the study. All observers have normal color vision (assessed by the Neitz OT anomaloscope). Observers J. S. and I. V. were paid participants. The Institutional Review Board at the University of Chicago approved all experimental procedures.

B. Apparatus

A two-channel Maxwellian view four-primary photostimulator was used to generate isolated rod and cone stimuli [12], which were viewed through a 2 mm artificial pupil. The theoretical basis for achieving independent control of the activities of four types of photoreceptors (S-, M-, and L-cones, and rods) in the human retina is silent substitution [13], and the details are provided by Shapiro et al. [14]. The primaries were derived from LED-interference filter combinations yielding dominant wavelengths of 459 nm (blue), 561 nm (greenish-yellow), 516 nm (green), and 658 nm (red), all with half-widths of about 10 nm. The radiances of the primaries were controlled by amplitude modulation of a 20 kHz carrier feeding into an eight-channel analog output Dolby sound card (M-Audio-Revolution 7.1 PCI) with a 24 bit digital-to-analog converter (DAC) operating at a sampling rate of 192 kHz. The outputs of the DACs were demodulated [15] and sent to voltage-to-frequency converters that provided 1 μs pulses at frequencies up to 250 kHz to control the LEDs [16]. The sound card with a demodulator has a precision of greater than 16 bits [15]. The sound card was controlled by self-developed software in a Macintosh G5 PowerPC computer.

C. Calibration Procedures

The photostimulator was calibrated using a two-step process. The first step pertained to the measurement of the spectral distribution and the linearization of physical light for each LED. The second part involved observer calibrations to compensate for individual differences in prereceptoral filtering. Details of the calibration procedures have been summarized elsewhere [12,17].

D. Stimuli

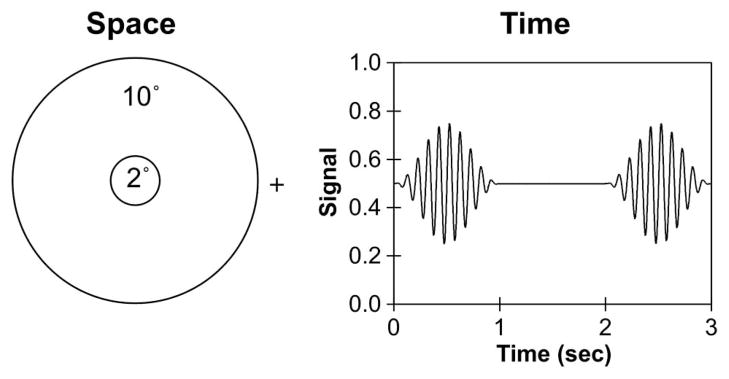
The stimuli were presented in a 2° circular field set within a steady 10° surround, positioned at 6° temporal eccentricity (see Fig. 1 for the spatial configuration). Three types of modulations were generated by the four-primary photostimulator at each light level: (1) isolated rod stimuli that only modulated rod excitation (Rod) while maintaining constant L-, M-, and S-cone excitations; (2) isolated cone luminance stimuli that modulated L-, M-, and S-cone excitations in phase (L + M + S) while rod excitations were kept constant; and (3) combined rod and cone stimuli that modulated the excitations of rods and all three cone types in phase (L + M + S + Rod). Note that, in a cone-based chromaticity space, luminance is typically specified as (L + M) [18]. Here we used (L + M + S) for cone luminance stimulus specifications because, to maintain a constant chromaticity while modulating luminance, Scone excitation was varied in the same proportion and phase as the L- and M-cone excitations. We normalized rod excitations such that, for an equal-energy-spectrum light, 1 photopic Troland (Td) was equal to 1 rod Td [14].

Fig. 1.

Spatial configuration and temporal profile of stimuli used for CFF measurements. The left panel shows a 2° central field set within a 10° surround. A fixation placed the stimuli at 6.0° temporal eccentricity. The right panel shows an example of a 10 Hz signal that was modulated sinusoidally in the center field within a 1 s raised cosine envelope that was alternated with a 1 s steady center field.

For all stimulus types in this study, the time-averaged chromaticity of the light in the center and the surround fields was set to L(L + M) = 0.6667 and S/(L + M) = 0.30. The center field was sinusoidally modulated around a mean illuminance of 2 photopic Td, 20 photopic Td, or 200 photopic Td. To minimize flicker adaptation, the modulated field was presented in a 1 s raised cosine envelope that alternated with a 1 s steady field (see right panel of Fig. 1 for the temporal profile of the stimuli). All the signals were modulated at 35% Michelson contrast. The surround was either dark or steady, with retinal illuminance ranging from 0.002 Td to a value equiluminant to the center illuminance in decade steps (0.002–2 Td for a 2 Td center, 0.002–20 Td for a 20 Td center, or 0.002–200 Td for a 200 Td center). Changes in center or surround illuminance were achieved with calibrated neutral density filters. We measured only CFFs following dark adaptation for two reasons. First, our past studies have shown that equiluminant-surround CFFs were comparable following dark adaptation and during the cone plateau following a bleaching light adaptation [10,11]; therefore, comparing CFFs with dim surrounds and an equiluminant surround could quantify the magnitude of suppression. Second, following bleaching light adaptation, rod CFFs could not be measured due to rod saturation.

E. Procedure

Each session consisted of one center illuminance (2 Td, 20 Td, or 200 Td) with different surround illuminances and one modulation type. Prior to the start of each session, the observer dark adapted for 30 min. There were two trials for each surround illuminance. The time needed to complete trials for a single surround illuminance was about 1–2 min. For each trial of each condition, the computer randomly set an initial temporal frequency between 5 and 30 Hz. The observer adjusted the temporal frequency to determine the CFF by pressing buttons on a gamepad sensed by the computer. Two buttons were programmed to increase or decrease temporal frequency in 1 Hz step sizes, while another two buttons were programmed to alter the frequency in larger steps of 5 Hz. Once the CFF was determined, the observer pressed a button to record the setting, and the next trial was initiated. Each condition was repeated 4–5 times on different days. The mean CFF and standard error for each combination of modulation type and surround illuminance are reported.

3. RESULTS

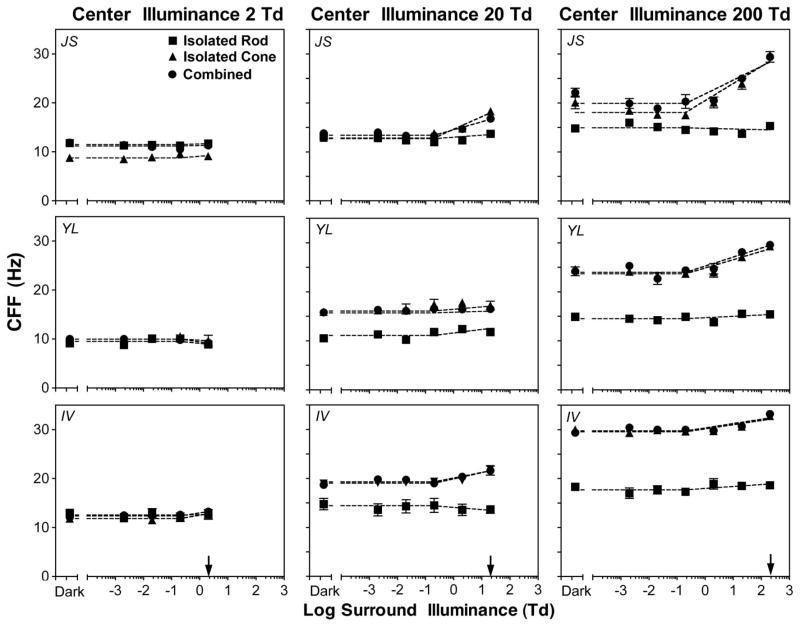
The CFFs (in hertz) as a function of surround illuminance for the isolated rod, isolated cone, and combined stimuli are shown in Fig. 2 (J. S., upper row; Y. L., middle row; and I. V., bottom row). With the 2 Td center (left column), CFFs for all three stimulus types were about equal for Y. L. and I. V.. Since CFFs were largely determined by response amplitude (see Section 4 for more details), equal rod and cone CFFs suggested consistent equal rod and cone inputs at this light level. For J. S., however, CFFs with the isolated cone stimuli were lower than those obtained with the isolated rod stimuli or combined stimuli, suggesting that rod input dominated cone input for the 2 Td center for this observer. Further, for all three observers, with the 2 Td center, CFFs for each of the stimulus types were approximately constant with different surround illuminance levels. With the 20 Td center, CFFs with the isolated rod stimuli were lower than those with the isolated cone or combined stimuli for Y. L. and I. V., consistent with cone dominance at this light level. For J. S., however, CFFs for all three stimulus types were about equal except that CFFs with the isolated rod stimuli were slightly lower than CFFs with the isolated cone or combined stimuli when surround illuminance was ≥2 Td, suggesting equal rod and cone inputs at this light level. CFFs with the isolated rod stimuli were about constant for all surround illuminances, while CFFs with the isolated cone or combined stimuli were the highest at equiluminant conditions for J. S. and I. V. For Y. L., the CFFs with all three stimulus types were about constant with all surround illuminance levels. With the 200 Td center, CFFs with the isolated cone and combined stimuli were comparable and were higher than CFFs with the isolated rod stimuli, suggesting cone dominance at this light level. CFFs with the isolated rod stimuli were constant at all surround illuminance levels except for the responses of I. V. For the isolated cone or combined stimuli, CFFs were approximately constant at surround illuminances of ≤0.2 Td and then increased monotonically with increasing surround illuminances.

Fig. 2.

CFF measurements as a function of surround illuminance for observers (top) J. S., (center) Y. L., and (bottom) I. V. (Left) 2 Td center, (middle) 20 Td center, (right) 200 Td center. The arrows indicate the center illuminance. The error bars are standard errors of the means. The majority of error bars are absent because they are covered by the plot symbols.

The CFF data for each stimulus type and center illuminance in Fig. 2 were fitted with an empirical linear model:

$$\text{CFF}=a+bx,$$ (1)

where x = 0 if the surround illuminance was ≤0.2 Td and x = log(surround illumiance/2) + 1 if surround ≥2 Td; therefore, x = 1 for 2 Td, x = 2 for 20 Td, and x = 3 for 200 Td. In this parsimonious model, the intercept, a, stands for the averaged CFFs at dim surrounds (≤0.2 Td), and the slope, b, represents the increase in CFF per log unit increase in surround illuminance when the surround illuminance is >0.2 Td. If b = 0 (or statistically, b is not significantly different from 0), then CFF would be constant at all surround illuminance levels and there would be no difference in measured CFFs at dim surrounds and equiluminant surrounds; that is, there is no suppression of flicker detection from dim surrounds. If b > 0 (or b is statistically greater than 0), equiluminant-surround CFFs would be higher than CFFs at dim surrounds, indicating the presence of suppression from dim surrounds. The magnitude of the suppression can be quantified as the difference in CFFs between dim surrounds to equiluminant-surround conditions. Specifically, the magnitude of suppression will be b for a 2 Td center, 2b for a 20 Td center, and 3b for a 200 Td center. In short, this empirical model has two desirable features in describing the data. First, it can test whether there is significant suppression statistically by testing whether b is greater than 0. Second, it can be used to estimate the magnitude of suppression between dim and equiluminant surrounds. The dashed lines in Fig. 2 show the prediction based on this empirical model. Overall, the model described the CFF data adequately: when the slope, b, was significant, the variance explained by the model (R²) ranged between 0.72 and 0.94; when the slope was not significant, R² was small because the intercept alone was sufficient to describe the data.

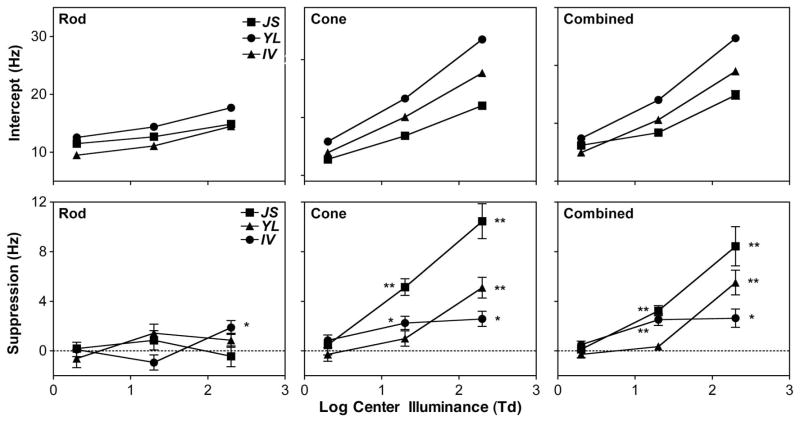
The fitted intercepts and the estimated magnitudes of suppression on equiluminant-surround CFFs from dim surrounds (≤0.2 Td), as a function of center illuminance for different stimulus types, are shown in Fig. 3 (top row, intercepts; bottom row, suppression magnitudes). Overall, the fitted intercepts increased with increasing center illuminance monotonically for all stimulus types and observers. For the isolated rod stimuli (bottom-left panel in Fig. 3), suppression from dim surrounds was absent at all three center illuminance levels for all three observers, except that, for I.V., a significant suppression was present at a magnitude of 1.9 Hz at a 200 Td center. For the isolated cone stimuli and the combined stimuli, there was no suppression at a 2 Td center for all three observers, but suppression was significant at 20 and 200 Td centers for all three observers, except for Y. L. at a 20 Td center. The magnitude of suppression was between 2.3 and 5.1 Hz at a 20 Td center for I. V. and J. S. and 2.6 and 10.4 Hz at a 200 Td center for all three observers. For each observer, there were nine stimulus types (isolated rod, isolated cone, and combined stimuli) and center illuminance (2, 20, and 200 Td) combinations. For three observers, therefore, there were in total 27 conditions (stimulus type × center illuminance × observer). CFFs measured under dim and equiluminant surrounds were significantly different among 11 out of the 27 conditions (labeled as “*” or “**” in the bottom row, Fig. 3), in which the averaged equiluminant-surround CFF was 25.2 (mean) ± 1.7 (sem) Hz (95% CI, 21.3–29.1 Hz). For all other 16 conditions in which CFFs were not reduced under dim surround, the equiluminant-surround CFF was 12.6 Hz ± 0.6 Hz (95% CI, 11.3–13.9 Hz). This analysis indicated that the equiluminant-surround CFF had to be high enough for dim surround to reduce equiluminant-surround CFF significantly.

Fig. 3.

Fitted intercept (a) and estimated suppression magnitude from the fitted slope b from Eq. 1 (suppression magnitude = b for a 2 Td center, 2b for a 20 Td center, and 3b for a 200 Td center) for the (left) isolated rod stimuli, (middle) isolated cone stimuli, and (right) combined stimuli. The error bars are standard errors. For each observer, the conditions with significant suppression are labeled: *, p < 0.05; **, p < 0.01.

4. DISCUSSION

Our measurements indicated that CFFs with the isolated cone stimuli and with the combined stimuli at ≥20 Td were comparable, suggesting dominating cone contributions to the combined CFFs at these light levels. Given that equiluminant-surround CFFs with the isolated cone stimuli and with the combined stimuli at ≥20 Td were most likely to be reduced by dim surrounds and suppression of rod flicker detection was observed only in one observer at 200 Td, we concluded that dim surrounds suppressed cone CFFs but only at a higher light level. Since complete suppression only occurred when the surround illuminance was ≤0.2 Td and given the absolute cone threshold is near 0.1 Td [19], we inferred that suppression from the dim surround is primarily driven by rod activities. These results can be understood in terms of the effect of dim surrounds on impulse response functions (IRFs). We first established the link between CFFs and IRFs by simulating how IRF parameters, which were likely to change under different stimulation conditions, could affect CFFs. Second, we discussed rod and cone IRFs estimated at different levels and explained why cone CFFs instead of rod CFFs were more likely to be suppressed. Finally, we speculated the potential neural pathway mediating lateral suppression.

An earlier study showed that dark-adapted rods altered the amplitude and timing of cone IRFs [11]. To understand how different IRFs affected CFFs, we conducted simulation analysis with IRFs modeled as the difference between an excitatory component (with a relative weight of ω₁, a time constant of τ₁, and n₁ stages) and an inhibitory component (with a relative weight of ω₂, a time constant of τ₂, and n₂ stages) [20,21]:

$$A(t)={\omega }_1{[t/{\tau }_1{e}^{({\tau }_1-t)/{\tau }_1}]}^{(n_1-1)}-{\omega }_2{[t/{\tau }_2{e}^{({\tau }_2-t)/{\tau }_2}]}^{(n_2-1)},$$ (2)

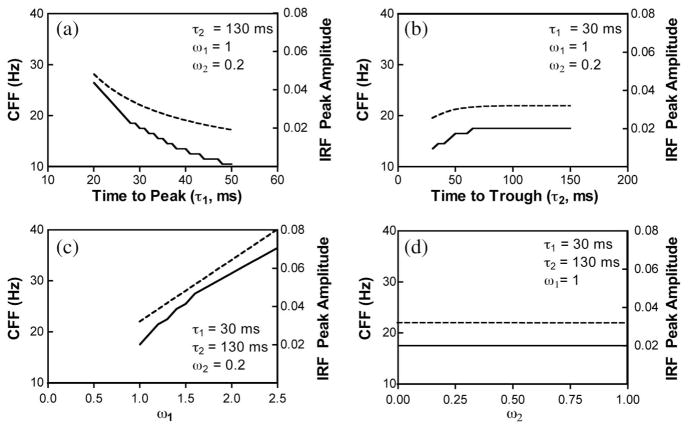
where A is the response amplitude at time t. In the literature, τ₁ is also referred to as time to peak and τ₂ as time to trough. For the simulation analysis, n₁ and n₂ in Eq. (2) were set to 7, and the excitatory and inhibitory components in Eq. (2) were normalized to have a unit area under the curve. To model CFF using IRF described in Eq. (2), we used sinusoidally modulated stimuli in various temporal frequencies (1 to 50 Hz in a step size of 1 Hz) for a fixed contrast and light intensity. We first convolved each stimulus with a certain temporal frequency with the IRF described in Eq. (2) and computed the maximum value of the convolved function. The maximum values from the stimuli with all of the temporal frequencies were then compared with a fixed decision criterion, with CFF defined as the temporal frequency at which the maximum convolved value was equal to the criterion. Figure 4 illustrates the effects of different IRF parameters (τ₁, τ₂, ω₁, and ω₂) on peak IRF amplitudes and CFFs, using unit light intensity with a contrast of 30% and a criterion of 0.15. The simulation results indicated that increasing times to peak (τ₁) reduced the IRF peak amplitudes and the predicted CFFs, while increasing the weights of the excitatory component (ω₁) increased the IRF peak amplitudes and CFFs. On the other hand, changing the values of the parameters of the inhibitory component (τ₂ and ω₂) had negligible effects on the IRF peak amplitudes and CFFs. The results indicated that CFFs are determined by the peak amplitudes of the IRFs, which in turn are largely determined by the excitatory components. The simulation results are consistent with physiological findings in primate ganglion cell recordings that higher CFFs were associated with higher peak IRF amplitudes and shorter times to peak [22]. Psychophysically, the estimated cone IRF peak amplitude was reduced and time to peak was longer under the dark-surround condition than under the equiluminant-surround condition [11].

Fig. 4.

Predicting CFFs using IRF: effects of IRF model parameters (time to peak, τ₁, time to trough, τ₂, the excitatory weight, ω₁, and inhibitory weight, ω₂) on IRF peak amplitudes (dashed lines, right y axis) and CFFs (solid lines, left y axis). (a) Varying τ₁ only with other parameters fixed at the values shown in the panel, (b) varying τ₂ only, (c) varying ω₁ only, and (d) varying ω₂ only. See text for more details.

It has been proposed that, for suppression to occur, the response amplitude and integration time resulting from the convolution of IRFs and stimuli must reach certain values [23]. This idea is consistent with our observation that an equiluminant-surround CFF had to be high enough for suppression to occur. Based on our estimated rod and cone IRFs from psychophysical data [20], the times to peak of the rod and cone IRFs did not differ dramatically at mesopic light levels [20]. On the other hand, when the light level was increased from 2 to 200 Td, the peak amplitude of the cone IRF increased by over threefold, while the peak amplitude of the rod IRF only increased modestly (by 34%). The ratio of the cone-to-rod IRF peak amplitudes was 1.9 at 2 Td, 2.6 at 20 Td, and 5.6 at 200 Td. When the rod or cone IRF was convoluted with temporally modulated stimuli, cone-mediated flicker detection was more likely to be suppressed by dim surrounds than rod-mediated flicker detection because of a great increase in cone IRF peak amplitude with increasing light levels but not in rod IRF peak amplitude. At a 2 Td center, both rod and cone responses were weak, and no suppression was observed. With increasing light levels, cone response amplitudes were high enough to be suppressed, but rod response amplitudes did not change dramatically (we only observed suppression of rod flicker detection in one observer at a 200 Td center). Dark-adapted rods suppressed mainly cone flicker detection [6–11] but not rod flicker detection, for an obvious reason; that is, under the majority of stimulation conditions, rod responses are not strong enough to be suppressed. It is reported that the rod signal from the two pathways can cancel each other at 15 Hz modulation, but only in a small background intensity range centered near 1.0 scotopic Td or 0.13 photopic Td [24,25]. The light levels we used in this study were much higher than the light levels at which self-cancellation occurs, ruling out the possibility of cancellation of the rod pathways to account for our results that rod CFFs were not suppressed.

A fundamental issue concerns determination of the neural sites that mediate lateral suppression of flicker detection. In the amphibian retina, an inhibitory feedback mechanism from horizontal cells to cones can explain lateral rod–cone interactions [26,27]. In the primate retina, horizontal cells are insensitive in the scotopic range, but rod suppression occurs only at dim-surround illuminances, indicating that primate horizontal cells are an unlikely locus of suppression from dark-adapted rods [10]. Our current study indicates suppression from dark-adapted rods occurred when the center light was in the intermediate or high mesopic range (20 or 200 Td), at which the signal is presumably transmitted through the cone bipolar cells, and the surround light was low ≤0.2 Td, which is presumably mediated by the rod bipolar pathway. Given this, we speculate that suppression of flicker detection from dark-adapted rods might be mediated by an inhibitory signal from AII amacrine cells to cone bipolar cells, or potentially from AII amacrine cells to ganglion cells directly [28].