Summary
The ‘Clinical antipsychotic trials in intervention effectiveness’ study, was designed to evaluate whether there were significant differences between several antipsychotic medications in effectiveness, tolerability, cost and quality of life of subjects with schizophrenia. Overall, 74 % of patients discontinued the study medication for various reasons before the end of 18 months in phase I of the study. When such a large percentage of study participants fail to complete the study schedule, it is not clear whether the apparent profile in effectiveness reflects genuine changes over time or is influenced by selection bias, with participants with worse (or better) outcome values being more likely to drop out or to discontinue. To assess the effect of dropouts for different reasons on inferences, we construct a joint model for the longitudinal outcome and cause-specific dropouts that allows for interval-censored dropout times. Incorporating the information regarding the cause of dropout improves inferences and provides better understanding of the association between cause-specific dropout and the outcome process. We use simulations to demonstrate the advantages of the joint modelling approach in terms of bias and efficiency.
Keywords: Competing risk, Dropout, Interval censoring, Joint analysis, Repeated measures
1. Introduction
The ‘Clinical antipsychotic trials in intervention effectiveness’ (CATIE) schizophrenia clinical trial (Lieberman et al., 2005; Rosenheck et al., 2006) was conducted between January 2001 and December 2004 at 57 clinical sites in the USA. The goals were to evaluate whether there were significant differences between five antipsychotic medications in effectiveness, tolerability, cost and quality of life. About three-quarters of the participants in the CATIE discontinued treatment for various reasons (lack of efficacy, side effects or reasons that were not related to efficacy or side effects that were regarded as ‘patient decision’). There were large differences in rates of discontinuation for the different treatments that could substantially affect the results of the analysis of the primary efficacy variable: PANSS, the positive and negative symptom score. For example, it appeared that olanzapine was associated with a significantly lower rate of dropout due to inefficacy than all the other treatments but somewhat higher rate of dropout due to side effects. In contrast, risperidone appeared to have the lowest rate of dropout due to side effects but one of the highest rates of dropout due to inefficacy. We hypothesized that using this additional information about potentially non-informative and informative reasons for dropout could remove some bias and improve the efficiency of treatment comparisons over time. Thus we propose a new approach of modelling repeated measures data and interval-censored competing risks data and apply it to the CATIE study to assess whether inferences about PANSS could be improved by using this joint model.
Methods for joint analysis of repeated measures and survival outcomes have received much attention in the statistics literature in recent years (Hogan and Laird, 1997; Henderson et al., 2000; Tsiatis and Davidian, 2004; Diggle et al., 2008). The goals of such analyses can be to assess influences on both longitudinal and survival outcomes jointly (Henderson et al., 2000; Zeng and Cai, 2005), to improve inference for the repeated measures outcome by accounting for the survival outcome (Wu and Carroll, 1988; Schluchter, 1992; Little, 1995) or to perform inference for the survival outcome while accounting for the repeatedly measured outcome (Faucett and Thomas, 1996; Wulfsohn and Tsiatis, 1997; Wang and Taylor, 2001; Brown and Ibrahim, 2003). Under assumptions of missingness completely at random and missingness at random using the maximum likelihood estimation method we can obtain unbiased estimates for the repeated measures outcome without accounting for dropout (Little and Rubin, 2002). When data are missing not at random the joint approach is necessary, to correct for bias in the estimates of the repeated measures outcome (Troxe et al., 2004).
We focus on the scenario of main interest in the CATIE study, in which the time-to-event variable is interval-censored dropout and the repeated measures outcome is the primary variable of interest. When a large percentage of study participants fail to complete the study schedule, the apparent profile in effectiveness may not reflect genuine changes over time but may be an artefact of selection bias, with participants with worse (or better) outcome values being more likely to drop out or to discontinue. Failure to account for data lost due to dropout may thus result in biased inferences about the effectiveness outcomes. Indeed it has been demonstrated that ignoring the dropout process (when it is related to the outcome process) and analyzing the data under missingness at random assumptions leads to bias in parameter estimates (e.g. Diggle et al., (2007)).
When dropout occurs for a variety of reasons, some of these reasons may be informative (non-ignorable, missingness not at random) whereas some may be non-informative (ignorable, missingness at random or missingness completely at random). For example, dropout due to lack of improvement may be informative, whereas dropout due to side effects may be unrelated to the measured effectiveness outcomes and thus non-informative. Accounting for cause-specific dropout is likely to improve inferences and to provide a better understanding of the association between dropout and outcome processes.
Several researchers have proposed models for such scenarios in recent years (Elashoff et al., 2007, 2008; Williamson et al., 2008; Hu et al., 2009; Li et al., 2009). All these approaches have considered semiparametric competing risk submodels to describe the dropout processes due to different causes and have estimated the parameters by using computationally intensive procedures (the EM algorithm or Markov chain Monte Carlo sampling). The joint model of Elashoff et al. (2007) used a linear mixed submodel for the repeated measures outcome, a generalized logistic submodel for the marginal probability of dropout due to a particular cause and cause-specific proportional hazards (Cox) models. These submodels were linked by common latent variables. Alternatively, the same researchers (Elashoff et al., 2008) used proportional hazards (Cox) submodels with common frailties for the multiple failure types. Williamson et al. (2008) described a joint model which was similar to that of Elashoff et al. (2008) but with different random-effect specification. All three approaches mentioned so far can be regarded as extensions of the approach of Henderson et al. (2000) for a single type of dropout. Hu et al. (2009) proposed a Bayesian alternative to the approach of Elashoff et al. (2008), and Li et al. (2009) developed methods for robust estimation based on the t- rather than normal distribution of the random effects. Simulation studies in all these references confirmed the expectation that in the presence of strong correlation between the repeated and the survival outcomes the joint model gave nearly unbiased results for all parameters whereas significant bias in slope estimates and underestimation of standard errors occurred when the repeated measures outcome was analysed separately.
So far, there has not been a joint model for longitudinal outcome and competing risk, cause-specific dropouts that are interval censored. This paper fills in this gap. Advantages of our approach are that it can easily handle interval-censored data, allows estimation of the hazard function for each specific cause of dropout and can be fitted in commercial software. We extend the work of Sparling et al. (2006) who considered interval-censored data with time-dependent covariates and proposed a class of parametric survival models that includes Weibull, log-logistic and a distribution similar to the log-normal distribution. We build on the work of Guo and Carlin (2004) who demonstrated how a parametric submodel for a single failure outcome and a repeated measures submodel with shared random effects (latent variables) can be jointly analysed in procedure NLMIXED. As noted by Lindsey (1998) when data are heavily interval censored, parametric regression models are robust and in general more informative than the corresponding non-parametric or semiparametric alternatives.
We apply the proposed approach to the CATIE data and assess the effect of accounting for dropout for various reasons on inferences regarding PANSS-scores. We also evaluate the relationship between each cause-specific dropout and PANSS-scores and provide guidance regarding the interpretation of results in the presence of different types of dropout.
The paper is organized as follows. Section 2 presents the model and describes its properties. Section 3 applies the model to the data from the CATIE study. Section 4 contains simulation results and Section 5 concludes with discussion and conclusions.
The computer code for running the simulation study can be obtained from
2. Models
Let yit be the repeated measures outcome for the ith subject at time t (i = 1, …, n; t = 1, …, ni) where n is the total number of subjects in the study and ni is the number of repeated observations on the ith subject. Each subject can drop out for one of K different causes. In the CATIE study all dropout times due to specific reasons of interest are regarded as interval censored because dropout was only known to have occurred in between prescheduled visits.
We denote by the pair (Ti, Ki) the dropout data on subject i, where Ti is the time to dropout or censoring, and Ki can take values 0,1, . . . ,K, where 0 denotes right censoring and 1−K denote the different reasons for dropout. The censoring is assumed independent of the dropout time and can include dropout reasons that are not considered as part of the K competing risks.
The model for the repeated measures outcome is specified as follows:
| (1) |
where xit and zit are the covariate vectors corresponding to the fixed and random effects respectively, β is the fixed parameter vector and bi ~ N.0, Σb/ is a subject-specific random effect, which is assumed independent of the errors εit ~ N.0, σ2/ and across subjects.
Using the notation that was introduced by Sparling et al. (2006), the cause-specific hazards are defined as follows:
| (2) |
where Ki = k corresponds to the kth reason for dropout, τit corresponds to time of observation, αk > 0 and κk are general hazard function parameters. These can be estimated from the data or fixed when a particular special case distribution is selected for analysis. Sparling et al. (2006) described the hazards in this general class in more detail. κk = 0 corresponds to a Weibull hazard with a decreasing hazard function for 0 < αk ≤1, constant for αk = 1 and increasing for αk > 1. κk = 1 corresponds to the log-logistic hazard. For αk = 1.5 and κk = 0.5 the hazard is very similar to the hazard for the log-normal distribution.
In equation (2) γitk are hazard rate parameters that can depend on fixed and random effects at each update time as follows:
| (3) |
where xitk and zitk are the covariate vectors corresponding to the fixed and random effects respectively for the kth cause, βk is a fixed parameter vector and ui ~ N.0, Σu/ is a subject-specific random effect that could be shared with the random-effect vector of the repeated measures response model. Of particular interest is the situation when ui =Λbi where Λ is a matrix of factor loadings to be estimated from the data. The random effects bi and ui are latent variables and the factor loadings are unknown coefficients that allow the variances of the random effects to be different for each outcome. The most common examples of random effects are random intercepts and slopes. It is possible to introduce dependence of the censoring on the dropout time by extending the model proposed and considering additional random effects.
The βk -parameters have an intuitive interpretation in the special case of Weibull and log-logistic models. For Weibull models individual βs are interpreted as the change in the log-relative-risk for a unit increase in the corresponding predictor. For log logistic models, individual βs are interpreted as the change in the log-odds of cumulative incidences. For other choices of κ-values interpretation is not intuitive so it may be better to test whether either the Weibull or the log-logistic models, fit the data well, rather than estimate κ.
A subject’s failure time ei can be observed precisely, or it can be censored. In the general formulation we allow for left, right and interval censoring for each competing risk. The following indicators for each of K possible dropout reasons are defined:
Note that in the competing risks situation the indicators are not independent of one another. If a subject drops out for one recorded reason then this subject is right censored for all other reasons. If a subject drops out for non-specified reasons then this subject is regarded as right censored in all dropout submodels.
For exactly observed, left-censored and right-censored dropout times ti, the contribution of the dropout processes to the conditional likelihood given the random effects is
| (4) |
Here fik denotes the event density for the kth reason for dropout and Fik denotes the corresponding cumulative distribution function. For interval-censored dropout times, a subject remains at risk of all causes of dropout until an unknown time within the interval when dropout for the kth reason actually occurs. Thus the contribution of the dropout process to the conditional likelihood is
| (5) |
However, this integral does not have a closed form expression, thus leading to a nested integral approximation for the entire likelihood. Because of this added computational complexity, we make the simplifying assumption that, if a subject is interval censored for a particular reason, then this subject is right censored for the other competing reasons at the beginning of the interval when dropout occurred. We choose the beginning of the interval because this is the latest time point at which we know for sure that the subject remained in the study. For closely spaced observation times this approximation is expected to introduce negligible bias.
Under our simplifying assumption, the contribution of the ith subject to the log-likelihood of the model conditional on the random effects is
Here θ denotes the parameter vector of all covariates. The event densities and the cumulative distribution functions are obtained from the assumed hazard functions. In the simple case of no time-dependent covariates the cumulative hazard is
| (6) |
and the density and cumulative distribution functions can be obtained by the usual formulae:
| (7) |
| (8) |
Details about the situation and formulae when there are time-dependent covariates can be found in Sparling et al. (2006).
Because there are random effects in all the expressions above, it is not possible to maximize the likelihood directly. It is necessary to use a stochastic or numerical approximation method first and then to maximize the approximation. We chose to use Gaussian quadrature and then to maximize the log-likelihood by using existing software. Using the general likelihood option in PROC NLMIXED allows us to write and maximize the likelihood above explicitly. In general, our proposed model can handle any combination of exactly observed, right-censored, left-censored or interval-censored observations during the study period.
3. Joint analysis of PANSS severity and competing risk dropout in the ‘clinical antipsychotic trials in intervention effectiveness’ study
In the CATIE study 1493 adult schizophrenia patients were initially randomly assigned to receive a first-generation antipsychotic (perphenazine) or one of four second-generation drugs (olanzapine, quetiapine, risperidone or ziprasidone) at 57 sites (clinics). Participants were followed for up to 18 months or until the initial randomly assigned treatment was discontinued for any reason (phase I). Other randomizations and treatments followed after phase I, but this paper focuses on the analysis of phase I data. Since ziprasidone was approved for use by the Food and Drug Administration after the study began, we did not consider ziprasidone in this paper. After excluding subjects on ziprasidone our analyseable sample size was 1054 subjects with a total of 4509 measurements.
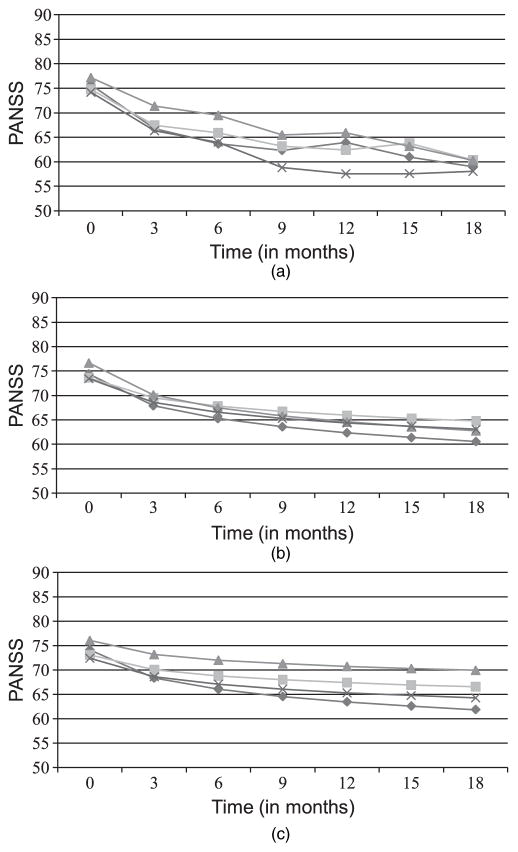
The main outcome of interest in the current paper is the efficacy outcome PANSS, the positive and negative symptom score. Higher PANSS-scores represent more severe schizophrenia symptoms. PANSS and additional indicators of side effects were recorded at baseline, 1 month and quarterly thereafter until 18 months. Average PANSS-scores by treatment and time are shown in Fig. 1(a) and in Table 1. Table 1 also includes standard deviations and sample sizes by treatment and time.
Fig. 1.
(a) Raw PANSS-means, (b) estimated PANSS-means based on separate PANSS-analysis and (c) estimated PANSS-means based on joint analysis of PANSS and different reasons for dropout in the CATIE study:
 olanzapine;
olanzapine;
 quetiapine;
quetiapine;
 , risperidone;
, risperidone;
 , perphenazine
, perphenazine
Table 1.
Means, standard deviations SD and sample sizes of PANSS-scores by treatment and time in the CATIE study
| Parameter | Results for the following times (months):
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 3 | 6 | 9 | 12 | 15 | 18 | |
| Olanzapine | ||||||||
| Mean | 75.7 | 69.7 | 66.8 | 63.7 | 62.3 | 63.9 | 61.0 | 59.0 |
| SD | 18.2 | 17.9 | 17.8 | 17.6 | 17.0 | 17.6 | 16.9 | 17.1 |
| N | 262 | 243 | 185 | 146 | 126 | 113 | 102 | 83 |
| Quetiapine | ||||||||
| Mean | 74.8 | 69.7 | 67.5 | 65.9 | 63.2 | 62.4 | 63.8 | 60.4 |
| SD | 17.0 | 17.1 | 17.8 | 15.6 | 14.8 | 16.7 | 15.8 | 13.6 |
| N | 260 | 239 | 165 | 107 | 84 | 70 | 56 | 49 |
| Risperidone | ||||||||
| Mean | 77.2 | 73.4 | 71.4 | 69.5 | 65.5 | 65.9 | 63.2 | 60.2 |
| SD | 16.5 | 18.0 | 18.5 | 17.7 | 15.5 | 16.3 | 16.4 | 17.5 |
| N | 269 | 243 | 165 | 122 | 99 | 87 | 76 | 62 |
| Perphenazine | ||||||||
| Mean | 74.2 | 69.4 | 66.3 | 64.0 | 58.8 | 57.6 | 57.6 | 58.0 |
| SD | 18.0 | 17.8 | 17.5 | 17.7 | 18.0 | 16.5 | 16.1 | 16.2 |
| N | 256 | 235 | 172 | 115 | 84 | 75 | 69 | 61 |
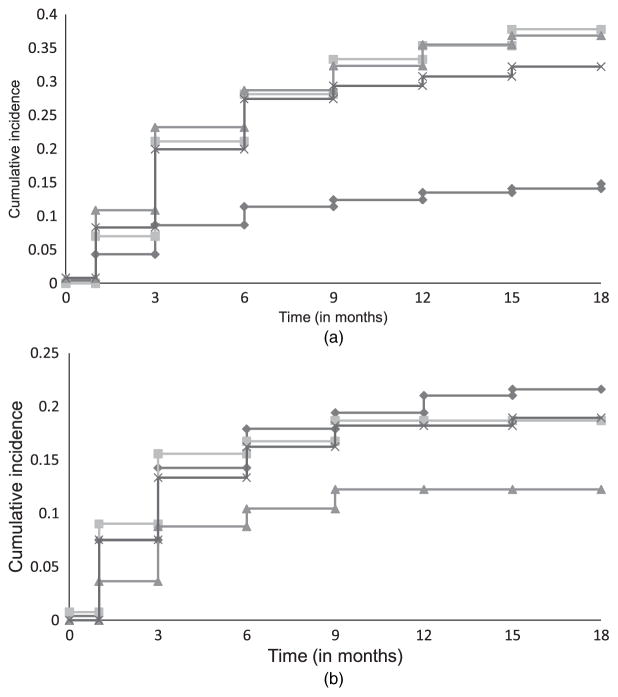
Differences in rates of incidence for discontinuation due to inefficacy and side effects among the different treatments are shown in Fig. 2(a) and 2(b) respectively. Discontinuation due to patient decision appeared to be a heterogeneous category and it was not possible to tease out potentially different reasons for discontinuation within this category. We did not model this as a separate reason for dropout, but rather treated it as non-informative censoring for the modelled dropout due to either inefficacy or side effects. It is unlikely that this heterogeneous dropout category is related to dropout due to side effects and dropout due to inefficacy. Thus the independence assumption between dropout and censoring appears reasonable. We considered two competing risks for dropout: inefficacy and side effects. All observed dropout times were interval censored.
Fig. 2.
Cumulative incidence for dropout due to (a) inefficacy and (b) side effects in the CATIE study:

 olanzapine; quetiapine;
olanzapine; quetiapine;
 , risperidone;
, risperidone;
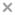 , perphenazine
, perphenazine
We first fitted separate models of total PANSS-score, of dropout due to inefficacy and of dropout due to side effects. For total PANSS-score we considered the linear mixed model (1) with the following fixed effects: three dummy variables for treatment (di1 = 1 if the ith subject was assigned to olanzapine and di1 = 0 otherwise; di2 = 1 if the ith subject was assigned to quetiapine and di2 = 0 otherwise; di3 = 1 if the ith subject was assigned to risperidone and di3 = 0 otherwise), log-time and the interaction between the treatment indicators and log-time. Thus we used the first-generation antipsychotic (perphenazine) as the reference treatment. We also assumed a random intercept and slope for PANSS–measures with a bivariate normal distribution with 0 means and unstructured variance–covariance matrix. For dropout due to inefficacy and dropout due to side effects we considered the hazards in equation (2) where we originally allowed the κc-parameters to be freely estimated from the data. Since the dropout models revealed that the estimated κc-parameters were not significantly different from 0, Weibull hazards appeared to provide a good fit to the data and hence we present results from Weibull submodels for both dropout reasons. Thus treatment effects on dropout are more easily interpretable as relative risks. We used the estimates from the separate models as starting values for the joint models.
We considered several joint models with different reasons for dropout that allow flexible modelling of dropout:
a joint model with shared random intercept and slope between the PANSS-submodel and the dropout submodels,
a joint model with shared random intercept between the PANSS-submodel and the dropout submodels, and
a joint model with shared deviations from the means of PANSS between the PANSS-submodel and the dropout submodels.
The most flexible of these models is the model with shared random intercept and slope:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where bri ~ N.0, Σb/ is independent of the errors εit ~ N.0, σ2/ and across subjects, k = 1 indicates dropout due to inefficacy, k = 2 indicates dropout due to side effects and λkl, l = 1, 2, are factor loadings for the random effects that will be estimated from the data. Here we assume a random intercept and slope for the continuous outcome and allow both dropout processes to depend on these random intercepts and slopes. The factor loadings define the variances of the random effects. The model with shared random intercept is a special case when λk1 = 0 for all k and the model with shared deviations from the mean is a special case when λk0 = λk1 for all k.
PROC NLMIXED was used for model fitting and estimation of additional treatment comparisons. The general option in PROC NLMIXED allowed specification of the closed form conditional likelihood and the random statement was used to specify the random effects distribution. The convergence criteria were strengthened from the default values of 10−8 to 10−12 to avoid premature convergence. 10 quadrature points were used in each direction. The choice of the number of quadrature points was made by comparing the estimates and standard errors with five, 10 and 15 quadrature points. 10 points were sufficient for accurate estimation and were chosen because the computational time was significantly less than when 15 quadrature points were used. Note that PROC NLMIXED cannot handle nested Gaussian quadrature and becomes computationally forbidding as the number of random effects increases.
Table 2 presents parameter estimates from the most flexible joint model (model 1), the corresponding joint model where all dropout was treated the same (model 2) and from the model for PANSS where dropouts were not modelled (model 3). Model 1 was selected among the considered models with different reasons for dropout (models (a), (b) and (c)) based on the Akaike information criterion AIC. AIC for this model was 38 416 compared with 38 570 for the model with shared random intercept for the PANSS-submodel and the dropout submodels, and 38 545 for the model with shared deviations from the means of PANSS between the PANSS submodel and the dropout submodels. Thus AIC was used to select the proper random-effects structure in the model with competing risk dropouts since the models with different random effects are not nested.
Table 2.
Maximum likelihood estimates and standard errors in the CATIE study
| Effect | Results for model 1 (shared intercept and slope) | Results for model 2 (common dropout)† | Results for model 3 (ignoring dropout) |
|---|---|---|---|
| PANSS | |||
| Intercept (β0) | 72.17 (1.08) | 72.28 (1.08) | 73.43 (1.05) |
| Olanzapine (β1) | 1.69 (1.49) | 1.57 (1.49) | 1.00 (1.47) |
| Quetiapine (β2) | 0.66 (1.50) | 0.65 (1.50) | 0.22 (1.48) |
| Risperidone (β3) | 3.64 (1.50) | 3.68 (1.49) | 3.21 (1.48) |
| Time (β4) | −2.41 (0.53) | −2.55 (0.52) | −3.52 (0.47) |
| Olanzapine by time (β5) | −1.44 (0.64) | −1.29 (0.64) | −1.18 (0.63) |
| Quetiapine by time (β6) | 0.57 (0.68) | 0.58 (0.68) | 0.51 (0.67) |
| Risperidone by time (β7) | 0.68 (0.66) | 0.62 (0.66) | 0.64 (0.65) |
| SD(r.i.) (σb11) | 15.88 (0.42) | 15.85 (0.42) | 15.88 (0.42) |
| SD(r.sl.) (σb22) | 4.44 (0.26) | 4.41 (0.26) | 4.27 (0.25) |
| Corr(r.e.) (ρb) | −0.43 (0.05) | −0.43 (0.05) | −0.46 (0.05) |
| SD(error) (σ11) | 9.03 (0.12) | 9.04 (0.12) | 9.07 (0.12) |
| Inefficacy | |||
| Intercept (β01) | −3.58 (0.19) | −2.37 (0.14)1 | — |
| Olanzapine (β11) | −0.97 (0.23) | −0.44 (0.16)2 | — |
| Quetiapine (β21) | 0.16 (0.19) | 0.12 (0.15)3 | — |
| Risperidone (β31) | 0.11 (0.19) | −0.08 (0.15)4 | — |
| Shape (α1) | 1.07 (0.06) | 0.98 (0.04)5 | — |
| Loading (intercept) (λ10) | 0.04 (0.01) | 0.03 (0.004)6 | — |
| Loading (slope) (λ11) | 0.06 (0.01) | 0.04 (0.01)7 | — |
| Side effects | |||
| Intercept (β02) | −3.54 (0.21) | −2.87 (0.14)1 | — |
| Olanzapine (β12) | 0.05 (0.21) | −0.44 (0.16)2 | — |
| Quetiapine (β22) | 0.07 (0.23) | 0.12 (0.15)3 | — |
| Risperidone (β32) | −0.48 (0.26) | −0.08 (0.15)4 | — |
| Shape (α2) | 0.87 (0.06) | 0.98 (0.04)5 | — |
| Loading (intercept) (λ20) | 0.01 (0.01) | 0.03 (0.004)6 | — |
| Loading (slope) (λ21) | 0.03 (0.01) | 0.04 (0.01)7 | — |
| −2 log−likelihood for entire model | 38364 | 37898 | 35605 |
| AIC | 38416 | 37936 | 35629 |
Estimates denoted by the same superscript number are the same because of the model specification of common dropout.
Likelihood ratio tests can be used to reduce the fixed predictors in the model once the model structure has been determined. Maximized log-likelihoods and likelihood-based criteria cannot be used to select between models with different data structures, i.e. between models with competing reasons for dropout, common dropout and ignoring dropout. Such a decision should be based on the scientific goals of the study and not on statistical criteria.
On the basis of the estimated regression coefficients and linear combinations of regression coefficients, the joint model with separate reasons for dropout (model 1) revealed that olanzapine was associated with a significantly greater improvement in PANSS over time than the other three medications: p = 0.03 versus perphenazine (β5), p = 0.001 versus risperidone (β5 − β7) and p = 0.002 versus quetiapine (β5 −β6). Quetiapine and risperidone were not significantly different from perphenazine as indicated by the estimates of β6 and β7. The model also showed a significantly lower risk for dropout due to inefficacy for subjects on olanzapine compared with subjects on perphenazine (p < 0.0001 for β11), risperidone (p < 0.0001 for β11 − β31) or quetiapine (p < 0.0001 for β11 − β21). In contrast, subjects on olanzapine and quetiapine had a significantly higher likelihood of dropout due to side effects than subjects on risperidone (p = 0.03 and p = 0.03 for β12 − β32 and β22 − β32 respectively). The factor loadings corresponding to dropout due to inefficacy (λ10 and λ11) were significantly larger than 0 (p < 0.0001 for both factor loadings); thus there was a significant positive association between PANSS-score and dropout due to inefficacy. The factor loadings corresponding to dropout due to side effects (λ20 and λ21) were also significantly larger than 0 but the effect was not nearly as large as for dropout due to inefficacy (p = 0.01 and p = 0.02 for intercept and slope respectively). Thus dropout due to inefficacy is much more likely to be informative than dropout due to side effects.
The model ignoring dropout (model 3) estimated noticeably steeper slopes for all treatments except for olanzapine. This was expected since more than 40% of the subjects on these treatments discontinued their assigned treatment because of inefficacy, resulting in the observed PANSS appearing lower. Failure to take this into account led to bias towards overestimating the effects of these treatments. In the model ignoring dropout the comparison between the slopes for olanzapine and perphenazine was not statistically significant (p = 0.06 for β5); hence this model failed statistically to distinguish the effectiveness of these treatments. Figs 1(b) and 1(c) show the estimated means by treatment over time for the separate and the best fitting joint model. The greater separation of treatment effects in the joint model with different reasons for dropout is evident when comparing the spread of treatment means between Figs 1(b) and 1(c).
The model treating all dropouts the same (model 2) gave estimates of PANSS-effects between those from the joint models with different dropout reasons and those from the model ignoring dropout. It also did not present a detailed picture of the differences in rates of dropout among treatments. For example, it estimated that olanzapine was associated with a significantly lower rate of dropout (p = 0.005 for β11) than perphenazine. This was indeed so for dropout due to inefficacy (Fig. 2(a)), but for dropout due to side effects olanzapine was not significantly different from perphenazine (Fig. 2(b)). Furthermore, this model estimated that olanzapine was associated with a significantly lower chance of dropout (p = 0.02 for β11 − β31) than risperidone, whereas as seen from the models with different reasons for dropout the differences in rates of dropout for inefficacy and for side effects for these two treatments went in opposite directions, i.e., compared with risperidone, olanzapine was associated with a significantly lower chance of dropout due to inefficacy but with a significantly higher chance of dropout due to side effects (Fig. 2(a) and Fig. 2(b)).
Although the analyses of the CATIE data clearly show that joint models with different reasons for dropout can improve inferences regarding treatment effects on the primary efficacy outcome PANSS, simulation studies are necessary to assess whether this approach can indeed capture the underlying true response better when compared with treating all dropout the same and with ignoring dropout. The next section presents such a simulation study in a situation when dropout due to inefficacy is informative and dropout due to side effects is non-informative.
4. Simulations
To investigate whether joint modelling of the repeated measures response and dropout due to different reasons can better capture the underlying response we performed the following simulation study. Without losing generality and to illustrate our main point regarding potential bias in parameter estimation we considered linear effects of time and only two treatments. We used the same time points as in the CATIE study. For speed of computation, in the model formulation (1)–(3), we considered only random slopes and modelled positive association between the repeated measures outcome and the risk of dropout due to inefficacy via positive factor loadings for the random slope (λ1 > 0 in equation (13)), and no association between the repeated measures outcome and the risk for dropout due to side effects by setting the factor loading for the random slope in the model for dropout due to side effects equal to 0 (λ2 = 0 in equation (13)). We considered two settings (with smaller and larger correlation between the efficacy measure and dropout due to inefficacy) and generated 200 data sets at each setting according to the following simulation model:
where k = 1 corresponds to dropout due to inefficacy and k = 2 corresponds to dropout due to side effects. The loading λ2 was set equal to 0, whereas the two settings assume λ0 = λ1 = 1 (smaller correlation) and λ0 = λ1 = 3 (larger correlation). The random slope bi was assumed normally distributed with zero mean and unit variance and the errors for the repeated measures outcome were assumed independent and identically distributed N.0, 1/. The parameter values of the regression parameters of the repeated measures outcome are provided in Table 3. Treatment 1 was associated with a larger improvement over time (β3 = −0.5), with a lower risk of dropout due to inefficacy (β11 = −1) and a higher risk of dropout due to side effects (β12 = 1) than treatment 0. Both scale parameters were set equal to 1 (α1 = 1 and α2 = 1). To emphasize model differences we considered high rates of dropout so that dropout for all causes could reach 85% (β01 = −3 and β02 = −4). Each data set generated consisted of 500 subjects: 250 for each treatment arm. All observations were interval censored to mirror the CATIE study.
Table 3.
Estimates and average standard errors for the repeated measures outcome in the simulation study
| Effect | True value | Results for the following models:
|
||
|---|---|---|---|---|
| Dropout separated by reason | Common dropout | Ignoring dropout | ||
| Simulation 1 | ||||
| Intercept | 72.00 | 72.00 (0.05) | 72.00 (0.05) | 72.02 (0.05) |
| Treatment 1 | 0.00 | 0.00 (0.08) | −0.01 (0.08) | −0.01 (0.08) |
| Time | −1.00 | −0.98 (0.08) | −1.07 (0.08) | −1.20 (0.07) |
| Treatment 1 by time | −0.50 | −0.49 (0.11) | −0.40 (0.10) | −0.38 (0.10) |
| Loading | 1.00 | 1.01 (0.04) | 0.96 (0.04) | 0.93 (0.04) |
| SD(error) | 1.00 | 1.04 (0.02) | 1.04 (0.02) | 1.04 (0.02) |
| Simulation 2 | ||||
| Intercept | 72.00 | 71.99 (0.05) | 72.00 (0.05) | 72.01 (0.05) |
| Treatment 1 | 0.00 | 0.00 (0.08) | 0.00 (0.08) | 0.00 (0.08) |
| Time | −1.00 | −0.87 (0.23) | −1.49 (0.24) | −2.53 (0.18) |
| Treatment 1 by time | −0.50 | −0.34 (0.30) | −0.24 (0.28) | −0.07 (0.26) |
| Loading | 3.00 | 3.00 (0.14) | 2.62 (0.14) | 2.27 (0.09) |
| SD(error) | 1.00 | 1.04 (0.02) | 1.04 (0.02) | 1.04 (0.02) |
| Simulation 3 | ||||
| Intercept | 72.00 | 71.99 (0.05) | 72.00 (0.05) | 72.01 (0.05) |
| Treatment 1 | 0.00 | 0.00 (0.08) | 0.00 (0.08) | 0.00 (0.08) |
| Time | −1.00 | −0.99 (0.22) | −1.49 (0.24) | −2.53 (0.18) |
| Treatment 1 by time | −0.50 | −0.44 (0.29) | −0.24 (0.28) | −0.07 (0.26) |
| Loading | 3.00 | 2.92 (0.04) | 2.62 (0.14) | 2.27 (0.09) |
| SD(error) | 1.00 | 1.04 (0.02) | 1.04 (0.02) | 1.04 (0.02) |
To each of the generated data sets we fitted a joint model with competing risks (a joint model with separate reasons for dropout), a model in which all dropout was treated as the same (a joint model with common reason for dropout) and a model for the repeated measures outcome in which dropout was ignored (which is herein referred to as the separate model). All models converged for all simulated data sets.
Average parameter estimates and average standard errors for the repeated measures outcome are provided in Table 3. The first block of Table 3 shows the results of the simulation with small correlation (simulation 1); the second block shows the results of the simulation with large correlation (simulation 2). The third block of Table 3 shows the results of fitting a joint model with large correlation and separate reasons for dropout in which the factor loading for dropout due to side effects is set to be equal to 0 (simulation 3). Thus the results from simulations 2 and 3 for the model with common dropout are identical. Similarly, the results from the separate model from the two simulations are identical.
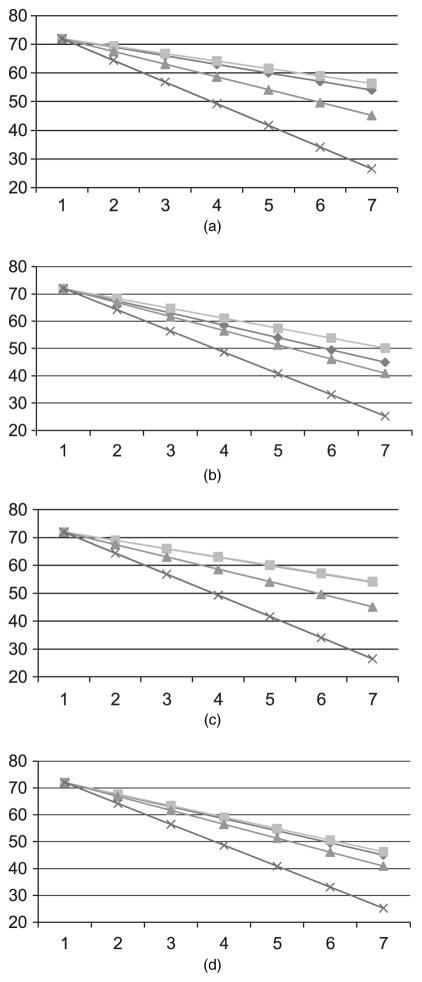
The joint model with separate reasons for dropout recovered the parameter estimates best whereas the separate model significantly overestimated the time effects in all settings. The joint model with common reason for dropout gave intermediate estimates. The bias in the slope estimates in the separate model and in the joint model with common dropout is also evident in Fig. 3, which shows the predicted average responses by treatment in simulation 2 and in simulation 3 compared with the true values from which we generated the data. In simulation 1 the bias of slope estimates was the smallest in the joint model with separate dropout also but the differences were not as evident graphically as in the settings with the stronger correlation. Hence this scenario is not shown in Fig. 3.
Fig. 3.
Estimated mean response for (a) treatment 0 in scenario 2, (b) treatment 1 in scenario 2, (c) treatment 0 in scenario 3 and (d) treatment 1 in scenario 3 of the simulation study:
 , truth;
, truth;
 , joint model, separate dropout;
, joint model, separate dropout;
 , joint model, common dropout;
, joint model, common dropout;
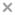 , separate model
, separate model
The graphs also show that for treatment 0 (which is associated with a higher dropout due to inefficacy and a lower dropout due to side effects) the joint model with separate reasons for dropout captures the underlying trend regardless of whether we estimate the factor loading for dropout due to side effects (λ2) or set it equal to 0, whereas for treatment 1 (which is associated with a lower dropout due to inefficacy and a higher dropout due to side effects) the joint model with separate reasons for dropout overcorrects the trend over time when λ2 is estimated. The joint model with separate dropouts is still the best approach overall as testing of treatment differences is the least biased under all scenarios for this model compared with the other two models (Table 3). However, the simulation results suggest that less biased and more efficient estimation occurs when the non-significant factor loading λ2 (average p = 0.08) is set equal to 0 (Figs 3(c) and 3(d)).
5. Discussion
In the current paper, we developed an approach for joint modelling of repeatedly measured outcomes and interval-censored cause-specific dropout to assess the influence of discontinuation of treatment for various reasons in the CATIE study in schizophrenia. Our model (like the models of Elashoff et al. (2007, 2008) and Williamson et al. (2008)) includes a linear mixed submodel for the repeated measures outcome and builds in the association between the longitudinal series and the competing risks via shared random effects. However, rather than semiparametric models, it assumes general survival distributions for the causespecific dropout processes that allow the testing of different hazard alternatives (e.g. Weibull versus log-logistic) for each reason for dropout. We can thus have both time-independent and time-dependent covariates and parameter estimates for some of the special case models that have intuitive interpretation. We demonstrated with the analysis of PANSS-scores in the CATIE study and using simulations that the method proposed reduces bias in the estimation of treatment effects. Important advantages of our approach are that it can easily handle interval censoring, allows estimation of the hazard function for each specific dropout cause and can be fitted in commercial software.
Our approach focused on data missing because of dropout and assumed that intermittent missing data were non-informatively missing (i.e. missing at random or missing completely at random). If intermediate efficacy scores are informatively missing (i.e. missing not at random) then additional modelling will be required to account for that. In the CATIE data, less than 10% of the intermediate PANS-scores were missing; thus it is unlikely that, even if they are informatively missing, the results will be substantially affected by treating them as non-informatively missing. Thus we did not explicitly model intermittent dropout.
In the CATIE study, the relationship between a particular reason for discontinuation of anti-psychotic treatment and efficacy measures of that treatment appeared to vary across the reasons for discontinuation. Dropout due to inefficacy appeared informative whereas dropout due to side effects was probably non-informative as evidenced by the repeated measures profiles of subjects who dropped out for different reasons. These features of the CATIE data called for analytic methods that could simultaneously address the multifaceted dependence of the measures and the causes of discontinuation. Mixed effects models that were used in the initial analysis by Lieberman et al. (2005) and Rosenheck et al. (2006) did not account for these features.
From the substantive clinical point of view, the joint modelling methods that were presented here lend support to previously published findings (Lieberman et al., 2005; Rosenheck et al., 2006). The phase I analysis of symptoms as measured with PANSS found no significant difference in changes in PANSS total scores between olanzapine (the best performing second-generation antipsychotic) and perphenazine (the comparison first-generation antipsychotic drug) after adjustment for multiple comparisons, using the approach of Hochberg (1988) that was chosen in previous CATIE analyses. However, whereas the previous phase-I-only analysis (Rosenheck et al. (2006), on-line supplemental Table G) found no significant effect between olanzapine and perphenazine even without Hochberg adjustment (p = 0.11), model 1 of the present analysis did find a statistically significant effect before Hochberg adjustment (p = 0.03). This difference does not represent a clinically meaningful contrast and there are other changes between the original approach and our approach that might explain this difference such as treating time as continuous and using baseline PANSS-scores as part of the response vector. However, comparing the results between the separate and joint models in our reanalysis of the CATIE study and the simulation study illustrates the potential of the joint analysis approach to increase model sensitivity to treatment differences by decreasing bias in the treatment estimates and potentially improving power.
The joint modelling efforts that are presented here also suggest greater likelihood of termination for lack of efficacy with perphenazine compared with olanzapine, but no significant difference in discontinuation due to side effects. Thus they confirm the results from the original analyses on time to discontinuation (Lieberman et al., 2005). It is useful to clarify that, whereas PANSS-scores represent overall changes in wellbeing over the many months of the trial, discontinuation for lack of efficacy represents an unstandardized clinician judgement with respect to a sentinel event at a single point in time. These analyses thus enhance our confidence in the original presentations of the CATIE results.
Compared with the original analyses of the CATIE data, our approach not only improves the power for detecting differences in treatment and simultaneously tests the effects of treatments on the repeated measures and dropout but also allows a quantitative assessment of the strength of the relationship between dropout due to various reasons and the efficacy outcome. Not surprisingly, the risk for dropout due to inefficacy was found to be significantly positively associated with PANSS-scores in the CATIE data whereas the relationship between the risk for dropout due to side effects and PANSS-scores was not as strong. Because dropout due to side effects was only weakly associated with PANSS-scores in the CATIE study, we can fit a simpler model that considers only dropout due to inefficacy together with PANSS-scores and assumes that all other dropout is independent censoring. Such a model gives very similar results for the PANSS regression coefficients and leads to the same substantive conclusions. However, it does not allow the estimation of treatment effects on dropout due to side effects and testing whether dropout due to side effects is informative.
Despite the advantages of our approach, it needs to be applied with caution. Misspecification of one part of the model could lead to compensatory changes in other parts of the model. For instance, it has been shown that incorrect specification of random effects in simpler models (Fieuws and Verbeke, 2004; Gueorguieva, 2005) can lead to bias in other parts of the models. Furthermore, our simulation suggests that, when there is no association between a particular reason for dropout and the repeated measures outcome, fitting a joint model in which the association parameter is estimated can lead to a small loss in efficiency and bias in finite samples. Thus, it is important to build the model in stages and to apply simplifying assumptions whenever possible. Finally, the approximation that we use for interval-censored data can lead to some bias when the gaps between observation times are large and the majority of the data are interval censored. In this case the times at risk of each event will be underestimated. However, in our simulation study presented in Section 4, the approximation appears to lead to little or no bias in the regression parameter estimates. Thus, even with entirely interval-censored data when the gaps between observation times are not too large the magnitude of bias due to this simplifying assumption is likely to be small. However, a larger simulation study is needed to confirm this observation for a variety of scenarios.
In the current paper we do not emphasize assessment of the goodness of fit or checking model assumptions. Since the hazard functions can be very flexibly selected, we expect that we can model the dropout processes closely. Additionally, the graphical diagnostics methods that was proposed by Dobson and Henderson (2003) for regularly scheduled repeated measurements can be extended to the models-proposed. Although a potential lack of robustness to departures from the normal distributional assumptions for the random effects may be of concern, studies of similar models have found little effect of such departures (Tseng et al., 2005). Further work is necessary to develop models for checking all aspects of the modelling assumptions.
Acknowledgments
The work in this paper was supported by National Institute of Mental Health grant 1R21MH-080959-01A1. This paper was based on results from the CATIE project, supported by the National Institute of Mental Health (N01MH90001). The aim of this project is to examine the comparative effectiveness of antipsychotic drugs in conditions for which their use is clinically indicated, including schizophrenia and Alzheimer’s disease. The project was carried out by investigators from the University of North Carolina, Duke University, the University of Southern California, the University of Rochester and Yale University in association with Quintiles, Inc.; the programme staff of the Division of Interventions and Services Research of the National Institute of Mental Health, and investigators from 56 sites in the USA (CATIE Study Investigators Group). Medication was provided by AstraZeneca Pharmaceuticals LP, Bristol-Myers Squibb Company, Forest Pharmaceuticals, Inc., Janssen Pharmaceutica Products, LP, Eli Lilly and Company, Otsuka Pharmaceutical Co., Ltd., Pfizer Inc. and Zenith Goldline Pharmaceuticals, Inc. The Foundation of Hope of Raleigh, North Carolina, also supported the project.
Contributor Information
Ralitza Gueorguieva, Yale University School of Medicine, New Haven, USA.
Robert Rosenheck, Veterans Affairs New England Mental Illness Research and Education Center and Yale University School of Medicine, New Haven, USA.
Haiqun Lin, Yale University School of Medicine, New Haven, USA.
References
- Brown ER, Ibrahim JG. A Bayesian semiparametric joint hierarchical model for longitudinal and survival data. Biometrics. 2003;59:221–228. doi: 10.1111/1541-0420.00028. [DOI] [PubMed] [Google Scholar]
- Diggle P, Farewell D, Henderson R. Analysis of longitudinal data with drop-out: objectives, assumptions and a proposal (with discussion) Appl Statist. 2007;56:499–550. [Google Scholar]
- Diggle P, Sousa I, Chetwynd A. Joint modelling of repeated measurements and time-to-event outcomes: the Fourth Armitage Lecture. Statist Med. 2008;27:2981–2998. doi: 10.1002/sim.3131. [DOI] [PubMed] [Google Scholar]
- Dobson A, Henderson R. Diagnostics for joint longitudinal and dropout time modelling. Biometrics. 2003;59:741–751. doi: 10.1111/j.0006-341x.2003.00087.x. [DOI] [PubMed] [Google Scholar]
- Elashoff RM, Li G, Li N. An approach to joint analysis of longitudinal measurements and competing risks failure time data. Statist Med. 2007;26:2813–2835. doi: 10.1002/sim.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elashoff RM, Li G, Li N. A joint model for longitudinal measurements and survival data in the presence of multiple failure types. Biometrics. 2008;64:762–771. doi: 10.1111/j.1541-0420.2007.00952.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faucett CJ, Thomas DC. Simultaneously modeling censored survival data and repeatedly measured covariates: a Gibbs sampling approach. Statist Med. 1996;15:1663–1685. doi: 10.1002/(SICI)1097-0258(19960815)15:15<1663::AID-SIM294>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- Fieuws S, Verbeke G. Joint modelling of multivariate longitudinal profiles: pitfalls of the random-effects approach. Statist Med. 2004;10:3093–3104. doi: 10.1002/sim.1885. [DOI] [PubMed] [Google Scholar]
- Gueorguieva R. Comments about joint modeling of cluster size and binary and continuous subunit-specific outcomes. Biometrics. 2005;61:862–866. doi: 10.1111/j.1541-020X.2005.00409_1.x. [DOI] [PubMed] [Google Scholar]
- Guo X, Carlin BP. Separate and joint modelling of longitudinal and event time data using standard computer packages. Am Statistn. 2004;58:16–24. [Google Scholar]
- Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;1:465–480. doi: 10.1093/biostatistics/1.4.465. [DOI] [PubMed] [Google Scholar]
- Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75:800–802. [Google Scholar]
- Hogan JW, Laird NM. Model-based approaches to analysing incomplete longitudinal and failure time data. Statist Med. 1997;16:259–272. doi: 10.1002/(sici)1097-0258(19970215)16:3<259::aid-sim484>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- Hu WH, Li G, Li N. A Bayesian approach to joint analysis of longitudinal measurements and competing risks failure time data. Statist Med. 2009;28:1601–1619. doi: 10.1002/sim.3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Elashoff RM, Li G. Robust joint modeling of longitudinal measurements and competing risks failure type data. Biometr J. 2009;51:19–30. doi: 10.1002/bimj.200810491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman JA, Stroup TS, McEvoy JP, Swartz MS, Rosenheck RA, Perkins DO, Keefe RS, Davis SM, Davis CE, Lebowitz BD, Severe J, Hsiao JK for the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) Investigators. Effectiveness of antipsychotic drugs in patients with chronic schizophrenia. New Engl J Med. 2005;353:1209–1223. doi: 10.1056/NEJMoa051688. [DOI] [PubMed] [Google Scholar]
- Lindsey JK. A study of interval censoring in parametric regression models. Liftim Data Anal. 1998;4:329–354. doi: 10.1023/a:1009681919084. [DOI] [PubMed] [Google Scholar]
- Little RJA. Modeling the drop-out mechanism in repeated-measures studies. J Am Statist Ass. 1995;90:1112–1121. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: Wiley Interscience; 2002. [Google Scholar]
- Rosenheck RA, Leslie DL, Sindelar J, Miller EA, Lin H, Stroup TS, McEvoy J, Davis S, Keefe RSE, Swartz MS, Perkins D, Hsian JK, Lieberman JA. Cost-effectiveness of second generation antipsychotics and perphenazine in a randomized trial of treatment for chronic schizophrenia. Am J Psychiat. 2006;163:2080–2089. doi: 10.1176/ajp.2006.163.12.2080. [DOI] [PubMed] [Google Scholar]
- Schluchter MD. Methods for the analysis of informatively censored longitudinal data. Statist Med. 1992;11:1861–1870. doi: 10.1002/sim.4780111408. [DOI] [PubMed] [Google Scholar]
- Sparling YH, Younes N, Lachi JM, Bautista OM. Parametric survival models for interval-censored data with time-dependent covariates. Biostatistics. 2006;7:599–614. doi: 10.1093/biostatistics/kxj028. [DOI] [PubMed] [Google Scholar]
- Troxel A, Ma G, Heitjan DF. An index of local sensitivity to nonignorability. Statist Sin. 2004;14:1221–1237. [Google Scholar]
- Tseng YK, Hsieh F, Wang JL. Joint modelling of accelerated failure time and longitudinal data. Biometrika. 2005;92:587–603. [Google Scholar]
- Tsiatis AA, Davidian M. Joint modelling of longitudinal and time-to-event data: an overview. Statist Sin. 2004;14:809–834. [Google Scholar]
- Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. J Am Statist Ass. 2001;96:895–905. [Google Scholar]
- Williamson PR, Kolamunnage-Dona R, Philipson R, Marson AG. Joint modelling of longitudinal and competing risk data. Statist Med. 2008;27:6426–6438. doi: 10.1002/sim.3451. [DOI] [PubMed] [Google Scholar]
- Wu MC, Carroll RJ. Estimation and comparison of changes in the presence of informative right censoring by modelling the censoring process. Biometrics. 1988;44:175–188. [PubMed] [Google Scholar]
- Wulfsohn MS, Tsiatis AA. A joint model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- Zeng D, Cai J. Simultaneous modelling of survival and longitudinal data with an application to repeated quality of life measures. Liftim Data Anal. 2005;11:151–174. doi: 10.1007/s10985-004-0381-0. [DOI] [PubMed] [Google Scholar]