An integer linear programming approach for finding deregulated subgraphs in regulatory networks

Abstract

Deregulation of cell signaling pathways plays a crucial role in the development of tumors. The identification of such pathways requires effective analysis tools that facilitate the interpretation of expression differences. Here, we present a novel and highly efficient method for identifying deregulated subnetworks in a regulatory network. Given a score for each node that measures the degree of deregulation of the corresponding gene or protein, the algorithm computes the heaviest connected subnetwork of a specified size reachable from a designated root node. This root node can be interpreted as a molecular key player responsible for the observed deregulation. To demonstrate the potential of our approach, we analyzed three gene expression data sets. In one scenario, we compared expression profiles of non-malignant primary mammary epithelial cells derived from BRCA1 mutation carriers and of epithelial cells without BRCA1 mutation. Our results suggest that oxidative stress plays an important role in epithelial cells of BRCA1 mutation carriers and that the activation of stress proteins may result in avoidance of apoptosis leading to an increased overall survival of cells with genetic alterations. In summary, our approach opens new avenues for the elucidation of pathogenic mechanisms and for the detection of molecular key players.

INTRODUCTION

In the last decade, microarray-based gene expression profiles played a crucial role in the study of disease-related molecular processes. Initially, microarray studies focused on single differentially expressed genes. Later, gene set analysis (GSA) and related approaches were taking into account that genes do not act individually but in a coordinated fashion (1–3). The disadvantage of this type of methods is that they can only reveal the enrichment of genes in predefined gene sets, e.g. canonical biological pathways. Other approaches like GRAIL (4) use text mining to identify key disease genes and the biological relationship among those key genes. In recent years, the research focus has shifted toward analysis methods that integrate topological data reflecting biological dependencies and interactions between the involved genes or proteins. In general, these graph-based approaches use scoring functions that assign scores or weights to the nodes or/and edges and make strong efforts to identify high-scoring pathways or subgraphs. A seminal work in this area is the publication by Ideker et al. (5) who proposed a method for the detection of active subgraphs by devising an appropriate scoring function and search heuristics. Other groups reported similar methods, which are all based on scoring protein–protein interaction (PPI) networks given experimental data (6–8).

In 2008, Ulitsky and co-workers presented an algorithm for detecting disease-specific deregulated pathways by using clinical expression profiles (9). In the same year, two Integer Linear Programming (ILP)-based approaches for uncovering deregulated networks have also been published (10,11). Recently, Dao et al. presented a randomized algorithm for efficiently finding discriminative subnetworks, which is based on color coding techniques (12).

Vandin et al. published a computational framework for a related problem, the de novo identification of significantly mutated subnetworks, in which they consider the neighborhood of mutated genes (13). Due to space constraints a complete overview of all related subnetwork-based approaches is out of scope of this work. An overview of several network algorithms and tools is given in Supplementary Table S1.

Considering regulatory networks, our group recently proposed a dynamic programming algorithm (14) to identify deregulated paths of a certain length relying on standard Gene Set Enrichment Analysis (GSEA) (1,15,16).

In the present work, we do not consider single deregulated paths, but subgraphs and present a novel branch-and-cut based approach for the determination of deregulated subgraphs that can be applied to both directed (e.g. regulatory networks) and undirected graphs (e.g. PPI networks). Given a network and node scores indicating the deregulation of the corresponding genes or proteins, our approach identifies the heaviest connected subnetwork of size k, i.e. the most deregulated subnetwork with the highest sum of node scores. In the case of directed graphs, we denote a subgraph as connected if all nodes of the subgraph are reachable from a designated root node via paths that contain only nodes belonging to the subgraph. We chose this connectivity model to find molecules (root nodes) that exert a dominating influence on their downstream targets. Such root nodes are very likely to be molecular key players responsible for the observed deregulation and may, thus, serve as promising targets for therapy purposes.

Since we are especially interested in the identification of genes and proteins that may play a key role in pathogenic processes, we evaluated the new approach by carrying out three different tests studying differences of regulatory processes based on the KEGG human regulatory pathways (17–19) and expression data. First, we analyzed gene expression profiles of non-malignant mammary epithelial cells from BRCA1 mutation carriers and non-BRCA1 mutation carriers (20) to explore the effect of the mutations on the regulatory processes and to gain new insights on how these mutations may contribute to the development of breast cancer. Second, we studied activity differences in regulatory networks between groups of short- and long-time survivors of astrocytomas using a freely available dataset of high-grade (grades III and IV) astrocytomas (21,22). Using these datasets, we also compared our novel approach with state-of-the-art methods.

Finally, we applied our algorithm to a dataset generated at Roche Pharma Research. This dataset consisted of gene expression data from two different colorectal adenocarcinoma cell lines treated with a cytotoxic substance. The goal of the experiment was to elucidate the mode of action of the employed agent. The binaries of the implementation of our algorithm and the used graph and gene score lists are freely available on our homepage http://genetrail.bioinf.uni-sb.de/ilp/.

MATERIALS AND METHODS

We present a novel branch-and-cut (B&C) approach for detecting deregulated subgraphs in biological networks based on expression differences of the involved genes or proteins. We will start with a detailed problem definition.

Problem definition

As input, the algorithm requires a directed graph that represents the biological network G = (V, E) and scores for each node. Given this labeled directed graph, we are interested in finding connected subgraphs of size k that maximize the sum of the scores. Here, we denote a subgraph G′ ⊂ G as connected if it contains at least one root node v_r from which all other nodes in G′ are reachable, i.e. for each node v in G′, a path from v_r to v consisting only of nodes in G′ exists.

Workflow

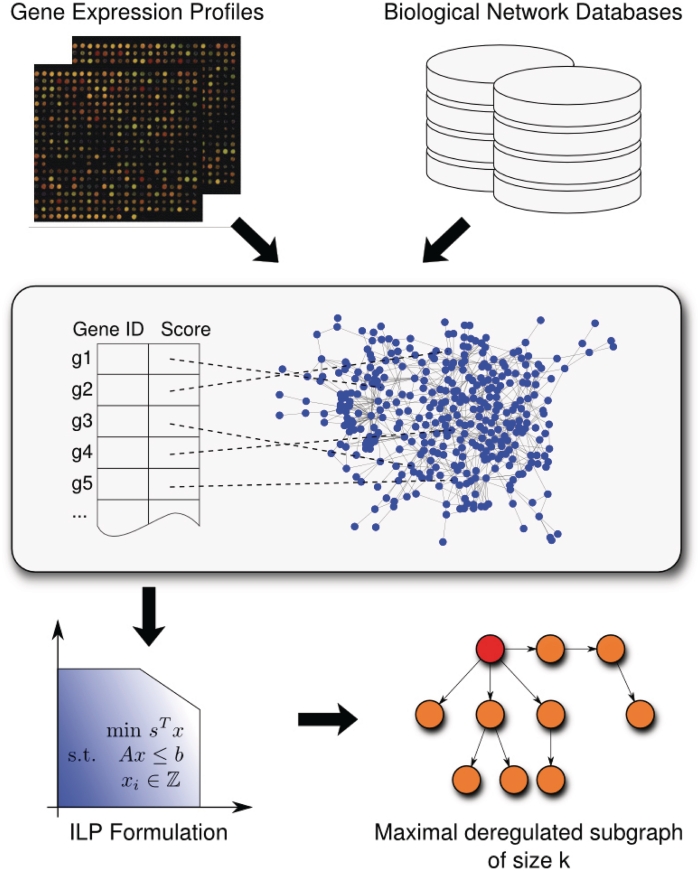
The workflow of our approach consists of three steps. In short, using normalized expression data, we compute a score for each gene that mirrors the expression differences of the gene between the sample and the reference group and that can be interpreted as its degree of deregulation. These gene scores are mapped to the corresponding nodes of the biological network G. Finally, we apply our approach to this labeled directed graph. An overview of the workflow is presented in Figure 1.

Figure 1.

Workflow of our algorithm for the computation of deregulated subgraphs. As input, it requires a biological network and a list of genes with scores that have been derived from expression data and mirror the degree of deregulation. After the scores of the genes have been mapped to the corresponding nodes of the network, our ILP-based B&C approach calculates the most deregulated subgraph that can be visualized using BiNA (23).

We start with the description of the methods for calculating the node scores and the procedures for preparing the input network. After the presentation of the ILP and the B&C approach, we list the tools used for the visualization and statistical evaluation of the obtained deregulated subgraph.

Normalization and calculation of the gene scores

Given the expression datasets of the sample and reference group, we first carried out quantile normalization (24) of the microarrays if necessary. To demonstrate the flexibility of our tool with respect to different pre-processing approaches, we selected three common methods, including fold-difference, two-tailed unpaired t-test and fold changes to determine a score for each transcript, and applied these to three different microarray data sets. In the next step, the transcript IDs are mapped to NCBI Gene IDs. If two or more transcript IDs are mapped to the same gene, we select the median score of the corresponding transcripts as its score. Hence, the resulting gene list contains one score for each gene on the microarray and this score mirrors its degree of deregulation.

Preparing the biological network

The B&C approach requires a directed graph as input. In this study, we considered the union of all KEGG human regulatory pathways including the KEGG cancer pathways. In the following, we denote this merged network as the KEGG human regulatory network.

We imported the KEGG regulatory pathways via the Biochemical Network Database (BNDB) (25) that facilitates the merging and integration of various external network databases. The usage of the BNDB has the advantage that we have access to the data of different databases using the same interface. For details of the import and merging procedures, see Refs (23,25) and the Supplementary Methods.

Since KEGG pathways also contain nodes for protein families, we transformed the original KEGG pathways by splitting the nodes of protein families into their components. Given a protein family, we replace the family node by a set of nodes where each node represents a family member. Each new node is connected to all neighbors of the original family node, i.e. it has the same set of in- and outgoing edges as the original family node, and receives the score of its corresponding gene. Here, we assume that all family members interact in the same manner with the neighboring nodes of the original family node. We also have to deal with nodes that still have no score. Here, we decided to set these scores to a constant value of ‘0’. The corresponding nodes do not contribute to the total score of the subnetwork, but may be chosen for connectivity reasons. Finally, for the mapping of the genes and their scores to the nodes of the network, we used the NCBI Gene identifiers.

ILP formulation and the B&C algorithm

For each node v_i ∈ G, we introduce two binary variables x_i and y_i. While the variable x_i ∈ {0, 1} indicates whether its corresponding node v_i is contained in the selected subgraph (x_i = 1) or not (x_i = 0), the variable y_i ∈ {0, 1} indicates whether its corresponding node v_i is the root node (y_i = 1) or not (y_i = 0). Let s_i be the score of node v_i then the optimization problem can be formulated as follows:

The following constraint ensures that the subgraph consists of k nodes:

(1)

We ensure that we obtain one root node by the constraint

The inequalities

ensure that the designated root node belongs to the nodes of the selected subgraph.

All remaining constraints concern the connectivity of the desired subgraph. Let In(i) be the set of indices of the predecessors of node v_i, where a node v_j is a predecessor of v_i if there is a directed edge from v_j to v_i. We ensure that a chosen node has either a predecessor in the selected subgraph or it is the designated root node by

Unfortunately, this kind of constraints is also fulfilled by cycles as every node in a cycle has a predecessor. Hence, a subgraph fulfilling the above constraints may contain disconnected cycles. Let be the set of node indices of a cycle, and analogously In() the set of indices of nodes which share an in-edge into this cycle, then the extension of the above constraint to the cycle is given by

(2)

In theory, the complete description of our optimization problem as given above requires one constraint for every cycle, resulting in a large number of inequalities of type (2) for the considered problem instances.

In practice, branch-and-cut-algorithms (B&C-algorithms) start with a basic set of constraints, solve the current mathematical problem and check afterwards if the result violates not yet considered constraints. If so, violated constraints are added (cut) and the solver is restarted. This process iterates until no further violated constraint could be identified.

In order to solve the mathematical problems efficiently, see e.g. Ref. (26), the integrality contraints are dropped (relaxation) and we obtain common linear problems. Unfortunately, the above constraints can also be fulfilled by non-integer values, i.e. x_i ∈ [0, 1] but x_i ∉ {0, 1}. Therefore, we expect usually non-integer solutions of the relaxed problems. However, it can be efficiently decided, whether the variable values of a result are integer and whether non-zero (not necessarily integer) values form disconnected cycles. Evaluating both criteria is equivalent to deciding if a result of the relaxed problem is a valid solution candidate for the original problem.

In case of a non-integer result and no further violated constraint, a so-called branching step is needed. The mathematical problem is subdivided into two or more subproblems (branch). An ordinary decision strategy is, e.g. assigning one variable to the next upper integer according to its value in the recent intermediate solution (first subproblem) and to the next lower integer (second subproblem). In this case, we have to deal with two new subproblems where one more variable is fixed. The subproblems are also addressed by the above procedure and the best solution is selected. This scheme is iterated until we obtain a feasible solution that does not violate any possible contraint and where all values are integer.

As our set of basic cycle constraints, we only consider cycles with two or three nodes. In order to identify violated constraints during the B&C process, we implemented an efficient algorithm that searches for unsatisfied inequalities of type (2).

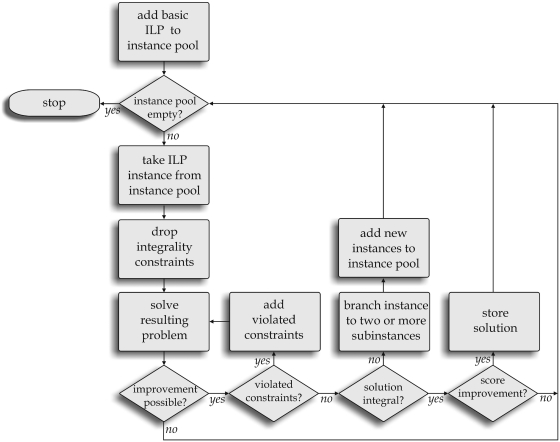
In this study, we used the ‘traditional mixed integer search’ B&C framework of CPLEX (27), version 12.1, which is freely available for academic applications. A general workflow of B&C algorithms is presented in Figure 2. For a detailed survey of B&C algorithms, the interested reader is referred to Refs (26) and (28).

Figure 2.

B&C workflow for solving the ILP. The ILP problem with only basic constraints is added to the instance pool (pool for considered ILP subproblems). After choosing one subproblem, the integrality contraints are dropped in order to solve the problem efficiently. In the case of identified violated constraints, they are added to the problem. If not, it has to be decided whether the solution is integer. If this is not the case, the current problem is subdivided into two or more subproblems depending on the branching strategy.

Visualization of the resulting subgraphs

For the visualization of the deregulated subgraphs, we use the Biological Network Analyzer (BiNA) (23), which is a Java application for the visualization of metabolic and regulatory networks. For our purpose, we implemented a plugin for BiNA, which can visualize the disease- or condition-specific subgraphs and facilitates the navigation through different network sizes k. In addition, the plugin provides the option to visualize different condition-specific networks in a union graph. If only two such networks are chosen for comparison, the edges are drawn using two different colors according to their affiliation, and common edges are painted using a third color. This way, the differences and similarities between the two studied conditions or states are graspable at a glance.

Statistical methods for the evaluation of the results

For testing the significance of a computed subgraph of size k and root node v_r, we carried out 1000 permutation tests where we permuted the scores of the network nodes and computed the best subgraph of size k with root v_r. The P-value was calculated as the number of permutations reaching an equal or better score than our original subgraph rooted in v_r divided by the number of permutations.

To compare our method to the results of standard GSA methods, we analyzed the input lists (sorted by their scores) with standard unweighted GSEA using GeneTrail (16,29). Among other functional categories already provided by GeneTrail, we also analyzed the curated gene set ‘c2.all.v2.5.symbols.gmt’ from the Molecular Signatures Database (MSigDB) (30), which contains additional gene sets from online pathway databases, publications in PubMed and knowledge of domain experts. Furthermore, we performed an over-representation analysis (ORA) of the nodes/genes of the deregulated subgraph as test set and the genes of the regulatory graph as reference set with GeneTrail.

RESULTS

To validate our B&C approach, we studied three different application scenarios that will be presented below. For all applications, we considered the KEGG human regulatory network and prepared the datasets as described in the ‘Materials and methods’ section. Preliminary tests with a broad range of sizes have shown that the most stable, significant and biologically interesting results are obtained for k ranging from 10 to 25 nodes. Hence, we will consider that range of subgraph sizes in all three applications.

Nonmalignant primary mammary epithelial cells

For a first test, we downloaded and analyzed the GSE13671 dataset (20) (Affymetrix HG-U133 Plus 2.0 microarray) from GEO (Gene Expression Omnibus) (31) that provides expression data from non-malignant primary mammary epithelial cells with and without BRCA1 mutations. We computed the fold difference for the mean of the BRCA1 mutation carriers against the mean of non-mutation carriers given the normalized and log-transformed expression values. The Affymetrix chip IDs were mapped to NCBI Gene IDs and the resulting list containing genes and corresponding scores served as input for our algorithm. As described above, we computed the most deregulated subgraphs for different subgraph sizes ranging from 10 to 25 nodes. To study the stability of the results, we considered the union of all nodes and edges that occur in at least one of the 16 optimal subgraphs. The compactness of this so-called union graph is an indicator of the stability of the identified deregulated components, i.e. the less nodes this union graph contains, the more stable are the identified core components.

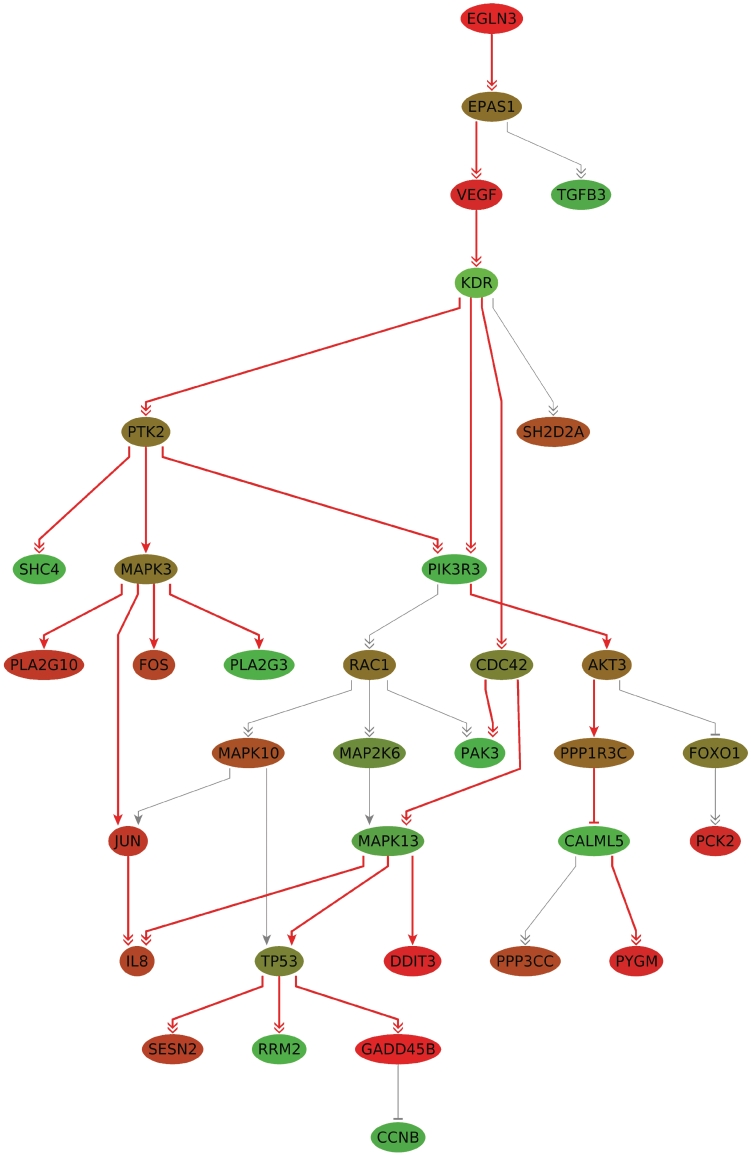
Figure 3 shows the best subgraph for 25 nodes (P < 0.001) and, additionally, the remaining nodes of the union graph as isolated vertices. The number of occurrences listed in Table 1 indicates the presence of a stable core component. This component consists of the path EGLN3 (PHD3) → EPAS1 (HIF-2α) → VEGF → KDR (VEGFR2) with the designated root node EGLN3 and, located farther downstream, the subgraph rooted in MAPK13 consisting of the nodes TP53, DDIT3, RRM2 and GADD45B.

Figure 3.

The most deregulated subgraph for BRCA1 mutation carriers against non-mutation carriers for a network size of 25 (red edges) with root node EGLN3 (P < 0.001). The nodes connected by gray edges are part of the union network of the deregulated subgraphs of size 10–25. The nodes are colored by the computed scores (fold differences), where shades of green correspond to downregulated and shades of red correspond to upregulated genes. The more intense the color, the higher the level of deregulation.

Table 1.

List of genes found in the 16 computed deregulated subgraphs of sizes 10–25 and number of occurrences for BRCA1 mutation carriers versus non-mutation carriers

Gene ID	Gene symbol	Gene description	Number of occurrences in the 16 deregulated subgraphs
7157	TP53	Tumor protein p53	16
6241	RRM2	Ribonucleotide reductase M2	16
5603	MAPK13	Mitogen-activated protein kinase 13	16
4616	GADD45B	Growth arrest and DNA damage-inducible, beta	16
1649	DDIT3	DN damage-inducible transcript 3	16
7422	VEGFA	Vascular endothelial growth factor A	16
3791	KDR	Kinase insert domain receptor (a type III receptor tyrosine kinase)	16
2034	EPAS1	Endothelial PAS domain protein 1	16
112 399	EGLN3	egl nine homolog 3 (Caenorhabditis elegans)	16
83 667	SESN2	Sestrin 2	15
998	CDC42	Cell division cycle 42 (GTP binding protein, 25 kD)	15
8503	PIK3R3	Phosphoinositide-3-kinase, regulatory subunit 3 (gamma)	14
5063	PAK3	p21 protein (Cdc42/Rac)-activated kinase 3	13
3576	IL8	Interleukin 8	11
5837	PYGM	Phosphorylase, glycogen, muscle	9
51 806	CALML5	Calmodulin-like 5	9
5507	PPP1R3C	Protein phosphatase 1, regulatory (inhibitor) subunit 3C	9
10 000	AKT3	v-akt murine thymoma viral oncogene homolog 3 (protein kinase B, gamma)	9
891	CCNB1	Cyclin B1	8
5533	PPP3CC	Protein phosphatase 3 (formerly 2B), catalytic subunit, gamma isoform	5
7043	TGFB3	Transforming growth factor, beta 3	5
3725	JUN	Jun oncogene	2
8399	PLA2G10	Phospholipase A2, group X	1
5879	RAC1	Ras-related C3 botulinum toxin substrate 1 (rho family, small GTP binding protein Rac1)	1
5608	MAP2K6	Mitogen-activated protein kinase kinase 6	1
5602	MAPK10	Mitogen-activated protein kinase 10	1
5595	MAPK3	Mitogen-activated protein kinase 3	1
5106	PCK2	Phosphoenolpyruvate carboxykinase 2 (mitochondrial)	1
50 487	PLA2G3	Phospholipase A2, group III	1
399 694	SHC4	SHC (Src homology 2 domain containing) family, member 4	1
2353	FOS	FBJ murine osteosarcoma viral oncogene homolog	1
2308	FOXO1	Forkhead box O1	1
9047	SH2D2A	SH2 domain protein 2A	1
5747	PTK2	PTK2 protein tyrosine kinase 2	1

When performing an ORA for the genes of the subgraph of size 25 as test set and the genes of the regulatory network as reference set, we find many KEGG and MSigDB pathways significantly enriched that are associated with cancer. An overview of significantly enriched pathways which cover at least four genes of the deregulated subgraph is given in Supplementary Table S2. Further elaborations on the pathways are given in the ‘Discussion’ section.

Comparison of high-grade glioma

As a second test, we analyzed the dataset GDS1815 (Affymetrix HG-U133A microarray) from GEO providing expression data of high-grade gliomas, for which additional clinical data is also available. Here, we were interested in the identification of deregulated processes that contribute to the malignancy of the brain tumors. To this end, we compared two groups of patients with strongly differing survival times. While the first group had survival times ≤40 weeks (Group 1, 12 expression profiles, average age 42 years, 12× WHO grade 4), the second group had survival times ≥300 weeks (Group 2, 12 expression profiles, average age 40 years, 9× WHO grade 3, 3× WHO grade 4). We used the independent two-tailed t-test to compute a score and a P-value for each gene. The P-values were required for the comparison of our method with two competing approaches (see below).

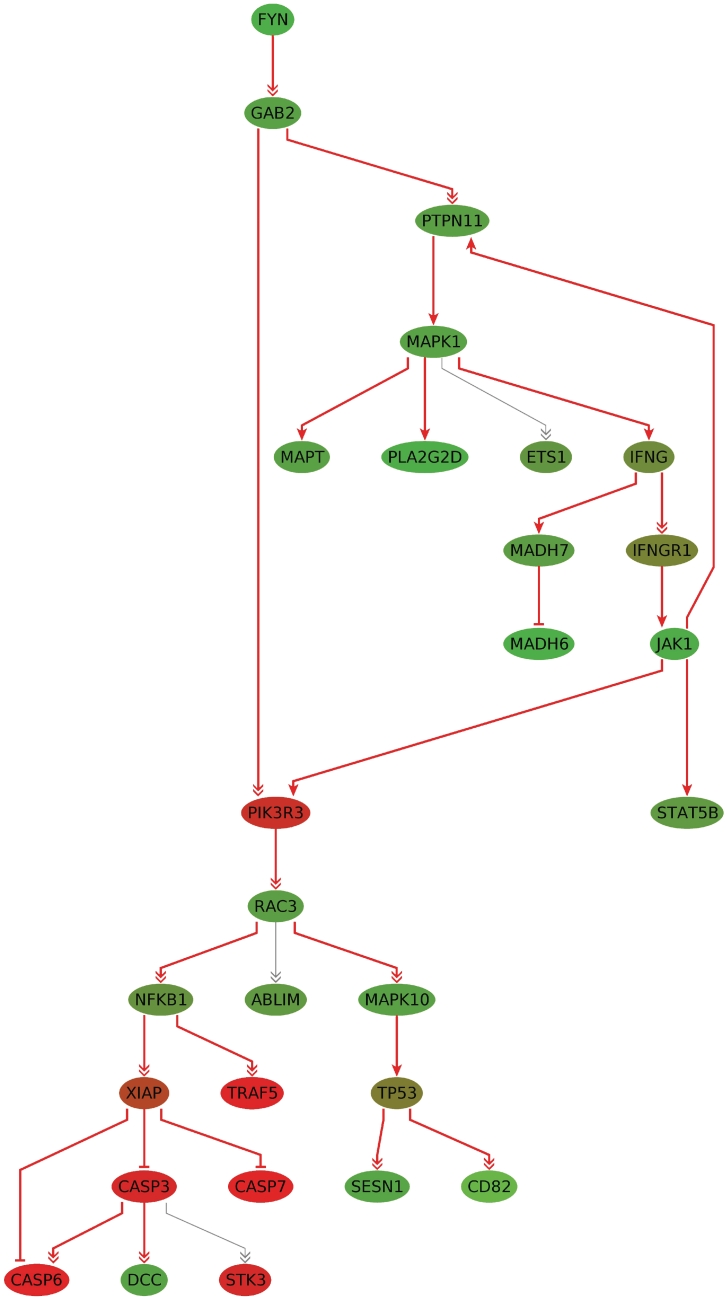
On a workstation with an Intel(R) Xeon(R) CPU (W3540, 2.93 GHz, 11 GB RAM), the calculation of the subgraphs of size 10–25 took 71 s in single thread mode. The results are again very stable, which is shown in the compactness of the union graph of size 10–25 consisting in total of 28 nodes. The subgraph of size 25 is shown in Figure 4. Many genes in this subgraph have been associated with glioma, including FYN, PIK3R3, RAC3, XIAP and several caspases. Other genes like TP53, NFKB, MAPK1 and IFNG are associated with cancer in general. An interpretation of these findings is given in ‘Discussion’ section.

Figure 4.

The subgraph of size k = 25 for the glioma dataset. The nodes connected by gray edges are part of the union network of the deregulated subgraphs of size 10–25. The nodes are colored by the computed scores (t-test test statistic values), where shades of green correspond to downregulated and shades of red correspond to upregulated genes. The more intense the color, the higher the level of deregulation.

We compared our results for this dataset with the results of the BioNet (32) implementation of the ILP-based approach by Dittrich et al. (11). A comparison with the ILP approach of Zhao et al. (10) was not possible as no software was available.

Since BioNet has been designed for undirected graphs, we could only apply it to the ‘undirected’ version of the KEGG human regulatory network. BioNet calculated an optimal subgraph of size 37 overlapping with our deregulated network of size 25 in 9 nodes (running time: 16 min). When reconsidering the original directed edges, the calculated deregulated network was not connected in our sense, i.e. not all nodes in the subgraph could be reached from the root node. This complicated the interpretation of the result. However, the subgraph of 37 nodes comprises the central component of our subgraph of size 25 consisting of the nodes FYN, GAB2, JAK1, PIK3R3, RAC3, MAPK10, TP53, SESN1 and CD82 (Supplementary Figure S1). To assess the significance of the overlap of the results of BioNet and our computed subnetwork, the hypergeometric test was applied. The chance for finding such an overlap by coincidence is <10⁻¹².

We also applied jActiveModules (version 2.23) (5) to our input graph and this dataset. A first iteration of the algorithm resulted in five networks with sizes ranging from 502 to 611 with scores from 11.354 to 11.678, which took about 90 min for the computation. The overlap with our deregulated subnetwork was between 17 and 24 nodes. We used the highest scoring network of size 573 (overlap with our subnetwork 24, score 11.678, P-value_overlap < 10⁻¹⁸) for an additional iteration, which yielded a best scoring network of size 1 with score 3.114. The second best scoring network was of size 138 and had an overlap of 17 nodes with our network. A third iteration using the latter network resulted in a best scoring network of size 65 (score 2.812) with an overlap of 16 nodes compared with our network. Another iteration on this network yielded only networks of sizes 1 or 2. Due to the differences in the subgraph sizes, a more detailed comparison of the two approaches is difficult.

Colorectal adenocarcinoma cell lines

In a third test, we analyzed gene expression data from two different colorectal adenocarcinoma cell lines (HT-29 and HCT-116). Both cell lines were treated with a cytotoxic substance and samples were taken at two different time points (8 and 24 h), untreated samples were used as control. Gene expression data for all treated and untreated samples was generated using the Affymetrix HG-U133 Plus 2.0 microarray. The raw and normalized expression data are available on our homepage (http://genetrail.bioinf.uni-sb.de/ilp). We compared the mean of the treated with the mean of untreated cell lines and computed fold changes for each comparison. Affymetrix Probeset IDs were mapped to NCBI Gene IDs and the resulting four different lists containing genes and their corresponding fold changes (scores) served as input for our algorithm. For the four resulting input lists, we determined the most deregulated subgraphs for k ranging from 10 to 25 nodes. The four obtained sets of subgraphs are again very stable. For example, in case of HCT-116, 24 h, we observed that, except for one transition, with increasing k only new nodes were added to the previous subgraph. This resulted in a union graph consisting of only 26 nodes. An overview of the genes along with their number of occurrences in the subgraphs can be found in the Supplementary Tables S3, S5, S7, S9

For the following analysis, we consider the computed subgraphs of size 25 (P < 0.001, see ‘Materials and Methods’ section). We performed an ORA with GeneTrail (29) using the subgraph's genes as test set and the regulatory graph's genes as reference set (Supplementary Tables S4, S6, S8, S10). For visual representation of the ORA results, we colored the subgraphs using the most significantly enriched regulatory pathways (Supplementary Figure S2).

When comparing these most significantly enriched regulatory pathways, the HCT-116 and the HT-29 subgraph both contain parts of the ‘TP53 signaling pathway’ at 8 h after treatment. Twenty-four hours after treatment only the subgraph of the HCT-116 cell line was significantly enriched for the ‘TP53 signaling pathway’. The components of the HT-29 subgraph showed a shift to chemokine signaling and toll-like receptor signaling.

DISCUSSION

We presented a novel ILP-based B&C approach for detecting deregulated connected subgraphs in biological networks. The optimization approach can be combined with every additive node-based scoring function that is appropriate to measure the deregulation of the corresponding genes or proteins. In this study, we used the regulatory pathways from KEGG. However, we can apply the method to any type of biological network. Using BN++ (23), we can access different data sources, e.g. regulatory network databases as KEGG (17–19) or Transpath (33) and PPI databases as DIP (34), HPRD (35), MINT (36) and IntAct (37). Only slight modifications are required to adapt the approach to undirected PPI networks or even to a combination of regulatory and PPI networks. In this case, each undirected edge has to be replaced by two directed edges. However, in the undirected case the concept of the root node does not apply, since every node is reachable from any node in the connected undirected network. In this case, our algorithm would only compute the most deregulated connected part of the input network. Since our algorithm was primarily designed for directed networks, we did not try applying our algorithm to the undirected case, so the effectiveness of our algorithm in this case is unproven. However, we are convinced that taking the direction of regulatory networks into account is one of the main advantages of our algorithm. Most other available algorithms neglect the direction of the input network, whereas our algorithm tries to use the additional information to identify the causes and the molecular key players of the deregulation.

The identification of patterns of pathway deregulation is a crucial task in differential network analysis. Moreover, the detection of the molecular key players that trigger the observed differences is a major challenge. With our connectivity model, we do not only identify the most deregulated subgraph, but also a root node which may be the cause for the deregulation as we have demonstrated with the first example. We applied our method to expression profiles of non-malignant primary mammary epithelial cells (PMECs) isolated from BRCA1 mutation carriers and women without BRCA1 mutations. BRCA1 germline mutations are associated with a predisposition for developing breast cancer. The cumulative breast cancer risk by 70 years of age in BRCA1 mutation carriers has been estimated to be 65% (38). Although familial breast cancers have been intensely researched, the exact processes influenced by the BRCA1 mutation which eventually result in the development of breast cancer are still elusive. Burga and co-workers found that the non-malignant PMECs from BRCA1 mutation carriers contained a subpopulation of progenitor cells, which showed an altered proliferation and differentiation in cell culture (20). In concordance to these morphologic observations, the comparison of the expression profiles of the PMECs with and without BRCA1 mutations revealed an upregulation of the EGFR pathway, which they discussed as possible cause for the altered growth and differentiation properties. Our study confirms these results as we also find EGF and p53 signaling pathway significantly enriched in our deregulated subgraph components (Supplementary Table S1). Additionally, we find significantly enriched pathways and categories that are associated with hypoxia and oxidative stress, as e.g. ‘Hypoxia review’, ‘Hypoxia normal up’ and ‘Oxstress breastca up’ from MSigDB. The designated root node of our deregulated network is the gene PHD3 (EGLN3), which is known to play an important role in hypoxia. Yan et al. (39) found that the occurrence of a HIF-1α-positive phenotype and a PHD3-negative phenotype is correlated with BRCA1 tumors. However, in this study we find that PHD3 is overexpressed in the non-malignant PMECs with BRCA1 mutations. Ginouves et al. discussed overactivation of PHDs during chronic hypoxia and its effects on HIFα (40). They found that PHDs are the key enzymes triggering a feedback mechanism, which leads to a desensitization of HIF1/2α and protects cells against necrotic cell death. Additionally, the GADD (growth arrest and DNA damage-inducible) genes (GADD45B, DDIT3) found in our deregulated subgraph are involved in cell cycle arrest, repair mechanisms and apoptosis. An increased expression of these genes has also been described in studies examining cells in stressful conditions (41,42). The genes GADD45B and DDIT3 (GADD153) are also overexpressed in the BRCA1 mutation carrier expression data. This is another indication that the cells seem to be in a stressful state, which may have origins in the processes involved in the hypoxia regulation. A study of Dai et al. (43) discussed the role of oxidative stress in dependence of obesity as a possible cause for increased breast cancer risk. Regarding cell cultures of PMECs, as in our case, this factor should admittedly be of no relevance. We hypothesize that the described different growth properties of the PMECs with BRCA1 mutations are responsible for a disturbance in O₂ homeostasis, so that this may induce oxidative stress. Additionally, the activation of the aforementioned stress proteins can result in avoidance of necrosis or apoptosis and in this way lead to an increased overall survival of cells with genetic alterations. If the cells in risk of cancerous transformation show a different growth behavior that results in oxidative stress, targeting the genes involved in these processes to induce cell death may be a possible starting point for preventing the outbreak of the disease. The idea of using, e.g. PHDs, HIF-1α or its downstream targets as a potential therapeutic strategy has been suggested by Ginouves et al. and Yan et al., respectively.

To compare the results of our algorithm to a standard GSEA, we subjected the input list containing the genes sorted by the absolute values of their fold differences to the GSEA variant implemented in GeneTrail. The analysis revealed many significantly deregulated pathways (P < 0.05, FDR adjusted), among others the KEGG pathways ‘cell cycle’, ‘DNA replication’ and ‘mismatch repair’. When regarding the MSigDB gene sets, we find the breast cancer related categories ‘BRCA ER neg’, ‘BRCA ER pos’, ‘Breast cancer estrogen signaling’ and ‘Breast ductal carcinoma genes’, as well as the hypoxia related category ‘Hypoxia reg up’ significantly deregulated. Interestingly, in this analysis neither the p53 signaling pathway nor the EGF signaling pathway was significantly deregulated.

Taken together, the non-malignant mammary epithelial cells with BRCA1 mutations exhibit many properties that are known from breast cancer. Our study indicates that the cells are in a stressful state potentially originated from the processes involved in the regulation of long-term oxidative stress. Moreover, it seems that it is a very thin line between a cancerous outcome and non-cancerous phenotype for BRCA1 mutated mammary epithelial cells considering the accumulated deregulation affecting multiple signaling pathways visible in our computed subgraphs. Finally, the GSEA analysis also reported hypoxia as a significant finding. However, since the GSEA results are presented as a long list of significant categories the relevance of hypoxia might have been underestimated. Thus, we can conclude that the causative chains of interactions and reactions in the deregulated subgraphs provide more structured information that facilitate the interpretation of the results.

In our second example comprising high-grade glioma expression data, the root node of the computed optimal subgraph was the gene FYN encoding a member of the Src kinase family that is a downstream effector of EGFR signaling, enhancing invasion and tumor cell survival in vivo (44). Silencing of this gene by promotor hypermethylation has been shown in gliomas and might be implicated in the initiation of glioma from neural stem cells (45). Src kinases including FYN are often activated in glioblastoma and silencing of the kinases with dasatinib combined with a monoclonal anti-EGFR antibodies significantly increased survival of xenograft glioblastoma mouse models (44). Another gene of the subgraph, PIK3R3, encodes a regulatory subunit of phosphoinositide 3-kinase and has been shown to be overexpressed in highly proliferating glioblastomas, while knock-down of PIK3R3 expression in cell lines strongly inhibited glioblastoma neurosphere growth (46). Overexpression of RAC3 might be associated with aggressive and invasive growth in glioblastoma (47,48). The inhibitor of apoptosis XIAP that inhibits its downstream targets CASP3 and CASP7 are also part of the subgraph. XIAP is widely expressed in glioblastoma and might be implicated in radio resistance of glioblastoma (49), while expression of CASP3 is generally low in glioblastoma suggesting a low apoptotic activity in these tumors (50). CASP7 is thought to be relevant for the apoptosis/necrosis balance in glioma, with knockdown of CASP7 resulting in an anti-apoptotic and pro-necrotic response that is often seen in glioblastoma (51). Other genes in the optimal subgraph include well-known cancer-associated genes like TP53, NFKB, MAPK1 and IFNG.

As a further application, we employed our algorithm to a data set generated at Roche Pharma Research providing the differential expression of two colorectal adenocarcinoma cell lines HCT-116 and HT-29 that were treated with a cytotoxic substance. After treatment with the substance, the cell lines were classified into weak responders and strong responders according to the EC50 value. This value reflects the dosage at which 50% of all cells die off. In this experiment, we classified all cell lines with a value <10 μM as strong responder, whereas weak responder cell lines showed an EC50 value >70 μM. According to in-house experiments, HT-29 shows a weak response (71 μM) after treatment with the compound, in contrast to HCT-116 (5 μM), which is a strong responder (H. Burtscher, unpublished results). In addition, it is known that HT-29 carries TP53 mutations, whereas HCT-116 is TP53 wildtype [see IARC TP53 DB (52), Roche Cancer Genome Database (53)]. Taken together, one could hypothesize that TP53 mutation status within these cell lines is a marker of response. However, when performing experiments with several different weak responder and strong responder cell lines, no correlation between TP53 mutation status and response status was detected.

Our new method confirms these results: at the 8-h time point, TP53 signaling is significantly enriched in the subgraph of both cell lines. This changes after 24 h where the TP53 signaling pathway is only significantly enriched in HCT-116 but not in HT-29 cell line. We hypothesize that, since HT-29 is a non-responder, other regulatory processes than those involved in apoptosis might become more important for the cell. In detail, we detect a shift of significant regulatory processes to chemokine signaling and toll-like receptor signaling with genes triggering the immune response.

Our new B&C approach and the one given by Dittrich et al. (11) differ in several important aspects. The key difference between the two approaches is the connectivity model. While the approach of Dittrich et al. has been designed for undirected graphs, the new formulation takes the directions of the reactions and interactions explicitly into account in order to analyze the signal propagation within the network, aiming especially at the identification of molecular key players. While Dittrich et al. transform the problem into a prize-collecting Steiner tree problem, we work directly on the original problem. Furthermore, we use a purely node-based formulation where edges do not appear as variables. Hence, we expect a better performance when the input graphs are large and contain many edges. While our approach considers subgraphs of a predefined size k, the network score in Ref. (11) controls the size of the resulting networks. Due to its efficiency, our algorithm enables the user to determine subgraphs for a broad range of sizes k. Furthermore, we observed that the incremental comparison and visualization of the resulting subgraphs (k → k + 1) does not only provide essential information about the stability of the results, but also on signal propagation spreading from the deregulated core components. Moreover, it is possible to get rid of the pre-defined size k if required or desired for a given application. This can be achieved since our algorithm works for any node-based scoring function, in particular also for the network score used by Dittrich et al. Hence, it suffices to select a suitable scoring function and to remove the size constraint (1). The comparison of our approach with the one by Dittrich et al. (11) on the glioma dataset showed that both approaches find similar subgraphs; however, our approach provides more structured information that facilitates the identification of molecular key players and the interpretation of the results.

In summary, the results of the three experiments provide convincing evidence that the novel B&C approach opens new avenues for the elucidation of pathogenic mechanisms and for the detection of molecular key players and putative target molecules. Since the approach is applicable for both directed and undirected graphs and makes no strong assumptions concerning the scoring function, it is suited for a broad range of application scenarios. One such scenario is the extension of our algorithm for the integration of miRNA data by adding additional nodes for miRNAs and edges for miRNA targets in our network, and by devising scoring functions suitable for capturing the miRNA–mRNA relationships. Due to its efficiency, our algorithm enables the user to scan a wide range of subgraph sizes in reasonable time facilitating the stability analysis of the obtained results. Furthermore, we showed that the application of our algorithm to previously analyzed data can yield new insights that may contribute to a better understanding of diseases.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Methods, Supplementary Figures 1 and 2, Supplementary Tables 1–10 and Supplementary References [5–14,17–19,23,25,33–37,54–61].

FUNDING

This work was supported by the DFG Priority Program SPP 1335: LE 952/3-1, KA 812/13-1. Funding for open access charge: DFG Priority Program SPP 1335.

Conflict of interest statement. None declared.