Binding Affinity Prediction for Ligands and Receptors Forming Tautomers and Ionization Species: Inhibition of Mitogen-Activated Protein Kinase-Activated Protein Kinase 2 (MK2)

Abstract

Treatment of ionization and tautomerism of ligands and receptors is one of the unresolved issues in structure-based prediction of binding affinities. Our solution utilizes the thermodynamic master equation, expressing the experimentally observed association constant as the sum of products, each valid for a specific ligand–receptor species pair, consisting of the association microconstant and the fractions of the involved ligand and receptor species. The microconstants are characterized by structure-based simulations, which are run for individual species pairs. Here we incorporated the multispecies approach into the QM/MM linear response method and used it for structural correlation of published inhibition data on mitogen-activated protein kinase (MAPK)-activated protein kinase (MK2) by 66 benzothiophene and pyrrolopyridine analogues, forming up to five tautomers and seven ionization species under experimental conditions. Extensive cross-validation showed that the resulting models were stable and predictive. Inclusion of all tautomers and ionization ligand species was essential: the explained variance increased to 90% from 66% for the single-species model.

Introduction

Quantitative prediction of binding affinities of ligands interacting with target macromolecules is one of the most important tasks for lead optimization and other procedures in computational medicinal chemistry. The majority of approved drugs and drug candidates contain tautomerism-prone heteroaromatic ring systems and heteroatom-rich substructures¹ as well as one or more ionizing groups.^2,3 Components of the receptor binding sites, e.g., several amino acid residues,^4,5 cofactors (porphyrin,^6,7 NAD⁺, biotin,³ and others), and nucleobases,⁸⁻¹⁰ are also prone to ionization and tautomerism under physiological conditions.

Structural differences of tautomer and ionization species lead to varying interactions with the binding site and cause the dependence of overall affinity on several factors. In addition to pH and temperature, the influence of medium polarity on tautomer and ionization equilibria plays a role because the interactions with the receptors may happen in an aqueous medium (blood/plasma, extra- and intracellular fluids) or in a nonpolar medium such as the bilayer core of the cell membrane.

The time scale of establishing the tautomeric equilibria depends on the nature of broken and created bonds. Tautomers that interchange by CH bond cleavage and formation can often be isolated because their half-lives (t_1/2) are measured in hours thanks to high (>30 kcal/mol) interconversion energy barriers. The CH-to-NH, −OH, and −SH tautomer conversions have much lower energy barriers (∼20 kcal/mol), and their t_1/2 values are in the range of a second.¹¹ For the NH-to-OH and OH-to-OH tautomerism, the rates are much faster: some keto–enol tautomers convert on the picosecond time scale.¹² The fast tautomer interconversions of the last two categories facilitate the description of the ligand binding to macromolecules because the tautomer fractions remain constant during the binding process and are fully characterized by the equilibrium constants, eliminating the need to consider the kinetics of the tautomer interconversion process.

Treatment of tautomers presents a challenge to methods utilizing classical force fields because of the increased occurrence of less common structures for which the parameters may not be readily available. Along with this nuisance, the static charge distribution and other approximations of the classical force fields contribute to the increasing use of combined quantum mechanics/molecular mechanics (QM/MM) methods in structure-based binding affinity predictions.^13,14 The application of hybrid QM/MM methods alleviates several issues in the classical description of biomolecular interactions and enables their more accurate description at a reasonable computational expense.¹⁵ We previously reported an extension of the linear response method¹⁶⁻²² by using the QM/MM energies of the time-averaged structures after MD simulation.^23,24 The QM/MM-LR approach was successfully applied to the affinity prediction of inhibitor binding to Zn-dependent matrix metalloproteinases (MMPs).¹² The model was capable of distinguishing subtle differences in the binding sites of two related MMPs and provide intricate selectivity clues²⁵ by including the phenomena that are out of reach of classical force fields, such as the coordination bonds made by the studied hydroxamates with the binding-site zinc and the proton transfer from the hydroxamate OH group to carboxyl of a neighboring Glu side chain in the binding site.

Treatment of multiple species resulting from ionization and tautomerism is a challenge for current force-field based simulations in spite of the progress in the area.²⁶ Keeping in mind the advantages the QM/MM techniques offer for the treatment of tautomers and polarizing interactions, we wanted to examine the ability of the QM/MM-LR approach to describe binding of ligands involving tautomer and ionization equilibria. Suitable chemotypes, forming several tautomers and ionization species in aqueous media under physiological conditions, were found among the inhibitors of mitogen-activated protein kinase (MAPK)-activated protein kinase 2 (MK2) for the complexes of which a number of X-ray structures were available.²⁷⁻³¹

MK2 has two isoforms, α and β, which are produced by alternative splicing with 400 and 370 residues, respectively.³¹ The enzyme consists of N-terminal proline-rich region (residues 10–44), catalytic region with DFG motif (residues 51–325), and C-terminal autoinhibitory region (residues 328–364). The C-terminal region includes a nuclear export signal (NES) of hydrophobic residues 356–368 and a nuclear localization signal (NLS) containing basic residues 373–389. The isoform β lacks the NLS region. During the presence of the inactive complex of p38α and MK2 in the nucleus, the C-terminal NLS is functional and the NES is masked. Upon stress stimulation, upstream kinases like MAPK kinase-6 activate p38, which in turn phosphorylates MK2, unmasking the NES, and this active complex translocates to cytoplasm. This cascade of events leads to coexport of activated p38 from the nucleus to cytoplasm.

MK2 is a serine/threonine protein kinase regulating, by a post-transcriptional mechanism, biosynthesis of tumor necrosis factor α (TNFα) that is overproduced in inflammatory diseases such as rheumatoid arthritis and inflammatory bowel disease. MK2 knockout mice showed reduced expression of TNFα when stimulated with lipopolysaccharide (LPS) and were resistant to developing disease in arthritis models.³² Mice that lack MK2 show increased stress resistance and survive LPS-induced endotoxic shock,³³ thanks to significant reduction in the production of TNFα. Unlike p38 MAP kinase inhibition leading to several serious side effects,³⁴ MK2 knockout mice are healthy and have a normal phenotype. The role of MK2 and the benefits of MK2 inhibition in other inflammatory diseases such as Alzheimer’s disease, atherosclerosis, and cancer are being actively investigated.³⁵

This study focuses on characterization of structural and energetic determinants of MK2 inhibitor binding involving multispecies equilibria using the newly developed MS-QM/MM-LR approach. The approach is applicable to binding predictions of speciated small molecules to speciated macromolecules, which are of interest in several areas of pure and applied chemistry.

Results and Discussion

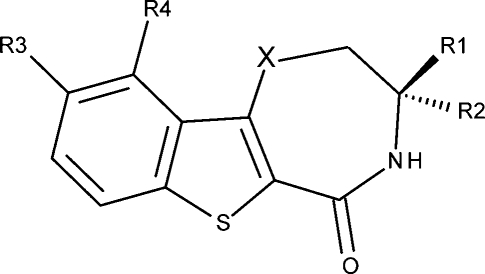
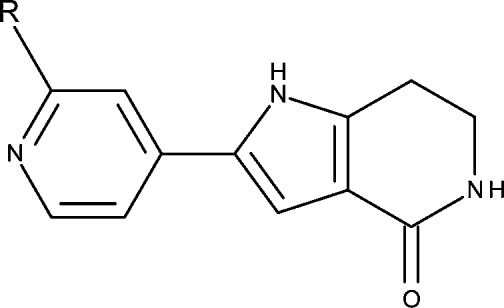
The structures, tautomer and species, and inhibitory activities of the studied 66 MK2 inhibitors,²⁷⁻²⁹ analogues of benzothiophene (benzothienodiazepinones, except 6 and 7) and pyrrolopyridine, are summarized in Tables 1 and 2, respectively. Under physiological conditions, the compounds exhibit ionization as well as prototropic and annular tautomerism: they form up to five different skeleton tautomers, with some tautomers creating two to four ionization species (Schemes 1 and 2), occasionally thanks to the ionization centers in the side moieties R (Tables 1 and 2). All potential tautomers within the two series are formed by the shifts of hydrogen between C and N, C and O, and N and O (Schemes 1 and 2), so the tautomer equilibria in an aqueous solution are expected to be established practically instantaneously.

Table 1. Benzothiophene Analogues: Structures, Considered Tautomers and Species, and MK2 Inhibition IC₅₀ Values (M).^28,29.

						considered		log(1/IC50)
ligand no.	X	R1	R2	R3	R4	tautomers	species	exp	calcd
1	NH	H	H	OCH3	H	T1,T2	S1,S5,S7	6.745	6.739
2	NH	CH3	H	OCH3	H	T1,T2	S1,S5,S7	7.398	7.635
3	NH	H	CH3	OCH3	H	T1,T2	S1,S5,S7	6.523	6.713
4	NH	(CH2)2CH3	H	OCH3	H	T1,T2	S1,S5,S7	5.818	5.486
5	NH	CH2OH	H	OCH3	H	T1,T2,T5	S1,S5,S7,S11	7.854	7.446
6	S	H	H	OCH3	H	T1,T3	S1,S9	5.963	5.547
7	CH2	H	H	OCH3	H	T1,T3	S1,S9	6.301	6.281
8	NH	CH2NH2	H	OCH3	H	T1,T2	S1,S2,S5,S6	8.301	8.436
9	NH	CH2NHCH2CH3	H	OCH3	H	T1,T2	S1,S2,S5,S6	6.244	6.021
10	NH	CH2NH(CH2)2CH3	H	OCH3	H	T1,T2	S1,S2,S5,S6	6.347	6.621
11	NH	CH2NHCH2Pha	H	OCH3	H	T1,T2,T5	S1,S2,S5,S6,S12	6.244	6.418
12	NH	CH2N(CH3)CH2Ph	H	OCH3	H	T1,T2,T5	S1,S2,S5–S7,S12	5.719	6.074
13	NH	CH3	H	OH	H	T1,T2	S1,S2,S5,S6–S8	6.721	6.944
14	NH	CH3	H	OCH2(3-OCH3-Ph)	H	T1,T2	S1,S5,S7	6.959	7.022
15	NH	CH3	H	OCH2-c-C3H5	H	T1,T2	S1,S5,S7	5.879	5.874
16	NH	CH3	H	O(CH2)2OCH3	H	T1,T2	S1,S5,S7	6.569	6.769
17	NH	CH3	H	OCH2CH(CH3)2	H	T1,T2	S1,S5,S7	6.398	6.238
18	NH	CH3	H	OCH2COOCH3	H	T1,T2	S1,S5,S7	7.523	7.212
19	NH	CH3	H	OCH2-c-C6H11	H	T1,T2	S1,S5,S7	5.463	5.593
20	NH	CH3	H	O–CH=CHb		T1,T2	S1,S5,S7	7.796	7.775
21	NH	CH3	H	O–CH2–CH2		T1,T2	S1,S5,S7	7.553	7.593
22	NH	CH3	H	N=CH–CH=CH		T1,T2,T4	S1,S5,S7,S10	9.000	8.549
23	NH	CH3	H	OC(Ph)=CH		T1,T2	S1,S5,S7	6.824	6.801
24	NH	CH3	H	N=C(Cl)-CH=CH		T1,T2,T4	S1,S5,S7,S10	8.699	8.474
25	NH	CH3	H	N=C(Ph)-CH=CH		T1,T2,T4	S1,S5,S7,S10	8.046	7.758
26	NH	CH3	H	N=C(4-Py)-CH=CHc		T1,T2,T4	S1,S5–S7,S10	7.854	7.967
27	NH	CH3	H	N=C(3-Py)-CH=CH		T1,T2,T4	S1,S5–S7,S10	8.301	7.705
28	NH	CH3	H	N=C(5-Pm)-CH=CHd		T1,T2,T4	S1,S5,S7,S10	7.638	7.356
29	NH	CH3	H	N=C(2-OCH3-Ph)-CH=CH		T1,T2	S1,S5,S7	7.699	7.517
30	NH	CH3	H	N=C(3-OCH3-Ph)-CH=CH		T1,T2,T4	S1,S5,S7,S10	7.387	7.199
31	NH	CH3	H	N=C(2-F-Ph)-CH=CH		T1,T2,T4	S1,S5,S7,S10	7.854	7.705
32	NH	CH3	H	N=C(2-CH3-Ph)-CH=CH		T1,T2,T4	S1,S5,S7,S10	7.523	7.771
33	NH	CH3	H	N=C(4-CH3-3-Py)-CH=CH		T1,T2,T4	S1,S2,S5–S7,S10	8.301	8.265
34	NH	CH2N-Tpe	H	OCH3	H	T1,T2	S1,S2,S5,S6	<4.699	4.879
35	NH	CH2N-Mof	H	OCH3	H	T1,T2,T5	S1,S2,S5,S7,S11	<4.699	4.812

^aPh: phenyl.

^bR3 and R4 join the phenyl ring to form cyclic derivatives in ligands 20–33.

^cPy: pyridyl.

^dPm: pyrimidinyl.

^eTp: tetrahydropyrrolyl.

^fMo: morpholinyl.

Table 2. Pyrrolopyridine Analogues: Structures, Considered Species,^a and MK2 Enzyme Inhibition IC₅₀ Values (M)²⁷.

			log(1/IC50)
ligand no.	R	considered species	exp	calcd
36	H	S1,S3,S5	6.767	6.561
37	Phb	S1,S3,S5	7.180	7.520
38	4-Pyc	S1,S2,S3,S5	7.252	7.339
39	3-Py	S1,S3,S5	7.319	7.486
40	3-Thd	S1,S3,S5	7.119	7.550
41	2-Npe	S1,S3,S5	7.284	6.934
42	2-Btf	S1,S3,S5	7.523	7.347
43	3-Qg	S1,S3,S5	8.071	7.994
44	2-OH-Ph	S1,S2,S3–S5	6.387	6.920
45	3-OH-Ph	S1,S2,S3–S5	7.602	7.829
46	4-OH-Ph	S1,S2,S3–S5	7.678	7.669
47	2-Cl-Ph	S1,S3,S5	6.218	6.430
48	3-Cl-Ph	S1,S3,S5	7.432	7.747
49	4-Cl-Ph	S1,S3,S5	7.495	7.568
50	2-F-Ph	S1,S3,S5	6.900	7.165
51	3-F-Ph	S1,S3,S5	7.523	7.659
52	4-F-Ph	S1,S3,S5	7.301	7.422
53	4-CF3-Ph	S1,S3,S5	7.149	7.181
54	4-COCH3-Ph	S1,S3,S5	7.292	7.228
55	4-OCH3-Ph	S1,S3,S5	7.260	7.205
56	4-NH2-Ph	S1,S3,S5	7.387	7.340
57	4-[CONH-c-C5H9]-Ph	S1,S3,S5	8.097	8.153
58	4-[CONH-c-C6H11]-Ph	S1,S3,S5	7.770	7.662
59	4-[CONHCH2Ph]-Ph	S1,S3,S5	8.097	7.786
60	4-[CONH(CH2)2Ph]-Ph	S1,S3,S5	7.337	7.508
61	4-[CONH(CH3)CH2Ph]-Ph	S1,S3,S5	7.252	7.309
62	Cl	S1,S3,S5	6.216	6.270
63	5-Pmh	S1,S3,S5	7.081	7.115
64	4-CN-Ph	S1,S3,S5	7.208	7.218
65	4-COOH-Ph	S2,S3,S5	7.658	7.683
66	4-[CONH-c-C3H5]-Ph	S1,S3,S5	7.824	7.816

^aAll compounds present as tautomers T1 and T2.

^bPhenyl.

^cPyridinyl.

^dThienyl.

^eNaphthyl (marked as 3-Np in the original publication).

^fBenzothienyl.

^gQuinolinyl.

^hPyrimidinyl.

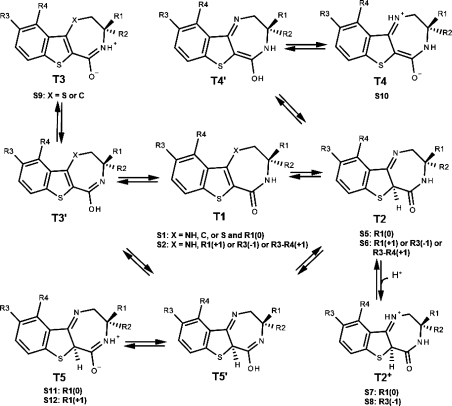
Scheme 1. Tautomer and Ionization Equilibria of Studied Benzothiophene Analogues (Table 1).

Species, present in at least 0.01% fraction under experimental conditions, are labeled S1–S12 and their parent tautomers are labeled as T1–T5. The neutral forms of the T3, T4, and T5 neutral-zwitterion pairs, marked with a prime, are present in negligible fractions and are listed only as intermediates in the formation of more abundant zwitterionic counterparts. The protonated form of T2 is shown as T2+. The charges of substituent groups are given in brackets. The R3–R4 substituent group for S2/T1 and S6/T2 refers to the cyclic derivatives (20–33, Table 1). Species S3 and S4 are not present in this series.

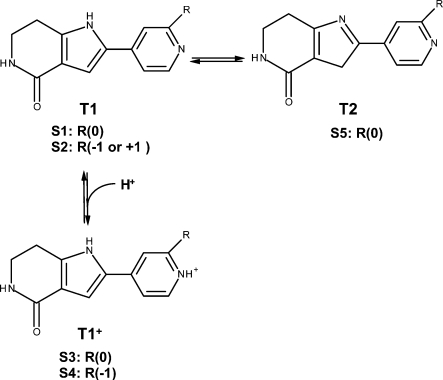
Scheme 2. Tautomer and Ionization Equilibria of the Studied Pyrrolopyridine Analogues (Table 2), Showing the Species Present in at Least 0.01% Fraction under Experimental Conditions.

Tautomers are labeled as T1–T2 and species are labeled S1–S5. Protonated form of T1 is shown as T1+. The charges of substituent groups are given in brackets. Species S1, S2, and S5 are similar to those in Scheme 1 in the approximate position of charged atoms with regard to the CO-NH in T1. Species S6–S12 are not present in this series.

Ligand Fractions of Tautomers and Ionization Species

Ligand fractions of tautomers and ionization species in aqueous solution were estimated for water under the conditions of experiments (pH 7.5 and 30 °C), using the SPARC³⁶ online calculator. The fractions of individual tautomers were calculated from the relative abundances of all possible tautomers at equilibrium (Schemes 1 and 2). Ionization estimates were only performed for tautomers with at least 0.01% fraction to determine the fraction of each species. The resulting 233 tautomers (T1–T5) and species (S1–S12) for the studied 66 compounds were grouped and numbered as shown in Schemes 1 and 2. The species classification is based on the ionization state as well as on the parent tautomer. As a result, the species with the same number may have different overall charges as indicated in Schemes 1 and 2.

The neutral-zwitterion tautomer pairs T3, T4, and T5 are mainly present as zwitterions, with the proton transferred from the hydroxyl in position 1 to N in position 2 or 5 (atom X in the Table 1 structure). Charged skeletons are produced by external protonation, as seen in benzothiophene tautomer T2⁺ (Scheme 1) and pyrrolopyridine tautomer T1⁺, with the protonated N in position 5 or in the pyridine ring, respectively. Further ionizable groups are present in the side chains R1, R3, R4, or cyclic substructures R3–R4. Combinations of the skeleton tautomers and the side chains ionized to varying degrees give rise to altogether 12 species.

While both series are dominated mainly by tautomers T1 and/or T2, the presence of other tautomers cannot be neglected. The formation of T2 and T5 results in the loss of planarity of thiophene ring forming a new chiral center, which exhibited stronger interactions with the MK2 enzyme when set in S configuration in all MD simulations (described below). An overview of speciation of individual compounds is given in Figure 1, with all details listed in Table S4 in Supporting Information.

Figure 1.

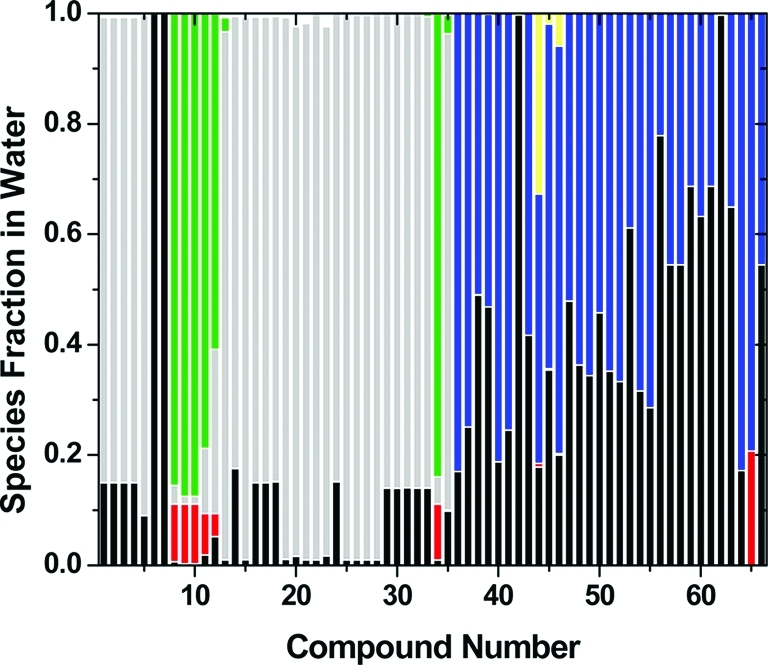
Species fractions of the studied benzothiophenes (1–35, Table 1) and pyrrolopyridines (36–66, Table 2) in water under experimental conditions: species S1/T1, S2/T1, S3/T1, S4/T1, S5/T2, and S6/T2 (Schemes 1 and 2) are shown in black, red, blue, yellow, gray, and green, respectively. Only major species (>10% in at least one compound) are shown.

The majority of the benzothiophene analogues (Table 1 and Figure 1) do not ionize in water under experimental conditions. For 26 of 35 compounds, species 5/tautomer 2 (S5/T2) is the predominant species. Compounds 6 and 7 are mainly present as S1/T1. Only compounds 8–12 and 34 are mostly available as ionized S6/T2 and S2/T1.

All pyrrolopyridine analogues (Table 2 and Figure 1) are present mainly as T1 in water. While neutral species S1 dominates (>70%) for compounds 42, 56, and 62 and ionized species S3 for compounds 36, 37, 40, 41, 46, 55, 64, and 65, most compounds share preferences for both species 1 and 3. Compound 65 with carboxyl group substituent is always ionized and present as both species S2 and S3. Compound 44 also exhibits preference for neutral species S4 in addition to species S1 and S3.

Protonation States of Ionizable Protein Residues

Protonation of ionizable residues of MK2 was determined by pK_a calculations using the PROPKA 2.0 web server³⁷ at the experimental conditions (pH 7.5 and 30 °C). This empirical structure-based approach includes desolvation effects and intramolecular interactions such as H-bonds and charge–charge interactions. The pK_a values for ionizable residues in the binding site (Figure 2 below), Glu139 (pK_a = 1.88), Asp142 (2.51), Asp207 (1.24), and Lys93 (12.83), differ from the pH 7.5 of experiment by 5 or more logarithmic units, indicating that the binding site has just one ionization state in fraction exceeding 0.01%, with the side chain carboxyl groups of both Glu and Asp residues deprotonated and the side chain ε-amino group of Lys93 protonated. No tautomerization is expected for the binding site residues.

Figure 2.

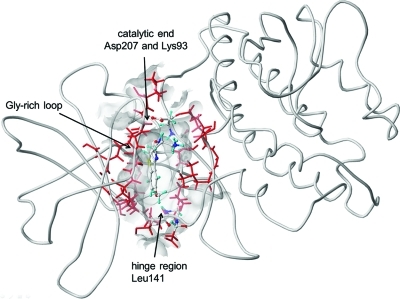
Time-averaged structure of MK2 with bound compound 8 (Table 1) used in step 4. The protein is shown as C_α-trace with the binding site indicated as transparent surface of the binding site residues Leu70, Gly71, Leu72, Gly73, Ile74, Ala91, Leu92, Lys93, Met138, Glu139, Cys140, Leu141, Asp142, Asn191, Leu192, Leu193, Thr206, and Asp207. The key residues and the ligand, shown in atom-type-colored ball and stick representation and the other binding site residues represented as red sticks are included in QM and optimized MM regions of the QM/MM geometry optimization, respectively (step 2). The ligand and all binding site residues were included in the flexible region in FlexiDock docking (step 1) and the QM-region in the single-point QM/MM energy calculation (step 4).

Multispecies Binding Equilibria

Individual ligand (L) and receptor (R) species present in the solution differ in structures of some fragments and, consequently, the binding event results in different structures of the complexes, which have different association microconstants. For the receptor, only the ionization or tautomer species of the fragments, which either directly participate in the binding or are in a sufficient proximity of the site to affect the binding, will differ in the association microconstant and need to be considered.

The mutually exclusive 1:1 binding of multiple ligand species (total number l) to a macromolecule receptor site species (total number s) is illustrated in eq 1 for the ith ligand species.

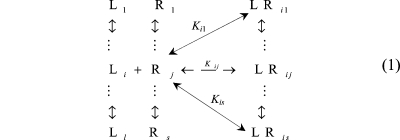1

The microconstants K_ij characterizing affinities of the l × s ligand–receptor complex species are defined, for the ith ligand species bound to the jth receptor species, as

2

The association microconstants are the relevant quantities for the correlation with structure. The measured equilibrium constant K of the ligand, however, contains the total concentration of the ligand–receptor complexes without distinguishing between complexes differing in interacting species. To express K as a function of K_ijs, a series of rearrangements needs to be made, as shown in eq 3: (1) the total bound concentration, [LR], is given as the sum of concentration of the l × s complex species, to get the third term; (2) in the numerator of the third term, each summand is formally multiplied by [L_i][R_j]/[L_i][R_j] and, in this way, the fractions of each ligand species, f_i = [L_i]/[L], and each receptor species, f_j = [R_j]/[R], are introduced, as shown in the fourth term; (3) finally, the microconstants K_ij are incorporated using their definition in eq 2.

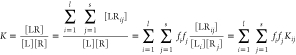3

The fractions f_i and f_j depend on the medium and remain constant as long as the medium is not changing. The test media and intra/extracellular body fluids are buffered, so the key property, the pH value, remains invariant and the fractions f_i and f_j can usually be calculated before optimization.

For ligand ionization, the expressions for the fractions f_i of the ith species can be derived from the definition of the ionization constants. In the case of two or more ionization groups, attention needs to be paid to the actual macroscopic pK_a values. If the pK_a values are closer than 3–4 units, the ionization tendencies of the two ionizable groups are not clearly separated, and mixed species may occur. Consequently, such pK_a values are no longer equal to the ionization microconstants, and multiple species with the same charge (e.g., neutral molecules and zwitterions as two species with the net zero charge, such as the neutral-zwitterion tautomer pairs T3–T5 in Scheme 1) can be present for a given pH value of the medium.

For the receptors, the equilibria can be affected by through-space proximity to other groups. Specialized techniques have been developed to estimate the ionization constants of individual ionizable groups³⁷⁻⁴⁷ and the equilibrium constants for tautomers.⁵

The prevalence of the ith bound species for a ligand can be calculated using the sum of all its complexes with the receptor species:

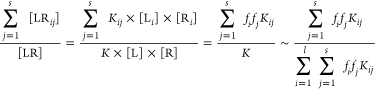4

The numerator and denominator come from eqs 2 and 3, respectively. The third quasi-equality in eq 4 ensures that the sum of prevalences for all l species of a ligand equals unity. The prevalence of the receptor species for the given ligand is calculated in a similar way; just the summations in the numerators of eq 4 would run through all l ligand species instead of the s receptor species.

Multispecies Inhibitor Studies

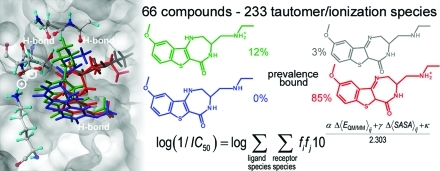
In the single-species QM/MM-LR approach, a linear combination of the QM/MM energy term and the solvent-accessible surface area (SASA) term is correlated with enzyme inhibition potency, which may be given as log(1/IC₅₀) values, where IC₅₀ is the concentration of an inhibitor that decreases the rate of an enzyme-catalyzed reaction by 50%. For reversible and competitive enzyme inhibition, the direct proportionality between IC₅₀ and ligand–receptor association constant is given by the Cheng–Prusoff equation.⁴⁸ For the multispecies correlation, which uses the total association constant K as the dependent variable, each of the species microconstants K_ij in eq 3 needs to be expressed as an exponential with the exponent equal to the linear combination of the ligand–protein QM/MM interaction energy term and the SASA term and eq 3 needs to be logarithmized. Assuming that the regression coefficients α, γ, and κ maintain the same values for each pair of ligand and receptor species, the inclusion of multiple species does not increase the number of the regression coefficients. The MS-QM/MM-LR correlation equation is then

5

The term ⟨ΔE_QM/MM⟩ denotes the binding energy defined as the difference between the QM/MM energies of the complex and those of the unbound interaction partners, all calculated for the time-averaged structures from MD simulations. The change in SASA upon binding is defined analogously. The QM/MM term in eq 5 replaced the van der Waals and electrostatic energy terms in the classical LR approach, which were scaled by coefficients α and β, respectively.¹⁶⁻²²

The QM/MM and SASA terms of 233 tautomers and species of 66 ligands complexed with MK2 enzyme were calculated using a slight modification of our previously published four-tier approach.^23,24 The protocol consists of (1) flexible docking with the poses selected based on the docking score, (2) QM/MM geometry optimization of the docked complexes, (3) MD simulation of the geometry optimized structures, solvated with explicit TIP3P water molecules,⁵⁵ and (4) for the time-averaged structures from step 3, calculation of the single-point QM/MM interaction energy term and the SASA term. The two terms were correlated with the enzyme inhibition potencies using eq 5.

Computational Protocol

In step 1 (docking), the studied inhibitors were docked into the recently published³⁰ X-ray structure of MK2 in active conformation, bound to a 3-aminopyrazole derivative (PDB code 3KGA(30)) with 2.55 Å resolution, taken from the Protein Data Bank.⁴⁹ MK2 features the β-sheet dominated N-terminal lobe and a purely α-helical C-terminal lobe, enclosing the ATP-binding site for which the inhibitors compete. The binding site (Figure 2) is lined by conserved glycine-rich motif GXGXXG of residues 71–76 and the hinge region, extending from the gate-keeper residue Met138 and including residues 139–142. The interaction of conserved Lys93 with the conserved Glu104 from helix C is considered a hallmark of the active conformation of protein kinases.⁵⁰ Docking was performed using the FlexiDock module from SYBYL-X. Two available X-ray structures, one for each series (for ligands 33(29) and 50(27)), were used to guide prepositioning of studied compounds. In addition to ligands, rotatable bonds of side chains of binding site residues were allowed to move during the docking procedure. This step was critical in selecting the optimal binding mode with the highest FlexiDock score, especially for more flexible compounds. The deviations between the optimal binding modes (poses) of individual tautomers/species of the same compounds were significant. The respective heavy-atom rmsd values varied between 0.55 and 10.95 Å and are summarized in Table S1 in Supporting Information. To speed up the QM/MM convergence, docked complexes were briefly minimized using Generalized Born implicit solvent method in Amber 10.

In step 2 (QM/MM optimization), geometries of minimized protein–ligand complexes were further optimized by the ONIOM method,^51,52 a hybrid QM/MM method available in Gaussian 09.⁵³ Ligands and key binding site components (backbone atoms of Cys140, Leu141, and Asp142; whole residues of Thr206 and Asp207) were included in the QM region, and the rest of the system was defined as the MM region. The ligand and binding site residues were allowed to move during geometry optimization, and the rest of the system was frozen (Figure 2). No tautomer/species conversion was observed during the geometry optimization procedure.

In step 3 (MD simulations), the entire hydrated and neutralized QM/MM-optimized complexes were heated and subjected to 1 ns MD simulation in Amber 10. Analysis of the trajectories for energy terms (potential, kinetic, and total energies), density, volume, temperature, pressure, and rmsd values of C_α atoms revealed that that the secondary and tertiary structure of the ligand–receptor complex remained stable throughout the simulation and all studied ligand–receptor complexes attained equilibrium within the 1 ns simulation period. For several compounds, 20 ns MD simulations were run, showing no major differences to the 1 ns trajectories.

The MD trajectories were also analyzed to track critical intermolecular interactions, including water bridges that were involved in ligand binding (see below). For all complexes, the conserved Lys93 was found to be interacting with a conserved Glu104 from helix C, indicating the active conformation of protein kinases.⁵⁰ The time-averaged structures from the final 900 ps of MD simulations were calculated using the ptraj program in AmberTools,⁵⁴ keeping only 100 water molecules closest to the ligands and stripping off the remaining water molecules and counterions used for neutralizing the system. The resulting structures were briefly minimized to remove unnatural features.

Step 4 (single-point QM/MM energy and SASA calculations) was performed for time-averaged structures resulting from step 3. The QM region consisted of ligands, binding site residues, and water molecule for complexes, in the cases when water-mediated interactions were observed. The heavy-atom rmsd values between the time-averaged structures of individual tautomers/species varied between 1.30 and 11.73 Å and are summarized in Table S2 in Supporting Information.

For steps 1–4, the computations for each ligand–receptor species took on average 15–20 min, 40–60 h, 200–240 h, and 12–24 h of single-processor time, respectively. For the 233 complexes, plus free interaction partners, this study used about ∼130000 h of CPU time.

Multispecies 3D-QSAR Correlation

The MK2 enzyme inhibition potencies, given as logarithmized 1/IC₅₀ values, were correlated with the QM/MM interaction terms and the SASA terms, both calculated in step 4. The nonlinear regression model (eq 5), with s = 1 as only one ionization/tautomer state was predicted for the binding site, was optimized using the Solver⁵⁵ software.

Contributions of individual steps of the calculation protocol to the correlation were examined, and the results are summarized in Table 3. The use of the FlexiDock scores in place of the QM/MM energies in eq 5 resulted in no correlation (r² = 0.002). The QM/MM energies and SASA, calculated from the geometry optimization step 2, gave r² = 0.202. The use of van der Waals and electrostatic energy terms from the MD simulation in the MS-LR fashion in eq 5, as summarized in step 3, slightly improved the correlation (r² = 0.353), but the signs of the coefficients α and β for the van der Waals and electrostatic energy terms, respectively, were incorrect. The full MS-QM/MM-LR treatment (eq 5) was necessary to achieve an agreement between experimental and calculated inhibitory activities, with the correct signs of the optimized coefficients α and γ (r² = 0.906).

Table 3. Linear Response Correlations Using eq 5 for Individual Steps: Optimized Coefficients and Descriptive Statistical Indices^a.

step	α × 10–3(mol/kcal)b	β × 10–4(mol/kcal)c	γ × 10–3(1/Å2)d	κ	r2	RMSE
1. docking	0.0878 ± 0.115			7.292 ± 0.238	0.002	0.741
2. QM/MM optimization	–0.3868 ± 21.25		–7.354 ± 46.51	4.107 ± 27.44	0.202	0.663
3. MD simulation	10.47 ± 54.29	5.709 ± 62.32	–11.61 ± 86.56	5.417 ± 38.22	0.353	0.597
4. single-point QM/MM	–1.326 ± 0.591		–7.761 ± 2.261	1.160 ± 0.358	0.906	0.228

^aThe squared correlation coefficient (r²) and the root-mean-square error (RMSE).

^bScales the QM/MM energy term (eq 5) in rows 2 and 4, and the vdW energy term in row 3.

^cScales the electrostatic energy term.

^dScales the SASA term.

An analysis of the importance of tautomeric and ionization species for the correlation is summarized in Table 4. The simplest model (row 1) uses only the QM/MM and SASA terms for tautomer 1 (no ionization species are included), in eq 5, which thus became a standard, one-mode QM/MM-LR equation and exhibits a comparatively weak correlation (r² = 0.662). The addition of ionization species for tautomer 1 (row 2) lead to a better performance (r² = 0.734). The consideration of all tautomers and no ionization species (row 3) brought further improvement (r² = 0.839). The model including all tautomers and all ionization species (row 4) provided the best results (r² = 0.906). The comparison of experimental and calculated inhibitory potencies for different species compositions (Table 4), shown in Figure 3, also confirms the need for inclusion of all tautomers and ionization species.

Table 4. The MS-QM/MM-LR Correlations (eq 5) for Different Tautomer and Species Composition: Optimized Coefficients and Statistical Indices.

							LOOc		MC-LGOd
tautomer	species	α × 10–3(mol/kcal)a	γ × 10–3(1/Å2)b	κ	r2	RMSE	q2	RMSE	q2	RMSE
single	single	–1.212 ± 1.289	–8.985 ± 8.451	1.151 ± 0.896	0.662	0.431	0.617	0.458	0.616	0.459
single	multi	–1.291 ± 1.026	–8.664 ± 7.211	1.000 ± 0.758	0.734	0.382	0.690	0.412	0.691	0.411
multi	single	–1.338 ± 0.801	–8.334 ± 5.002	0.960 ± 0.507	0.839	0.297	0.819	0.315	0.819	0.315
multi	multi	–1.326 ± 0.591	–7.761 ± 2.261	1.160 ± 0.358	0.906	0.228	0.897	0.237	0.894	0.241

^aScales the QM/MM energy term.

^bScales the SASA term.

^cLeave-one-out cross-validation: the results reported as RMSE and the squared predictive correlation coefficient (q²).

^dMonte Carlo leave-group-out cross-validation: the compounds were randomly divided into 7 groups, and each group of ∼9 compounds was used once as a test set; the procedure was repeated 10 times.

Figure 3.

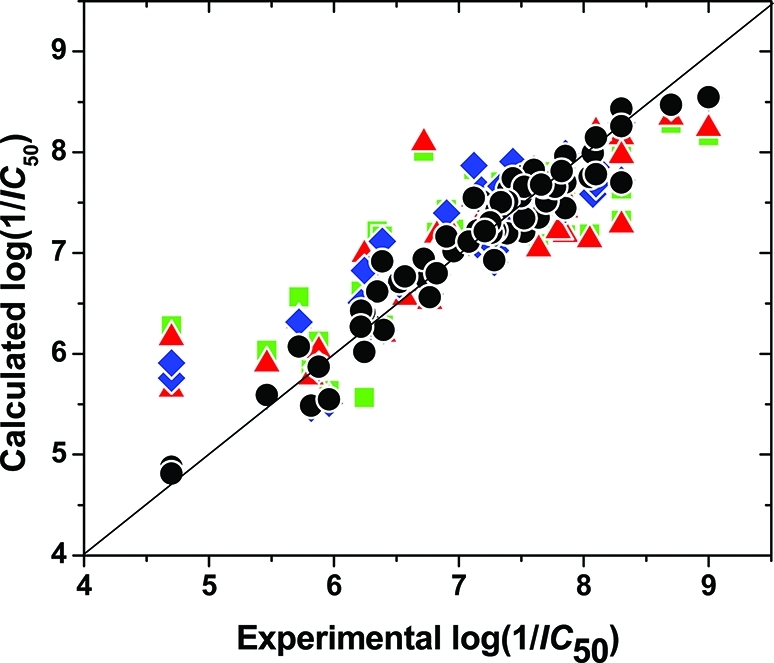
Correlations between experimental and calculated MK2 inhibition potencies for studied compounds are shown for all models: single-tautomer, single-species (green squares), single-tautomer, multispecies (red triangles), multitautomer, single-species (blue diamonds), and multitautomer, multispecies (black circles).

The agreement between the model and experiment is very satisfactory, especially for the complete setup (row 4). The LOO-cross-validation and, more importantly, the rigorous MC-LGO cross-validation confirmed that all models are stable, exhibit no overfitting, and have adequate predictive power because the values of the predictive indices RMSE and q² are similar to those of the descriptive indices RMSE and r². Interestingly, the optimized values of the coefficients α and γ did not vary significantly with the addition of species, which is also a sign of extraordinary stability of the models. As an additional model validation attempt, we performed the correlations with swapped values of the fractions f_i of individual tautomers/species in water. The numbers of tautomers/species differ but are equal to three for most compounds (Tables 1 and 2). Therefore, we swapped the f_i values in the correlation eq 5 for the first three species (the f_i values for compounds 6 and 7, having only two species, were always exchanged). The descriptive abilities of the correlations using eq 5 were characterized by r² = 0.906 for the correct (1–2–3) order of the f_i values, r² = 0.831 for the order 3–2–1 (the f_i values for species 1 and 3 were exchanged), r² = 0.807 for the 2–1–3 order, r² = 0.629 for the 1–3–2 order, r² = 0.702 for the 2–3–1 order, and 0.673 for the 3–2–1 order. The swapping of some f_i values, although providing only limited randomization, clearly leads to deterioration of the correlation.

For compounds 34 and 35 with semiquantitative enzyme inhibitory potencies (Table 1), which were excluded from the model fitting process, predictions were made using all models. Activities of both compounds were predicted to be very close to the observed limits using the complete model (Table 4, line 4) although not below them (Figure 3).

Contribution of the QM/MM energy to the correlation with inhibitory potency is greater than that of the SASA term. Coefficient γ associated with SASA term is approximately 7 times larger than that of the QM/MM term; however, when the overall contributions, i.e., the products of coefficients and the variables, are considered, the values of the QM/MM contributions are ∼10 times larger than those of the SASA term. There is no cross-correlation between the QM/MM energy and SASA terms (r² = −0.334).

Standard deviations of inhibitory activities (IC₅₀) were only published for the series 2 compounds (36–66, Table 2) and are listed in Table S3 in Supporting Information. No information was published about the error distribution, so a detailed comparison of model performance with respect to experimental errors cannot be made. However, we can use the standard deviations as the estimates of experimental variance. On the logarithmic scale, which was used in the correlation, the average error interval for log(1/IC₅₀) is 0.220 (Supporting Information Table S3), with the average log(1/IC₅₀) located asymmetrically in this interval. The average error interval, which includes both positive and negative deviations, is smaller than RMSE = 0.228 for the best prediction (step 4 in Table 3), indicating that the complexity of the model is adequate: the model is not overly detailed and does not describe experimental errors.

Critical MK2–Inhibitor Interactions

Important interactions between MK2 and inhibitors were tracked by the analysis of MD trajectories of 233 complexes from the production phase.

H-Bond Interactions

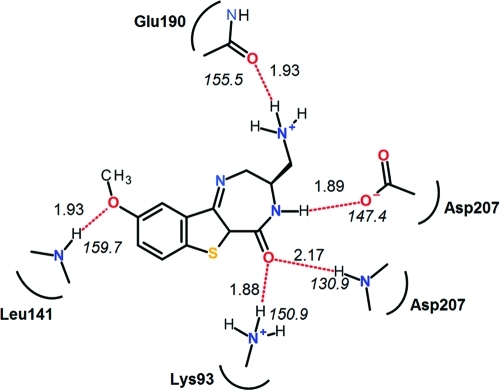
H-bond interactions, both at the catalytic end (Asp207 and Lys93) and in the hinge region (Leu141), shown in Figure 2, are typical for all compounds exhibiting higher inhibitory potencies. The amino and carbonyl groups in the lactam ring make H-bond interactions with catalytic Asp/Lys pairs and methoxy oxygen (Table 1) or pyridinyl nitrogen (Table 2) groups interact with the backbone NH group of Leu141 in hinge region (Figure 4). The magnitudes of the average bond lengths (<2 Å) and angles (>150°, i.e., not deviating much from the ideal 180° magnitude) indicate strong H-bond interactions that seem to be critical for enzyme inhibition.

Figure 4.

Interaction map of compound 8 (Table 1) as species 5/tautomer 2 (Scheme 1) in the binding site of MK2. Nitrogen, oxygen, and sulfur atoms are printed in blue, red, and yellow colors, respectively. H-Bond interactions are drawn in red color, and the bond lengths and bond angles (in italics) for the time-averaged structure are shown.

Water-Mediated Interactions

Water-mediated interactions were observed in many studied ligands bound to MK2. The protonated N atom in position X (Table 1) of the lactam ring in tautomers T2 and/or T4 of compounds 23 and 33 makes the water-mediated H-bond interaction with the backbone carbonyl oxygen of Glu190. Additionally, in compound 33, a water molecule creates an H-bonded bridge between the protonated N atom of pyridine ring and the carboxyl group of the Asp142 side chain in the hinge region. Water-mediated interactions were also observed for tautomer T2 of compounds 5, 8, 9, 11, 17, and 19, as well as for tautomers T2 and T4 of compounds 25, 26, and 29 (Table 1), in which the protonated N atom in the X position of the lactam ring forms H-bond interaction with the backbone carbonyl oxygen of Leu70 in the glycine-rich loop through a water molecule. Pyrrolopyridines (Table 2) binding as S3/T1 possess protonated pyridine ring, which interacts either directly with Glu139 backbone carbonyl oxygen (compounds 40, 41, 43–46, 49, 52, and 57) or with Leu141 backbone NH group through a water-mediated interaction (compounds 36, 38, 39, 56, 58, 59, and 60).

Hydrophobic Interactions

Hydrophobic interactions with the hinge region (Figure 2) are formed by several substructures in the part of the molecules that is opposite to the lactam ring. In benzothiophene series (Table 1), the rings attached in positions R₃–R₄ make compounds 22–33 relatively potent inhibitors. On the contrary, the absence of the aryl ring attached to the pyridyl ring decreases the potency of pyrrolopyridines 36 and 62 (Table 2). However, the structural dependence is more complex: substituents in the o-position of the aryl ring attached to the pyridyl ring negatively affect potency for pyrrolopyridines 44, 47, and 49 (Table 2). The side chain atoms of residue Leu70 (glycine-rich loop, Figure 2) and Leu193 make hydrophobic interactions from both sides of the binding site with many compounds having aryl ring substituents positioned near the hinge region of the MK2 enzyme.

Prevalences of Bound Tautomers and Species

The prevalences, as predicted by eq 4 with the K_ij values calculated from eq 5 with optimized coefficients (last lines of Tables 3or 4), are summarized in Tables S4 and S5 in Supporting Information. The majority (28 of 35) of benzothiophenes (1–5, 12–33, and 35; Table 1) preferably bind as neutral species 5/tautomer 2 (Scheme 1). Several benzothiophenes (1–4, 12–14, 17, 18, 24, 29, 30, and 35) also exhibit some fraction of bound S1/T1 species. Only compounds 6 and 7 bind exclusively as S1/T1 (Scheme 1). Compounds 8–10 and 34 prefer to bind as protonated S6/T2 thanks to the presence of amino substituent in the lactam ring. Compound 11 shows almost equal binding preferences for S2/T1, S5/T2, and S6/T2. Compounds 9 and 11 bind (∼10%) in S2/T1 form as well.

Pyrrolopyridine analogues (Table 2, Scheme 2) mostly bind in neutral form as S1/T1 (42, 50, 60, and 62) or protonized as S3/T1 (36, 41, 43, 45, 46, 49, 54–57, 64, and 65) or both (37–40, 43, 47, 48, 51–53, 58, 59, 61, 63, and 66). Compound 44 binds as both S3/T1 and S4/T1 species, the latter having the phenyl ring hydroxyl group in the deprotonated form. The predominantly bound tautomer 1 has the planar lactam ring attached to aromatic pyrrole ring. All compounds from this series make favorable interactions with the Asp/Lys catalytic pair, which may explain their comparatively narrow potency range.

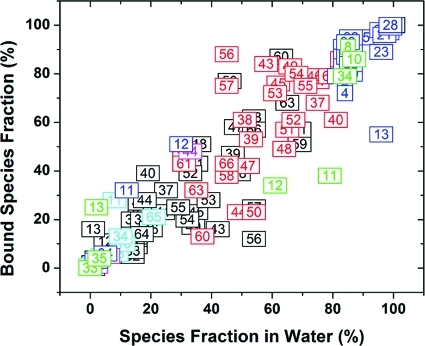
The fractions of free vs bound tautomers and species for all studied inhibitors are plotted in Figure 5. For the majority of the compounds, the prevalent species in solution are the bound species as well. Nevertheless, the correlation is rather loose and there are several noticeable differences between binding prevalences and the fractions in solution.

Figure 5.

A comparison of predicted bound species prevalences and species fractions in the aqueous solution for studied ligands (the numbers correspond to the compound numbers in Tables 1 and 2). Species 1–6 (Schemes 1 and 2) are referred to by black, cyan, red, magenta, blue, and green colors, respectively. Only major species (at least one compound with >10%) are shown here.

For example, compounds 11 and 12 (Table 1, Scheme 1) are mainly present as protonated species S6 in solution (>60%) but they are bound as nonionized species S5. Compound 13 binds to a significant extent as species S1, S5, and S6, although only species S5 is prevalent in solution. Compound 50 (Table 2, Scheme 2) is present as both species S1 and S3 in solution but shows a higher preference for species S1 while binding.The situation is opposite for compounds 43, 56, and 57, which prefer to bind as species S3, even though they have about equal concentrations of species S1 and S3 in solution.

Conclusions

The QM/MM linear response method was extended for multiple ligand and receptor species, resulting from tautomerism and ionization, using rigorous thermodynamic principles, to fill a gap in the armory of the computational methods for structure-based, ensemble-utilizing, and empirically calibrated prediction of binding affinities. Ionization and tautomerism, as widespread phenomena among the drug-like molecules, need to be included in the methods for prediction of binding affinities to bring the models closer to reality. Our approach is based on performing the simulations individually for each species pair and combining the results of these simulations in a correlation equation that is calibrated using the experimental data. Interestingly, inclusion of multiple species does not increase the number of optimized coefficients, at least in the studied case: the same regression coefficients could be used for all species without a detrimental impact on the quality of the fit. The developed MS-QM/MM LR method was applied to a set of 66 MK2 inhibitors forming up to five tautomers and seven ionization species under the experimental conditions. The treatment of multiple ligand species significantly improved the correlation between experimental inhibition potencies and the QM/MM interaction energy and SASA terms for the time-averaged structures from MD simulations. The structural and energetic information obtained from the time-averaged structures highlights the critical interactions necessary for optimal enzyme inhibition. Strength of the H-bond interactions of ligands with the backbone amide group of Leu141 in the hinge region, and carboxyl and ε-amino groups in the side chains of catalytic Asp207 and Lys93, respectively, significantly affect the inhibition potency. Additional interactions with backbone carbonyl group of Glu190 and glycine-rich loop made by some potent inhibitors represent hints for further improvements in potency. If future studies, preferably dealing with the experimentally observed prevalences of bound species, confirm the utility of the MS-QM/MM-LR approach, it may become a welcome addition to the methods for lead optimization in drug design.

Experimental Section

Data Set

The MK2 inhibitory activities for 66 benzothiophene and pyrrolopyridine derivatives were reported by Anderson et al.²⁷⁻²⁹ The X-ray structures of the MK2 complexes with a benzothiophene analogue 33 (Table 1), a pyrrolopyridine analogue 50 (Table 2), and an untested 3-aminopyrazole derivative with the PDB⁴⁹ codes 3FYJ,²⁹2P3G,²⁷ and 3KGA,³⁰ respectively, facilitated the use of structure-based techniques. The structure 3FYJ was preferred to 3FYK(29) because its ligand is larger and provides more clues for docking larger benzothiophene analogues. The inhibitors compete with ATP for binding to MK2. The isoeffective concentrations (IC₅₀) were determined in the assay, monitoring the amount of HSP-peptide (KKKALSRQLSVAA) that was phosphorylated by MK2 after 30 min incubation at pH 7.5 and 30 °C.²⁷⁻²⁹ Experimental errors were only given for the pyrrolopyridine series²⁷ and are listed in Table S3 in Supporting Information.

Tautomerism and Ionization of Ligands

The enzyme inhibitory IC₅₀ values of the studied ligands were determined at pH 7.5 and 30 °C. The relative abundances of all possible tautomers at equilibrium were estimated under the conditions of the experiment. Subsequently, ionization estimates were performed only for tautomer having the fraction of at least 0.01% to determine the fraction of individual species as a function of pH. In both cases, the SPARC web server³⁶ was used.

Ionization and Tautomerism of Binding Site Residues

The protonation states of ionizable protein residues were estimated by pK_a calculations using the PROPKA 2.0 web server³⁷ at the experimental conditions (pH 7.5 and 30 °C). There was one dominant ionization state of the binding site (Figure 2) predicted, with Glu and Asp side chain carboxyl groups deprotonated and Lys side chain ε-amino groups protonated. No tautomerism was expected for the binding site residues (Figure 2).

Ligand Preparation

Ligand structures were built in Sybyl-X 1.1.⁵⁶ Geometry optimization and Mulliken charge⁵⁷ calculations were done in Jaguar⁵⁸ (Schrodinger) using the DFT/B3LYP method⁵⁹ with basis set 6-31G**.^60,61 Charge and spin multiplicity were entered manually for different protonation states.

Protein Preparation

The recently published X-ray structure of MK2 in active conformation bound to a 3-aminopyrazole derivative (PDB⁴⁹ code 3KGA(30)) with 2.55 Å resolution is of better quality than other available structures (3FYJ,²⁹3FYK,²⁹2P3G²⁷), as documented by resolution (2.55 Å vs >3.5 Å) and distribution of φ–ψ dihedrals (90% vs <70%) in the most favored regions. The 3KGA structure was modified with Biopolymer structure preparation tool in Sybyl-X:⁵⁶ the bound ligand and water molecules were removed, heavy atoms missing from residues were added, and the N-terminal and the C-terminal residues were capped with N-acetyl and N-methyl amide groups. Protonation types were set for His (ε-N protonated), Glu (negatively charged), and Lys (positively charged) residues. Hydrogen atoms were added, and charges were loaded using the AMBER 7 FF02⁶² force field. The resulting structure was briefly (100 steps) minimized only for H-atoms by the Powell conjugate gradient method in Sybyl-X.⁵⁶

Flexible Protein–Ligand Docking

Docking of ligands into MK2 binding site was performed using the FlexiDock program in Sybyl-X.⁵⁶ FlexiDock deploys a genetic alghorithm-based optimization in torsional space for both the protein binding site (rotatable bonds in side chains) and the ligand. The fitness function uses a subset of the Tripos force field: the van der Waals, electrostatic, torsional, and constraint energy terms. The number of rotatable bonds in the binding site residues (see Figure 2) of the protein was up to 57 and that of ligands ranged from 1 to 8. The number of generations used varied from 35000 to 60000 depending upon the total number of rotatable bonds, satisfying the rule-of-thumb recommendation of 500–1000 generations per each rotatable bond in protein and ligand plus six. The site-point scoring feature was activated in FlexiDock by defining the H-bond interaction partners in the protein and ligands: the backbone NH of Leu141 in the hinge region of MK2 as H-bond donor, and, as acceptor, the first atom, if it was O or N, in substituent R₃ of benzothiophenes (Table 1) or the N atom in the pyridyl ring of pyrrolopyridines (Table 2). The available X-ray structures for the data set series, with the PDB⁴⁹ codes 3FYJ (compound 33 In Table 1 below)²⁹ and 2P3G (compound 50 in Table 2 below),²⁷ were used to aid the prepositioning of benzothiophene and pyrrolopyridine analogues, respectively, in the binding site prior to docking. The protein parts of these structures were aligned with that of the 3KGA structure by homology in Biopolymer module in Sybyl-X. The remaining ligands from both the series were superimposed using the fit atoms method. The best structures were chosen based on the FlexiDock scores and visual inspection. As tautomers with nonplanar lactam ring for most benzothiophenes (Table 1) did not always make catalytic end H-bond interactions, the H-bond distances to catalytic residues Asp207 and Lys93 were not considered mandatory for the pose selection.

The difference in the docked poses (conformations) of tautomers/species of individual compounds were reported as the heavy-atom rmsd values (Table S1 in Supporting Information), calculated using Chimera.⁶³ For all compounds, species 1 served as reference structure except for compound 65, where species 2 was used for this purpose. The same approach was used to calculate the heavy-atom rmsd values for the time-averaged ligand geometries of tautomers/species after MD simulation (steps 3/4), which are summarized in Table S2 in Supporting Information.

QM/MM Geometry Optimization

Docked protein–ligand complexes were briefly (1000 steps) optimized to remove any bad contacts by modified Generalized Born implicit solvent model in Amber 10. Optimization started with steepest descent method to quickly remove the largest strains and was switched after 100 cycles to the conjugate gradient method with root-mean-square of 1 cal/(mol × Å) as the convergence criterion for fine optimization close to the energy minimum. The nonbonded cutoff was set to 16.0 Å. Input files for ONIOM calculations^51,52 in Gaussian 09⁵³ were prepared in GaussView 5.0.⁶⁴ Ligands and selected binding site components (entire residues of Thr206 and Asp207, backbone atoms of Cys140, Leu141, and Asp142) were included in the QM region, and the rest of the system was defined as the MM region. The partitioning of the system in ONIOM was based on published recommendations:⁶⁵ the QM/MM cuts were always made between the C–C bonds and at least three bonds away from any potential interacting atoms. In the MM region, the remaining binding site residues (Figure 2) were allowed to move during geometry optimization and the rest of the system was frozen. Charges were manually entered for both QM (along with spin multiplicity) and MM regions. The defined QM and MM regions were treated with DFT/B3LYP functional⁵⁹ using 6-31G(d,p) basis set^60,61 and Amber ff99SB force field,⁶⁶ respectively. Electronic embedding option was activated during calculations.

MD Simulation

Molecular dynamics simulations were performed using Amber 10 package⁶⁷ under isothermal/isobaric (NPT) conditions with Amber ff99SB⁶⁶ and general Amber (GAFF)⁶⁸ force fields for protein and ligand molecules, respectively.

Structure Preparation

The Leap program from Antechamber tools (AmberTools 1.4)⁵⁴ was used to prepare the parameter/topology (prmtop) and input coordinate (inpcrd) files using the Mulliken charges⁵⁷ from the QM/MM optimization, which were kept for protein–ligand complexes during MD simulations. For each system, protein–ligand complexes and unbound ligands were simulated separately. The unbound protein was simulated only once. The net charge of the protein–ligand complexes varied from +3 to +6 depending upon the overall charge of the ligand and was neutralized by adding Cl^– ions at positions of high positive electron potential around the complexes. The system was immersed in a truncated octahedral box of pre-equilibrated TIP3P⁶⁹ water molecules⁵⁵ in the way that no atoms in the protein–ligand complexes were closer than 8 Å to any of the sides of the water box. The counterions and solvent molecules were briefly minimized for 1000 steps to remove any bad contacts with the complexes, whereby the protein and ligands were position-restrained using force constant of 500 kcal/(mol × Å²).

Heating, Equilibration, and Production Phases

To allow the readjustment of solvent molecules to the potential field of the ligand–receptor complex, the solvent equilibration step was performed in three stages. During the first heating phase, MD simulation was carried out for 10 ps, with constant volume periodic boundaries with an initial temperature of 0 K, allowing to heat up to 100 K. The second heating phase was performed for 20 ps under constant pressure periodic boundaries with an average pressure of 1 atm. Isotropic position scaling was used to maintain the pressure, and a relaxation time of 2 ps was used. The system was allowed to heat up from the initial temperature 100 K to the final temperature 300 K. The final solvent equilibration step was performed for 50 ps under constant pressure periodic boundary conditions as mentioned above. The Langevin dynamics was used in all stages to control the temperature using a collision frequency of 1.0 ps^–1. During these three stages, the protein–ligand complexes were position-restrained with a force constant of 10 kcal/(mol × Å²). The final production phase with the entire system was carried out under isothermal/isobaric conditions for 1 ns including 100 ps equilibration phase. The SHAKE algorithm⁷⁰ was used to constrain bonds involving hydrogen, allowing time step of 2 fs, for a total of 500000 steps. The trajectory file was written for every 100 steps, resulting in 5000 frames. The cutoff was set to 10 Å in all steps.

Tracking H-Bond and Water-Mediated Interactions.

MD trajectory analysis for H-bond and water-mediated interactions for 233 complexes from the production phase was performed using the ptraj program in AmberTools 1.4.⁵⁴ The default cutoff values for distance (3.5 Å) and angle (no value) were chosen. The following pairwise interactions were monitored: (1) the backbone NH of Leu141 in the hinge region of MK2 as H-bond donor, and, as H-bond acceptor, the first atom, if it was O or N, in substituent R₃ of benzothiophenes (Table 1) or the N atom in the pyridyl ring of pyrrolopyridines (Table 2), (2) Asp207 carboxyl oxygen atoms and the NH group of the six- or seven-membered lactam ring of ligands, and (3) the O atom of the lactam ring and the amino group of the Lys93 side chain. To keep track of important water-mediated interactions, “solvent” keywords solventneighbor (value = 6), solventdonor (WAT O), and solventacceptor (WAT O H1 and WAT O H2) were specified. The solventneighbor value specifies the maximum number of possible interactions per a given donor or acceptor.

Time-Averaged Structures

Time-averaged structures were calculated from 4000 trajectory frames (final 900 ps) of the production phase of the MD simulation using the ptraj program in AmberTools 1.4.⁵⁴ The hundred water molecules closest to the ligands were kept for all complexes, and the remaining waters and ions were stripped. The structures were briefly minimized to relieve conflicts, resulting in structures with close-to-standard bond length and angles and the dihedrals representing the ensemble.

Single Point QM/MM Energy Calculations

The time-averaged structures from MD simulations were used for single point QM/MM energy calculation in ONIOM^51,52 using DFT/B3LYP functional⁵⁹ method with 6-31G(d,p) basis set^60,61 for QM region and Amber ff99SB⁶⁶ force field for MM region, respectively. Electronic embedding option was activated during calculations. The QM region consisted of ligands, binding site residues (Figure 2), and a water molecule for complexes, where water-mediated interactions were observed. The binding energy term ⟨ΔE_QM/MM⟩ term was calculated as the difference between the QM/MM energies of the complex and those of the unbound interaction partners.

SASA Term Calculation

The solvent accessible surface area (SASA) terms for time-averaged structures of protein–ligand complexes and unbound interaction partners were calculated using the program Naccess,⁷¹ which implements the Lee and Richards algorithm.⁷² The default values (probe radius 1.4 Å; z-slices 0.05 Å; van der Waals radii) were used in the calculations. The burial of solvent accessible surface area upon protein–ligand binding was calculated as the difference between the SASAs of the complex and those of unbound interaction partners.

Regression and Cross-Validation

The coefficient values in the model (eq 5) were optimized by nonlinear regression analysis in the Premium Solver Platform.⁵⁵ The stability and predictive power of the model was tested by the Monte Carlo leave-group-out (MC-LGO) cross-validation. In this test, compounds were randomly divided into seven groups of about equal size and the model calibration process involved only compounds from six groups in any given cycle leaving one of the groups outside as the test set. The resulting model was used to predict the activities for the omitted test set compounds. This process was repeated 10 times, reshuffling the compounds in each group, resulting in 70 models in total. The leave-one-out (LOO) cross-validation was also performed, omitting and predicting one compound at a time.

Glossary

Abbreviations Used

LGO

leave-group-out (cross-validation)

LOO

leave-one-out (cross-validation)

LPS

lipopolysaccharide

LR

linear response (method)

MAPK

mitogen-activated protein kinase

MC

Monte Carlo

MD

molecular dynamics

MK2

MAPK-activated protein kinase 2

MS

multispecies (approach)

NES

nuclear export signal

NLS

nuclear localization signal

ONIOM

our own N-layered integrated molecular orbital and molecular mechanics

QM/MM

quantum mechanics/molecular mechanics

QSAR

quantitative structure–activity relationship

rmsd

root-mean-square deviation

RMSE

root-mean-square error

SASA

solvent-accessible surface area

t_1/2

half-life

TNFα

tumor necrosis factor α

Supporting Information Available

Tables (XLS) summarizing the heavy-atom rmsd values between the docked poses (step 1) and between the time-averaged poses (steps 3/4) of tautomer/species for individual compounds, published standard deviations of inhibitory activities of pyrrolopyridines (Table 2), fractions of free tautomers/species and prevalences of bound tautomers/species for benzothiophenes (Table 1) and pyrrolopyridines (Table 2), respectively. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States