The Black Queen Hypothesis: Evolution of Dependencies through Adaptive Gene Loss

ABSTRACT

Reductive genomic evolution, driven by genetic drift, is common in endosymbiotic bacteria. Genome reduction is less common in free-living organisms, but it has occurred in the numerically dominant open-ocean bacterioplankton Prochlorococcus and “Candidatus Pelagibacter,” and in these cases the reduction appears to be driven by natural selection rather than drift. Gene loss in free-living organisms may leave them dependent on cooccurring microbes for lost metabolic functions. We present the Black Queen Hypothesis (BQH), a novel theory of reductive evolution that explains how selection leads to such dependencies; its name refers to the queen of spades in the game Hearts, where the usual strategy is to avoid taking this card. Gene loss can provide a selective advantage by conserving an organism’s limiting resources, provided the gene’s function is dispensable. Many vital genetic functions are leaky, thereby unavoidably producing public goods that are available to the entire community. Such leaky functions are thus dispensable for individuals, provided they are not lost entirely from the community. The BQH predicts that the loss of a costly, leaky function is selectively favored at the individual level and will proceed until the production of public goods is just sufficient to support the equilibrium community; at that point, the benefit of any further loss would be offset by the cost. Evolution in accordance with the BQH thus generates “beneficiaries” of reduced genomic content that are dependent on leaky “helpers,” and it may explain the observed nonuniversality of prototrophy, stress resistance, and other cellular functions in the microbial world.

Opinion/Hypothesis

There is a tendency in evolutionary discourse to describe life’s history as a progression towards increasing complexity. However, there is no reason to expect that complexity will be selectively advantageous at all times and for all species. Indeed, Gould (1) argued that the appearance of progress in the fossil record is a mere artifact: because there is a minimum complexity necessary to sustain life but no apparent upper limit to complexity, even undirected change may produce more complex species by a “drunkard’s walk” mechanism while preserving relatively simple bacteria as the dominant mode of life. In fact, nature offers numerous examples of “reductive evolution,” where simple organisms derive from more complex ancestors. This phenomenon is typified by macro- and microscopic parasites and symbionts, particularly those that reside inside their hosts (e.g., see reference 2). Such organisms tend to lose the capacity to synthesize metabolites provided by their hosts. For example, tapeworms lack digestive tracts, absorbing all their required nutrients transdermally from their host’s gut (3). Similarly, many host-associated bacteria (e.g., Lactobacillus spp.) are no longer able to synthesize certain essential metabolites, such as amino acids (4, 5).

Genome size in eukaryotes is subject to diverse evolutionary forces and is not necessarily associated with genetic or phenotypic complexity (6–8). In bacteria, however, reductive genome evolution often causes losses of function. Based on analyses of the ratio of synonymous to nonsynonymous mutations in protein-coding genes, DNA loss in parasitic and symbiotic bacteria appears to be driven by genetic drift associated with transmission bottlenecks, insulation from horizontal gene transfer (HGT), and the relaxation of selection on certain functions (9). In experimentally evolved populations of Salmonella enterica, genetic drift caused by daily single-cell bottlenecks drove massive and often deleterious gene loss, consistent with hypotheses about the evolution of endosymbionts (10). In contrast, adaptive gene loss has been observed in experimentally evolved populations of Escherichia coli that experienced a more permissive daily bottleneck of ~5 × 10⁶ cells (11); for example, a single operon-scale deletion arose independently in 12 replicate lines that conferred an advantage of ~1% in competition with the ancestor (12). In nature, some free-living bacteria also have reduced genomes, and in these cases large population sizes and the apparent absence of transmission bottlenecks suggest that selection, not drift, must be responsible. For example, Prochlorococcus and “Candidatus Pelagibacter,” which are the most abundant phototrophic and heterotrophic marine genera, respectively, both exhibit reduced genomes (13, 14). The effective population sizes of these organisms vastly exceed those in any laboratory experiment, and therefore selection almost certainly drove their genome reduction. The most likely explanation for the fitness advantage conferred by genomic and metabolic “streamlining” in both natural and experimental populations is that it reduces the amount of carbon and other limiting nutrients required to produce a new cell (12, 15, 16).

To be evolutionarily successful, however, genomic streamlining also requires that the lost functions are dispensable to the organism, such that the cost of gene loss is less than the benefit. It was thus surprising to find that the Prochlorococcus strains with streamlined genomes had a greatly diminished capacity to survive oxidative stress in comparison with a marine isolate of the related Synechococcus group (17), despite the fact that both organisms are oxygen-producing photoautotrophs. Consistent with their physiological differences, genomic comparisons revealed that Prochlorococcus isolates had a smaller suite of oxidative-stress genes than Synechococcus (18).

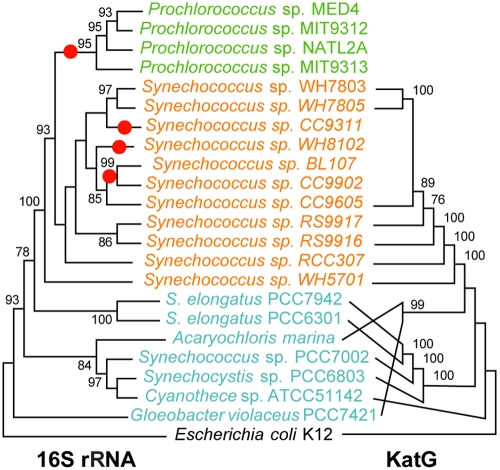
One stress response gene of particular relevance encodes catalase-peroxidase (katG), a large, Fe-dependent enzyme that is thought to be the primary defense against external hydrogen peroxide (HOOH) in cyanobacteria (19, 20). None of the sequenced Prochlorococcus genomes contain katG, whereas most Synechococcus genomes do (Fig. 1) (18). Previous studies found that the katG gene has undergone extensive HGT, in some cases even jumping from bacteria to eukaryotes (21, 22). The discrepancy between the rRNA gene and katG gene phylogenies (Fig. 1) also suggests that HGT of the latter has occurred in the cyanobacteria, although all of the katG genes are monophyletic in Synechococcus. Therefore, the simplest explanation for the variable presence or absence of katG in the combined Synechococcus-Prochlorococcus clade is that this gene was present in their common ancestor but was later lost in several lineages, including the entire Prochlorococcus genus (these losses are shown as red dots in Fig. 1). Also, the pan-genome of the sequenced Prochlorococcus genomes includes a large repertoire of accessory genes, many of which occur in only a single isolate, implying that these organisms are as prone to HGT as many other bacteria (23). The absence of a commonly transferred gene, such as katG, from the Prochlorococcus pan-genome suggests that its acquisition would provide no net benefit, even though the gene product increases resistance to oxidative stress. Notably, catalase is also missing from the streamlined “Candidatus Pelagibacter ubique” HTCC1062 genome (16), and this organism has other conspicuous nutritional dependencies that have apparently arisen through gene loss (24, 25). Together, Prochlorococcus and “Ca. Pelagibacter” comprise 50% or more of the microbiota in some surface regions of the ocean (26); their katG deficiencies thus imply that a minority of organisms are sufficient to reduce the HOOH in these waters to a level that allows the dominant types to thrive.

FIG 1 .

Comparison between the phylogenies of the catalase-peroxidase and small subunit rRNA genes for cyanobacteria with sequenced genomes. Although there are some differences in branching order between the two trees, the marine Synechococcus KatG proteins form a well-supported monophyletic clade, implying that this protein was present in the clade’s ancestor and was subsequently lost in several lineages (indicated by red dots on the rRNA tree), including Prochlorococcus. Green, representatives of the Prochlorococcus clade; orange, marine Synechococcus clade; cyan, other Cyanobacteria. Bootstrap values less than 75% are omitted. Only the tree topologies are shown; branch lengths do not represent genetic distances. Tree construction methods are described in the supplemental material. (Alignments and distance matrices used to produce the figure have been deposited at http://www.datadryad.org [http://dx.doi.org/10.5061/dryad.7j8c5s5j].)

A lack of defenses against HOOH is potentially costly. HOOH is generated in the ocean by the photooxidation of dissolved organic carbon (27), and sterile filtered seawater exposed to sunlight accumulates enough HOOH in a few hours to kill axenic Prochlorococcus cultures (17). But fortunately for Prochlorococcus, other members of its natural community act as a sink for HOOH (28) and keep concentrations low enough for Prochlorococcus to thrive. The sink effect occurs because HOOH is roughly as membrane permeative as water (29), so the cells that protect their interiors by detoxifying intracellular HOOH eventually also reduce the level of extracellular HOOH and thus protect neighboring cells. In this way, some marine microbes act as “helpers” that protect the vulnerable majority—the “beneficiaries”—from HOOH as a side effect of protecting themselves (17).

Placing this ecological interaction into an evolutionary context, the loss of HOOH resistance can be described as a community-dependent adaptive event. It is adaptive because resources may be shunted from HOOH defense to growth, but only because other members of the community condition the environment such that a robust oxidative-stress response becomes dispensable to the beneficiaries. The surprising HOOH sensitivity for the numerically dominant members of the oligotrophic marine community leads us to propose that there is some more general evolutionary process driving this dependency.

To better understand the proposed evolutionary process, we can separate it into several underlying components. First, there is a selective advantage of becoming a beneficiary, which drives the loss of genes from some organisms and, by default, turns other community members into helpers. The helpers are thus passive players in this process—perhaps the unlucky ones that were the slowest to change. Second, the fitness advantage of losing the gene and its encoded function must be frequency dependent, such that when the helpers become sufficiently rare the benefit of any further loss is negated by its cost, preventing the extinction of the function from the community. Last, we emphasize that HOOH removal differs from many other functions by being “leaky,” so that its detoxification by some members of the community inevitably benefits other cells in their vicinity. Together, these component processes suggest a novel mechanism for reductive evolution, and in the sections that follow we formulate this into an explicit hypothesis and discuss how it may apply to other microbial systems.

THE BLACK QUEEN HYPOTHESIS

One well-known theory of coevolution, the Red Queen Hypothesis (30), uses a metaphor derived from Lewis Carroll’s Through the Looking-Glass (31)—“it takes all the running you can do, to keep in the same place,” spoken by the (red) Queen of Hearts—to describe the evolutionary race between ecological antagonists, such as parasites and their hosts. This hypothesis sought to explain the surprising prevalence of extinction in the fossil record, and it posited that all species experience a constantly deteriorating environment as a consequence of coevolution with other species.

In contrast, the evolution of functional dependency on helpers by definition generates commensalistic or even mutualistic interactions. We present here an alternative theory of coevolution that we name the “Black Queen Hypothesis” (BQH). Similar to the red queen, the black queen refers to a playing card, in this case the queen of spades in the game Hearts. In Hearts the goal is to score as few points as possible. The queen of spades, however, is worth as many points as all other cards combined, and therefore a central goal of the game is to not be the player that ends up with that card. (We discuss the “shooting the moon” strategy later.) In the context of evolution, the BQH posits that certain genes, or more broadly, biological functions, are analogous to the queen of spades. Such functions are costly and therefore undesirable, leading to a selective advantage for organisms that stop performing them. At the same time, the function must provide an indispensable public good, necessitating its retention by at least a subset of the individuals in the community—after all, one cannot play Hearts without a queen of spades. The detoxification of HOOH fulfills both of these criteria, and therefore the BQH predicts that this function will be performed by helpers that comprise only a fraction of the community.

Treated formally, the BQH specifies the conditions under which it is advantageous for an organism to stop performing a function. Any loss of a functional gene comes with a potential cost in fitness; therefore, in order to invade a population, a loss-of-function (LOF) mutation must also provide a gain in fitness that outweighs this cost. In most cases, the relative fitness benefit (B) is determined by the saving in energy or other resources that results from gene loss. For an ancestral organism and a LOF mutant that have cell quotas for a limiting resource of Q_A and Q_M, respectively:

$$B=\frac{Q_A-Q_M}{Q_A}$$ (1)

For example, owing to the high iron content of katG, Prochlorococcus requires ~0.2% less iron per cell than a putative catalase-positive ancestor (17), so the benefit of losing the katG gene is ~0.2% in iron-limited waters (e.g., see reference 32), provided that detoxification by other organisms prevents the buildup of HOOH. If we assume that this saving provides a proportional increase in the net growth rate of Prochlorococcus, then a LOF mutant could invade the ancestral population at rate Bμ, where μ is the ancestral growth rate. In the absence of countervailing selective pressure, the mutant would sweep through the population rather quickly, even given the massive global population size of Prochlorococcus. For B = 0.002 and assuming that the ancestral type doubles once per day (μ of ~0.69 day⁻¹), then the LOF mutant increases relative to the overall population at a rate of ~0.0014 day⁻¹. Assuming a constant and homogenous global Prochlorococcus population of ~1 × 10²⁵ cells (10⁴ cells ml⁻¹ to a 10-m depth over 1/4 of the Earth’s surface), the mutant would constitute 99% of the population in fewer than 125 years.

The fitness cost (C) for gene loss can be calculated from the fitness of a LOF mutant in an environment where the public good provided by the function is absent, adjusted by (i) the degree to which other members of the community provide that public good—i.e., how much “help” the surrounding community provides—and (ii) any residual activity of the mutant. Let k be the per capita rate constant for the function under consideration. For a given strain, let μ₀ be the per capita growth rate when k equals 0, and let k_M be the functional rate necessary to allow growth at the species’ maximum rate, μ_M. We can calculate the effective k for any given organism as the sum of its internal rate k₀ plus the contribution from the surrounding community, calculated using the values of k for each community member modified by a “leakiness coefficient,” L, that measures the proportion of its activity that generates public goods available to others:

$$k=k_0+{\displaystyle \sum _{i=1}^s{N}_i{L}_i{k}_i}$$ (2)

where S is the number of strains, and N is the density of the ith strain. As a simple example, let us assume that μ increases linearly with k between k = 0 and k = k_M. Then, for k ≥ 0 and k ≤ k_M, the cost C is

$$C=\frac{{\mu }_M-\mu }{{\mu }_M}=\frac{\left(k_M-k\right)\left({\mu }_M-{\mu }_0\right)}{{\mu }_M{k}_M}$$ (3)

which reduces to (k_M − k)/k_M when the mutant cannot survive alone (i.e., μ₀ = 0). While equations 2 and 3 assume for simplicity that the relevant functions are linear, the general conclusions should still hold with more complex interactions.

The BQH thus predicts that a LOF mutant will be able to expand in its ancestral population if B is greater than C, i.e., when benefits outweigh costs. In the special case of a mutant expanding in an environment occupied only by itself and its ancestor, the mutant will expand until the ancestors reach a concentration that provides exactly enough of the public good to facilitate an equal growth rate for the ancestor and the mutant. As long as the function loss gives the mutant a growth advantage over its ancestor but the mutant retains a requirement for the public good produced by the function, then there are conditions where the two will coexist even if they compete for the same limiting resource in a spatially and temporally homogenous environment (33).

However, in a mixed community with unrelated organisms that provide the public good at a sufficient level but are not in direct competition with the mutant and its ancestor, we would expect the LOF mutant to drive its ancestor to extinction. Indeed, in a mixed community, the BQH predicts that functional loss will proceed in every species in the community until B is less than or equal to C for all individuals. At this point, vulnerable organisms cannot increase further without reducing the public good to a level at which any additional loss of function would be deleterious. As LOF mutants replace their ancestors, the community will come to be populated by lineages of helpers and beneficiaries, just as in the case of Prochlorococcus and its marine cohabitants. Although these interactions might appear superficially to be altruistic, in fact this bifurcation arises through classic Darwinian selection acting on individuals. Importantly, this reductive evolution occurs because of the leakiness of the function that provides the public good.

So far, we have assumed that evolution happens in a well-mixed environment, such as a patch of the ocean’s surface layer, so that every organism has equal access to the public good. If we relax this assumption, then the cost-benefit analysis becomes more complex. Specifically, the effects of leakiness are altered when the most likely recipients of the public good are nearby organisms and often relatives. Previous studies have demonstrated that spatial structure plays a key role in the evolution of certain microbial phenotypes, including secretion of growth factors (34) and allelopathic compounds (35), that impose costs on some individuals while providing benefits to others. Hamilton’s rule (reviewed in a microbial context in reference 36) states that these seemingly altruistic phenotypes will be favored by selection when rB is greater than C, where B is the fitness benefit to the recipient of an altruistic action, C is the fitness cost to the altruist, and r is the genetic relatedness between these individuals. Both Hamilton’s rule and the BQH use a cost-benefit analysis to evaluate whether selection will favor traits associated with the production of public goods. However, Hamilton’s rule emphasizes the cost to the individual that produces a public good and whether that cost is more than offset by the benefits to its relatives. In contrast, the BQH (equation 1) focuses on the benefit to an individual that can avoid paying a cost because its community provides the public good, without regard to the relationship between the producer and user of the public good. Thus, kin selection sustains the active production of public goods under Hamilton’s rule, whereas physiological leakiness and density-dependent interactions are key to the BQH (equations 2 and 3). These differences do not mean that spatial structure and genetic relatedness are irrelevant to the BQH; undoubtedly, these factors can influence which lineages undergo reductive evolution, the resulting level of public good, and other important aspects of the system. The intersection of Hamilton’s rule and the BQH is therefore worthy of further exploration, both theoretically and empirically. However, introducing spatial structure and its effects on genetic relatedness should not change the fundamental possibility that reductive evolution will proceed in a manner generally consistent with the BQH.

THE BQH APPLIED TO OTHER MICROBIAL FUNCTIONS

Our discussion of the BQH has focused thus far on HOOH cross-protection in marine systems, but other microbial interactions may also generate similar evolutionary dynamics. Any function that is both costly to perform and leaky is a potential target for loss. In this section, we suggest that nitrogen fixation, inorganic nutrient acquisition, and biofilm matrix deposition meet these criteria and thus may be analyzed ecologically and evolutionarily in the framework of the BQH. (See also reference 33 for a related analysis of bacteria that employ detoxification mechanisms for resistance to antibiotics.) While the potentially social aspects of these functions have been considered previously (e.g., see references 37 and 38 and references below), we suggest that the BQH helps unite them in a common and generally applicable framework.

Biological nitrogen fixation is one of the most energetically demanding of metabolic functions, and it ultimately limits community productivity in many environments (39). However, it is performed by a relatively small subset of organisms; for example, in the oceans, nitrogen-fixing species (diazotrophs) constitute less than 1% of the total cyanobacterial population (40). Phylogenetic analysis of the nitrogenase operon strongly suggests that either (i) the last common ancestor of all extant life was a diazotroph or (ii) HGT of these genes has been widespread (41). There must have been either selection that caused the majority of lineages to lose this function or an absence of net benefits to its acquisition in many species, despite the dependence of so many communities on this function. The vertical transmission of fixed N from a diazotroph to its progeny is imperfect, and therefore some of the fixed N becomes a public good. Hence, N provision, like HOOH removal, is a leaky process, and the BQH may explain the rarity of this important function.

In other environments, the low solubility of iron in the presence of oxygen limits growth (42). Iron acquisition in these habitats often depends on the secretion by microorganisms of high-affinity iron-binding siderophores that maintain a pool of dissolved and biologically available iron. However, the siderophore-bound iron is not only available to the species responsible for producing the siderophores but also to siderophore-deficient organisms (43, 44). Indeed, the provision of siderophore-producing helpers facilitates the growth of previously “unculturable” beneficiaries, indicating that some microbes are unable to acquire sufficient iron for growth without help (43). Strikingly, siderophore production is rare in unicellular cyanobacteria compared to filamentous genera (45), despite the abundance of unicellular species in iron-limited “high-nutrient, low-chlorophyll” regions of the ocean (32). Thus, although the production of these extracellular molecules is vital to the productivity of many communities, the production costs are shared unevenly among the taxa in those communities. In a similar vein, the highly abundant but streamlined marine heterotrophic bacterium “Ca. Pelagibacter ubique” has lost the genes required for assimilatory sulfate reduction, which are present in all other known aerobic marine bacteria. As a consequence, “Ca. Pelagibacter ubique” is dependent on external sources of reduced sulfur for growth (24), and this auxotrophy is adaptive only because it can obtain dimethylsulfoniopropionate (DMSP) from the exudations of diverse phytoplankton helpers (46).

Last, much of microbial life exists in biofilms, whose residents are embedded in a sticky matrix of secreted polymers. While much effort has been expended on understanding the composition and ecological effects of biofilm matrix production, both in environmental and clinical settings, few studies have investigated the contribution of individual species in mixed communities to matrix deposition. However, coculture experiments with bacteria and algae have indicated that heterotrophic bacteria play a crucial role in the production of phototrophic biofilms (i.e., periphyton) and that algae-only assemblages develop slower (47) and are less stable (48) than assemblages that include bacteria. The most productive niches in streams are those with high water velocities, and organisms must invest resources in strong adhesion to exploit the available resources (49). The fact that algae appear to depend on bacterial help to persist in these high-energy environments is consistent with the coevolutionary dynamics expected under the BQH.

All these examples involve the following: (i) products that are energetically or nutritionally expensive; (ii) functions that are performed and products produced by only a fraction of the community; (iii) functions that are leaky enough for the resulting public goods to be used by other species; and (iv) products that are vital to the community, not just the producer. Although the details of the model will depend on particular functions, habitats, and communities, the BQH rests on these four general points. For some public goods, leakiness may be highly evolvable (e.g., if it involves active transport into or out of cells). In these cases, the development of the helper-beneficiary dyad likely also requires some benefit to the helper; otherwise, the helpers would not compete well against those with more stingy strategies. In contrast, for other functions, such as those where the resulting public good is disseminated by mere diffusion (e.g., HOOH removal), some degree of helping is essentially unavoidable; if a function is required for any species, then some of the benefit becomes available to the entire community.

ARE BENEFICIARIES “CHEATERS”?

Under the BQH, beneficiaries take advantage of helpers for their growth and even survival, as seems to be the case for Prochlorococcus at the ocean’s surface. This relationship raises the question: are beneficiaries evolutionary “cheaters?”

Cheaters are typically thought of as mutants within a single-species population that stop performing some function that is costly to the individual but beneficial to the group as a whole, thereby gaining a fitness advantage at the expense of their conspecifics (36). This dynamic is certainly similar to the BQH, but importantly, there is no requirement under the BQH that the helpers and beneficiaries be related; in fact, they may often belong to different species, different trophic levels, and even different phylogenetic domains. Moreover, the idea of cheating implies that there is some direct negative effect of the cheaters on the cooperators. For example, in the socially aggregative bacterial species Myxococcus xanthus, spore dissemination requires that most of the aggregating individuals become nondividing stalk cells that form the base and exterior layer of the fruiting body. Experiments have demonstrated that mutant cheaters that rarely become stalk cells produce disproportionate numbers of spores and can invade wild-type populations; as the mutants increase in abundance, they can depress the overall spore production of the population (50). In contrast, it is not the case with the BQH that the fitness of helpers is necessarily diminished. Under the BQH, the beneficiaries would harm the helpers only if both organisms are limited by the same resource, such that increased resource consumption and growth by the beneficiaries reduce resource availability to and growth by the helpers. Thus, the term “cheater” might apply to the initial invasion of a beneficiary mutant into its ancestral helper population, provided that both the helper and beneficiary subpopulations are limited by the same resource.

But what if the helpers and beneficiaries are limited by different substrates, each of which is unavailable (or at least not limiting) to the other population? In that case, the relationship would be commensal. Prochlorococcus and its heterotrophic helpers probably do not compete for carbon and energy sources; in fact, they occupy different trophic levels, with the heterotrophs potentially dependent on Prochlorococcus as their main source of organic carbon. Heterotrophic bacteria in the oceans are generally thought to be limited by photosynthetic carbon fixation (51), a process dominated by Prochlorococcus in many regions (14). If genome reduction allowed Prochlorococcus to increase its rate of primary production, it may have simultaneously increased the organic carbon supply for the helper community. In this case, both Prochlorococcus and the helpers would have benefitted and their association is not merely commensalistic but mutualistic. Thus, the BQH describes a general evolutionary process that may sometimes include cheating but, in other ecological contexts, can result in neutral or positive interactions between species.

SHOOTING THE MOON

Hearts players will be familiar with an alternative route to victory called “shooting the moon.” This risky strategy requires a player to capture all point-scoring cards, including the Queen of Spades, the exact opposite of the typical strategy of minimizing one’s points. At the risk of belaboring the card game metaphor, we suggest there may be an analog of shooting the moon for the BQH. In particular, might a species, having become a helper for one function, therefore be more likely to become a helper for other, unrelated functions? Such an outcome would involve passive evolution toward a niche with high resource requirements, but with the advantage of high “job security” for the helper owing to the dependence of the community on its continued well-being.

The fact that the process of function loss should accelerate for beneficiaries but not for helpers suggests that this scenario is plausible. Equation 1 represents the benefit of function loss as a proportion of the total cell quota for some limiting nutrient relative to the resource demands of the function. After one function has been lost, the cell quota decreases, thereby providing a proportionately greater benefit from any future savings of a fixed quantity of limiting resource. If all else were equal, the selective advantage for a new LOF mutant in an existing population of beneficiaries would thus be greater than that for the same mutation in the helpers. And with each successive functional loss from the beneficiary, this gap would increase. Thus, it would become increasingly difficult over time for helpers to produce successful beneficiary lineages. In the long run, one can envision a community that is numerically dominated by functionally limited beneficiaries that are well adapted to compete for their own limiting nutrients, with a smaller and perhaps more diverse assemblage of helper organisms that serve as repositories for the many functions necessary for community prosperity. It is also worth noting the parallels between these two alternative evolutionary trajectories and the ideas of r- and K-selected organisms (52) and of “copiotrophs” and “oligotrophs” (53); one could speculate that the dynamics implicit in the BQH have been important in promoting the division between these alternative life history strategies in some ecological circumstances.

One additional corollary of “shooting the moon” is that helper lineages should tend to be numerically rare but always present owing to the community’s requirement for the public goods they produce. In this way, they fit the definition of “keystone species,” which have ecological importance much greater than one would surmise from their abundance. While future work is required to determine the specific abundances of, for example, HOOH-scavenging organisms in the oligotrophic surface waters of the world’s oceans, it seems likely they will be minorities, because initial genomic studies imply that the numerically dominant organisms in those habitats (e.g., Prochlorococcus and “Ca. Pelagibacter”) are deficient in this regard. The BQH offers an explanation for the persistence of these rare but indispensable keystone species.

CONCLUSION

The Black Queen Hypothesis seeks to explain reductive genome evolution in some free-living microbial lineages, and it can also explain why certain essential functions are nonetheless rare within some communities. It presents a scenario whereby individual-level selection creates a division of labor in microbial communities that, like organizations in humans and other social animals, is often to the advantage of all. Unlike the case with many theories of coevolution, the relationships between helpers and beneficiaries do not arise from their direct interaction but rather because the beneficiary can simply stop performing a costly function that is provided by the leaky helper. The BQH also provides a new framework for looking at several classic problems in microbial ecology. How are microbial communities organized? Why do many organisms fail to grow in pure cultures? Are there unknown niches, even in relatively homogenous environments, that allow the persistence of many species competing for a few limiting resources (i.e., the Paradox of the Plankton [54])? And what forces lead to the dependence of communities on rare keystone organisms, whose extinction can lead to instability and potential catastrophe (e.g., see references 55 and 56)?

SUPPLEMENTAL MATERIAL

Text S1

Supplemental material for this article may be found at Text S1, DOCX file, 0.1 MB.