Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2012 Feb 10;28(7):914–920. doi: 10.1093/bioinformatics/bts078

WaVPeak: picking NMR peaks through wavelet-based smoothing and volume-based filtering

Zhi Liu 1, Ahmed Abbas 2, Bing-Yi Jing 3,*, Xin Gao 2,*
PMCID: PMC3315717  PMID: 22328784

Abstract

Motivation: Nuclear magnetic resonance (NMR) has been widely used as a powerful tool to determine the 3D structures of proteins in vivo. However, the post-spectra processing stage of NMR structure determination usually involves a tremendous amount of time and expert knowledge, which includes peak picking, chemical shift assignment and structure calculation steps. Detecting accurate peaks from the NMR spectra is a prerequisite for all following steps, and thus remains a key problem in automatic NMR structure determination.

Results: We introduce WaVPeak, a fully automatic peak detection method. WaVPeak first smoothes the given NMR spectrum by wavelets. The peaks are then identified as the local maxima. The false positive peaks are filtered out efficiently by considering the volume of the peaks.

WaVPeak has two major advantages over the state-of-the-art peak-picking methods. First, through wavelet-based smoothing, WaVPeak does not eliminate any data point in the spectra. Therefore, WaVPeak is able to detect weak peaks that are embedded in the noise level. NMR spectroscopists need the most help isolating these weak peaks. Second, WaVPeak estimates the volume of the peaks to filter the false positives. This is more reliable than intensity-based filters that are widely used in existing methods.

We evaluate the performance of WaVPeak on the benchmark set proposed by PICKY (Alipanahi et al., 2009), one of the most accurate methods in the literature. The dataset comprises 32 2D and 3D spectra from eight different proteins. Experimental results demonstrate that WaVPeak achieves an average of 96%, 91%, 88%, 76% and 85% recall on 15N-HSQC, HNCO, HNCA, HNCACB and CBCA(CO)NH, respectively. When the same number of peaks are considered, WaVPeak significantly outperforms PICKY.

Availability: WaVPeak is an open source program. The source code and two test spectra of WaVPeak are available at http://faculty.kaust.edu.sa/sites/xingao/Pages/Publications.aspx. The online server is under construction.

Contact: statliuzhi@xmu.edu.cn; ahmed.abbas@kaust.edu.sa; majing@ust.hk; xin.gao@kaust.edu.sa

1 INTRODUCTION

In the last two decades, nuclear magnetic resonance (NMR) has played a significant role in protein structure elucidation (Wüthrich, 1986). NMR is a powerful technique to determine the 3D structures of proteins at the atomic level. Different from X-ray crystallography, the dominant structure determination technique, NMR allows the study of proteins in vivo. It can therefore be used to study small- and medium-sized proteins that cannot be crystalized. The 3D structures determined by NMR, on the other hand, may reveal intravital characteristics and dynamics of the proteins.

After the spectra are collected, NMR structure determination usually involves several time-consuming steps, i.e. peak picking, chemical shift assignment, nuclear Overhauser effect spectroscopy (NOESY) assignment and structure calculation (Wüthrich, 1986). These steps can take experienced NMR spectroscopists weeks or even months. Among the four steps, peak picking is a prerequisite for all following steps, and thus required much attention from spectroscopists. The goal of peak picking is to identify cross-signals, which contain the chemical shift information of the spin systems, from the noisy NMR spectra.

Computational approaches have been widely applied to accelerate the post-spectra processing stage of NMR structure determination (Alipanahi et al., 2009, 2011; Altieri and Byrd, 2004; Gronwald and Kalbitzer, 2003; Güntert, 2009; Herrmann et al., 2002; Jang et al., 2010, 2011; Williamson and Craven, 2009). However, peak picking is the most sensitive and, thus far, it has been difficult to design automatic methods that can deal with this sensitivity. There are two reasons for this difficulty. First, the outputs of peak picking serve as the inputs for both the assignment and structure calculation steps. Any practical peak-picking method must therefore be very accurate. Second, there are various sources of errors in NMR spectra, including random noise, sample impurities, artifacts and water bands, which makes peak picking a very challenging problem.

The first automatic peak-picking method was proposed in 1990 (Kleywegt et al., 1990). Symmetry was both assumed and used to identify peaks in 2D 1H NMR spectra. Since then, a variety of methods have been explored to solve the peak-picking problem, which include peak-property-based methods (Garret et al., 1991; Johnson and Blevins, 1994), machine learning methods (Antz et al., 1995; Carrara et al., 1993; Corne et al., 1992; Rouh et al., 1994), and spectra-decomposition-based methods (Alipanahi et al., 2009; Koradi et al., 1998; Korzhneva et al., 2001; Orekhov et al., 2001).

Among the existing automatic methods, AUTOPSY (Koradi et al., 1998) and PICKY (Alipanahi et al., 2009) are the most accurate. Both of these methods attempt to estimate the noise level of the given spectrum. The noise is assumed to be white Gaussian noise and is estimated within small regions of the spectrum. All the data points that have lower intensities than the estimated noise level are eliminated, which eliminates most parts of the spectrum. The remaining spectrum looks like a set of disconnected components. Instead of dealing with all the components altogether, both AUTOPSY and PICKY extract separate components. AUTOPSY extracts components by a simple flood fill algorithm, whereas PICKY further subdivides weakly connected components into smaller ones. After the components are formed, both methods conduct peak picking within each component. AUTOPSY first identifies strong, obvious peaks from components. Each of these components is then decomposed as the outer product of 1D lineshapes. The lineshapes are then clustered and used to detect overlapping peaks from the remaining components. Different from AUTOPSY, which uses symmetry properties of peaks, PICKY directly applies SVD on each of components. Since the components formed by PICKY are much smaller and simpler than the ones formed by AUTOPSY, rank-one SVD seems to be powerful enough to identify peaks from the components. However, both AUTOPSY and PICKY have a quite high false positive rate. Therefore, a refinement step is performed in each method to reduce the number of false peaks. In AUTOPSY, the integration, symmetrization and filtering modules are applied. In PICKY, the peaks are first sorted according to the intensities. A certain number of the strongest peaks (usually 1.2K, where K is the expected number of peaks) is kept. The peaks from different NMR spectra, which share common atoms, are used to cross-eliminate false positive peaks.

Although AUTOPSY and PICKY have demonstrated impressive accuracy on different benchmark spectra, they both have two bottlenecks. The first is that all the data points with low intensities are eliminated in both methods. However, a number of true peaks actually have low intensities due to various reasons, including the sensitivity of the NMR spectrometer, the strength of the magnetic field, the characteristics of the target proteins and the local dynamics of the spin systems. Unfortunately, spectroscopists need the most help to deal with these weak peaks. An ideal peak-picking method should therefore be able to identify the weak peaks instead of disregarding them.

The second bottleneck is the way the two methods eliminate the false positive peaks. Apparently, a brute force method that selects all the local maxima as peaks should have higher sensitivity than any other method. The issue is that since the real spectra are very noisy, the brute force method will generate a huge number of peaks, making it almost impossible for users to identify the true ones. On the other hand, all peak-picking methods try to smooth the spectra such that there is a good tradeoff between the sensitivity and the specificity. For example, PICKY first eliminates all the weak data points and then smoothes the components by rank-one SVD. The problem now is how to rank the peak candidates in an order such that the true peaks are at the top. The existing methods use either intensity-based ranking or cross-references from other spectra. However, the intensity of a single data point is not informative enough to distinguish a true peak from a false one. Cross-references from other less reliable spectra, on the other hand, may eliminate some true peaks.

In this article, we introduce WaVPeak, a fully automatic peak-picking method that is based on wavelet-based smoothing and volume-based filtering and overcomes the two bottlenecks of the existing methods. We first propose the use of the Daubechies 3 wavelet for the peak-picking problem. We suggest and demonstrate that this wavelet is the most suitable one for this problem because it can smooth the spectrum, sharpen the peak shapes and maintain the peak locations. In this way, no data point will be eliminated. Furthermore, the weak peaks that are embedded in the noise will be recovered and will become visible. Then, a brute force method is applied to isolate all the local maxima in the wavelet-smoothed spectrum. However, the number of local maxima in the wavelet-smoothed spectrum is much smaller than the number in the original spectrum. The peak candidates are then sorted according to the estimated volume of the peak shapes, which has a much stronger distinguishable power than intensity-based sorting has.

2 METHODS

WaVPeak consists of three main steps, i.e. wavelet-based smoothing, brute force peak picking and volume-based filtering. Given any spectrum, it is first smoothed by wavelets. A brute force algorithm is then applied to identify all the local maxima as the initial peak candidates. The initial peaks are ranked according to their estimated volume. The details of the wavelet-based smoothing and volume-based filtering are discussed in this section.

2.1 Wavelet-based smoothing

Wavelets are mathematical functions that cut up data into different frequency components. Subsequently, each component is studied with a resolution matched to its scale. Wavelets have advantages over traditional Fourier methods in analyzing physical situations in which the signal contains discontinuities and sharp spikes. Interestingly, wavelets were developed independently in the fields of mathematics, quantum physics, electrical engineering and seismic geology.

Interchanges between these fields during the last 20 years have led to many new wavelet applications, especially image processing and de-noising noisy data. Wavelets have also been employed in various tasks to do with NMR signal processing (Barache et al., 1997; Dancea and Güntert, 2005; Gronwald and Kalbitzer, 2004; Günther et al., 2000, 2002; Hu et al., 2011; Lang et al., 1996; Neue, 1996; Shao et al., 2000). Such tasks include analyzing the dynamical behavior of NMR signals (Barache et al., 1997; Hu et al., 2011; Neue, 1996), de-noising the NMR spectra (Dancea and Güntert, 2005; Günther et al., 2000), suppressing water peaks from the spectra (Gronwald and Kalbitzer, 2004; Günther et al., 2002), and increasing the resolution of the spectra (Shao et al., 2000).

Despite such applications of wavelets in NMR signal processing, wavelet-based automatic peak picking has not been the focus of research attention. The most relevant work is Dancea and Güntert, 2005. Dancea and Güntert combined different wavelet procedures together in a consensus manner to de-noise the 15N-NOESY spectrum in order to generate a 3D structure for the Sud protein from Wolinella succinogenes. They considered the consensus results from three wavelet-base functions, i.e. Symmlet, Daubechies (Daubechies, 1992) and Coiflet. Although the structure was accurately determined, the proposed multi-stage de-noising technique was specific for one particular spectrum and could not be easily generalized.

De-noising or smoothing by wavelets is an indispensable step for automatic NMR peak picking due to the various sources of noise in the spectra. It is an important step as the de-noising is carried out without smoothing the sharp structures. The result is a cleaned-up signal that still captures important details. The de-noising consists of three steps:

  1. transforming the spectra to the wavelet domain using some appropriate 2D wavelets (more discussion below);

  2. applying thresholding methods (e.g. hard or soft thresholding), i.e. setting all coefficients to zero that are less than a particular threshold (we adopt soft thresholding later in this article); and

  3. inverse-transforming the thresholded coefficients to reconstruct the data set in the signal domain.

We now elaborate more on 2D wavelets in Step 1. First, 2D wavelets can be constructed from 1D wavelets (see Mallat, 1989). Given a 1D scale function, ϕ(x), and its corresponding wavelets, ψ(x), we define the 2D scale function as

graphic file with name bts078um1.jpg

and the corresponding 2D wavelets as

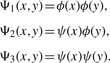graphic file with name bts078um2.jpg

The critical issue then becomes how to choose the 1D wavelets ϕ(x) and ψ(x) as different wavelets serve different purposes. Since our objective is to identify peaks, the ideal wavelet function should resemble the shapes of true peaks, i.e. a cone shape in our NMR peak-picking problem. We have explored various wavelet families with different parameters on MATLAB, including Daubechies, Symlets, Coiflets and Biorthogonal. It turns out that Daubechies 3, Symlets 3 and Biorthogonal 2.4 significantly outperform others on the peak-picking accuracy, when evaluated with real NMR spectra. The accuracy of these three wavelets is very similar with Daubechies 3 having slightly higher sensitivity. Therefore, in WaVPeak, we use 2D Daubechies 3 as the default wavelet.

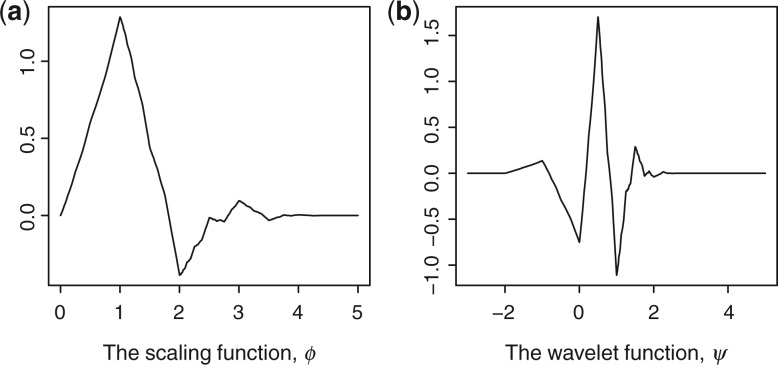
Figure 1 illustrates the scaling function, ϕ, and the wavelet function, ψ, of the 1D Daubechies 3 wavelet. Clearly, both functions produce a cone shape, which looks like a peak shape after smoothing. This can be further confirmed from Figure 2, which shows the original spectrum of the 15N-HSQC of the VRAR protein with wavelet-based smoothing using Daubechies 3. Clearly, the original spectrum is much noisier than the wavelet-smoothed spectrum. Furthermore, the peak shapes are smoothed and sharpened in the smoothed spectrum as well.

Fig. 1.

Fig. 1.

Open in a new tab

The scaling and wavelet functions of the Daubechies 3 wavelet.

Fig. 2.

Fig. 2.

Open in a new tab

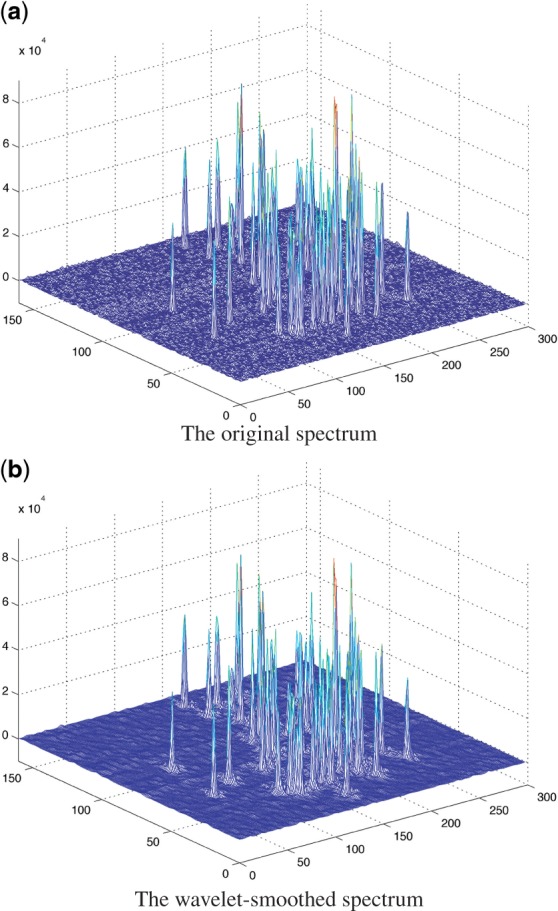
The original spectrum and the Daubechies 3 wavelet-smoothed spectrum of 15N-HSQC of protein VRAR.

2.2 Volume-based filtering

After the initial peaks are identified by the brute force algorithm on the wavelet-smoothed spectrum, we need to identify the true peaks from the relatively large set of initial peaks. The idea is to rank the initial peaks according to a certain criterion, so that all the true peaks are ranked as highly as possible. Traditional methods use the intensity of the peak location as the filtering criterion. However, the intensity of one single data point can be badly biased by various sources of noise in the NMR spectrum; intensity is thus not a reliable criterion.

Here, we propose the use of the volume of the peak instead of the intensity. However, the number of data points that belong to a certain peak shape is not apparent. We therefore need to select a region around the peak location in order to estimate the volume. A trivial solution is to set a predefined window size, such as three. This region includes all the data points that differ by at most one in all the dimensions. To estimate the volume of the peak shape in this region, we assume that the region of the entire peak shape is at least larger than this small region with a window size of three. The volume can thus be estimated as the sum of the volume of the ‘pillars’ (in this case, nine), each of which corresponds to a part of the peak shape over a grid. The volume of a pillar can then be simply estimated as the area of the grid multiplied by the intensity of the data points corresponding to that grid. Note that in a given spectrum, the area of the grid is a fixed value. Therefore, we can use the sum of all the intensities in this region to estimate the volume of the peak.

However, in real spectra, the span of a peak shape over different dimensions can have different numbers of data points. Figure 3 shows an example of a peak shape on a 2D spectrum. This peak shape spans over three and five data points on the two dimensions, respectively. Thus, taking a fixed region of size 3×3 does not give a good estimation of the volume of the peak. In order to solve this problem, we propose a self-adapted, window-based volume estimation.

Fig. 3.

Fig. 3.

Open in a new tab

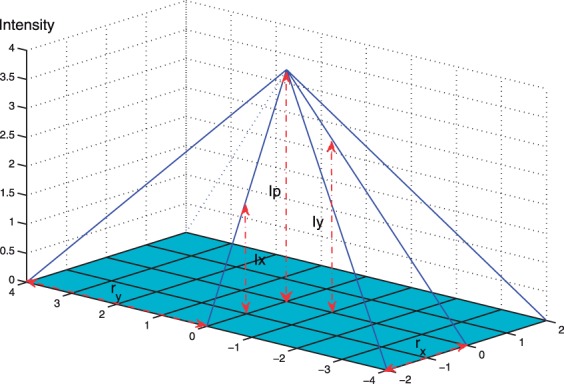
A peak shape with different spans over the x- and y-dimensions.

As shown in Figure 3, the ideal size of the window is 3×5, which includes all the data points that differ by at most one in one dimension and by at most two in the other dimension. From Figure 3, it is easy to show that:

graphic file with name bts078um3.jpg

where rx and ry are the levels of neighbors being considered for dimensions x and y, respectively, and Ip, Ix, Iy are the intensities for the peak, the direct neighbor of this peak on x-dimension, and the direct neighbor of this peak on the y-dimension, respectively. Consequently, we have

graphic file with name bts078um4.jpg

To adjust the size of the region in which we calculate the volume, we set the level size that corresponds to the dimension with the smaller r value to be one. Without loss of generality, assume rx < ry. The level size for the y-dimension is set to 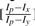Inline graphic. The generalization to higher dimensional spectra is straightforward. Algorithm 1 gives the pseudocode of the self-adapted, window-based filtering algorithm for an arbitrary spectrum.

graphic file with name bts078i2.jpg

2.3 Evaluation criteria

In order to evaluate a peak-picking method objectively, we adopt three criteria, i.e. recall, precision and F-score. Let TP denote the number of true peaks that are discovered by the method, FP the number of false peaks returned by the method and FN the number of true peaks that are not discovered by the method. Recall is defined as TP/(TP+FN), where TP+FN is the total number of ideal peaks. Similarly, precision is defined as TP/(TP+FP), where TP+FP is the total number of peaks returned by the method.

Recall measures the ability of the method to discover the true peaks, whereas precision measures the ability to reject false peaks. In the peak-picking problem, recall is more important than precision because a false peak can be possibly eliminated in the following NMR data analysis process.

We further apply the F-score to measure the tradeoff between recall and precision, where the F-score is defined as the harmonic mean of recall and precision, i.e. 2·Recall·Precision/(Recall+Precision).

3 RESULTS

3.1 Data set

To fairly evaluate the performance of WaVPeak, we test WaVPeak on the spectra set proposed in Alipanahi et al. (2009), which is one of the largest benchmark sets on the peak-picking problem. The set contains 32 spectra extracted from 15N-HSQC, HNCO, HNCA, HNCACB and CBCA(CO)NH from eight proteins, i.e. TM1112, YST0336, RP3384, ATC1776, CASKIN, HACS1, VRAR and COILIN.

3.2 Performance on the benchmark set

WaVPeak is applied on each spectrum of the benchmark set to automatically pick peaks. Although different spectra in the data set share the common 15N and 1H atoms, the cross-referencing is not applied in our experiments so that we may objectively test the peak-picking accuracy of the proposed method.

The Daubechies 3 wavelet is employed to smooth the original spectrum. Figure 2 shows one example of a wavelet-smoothed 15N-HSQC spectrum of the VRAR protein. The smoothed spectrum is much smoother than the original spectrum. Furthermore, the property of the Daubechies 3 wavelet ensures that the peak shapes are more obvious in the smoothed spectrum. A brute force algorithm is then used to select all the local maxima in the smoothed spectrum to build the initial peak list. Note that due to the smoothness of the wavelet-smoothed spectrum, the number of local maxima becomes an order of magnitude smaller than the number in the original spectrum.

All initial peaks are then ranked according to the volume-based estimation. In the first round, the default window size (differing by at most one step size in each dimension) is used to define the neighbors. Then, the top N peaks are extracted, where N is the length of the target protein, which is given as the input. The window size is adjusted according to Algorithm 1. The initial peaks are then re-ranked according to the estimated volume in the updated neighborhood. Finally, the top M peaks are selected as the prediction results, where M is either given by the users or is set to 1.2K as the default (where K is the expected number of peaks in this spectrum).

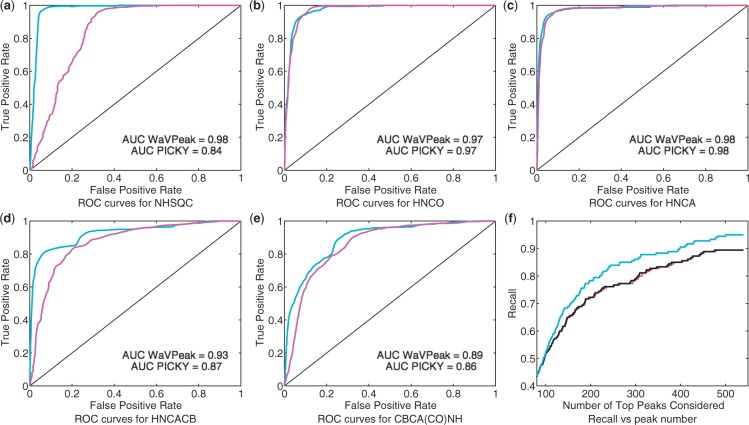
We compared the performance of the publicly available version of PICKY with WaVPeak, with a default noise cutoff threshold of 5 according to Alipanahi et al. (2009). Table 1 lists the performance of PICKY and WaVPeak on the benchmark set when the top 1.2K peaks are considered. It can be seen that when the same number of peaks is considered, WaVPeak has a consistently better recall than PICKY on four of the five types of spectra. It is well acknowledged in the NMR community that 15N-HSQC is the most reliable and clean spectrum among the five, whereas the HNCACB and CBCA(CO)NH spectra are the noisier. WaVPeak has an average improvement of 3%, 2%, 16% and 13% on recall over PICKY on 15N-HSQC, HNCO, HNCACB and CBCA(CO)NH, respectively. On the other hand, the precision of WaVPeak is comparable to that of PICKY on 15N-HSQC, HNCO and HNCA. The improvement in precision is significant for CBCA(CO)NH. However, PICKY has a much higher precision than WaVPeak on HNCACB. Since the number of top peaks is the same for both methods, this higher precision of PICKY seems to conflict with the lower recall. This is due to the fact that PICKY detects fewer than 1.2K peaks in the three HNCACB spectra. Figure 4a–e show the receiver operating characteristic (ROC) curves of PICKY and WaVPeak when different numbers of top peaks are considered. Therefore, WaVPeak is consistently and significantly more sensitive than PICKY, and the overall performance (F-score in Table 1 and area under curves (AUCs) in the Figure 4a–e is also better than that of PICKY.

Table 1.

Comparison between WaVPeak and PICKY on the 32 spectra of the eight proteins in the benchmark set

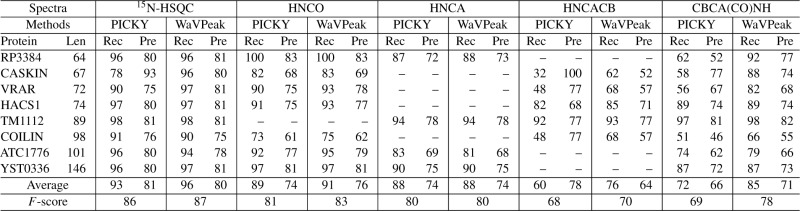graphic file with name bts078i3.jpg
Open in a new tab

To make the comparison, the top 1.2K peaks are considered, where K is the expected number of peaks. For PICKY, the peaks are sorted according to the intensity, whereas for WaVPeak, the peaks are sorted according to the volume. Recall, precision and F-score are listed as percentiles.

Fig. 4.

Fig. 4.

Open in a new tab

(a)–(e) ROC curves of WaVPeak and PICKY for NHSQC, HNCO, HNCA, HNCACB and CBCA(CO)NH, respectively. The curves for WaVPeak are cyan and the curves for PICKY are magenta. The areas under the curve (AUC) for both methods are given in the figures as well. (f) The relationship between the number of top peaks considered and the recall value for the CBCA(CO)NH spectrum of ATC1776. The magenta, black and cyan curves are for PICKY (with the default intensity-based filtering), Daubechies 3 wavelet plus intensity-based filtering and Daubechies 3 wavelet plus volume-based filtering, respectively.

It is clear from Table 1 that PICKY has a higher recall than WaVPeak on only 3 of the 32 spectra. It should be noted that on eight spectra, WaVPeak is able to identify significantly more true peaks than PICKY identifies (the improvement in recall is over 15%). These spectra are the 15N-HSQC spectrum of CASKIN, the HNCACB spectra of CASKIN, VRAR and COILIN, and the CBCA(CO)NH spectra of RP3384, CASKIN, VRAR and COILIN. With the exception of the CBCA(CO)NH spectrum of RP3384, PICKY's noise level elimination step overestimates the noise level. The hard-threshold-based elimination step then removes many true peaks. Some of these true peaks still have relatively strong intensities, but these intensities are lower than the estimated noise level. The others are weak peaks that are completely embedded in the noise, which are impossible for any hard-threshold-based method to discover. Therefore, PICKY has very low recall on these seven spectra, but quite high precision due to the small number of total peaks returned. For CBCA(CO)NH of RP3384, PICKY returns a large number of peaks. However, the recall is still 20% lower than that of WaVPeak. This further confirms that the wavelet-smoothed spectrum can discover the baseline peak shapes of the weak peaks that are embedded in the noise level, and the volume-based filtering can select the peaks, though they have very low intensities.

In Alipanahi et al. (2009), the cross-reference step is used to refine the peak lists of different spectra that share common atoms. This, apparently, is an efficient way to remove the false positives in practice. However, this assumes that a set of spectra are available. Our focus is to discover a more powerful and general method for peak picking for any given spectrum. Therefore, WaVPeak does not have a default cross-referencing step. It should be noted that cross-referencing can be easily implemented and applied as a post-processing step for any peak-picking method. When compared with the accuracy of PICKY after cross-referencing, WaVPeak without cross-referencing still has comparable F-scores (87% versus 87%, 82% versus 83%, 81% versus 80%, 72% versus 70% and 78% versus 78% for the five types of spectra, respectively).

3.3 Effects of wavelet-based smoothing and volume-based filtering

Table 1 demonstrates the performance of WaVPeak when the top 1.2K peaks are considered. It is also necessary to see how the accuracy changes when different number of peaks are considered. When the accuracy of WaVPeak and PICKY is compared using different numbers of peaks, the results are very similar to those presented in Table 1.

We further evaluate the contribution of wavelet-based smoothing and volume-based filtering. To measure the contribution of wavelet-based smoothing, we compare the smoothing module of WaVPeak plus the traditional intensity-based filtering by PICKY, which includes intensity-based filtering as a default. To evaluate the contribution of volume-based filtering, we compare the smoothing module of WaVPeak with different filtering methods, including intensity-based filtering and self-adapted, window-based filtering.

Figure 4f shows the recall curve of the three methods when different numbers of peaks are considered in the CBCA(CO)NH spectrum of the ATC1776 protein. The expected number of peaks is 180. Therefore, when <180 top peaks are considered, the recall for all methods is relatively low. The three methods have the same recall when <80 top peaks are taken into account. When we consider >80 peaks, wavelet-based smoothing plus the self-adapted, window-based filtering, i.e. WaVPeak, consistently has highest recall, whereas wavelet-based smoothing plus intensity-based filtering has the second highest recall. Note that the list of initial peaks for the wavelet-smoothed spectrum is the same for the two different filtering methods. The filtering method only re-ranks the peaks according to different measures. This clearly demonstrates that volume has much stronger power to distinguish peaks than intensity has. When using intensity-based filtering, wavelet-based smoothing has slightly better recall than PICKY. This demonstrates the power of the wavelet to discover the weak peaks that are discarded in PICKY's noise level elimination. By combining wavelet-based smoothing and self-adapted windows, WaVPeak has significantly higher recall than PICKY has. When triple the expected number of peaks are considered, WaVPeak has 95% recall, whereas the recall of PICKY is 89%.

3.4 Implementation details

One other advantage of WaVPeak is that it can be easily implemented. WaVPeak does not have as many steps as the other methods. WaVPeak is also an open source program. The MATLAB version of the source code with two testing spectra are available at http://faculty.kaust.edu.sa/sites/xingao/Pages/Publications.aspx. We are currently developing a web server and making WaVPeak a plug-in for interactive NMR data processing tools, such as SPARKY (Goddard and Kneller, 2007).

4 DISCUSSION

WaVPeak is proposed as a general peak-picking approach for any NMR spectrum. Therefore, WaVPeak does not use the properties of the specific spectra or the specific amino acids. Such properties, of course, will be useful to improve the accuracy of WaVPeak. One efficient way to reduce the number of false positive peaks further is to take the consensus of the peak lists from different peak-picking methods, such as PICKY and WaVPeak. This can significantly increase the precision (data not shown) while maintaining comparable recall. We have made WaVPeak an open source program so that expert knowledge can be easily encoded. Furthermore, we will make WaVPeak a plug-in to SPARKY or NMRView so that users can do interactive peak picking.

WaVPeak estimates the volume within self-adapted rectangular regions. The rectangular regions, however, may not be ideal, especially for peaks with a lot of overlap. In such a case, the volume of one peak may be added to that of another overlapped peak. A possible solution is to use a V–N plot to identify true peaks. For each of the initial peak candidates, we can start with the smallest diamond-shaped neighborhood region (differing by at most one step size in at most one dimension), and gradually increase the size of the region. This will generate a series of alternating diamond-shaped and rectangular regions. Consequently, we will have a series of estimated volumes for these regions. We can then plot the volume in relations to each neighborhood, which will be referred to as the V–N plot. The V–N plot (or its smoothed version) may reveal a lot of information about the patterns of the true peaks. For instance, if two peaks overlap a lot with each other or are even completely overlapping, it is possible that we only observe one peak in the wavelet-smoothed spectrum. However, in the V–Nplot, we can see that the AUC is almost twice the area of the other curves. If a local maximum is a fake peak, it is very unlikely that it has a regular and smooth peak shape. In the V–N plot, the curve will not be smooth either. The gradient change of the curve might be informative in identifying false peaks.

In evaluating the performance on the benchmark set in Section 3, the top M peaks are selected as the prediction results, where M is either given by the user or is set to 1.2K as the default. In reality, it would be desirable to have a fully automatic data-driven method to identify true peaks with high recall rates among the candidate peaks obtained after wavelet-based smoothing. This is, in fact, a multiple testing problem, which has received much attention in the statistical literature since the seminal article by Benjamini and Hochberg (1995). Work is currently underway to clarify how it can help in resolve our peak-picking problem.

5 CONCLUSION

In this article, we introduced WaVPeak, an automatic peak-picking method that is based on wavelet-based smoothing and volume-based filtering. Experimental results demonstrate that the wavelet-based smoothing outperforms existing decomposition techniques for this task, and volume-based filtering outperforms traditional intensity-based filtering. The combination of these two ideas results in a novel method that is significantly more accurate than the state-of-the-art peak-picking methods.

ACKNOWLEDGEMENTS

The spectra for TM1112, YST0336, RP3384 and ATC1776 were generated by Cheryl Arrowsmith's Lab at the University of Toronto. The spectra for COILIN, VRAR, HACS1 and CASKIN were provided by Logan Donaldson's Lab at York University. We are grateful to Ming Li for making PICKY publicly available. We thank Virginia Unkefer for proof-reading the manuscript.

Funding: This work was supported by the King Abdullah University of Science and Technology (KAUST) Award No. GRP-CF-2011-19-P-Gao-Huang, KAUST GMSV Collaborative Award, Hong Kong Research Grant Council grants (HKUST6019/10P), the National Nature Science Foundation of China (71071155), the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (10XNL007), and in part by NSFC (71071155).

Conflict of Interest: none declared.

REFERENCES

  1. Alipanahi B., et al. PICKY: a novel SVD-based NMR spectra peak picking method. Bioinformatics. 2009;25:i268–i275. doi: 10.1093/bioinformatics/btp225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alipanahi B., et al. Error tolerant NMR backbone resonance assignment and automated structure generation. J. Bionform. Comput. Biol. 2011;9:15–41. doi: 10.1142/s0219720011005276. [DOI] [PubMed] [Google Scholar]
  3. Altieri A., Byrd R. Automation of NMR structure determination of proteins. Curr. Opin. Struct. Biol. 2004;14:547–553. doi: 10.1016/j.sbi.2004.09.003. [DOI] [PubMed] [Google Scholar]
  4. Antz C., et al. A general Bayesian method for an automated signal class recognition in 2D NMR spectra combined with a multivariate discriminant analysis. J. Biomol. NMR. 1995;5:287–296. doi: 10.1007/BF00211755. [DOI] [PubMed] [Google Scholar]
  5. Barache D., et al. The continuous wavelet transform, an analysis tool for NMR spectroscopy. J. Magn. Reson. 1997;128:1–11. [Google Scholar]
  6. Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. Roy. Stat. Soc. B Met. 1995;57:289–300. [Google Scholar]
  7. Carrara E., et al. Neural networks for the peak-picking of nuclear magnetic resonance spectra. J. Neural Netw. 1993;6:1023–1032. [Google Scholar]
  8. Corne S., et al. An artificial neural network for classifying cross peaks in two dimensional NMR spectra. J. Magn. Reson. 1992;100:256–266. [Google Scholar]
  9. Dancea F., Güntert U. Automated protein NMR structure determination using wavelet de-noised NOESY spectra. J. Biomol. NMR. 2005;33:139–152. doi: 10.1007/s10858-005-3093-1. [DOI] [PubMed] [Google Scholar]
  10. Daubechies I. Ten Lectures on Wavelets. Philadelphia: SIAM; 1992. [Google Scholar]
  11. Garret D., et al. A common sense approach to peak picking in two-, three-, and 4D spectra using automatic computer analysis of contour diagrams. J. Magn. Reson. 1991;95:214–220. doi: 10.1016/j.jmr.2011.09.007. [DOI] [PubMed] [Google Scholar]
  12. Goddard T., Kneller D. SPARKY 3. San Francisco: University of California; 2007. [Google Scholar]
  13. Gronwald W., Kalbitzer H. Automated structure determination of proteins by NMR spectroscopy. Prog. Nucl. Magn. Reson. 2003;44:33–96. [Google Scholar]
  14. Gronwald W., Kalbitzer H. Automated structure determination of proteins by NMR spectroscopy. Prog. Nucl. Magn. Res. Sp. 2004;44:33–96. [Google Scholar]
  15. Güntert T. Automated structure determination from NMR spectra. Eur. Biophys. J. 2009;38:129–143. doi: 10.1007/s00249-008-0367-z. [DOI] [PubMed] [Google Scholar]
  16. Günther U., et al. NMRLAB—advanced NMR data processing in matlab. J. Magn. Reson. 2000;145:201–208. doi: 10.1006/jmre.2000.2071. [DOI] [PubMed] [Google Scholar]
  17. Günther U., et al. WAVEWAT—improved solvent suppression in NMR spectra employing wavelet transforms. J. Magn. Reson. 2002;156:19–25. doi: 10.1006/jmre.2002.2534. [DOI] [PubMed] [Google Scholar]
  18. Herrmann T., et al. Protein NMR structure determination with automated NOE-identification in the NOESY spectra using the new software ATNOS. J. Biomol. NMR. 2002;24:171–189. doi: 10.1023/a:1021614115432. [DOI] [PubMed] [Google Scholar]
  19. Hu M., et al. Wavelet transform analysis of NMR structure ensembles to reveal internal fluctuations of enzymes. Amino Acids. 2011 doi: 10.1007/s00726-011-0895-1. doi: 10.1007/s00726-011-0895-1. [DOI] [PubMed] [Google Scholar]
  20. Jang R., et al. Towards automated structure-based NMR resonance assignment. Vol. 6044. Berlin Heidelberg: Springer-Verlag; 2010. pp. 189–207. of Lecture Notes in Computer Science. [Google Scholar]
  21. Jang R., et al. Towards fully automated structure-based NMR resonance assignment of 15N-labeled proteins from automatically picked peaks. J. Comput. Biol. 2011;18:347–363. doi: 10.1089/cmb.2010.0251. [DOI] [PubMed] [Google Scholar]
  22. Johnson B., Blevins R. NMR View: a computer program for the visualization and analysis of NMR data. J. Biomol. NMR. 1994;4:603–614. doi: 10.1007/BF00404272. [DOI] [PubMed] [Google Scholar]
  23. Kleywegt G., et al. A versatile approach toward the partially automatic recognition of cross peaks in 2D1H NMR spectra. J. Magn. Reson. 1990;135:288–297. [Google Scholar]
  24. Koradi R., et al. Automated peak picking and peak integration in macromolecular NMR spectra using AUTOPSY. J. Magn. Reson. 1998;135:288–297. doi: 10.1006/jmre.1998.1570. [DOI] [PubMed] [Google Scholar]
  25. Korzhneva D., et al. MUNIN: application of three-way decomposition to the analysis of heteronuclear NMR relaxation data. J. Biomol. NMR. 2001;21:263–268. doi: 10.1023/a:1012982830367. [DOI] [PubMed] [Google Scholar]
  26. Lang M., et al. Noise reduction using an undecimated discrete wavelet transform. IEEE Signal Proc. Lett. 1996;3:10–12. [Google Scholar]
  27. Mallat S. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989;11:674–693. [Google Scholar]
  28. Neue G. Simplification of dynamic NMR spectroscopy by wavelet transforms. Solid State Nucl. Magn. Reson. 1996;5:305–314. doi: 10.1016/0926-2040(95)01196-x. [DOI] [PubMed] [Google Scholar]
  29. Orekhov V., et al. MUNIN: a new approach to multi-dimensional NMR spectra interpretation. J. Biomol. NMR. 2001;20:49–60. doi: 10.1023/a:1011234126930. [DOI] [PubMed] [Google Scholar]
  30. Rouh A., et al. Bayesian signal extraction from noisy FT NMR spectra. J. Biomol. NMR. 1994;4:505–518. doi: 10.1007/BF00156617. [DOI] [PubMed] [Google Scholar]
  31. Shao X., et al. Resolution of the NMR spectrum using wavelet transform. Appl. Spectrosc. 2000;54:731–738. [Google Scholar]
  32. Williamson M., Craven C. Automated protein structure calculation from NMR data. J. Biomol. NMR. 2009;43:131–143. doi: 10.1007/s10858-008-9295-6. [DOI] [PubMed] [Google Scholar]
  33. Wüthrich K. NMR of Proteins and Nucleic Acids. New York: John Wiley and Sons; 1986. [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES