A new approach to bias correction in RNA-Seq

Abstract

Motivation: Quantification of sequence abundance in RNA-Seq experiments is often conflated by protocol-specific sequence bias. The exact sources of the bias are unknown, but may be influenced by polymerase chain reaction amplification, or differing primer affinities and mixtures, for example. The result is decreased accuracy in many applications, such as de novo gene annotation and transcript quantification.

Results: We present a new method to measure and correct for these influences using a simple graphical model. Our model does not rely on existing gene annotations, and model selection is performed automatically making it applicable with few assumptions. We evaluate our method on several datasets, and by multiple criteria, demonstrating that it effectively decreases bias and increases uniformity. Additionally, we provide theoretical and empirical results showing that the method is unlikely to have any effect on unbiased data, suggesting it can be applied with little risk of spurious adjustment.

Availability: The method is implemented in the seqbias R/Bioconductor package, available freely under the LGPL license from http://bioconductor.org

Contact: dcjones@cs.washington.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In the last few years, RNA-Seq has emerged as a promising alternative to microarrays in quantifying RNA abundance. But, as microarray technology has brought with it technical challenges ranging from developing robust normalization to accounting for cross-hybridization, RNA-Seq presents a new set of challenges. As first noted by Dohm et al. (2008), a particular challenge is the often complex and protocol-specific influence of nucleotide sequence on quantification.

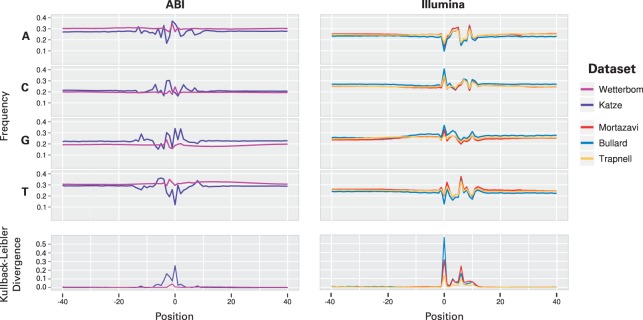
In an ideal experiment, the number of RNA-Seq reads mapping to a particular position in the genome is a function of RNA abundance and should not be additionally dependent on the sequence at that position. Yet, this is not the case. As illustration, Figure 1 plots this non-uniformity in nucleotide frequencies on five datasets (Table 1), each using a different protocol.

Fig. 1.

Nucleotide frequencies are plotted relative to the start (labeled position 0) of each mapped read, respecting strand, and grouped by platform (Illumina or ABI SOLiD). The datasets plotted here are those used for evaluation, listed in Table 1. The sequence is taken from the genomic context surrounding the read, so that −40 to −1, for example, fall outside the read sequence itself. The symmetrized Kullback–Leibler divergence is used to summarize the difference in nucleotide frequency compared with a fixed estimate of background nucleotide frequencies made by sampling many positions near mapped reads. Under the assumption that reads are sampled uniformly from transcripts, each of the plots should be essentially flat.

Table 1.

Datasets on which the methods are evaluated

Experiment	Species	Platform	Protocol	Read length
Wetterbom et al. (2010)	Chimp.	ABI	mRNA	33
Katze,M.G. (unpublished data)	Macaque	ABI	WT	50
Bullard et al. (2010)	Human	Illumina	mRNA	35
Mortazavi et al. (2008)	Mouse	Illumina	mRNA	33
Trapnell et al. (2010)	Mouse	Illumina	mRNA	75

The protocol column lists whether a poly-A priming step to select for polyadenylated transcripts was used (mRNA), or depletion of ribosomal RNA with no step to select for polyadenylated transcripts (WT).

These biases may adversely effect transcript discovery, as low level noise may be overreported in some regions, and in others, active transcription may be underreported. They render untrustworthy comparisons of relative abundance between genes or isoforms, and any test of differential expression hangs on the assumption that these biases are identical between replicates, an undesirable assumption given that the causes of the bias are not well understood. Additionally, in many tests of differential expression higher read count will result in higher statistical confidence. It follows that the sensitivity of such a test will also be biased by sequence, affecting downstream analysis such as gene ontology enrichment tests.

This bias, though observed primarily in the 5′ end of a read, is not resolved by trimming the reads prior to mapping (Hansen et al., 2010) (Section 1 in Supplementary Material), suggesting it is not a result of erroneous base calling, and that a more sophisticated means of correction is needed.

Li et al. (2010) propose two models. The first is a Poisson linear model, in which read counts across a transcript follow an inhomogeneous Poisson process. The read count at position i within the transcript is Poisson distributed with parameter λ_i, where, log(λ_i) is the sum of independent weights determined by the nucleotide at each position surrounding the read start, in addition to a term capturing the abundance of the transcript.

The second model is based on multiple additive regression trees, or MART (Friedman and Meulman, 2003). In their tests, the MART model shows a moderate improvement over the Poisson linear model. Both models are fit to a number of abundant test genes, requiring existing gene annotations for the reference genome.

Another model, proposed by Hansen et al. (2010), directly estimates the distribution of initial heptamers within reads, then estimates a presumed background heptamer distribution, sampled from the ends of reads. The read count at a given position is then adjusted by the ratio of the foreground and background heptamer probabilities. Specifying two distributions over heptamers (i.e. foreground and background distributions) requires 2(4⁷−1)=32 766 parameters, so while no gene annotations are needed to train such a model, a significant number of reads are required, and a number that increases exponentially with k, if it were desirable to model k-mers for k>7.

Lastly, Roberts et al. (2011) have recently published a description of another approach, in which sequence probabilities are modeled by variable-order Markov chains. The structure of these Markov chains are hard-coded, chosen in advance using a hill-climbing algorithm on a representative dataset. This method is implemented in the latest version of Cufflinks (Trapnell et al., 2010), and tightly incorporated into its estimation of transcript abundance, requiring either predicted or existing gene annotations.

Here we propose a new approach, using Bayesian networks to model sequence probabilities. Unlike the methods of Roberts or Li, our model requires no gene annotations, nor even the assumption that the short reads are derived from RNA. In this sense, we build on the work done by Hansen et al. (2010), generalizing their approach in a way we find to be more robust and effective at correcting for bias in a variety of protocols. Due to the weak assumptions required by our model, it is applicable and potentially useful in any setting in which short reads are aligned to a reference sequence.

2 METHODS

2.1 Principle

We begin with a natural model of an RNA-Seq experiment (and one that is often assumed, whether implicitly or otherwise). The number of reads x_i aligned to genomic position i is an unbiased estimate of RNA abundance. Furthermore, we assume reads may be treated as independent and identically distributed samples. That is, if N reads are generated, and m_i is the event that a generated read maps to position i, then E[x_i]=NPr[m_i].

The experiment may be considered unbiased with regards to sequence if, having observed the nucleotide sequence s_i surrounding position i, the expected number of reads sampled from position i is independent of s_i, i.e. if

From Bayes' rule,

This suggests a natural scheme in which observations may be reweighted to correct for bias. First, define the sequence bias b_i at position i as b_i=Pr[s_i]/Pr[s_i|m_i].

Now, if we reweight the read count x_i at position i by b_i, we have,

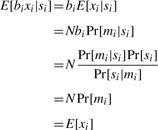Thus, the reweighted read counts are made unbiased.

To estimate the bias b_i, we must make estimates of the background sequence probability Pr[s_i] and the foreground sequence probability Pr[s_i|m_i], the latter being the probability of the sequence given a read being sampled from its position. Estimating bias is therefore a problem of finding a model of sequence probability that is sufficiently complex to capture the common features of the training data yet avoids overfitting.

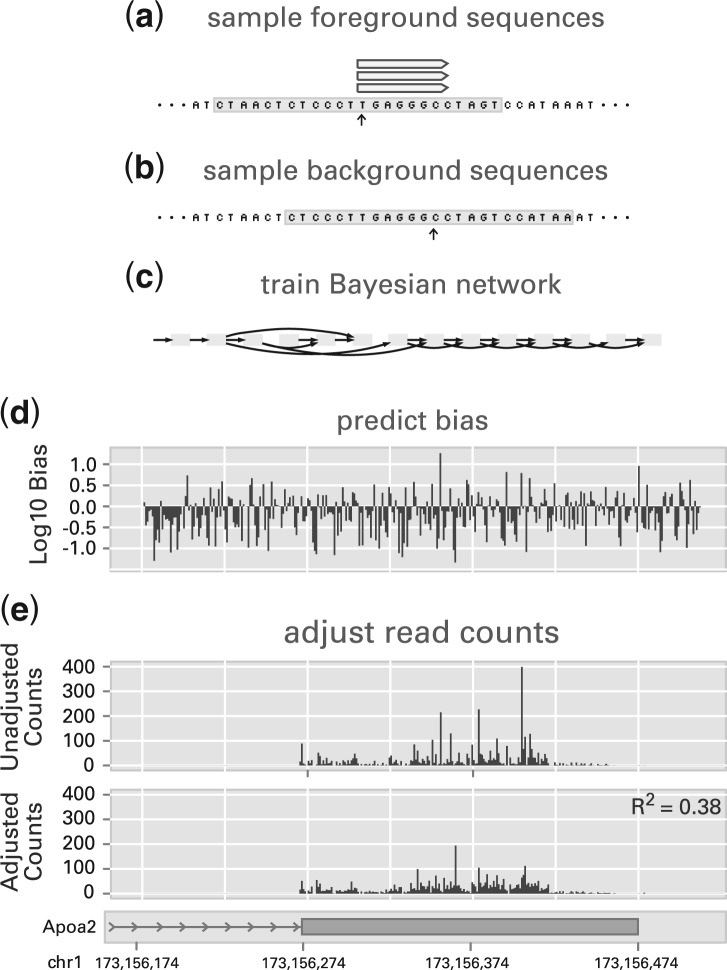
Toward that end, we propose training a Bayesian network using examples of foreground and background sequences. By training the model discriminatively and penalizing model complexity, we can avoid a model that is overparametrized, excluding parameters that are insufficiently informative in discriminating between foreground and background. The Bayesian network can then be used to evaluate sequence probability, and thus bias, at any genomic position. Figure 2 gives a schematic overview of the proposed model.

Fig. 2.

An overview of the approach taken: (a) foreground sequences are sampled from the regions surrounding the starts of mapped reads; (b) background sequences are sampled by randomly offsetting foreground positions; (c) a Bayesian network is trained to discriminate between the set of sampled foreground and background sequences; (d) and the model is evaluated at each position within a locus, predicting bias. The predicted bias can then be used to adjust read counts, as in (e). In (d) and (e), we show the results of this method applied to the 3′ UTR of Apoa2, using data from Mortazavi et al. (2008). In bias coefficients predicted across 10 million positions of chromosome 1, the log10 bias of 95% of the positions were between −1.14 and 0.63, suggesting that most adjustments are not large. The R² measure, detailed in Section 3.2, gives the relative increase in log-likelihood under a uniform sampling model, after correcting for bias, with 1.0 indicating a perfect fit, and the score of 0.38 here indicating a significant increase.

We have so far ignored one complication: the RNA abundance that we wish to estimate is not itself independent of the nucleotide sequence. Notably, exonic DNA tends to be more GC-rich than intergenic DNA. If background sequences are sampled uniformly from the genome. we run the risk of incorrectly adjusting for biological sequence bias, rather than technical sequence bias. To avoid this, we propose using paired training data. Each foreground training sequence is paired with a background sequence taken from a nearby position that is likely to have similar abundance and general nucleotide composition. Alternatively, we could pair foreground samples with background samples from within the same transcript, but we prefer to avoid dependence on existing gene annotations.

The methods proposed by Hansen et al. (2010) and (Roberts et al., 2011) also treat bias correction as a problem of estimating foreground and background sequence probabilities. They differ primarily in how these sequence probabilities are estimated. Li et al. (2010) estimate reweighting coefficients (b_i, in our notation) directly, given training data consisting of long annotated, highly expressed transcripts.

2.2 Estimation

To estimate sequencing bias, we train a Bayesian network in which each node represents a position in the sequence, relative to the read start, and edges encode dependency between positions. Bayesian networks have been applied to recognize motifs in nucleotide sequences in the past, in particular in modeling splice sites (Cai et al., 2000; Chen et al., 2005) and transcription factor binding sites (Ben-Gal et al., 2005; Grau et al., 2006; Pudimat et al., 2005).

In our model, we do not rely on constraining the set of networks (e.g. to trees), and instead approximate the NP-Hard problem of determining the optimal network structure using a fast hill-climbing algorithm. Furthermore, we train our model discriminatively; only parameters that are deemed informative in discriminating between foreground and background sequences are included in the model. We thus seek to train a model that reduces bias, without including uninformative parameters that would only increase variance.

2.2.1 Sampling

The model is trained on n sequences, one half labeled as foreground, the other background, sampled from the reference genome. To obtain the foreground sequences, we take sequences surrounding (extending 20 nt to either side, by default) the start positions of a randomly sampled set of n/2 aligned reads. To avoid the risk of the method being overfit to reads deriving from a few highly expressed genes, we ignore duplicate reads, which we define as two reads mapping to the same location in the genome. The nucleotide sequence is taken from the genome, rather than the reads themselves, allowing us to include positions outside of the read.

To obtain background training sequences, we randomly offset the positions from which the foreground sequences were sampled. The offset is drawn from a zero-mean Gaussian (with σ²=10, by default), and rounded to the nearest integer, away from zero. By using such a scheme, we attempt to mitigate the effects of biological sequence bias, sampling positions that are more likely to be biologically similar.

This procedure produces a training set of n sequences with accompanying labels T={(s₁, x₁), (s₂, x₂),…, (s_n, x_n)}. The label x_i is binary, indicating classification as background (x_i=0) or foreground (x_i=1).

2.2.2 Training

To determine the structure and parameters of the Bayesian network, we use a hill-climbing approach similar to the algorithm described by Grossman and Domingos (2004). The network structure is determined by greedily optimizing the conditional log-likelihood:

where Pr[x] is flat (i.e. Pr[x=0]=Pr[x=1]=0.5) since we sample foreground and background positions equally.

As we will be estimating parameters and evaluating the likelihood on the same set of samples, simply maximizing the likelihood would severely overfit the training set. We thus penalize model complexity heuristically using the Bayesian information criterion (Schwarz, 1978). Where m is the number of parameters needed to specify the model, we maximize, ℓ′=2ℓ − m log n.

Some benefit might be obtained from a more highly tuned complexity penalty. However, since the model is trained greedily, additional parameters will be decreasingly informative, and increasingly similar between foreground and background. Adding more parameters will have little effect. Only when m is allowed to grow exponentially does the prediction become polluted by small deviations between thousands of uninformative parameters.

At each step of the optimization procedure, every possible edge or position addition, removal or edge reversal that produces a valid, acyclic network is evaluated, and the alteration that increases the score ℓ′ the most is kept. This process is repeated until a local maximum is found, in which no single alteration to the network will increase the score. Given the network structure, the parameters are estimated directly from the observed nucleotide frequencies in the training data.

The run time of the training procedure is further reduced in practice by imposing the following two restrictions on the structure of the network, First, the in-degree (i.e. number of parents) of any node must be less than some number p_max. Secondly, for all edges (i,j), |j−i|≤d_max for some number d_max. This latter rule encodes the assumption that distant nucleotides are effectively independent. We choose p_max=4 and d_max=10, as reasonable default values (Section 2 in Supplementary Material).

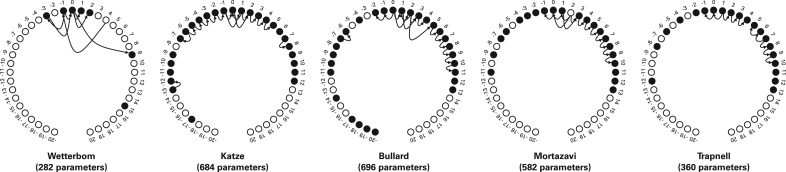
Figure 3 shows examples of the structure learned when this procedure is applied to several datasets, using 100 000 reads from each.

Fig. 3.

The network structures learned on each of the datasets are displayed. Positions are relative to the read start, which is labeled 0. Hollow circles indicate positions that were not included in the model, being deemed uninformative, given the other positions and edges. The number of parameters needed to specify each model is listed in parenthesis below. Applied to data with less bias, a sparser model is trained, as evinced by the Wetterbom dataset. Note that dependencies (i.e. arrows) tend to span a short distances, and nodes tend to have a small in-degree (i.e. have few inward arrows). In practice, we save time in training by prohibiting very distant dependencies (>10, by default) or very high in-degrees (> 4, by default).

3 RESULTS

Since we cannot observe directly the underlying RNA abundance, our evaluation strategy relies on testing three assumptions we make of an ideal, unbiased RNA-Seq experiment.

1. Positional nucleotide frequencies (as in Fig. 1), measured from reads within exons, should not differ greatly from frequencies measured by sampling uniformly within the same exons.

2. Read counts across a single exon should follow, approximately, a Poisson process.

3. Adjusting for bias in RNA-Seq should increase the agreement between RNA-Seq and another method of quantification.

Evident from Figure 2, the assumption of uniform read coverage often does not hold in typical RNA-Seq datasets. Although the bias corrected read counts across the exon pictured in this example are visibly more uniform, we sought a simple, objective tests that could be applied genome-wide. To this end, we used cross-validation tests (i.e. methods were trained and tested on disjoint subsets of the same RNA-Seq datasets) of a quantitative measure of the increase in uniformity of nucleotide frequencies (Kullback–Leibler divergence in Section 3.1) and increase in uniformity of read coverage (Poisson regression in Section 3.2). Additionally, we compare RNA-Seq-based estimate of gene expression to quantitative real-time PCR (qRT-PCR) based estimates for the same genes, showing increased correlation between the two methods after bias correction (Section 3.3).

To evaluate the first two assumption, we applied our procedure (labeled ‘BN’) as well as those of Li et al. (2010) (‘GLM’ and ‘MART’) and Hansen et al. (2010) (7mer), which are implemented in the R packages mseq and Genominator, respectively, to four publicly available datasets (Bullard et al., 2010; Mortazavi et al., 2008; Trapnell et al., 2010; Wetterbom et al., 2010), as well as an unpublished dataset of our own (Table 1).

Each method was trained on data taken from chromosomes 1–8 of the genome from which the reads were mapped (including chromosomes 2a and 2b of the Chimpanzee genome). For evaluation, we drew a set of long, highly expressed exons from the remaining chromosomes. In particular, for each reference sequence, beginning with the set of exons annotated by Ensembl release 60 (Hubbard et al., 2009), we removed any exons with known alternate splice sites, then chose the top 1000 exons by read count, restricting ourselves to those at least 100 nt long.

The differences in the methods being tested necessitated training procedures unique to each. The total number of reads used to train each method is listed in Section 3 in Supplementary Material, and below we describe the procedure used for each.

Li et al. (2010) recommends that their MART and GLM models be trained using the 100 most abundant genes. We used 1000 exons from chromosomes 1–8, otherwise chosen in a manner identical to that which was used to select the test exons. Both the GLM and MART models were trained considering the initial read position and 20 nt upstream and downstream, and otherwise using default parameters.

Hansen et al. (2010) recommends using all the reads to estimate heptamer frequencies used by their model. The training procedure works by simple tallying of frequencies. The implementation of this model in the Genominator package uses a great deal of memory, and we were unable to train with the volume of data we wished, so we reimplemented the model and trained it on all of the reads aligned to chromosomes 1–8.

We evaluated several variations of the heptamer model. The suggested method involved averaging the frequencies of the first two heptamers of each read. Yet, we found that in every case, this performed worse than simply counting the frequencies of the initial heptamer, and thus we report only the latter. The background frequencies are estimated from positions 18–23 in each read.

Our own method was trained on the 100 000 randomly selected reads from chromosomes 1–8, considering the initial read position and 20 nt upstream and downstream.

All datasets were mapped using Bowtie (Langmead et al., 2009) using default parameters against, respectively, the hg19, mm9, rheMac2 and panTro2 genome assemblies obtained from the UCSC Genome Browser (Karolchik et al., 2008).

3.1 Kullback–Leibler divergence

Plotting the nucleotide frequencies (Fig. 1), we observe an obvious bias. To quantify the non-uniformity observed in these plots, we use the symmetrized Kullback–Leibler (KL) divergence (Kullback and Leibler, 1951).

If f_x is the background frequency of a k-mer x, and f′_x the observed frequency, the KL divergence is computed as

where the sum is over all k-mers. This can be thought of as a measure dissimilarity between two probability distributions. If f_x and f′_x for a k-mer x are approximately equal, their log-ratio will be approximately zero, leading to a small KL divergence (exactly zero, when the distributions are equal). Conversely, very different k-mer frequencies will result in a larger KL divergence.

When computing the KL divergence, there is a risk of the measure being dominated by a small number of reads with many duplicates. Yet, given the high coverage of the exons being tested, if duplicate reads are excluded, it may not capture the full effect of bias correction. To account for these opposing concerns, we adopt the following method: all reads contained within the exon being tested are ranked by the number of duplicates. We then exclude reads that are ranked in the lower half, and count each read ranked in the upper half only once, ignoring duplicates.

Under the assumption of uniform sampling, the set of reads ranked in the upper half should not depend on sequence, and we should expect the KL divergence to be low. We compute the divergence by reweighting the read counts using the predicted bias coefficient before ranking the reads, choosing those reads ranked in the upper half of each exon, ignoring duplicate reads, and then tallying frequencies of overlapping k-mers. The k-mer distribution obtained is then compared to a background distribution obtained by redistributing reads uniformly at random within their exons.

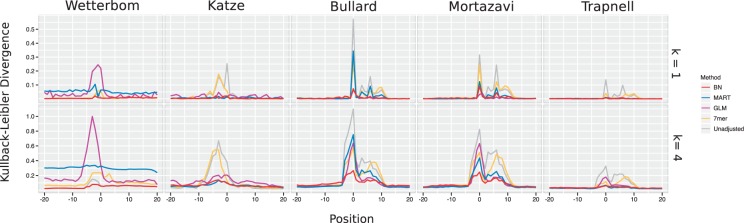
We repeated the procedure for k ∈{1, 2, 3, 4, 5, 6}. The results of this analysis are plotted in Figure 4, for k = 1 and k = 4. The remaining cases are plotted in Section 4 in Supplementary Material.

Fig. 4.

The KL divergence compares the frequency of k-mers (here, for k=1 and k=4) surrounding the starts of aligned reads to the frequencies expected under the assumption of uniform sampling from within exons. A large divergence indicates significant bias. Plotted here is the divergence from unadjusted read counts as well as after adjusting read counts using each method.

3.2 Poisson regression

In this comparison, we measure the uniformity of the data, or more precisely how well the counts conform to a Poisson process. The assumption of positional read counts following a Poisson distribution is known to be a poor fit (Srivastava and Chen, 2010), but measuring the improvement in the fit derived from correcting for bias remains a principled and easily interpreted criterion. This increase in uniformity is illustrated in Figure 2.

We perform maximum-likelihood fitting of two models. In the null model, the Poisson rate is fixed for each test exon. That is, for position j within exon i, the rate is λ_ij = a_i where a_i is the parameter being fit. For comparison, we then fit a model in which the rate is also proportional to the predicted bias coefficients: λ′_ij = a_ib_ij.

If the null model has log-likelihood L, and the bias-corrected model L′, a simple goodness of fit measure is the improvement in log-likelihood [a statistic commonly known as McFadden's pseudo-coefficient of determination (McFadden, 1974)], defined as, R² = 1 − L′/L.

This measure can be interpreted as the improvement in fit over the null model, with R² = 1 indicating a perfect fit, occurring when the model being evaluated achieves a likelihood of 1. Smaller number indicate an increasingly worse fit, with R² = 0 representing no improvement over the null model, and R² = 0.5, for example, indicating the model has a log-likelihood equal to half that of the null model (a large improvement, corresponding to, for example, the likelihood increasing over 100-fold if the initial log-likelihood was −9.6, which is the mean per-position log-likelihood under the null model). This measure has the added advantage that it can take on values <0, indicating that the model has worse fit than the null model (i.e. when adjusting read counts according the bias coefficients leads to less uniform read coverage).

We compute R² for each of the test exons, giving us a sense of the variability of the effectiveness of each model. The results of this analysis are plotted in Figure 5. To summarize each model with a single number, we can examine the median R² value, as listed in Table 2. Our method shows a highly statistically significant improvement in performance over other methods in all but one comparison, in which the MART method performs equally.

Fig. 5.

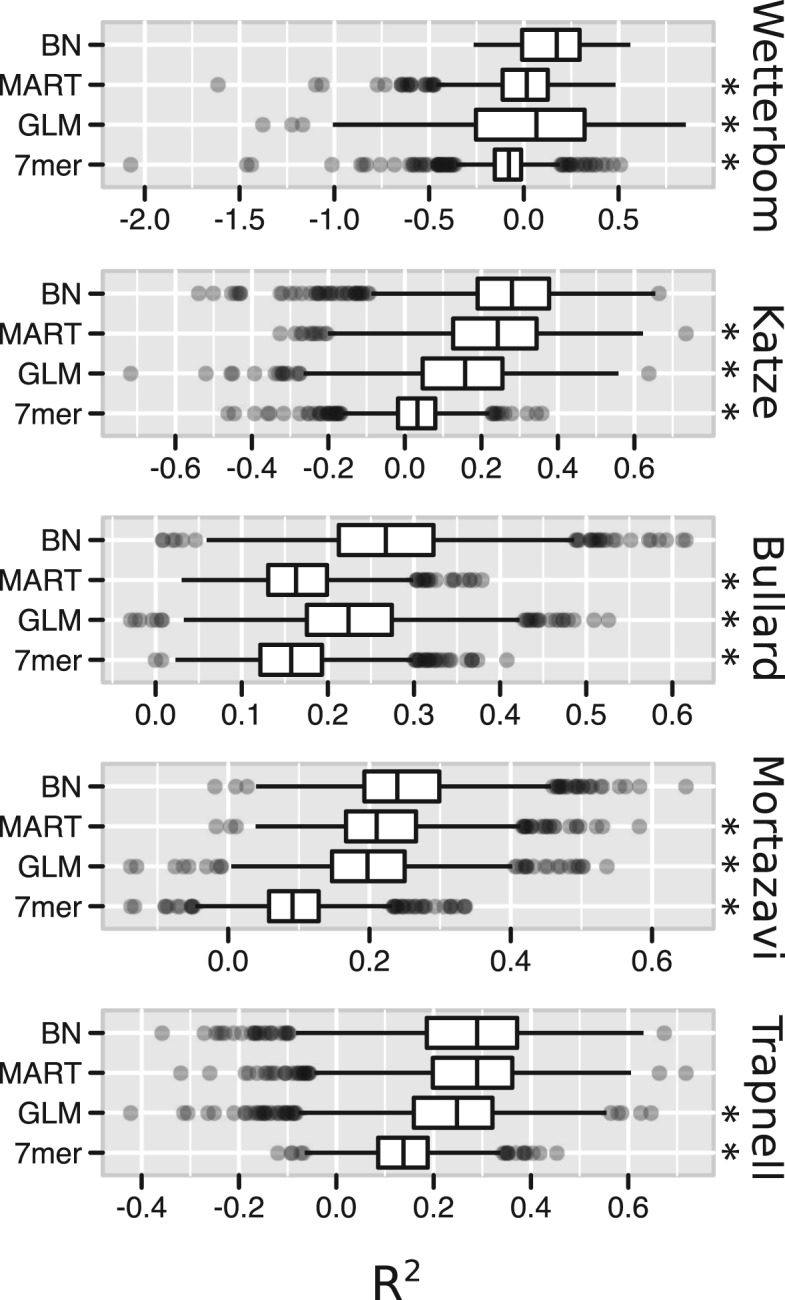
For each of the 1000 test exons, we compute McFadden's pseudo-coefficient of determination R², equivalent to the improvement in log-likelihood under the bias-corrected model. The statistic is positive, and increases as uniformity is increased, and negative when uniformity is decreased. Marked with asterisks are methods over which the BN approach showed a statistically significant improvement when applied to the same data, according to a one-sided Wilcoxon signed-rank test. In each of those marked, we observed P < 10⁻²³. Boxes are plotted to mark the 25, 50 and 75% quantiles, with whiskers extending to 1.5 times the interquartile range (i.e. the span between the 25% and 75% quantiles), and dots marking more extreme values.

Table 2.

The median R² goodness of fit statistic across test exons

	BN	MART	GLM	7mer
Wetterbom	0.174	0.016	0.066	−0.079
Katze	0.280	0.243	0.158	0.033
Bullard	0.267	0.163	0.224	0.157
Mortazavi	0.240	0.210	0.197	0.091
Trapnell	0.289	0.289	0.248	0.138

The R² statistic measures increased uniformity in read coverage, after correcting for bias. Here the median R² across the test exons is listed for each method and sample. A higher R² indicates a better fit. The highest value in each row is highlighted in bold.

3.3 qRT-PCR correlation

We used sequencing data previously published by Au et al. (2010) to evaluate the effect bias correction has on correlation to measurements made by TaqMan RT–PCR, made available by the the Microarray Quality Control project (Shi et al., 2006). The RNA-Seq data shows a pattern of bias similar to that seen in the other samples sequenced on an Illumina platform (Section 6 in Supplementary Material). This evaluation does not rely on an assumption that qRT-PCR is necessarily more accurate than RNA-Seq-based quantification, only that qRT-PCR is not biased in the same way as the RNA-Seq data.

To evaluate the efficacy of each of the bias correction methods considered, we counted reads overlapping each gene, defining the gene by the union of every transcript in release 60 of the Ensembl gene annotations. Counts were then normalized by dividing by the length of these genes. We then removed any genes with a read count <10, or that did not correspond to a unique TaqMan probe.

Each method was trained in a manner identical to that used in the analysis of Sections 3.1 and 3.2, but without restricting the training data to the first eight chromosomes. After adjusting read counts according to the predicted sequence bias, we computed the Pearson's correlation coefficient r between log read counts and log TaqMan expression values, which are averaged across three replicates. These correlations are listed in Table 3. Our method shows a statistically significant increase in correlation compared with the other methods.

Table 3.

The Pearson's correlation coefficient r between log-adjusted read counts and log-adjusted TaqMan values

Method	Correlation
Unadjusted	0.6650**
7mer	0.6680**
GLM	0.6874**
MART	0.6998*
BN	0.7086

We estimated the statistical significance of the improvement in correlation using the BN method over the other methods using a simple boostrap procedure. A bootstrap sample is formed by sampling, with replacement, 648 genes from the original set of the same size. The correlation is then computed for this set, using the adjusted count from each method. We repeated this procedure one million times, and counted the number of times each of the competing methods achieved a higher correlation than the BN method. Those marked with a single asterisk achieved a higher correlation fewer than 1000 times, resulting in a P < 10⁻³. Those marked with two asterisks achieved a higher correlation in none of the bootstrap samples, indicating a P < 10⁻⁶.

3.4 Robustness

Training our model on more reads leads to more accurate estimation of bias, but an increasingly long training time. For example, in our tests, fitting our model to 100 000 reads from the Mortazavi data, training time was approximately 45 min, running on one core of a 3 GHz Intel Xeon processor. However, limiting the training to 25 000 reads leads to a model that is nearly as accurate while requiring <4 min to train. A full discussion of this trade-off is provided in Section 6 in Supplementary Material.

The quality of the solution depends also on two other parameters: the standard deviation at which background sequences are sampled, and the weight applied to the penalty term of the BIC, yet it is not particularly sensitive to their values. (The median R² goodness-of-fit statistic used in Section 3.2 varied by <25% as these parameters were varied over a range of 10⁴. See Section 2 in Supplementary Material.) The same is true of the p_max and d_max parameters, used restrict the in-degree and edge distance of the model, respectively, in order to control training time. Our tests show that these parameters need only be greater than zero for an adequate model to be trained for the Mortazavi data. In all our evaluation, no special tuning of the parameters was performed, suggesting it can be used effectively across datasets without any intervention.

Additionally, experimental and theoretical analysis suggest that the procedure is very resistant to inclusion of extraneous parameters. In Section 11 in Supplementary Material, we prove an upper bound on the probability of our model predicting any bias, if the experiment is in fact unbiased, showing that there very little risk in the applying the method to an unbiased data set. In particular, if >10 000 reads are used in the training procedure, the probability that any adjustment at all will is made is <0.0004.

4 DISCUSSION

We have demonstrated that sequence bias can confound, sometimes severely, quantification in RNA-Seq experiments, and we have introduced an effective method to account for this bias without the need of existing gene annotations. The analysis provided demonstrates that our method shows significant improvement in three aspects: uniformity of read coverage, consistency of nucleotide frequencies and agreement with qRT-PCR.

In our results, estimating initial heptamer frequencies was not seen to be as effective as the other models, even when data generated using random hexamer priming was used. A possible explanation is, given the large number of parameters needed to estimate heptamer frequencies (4⁷ = 16 383), these parameters are estimated with less accuracy than in models requiring fewer parameters. Yet, we trained the 7mer model on a minimum of 1.9 million reads (Section 3 in Supplementary Material), a number that based on theoretical results, following from work by Birch (1964) and included in Section 10 in Supplementary Material for completeness, suggests should lead to accurate estimates

A perhaps more significant factor is that this method does not capture bias outside of the initial heptamer, though many datasets clearly are affected by bias in other positions. Thus to improve the performance, it seems necessary to increase the size of the k-mers being considered. However, exponentially more reads would be required for an accurate estimate since the accuracy of the model, as quantified by its KL divergence from the true distribution, is (r−1)/2n, where r=4^k is the number of parameters that must be estimated (Section 10 in Supplementary Material).

Our method generalizes this approach, attempting to overcome this problem by using an estimation of sequence probability that requires fewer parameters and can account for bias outside of the initial heptamer. In all our tests, this approach was at least as effective as those of Li et al. (2010), despite not requiring gene annotations or manual selection of training examples.

We have not performed any direct comparison to the method described by Roberts et al. (2011) and implemented in Cufflinks (Trapnell et al., 2010). Though this method is superficially similar to our own, a proper comparison is difficult, as the software cannot be applied independently of estimating transcript abundance in FPKM (fragments per exonic kilobase, per million mapped reads) using Cufflinks. Fairness would dictate that competing methods be substituted in FPKM estimation, or that a separate interface be written to the Cufflinks bias correction method—both comparisons requiring significant effort.

Though the Cufflinks method and our own both use graphical models to estimate sequence probabilities, we make no restriction on the graph other than acyclicity. We go to considerable effort to efficiently approximate the optimal structure for each dataset rather than using a fixed structure, as in Cufflinks. A ‘one size fits all’ approach likely works quite well in many cases, yet the observed specificity of the bias to protocol and platform argues against it. For example, the structures learned by our method (Fig. 3) are considerably different between those sequenced on an Illumina platform versus an ABI platform, and even vary within platform.

During the review of this article, another method addressing sequence bias in RNA-Seq was published by Zheng et al. (2011). Rather than fitting a model of the specific base-level sequence bias surrounding read start, they propose making adjustments according to summary statistics at the gene level. Such an approach is disadvantaged in its inability to model the very specific pattern of sequence bias we have observed. Yet, such an approach is efficient, and though we have not yet evaluated it, claimed to be effective.

Because we do not require annotations, ChIP-Seq, and other high-throughput sequencing experiments, may also benefit from our model. In a preliminary investigation, we found the sequence bias in one ChIP-Seq experiment (Cao et al., 2010) was less than that observed in any of the RNA-Seq data we evaluated; however, our method is still able to effectively correct for the bias that was observed (Section 7 in Supplementary Material). Protocol differences, as we have seen, can result in significant differences in observed nucleotide frequencies, so we cannot safely assert that bias in ChIP-Seq data is always low. Given the weak assumptions made by our model, our estimation of bias could easily be incorporated into ChIP-Seq peak-calling algorithms, and potentially improve accuracy.

To determine the extent to which polymerase chain reaction amplification is responsible for the observed bias, we evaluated data from the FRT-Seq method proposed by Mamanova et al. (2010). FRT-Seq avoids the PCR amplification step during library preparation with reverse transcription occurring on the flowcell surface. We observed that this data is not free from sequence bias, yet unlike other data generated on the Illumina platform, it appears to be effected only by relatively few positions adjacent to the read start (Section 8 in Supplementary Material). Other protocol improvements might further reduce sequence bias. Notably, promising work by Jayaprakash et al. (2011) proposes a pooled adapter strategy to deal with this issue in small RNA sequencing experiments.

RNA-Seq is most often used to compare levels of expression, and so a natural concern is the consistency of the bias between samples. In the data we examined, the bias appears to be largely, but not entirely consistent (Section 9 in Supplementary Material). Similarly, in Figure 1, the three datasets sequenced on the Illumina platform display similar patterns of non-uniformity, yet differ in magnitude, suggesting that batch effects in RNA-Seq remain a legitimate concern that should not be dismissed without evaluation.

In summary, we have demonstrated a relatively simple graphical model that effectively corrects for sequence bias pervasive in RNA-Seq, and to a lesser extent, ChIP-Seq experiments. In our tests, this model performs at least as well, and often better than existing methods, and involves fewer requirements or assumptions. Our model leads to more accurate quantification, and would likely provide a positive benefit when incorporated into downstream analysis.

Funding: Federal funds from the National Institute of Allergy and Infectious Diseases, National Institutes of Health, Department of Health and Human Services, under Contract No. HHSN272200800060C and by the Public Health Service grant (P51RR000166) from the National Institutes of Health, in whole or in part.

Conflict of Interest: none declared.