Abstract
Census data on endangered species are often sparse, error-ridden, and confined to only a segment of the population. Estimating trends and extinction risks using this type of data presents numerous difficulties. In particular, the estimate of the variation in year-to-year transitions in population size (the “process error” caused by stochasticity in survivorship and fecundities) is confounded by the addition of high sampling error variation. In addition, the year-to-year variability in the segment of the population that is sampled may be quite different from the population variability that one is trying to estimate. The combined effect of severe sampling error and age- or stage-specific counts leads to severe biases in estimates of population-level parameters. I present an estimation method that circumvents the problem of age- or stage-specific counts and is markedly robust to severe sampling error. This method allows the estimation of environmental variation and population trends for extinction-risk analyses using corrupted census counts—a common type of data for endangered species that has hitherto been relatively unusable for these analyses.
One of the first questions a resource manager asks about threatened and endangered species is, “How bad is it?” At its most formal level, this question can be converted into a population viability analysis (PVA), complete with estimates of extinction risk and minimum viable-population sizes. But even if a detailed PVA is not done, the ability to summarize the trajectory of populations is crucial. Such a summary can be used to inform managers on how much improvement must be made in survival or reproduction to arrest a declining trend. It can be used to assign priorities among different populations with different trends and to quantify the short-term risks of waiting while managers or scientists seek more definitive information. One of the more practical methods for addressing these questions was presented by Dennis et al. (1), wherein they illustrate how treating a time series of population counts as a diffusion process can yield estimates of extinction risk. This diffusion approximation has since been used to estimate extinction risks for numerous species of conservation concern (1–4).
An oft-cited limitation of this method, however, is the sensitivity of its parameter estimates to sampling error (refs. 5 and 6 but also see ref. 7). Estimates of environmental variance (see refs. 1, 3, and 8) are usually small, and are much smaller than the severe sampling-error variance that plagues the data sets for many threatened and endangered species. Although improving the quality of data collection is an obvious recommendation, this is not possible for historical data. Furthermore, severe sampling error may be very difficult to remove because of a variety of logistical constraints. Finally, not only is sampling error severe in many cases, it often changes through time as methods are improved, personnel changes, or entirely new methods of sampling are adopted. A less commonly recognized limitation is that for many species, only particular age classes or life stages are amenable to census. For instance, spawners are counted for salmon, nesting or breeding adults are often counted for birds, mothers with cubs are counted for grizzly bears, and egg counts are used for many other species. Counts of only a subset of the population pose difficulties, because most risk analyses require that the count at time t + 1 stems from the count at time t—an assumption that fails with many age- or stage-specific counts.
Here I use stochastic age-structured matrix models to generate data, to which I add high and erratic sampling errors. I then demonstrate the severe estimation errors that can occur when age- or stage-specific counts are used as a surrogate for population counts. Finally, building on the previous work of Dennis et al. (1), I develop an alternative, more robust method for estimating population parameters from highly corrupted age- or stage-specific counts.
The Method and Parameter Estimation of Dennis et al.
The population dynamics model used by Dennis et al. (1) originates from the observation that at the population level, stochastic age-structured models with no density dependence behave as a stochastic, discrete time model with exponential growth or decline:
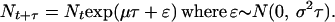 |
1 |
The probability distribution of population size at time t + τ is lognormal. The parameter μ determines the rate at which the median increases through time, whereas σ determines the rate of spread of the distribution, in other words, the variability of population size at time t + τ. By a diffusion approximation, the long-term trends, extinction probabilities, and times to extinction are calculated easily (1).
When censuses are conducted yearly and there are no missing census points, the maximum likelihood estimates of μ and σ2 are (equations 24 and 26 in ref. 1):
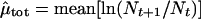 |
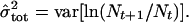 |
2 |
Note that μ̂tot and
σ̂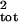 refer to the parameters that are
estimated from the true population size with no sampling error.
refer to the parameters that are
estimated from the true population size with no sampling error.
Using Age- or Stage-Specific Counts as Surrogates for Population Level Counts.
When only age- or stage-specific data are available, one option is to
assume that these data have the same statistical properties as total
population counts and simply to use them in lieu of population counts.
For example, the estimates μ̂age and
σ̂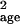 could be calculated by using
At in place of
Nt in Eq. 2, where
At is the age- or stage-specific count at
time t. However, unless the variability among ages is
similar and correlated, the variability measured in one age class will
differ from the variability at the population level (which is what we
are trying to estimate). Another option is to transform the data by
using a running sum to obtain a count that more closely approximates
the total population,
could be calculated by using
At in place of
Nt in Eq. 2, where
At is the age- or stage-specific count at
time t. However, unless the variability among ages is
similar and correlated, the variability measured in one age class will
differ from the variability at the population level (which is what we
are trying to estimate). Another option is to transform the data by
using a running sum to obtain a count that more closely approximates
the total population,
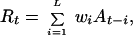 |
3 |
where L is the number of counts added together to give the running sum count at time t and wi is the weight given to each count. The optimal transformation would use survivorship and fecundity information to calculate a proper wi and L. However, in the examples presented here, I assume that survivorship and fecundity information is limited, and the best weighting cannot be determined. Instead, I use a uniform weighting of wi = 1 for all i. L is determined by using basic knowledge of the species' generation time. One approach is to use the running sums directly as a surrogate for population counts:
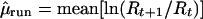 |
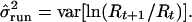 |
4 |
Unfortunately, this straightforward method suffers from bias problems. When sampling error is absent, it gives variance estimates that are highly underestimated (Fig. 1 Upper Right), because the running sum transformation filters out variance. When sampling error is present, it can highly overestimate the variance (Fig. 1 Lower Right).
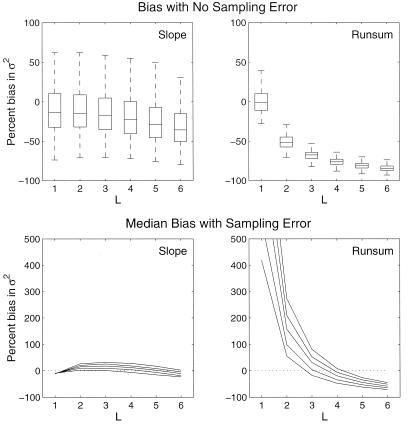
Figure 1.
Effect of L, the number of counts added together, on the
biases in the estimates of σ̂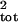 with the slope
(Left) and running sum (Right) methods.
The data are from 500 100-year realizations of the stochastic
exponential growth model (Eq. 1) with μ = −0.05 and
σ2 = 0.05. The results are relatively
insensitive to the level of μ (μ < 0) or
σ2. The median bias and variability in the
parameter estimates when no sampling error is present are shown
(Upper). The median biases when sampling error is 2, 4, 6,
8, or 10 × σ2 are shown
(Lower).
with the slope
(Left) and running sum (Right) methods.
The data are from 500 100-year realizations of the stochastic
exponential growth model (Eq. 1) with μ = −0.05 and
σ2 = 0.05. The results are relatively
insensitive to the level of μ (μ < 0) or
σ2. The median bias and variability in the
parameter estimates when no sampling error is present are shown
(Upper). The median biases when sampling error is 2, 4, 6,
8, or 10 × σ2 are shown
(Lower).
An Alternative Approach.
To circumvent these bias problems, I developed an alternative estimation method, the slope method. This method was motivated by the observation that in a stochastic exponential process, the mean and variance of ln(Nt+τ/Nt) are linear functions of τ with slopes of μ and σ2. Because population counts through time are highly correlated, a running sum of those counts (if not too long) retains much of the lognormal properties of the component counts. Correspondingly, the mean and variance of ln(Rt+τ/Rt) are approximately linear functions of μ and σ2. With the slope method, the parameter estimates are
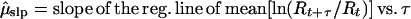 |
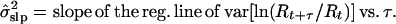 |
5 |
One of the strengths of the slope method is its robustness to
extreme lognormal observation error, Xs,
because
ln(Xs⋅Nt+τ/Xs⋅Nt)
∼N(μτ, σ2τ + constant) (see
Figs. 1 and 2). The slope method
underestimates σ̂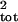 when sampling error is
absent (Fig. 1 Upper Left), because of correlation between
Rt and
Rt+τ and serial correlation among
ln(Rt+τ/Rt),
ln(Rt+τ+1/Rt+1),
ln(Rt+τ+2/Rt+2),
… This bias, however, is much less than the bias with the running
sum method—a negative 15% vs. a negative 75% bias (L
= 4). With a very long time series, subsampling
Rt to remove serial correlation might give
better estimates, but with shorter data sets (20–50 years), the errors
caused by removing data seem to be more severe than the bias caused by
serial correlation.
when sampling error is
absent (Fig. 1 Upper Left), because of correlation between
Rt and
Rt+τ and serial correlation among
ln(Rt+τ/Rt),
ln(Rt+τ+1/Rt+1),
ln(Rt+τ+2/Rt+2),
… This bias, however, is much less than the bias with the running
sum method—a negative 15% vs. a negative 75% bias (L
= 4). With a very long time series, subsampling
Rt to remove serial correlation might give
better estimates, but with shorter data sets (20–50 years), the errors
caused by removing data seem to be more severe than the bias caused by
serial correlation.
Figure 2.
Illustration of the slope method for estimating the variance and mean of ln(Nt+1/Nt) from ln(Rt+τ/Rt), where Nt is the total uncorrupted population count and Rt is a running sum of age- or stage-specific counts. The slope of var[ln(Rt+τ/Rt)] vs. τ is an estimate of σ2. The slope of mean[ln(Rt+τ/Rt)] vs. τ is an estimate of μ (in this case μ < 0). The effect of sampling error on the var[ln(Rt+τ/Rt)] vs. τ line is to raise the line while keeping the slope (used to estimate σ2) approximately the same (A). The effect of sampling error on the mean[ln(Rt+τ/Rt]) versus τ line is to increase the variance of the data around the line (B).
The Errors Between the True and Estimated μ and
σ .
.
Estimates of μ and σ2 include two different
sources of error: (i) error caused by using a finite rather
than an infinite time series and (ii) error caused by
observation errors and counts that are not a representative sample of
all ages. The first is the error between
μ̂tot, σ̂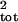 and
μ, σ2. Dennis et al. (1)
demonstrate how to calculate this type of error. The second type is the
error between the true μ̂tot and
σ̂
and
μ, σ2. Dennis et al. (1)
demonstrate how to calculate this type of error. The second type is the
error between the true μ̂tot and
σ̂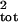 and values calculated from corrupted age
or stage counts.
and values calculated from corrupted age
or stage counts.
To explore this second type of error, I studied the behavior of time
series generated from stochastic matrix models. One thousand simulated
20-year time series provided true population counts,
Nt, and corresponding age- or
stage-specific counts, which I later corrupted with sampling error. I
then compared the true μ̂tot and
σ̂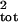 , calculated by using
Nt, with the estimates from the three
methods using the corrupted counts. The stochastic matrix models I used
were based on published age- or stage-structured matrix models for
endangered Chinook salmon, sea turtles, and petrels. These species
represent three very different life histories, but in each case, only a
subset of age/stage classes are countable. The magnitude of
environmental variation added to the survivorship and fecundity
parameters in the matrices was determined by direct data on fecundity
variation or by fitting the model to reflect the variability observed
in an available 20-year time series for each species (or a related
species). To the age- or stage-specific counts, one of the following
four types of sampling error was added. Note that the sampling error
variance added was 5–20 times higher than the environmental variance.
, calculated by using
Nt, with the estimates from the three
methods using the corrupted counts. The stochastic matrix models I used
were based on published age- or stage-structured matrix models for
endangered Chinook salmon, sea turtles, and petrels. These species
represent three very different life histories, but in each case, only a
subset of age/stage classes are countable. The magnitude of
environmental variation added to the survivorship and fecundity
parameters in the matrices was determined by direct data on fecundity
variation or by fitting the model to reflect the variability observed
in an available 20-year time series for each species (or a related
species). To the age- or stage-specific counts, one of the following
four types of sampling error was added. Note that the sampling error
variance added was 5–20 times higher than the environmental variance.
(i) Unbiased error. The sampling error was drawn from the lognormal distribution, exp[N(μ = 1.0, σ2 = 0.5)]. More than 50% of the corrupted counts were over 25% too high or 25% too low.
(ii) Unbiased but density-dependent error. Percentage-wise large errors were more common when counts were small. Sampling error was drawn from the lognormal distribution, exp[N(μ = 1.0, σ2 = y)], as follows: counts < 100, y = 0.5 + (1 − count/100)⋅0.5; counts > 100, y = 0.5.
(iii) Unbiased but erratic error. The accuracy of the counts was changed every 5 years. The sampling error was drawn from the lognormal distribution, exp[N(μ = 1.0, σ2 = y)], as follows: years 1–5, y = 0.5; years 6–10, y = 1.0; years 11–15, y = 0.25; and years 16–20, y = 0.5.
(iv) Biased and erratic error. Bias and accuracy of the counts changed every 5 years. The sampling error was drawn from the lognormal distribution, exp[N(μ = x, σ2 = y)], as follows: years 1–5, (x, y) = (0.5, 0.5); years 6–10, (x, y) = (1.0, 1.0); years 11–15 (x, y) = (1.5, 0.25); and years 16–20 (x, y) = (0.75, 0.5).
Spring/Summer Chinook Salmon.
The following is a modified Leslie matrix for Snake River spring/summer Chinook salmon (8) in which the spawner class is separate.
 |
6 |
The ɛi terms represent environmental variability and were drawn from a multivariate lognormal distribution, exp[N(μ = 0, σ2 = 0.02)], with correlation 0.99 between the ɛis. All simulations were started with the age distribution: [8490 450 397 285 379]. This distribution is not the equilibrium age structure; it has a much higher number of 1- to 2-year-old fish. This distribution was chosen to illustrate the behavior of the parameter estimates when the age structure is far from equilibrium. In this case, the perturbed age structure creates a large pulse that travels through all of the time series.
For the running sum transformation, 5 consecutive spawner counts were added together,
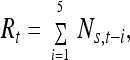 |
7 |
where Ns,t is the spawner count at time t. The maximum spawner return age for this stock is 5, and a running sum of 5 counts is related to the number of total current and potential spawners in the population at time t.
Loggerhead Sea Turtles.
Crowder et al. (9) estimated the following matrix for loggerhead sea turtles divided in the age classes; egg, and yr 1–7, yr 8–15, yr 16–32, and yr 32+ :
 |
8 |
The environmental variance terms, ɛi, were drawn from the multivariate lognormal distribution, exp[N(μ = 0, σ2 = xi)], where x1 = 0.5, x2 = 0.01, x3 = 0.01, x4 = 0.01, and x5 = 0.01, and correlation of 0.99 between ɛis. These distributions were chosen to reflect the enormous variability in the annual number of nesting females (and hence, egg counts) that is a characteristic of many sea turtle populations (10, 11), and the observed variance patterns in a 26-year time series of egg counts of green turtles (Chelonia mydas) in Costa Rica (10). Unlike the salmon matrix, the sea turtle matrix does not tend to produce population cycles. This difference makes age- or stage-specific counts more robust as population estimators. However, high variability in one age class (in this case, the sampled egg class) relative to others also leads to biased parameter estimates.
Because sea turtle life spans are 30+ years, a biologically motivated running sum would include roughly 30 egg counts, weighted more toward recent egg counts. However, with a 20-year time series, the running sum cannot include more than ≈5–6 counts, while still leaving enough data points for estimation. For the example here, three egg counts were added together to produce each running sum.
Hawaiian Dark-Rumped Petrel.
Breeding-colony censuses of this petrel include mainly birds aged 6–23 years. Juveniles comprise ≈50% of the population but most (70%) do not return to the colony and are not counted (12). Simons (12) estimated parameters for a 35 × 35 Leslie matrix for this endangered petrel by using juvenile survivorship (1–5 yr) = 0.8034 + ɛ1, adult survivorship (6–35 yr) = 0.93 + ɛ2, juvenile fecundity = 0, and adult fecundity = 0.294 + ɛ3 (matrix not shown). The environmental variability terms, ɛi, were drawn from the multivariate lognormal distribution, exp[N(μ = 0, σ2 = xi)], where x1,2 = 0.01 and x3 = 0.1, with 0.99 correlation. The variance in adult fecundity reflects that observed by Simons. I did not have estimates of the variability in survivorships and chose moderately low levels. Simulations indicated that the results were not qualitatively sensitive to the level of variation in the survivorships.
The breeding-bird counts were transformed by
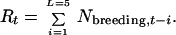 |
9 |
L = 5 was chosen as follows: the breeding bird count at time t contributes age-1 birds in year t, age-2 birds in year t + 1, age-3 birds in year t + 2, etc. Because petrels begin breeding on average at age 5, breeding-bird counts (t − 4 to t) contribute to the current total population size. With information on adult fecundity and juvenile survivorship, a better weighting could be determined. I assume that such information is unavailable, as it often is, and I used a uniform weighting instead.
Results
For each time series, μ̂tot and
σ̂ were calculated from the true total
population count by using Eq. 2. Estimates of
μ̂tot and σ̂
were calculated from the true total
population count by using Eq. 2. Estimates of
μ̂tot and σ̂ then were calculated by using the uncorrupted and corrupted age- or
stage-specific counts: μ̂age and
σ̂
then were calculated by using the uncorrupted and corrupted age- or
stage-specific counts: μ̂age and
σ̂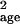 with Eq. 2 directly from the
corrupted counts, μ̂run and
σ̂
with Eq. 2 directly from the
corrupted counts, μ̂run and
σ̂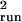 with Eq. 4 from the running
sums, and μ̂slp and
σ̂
with Eq. 4 from the running
sums, and μ̂slp and
σ̂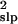 with Eq. 5. The percent
differences between the estimated and true
μ̂tot and σ̂
with Eq. 5. The percent
differences between the estimated and true
μ̂tot and σ̂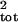 then were calculated. Two risk metrics, the mean rate of population
growth [λ = exp(μ̂ + σ̂2)]
and the probability of a 90% decline within a given time horizon (1),
were calculated by using the estimated and true
μ̂tot and σ̂
then were calculated. Two risk metrics, the mean rate of population
growth [λ = exp(μ̂ + σ̂2)]
and the probability of a 90% decline within a given time horizon (1),
were calculated by using the estimated and true
μ̂tot and σ̂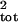 .
The probability of extinction could not be calculated because this
requires an estimate of total population size, which is impossible to
derive purely from age- or stage-specific counts with little other
information.
.
The probability of extinction could not be calculated because this
requires an estimate of total population size, which is impossible to
derive purely from age- or stage-specific counts with little other
information.
Effect of Counts That Do Not Reflect the Population.
The first complication I examined concerned simply the effect of age-
or stage-specific counts (no sampling error) on parameter estimates.
Figs. 3 and
4 (Top) show the difference
between the true parameters and their estimates,
μ̂age and σ̂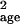 ,
calculated by using age- or stage-specific counts directly. In general,
these specific counts were poor surrogates for population counts. The
parameter σ̂
,
calculated by using age- or stage-specific counts directly. In general,
these specific counts were poor surrogates for population counts. The
parameter σ̂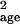 was overestimated highly
(1,000–7,000%). The parameter μ̂age was
biased 100% upward for the salmon example (this bias was not present
if the simulations were started with the age distribution at
equilibrium). The bias in the parameter estimates had strong effects on
the calculated risk metrics. The population rate of decline was
overestimated by a median of 150% for the salmon and 53% for sea
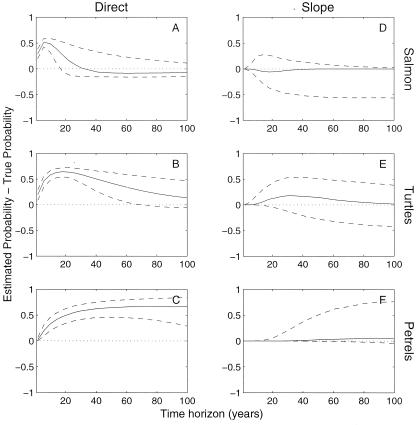
turtles (Fig. 5). Although the estimate
was good for the petrels, it became biased upward when sampling error
was present (next section). Similarly, the estimates of probability of
a 90% decline within a given time horizon were biased highly for
salmon and sea turtles (similar to Fig. 6
A–C).
was overestimated highly
(1,000–7,000%). The parameter μ̂age was
biased 100% upward for the salmon example (this bias was not present
if the simulations were started with the age distribution at
equilibrium). The bias in the parameter estimates had strong effects on
the calculated risk metrics. The population rate of decline was
overestimated by a median of 150% for the salmon and 53% for sea
turtles (Fig. 5). Although the estimate
was good for the petrels, it became biased upward when sampling error
was present (next section). Similarly, the estimates of probability of
a 90% decline within a given time horizon were biased highly for
salmon and sea turtles (similar to Fig. 6
A–C).
Figure 3.
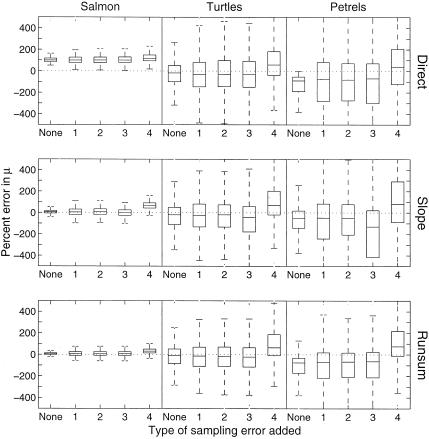
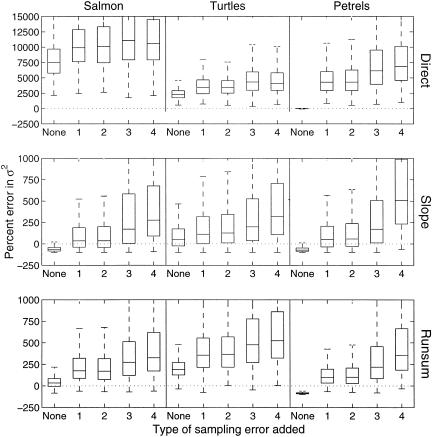
Effect of severe sampling error on estimates of μ̂tot by directly using age or stage counts as surrogates for population counts (Direct), by using the slope method (Slope), or by using the running sum method (Runsum). In the boxplots, the middle line indicates the median; the box encloses 75% of the data; and the whiskers indicate the range of the entire data. The four types of sampling error are unbiased lognormal error (1), unbiased lognormal error with variance that depends on the count size (2), unbiased lognormal error with variance that changes every 5 years (3), and biased lognormal error with variance and bias that change every 5 years (4).
Figure 5.
Effect of severe sampling error on estimates of the mean rate of population decline, λ. Note that the scale (Top) is much larger, because of larger errors associated with the direct method. See Fig. 3 for a description of the boxplots and sampling-error types.
Figure 6.
Effect of parameter estimates on the probability of a 90% decline in a given time horizon for salmon (Top), sea turtles (Middle), and petrels (Bottom). On the Left, the parameters were calculated by using the direct method (Eq. 2) from corrupted age- or stage-specific counts. On the Right, the parameters were estimated by using the slope method (Eq. 5). The solid lines show the median absolute difference between the probability of a 90% decline calculated with the corrupted counts vs. that calculated with the true population counts. The dashed lines show the range of 75% of the differences.
The true μ̂tot and
σ̂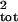 were much more accurately estimated by
using the running sum and slope methods [compare Figs. 3 and 4
(Top) to Figs. 3 and 4 (Middle and
Bottom)]. Note the scale in the lower panels (Fig. 4) is an
order of magnitude smaller because of the smaller error with these
methods. The bars marked “None” indicate the simulations with no
sampling error. Both methods greatly improved the estimation of
σ̂
were much more accurately estimated by
using the running sum and slope methods [compare Figs. 3 and 4
(Top) to Figs. 3 and 4 (Middle and
Bottom)]. Note the scale in the lower panels (Fig. 4) is an
order of magnitude smaller because of the smaller error with these
methods. The bars marked “None” indicate the simulations with no
sampling error. Both methods greatly improved the estimation of
σ̂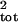 . The median bias of
σ̂
. The median bias of
σ̂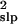 was −45%, +51%, and −72% for salmon,
sea turtles, and petrels. The median bias of
σ̂
was −45%, +51%, and −72% for salmon,
sea turtles, and petrels. The median bias of
σ̂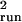 was +41%, +190%, and −87%. Estimation
of μ̂tot improved greatly for salmon; the
new estimates were unbiased and tight but there was little improvement
for the other species. The better estimates of
σ̂
was +41%, +190%, and −87%. Estimation
of μ̂tot improved greatly for salmon; the
new estimates were unbiased and tight but there was little improvement
for the other species. The better estimates of
σ̂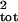 translated into significantly better risk
estimates. The median overestimation of population growth rate ranged
between 0.3% and 4% with low variability (Fig. 5). The estimates of
probability of a 90% decline in a given time frame also improved and
were relatively unbiased, although variable (similar to Fig. 6
C and D).
translated into significantly better risk
estimates. The median overestimation of population growth rate ranged
between 0.3% and 4% with low variability (Fig. 5). The estimates of
probability of a 90% decline in a given time frame also improved and
were relatively unbiased, although variable (similar to Fig. 6
C and D).
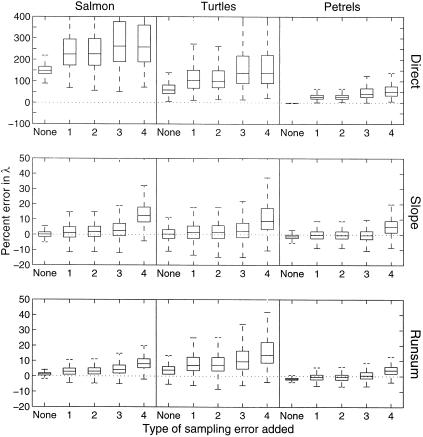
Figure 4.
Effect of severe sampling error on estimates of
σ̂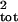 . Note that the scale (Top)
is much larger, because of larger errors associated with the direct
method. See Fig. 3 for a description of the boxplots and sampling-error
types. Directly using age- or stage-specific counts leads to large
biases in the estimate of σ̂
. Note that the scale (Top)
is much larger, because of larger errors associated with the direct
method. See Fig. 3 for a description of the boxplots and sampling-error
types. Directly using age- or stage-specific counts leads to large
biases in the estimate of σ̂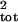 , and sampling
error greatly exacerbates the problem. The slope method allows
significantly fewer biased estimates in the face of severe sampling
error.
, and sampling
error greatly exacerbates the problem. The slope method allows
significantly fewer biased estimates in the face of severe sampling
error.
Effect of Severe Sampling Error.
When age and stage counts were used as direct surrogates for population
counts, high sampling error caused substantial overestimation of
σ̂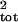 (Fig. 4). The most extreme increase
occurred for the petrels. In this case, σ̂
(Fig. 4). The most extreme increase
occurred for the petrels. In this case, σ̂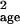 gave an unbiased estimate when no sampling error was present but
overestimated by a median 4,300–6,900% with sampling error added. The
other two species showed smaller but still large overestimates. The
corresponding estimates of population growth were highly biased (Fig.
5), and the estimates of the probability of a 90% decline were highly
biased and variable for all species, including petrels (Fig. 6
A–C).
gave an unbiased estimate when no sampling error was present but
overestimated by a median 4,300–6,900% with sampling error added. The
other two species showed smaller but still large overestimates. The
corresponding estimates of population growth were highly biased (Fig.
5), and the estimates of the probability of a 90% decline were highly
biased and variable for all species, including petrels (Fig. 6
A–C).
In contrast, the running sum and slope methods filtered out much of the
high sampling error. With the slope method, the median upward bias in
the σ̂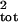 estimate was 35–275%, 100–250%,
and 50–500% for the salmon, sea turtles, and petrels (Fig. 4). With
the running sum method, the median bias was 175–325%, 300–400%, and
100–300%. This bias compares to median upward biases of
2,500–11,000%, when the corrupted counts were used directly. The
resulting estimates of mean population growth with the slope method
were unbiased and the upper and lower quartiles of the estimates varied
between 5% low and 5% high for all except the worst sampling error
(Fig. 5). The probability of a 90% decline within a given time frame
was relatively unbiased (Fig. 6 D–F) but was
highly variable.
estimate was 35–275%, 100–250%,
and 50–500% for the salmon, sea turtles, and petrels (Fig. 4). With
the running sum method, the median bias was 175–325%, 300–400%, and
100–300%. This bias compares to median upward biases of
2,500–11,000%, when the corrupted counts were used directly. The
resulting estimates of mean population growth with the slope method
were unbiased and the upper and lower quartiles of the estimates varied
between 5% low and 5% high for all except the worst sampling error
(Fig. 5). The probability of a 90% decline within a given time frame
was relatively unbiased (Fig. 6 D–F) but was
highly variable.
Difference Between the Running Sum and Slope Methods.
Comparing Figs. 3 and 4, it would seem that using running sums as a
direct surrogate for population counts often gives less variable and no
more biased estimates than the slope method. The sea turtle example is
the exception and points out one of the weaknesses of the running sum
method. The running sum estimates, especially
σ̂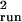 , are sensitive to L, the
number of counts added together to create a running sum count. This
sensitivity can be demonstrated by using the simple stochastic
exponential process (Eq. 1). With no sampling error, the
bias in the estimate of σ̂
, are sensitive to L, the
number of counts added together to create a running sum count. This
sensitivity can be demonstrated by using the simple stochastic
exponential process (Eq. 1). With no sampling error, the
bias in the estimate of σ̂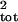 increases from
−50% to −80% as L increases from 2 to 6 (Fig. 1
Upper). For the slope method, in contrast, the bias
increases from −10% to −30%. With sampling error, the sensitivity
of the running sum estimates becomes severe, with the bias changing
rapidly from +50–300% to −80% when L is changed from 2
to 6 (Fig. 1 Lower). In comparison, the slope method
estimates are relatively insensitive to L and high sampling
error. In practice, choosing the optimal L may be difficult,
because basic life history information is not available, e.g., mean age
of return to breeding sites, mean lifespan, maximum breeding age, etc.
Thus, robustness to poor choices for the running sum transformation is
important.
increases from
−50% to −80% as L increases from 2 to 6 (Fig. 1
Upper). For the slope method, in contrast, the bias
increases from −10% to −30%. With sampling error, the sensitivity
of the running sum estimates becomes severe, with the bias changing
rapidly from +50–300% to −80% when L is changed from 2
to 6 (Fig. 1 Lower). In comparison, the slope method
estimates are relatively insensitive to L and high sampling
error. In practice, choosing the optimal L may be difficult,
because basic life history information is not available, e.g., mean age
of return to breeding sites, mean lifespan, maximum breeding age, etc.
Thus, robustness to poor choices for the running sum transformation is
important.
The decreased bias provided by the slope method comes with a cost. Its
variance estimate, σ̂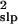 , is much more variable
than the estimates from the direct or the running sum methods (Fig. 1
Upper). When sampling error, age-structure perturbations, or
age-specific variability are high, the significantly reduced bias
provided by the slope method will outweigh the increased variability in
its variance estimate (Fig. 1 Lower). When the data do not
suffer from such problems (e.g., the expected sampling error variance
is less than the environmental variance), standard methods (1) or
σ̂
, is much more variable
than the estimates from the direct or the running sum methods (Fig. 1
Upper). When sampling error, age-structure perturbations, or
age-specific variability are high, the significantly reduced bias
provided by the slope method will outweigh the increased variability in
its variance estimate (Fig. 1 Lower). When the data do not
suffer from such problems (e.g., the expected sampling error variance
is less than the environmental variance), standard methods (1) or
σ̂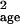 should give better parameter estimates.
The slope method should be viewed as a complement to the methods
introduced by Dennis et al. and specifically as a tool for
data sets beset by high nonprocess error variance. Finally, note that
the slope method has greater data needs. In its current form, the
method does not allow missing data, and in addition, 15 to 20 years of
data seem to be a minimum (for an L of 4). Using the method
with only 10 years will result in severe underestimates of
environmental variance. This problem rapidly dissipates as the time
series' length increases to 20 years.
should give better parameter estimates.
The slope method should be viewed as a complement to the methods
introduced by Dennis et al. and specifically as a tool for
data sets beset by high nonprocess error variance. Finally, note that
the slope method has greater data needs. In its current form, the
method does not allow missing data, and in addition, 15 to 20 years of
data seem to be a minimum (for an L of 4). Using the method
with only 10 years will result in severe underestimates of
environmental variance. This problem rapidly dissipates as the time
series' length increases to 20 years.
Discussion
Limited and error-riddled data are common for many species for which management decisions and status assessments must be made. Although improving sampling techniques is always warranted, certain constraints are often impossible to remove. Age- or stage-specific counts are one of these problems. Commonly, one segment of the population, often the juvenile segment, is unobservable. In addition, sampling error can be extreme or changing from year to year as methods and personnel change. In this paper, I introduce a slope method for estimating population parameters in the face of these two problems. The main advantage of this method is that it allows estimates of rates and risks of population decline with a well established tool (diffusion approximations) by using age- or stage-specific censuses that are corrupted with sampling error. Previously, the parameters for simple count-based extinction analyses could not be estimated with this common type of data.
One of the interesting features of the slope method is its ability to separate environmental variance from sampling error variance by using the different statistical properties of each, even when the sampling error is severe, e.g., orders of magnitude greater than the environmental variance. Previous methods have used strategies that partition the two sources of variability when the magnitude of the sampling-error variance is known or the ratio to the environmental variance is known (13–16). However, it is uncommon in conservation settings that the magnitude of the sampling error, absolute or relative, is known. Our consequent inability to estimate environmental variance in the face of sampling error variance has been one of the greatest obstacles to the estimation of parameters for population extinction analyses. The slope method presents a different strategy, separating the environmental variance from much larger sampling-error variance, by observing that the variance of the ratio of logarithm counts separated by n years should be governed by the function (environmental variance⋅n + sampling-error variance).
Like any model, the application of a diffusion approximation can be abused, and its success depends on certain assumptions. It, or any other population viability analysis, is likely to encounter troubles if there are substantial environmental trends or if variability does not conform to some well behaved distribution like a lognormal distribution. Fortunately, both of these assumptions can be tested readily. More problematic is the question of density dependence. This possibility can be tested (17), although, should populations grow, they will obviously climb out of the region of no density dependence. Conversely, if populations continue to shrink to only a handful of individuals, they are likely to enter a region of density depensation (or Allee effects). An oft-mentioned concern is autocorrelation in the environmental variability. The behavior of stochastic exponential population processes with correlated environmental variability is discussed in refs. 1 and 18. In short, the same diffusion approximation is valid for correlated variance. The μ parameter is unaffected but the σ2 estimate must be increased by the level of correlation. Methods for estimating σ2 in short time series with correlated noise are covered in ref. 18. In its current form, the slope method assumes that the environmental noise is relatively uncorrelated and will underestimate σ2 in time series with correlated noise. However, keep in mind that the slope method is used in situations where nonenvironmental variance is very high, in which case σ2 will tend to be overestimated.
Even when all of the assumptions are met, one needs to be cautious when interpreting and using the risk metrics estimated by simple diffusion approximations. Probabilities of reaching a specific threshold (e.g., extinction) have been criticized harshly, because they tend to be biased and have large confidence intervals for short or error-ridden data sets (5, 6). In the examples here, the slope method removed much of the bias in the estimated probability of a 90% decline within a given time frame, but the estimates were highly variable for two of the three species. Success at estimating probabilities for one species, salmon, suggests that estimating probabilities of hitting thresholds (such as extinction) is not necessarily doomed. It may be possible to delineate regions of parameter space [μ, σ2, time horizon, time-series length] where estimates of extinction probability are likely to be poor. Previously, this region would have included the entire parameter space for error-ridden data. The methods developed here considerably shrink the region of poor estimates.
On the other hand, the reliance on a risk metric with recalcitrant estimation problems is difficult to justify when an equally useful parameter, λ, the expected mean annual rate of population change, is readily available and is well estimated, even with very poor data. Without pretending to predict an extinction risk, λ itself provides some answers to the question, “How bad is it?” If λ is low, populations generally are at greater risk and will require larger improvements in survival or fecundity to mitigate the risk. In addition, the lower λ and the smaller the initial population size, the less time there is to “wait and learn more” before taking action. In addition, for threatened and endangered populations, a λ greater than 1 (headed toward recovery) is the legal imperative for management. This is not to argue that λ captures the same aspects of risk that probability of extinction does, or that probabilities of extinction should be abandoned. Small populations with λ greater than 1 but high environmental variability will still have high extinction risks. But until estimation methods are improved further, numerical estimates of the probability to hit a given threshold such as extinction will be dubious for many species (but not all). In those cases, where probability estimates are expected to be poor, I believe that λ is the more useful risk metric. It is certainly the most reliably estimated.
Acknowledgments
I thank T. Cooney, C. Jordan, R. Hinrichsen, P. Kareiva, P. Levin, M. McClure, P. McElhany, and B. Sanderson for helpful discussions throughout the development of these methods. I also thank M. Marvier for the salmon matrix used here.
References
- 1.Dennis B, Munholland P L, Scott J M. Ecol Monogr. 1991;61:115–143. [Google Scholar]
- 2.Gerber L, DeMaster D, Kareiva P. Cons Biol. 1999;13:1215–1219. [Google Scholar]
- 3.Morris W, Doak D, Groom M, Kareiva P, Fieberg J, Gerber L, Murphy P, Thomson D. A Practical Handbook for Population Viability Analysis. Washington, DC: The Nature Conservancy; 1999. [Google Scholar]
- 4.Nicholls A O, Viljoen P C, Knight M H, Van Jaarsveld A S. Biol Cons. 1996;76:57–67. [Google Scholar]
- 5.Fieberg J, Ellner S P. Ecology. 2000;81:2040–2047. [Google Scholar]
- 6.Ludwig D. Ecology. 1999;80:298–310. [Google Scholar]
- 7.Meir E, Fagan W F. Cons Biol. 1999;14:148–154. [Google Scholar]
- 8.Cumulative Risk Initiative. A Standardized Quantitative Analysis of Risks Faced by Salmonids in the Columbia River Basin. Washington, DC: Natl. Marine Fisheries Service; 2000. [Google Scholar]
- 9.Crowder L B, Crouse D T, Heppell S S, Martin T H. Ecol Appl. 1994;4:437–445. [Google Scholar]
- 10.Bjorndal K A, Wetherall J A, Bolten A B, Mortimer J A. Cons Biol. 1999;13:126–134. [Google Scholar]
- 11.Limpus C J. In: Biology and Conservation of Sea Turtles. Bjorndal K A, editor. Washington, DC: Smithsonian Institution Press; 1995. pp. 605–609. [Google Scholar]
- 12.Simons T R. J Wildl Management. 1984;48:1065–1076. [Google Scholar]
- 13.Carpenter S R, Cottingham K L, Stow C A. Ecology. 1994;75:1254–1264. [Google Scholar]
- 14.Cook J R, Stefanski L A. J Am Stat Assoc. 1994;89:1314–1328. [Google Scholar]
- 15.Ludwig D, Walters C J. Can J Fish Aquat Sci. 1981;38:711–720. [Google Scholar]
- 16.Ludwig D, Walters C J. Can J Fish Aquat Sci. 1989;42:1066–1072. [Google Scholar]
- 17.Dennis B, Taper M L. Ecol Monogr. 1994;64:205–224. [Google Scholar]
- 18.Tuljapurkar S D. Theor Popul Biol. 1989;35:227–294. doi: 10.1016/0040-5809(89)90001-4. [DOI] [PubMed] [Google Scholar]