Floating-electrode enhanced constriction dielectrophoresis for biomolecular trapping in physiological media of high conductivity

Abstract

We present an electrokinetic framework for designing insulator constriction-based dielectrophoresis devices with enhanced ability to trap nanoscale biomolecules in physiological media of high conductivity, through coupling short-range dielectrophoresis forces with long-range electrothermal flow. While a 500-fold constriction enables field focusing sufficient to trap nanoscale biomolecules by dielectrophoresis, the extent of this high-field region is enhanced through coupling the constriction to an electrically floating sensor electrode at the constriction floor. However, the enhanced localized fields due to the constriction and enhanced current within saline media of high conductivity (1 S/m) cause a rise in temperature due to Joule heating, resulting in a hotspot region midway within the channel depth at the constriction center, with temperatures of ∼8°–10°K above the ambient. While the resulting vortices from electrothermal flow are directed away from the hotspot region to oppose dielectrophoretic trapping, they also cause a downward and inward flow towards the electrode edges at the constriction floor. This assists biomolecular trapping at the sensor electrode through enabling long-range fluid sampling as well as through localized stirring by fluid circulation in its vicinity.

INTRODUCTION

The ability to selectively manipulate bio-particles such as cells,¹ DNA,² and proteins,³ as well as nanomaterials, such as nanofibers,⁴ nanotubes,⁵ and nanowires⁶ at localized fluid/device interfaces, within media of a wide range of conductivity, is fundamental to many applications in biomedicine and nanofabrication. Electrokinetic methodologies are uniquely poised for particle manipulation,⁷ since they are based on the inherent charge distributions within the manipulated materials, their scaling laws are highly compatible with microfluidic systems, and their instrumentation is relatively simple to assemble. Dielectrophoresis (DEP), which causes the translation of neutral particles to particular localized regions of high or low field intensity due to their polarization in a non-uniform electric field, allows for highly selective trapping of bio-particles and nanomaterials based on the characteristic frequency response of the conductivity and dielectric permittivity of particle versus those of the media.^{8, 9} However, since the DEP trapping forces scale as the cube of the equivalent radius of the particle, their application towards the manipulation of sub-micron sized bio-particles, such as proteins or single-stranded DNA (ss-DNA) fragments of low polarizability has been rather limited.^{10, 11, 12} Recent work on biomolecular sensing has identified mass transport of target biomarkers towards immobilized capture probes as the key bottleneck to enhancing detection speed, sensitivity, and selectivity.^{13, 14, 15} This has led to a closer consideration of DEP methodologies for trapping double-stranded (ds-DNA), ss-DNA target molecules,^{16, 17, 18, 19} and RNA (Ribonucleic acid) species.²⁰ However, DEP trapping within media of high conductivity for enhancement of DNA hybridization kinetics poses distinct challenges. The enhanced current flow under applied fields within media of high conductivity (1 S/m) causes Joule heating.^{21, 22} The resulting temperature gradients cause bulk electrothermal flow, which can dissipate the DEP trapping. Strategies for enhancing the net trapping force on nanoscale biomolecules over dissipative fluid flow due to Joule heating include the application of DEP to DNA immobilized on nanoparticles^{23, 24} or applying DEP towards the direct manipulation of DNA within devices containing sharp insulating tips or constrictions to enhance field gradients (E.dE/dx or ∇E²). In our recent work,²⁵ we have extended this latter approach by coupling the dielectric constriction to an electrically floating electrode with immobilized DNA capture probes to enable low frequency (∼1 KHz) DEP trapping of ss-DNA target (∼150 bases) in high conductivity saline media (σ_m ∼ 1 S/m), without electrolysis. As a result, we demonstrated the simultaneous pre-concentration, hybridization, and electrochemical sensing of target DNA, without any wash steps. The polarization of DNA in the 1–10 kHz frequency range to cause positive DEP, due to particle permittivity exceeding medium permittivity, is usually attributed to the predominant influence of the counter-ion cloud around the DNA molecules. This is supported by observations of weaker dielectrophoretic effects on ss-DNA versus ds-DNA,¹⁰ since ss-DNA, due to lower charge density undergoes only a limited degree of stretching along its length, in comparison to ds-DNA.¹¹ At these frequencies, the DEP response is interpreted to arise due to the influence of counterion fluctuations on the rotation of the DNA molecule with a quasi-permanent dipole, with relaxation times that depend on the square of the molecular weight.² At high salt concentration, the counterion fluctuations can take place over distances equivalent to the DNA’s persistence length,²⁶ that is, over about 50 nm. Hence, using device structures with ∼1 μm or smaller constrictions, positive DEP trapping of ss-DNA has been observed, even within high conductivity saline media.^{25, 27} In this current work, we focus on developing an electrokinetic framework to describe the profiles of electric fields, temperature, and force fields within this device to explore the role of Joule heating on the balance of DEP trapping forces versus dissipative electrothermal flow. While prior work on modeling electrodeless or insulator-based DEP devices utilizes 2D symmetry considerations for describing the electric fields, the presence of a metallic electrode at the floor of the constriction, as well as differential heat dissipation at the channel floor versus midway through the channel due to Joule heating requires a consideration of electric fields and force fields in all three dimensions.²⁸ The implications of this analysis on DEP force fields, temperature gradients, and the net balance between DEP trapping versus electrothermal flow are elucidated. We envision that these findings can enable a better understanding of the design considerations underlying the application of insulator constriction-based DEP within high-conductivity media for effective trapping of nanomaterials and biomolecules of low polarizability, such as ss-DNA and proteins.

METHODS

Device geometry

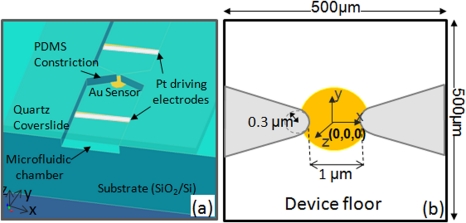
The device geometry of a dielectric constriction coupled to an electrically floating sensor electrode with immobilized DNA capture probes is shown in Figures 1a, 1b. Our model considers this device in the absence and presence of the electrically floating sensor electrode to highlight its role on the electric field profiles and the ensuing force fields. A SiO₂/Si wafer substrate was patterned with the Au disk electrode for immobilization of DNA capture probe molecules and Pt drive electrodes with 500 μm spacing for application of the DEP driving field (350 V/cm and frequency of ∼1 kHz). The microfluidic channel of few millimeters in length (y-direction), 500 μm in width (x-direction), and 5 μm in depth (z-direction) was constructed with highly insulating silicon nitride or high-density PDMS (Polydimethylsiloxane) layers using reactive ion etching methods to fabricate sharp 500 × field focusing for constrictions in the x-direction (500 μm reduced to 1 μm, henceforth termed as 500×). The dielectrophoretic trapping of ss-DNA was carried out in a high conductivity buffer with ∼50 mM sodium chloride (∼1 S/m) containing target DNA at 1 nM concentration, and added components of 1 mM mercaptohexanol (to keep the DNA capture probe monolayer intact during DEP), 10% v/v fetal calf serum (to reduce non-specific binding), and 10 mM trizma buffer (to adjust pH to 6.5).²⁹

Figure 1.

(a) Device geometry for the insulator constriction coupled to an electrically floating Au electrode sensor with immobilized DNA capture probe molecules. (b) Device geometry of the modeling studies showing the microchannel and electrode dimensions, as well as the x-, y-, and z-directions.

Device modeling

To elucidate the device-level computation of the response of bio-particles and the bulk fluid under dielectrophoresis conditions, we focus on the interplay of multi-physical parameters of the electric fields, temperature profiles, and force fields for 500 × constriction devices coupled to an electrically floating electrode. These parameters are computed using finite element methods with the commercial software ESI-CFD ACE + (ESI CFD, North America, Huntsville, AL). The electric potential within the microfluidic device can be mapped through solving the Laplace equation

$$\nabla ·((\sigma +j\omega \varepsilon )\nabla \phi )=0.$$ (1)

The electric field distribution can be obtained using the relation

$$\overrightarrow{E}=-\nabla \phi .$$ (2)

Based on the electric field distribution in the device, its gradient can be calculated, which in turn can be used to determine the dielectrophoretic force in the device. At steady state, the average dielectrophoretic force, ${\overrightarrow{F}}_{\mathit{DEP}}$, on a homogeneous spherical particle with dielectric permittivity ɛ_p, conductivity σ_p, and radius a suspended in a fluid with dielectric permittivity ɛ_m and conductivity σ_m in a non-uniform AC electric field E is given by

$${\overrightarrow{\mathbf{F}}}_{\mathit{DEP}}=2\pi a^3{\varepsilon }_m\mathrm{Re}\underset{K_{\mathit{CM}}}{\underbrace{\left(\frac{{\varepsilon }_p^{*}-{\varepsilon }_m^{*}}{{\varepsilon }_p^{*}+2{\varepsilon }_m^{*}}\right)}}\nabla {\overrightarrow{E}}^{\hspace{1em}2}.$$ (3)

Here, K_CM is the Clausius-Mossotti factor, which depends on the frequency (ω) of the applied field as given by: ɛ* = ɛ + σ/jω. Since the DEP force is experienced by the polarized particles, only in non-uniform electric fields, it is proportional to the gradient (or spatial non-uniformity) of the square of the electric field. In prior work, since the trapping of ss-DNA at low frequencies has been reported to occur due to positive DEP forces,^{25, 26, 27, 30} for computational simplicity, we herein assume a K_CM of ∼1, even though this value can range anywhere from 0 to 1 for experimental positive DEP conditions. Considering 50 nm particles to be trapped in the constriction (such as ss-DNA fragments of 150 bases), the DEP force can be given by

$${\overrightarrow{F}}_{\mathit{DEP}}=5.35\times {10}^{-31}\nabla {\overrightarrow{E}}^2.$$ (4)

Equation 4 assumes that the DEP force profile is chiefly governed by the profile of the electric field gradient in the device, even though the absolute value of the force can vary with the variation in the constants such as particle size and electrical properties of the medium and particle. Under the applied field for DEP, the significantly high electrical conductivity of the fluidic media in the channel, leads to enhanced current flow, and hence Joule heating. This in turn gives rise to a temperature increase in the channel. Since the electric field in the channel is not uniform, the heating and hence the temperature profile is also non-uniform. By heat transfer relation, the temperature in channel can be computed as

$$\rho c_p(\frac{\partial T}{\partial t}+u·\nabla T)=\nabla ·(k\nabla T)+⟨\sigma {\overrightarrow{E}}^2⟩.$$ (5)

Here, ρ is the mass density of the fluid; k is the thermal conductivity; c_p is the specific heat; u is the convection velocity; and $⟨\sigma {\left|\overrightarrow{E}\right|}^2⟩$ is the average Joule heating term. The convection term of heat transfer can be neglected owing to the micro-scale geometry of the device where thermal conduction is the main heat transfer mode.³¹ At steady state, heat generated in the system is equal to the heat dissipated. Thus, the temperature profile can be computed as

$$k{\nabla }^{2}T+⟨\sigma {\left|\overrightarrow{E}\right|}^2⟩=0.$$ (6)

The localized Joule heating gives rise to temperature gradients in the fluidic channel, which in turn leads to localized variations in the electrical properties (conductivity and permittivity) of the fluid. Thus, under the applied electric field, these variations in the electrical properties give rise to bulk fluid forces, called the electrothermal forces (${\overrightarrow{F}}_{\mathit{ET}}$). Electrothermal forces are given by³²

$${\overrightarrow{F}}_{\mathit{ET}}={\rho }_q\overrightarrow{E}-\frac{1}{2}{\left|\overrightarrow{E}\right|}^2\nabla \varepsilon .$$ (7)

Here, ρ_q is the charge density, ɛ is the dielectric permittivity, and $\overrightarrow{E}$ is the applied electric field. The first term on the right hand side of the equation is the Coulomb force (${\overrightarrow{F}}_C$), while the second term is the dielectric force (${\overrightarrow{F}}_D$). The electrothermal force acts on the bulk fluid, leading to fluid motion. The velocity profile (v_x, v_y, v_z) caused by ${\overrightarrow{F}}_{\mathit{ET}}$ can then be calculated from the Navier-Stokes equation

$$\eta {\nabla }^{2}v-\nabla p+⟨{\overrightarrow{F}}_{\mathit{ET}}⟩=0,$$ (8)

where, η is the viscosity, p is the pressure, and $⟨{\overrightarrow{F}}_{\mathit{ET}}⟩$ is the average volumetric force on the fluid. The material properties used within the model are summarized in Table TABLE I..

TABLE I.

Survey of the material properties used within the model.

Parameter	Value
Conductivity of fluidic media (σm)	1 S/m
Conductivity of PDMS constriction (σc)	4 × 10−13 S/m
Conductivity of gold electrode (σAu)	3.9 × 107 S/m
Relative permittivity of fluidic medium (ɛm)	77
Relative permittivity of constriction (ɛc)	2.5
Thermal conductivity of fluidic medium (km)	6.13 × 10−1 W/m K
Thermal conductivity of PDMS constriction (kc)	1.5 × 10−1 W/m K
Thermal conductivity of gold electrode (kAu)	311 W/m K
Thermal conductivity of silicon floor (kSi)	149 W/m K
Thermal conductivity of quartz ceiling (kQuartz)	7.5 W/m K
Dynamic viscosity of fluidic medium (μ)	1 × 10−3 kg/m s
Particle radius (spherical equivalent of ss-DNA) (a)	5 × 10−8 m
Claussius-Mossotti factor (kCM)	1
Applied voltage	17.5 V
Ambient temperature	300 K

RESULTS

Influence of the dielectric constriction on electric field profiles and DEP force fields

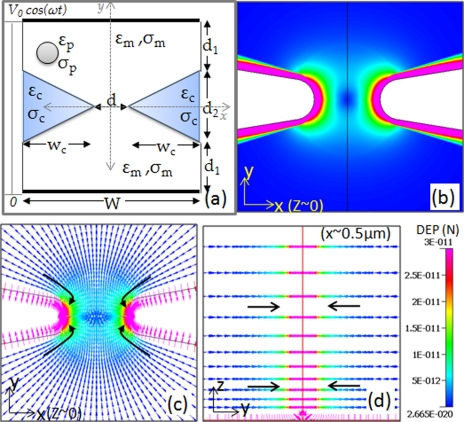
We begin with a consideration of the influence of a dielectric constriction in the microchannel on the electric field lines. While prior work has described the modification of electric field profiles due to the insulator edges, the relationship of bending of the field lines to the dielectric properties of the constriction material versus those of the fluidic media have not been elucidated. For this purpose, we consider the constriction device as a set of “lossy” capacitors as shown in Figure 2a, with the left side constriction, constricted fluidic medium in the gap and right side constriction being parallel to each other, so that the conduction and displacement currents are divided in proportion to their respective dielectric parameters (conductivity, σ, and permittivity, ɛ) for the particles (subscript p), constriction (subscript c), and the fluidic media (subscript m). At low frequencies, the conduction current and field are determined by σ_m and σ_c, while at high frequencies the displacement current and field are determined by ɛ_m and ɛ_c. For highly insulating constrictions, since σ_m ≫ σ_c, all the conduction current and field is forced through the medium in the gap at low frequencies. Similarly, since ɛ_m > ɛ_c, much of the displacement current and field passes through the fluidic medium at constriction gap at high frequencies. Based on this analysis, the constriction causes local enhancement of the field and its gradient at the edge of the constriction gap, both at low and high electric field frequencies, thereby causing enhancement of the ${\overrightarrow{F}}_{\mathit{DEP}}$ as shown in Figure 2b, as per Eq. 3. It should be noted that the localized field enhancements depend on channel to constriction width, i.e., W to d, whereas the field gradient due to the constriction depends on curvature of the constriction, i.e., ∼w_c/d₂ (Figure 2a). Furthermore, the constriction as shown in Figure 2a, only affects the fields in x- and y-directions, with no net z-component for the constricted electric field. From the DEP force field simulation shown in Figure 2b for a 500 × constriction, it can be noticed that the magnitude of the DEP force is highest at the constriction edge (Figures 2c, 2d), since the electric field gradient is highest at these points. The ${\overrightarrow{F}}_{\mathit{DEP}}$ vector (for positive dielectrophoresis) is pointed towards the constriction edge due to the highest electric field at these points. In summary, a 500-fold constriction in the channel width leads to ∼1000-fold increase in the electric field magnitude, with an even higher enhancement in field gradients at the constriction-edges, thereby causing a positive DEP trapping force directed towards the constriction edge.

Figure 2.

(a) Schematic to explain how the constriction geometry causes a field enhancement due to division of the low frequency conduction and high frequency displacement currents in proportion to their respective dielectric parameters (σ, ɛ); (b) magnitude of the ${\overrightarrow{F}}_{\mathit{DEP}}$ force field shows a significant region of high force field (∼10⁻¹¹ N) in the vicinity of the constriction; (c) the trapping force (${\overrightarrow{F}}_{\mathit{DEP}}$) in the x-y plane (x, y, z ∼ 0) is directed towards the constriction edge due to the high electric field and field gradient in this region; and (d) the trapping force (${\overrightarrow{F}}_{\mathit{DEP}}$) in the y-z plane (x ∼ 500 nm, y, z) is directed towards the constriction edge in the center of the microchannel.

DEP force fields for floating electrode coupled to insulator constriction

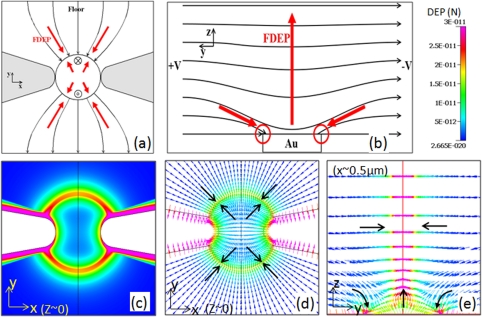
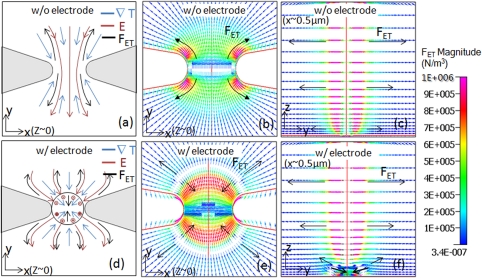
A sensor electrode with immobilized DNA capture probes forms an integral part of the electrical detection system for sensing the capture and hybridization with trapped ss-DNA targets under DEP. Hence, we present an analysis of the modified fields at the constriction due to presence of an electrically floating sensor electrode at the device floor (Figure 3a), as well as its influence through the channel depth (Figure 3b). In prior work, we have observed that a constriction coupled to an electrically floating electrode of equivalent size results in the highest degree of ss-DNA trapping; hence, herein we focus on the explanation in terms of the electric fields and DEP trapping forces. An electrically floating metal electrode in the path of the enhanced electric field due to the insulator constriction causes the electric field lines to terminate at the metal, perpendicular to the electrode surface, since the tangential field at the surface of the metal must be zero. The field lines in the plane right above the electrode surface must also terminate perpendicular to the electrode surface. Hence, the net electric field displays a z-component, which has important implications on the DEP and electrothermal force fields, as discussed subsequently. Furthermore, the electrode varies the x-y profile of the field at the device floor, while midway in the constricted channel this field profile is somewhat similar to the case of the constriction without the floating electrode. At the device floor, while the degree of enhancement to the field magnitude and the gradient is somewhat similar to that for the constricted device without the electrode, the primary difference is the extent of this enhancement. While the enhancement is primarily focused at the constriction edges for the case of the constriction without the electrode (Figure 2b); upon coupling to the electrode, the enhancement is extended to the entire electrode edge at the device floor, as well as across the constriction edge, as shown in Figure 3c. However, at midway depths in the channel, the influence of the electrode is diminished, and the profiles resemble the case for the constriction without the electrode. The directions of the DEP force fields in Figures 3d, 3e confirm that the ${\overrightarrow{F}}_{\mathit{DEP}}$ is directed towards the electrode edges at the device floor, as well as for channel depths up to ∼5%, in the region close to the electrode edges. In the region right above the center of the electrode, however, there is a reduction in the electric field density as shown in Figure 3b, resulting in DEP force directed upwards in channel depth, away from the low field region. In summary, coupling a floating electrode to the insulator constriction can cause localized enhancement of the extent of fields and field gradients due to focusing of field lines from multiple z-sections towards the device floor. While this analysis is presented for a disk electrode, we envision that electrode designs that are fabricated with a greater proportion of edges and are able to cause bending of field lines over a greater depth in the z-direction would display a greater extent of enhanced fields and gradients.

Figure 3.

(a) Influence of the electrically floating electrode on the x-y profile of the electric field. Field lines directed into the paper (x) and out of the paper (•) are also shown. ${\overrightarrow{F}}_{\mathit{DEP}}$ is directed towards the electrode edges; (b) Influence of the electrically floating electrode coupled to the insulator constriction on the electric field profiles in the z-plane. There is a net enhancement in extent of the high field region, since the electrode causes field lines from z-planes neighboring the device floor to terminate at the electrode surface; (c) the DEP force field for insulator constriction coupled to a floating electrode shows a significantly enhanced region of high trapping forces (∼10⁻¹¹ N) at the device floor (x, y, z ∼ 0); (d) the ${\overrightarrow{F}}_{\mathit{DEP}}$ is directed towards the electrode edges at the device floor (x, y, z ∼ 0); and (e) in the y-z plane (x ∼ 500 nm, y, z) ${\overrightarrow{F}}_{\mathit{DEP}}$ is directed towards electrode edges from the few upper z-planes and upwards (away from the electrode) in channel depth from the center of the electrode.

Temperature profiles

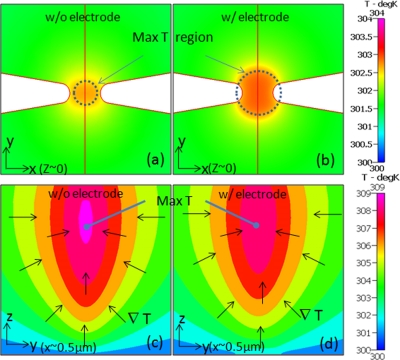
The application of electric fields (>100 V/cm) within fluids of significant electrical conductivity (>0.1 S/m) leads to enhanced current flow, and hence Joule heating. This in turn gives rise to temperature rise in the channel. The nonuniform electric field in the channel results in non-uniform Joule heating. Furthermore, owing to the varying heat dissipation profiles within different regions of the channel, the temperature profiles are also non-uniform. We begin with a physical picture of the temperature gradients based on the field profiles and heat dissipation characteristics in the x-y plane, as well as across y-z section of the device. For the 500 × constricted channel without a floating electrode, the electric field density at the constriction gap (y = 0 plane) can be assumed as somewhat equivalent through all points across the constriction width. This results in a region of maximum temperature within the fluidic medium at the center of the constriction (x,y = 0,0), due to the active heat dissipation at the fluidic interfaces with the device walls. Furthermore, since the floor and ceiling of the micro-channel act as the predominant heat sinks for the generated heat in the fluid, a hot spot develops midway through the channel. In the case of our specific design, since the thermal properties (heat capacity and thermal conductivity) of the channel floor (Si/SiO₂) differ from those of the channel ceiling (PDMS/quartz), with the floor acting as a better heat sink, the maximum temperature point is shifted nominally towards the ceiling of the channel. The temperature rise above ambient, due to Joule heating is strongly dependent on applied electric field (fixed at 350 V/cm in the current study) and conductivity of the media (fixed at 1 S/m to ensure optimal DNA hybridization conditions). The temperature profile simulations at the constriction device floor in the presence and absence of the floating electrode are shown in Figures 4a, 4b, respectively. In both cases, the temperatures are only marginally above the ambient for a 350 V/cm electric field, with the high temperature region spread to a slightly greater extent on the latter device, since the electrode of high thermal conductivity acts as an isothermal surface. However, the temperature close to the hotspot at the midway depth of the device rises steadily to 8°–10°K above ambient, as shown in the z-profiles in Figures 4c, 4d, for the constriction device with and without the floating electrode, respectively. The greater extent of enhanced electric field at the device floor for the constriction device coupled to floating electrode versus that without the electrode (Figure 3c versus Figure 2b), causes a greater extent of the high temperature region at the device floor. This electric field enhancement at the floor results in a net lowering of the density of field lines at depths above the electrode, which explains the lower temperatures at the hotspot in comparison to the constriction device without the electrode. This may also be attributed to the higher degree of heat dissipation due to presence of the high-thermal conductivity Au layer at the constriction floor. Hence, at the floor of the device, the maximum temperature is evenly distributed throughout the electrode surface rather than being concentrated within a narrow region, as observed for the constriction channel without electrode (Figure 4a versus Figure 4b). The temperature gradient vector is directed towards the highest temperature region, which is towards the constriction center in the x-y plane, whereas it is pointed towards the hotspot in the y-z section (Figures 4c, 4d). In absence of the electrode, the highest temperature attained within the hotspot is 36.2 °C (309.2 K), with the magnitude of temperature gradient of ∼6.5 × 10⁶K/m, around the highest temperature zone. In presence of the electrode, the highest temperature attained within the hotspot is 35.8 °C (308.8 K), with the magnitude of temperature gradient of ∼6.1 × 10⁶K/m. In summary, DEP fields (350 V/cm) applied within media of ∼1 S/m conductivity result in a significant temperature rise due to Joule heating, especially in the hotspot region near the constriction at midway of the channel depth (∼8°–10° K above ambient). While this rise is not likely to cause any significant damage to the DEP trapped ss-DNA targets, the temperature gradients can result in a significant degree of electrothermal flow. The temperature rise at the device floor is moderate (∼2°–3° K from ambient). At higher applied fields (∼1000 V/cm), the temperature at the hotspot can be high enough to alter the conformations of DEP trapped bio-molecules, such as proteins.

Figure 4.

Temperature profiles in the constriction region in xy-plane at the device floor for: (a) without (w/o) electrode and (b) with (w/) electrode in constriction channel. Temperature profiles in yz-plane at the center of constriction channel are shown for constriction channel (c) without electrode and (d) with electrode.

Electrothermal force profiles

The temperature gradients (∇T) due to localized Joule heating result in gradients in the fluid conductivity and permittivity, thereby leading to the fluid flow. Since, the electrothermal force arises due to temperature differences, the time averaged force per unit volume can be expressed in terms of temperature gradients as follows:

$$⟨{\overrightarrow{\mathbf{F}}}_{\mathit{ET}}⟩=-\frac{1}{2}(\frac{\nabla \sigma }{\sigma }-\frac{\nabla \varepsilon }{\varepsilon })·\overrightarrow{\mathbf{E}}\frac{\varepsilon \overrightarrow{\mathbf{E}}}{1+{(\omega \tau )}^2}-\frac{1}{4}{\left|\overrightarrow{\mathbf{E}}\right|}^2\nabla \varepsilon \mathrm{,}$$ (9)

$$⟨{\overrightarrow{\mathbf{F}}}_{\mathit{ET}}⟩=-\underset{F_C}{\underbrace{\frac{1}{2}(\frac{1}{\sigma }\frac{\partial \sigma }{\partial T}-\frac{1}{\varepsilon }\frac{\partial \varepsilon }{\partial T})\nabla \mathbf{T}·\overrightarrow{\mathbf{E}}\frac{\varepsilon \overrightarrow{\mathbf{E}}}{1+{(\omega \tau )}^2}}}-\underset{F_D}{\underbrace{\frac{1}{4}\left(\frac{1}{\varepsilon }\frac{\partial \varepsilon }{\partial T}\right)\varepsilon {\left|\overrightarrow{\mathbf{E}}\right|}^2\nabla \mathbf{T}}}.$$ (10)

As apparent from Eq. 10, the electrothermal forces are frequency (ω) dependent. At low frequency, the Coulomb forces (${\overrightarrow{F}}_C$) are dominant, while at high frequencies the dielectric forces (${\overrightarrow{F}}_D$) become dominant.³² Since our experimental DEP trapping work was conducted at low frequencies, we only consider Coulomb forces (${\overrightarrow{F}}_C$) within the subsequent analysis. As per Ref. 33, the temperature dependence of the conductivity and permittivity is given by: $\frac{1}{\sigma }\frac{\partial \sigma }{\partial T}=2\%$, $\frac{1}{\varepsilon }\frac{\partial \varepsilon }{\partial T}=-0.4\%$ over the temperature range of interest (∼0–30 °C). Hence,

$$\frac{1}{\sigma }\frac{\partial \sigma }{\partial T}-\frac{1}{\sigma \varepsilon }\frac{\partial \varepsilon }{\partial T}>0.$$ (11)

As apparent from Eqs. 10, 11, ${\overrightarrow{F}}_C$ is directed parallel or anti-parallel to the direction of electric field, which can be estimated based on the sign of $\nabla \mathit{T}·\overrightarrow{E}$. When the temperature gradient is parallel to the electric field, the Coulomb force is directed against the electric field and vice versa. In the subsequent sections, we analyze the magnitude and direction of the Coulomb force portion of ${\overrightarrow{F}}_{\mathit{ET}}$ for the constriction device, in absence and presence of the electrode.

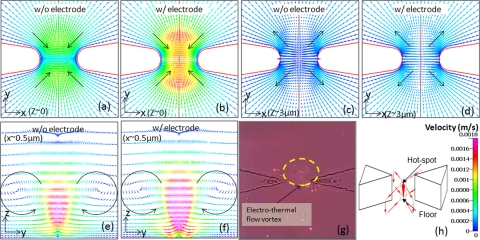
For the constriction device in absence of the floating electrode, the electric field lines do not have a z-component, as discussed within Sec. 3A. Hence, the Coulomb ${\overrightarrow{F}}_{\mathit{ET}}$ force does not have a z-component as well. Since the temperature gradients are highest within the constriction region; ${\overrightarrow{F}}_{\mathit{ET}}$ is most significant in this region, as shown in Figures 5a, 5b, 5c. As shown in the schematic of the vector directions for ∇T, $\overrightarrow{E}$ and ${\overrightarrow{F}}_{\mathit{ET}}$ in Figure 5a, ∇T and $\overrightarrow{E}$ are parallel and directed towards the constriction in the upstream region of the channel (y > 0), while they are anti-parallel in the downstream region of the channel (y < 0), with ∇T directed towards the constriction in the channel and towards the hotspot in the constriction region. Hence, ${\overrightarrow{F}}_{\mathit{ET}}$ is directed anti-parallel to $\overrightarrow{E}$ for the upstream region of the channel (y > 0) and is directed parallel to $\overrightarrow{E}$ for the downstream region of the channel (y < 0). In either situation, the dissipative action of ${\overrightarrow{F}}_{\mathit{ET}}$ on the DEP trapping is clear, since ${\overrightarrow{F}}_{\mathit{ET}}$ is directed away from the constriction, which is in the opposite direction of ${\overrightarrow{F}}_{\mathit{DEP}}$, which is always directed towards the constriction edge. It may be noted that exactly at center of the constriction, where ${\overrightarrow{F}}_{\mathit{ET}}$ switches direction, there is a very small region of zero ${\overrightarrow{F}}_{\mathit{ET}}$, since ∇T (which is parallel to z-axis) is perpendicular to $\overrightarrow{E}$ (which is parallel to the xy-plane).The electrothermal force simulations in Figures 5b, 5c confirm the direction of ${\overrightarrow{F}}_{\mathit{ET}}$ based on the analysis presented above and show their magnitudes in N/m³ units. It is readily apparent from Figure 5c that the magnitude of ${\overrightarrow{F}}_{\mathit{ET}}$ is lowest at the fluid interfaces with device walls (floor and ceiling) and rises continuously towards the hotspot in the channel depth due to the maximum temperature gradients at these points. Hence, while the ${\overrightarrow{F}}_{\mathit{ET}}$ differs across the channel depth, ${\overrightarrow{F}}_{\mathit{DEP}}$ is invariant with channel depth, since the electric field profiles in the different z-sections are similar to that of the device floor at the x-y plane. In a subsequent section, the balance of these ${\overrightarrow{F}}_{\mathit{ET}}$ and ${\overrightarrow{F}}_{\mathit{DEP}}$ forces will be compared in terms of their influence on net particle mobility.

Figure 5.

Constriction device without (w/o) electrode (a)-(c) and with (w/) electrode (d)-(f) are analyzed as follows: (a) and (d) show schematics of the direction of electric field (red), temperature gradient (blue), and the resulting Coulomb forces (black), without and with the electrodes, respectively (color images available on web version). (b) and (e) show simulations of electrothermal Coulomb force (F_ET) profiles acting on the bulk fluid at constriction channel floor for device without and with electrode, respectively. (c) and (f) show the F_ET profile in the yz-plane (x ∼ 500 nm, y, z) near the constriction edge with the z-component of the force for device without and with electrodes, respectively.

The direction and magnitude of ${\overrightarrow{F}}_{\mathit{ET}}$ for the constriction device coupled to the electrically floating electrode are shown in Figures 5d, 5e, 5f. As shown in the schematic of the vector directions for ∇T, $\overrightarrow{E}$, and ${\overrightarrow{F}}_{\mathit{ET}}$ in Figure 5d, within the upstream region of the channel (y > 0), $\overrightarrow{E}$ is pointed towards the electrode edges and ∇T is pointed towards the center of the device (x,y = 0,0); and hence they are parallel. In the downstream region of the channel (y < 0), $\overrightarrow{E}$ is pointed away from the electrode edges and ∇T is pointed towards the center of the device (x,y = 0,0); and hence they are anti-parallel. Hence, here too, ${\overrightarrow{F}}_{\mathit{ET}}$ is anti-parallel to $\overrightarrow{E}$ in the upstream half of channel (y > 0) and parallels $\overrightarrow{E}$ in the downstream half of the channel (y < 0) as shown in Figure 5e, leading to its dissipative action on trapping ${\overrightarrow{F}}_{\mathit{DEP}}$, which is pointed towards electrode edges. However, since the electric field profiles of this device display a z-component as discussed within Sec. 3B, the electrothermal force profiles too show a magnitude in the z-direction. Across the channel depth, as shown in Figure 5f, ${\overrightarrow{F}}_{\mathit{ET}}$ increases continuously as the hot spot region is approached, and it is directed outwards from the constriction center within each x-y device section. Hence, the major differences between the ${\overrightarrow{F}}_{\mathit{ET}}$ profiles for the constriction device with and without the floating electrode are at the device floor.

Velocity profiles

Based on the electrothermal force, the net velocity profiles on the fluid can be determined based on conservation of momentum, as described by the Navier-Stokes equation. For a given body force and assuming an incompressible fluid of low Reynolds number, the steady state Navier-Stokes equation can be written as previously described in Eq. 8. In this case, $⟨{\overrightarrow{F}}_{\mathit{ET}}⟩$ can be approximated as: $⟨{\overrightarrow{F}}_{\mathit{ET}}⟩=⟨{\overrightarrow{F}}_C+{\overrightarrow{F}}_D⟩$. Since the pressure in the fluid is constant, and we only consider low frequencies where electrothermal force is dominated by the Coulomb force, the equation is reduced to the following, for determining the velocity profiles in the x, y, and z-directions (v_x, v_y, and v_z)

$$\eta {\nabla }^2\overrightarrow{v}+⟨{\overrightarrow{F}}_C⟩=0.$$ (12)

For the constriction device without the floating electrode at the floor, since the electrothermal forces are dominant at the constriction edges and are directed away from the constriction region, the net fluid flow should occur away from the constriction. However, across the channel depth, the magnitude of the electrothermal force is highest at the hotspot that is midway through the channel depth, since the temperature and its gradient are highest in this region. Furthermore, since the magnitude of the electric field is highest at the constriction edges, the flow at the edges is the dominant factor in determining the overall flow profile. The overall fluid flow is dominated by the net highest force, with rest of the fluid flow occurring, so that the net mass and momentum are conserved. Hence, the velocity profiles of the fluid in Figure 6 show that the fluid flow out of the constriction follows the profile of the constriction edges from the hot spot, where the ${\overrightarrow{F}}_{\mathit{ET}}$, and hence, the outgoing fluid velocity magnitudes from the constriction are the highest. Towards the channel floor, on the other hand, the fluid is directed back towards the constriction to obey mass conservation principles. This net rotational flow gives rise to four vortices as shown schematically in Figure 6h. Finally, since the fluid volume going out of the hot spot needs to be replaced by an equal volume of the incoming fluid at the bottom, the fluid from the four vortices flow up to the midway depth point of the channel at the constriction center, with the maximum incoming fluid velocity being higher than the maximum outgoing fluid velocity. In presence of the floating electrode at the constriction floor, the net velocity profiles are somewhat similar to that of the constriction device in absence of the electrode. However, since the electrothermal forces are directed inwards towards the electrode center at the device floor due to the z-component of the electrothermal force, they support the formation of the vortex flow pattern, wherein fluid goes out from the hot spot and comes back in at the floor. Hence, the incoming fluid velocity is higher as compared to the constriction device without electrode. This in turn leads to a significant increase in the z-component of the velocity to compensate for the greater volume of the incoming fluid. Hence, within the hotspot region, while the direction of fluid flow due to electrothermal flow opposes trapping due to the DEP force, the fluid flow due to electrothermal flow at the channel floor can assist DEP trapping of bio-particles through enabling long-range fluid sampling by pushing the fluid towards the sensor electrode at the channel floor, as well as localized stirring by circulating a greater volume of the fluid in the vicinity of the sensor electrode.

Figure 6.

Electrothermal force induced fluid velocity profiles for the constriction channel device in xy-plane at the device floor: (a) without (w/o) electrode, and (b) with (w/) electrode, at the channel hot-spot: (c) without electrode and (d) with electrode. The yz-plane velocity profiles showing the two circulating fluid vortices for half of the channel are shown for (e) without electrode, and (f) with electrode. (g) Experimental result showing the formation of electrothermal flow vortex near the constriction in constriction channel device; (h) shows overall fluid flow in the constriction channel device with four vortices.

Balance of forces on the bio-particles

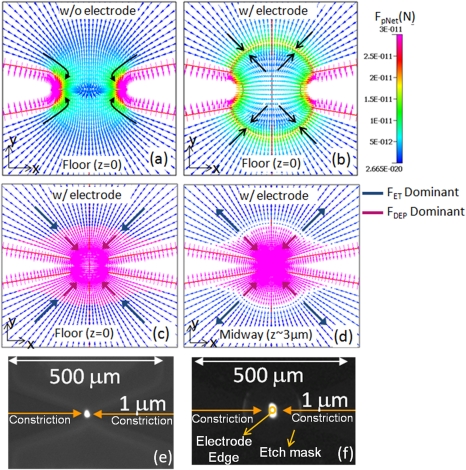
Finally, we examine the balance of ${\overrightarrow{F}}_{\mathit{ET}}$ and ${\overrightarrow{F}}_{\mathit{DEP}}$ forces on the net mobility for the bio-particles. The bulk fluid flow acts on the bio-particle in the form of drag force thereby affecting the particle trajectory. Particle terminal velocity in the fluid can be given by

$${\overrightarrow{v}}_p={\overrightarrow{v}}_f+\frac{{\overrightarrow{F}}_p}{\gamma }.$$ (13)

Here, ${\overrightarrow{v}}_p$ is the particle velocity, ${\overrightarrow{v}}_f$ is the fluid velocity, ${\overrightarrow{F}}_p$ is the force acting on the particle, which in this case is the dielectrophoretic force (${\overrightarrow{F}}_p={\overrightarrow{F}}_{\mathit{DEP}}$), and γ is the drag coefficient for the particle. Assuming a spherical particle of radius, a, the drag coefficient is given by

$$\gamma =6\pi \eta a.$$ (14)

From this analysis, net force on the particle can be computed as

$${\overrightarrow{F}}_{\mathit{pTotal}}=\gamma {\overrightarrow{v}}_f+{\overrightarrow{F}}_{\mathit{DEP}.}$$ (15)

Based on a Clausius-Mossotti factor (K_CM) of ∼1, the dielectrophoretic force for ss-DNA fragments (a∼50 nm) is ∼2 orders of magnitude higher than the electrothermal drag for a 500 × constriction device without the electrode. Hence, the bio-particles move predominantly under the influence of ${\overrightarrow{F}}_{\mathit{DEP}}$ in the vicinity of the constriction. For the constriction device coupled to the floating electrode, the situation is similar with a larger extent of DEP trapping force at the device floor and its complementary action with the fluid velocity profile under electrothermal flow at the device floor. However, the dominance of the DEP forces is limited to the constriction region. Away from the constriction, the magnitude of the DEP forces drop very rapidly and while the electrothermal forces, owing to the greater extent of fluid motion are still significant. In fact, further away from the constriction,the electrothermal drag force dominates over the DEP force on the particles. Since the electrothermal force is effective over a greater spatial region than DEP forces, it can assist in bringing more particles towards the constriction. Thus, as shown in Figures 7c, 7d, the net force on the particle is exactly similar to the DEP force in the vicinity of the constriction, while the dominant force on the particle away from the constriction is the electrothermal drag. The velocity profile due to this electrothermal force, as discussed in Sec. 3E, is directed towards the constriction at the floor of the device, whereas, midway through the channel depth, it is directed away from the constriction. Furthermore, in the case of the constriction device with the floating electrode, the incoming electrothermal force at the device floor is higher due to the presence of electrode. Thus, the presence of sensor electrode at the floor of the device not only helps to integrate the pre-concentration of the DNA with hybridization and sensing but also enhances the electrothermal forces to assist the DEP aided pre-concentration. The force profiles for the constriction device in absence and presence of the electrode differ only at the device floor and are rather similar through rest of the channel depth, and hence the Figures 7a, 7b show the force profiles at the device floor. The fluorescence microscopy images of Figure 7e (constriction only) and Figure 7f (constriction coupled to a floating electrode) present an experimental verification of the enhanced trapping of ss-DNA due to presence of the electrode; and this is especially the case within media of high conductivity where Joule heating and electrothermal flow become significant.

Figure 7.

Net force on the particle, ${\overrightarrow{F}}_{\mathit{DEP}}$ + ${\overrightarrow{F}}_{\mathit{ET}}$ (drag) at constriction device channel at device floor (a) without (w/o) electrode and (b) with (w/) electrode. The colors represent the regions of dominance of DEP (magenta) and ET (blue) and show how the two forces act in the same direction at (c) the device floor while act against each other at (d) the hot spot. Fluorescence microscopy images of constriction device without electrode in (e) and with electrode in (f) show the enhanced trapping of ss-DNA in high-conductivity media due to the presence of the floating electrode. The outer ring in (f) is due to the “etch mask” profile to expose the edges of the metal electrode.

CONCLUSIONS

We have presented an electrokinetic framework for the application of insulator dielectrophoresis within media of high-conductivity for effective trapping of bio- and nanostructures of low polarizability, such as ss-DNA and proteins. Our specific conclusions are summarized below:

• (1)A 500-fold constriction device enables a high degree of focusing of electric field lines, and the extent of this high-field region can be vastly enhanced through coupling the constriction to an electrically floating electrode at the constriction floor, to cause the focusing of field lines from multiple z-sections.
• (2)The application of electric fields of ∼350 V/cm to enable dielectrophoretic trapping of nanoscale biomolecules within media of conductivity of ∼1 S/m causes a temperature rise due to Joule heating. While the presence of a high thermal conductivity electrode at the constriction channel floor enables an isothermal surface for significant heat dissipation at the channel floor, a hotspot region with temperatures of ∼8°-10° K above the ambient is generated midway within the channel depth at the constriction center, causing a significant degree of electrothermal flow.
• (3)The electrothermal flow causes a set of vortices that drive the fluid outwards away from the hotspot that emerges midway through the channel, followed by a downward and inward motion towards the electrode edges at the constriction floor and then finally back upwards from the constriction floor towards the hotspot. While the electrothermal flow opposes dielectrophoretic trapping in the vicinity of the hotspot region, the electrothermal flow at the channel floor was found to assist the trapping of biomolecules through enabling long-range fluid sampling towards the sensor electrode at the channel floor, as well as through localized stirring by circulating a greater volume of the fluid in the vicinity of the sensor electrode. For ss-DNA molecules of ∼50 nm equivalent radii, the trapping forces far exceed the electrothermal dissipative forces at all z-sections of the device.