Inferring Coancestry in Population Samples in the Presence of Linkage Disequilibrium

Abstract

In both pedigree linkage studies and in population-based association studies there has been much interest in the use of modern dense genetic marker data to infer segments of gene identity by descent (ibd) among individuals not known to be related, to increase power and resolution in localizing genes affecting complex traits. In this article, we present a hidden Markov model (HMM) for ibd among a set of chromosomes and describe methods and software for inference of ibd among the four chromosomes of pairs of individuals, using either phased (haplotypic) or unphased (genotypic) data. The model allows for missing data and typing error, but does not model linkage disequilibrium (LD), because fitting an accurate LD model requires large samples from well-studied populations. However, LD remains a major confounding factor, since LD is itself a reflection of coancestry at the population level. To study the impact of LD, we have developed a novel simulation approach to generate realistic dense marker data for the same set of markers but at varying levels of LD. Using this approach, we present results of a study of the impact of LD on the sensitivity and specificity of our HMM model in estimating segments of ibd among sets of four chromosomes and between genotype pairs. We show that, despite not incorporating LD, our model has been quite successful in detecting segments as small as 10⁶ bp (1 Mpb); we present also comparisons with fastIBD which uses an LD model in estimating ibd.

EVEN in large populations, sampled individuals may share genome inherited from a common ancestor on the order of tens of generations ago, at a time depth of up to 2000 years, and the probabilities are increased in samples from small populations, structured populations, or in individuals ascertained for particular traits. Generally, such segments of genome that are shared identically by descent (ibd) in remote relatives are rare but not short (Donnelly 1983). For example, the probability that a pair of human individuals separated by 20 meioses share any of their autosomal genome is ∼0.001, but, if it exists, an ibd segment is of order 5 × 10⁶ bp (5 Mbp). For closer relatives, separated by 12 meioses, the chance of sharing some segment of autosomal genome is 0.148, while the expected length of the segment is of the same order of magnitude (8 Mbp).

Modern dense SNP marker data provide information to detect such ibd segments in unknown relatives and thus increase information for genetic linkage mapping (Leutenegger et al. 2003; Albrechtsen et al. 2009). Indeed, the first such method developed by Leutenegger et al. (2003) to detect segments of homozygosity by descent in individuals affected by Taybi–Linder syndrome has recently led to gene discovery (Edery et al. 2011). In population samples also, detection of unknown remote segments of ibd enables association tests either to use (Browning and Browning 2010) or to adjust for (Choi et al. 2009) this coancestry in association methods of gene mapping. Combining inheritance information within the pedigrees of a genetic epidemiological study with inferred ibd among members of different pedigrees has the potential to increase both the power and resolution of linkage mapping (Glazner and Thompson 2011).

In pedigrees ibd is well defined relative to the specified founders of the pedigree, but the appropriate definition is less clear where relationships are unspecified. There is no absolute measure of ibd ; it is always relative to some time point. This time depth, t, is related to two key parameters of the ibd process: the pointwise pairwise probability of ibd, β, and the expected length of an ibd segment between a pair of chromosomes. This length depends on β but also on the overall rate of change of ibd state along a chromosome, α. In a population of constant effective population size N_e

$$\beta =1-{\left(1-{\left(2N_{\text{e}}\right)}^{-1}\right)}^t,$$

but in natural populations N_e is neither constant nor accurately known. A segment of ibd in two current chromosomes resulting from a common ancestor t generations ago will be broken at rate 2t per Morgan (or 100 Mbp) along the chromosome, by recombination events in the chain of 2t ancestral meioses. In practice, it is more convenient to measure rates of ibd change on a scale of centimorgans or megabase pair, so α = 2t/100 per Mbp. However, in a population, segments of ibd result from common ancestors at different time depths, and there is no simple relationship between the segment lengths of ibd and the defining time depth t of ibd. In effect, the choice of β and of a rate parameter α defines ibd. While Browning and Browning (2010) adopt the approach of choosing values of β and α appropriate to the levels and lengths of ibd they aim to detect, in this article we regard them as parametrizing a prior distribution on these levels and lengths, and we examine sensitivity to this prior.

A major issue in the inference of ibd is the presence of linkage disequilibrium (LD). Among chromosomes or individuals, the signature of ibd is haplotypic similarity, but, at the population level, LD also results in haplotypic similarity. LD is maintained by linkage, but arises from the history of a population. At small chromosomal scales, LD may reflect the genetic background of an original mutant variant and thus coancestry of chromosomes relative to that mutant origin. At larger scales, LD may result from population admixture or substructure and is also a reflection of the relationship structure within a population. Clearly, only segments of ibd significantly longer than the extent of LD can be distinguished from the LD background. However, segments of genome resulting from common ancestors up to 25 generations ago are of the order 2 Mbp. Such segments are typically at least an order of magnitude longer than the extent of LD, and these are the segments we seek.

In this article, our major focus is the impact of LD on the detection of segments of ibd from population data, using a model that does not incorporate LD. This is important because LD is complex to model and dependent on population history. Whereas adequate samples for the estimation of allele frequencies may be available, from the same or from a comparable population, accurate estimation of haplotype frequencies requires far more data. In smaller populations, or nonhuman populations, such data may be unavailable. To undertake this study of the impact of LD on ibd inference, we have developed two innovations, First, to make maximal use of data on the genotypes and haplotypes of individuals, we have developed a general and flexible model for the patterns of ibd among a set of n chromosomes and for the changes in ibd along the genome. By using an improved ibd model, our goal is to compensate for not modeling LD. Second, to undertake the study, we required a method to generate realistic haplotypes to populate the founder population relative to which we measure ibd. Since our goal is the study of the impact of LD, these sets of haplotypes should include the same SNP markers and be generated according to the same allele frequencies and should differ only in the level of LD they exhibit. Our new beaglesim achieves this. The method uses the chromosomes of a real population to provide a base LD structure across the genome. A single parameter, γ, then controls the LD level relative to this base.

In Methods we first provide a description of other recent hidden Markov model (HMM) models used in ibd inference, and then introduce our new model for latent ibd among a set of n chromosomes. We describe a model for the observable data conditional on latent ibd, and an implementation of the ibd inference procedure for the case n = 4. We also describe our new simulation approach, beaglesim, for generating the realistic sets of haplotypes differing only in LD level that are required for our study. Finally, we discuss the choice of model parameters for our analyses. In the RESULTS section we first show the performance of our beaglesim simulation method, and then describe our results on the effect of LD in inference of ibd segments, given either haplotypic or genotypic data on pairs of individuals. We summarize the ability to detect ibd segments as a function of the length of the segment. Finally, we compare results with those of fastIBD (Browning and Browning 2011) run on the same data sets. We conclude with a Discussion.

Methods

Previous models for detecting ibd segments in populations

There have been several recent HMM approaches to the detection of ibd segments in individuals not known a priori to be related. To place our model and approach in context, we first summarize these. Using genotypic data on affected individuals, Leutenegger et al. (2003) used a two-state HMM to model the ibd /non-ibd between the two homologous chromosomes of these offspring individuals to detect unspecified additional relationships between their parents to increase the power for gene mapping. Browning (2008) used the same two-state ibd model for pairs of phased haplotypes sampled from a population, while another approach that relies on the availability of haplotypic data is that of Gusev et al. (2009). The first model for ibd between pairs of diploid individuals was that of Purcell et al. (2007), but this approach modeled the ibd as that of two independent pairs of haplotypes each following a model equivalent to that of Leutenegger et al. (2003). The ibd state is summarized as 0, 1, or 2 shared ibd between the two individuals. However, the inbreeding coefficient of offspring is the kinship coefficient of parents, and in most populations ibd within individuals is at least as great as ibd between. The approach of Browning and Browning (2010, 2011) also seeks only ibd between individuals and uses a two-state model of any ibd /no ibd between two diploids to analyze genotypic data. Thompson (2008) provided a Markov model for the 15 states of ibd among the four chromosomes of two individuals, and Thompson (2009) extended this model to any number n of chromosomes. However, the state transitions permitted under this model become increasingly restrictive for larger n, and the model of this article provides a less restrictive generalization. Moltke et al. (2011) have recently also provided a model for n chromosomes, but, to facilitate MCMC sampling of ibd, their latent ibd model is simplified, both in its pointwise state probabilities and in its permitted transitions.

All the above methods use similar data models. Basically, ibd DNA is of the same allelic type, while non-ibd DNA is of independent allelic types, and allele frequencies are assumed known or estimated from large population samples. The data model of Purcell et al. (2007) is different in that it treats the alleles of the population sample as a finite pool and assigns them without replacement to non-ibd DNA, resulting in negative correlations in these allelic types. In these earlier models LD is not accommodated; the data at each locus depend only on the latent ibd state at that locus. Albrechtsen et al. (2009) extended the basic data model to allow for pairwise LD among loci, but only the approach of Browning (2008) and Browning and Browning (2010) uses a full LD model. In this case, allele frequencies are not used directly, but only through the haplotype clusters of the BEAGLE model fitted empirically to a large population sample (Browning and Browning 2007). While most of the methods consider the data input as genotypic, the methods of Thompson (2008, 2009) and the current article allow for either haplotypic or genotypic data. As indicated by Leutenegger et al. (2003), allowance for genotyping error is important, and this is also accommodated in Thompson (2009), Browning and Browning (2010), and Moltke et al. (2011), as well as in the model presented here.

A model for ibd among n chromosomes

At any point in the genome, a set of n chromosomes partitions into k subsets, those within a subset being ibd. A useful one-parameter model for such a partition of n labeled exchangeable objects is that given by Ewens’ sampling formula (Ewens 1972; Balding and Nichols 1994), which may be expressed in terms of β, the pointwise probability of ibd between a pair of chromosomes (Thompson 2008, Equation 2).

To construct a HMM for the ibd process along the genome that has the correct equilibrium state distribution, we consider transitions that follow a modification of the “Chinese restaurant process” or CRP (Tavaré and Ewens 1997). As in Thompson (2008), the matrix-transition rates are expressed in terms of the relative rates β: (1 − β) of gain and loss of ibd between any pair of chromosomes. A new “potential chromosome” is added to an ibd group size j at rate jβ and forms a new subset not ibd to any existing group at rate (1 − β). Instantaneously with an addition, a random one of the (n + 1) chromosomes is removed, and (if not removed) the new chromosome assumes the identity of the removed chromosome. This defines a Markov rate matrix Q and hence the jump chain of the process and relative rates of leaving each state.

Further details of the n-chromosome model, including proof of the equilibrium distribution, is given in Appendix A. The transition matrix for the case n = 4 is given in Appendix B. Note that the matrix as stated has no chromosomal scale: β and η = (1 − β) are probabilities. The scale of changes in ibd state in terms of either genetic (centimorgans) or physical (megabase pairs) distance is provided by the rate parameter α (see Introduction). The matrix Q is multiplied by an overall rate parameter α per megabase pairs. This model is a generalized version of earlier models of Leutenegger et al. (2003) and Thompson (2008, 2009). As in those models, there are just two parameters: the pointwise pairwise probability of ibd (β) and a single overall rate parameter (α) controlling the scale of lengths of ibd segments.

To provide an understanding of the appropriate order of magnitude of the parameter α, consider the following. Note that the total rate of occurrence of potential transitions arising from the CRP is α(nβ + (1 − β))/Mbp (see Appendix A) or ∼α if β is small and n = 4. The distance to the next potential transition is exponentially distributed, with mean approximately α⁻¹ Mbp. For a pair of chromosomes, the rate of loss of ibd is 2α(1 − β), or the length of an ibd segment is approximately (2α)⁻¹ Mbp. Thus, for example, for segments on average 1 Mbp, α ≈ 0.5. However, as discussed below, in this article we do not try to tune α to specific segment lengths.

The new model permits some transitions among ibd states that were not permitted under earlier models and is designed to reflect more closely changes that occur in reality in the ancestry of a set of extant chromosomes. At any change event, any one chromosome can move from one ibd group to any other or become non-ibd with all other chromosomes. However, where chromosomes share ancestral recombination breakpoints, other transitions may occur Thompson (2009). Thus the model is further modified as in Thompson (2009). Before multiplying by α, the rate matrix Q is modified to Q*, where for ibd states w and z,

$$Q_{wz}^{*}=\left(1-\delta \right)Q_{wz}+\delta {\pi }_z\hspace{1em}\mathrm{for}\hspace{0.17em}z\ne w\hspace{0.17em}\mathrm{and}\hspace{0.17em}{Q}_{ww}^{*}=-{\displaystyle \sum }_{z\ne w}{Q}_{wz}^{*},$$ (1)

where π_z is the equilibrium probability of ibd state z. That is, with probability (1 − δ), transitions follow the rate matrix Q, but with probability δ the transition is to a state randomly chosen from the equilibrium distribution. This modification does not have any population–genetic interpretation, but maintains the correct distribution while allowing, with small probability, any state change.

Table 1 shows the proportion of genome and of segments in each of the 15 ibd states among four chromosomes at four different values of β. For β = 0.01, 94% of the genome is expected to be in the no-ibd state, with each of the 6 states with a single-pair ibd making up almost all the remainder. There are long stretches of no ibd, and almost 50% of segments are in that state, as the process enters and leaves one of the other states. When β = 0.1, only 55% of the genome is in the no-ibd state, and segments of no ibd are 10 times shorter and their proportion is 50% lower, as transitions among other ibd states start to have nonnegligible probability. In our analyses, we focus on the two intermediate values of β; β = 0.02 is approximately the value in our simulated population, while β = 0.05 is the value we typically use in our analysis model. In Table 1, proportions of genome and relative segment lengths are computed for δ = 0.1 since that is the value that is used in our analyses, but the values in Table 1 would be almost the same for δ = 0.

Table 1 . Proportions of genome and of segments for the different ibd state types.

ibd state	All ibd	Three ibd	Two pairs	One pair	No ibd
(a1,a2,a3,a4)	(0,0,0,1)	(1,0,1,0)	(0,2,0,0)	(2,1,0,0)	(4,0,0,0)
Number	1	4	3	6	1
Percentage of genome: (each state); any δ
β = 0.01	0.0006	0.0192	0.0096	0.951	94.18
β = 0.02	0.0045	0.0739	0.0369	1.811	88.72
β = 0.05	0.0649	0.4113	0.2056	3.907	74.23
β = 0.1	0.4545	1.3636	0.6818	6.136	55.23
Segment length (units α−1 Mbp); δ = 0.1
β = 0.01	0.273	0.354	0.268	0.507	8.786
β = 0.02	0.276	0.350	0.265	0.490	4.400
β = 0.05	0.284	0.341	0.258	0.443	1.768
β = 0.1	0.299	0.326	0.246	0.382	0.889
Percentage of segments: (each state); δ = 0.1
β = 0.01	0.01	0.24	0.16	8.41	48.08
β = 0.02	0.04	0.48	0.32	8.47	46.22
β = 0.05	0.22	1.18	0.78	8.61	41.04
β = 0.1	0.82	2.26	1.50	8.67	33.59

Results are given under the population prior model, as a function of β (δ = 0.1).

An HMM for ibd estimation

The latent state of our HMM is the ibd state among the chromosomes, specified as the unordered labeled partition of the chromosomes into the ibd subsets. The Markov model for the change of ibd state along the chromosome is then that described above.

We use a data model that is a direct extension of that of Leutenegger et al. (2003). Allele frequencies q_l,j of allele j at marker locus l are assumed known; in practice they can be well estimated from population samples. The chromosomes in a given ibd group at locus l all have allelic type j with probability q_l,j, while the allelic types of chromosomes in different ibd groups are independent. Just as we use the model of Equation 1 to avoid overconstraining zero transition probabilities in the HMM, we make a small allowance for genotyping error to eliminate zero emission probabilities. A simple error model is that, for each ibd state w,

$$P\mathrm{r}\left(\mathrm{data}\hspace{0.17em}|\hspace{0.17em}w;\mathit{\epsilon }\right)=\left(1-\mathit{\epsilon }\right)\mathrm{Pr}\left(\text{data}\hspace{0.17em}|\hspace{0.17em}w;\mathit{\epsilon }=0\right)+\mathit{\epsilon } \mathrm{Pr}\left(\text{data}\hspace{0.17em}|\hspace{0.17em}{w}_0\right),$$ (2)

where w₀ is the no-ibd state. That is, with probability (1 − ε) there is no error, while with probability ε each of the four chromosomes is independently observed of allelic type in accordance with the locus-specific allele frequencies. While this simple all-or-none error model works well for n = 4 chromosomes, for larger numbers of chromosomes it may be too extreme. An alternative would be a model of independent errors over loci and over chromosomes, possibly with a restriction on the number of errors at a locus (for example, the model of Sieberts et al. 2002). Note that our HMM does not attempt to accommodate LD in the analysis of data. LD is complex to model, and large samples are needed for accurate estimation of haplotype frequencies (Browning and Browning 2007). One of our main objectives is to study the impact of LD in the data on estimation under our model.

With the Markov model for locus-to-locus transitions in the ibd partitions along the chromosome, and data probabilities defined locus-by-locus independently given the latent ibd state, we have an HMM framework. Standard HMM computations (Baum et al. 1970) provide the probability of ibd states at each marker locus conditional on the data jointly at all marker loci. For n = 4 chromosomes, we have implemented these HMM computations in our IBD_Haplo software (main program ibd_haplo). If the data on the four chromosomes are phased (haplotypic data) there are 15 latent ibd states (including the no-ibd state), while for unphased genotypic data on a pair of diploid individuals there are 9. At any locus, if there are missing data, the remaining data are not considered, but the locus is still included in the computation of ibd state probabilities. The result of Kemeny and Snell (1976, p.124) shows that, as for the earlier model of Thompson (2009), the transition model described above remains Markov when a reduction is made from the 15 haplotypic states to the 9 genotypic states. Our program also allows for partially phased data; in some regions data may be haplotypic but in others genotypic.

The ibd_haplo program is fast; for example, running 500 pairs of individuals over 7000 markers takes less than 90 sec on a desktop computer. The output produced is large; for each set of 4 chromosomes or pair of genotypes, for each marker locus, probabilities of each of the 15 (or 9) ibd states are tabulated. To process these large output files we have written an R-package, IBDhaploRtools, which reads this output and produces a variety of summary statistics. The output state probabilities are reduced to a call (or no-call) using a calling threshold. For the results of this article we used a calling threshold of 0.9, the probability a single 1 of the 15 (or 9) ibd states must reach this threshold for the state to be called. Lower values (e.g., 0.8) provide too many incorrect calls, while higher values (e.g., 0.95) result in a high proportion of no-calls.

Data simulation

To obtain realistic simulated data with which to test our approach, we first simulate descent of genome. Each founder chromosome is given a unique founder genome label (FGL) and descendant chromosomes are specified as a list of segments consisting of the FGL from which that segment descends and its base pair boundaries. In each meiosis, distances to the next recombination crossover are generated along the chromosome as exponential random variables with mean 10⁸ bp, and the offspring chromosome is thereby constructed from the two in the parent. This process provides the set of chromosomes in the current population. Among a set of current chromosomes, the true simulated ibd is then obtained by comparison of the FGL segment lists: where the FGL is the same, the chromosomes are ibd.

For the current study, we simulated descent in a constant population of 3500 males and 3500 females over 200 generations. At each generation, repeated 3500 times, a random male and a random female are chosen to generate a son and a daughter. In effect, this population is very close to a random mating population of 14,000 chromosomes, but has the advantage that there are pedigrees (siblings, half-siblings, and cousins) embedded within it. For this study, we selected 500 pairs of individuals from the final generation of the population.

We then create realistic haplotypes to assign to the FGL, and thence to the sampled individuals via their FGL-segment lists. To do this we use a novel simulation approach, beaglesim, based on the BEAGLE software of Browning and Browning (2007). Unlike other simulation approaches that evolve population chromosomes (Peng and Amos 2010; Yuan et al. 2011), our approach uses directly an initial set of real haplotypes from a population with significant structure and/or LD. For this purpose we used data on 1917 male X chromosomes from the Framingham Heart Study (FHS) data (Cupples et al. 2009), chosen so that there were no reported relationships among them. Availability of this good-sized naturally phased chromosome eliminated the need for statistical phasing. Markers with minor allele frequency <5% were eliminated, as were ∼100 markers over about 3 Mbp around the centromere. There remained 6913 markers over ∼140 Mbp. The level of missing data was low; the overall level over the 6913 markers in 1917 chromosomes was 0.15%.

For beaglesim, first a BEAGLE model is estimated, on the basis of the set of real haplotypes. This model is expressed in terms of marker-to-marker transitions among haplotype clusters along the chromosome (Browning and Browning 2007). Variation in the LD structure along the chromosome, resulting from variation in recombination rates across the chromosome or from chance events of history, is reflected in the fitted BEAGLE model. Next, haplotypes are independently simulated from the fitted model. This process has the advantage that any number of chromosomes may be generated, so we are not limited by the size of the original real data set, and also that the resultant simulated chromosomes can be made public, since they are not the real data of any individual.

More importantly, the beaglesim approach permits generation of data sets with the same markers, same allele frequencies, and same general LD structure, but at different levels of LD. Since the BEAGLE model is specified in terms of marker-to-marker transitions, rather than, for example, genetic or physical distance, we adopt the same framework in attenuating the LD. In generating each simulated haplotype, at each marker with probability γ the current haplotype cluster is randomly switched in accordance with the haplotype cluster frequencies, thus breaking the LD. For example, if γ = 0.05, LD is broken on average every 20 markers. For the results in this article we use four such generated data sets: γ = 0 (original BEAGLE model), γ = 0.05, γ = 0.1, and γ = 1 (no LD).

Choice of parameter values

Since ibd is relative, there are no “true” values of the parameters α and β of the latent ibd process; choice of these parameters defines the time depth of the ibd that is sought. In fact, in our simulated population, relative to the founders, the level of pointwise kinship at the 200th generation is approximately β = 0.02, and the mean length of segments in some state of ibd is about 0.5 Mbp. Since pairwise ibd is broken at a rate 2α(1 − β) this indicates an α value of about 1. However, in any real study, the characteristics of the founding population and the subsequent demographic history would be unknown, and we therefore do not choose our parameter values on this basis.

For the results shown in this article, we adopt β = 0.05 and δ = 0.1. We have found that a smaller value of the rate-change parameter α gives better performance and adopt α = 0.05 also. A high value of α makes frequent changes in inferred ibd state more probable, while the lower value provides a “flat prior,” allowing the genetic marker data to dictate state changes (see Discussion). We have systematically examined performance of our inferences under values of β, α, and δ over the range 0.005 to 0.2, and additionally with δ = 0 and δ = 1. Results (not shown) are quite robust to the value of β, and of δ provided neither 0 nor 1. Results were more sensitive to the value of α, resulting in additional studies for α values from 0.01 to 2.0 at the values β = 0.05 and δ = 0.1 (see Results).

We used the marker allele frequencies of our original 1917 FHS chromosomes, rather than the frequencies in our small current sample or in the current 200th generation of the population. Thus we mimic the situation when we might have information from a substantial sample from a comparable population, such as in published HapMap (International Hapmap Consortium 2005) data or in a large case-control study (Wellcome Trust Case Control Consortium 2007). Recall that we had eliminated SNPs with minor allele frequencies <5%. Shared alleles that are assumed rare are strong evidence of ibd and can distort results if this assumption is incorrect. Although in our simulated data we did not include genotyping errors, in all our analyses we adopt ε = 0.01. This level is higher than expected as an overall rate in real SNP data, but error rates vary among SNPs, and it is important to make sufficient allowance for error (Leutenegger et al. 2003). Failure to allow for error when in fact it is present has greater impact than assuming too large an error rate.

Software availability

The following software referred to in this article is available at http://www.stat.washington.edu/thompson/Genepi/pangaea.shtml:

1. The IBD_Haplo software (which consists primarily of the ibd_haplo program) runs as a part of our MORGAN-3 package. The analyses of this article were run with the version of ibd_haplo in MORGAN 3.0.3 (November 2011 release).

2. A small collection of programs has been released (October 2011) under the name Create_IBD. This includes the beaglesim procedure (both as R-code and as a C-program) and programs for the population ibd simulation, and for the assignment of haplotypes to descendant chromosome segments.

3. The R-package, IBDhaploRtools, is used in analysis of ibd_haplo output. Version 1.2 (November 2011 release) performs the result summaries included in this article. The R-package also contains a tutorial, generated from an Sweave document, enabling the user to replicate the steps of analysis used to produced the tables and figures of this article from ibd_haplo output files.

4. Data files from this study are provided as supporting information in the form of two compressed file archives; see Supporting Information, File S1 for details. The first archive (see File S2) includes the simulation truth of the ibd among the 500 pairs of individuals used in this study and the marker information and data haplotypes of the relevant individuals generated at four different LD levels (γ = 0.0, 0.05, 0.1, 1.0). The second archive (see File S3) contains interim output of our analyses in the form of Rdata files of inferred ibd states, together with an Sweave wrapper document that uses these files in conjunction with the IBDhaploRtools R-package to recreate the tables and figures of this article. In principle, the results of File S3 and of this article can be recreated from only the data in File S2, using the ibd_haplo program, but this involves many huge intervening input and output files.

Results

The data set and the haplotypes

For our analysis of detection of ibd we used the first 100 female individuals of the final (200th) generation of the population simulation described in Data simulation. Choice of females avoids the presence of full sibs in our sample. In the 200 chromosomes of these 100 individuals there were 48,800 total FGL segments. Although at a single locus typically only 1% of the original 14,000 FGL survive in the population, over the chromosome, 2228 different FGL are represented among these 200 chromosomes.

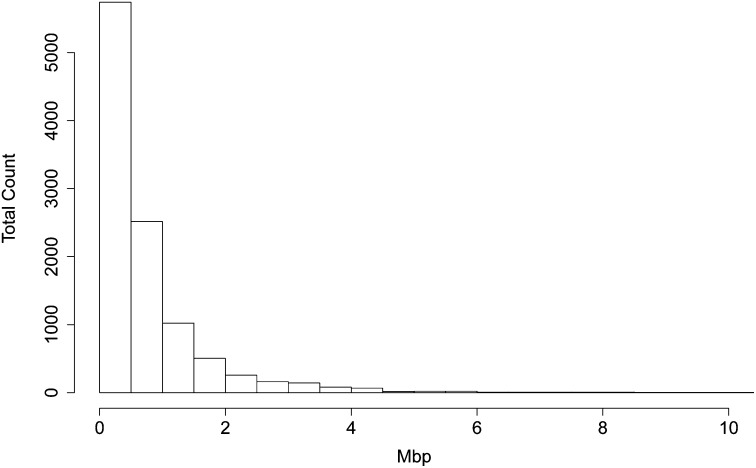
For our analysis of detection of ibd we used 500 pairs of individuals sampled with replacement from these 100 female individuals. The distribution of lengths of segments in each of the 14 ibd states (excluding the no-ibd state) among the four chromosomes of each of the 500 pairs of individuals is shown in Figure 1. This same ibd structure underlies each of the haplotypic or genotypic data sets analyzed. Note that over 50% of the ibd segments are <0.5 Mbp in length. Typically, we seek more recent coancestry, and hence longer ibd segments. We use the greater time depth in this article since we wish to explore the lower limits of ibd detection.

Figure 1 .

Histogram of the true lengths of the 10,603 segments in any state of ibd (excluding the no-ibd state) among the 500 pairs of individuals.

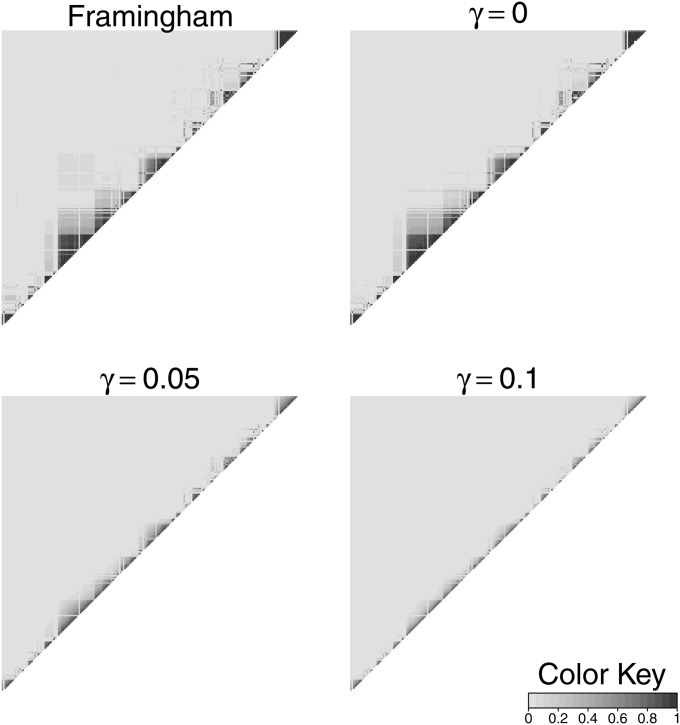
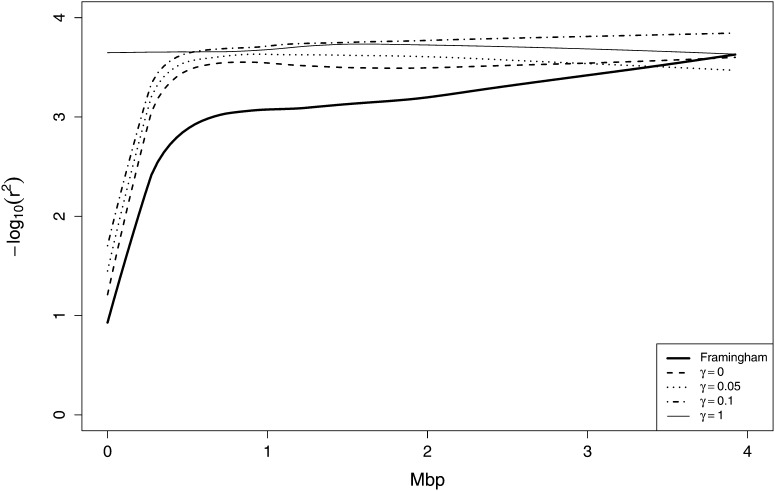
To investigate the performance and appropriate parameter choice for beaglesim we investigated the pattern of LD in our original data set of 1917 chromosomes, and in sets of 1917 chromosomes generated by beaglesim at varying levels of the attenuation parameter γ. Figure 2 shows the pattern of pairwise allelic correlations r² over 200 markers in a 5.16-Mbp region of the chromosome, for the original data, and for three γ values. The value γ = 0, which represents simulation from the original BEAGLE model, shows a pattern remarkably similar to the original data, although long-range LD (>0.5 Mbp) is reduced. This is to be expected since, even with as many as 1917 haplotypes, the fitting process of the BEAGLE model will have insufficient data to maintain significance of separate haplotype clusters over large genetic distances. A value γ = 0.05 shows reduced but still significant LD in a similar pattern, while γ = 0.1 retains only the strongest LD and over short ranges. As an additional assessment, curves of −log₁₀(r²) were fitted to r²-values between each marker and its 50 neighbors to each side of it. These curves are shown in Figure 3 and confirm that the long-range LD (0.5–2 Mbp) is substantially larger for the original chromosomes than for γ = 0. Also apparent is that, at distances >0.5 Mbp, the r²-values resulting from γ = 0.05 and γ = 0.1 are effectively the same as those for the case of no LD (γ = 1).

Figure 2 .

Linkage disequilibrium in a 5.16-Mbp segment of the chromosome, in the original set of 1917 chromosomes, and in sets of 1917 chromosomes generated by beaglesim, at attenuation levels γ = 0, 0.05, and 0.1.

Figure 3 .

Curves of −log₁₀(r²) by distance between markers, fitted for each marker with each of the 50 markers to each side of it, for the original set of 1917 chromosomes, and in sets of 1917 chromosomes generated by beaglesim, at attenuation levels γ = 0, 0.05, 0.1, and in the absence of LD (γ = 1).

The results of ibd segment inference

At each of the chosen LD levels, haplotypes were generated and assigned to the 100 sampled generation-200 individuals as described in Data simulation. The ibd_haplo program was run on the data set of 500 pairs from among these 100 individuals. The data on each pair were considered both as four haplotypes and as a pair of genotypes. Except where otherwise specified, results were run at α = 0.05, β = 0.05, δ = 0.1, and results are typically shown for the LD level γ = 0.1.

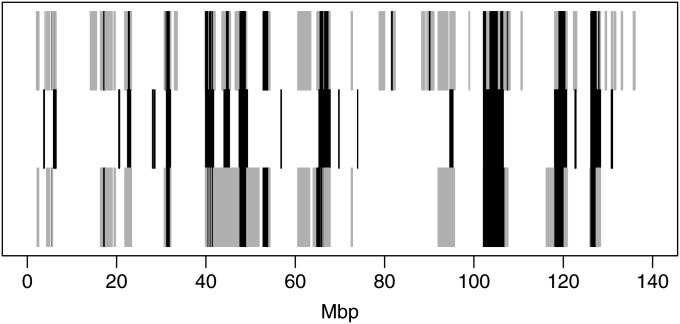
One example of the calls made for a set of four chromosomes in a pair of individuals is shown in Figure 4. The results for haplotypic data (above) and for genotypic data (below) may be compared with the true latent ibd for this pair of individuals (center). This example contains about seven larger segments of ibd, including three in a cluster at 40–47 Mbp, as well as about 12 smaller segments. The larger segments are well detected, although the genotypic analysis misses the central one of the cluster, with a large area of no-calls. Smaller segments may be missed, and there are some false positives. For this pair, the haplotypic and genotypic analysis results are similar, although the haplotypic data seem to produce more short areas of no-calls. We return to the detection of ibd as a function of segment length below, but first summarize results in terms of overall proportions of ibd calls.

Figure 4 .

Example of the true ibd and the calls across the 140-Mbp chromosome, based on ibd_haplo output using haplotypic and genotypic data, for 1 of the 500 pairs of individuals. Middle: the true ibd state with dark shading shows any state of ibd and white the no-ibd state. Top: the inferred state using haplotypic data. Bottom: for the same data analyzed as a pair of genotypes. In the inferred results, the lighter shading represents a no-call.

Table 2 shows the simulation truth and inferred results for the percentage of genome in each class of ibd state, the mean segment lengths, and mean percentages of segments, analogous to Table 1, which showed the model-based expectations. For the inferred results, the no-call regions were excised before computation of percentages and lengths. For the proportions, the prior results at β = 0.02 are given for comparison; for the lengths, the prior is not shown, since the model-based length contains the arbitrary scaling parameter α (see Discussion). Notable in the results is the excellent agreement of our prior model for ibd states at β = 0.02 and the values simulated in our population descent. The agreement between the simulation truth and the inferences is also excellent, except for the rarest high-ibd states. Particularly for the all-ibd state there are few realized segments of this type. Haplotypic and genotypic data perform broadly similarly, although the genotypic analyses have higher failure to detect ibd segments and hence more genome and longer length of no ibd. Also importantly, analysis results are similar at β = 0.02 and at β = 0.05. Use of the higher prior probability of ibd in the analysis model does not adversely affect the results.

Table 2 . Proportions of genome and of segments for the different ibd state types.

ibd state	All ibd	Three ibd	Two pairs	One pair	No ibd
Percentage of genome
Simulated	0.0042	0.20	0.12	11.58	88.10
Prior, β = 0.02	0.0045	0.30	0.11	10.87	88.72
Inferred: β = 0.02 Hap.	0.0217	0.41	0.15	12.65	86.76
Gen.	0.0189	0.27	0.14	10.30	89.27
Inferred: β = 0.05 Hap.	0.0303	0.51	0.19	13.71	85.55
Gen.	0.0304	0.32	0.17	11.17	88.31
Segment length (Mbp)
Simulated	0.71	0.44	0.40	0.78	6.44
Inferred: β = 0.02 Hap.	0.25	0.40	0.42	0.88	6.72
Gen.	0.26	0.46	0.57	1.21	11.49
Inferred: β = 0.05 Hap.	0.27	0.36	0.38	0.78	5.57
Gen.	0.29	0.42	0.49	1.09	9.57
Percentage of segments
Simulated	0.02	1.55	1.02	50.69	46.73
Prior, β = 0.02	0.04	1.92	0.96	50.82	46.22
Inferred: β = 0.02 Hap.	0.30	3.62	1.27	50.01	44.81
Gen.	0.42	3.34	1.45	49.59	45.20
Inferred: β = 0.05. Hap.	0.33	4.08	1.45	50.24	43.90
Gen	0.51	3.70	1.70	49.50	44.58

Results are given both as for the simulated data, under the prior model for β = 0.02, and as inferred using ibd haplo using either haplotypic (Hap.) or genotypic (Gen.) data with γ = 0.1 and for β = 0.02 and β = 0.05 in the analysis (δ = 0.1). For clearer comparison with the simulation truth and model prior, the no-call sites have been excised from the ibd haplo output, and proportions and lengths computed using only the marker locations at which a call was made.

Table 3 presents the key results on the impact of LD on ibd inference, with the results tabulated as percentages over the 6913 markers over all the 500 pairs of individuals. Since our analysis model does not include LD, one might expect best performance for the no-LD case (γ = 1). However, it can be seen that the haplotypic similarities resulting from LD actually decrease the percentage of false-negative calls. Table 3A shows the results for the 12% of markers at which the simulation truth is some state of ibd. We see that, except at very high LD (γ = 0), incorrect ibd states are rarely called, but that the rate of no-calls increases with increasing LD and is substantially higher for genotypic data than for haplotypic data. Table 3B shows the results for the 88% of genome that is in the no-ibd state. Here, in the absence of LD results are excellent but increasing LD leads to increased no-calls and false-positive calls of ibd. Generally haplotypic data perform better than genotypic data, because there is more information used, but at high LD levels haplotypic similarity leads the haplotypic data uniquely to perform more poorly than the genotypic, with higher false-positive and no-call rates.

Table 3 . The ibd segment inference results at decreasing LD levels.

γ:	0.0		0.05		0.1		1.0
% by mrk:	Hap.	Gen.	Hap.	Gen.	Hap.	Gen.	Hap.	Gen.
A. Given ibd (12%)
Correct	57.8	43.7	69.6	53.2	74.7	57.8	80.5	61.3
Other ibd	11.5	9.7	4.9	4.4	2.3	2.0	0.4	0.4
False neg.	3.5	10.6	4.5	12.1	5.6	13.3	8.0	17.5
No call	27.3	36.0	21.0	30.3	17.4	26.9	11.1	20.8
B. Given no ibd (88%)
Correct	47.5	57.4	66.1	70.9	80.4	81.0	99.2	97.9
False pos.	17.2	12.1	8.5	6.5	3.8	3.4	0.1	0.1
No call	35.2	30.5	25.4	22.6	15.7	15.6	0.7	1.9

Results are shown at decreasing LD levels, that is, increasing γ, and are tabulated as percentages over the 6913 markers over all 500 pairs of individuals. They are given for analyzing the data on the 500 pairs both as four haplotypes (Hap.) and as pairs of genotypes (Gen.). Results are separated into (A) the 12% of genome in which the latent ibd-state involved some ibd and (B) the 88% of genome in the no-ibd state.

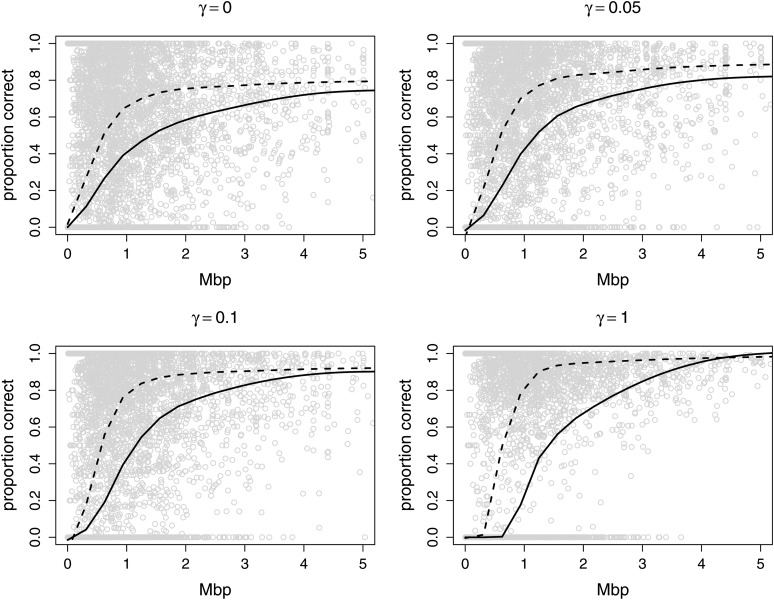
Figure 5 shows the results for all true segments of some state of ibd (that is, excluding the no-ibd state), by segment length and for the same four levels of LD. For both haplotypic (dashed lines) and genotypic (solid lines) analyses, shown are the proportion of markers within each segment that provide a call for the correct state of ibd. Again we see improved performance with decreasing LD (increasing γ) and the better performance of haplotypic analysis as compared to genotypic. With haplotypic data, for segments over 1 Mbp, >80, 90, and 95% of markers within a segment provide a correct call at γ = 0.05, 0.1, and 1, respectively.

Figure 5 .

Among the 10,603 segments in any state of ibd (see Figure 1), the proportion of markers that provided a call of the correct ibd state at a calling threshold of 0.9, by length of the segment. The four subfigures are for the values of γ shown; γ = 0 (high LD), γ = 0.05, γ = 0.1, and γ = 1.0 (no LD). The points and the solid fitted lines are for the genotypic data, while the dashed lines show the improvement obtainable using phased haplotypic data.

In Figure 5 points on the lower axis represent segments that fail to be called. Defining failure-to-detect as corresponding to <20% of markers in a segment providing a correct ibd call, 23, 7, and 2.5% of segments >1, 2, and 3 Mbp in length fail to be detected using genotypic data. For these large segments, the exact cut-off (20%) and the LD level (γ) have little impact on these results. The two extremes, γ = 0 and γ = 1, provide an interesting contrast with regard to small segments. At very high LD (γ = 0), haplotypic data apparently perform adequately even for the shortest segments. However, this is simply the result of LD being interpreted as ibd regardless of the true ibd state. In the case of no-LD (γ = 1) small segments with few SNP markers cannot provide evidence of ibd. As soon as there are sufficient markers for ibd to be recognized, performance improved rapidly, but this is not until about 0.3 Mbp for haplotypic data, and 0.65 Mbp for genotypic. Recall the average density of our SNP markers is 50/Mbp, so this corresponds to about 15 and 33 markers, respectively.

Table 4 shows the effect of varying the scaling parameter α, with other parameters at their standard values β = 0.05, γ = 0.1, and δ = 0.1. Small values of α correspond to small change rates in ibd states. “True” values of α for our simulated data are in the range 0.5–2.0; that is, such values would give prior expected segment lengths corresponding to those observed in our simulated data for the ibd states, including those for the no-ibd state. However, such values provide low performance, with high percentages of no-calls. Performance is much better at the α = 0.05 level which we use in our analyses, and it starts to degrade rapidly for α > 0.1. On the other hand, too small a choice of α (0.01) leads to many smaller ibd segments being missed, and hence a higher proportion of false negatives, particularly for the genotypic analysis.

Table 4 . The ibd segment inference at decreasing levels of smoothing.

α:	0.01		0.05		0.1		0.5		2.0
% by mrk:	Hap.	Gen.	Hap.	Gen.	Hap.	Gen.	Hap.	Gen.	Hap.	Gen.
A. Given ibd (12%)
Correct	75.6	56.8	74.7	57.8	73.5	56.9	64.9	45.6	48.3	24.9
Other ibd	1.7	1.5	2.3	2.0	2.7	2.5	4.3	3.8	6.1	4.5
False neg.	9.4	20.9	5.6	13.3	4.0	10.3	1.5	4.7	0.5	2.6
No call	13.3	20.8	17.4	26.9	19.8	30.3	29.3	45.9	45.2	68.0
B. Given no ibd (88%)
Correct	90.0	89.7	80.4	81.0	74.1	75.2	52.6	55.9	29.3	34.3
False pos.	2.2	2.3	3.8	3.4	4.7	3.9	6.6	4.4	6.4	3.2
No call	7.8	8.0	15.7	15.6	21.2	20.9	40.7	39.7	64.3	62.5

Results are shown at decreasing levels of smoothing, that is, increasing prior change-rate parameter α, and are tabulated as percentages over the 6913 markers over all 500 pairs of individuals. They are given for analyzing the data on the 500 pairs both as four haplotypes (Hap.) and as pairs of genotypes (Gen.). Results are separated into (A) the 12% of genome in which the latent ibd-state involves some ibd and (B) the 88% of genome in the no-ibd state.

Comparison of ibd_haplo and fastIBD

In Browning and Browning (2010, 2011) the performance of fastIBD was compared to that of PLINK (Purcell et al. 2007) and GERMLINE (Gusev et al. 2009). Here we compare ibd_haplo to fastIBD. We made two series of runs for fastIBD, the first using as the base population the same set of 100 final individuals from the simulation population and the second using an additional 900 individuals. In both cases, the initial ibd inference was run at a threshold of 10⁻⁶ as recommended by the fastIBD documentation, and results were then extracted at this threshold, and at a stricter 10⁻¹⁰ threshold. The recommended fastIBD parameter values and workflow was followed, with 10 runs from different seeds, and the provided script was used to consolidate results. Although fastIBD analyzes all pairs in a data set, for comparison purposes we extracted the results for the same 500 pairs of individuals used in our ibd_haplo study.

Exact comparisons of performance are complicated by the different protocols and objectives of the two programs. With regard to fastIBD runtime, each single run with the 100-individual base data set, including the BEAGLE imputation and phasing steps, is very comparable to the time for a single run of ibd_haplo on the 500 pairs of individuals sampled from this data set (60–90 sec). With a base population of 1000 individuals used for phasing and imputation, fastIBD times are at least an order of magnitude longer; 10 runs at each of five different LD levels and the subsequent consolidation of results can take up to 16 hr. A second key difference is that fastIBD does not seek within-individual ibd. We therefore considered the three ibd states that have only ibd within but not between the individuals as non-ibd when evaluating fastIBD results.

Results are shown in Table 5. In presenting the ibd_haplo results from Table 3, inference of the correct ibd state is combined with calls of other ibd states, since fastIBD does not distinguish among ibd states. Also, since fastIBD does not infer within-individual ibd, results for ibd_haplo are given both including (as ibd) and excluding states of only within-individual ibd (states 2, 5, and 8 in Appendix B). For haplotypic data, this makes almost no difference, but for genotypic data true-positive rates are reduced by excluding the within-individual ibd states. This is as expected, since genotypic data provides clearer evidence of within- than between-individual ibd.

Table 5 . Comparisons of ibd inference using using ibd_haplo and using fastIBD.

Program:		True-positive ibd inference				False-positive ibd inference
Input	Scoring	LD level γ				LD level γ
		0.0	0.05	0.1	1.0	0.0	0.05	0.1	1.0
ibd_haplo:	All ibd	69.3	74.5	77.0	80.9	17.2	8.5	3.8	0.1
Hap data	Btw ibd	69.8	74.5	77.5	81.3
ibd_haplo:	All ibd	53.4	57.6	59.8	61.7	12.1	6.5	3.4	0.1
Gen data	Btw ibd	46.1	49.7	52.3	53.3
fastIBD:	Strict	31.4	41.2	46.4	56.9	0.6	0.7	0.8	1.0
100 base	Loose	56.3	64.6	68.9	82.9	2.2	2.3	2.3	4.0
fastIBD:	Strict	41.5	51.4	56.9	71.7	0.7	0.9	0.9	1.5
1000 base	Loose	66.5	73.3	77.6	90.4	3.4	3.1	3.1	8.9

Results are shown at decreasing levels of LD (that is, increasing γ), and are tabulated as percentages over the 6913 markers over all 500 pairs of individuals. The ibd haplo program was run for both haplotypic (Hap.) and genotypic data (Gen.). For scoring ibd all states involving any ibd were scored (All ibd), as in Table 3, and then also only between-individual ibd was scored (Btw ibd), since fastIBD does not seek within-individual ibd. The fastIBD program was run using only the same 100 individuals for the BEAGLE imputation and phasing step as used in ibd haplo, and then also using an additional 900 individuals for a base sample of 1000. The ibd was scored using a strict (10⁻¹⁰) threshold and a looser threshold (10⁻⁶).

Very broadly, the two programs give comparable results, but there are some important differences. Using the strict ibd level and only 100 base individuals, fastIBD misses much ibd. The 1000-base individual set provides better performance, but still misses much ibd, especially at high LD levels. Through modeling this high LD, fastIBD cannot then detect ibd segments that result in comparable levels of haplotypic similarity. The looser ibd criterion has higher true-positive detection rates, but at the expense of higher false-positive rates. For the true positives, the fastIBD-100-loose results are comparable to ibd_haplo with haplotypic data at low LD and genotypic data at high LD.

By adjusting for LD, fastIBD controls false-positive rates at high LD. However, the longer segments of haplotypic similarity generated in independent chromosomes at high LD are false positives only in the context of the simulated descent from these founder chromosomes. In a real population, these similar haplotype segments could be the result of ibd at a time depth comparable to the 200 generations of our simulation. In the absence of LD, fastIBD shows relatively high false-positive rates, whereas ibd_haplo has a very low rate.

Discussion

We have shown that our HMM model can be used to detect segments of ibd, of the order of 1 Mbp among the four chromosomes of two individuals. Our model allows for any state of ibd between and within the individuals and accommodates missing data and possible typing error. If haplotypic information is available, performance is improved, but even with more readily available genotypic data, segments of this length are typically well detected. Such a length results, in expectation, from a 100-meiosis separation between the chromosomes, far beyond the likely available knowledge of coancestry.

Our analysis model does not include LD, and to examine the impact of LD we simulated founder chromosomes at various levels of LD, using our beaglesim approach. While this approach is dependent on the availability of a large sample of real high-LD chromosomes to fit the initial BEAGLE model (Browning and Browning 2007), it can then generate arbitrary numbers of independent chromosomes with quite realistic LD patterns at varying levels via the parameter γ, which controls the range of the LD. Even the original BEAGLE model (γ = 0) will tend to remove long-range LD that likely results from cryptic relatedness or admixture, but the block patterns typical of the real data persist even at higher levels of γ (for example, γ = 0.1). The BEAGLE model output is expressed as marker-to-marker transitions and incorporates any features of the LD patterns along the chromosome that are due to variable marker spacing or variation in recombination rates. Hence our beaglesim procedure for attenuating LD using the parameter γ is also on a marker-to-marker basis. However, if desired, clearly it could be easily modified so that the probability of breaking from the BEAGLE haplotype clusters depends on physical or genetic distance.

Several other approaches exist for simulating haplotypes with particular levels of LD. Programs such as fastsimcoal (Excoffier and Foll 2011) and MaCS (Chen et al. 2009) sample realizations of the coalescent process along a chromosome, which, along with a mutational model, describe the joint distribution of markers. Forward simulations begin with a set of real haplotypes (Peng and Amos 2010) or artificial haplotypes with high levels of LD (Yuan et al. 2011) and evolve a population forward in time according to the desired model. These methods simulate the process giving rise to the LD, which is necessary if that process is the object of study. For our study, we are interested in LD only as a confounding factor and do not require that the LD be influenced by any particular population genetic process. However, we do require sets of founder chromosomes with not only the same marker locations and and population allele frequencies, but also the same pattern of LD across the chromosome, differing only in the overall LD level; beaglesim achieves this.

In our study we aimed to detect segments of coancestry relative to founders at 200-generation time depth and examined the impact of LD in the founder chromosomes of the population. While the haplotypic similarities resulting from LD led to “false-positive” calls of ibd relative to our simulation truth, in reality LD results from the same coancestry that underlies ibd, but at greater time depth. Thus, were ibd to be measured relative to greater time depths, these false-positive calls should be true. There is no absolute definition of ibd, nor, outside of a simulation study, of what ibd is true. Rather, our goal has been to examine the limits of detection given a population of given size and structure. In genetic epidemiological studies, individuals will be ascertained for a trait of interest, which leads in turn to the chance of more recent coancestry, and larger segments of ibd in regions harboring relevant genes. The relevant time depth for inference of ibd is that of a mutation underlying a trait. While this is unknown, the results of this article show that we can, even in the case of randomly sampled individuals, achieve good overall performance at time depths that might correspond to 5000 years.

The parameter β is the overall level of population kinship and, in effect, determines the time depth of what is to be considered ibd. While the true level of ibd in our simulated population corresponded to β = 0.02, results were quite robust to the use of β = 0.05 in our analyses, and even to higher β-values (results not shown). The amount of ibd that will be called is determined also by the calling threshold. A high threshold will lead to many segments being missed and a high level of no-calls, while a low threshold leads to increasing calls of incorrect ibd states. We have found that the 0.9 threshold provides a good balance and recommend that β rather than the calling threshold be varied in analyses to check the consistency of segments detected at different kinship levels.

An unexpected result of our study is the role of the scaling parameter α in our population with relatively high population kinship β. In the studies of Browning and Browning (2010), β = 0.0001, and under their model the length of an ibd segment is (α(1 − β))⁻¹, so that α ≈ 1 is chosen to seek segments of ∼1 Mbp. In our study, we found that such a high value of α led to many no-calls and generally poor results and that results were much improved by using an α-value substantially smaller than that corresponding to the lengths of segments of ibd we aim to detect. The prior expected length of any segment is exponential with mean proportional to α⁻¹. A large α makes change of ibd -state a priori probable and leads to many inferred state changes. A smaller α provides a much flatter a priori distribution of segment lengths and enables the genetic marker data to dictate where there is evidence for a change in ibd state. This smaller α, resulting in longer segments, also means there will be a larger number of markers available to provide evidence of the correct ibd state in the segment.

The interplay between presence of LD at the population level and the ability to infer shorter segments of ibd is evident also in the comparison of ibd_haplo and fastIBD. At high LD, the fastIBD fitting of an LD model controls false-positive rates, but at the expense of lower true-positive rates. By not modeling LD, ibd_haplo has high false-positive rates, but also higher true-positive rates. At low LD, fastIBD can achieve high true-positive rates, but at the expense of higher false-positive rates than those of ibd_haplo. It is likely that ibd_haplo performs better with smaller α not only because of our relatively high β but also because we do not model LD. If ibd is permitted to change too frequently, there will be a tendency for many short segments of haplotypic similarity resulting from LD to be inferred as ibd. Where the LD is explicitly modeled, as in fastIBD, there may be no need to discourage state changes; the higher α recommended for that software can be used.

In our population simulation of the descent of genome we assumed a uniform recombination rate, and in our ibd_haplo analyses marker locations were specified in terms of megabase pairs rather than in terms of genetic distance. However, this was for convenience only. If a genetic map is known, or if local variations in recombination rate can be scaled using a framework map, marker locations may be specified in terms of genetic distance. There is no difference in the ibd_haplo implementation or in the processing of output; it is simply a variable rescaling of the chromosome on a marker-to-marker basis. Extreme hotspots of recombination would result both in low LD and in more transitions in ibd per available marker. The former would improve ibd_haplo performance in the region, while the latter might lead to failure to detect some ibd transitions.

In detecting ibd segments, our method performs better with haplotypic data than with genotypic data. This is simply because the additional phase information provided to the program provides much more evidence as to the true underlying local ibd state among the chromosomes. Where there are sufficient data to use fastIBD, information on haplotypes is recovered via the fitted LD model. Having no LD model, ibd_haplo cannot use this information. In the future, as sequence data become available and increasing read lengths cover more than one heterozygous site in an individual, phased data on diploid individuals may become the rule. This can only improve the ability of ibd_haplo to detect ibd segments.

A key feature of our approach is not to analyze chromosomes pairwise, but to make use of the joint information in a set of four chromosomes. For this case, with 15 haplotypic ibd states and with only 9 genotypic ibd states, the HMM forward–backward computation is efficient. However, with more chromosomes the number of ibd states increases rapidly, even when these are reduced to genotypic form (Thompson 1974). While exact HMM computations become infeasible for larger numbers of chromosomes, an MCMC approach can use the same underlying models to detect ibd segments, as has recently been done for the simpler and more restricted state model of Moltke et al. (2011). The balance between the gains of joint information and the increasing computational and modeling complexities remains to be studied.

Appendix A

In terms of the parameter θ of Ewens’ sampling formula (Ewens 1972), a partition z of the n chromosomes into |z| subsets x has probability

$$\pi \left(z\right)={\left(\stackrel{n-1}{{\displaystyle \prod }_{j=1}}\left(\theta +j\right)\right)}^{-1}{\theta }^{\left|z\right|-1}{\displaystyle \prod }_{x\in z}\left(\left|x\right|-1\right)\text{!}.$$ (3)

Note that |z| is the number of subsets in the partition z, while |x| is the number of elements (chromosomes) in subset x.

For a partition of 2 objects, it immediately follows that the probability that |z| = 1 (the two chromosomes are ibd) is β = 1/(1 + θ). For the model as described in the text, potential state changes occur at total rate α(nβ + (1 − β)) = α(n + θ)/(1 + θ) independently of the current state. This does not imply equal sojourn times, since, as seen in the examples in Appendix B, the chance that the described process of adding and deleting a chromosome results in a state change does depend on the current state. However, for purposes of the following we consider all “transitions,” whether or not they result in a state change. At a transition point, a new chromosome is added to a subset size j with probability j/(n + θ) and as a new singleton with probability θ/(n + θ), corresponding to the relative rates jβ and (1 − β) given in the text. Then we randomly delete one of the n + 1 chromosomes. If the newly inserted chromosome is not deleted, it receives the label of the deleted chromosome.

Consider a transition from state z to state w, with the transition probability p(w|z). To show that this process retains the distribution (3) we show π(z)p(w|z) = π(w)p(z|w). Note that w = z if the deleted chromosome is either the new chromosome or any other chromosome in the set to which the new chromosome was added. The case z = w trivially satisfies the required condition, so consider w ≠ z.

• Case 1: Suppose w is formed from z by inserting the new chromosome into z as a singleton and deleting one chromosome from a subset size j. Then

  $$p\left(w|z\right)=\frac{\theta }{n+\theta }\frac{1}{n+1}\left(1+I\left(j=2\right)\right),$$

where I(j − 2) = 1 if j = 2 and 0 otherwise. (This extra term derives from the fact that if j = 2 the same state will result whichever of the two chromosomes is deleted.) Conversely, z is formed from w by inserting the new chromosome into a subset size j − 1 of w and deleting the relevant singleton:

$$p\left(z|w\right)=\frac{j-1}{n+\theta }\frac{1}{n+1}\left(1+I\left(j=2\right)\right).$$

Again, if j = 2 either chromosome may play the role of the deleted singleton. Thus we have

$$\frac{\pi \left(z\right)}{\pi \left(w\right)}=\frac{{\theta }^{\left|z\right|}{\displaystyle {\prod }_{x\in z}\left(\left|x\right|-1\right)}\text{!}}{{\theta }^{\left|w\right|}{\displaystyle {\prod }_{x\prime \in w}\left(\left|x\text{,}\prime \right|-1\right)\text{!}}}=\frac{1}{\theta }\frac{\left(j-1\right)\text{!}}{\left(j-2\right)\text{!}}=\frac{j-1}{\theta }=\frac{p(z|w)}{p(w|z)}.$$

• Case 2: Suppose w is formed from z by inserting the new chromosome into a subset size j of z and deleting one chromosome from a subset size l of z. Then

  $$p\left(w|z\right)=\frac{j}{n+\theta }\frac{1}{n+1}.$$

Conversely, z is formed from w by inserting the new chromosome into the subset size l − 1 of w and deleting the relevant chromosome in the subset size j + 1 of w:

$$p\left(z|w\right)=\frac{l-1}{n+\theta }\frac{1}{n+1}.$$

Thus we have

$$\frac{\pi \left(z\right)}{\pi \left(w\right)}=\frac{{\theta }^{\left|z\right|}{\displaystyle {\prod }_{x\in z}\left(\left|x\right|-1\right)\text{!}}}{{\theta }^{\left|w\right|}{\displaystyle {\prod }_{x\prime \in w}\left(\left|x\text{,}\prime \right|-1\right)\text{!}}}=\frac{\left(j-1\right)\text{!}\left(l-1\right)\text{!}}{j\text{!}\left(l-2\right)\text{!}}=\frac{l-1}{j}=\frac{p\left(z|w\right)}{p\left(w|z\right)}.$$

Appendix B

For the case n = 4, we label the four chromosomes a, b, c, and d. For diploids, a and b denote the two chromosomes of one individual and c and d the two chromosomes of the other. We represent the states via the partition of the chromosomes. Thus, for example, the state (abd)(c) denotes that a, b, and d are ibd and c is not. However, we retain the usual ordering of the 15 states, the first 8 corresponding to states in which there is ibd within individuals. Note that states 2, 5, and 8 are states in which ibd is only within individuals and not between them.

The unscaled transition rate matrix among the 15 ibd states is shown in Table B1, where for conciseness we write η = 1 − β and omit the diagonal terms. We give three examples of the derivation of rows in Table B1:

1. Consider first transitions from any of the three states in which two pairs are ibd, for example, the state (ac)(bd). Transitions to either of the two states in which only a single pair remains ibd is possible. These transitions occur at rate 2(1 − β) = 2η, since the new chromosome must form a new group, and either one of the two in the dissolved pair is the one removed. Transitions are also possible to any one the four states in which three chromosomes are ibd. Each of these transitions occurs at rate 2β, since the new chromosome must join a group size 2, and the specific chromosome that is changing its ibd group must be the one deleted. The total rate of leaving the original state is 2 × (2(1 − β)) + 4 × (2β) = 4(1 + β).

2. Next consider any state with three chromosomes ibd, for example, (abc)(d). The new chromosome may join the trio, rate 3β, and the singleton may be deleted, leading to the state (abcd). The new chromosome may join the singleton, rate β, and each possible deletion from the trio leads to one of the three states of two ibd pairs. The new chromosome may form a singleton, rate (1 − β) = η, and each of the three possible deletions from the trio gives one of the six states with a single ibd pair.

3. Consider finally the state of no-ibd, (a)(b)(c)(d). The rate of change to each of the six states with one pair ibd is 2β, since, for example, an ibd pair (bc) may be formed either by the new chromosome joining c (rate β) with b being deleted or by the new chromosome joining b with c being deleted. The total rate of leaving the no-ibd state is thus 6 × 2β = 12β.

Table B1 . The unscaled transition rate matrix among the 15 ibd states.

	State	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	(abcd)	—	0	η	η	0	η	η	0	0	0	0	0	0	0	0
2	(ab)(cd)	0	—	2β	2β	2η	2β	2β	2η	0	0	0	0	0	0	0
3	(abc)(d)	3β	β	—	0	η	0	0	0	β	β	η	0	η	0	0
4	(abd)(c)	3β	β	0	—	η	0	0	0	β	β	0	η	0	η	0
5	(ab)(c)(d)	0	2β	2β	2β	—	0	0	0	0	0	β	β	β	β	2η
6	(acd)(b)	3β	β	0	0	0	—	0	η	β	β	η	η	0	0	0
7	(a)(bcd)	3β	β	0	0	0	0	—	η	β	β	0	0	η	η	0
8	(a)(b)(cd)	0	2β	0	0	0	2β	2β	—	0	0	β	β	β	β	2η
9	(ac)(bd)	0	0	2β	2β	0	2β	2β	0	—	0	2η	0	0	2η	0
10	(ad)(bc)	0	0	2β	2β	0	2β	2β	0	0	—	0	2η	2η	0	0
11	(ac)(b)(d)	0	0	2β	0	β	2β	0	β	2β	0	—	β	β	0	2η
12	(ad)(b)(c)	0	0	0	2β	β	2β	0	β	0	2β	β	—	0	β	2η
13	(a)(bc)(d)	0	0	2β	0	β	0	2β	β	0	2β	β	0	—	β	2η
14	(a)(bd)(c)	0	0	0	2β	β	0	2β	β	2β	0	0	β	β	—	2η
15	(a)(b)(c)(d)	0	0	0	0	2β	0	0	2β	0	0	2β	2β	2β	2β	—