Unified modeling of gene duplication, loss, and coalescence using a locus tree

Abstract

Gene phylogenies provide a rich source of information about the way evolution shapes genomes, populations, and phenotypes. In addition to substitutions, evolutionary events such as gene duplication and loss (as well as horizontal transfer) play a major role in gene evolution, and many phylogenetic models have been developed in order to reconstruct and study these events. However, these models typically make the simplifying assumption that population-related effects such as incomplete lineage sorting (ILS) are negligible. While this assumption may have been reasonable in some settings, it has become increasingly problematic as increased genome sequencing has led to denser phylogenies, where effects such as ILS are more prominent. To address this challenge, we present a new probabilistic model, DLCoal, that defines gene duplication and loss in a population setting, such that coalescence and ILS can be directly addressed. Interestingly, this model implies that in addition to the usual gene tree and species tree, there exists a third tree, the locus tree, which will likely have many applications. Using this model, we develop the first general reconciliation method that accurately infers gene duplications and losses in the presence of ILS, and we show its improved inference of orthologs, paralogs, duplications, and losses for a variety of clades, including flies, fungi, and primates. Also, our simulations show that gene duplications increase the frequency of ILS, further illustrating the importance of a joint model. Going forward, we believe that this unified model can offer insights to questions in both phylogenetics and population genetics.

Understanding the way new gene functions arise in genomes is a fundamental and long-studied question in evolutionary biology. Gene duplication, in particular, has been recognized as a powerful way of generating new functions through neofunctionalization and subfunctionalization (Ohno 1970; Lynch and Conery 2000), and gene losses can dramatically shape gene families (Niimura and Nei 2007). “Phylogenomics” (Eisen 1998) is the use of phylogenetics to systematically reconstruct the ancestry of thousands of gene families across many related genomes, and in recent years it has been pursued in a variety of ways (Zmasek and Eddy 2002; Li et al. 2006; Huerta-Cepas et al. 2007; Wapinski et al. 2007; Butler et al. 2009; Datta et al. 2009; Vilella et al. 2009; Mi et al. 2010).

The key idea in many of these approaches is that gene duplications and losses lead to incongruence (topological differences) between two important kinds of phylogenetic trees, the gene tree and the species tree (Goodman et al. 1979; Page 1994). The gene tree describes how a set of gene sequences has diverged from one another, while the species tree describes how a set of species has speciated. The gene tree can be thought of as evolving “inside” the species tree (Fig. 1), and this nesting can be reconstructed by reconciliation methods, in which the task is to infer the events responsible for the observed incongruence between two such trees (Goodman et al. 1979). Building on this idea, many models have been developed that use phylogenetic incongruence to infer the number, age, and location of gene duplication and loss events across several genomes (Page 1994; Arvestad et al. 2004; Durand et al. 2006; Rasmussen and Kellis 2011).

Figure 1.

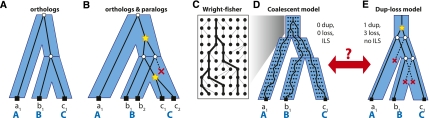
Different views of gene trees and species trees. (A) In the dup-loss model, a congruent gene tree and species tree indicates that all genes are orthologs. (B) Incongruence indicates the presence of gene duplications (stars) and gene losses (red “X”). (C) An example of the Wright-Fisher (WF) process and the coalescence of three lineages within the population. (D) A multispecies coalescent is a combination of WF processes for each branch of the species tree. In this model, no duplications or losses are allowed, but a gene tree can be incongruent due to a phenomenon known as incomplete lineage sorting (ILS). (E) In the dup-loss model, the same gene tree in panel D can be explained using one gene duplication and at least three gene losses. ILS cannot be modeled in the dup-loss model.

While these models (which we refer to as dup-loss models) have been successful in many situations, there still remain several important challenges in accurately inferring these events (Li et al. 2006; Hahn 2007; Huerta-Cepas et al. 2007; Rasmussen and Kellis 2007). These challenges stem from the fact that incongruence can occur due to phenomena other than duplications and losses, and therefore one must use caution when interpreting incongruence. Several of the more recent approaches have dealt with this complication by expanding their models to incorporate other important phenomena. For example, in prokaryotes, horizontal gene transfer (HGT) is a major cause of incongruence, and developing models that incorporate HGT is an active area of research (Doyon et al. 2010; David and Alm 2011; Tofigh et al. 2011). Another source of incongruence is due to uncertainty in the reconstruction of the gene tree, and methods that account for this have shown dramatic improvements (Durand et al. 2006; Åkerborg et al. 2009; Rasmussen and Kellis 2011).

However, despite such efforts, dup-loss models have yet to capture an important and potentially prominent effect called incomplete lineage sorting (ILS) or deep coalescence (Fig. 1D; Wakeley 2009). When a population of individuals undergoes several speciations in a relatively brief period of time, there can exist polymorphisms maintained throughout that time that eventually fix differently in descendant lineages. This effect alone is enough to cause a gene tree to be incongruent with its species tree, and it occurs most frequently in branches of the species tree that represent small time spans (few generations) or large population sizes (Pollard et al. 2006; Hobolth et al. 2007). While ILS can be inferred using coalescent models (Pamilo and Nei 1988; Rosenberg 2002; Rannala and Yang 2003; Degnan and Rosenberg 2009), these models have been developed for very different purposes, such as estimating population sizes, divergence times, or migration rates (Hey and Machado 2003; Rannala and Yang 2003; Liu and Pearl 2007). Typically, these analyses only require a subset of genes from the genome; therefore, one can choose genes that happen to be one-to-one orthologous and effectively avoid considering complications due to gene duplications and losses. In studies in which duplications are considered, they have been modeled in specific ways, such as a single duplication or a single species, and the primary focus has been to model other phenomena such as gene conversion (Innan 2003; Thornton 2007; Zhang and Rosenberg 2007; Innan 2009).

Currently, dup-loss models have only dealt with the influence of ILS in limited ways. Either ILS is assumed to be negligible and is ignored, or several post-processing steps are performed in order to mitigate its impact. For example, several reconciliation methods (Huerta-Cepas et al. 2007; Vilella et al. 2009) augment the usual strict interpretation of incongruence in order to identify extreme forms of incongruence that are unlikely to be due to duplication and loss, for example, when a duplication is followed by losses in each descendant lineage (Fig. 1E). Notice that such a gene tree can easily be explained without duplications, if instead it is explained with ILS in a pure coalescent model (Fig. 1D). Another strategy has been to collapse short branches within the species tree where ILS is thought to occur frequently, and perform reconciliation to a species tree that is not fully resolved (Vernot et al. 2008). While these strategies work in specific cases of ILS, they are not general. In particular, as more genomes are sequenced, they will add new branches to the species tree, further breaking up long branches into smaller ones and increasing the frequency of ILS throughout the species tree.

Here, we present the first general probabilistic model for joint modeling of gene duplications, losses, and incomplete lineage sorting (ILS) across multiple species. Our model, DLCoal (Duplication, Loss, and Coalescence), provides a framework for studying all three phenomena and how they interact with one another. Using our model, we find that duplications can actually increase the probability of ILS and that what different researchers refer to as “gene trees” in the dup-loss and coalescent fields are actually different objects, which we distinguish by introducing a third tree called the locus tree. Using the model, we have developed a new reconciliation algorithm, DLCoalRecon, which addresses a pressing need for inferring duplications and losses despite the presence of ILS. We show its improved accuracy over a standard reconciliation method on both real and simulated data sets. A program implementing this algorithm is freely available for download.

The model

In this work, we present a probabilistic model for gene family evolution that includes gene duplications, losses, and coalescence. We define our model by building on features of existing dup-loss and multispecies coalescent models.

Duplication-loss models

In a dup-loss model (Fig. 1A,B), gene duplications and losses are thought to be the main cause of incongruence (Goodman et al. 1979; Page 1994). Therefore, gene-tree species-tree congruence strongly implies that all genes within the gene family are orthologous and that the gene has always been present as a single copy throughout the history of the species (Fig. 1A). The internal nodes of such a gene tree are called speciation nodes (white circles) since they represent sequence divergence due to speciation. A duplication event copies a gene to a new locus in the genome, where it begins to diverge. This is represented by additional internal nodes called duplication nodes (stars), which can be located anywhere along the length of a species tree branch. In contrast, the gene loss event (red “X”) deletes a gene from the genome. Notice, these events can occur multiple times, allowing the gene tree to possibly differ greatly from the species tree (Fig. 1B). A pair of genes are called orthologous if their most recent common ancestor (MRCA) is a speciation node, and they are called paralogous if their MRCA is a duplication node.

Coalescent models

In applications of the coalescent model, incomplete lineage sorting (ILS) is thought to be the main source of incongruence. This model can be derived from lower-level population models, such as the Wright-Fisher or Moran model (Wakeley 2009). The Wright-Fisher (WF) model contains several assumptions, including a fixed population size N, nonoverlapping generations, random mating, and neutrality. It also assumes no recombination, which is reasonable for the mitochondrial chromosome as well as any small region within autosomes, such as a single gene. In any case, we refer to the WF process as operating on “chromosomes” and for diploid species, the population has 2N chromosomes. When tracing the ancestry of k chromosomes backward in time, the WF model defines the number of generations t until one pair finds a common ancestor, or coalesces (Fig. 1C). Given a large population size, this process can be approximated with the coalescent (Kingman 1982), which assumes that t follows the exponential distribution with rate parameter 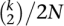. The process is repeated until all lineages coalesce into a single common ancestor, and the tree generated by this process is called a coalescent tree. Alternatively, the process can be terminated at some predetermined time possibly before all lineages fully coalesce, which has been referred to as a censored coalescent (Rannala and Yang 2003).

In the multispecies coalescent (Fig. 1D), each branch of the species tree is viewed as containing a WF process (Tajima 1983; Pamilo and Nei 1988; Rosenberg 2002; Rannala and Yang 2003; Degnan and Rosenberg 2009). This means that a gene tree is really a “traceback” of the ancestral lineages through this combined structure. Again, the coalescent can be used to approximate how a gene tree's topology and branch lengths should be distributed. The multispecies coalescent process is initialized with a family of extant genes present in the leaves of the species tree. Within each species branch, gene lineages present at the bottom of the branch are coalesced according to the censored coalescent. By visiting the species branches bottom-up, the process generates a gene tree connecting all gene lineages up to the root of the species tree, where a final (uncensored) coalescent process joins the remaining gene lineages.

Note that if a species branch has a large population size or a short time span, it is possible that two or more gene lineages may not coalesce at their first opportunity, a phenomenon called incomplete lineage sorting (ILS). Therefore, with ILS, a gene tree can be incongruent with the species tree, even though no gene duplications or losses have occurred.

A new model for duplication, loss, and coalescence

Building on these previous models, we now define a way to combine the multispecies coalescent with dup-loss models. Consider the gene family illustrated in Figure 2A. Without duplications, the multispecies coalescent process would be sufficient to model the ancestry of the genes a₁, b₁, and c₁. However, in this example, a duplication event occurred along the branch ancestral to species B and C. At that moment in time, there is a population of 2N chromosomes, and the duplication only occurs in one of them (star). Also, note that our “traceback” from genes b₁ and c₁ goes through a chromosome present at the duplication time, which is very likely to be a distinct chromosome if the population size N is large.

Figure 2.

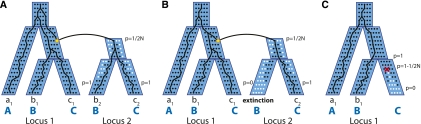
Duplication and loss events within a multispecies coalescent. (A) A duplication occurs in one chromosome and creates a new locus, “locus 2,” in the genome. At locus 2, the Wright-Fisher model dictates how the frequency p of the daughter duplicate (black dots) competes with the null allele (white dots) until it eventually fixes (p = 1). A gene tree is therefore a “traceback” in this combined process. (B) A new duplicate can undergo hemiplasy, and fixes in some lineages and goes extinct in others. (C) Similar to duplication, a gene loss (deletion) starts in one chromosome and drifts until it fixes or goes extinct.

When a duplication occurs, it creates a new locus in the genome, which we call “locus 2” (let “locus 1” denote the original locus), and its ancestry can be represented with a separate tree. Conceptually, every chromosome in the population has locus 2, but all of them except one have a null allele. We can then think about how this new duplicate (the non-null allele) spreads throughout the population according to the WF process (black and white dots in Fig. 2A).

Duplicate sweep

There are many possible outcomes as the new duplicate spreads throughout the population. Let us first consider the case in which the duplicate fixes and is therefore present in every chromosome of the extant species B and C (Fig. 2A). Note that the duplicate's frequency p is initially 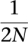and eventually fixes to 1 at the leaves of the locus 2 tree. This means that the sampled genomes of A, B, and C will contain genes a₁, b₁, b₂, c₁, and c₂, and their phylogenetic tree will be a traceback in the combined WF processes of locus 1 and locus 2. By modifying the coalescent process, we can define the distribution of branch lengths for the gene tree. First, note that the root of the locus 2 tree has only one individual with the non-null allele (black circle). This has the effect of forcing complete coalescence of all gene lineages in locus 2, and only allowing one lineage to trace back into the locus 1 tree. Thus, the descendants of the daughter duplicate (locus 2) behave differently from those of the mother duplicate (locus 1). In the following sections, we define a special process called the bounded coalescent that will model this condition. The second modification is that the duplication creates an additional lineage within the locus 1 tree that must coalesce. Thus, there is another opportunity for ILS (Fig. 2A), and it is for this reason that duplications tend to increase the frequency of ILS (see Results).

Gene loss within the multispecies coalescent

Conversely, we also define a model of gene loss (deletion) in the multispecies coalescent. When a loss occurs, a single gene is deleted from only one chromosome of the population (Fig. 2C). We can therefore represent the frequency of the non-null allele at this point as 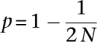. According to the WF process, this deletion will drift and either fixes or goes extinct.

DLCoal: A three-tree model

After considering the effect of gene duplication and loss in an example gene family, we now propose a general model. First, notice that the blue tree in Figure 2A is not a species tree (e.g., species B and C are represented multiple times), and yet it is distinct from the gene tree. Therefore, it is a third kind of tree, which we refer to as the locus tree, because it describes how new loci are created and destroyed. We can now propose a generative process that describes how all three trees are related (Fig. 3A).

Figure 3.

Generative process for the DLCoal model. (A) Given a species tree S with known topology and divergence times, a top-down dup-loss process generates a locus tree T^L, which contains duplication nodes (star), and each daughter duplicate is indicated by a daughter edge δ^L (dark red). From the locus tree, the bottom-up multilocus coalescent (MLC) process generates a gene tree T^G. Mappings between the trees represented by R^G and R^L indicate how one tree “fits inside” the other. This diagram depicts the same gene family as Figure 2A. (B) The multispecies coalescent and dup-loss model are special cases of DLCoal. When there are no duplications or losses (i.e., locus tree and species tree congruence), the model simplifies to the multispecies coalescent. (C) When ILS is assumed not to occur (i.e., gene tree and locus tree congruence), the model simplifies to the birth–death model for duplication and loss.

Species tree

We are given a species tree 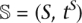with topology S and branch lengths t^S. The topology S is a graph [V(S), E(S)], with vertices V(S) and a set E(S) of directed edges (v, u). Let e(v) be the edge [v, ρ(v)], where ρ(v) is the parent of node v. Let t(v) be the length of branch e(v) expressed in units of time (generations). We use τ(v) to represent the age of a node v (i.e., the length of any path from v to the leaves). We assume that the population sizes N are given, and let N(v) represent the constant population size for branch e(v).

Locus tree

The locus tree is generated by a top-down birth–death process within the species tree (Arvestad et al. 2003; Dubb 2005; Åkerborg et al. 2009; Rasmussen and Kellis 2011). We assume a constant rate of gene duplication λ and gene loss μ expressed in events/gene per generation. The locus tree has topology T^L and has branch lengths t^L expressed in generations. The birth–death process also generates a reconciliation R^L that maps each node v ∈ V(T^L) to a node or branch in the species tree S. For each duplication node, one of the children is randomly denoted a daughter and the other a mother. Let δ^L be the set of all daughter nodes in the locus tree. An edge e(v) is called a daughter edge if v is a daughter node. We define the population sizes N^L for the locus tree using the population sizes of the species tree, namely, N^L(u) = N(R^L(u)).

Gene tree

Lastly, a gene tree 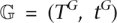is generated bottom-up using a multilocus coalescent (see Methods) within the locus tree. The process also generates a reconciliation R^G that maps vertices of the gene tree T^G to branches in the locus tree T^L. It is the gene tree along which molecular sequences evolve.

Simplifying assumptions

In this present definition of the model, we have made the following simplifying assumptions: We assume that the daughter of a duplication immediately begins at a locus unlinked with the mother gene (e.g., another chromosome or a distant location on the same chromosome); therefore, we can assume that coalescence within the mother and daughter lineages occurs independently. We also at this time assume no gene conversion between duplicated loci and that each duplication event creates a unique new locus.

Furthermore, we make several assumptions about the influence of the allele frequency of a new duplicate. We assume that the rate of gene duplication and loss is not dependent on the frequency of a gene in the population. We also at this time make an assumption about the fixing or extinction of new duplications or deletions. As we discuss in the next section, it is possible for a mutation such as a duplication or loss to not fully fix in all descendant lineages, an effect that has been called hemiplasy (Avise and Robinson 2008). Although this is likely an important phenomenon, we leave it for future work and instead optimize this present model for studying ILS. Thus, our hemiplasy assumption is that all duplications and losses either always go extinct or never go extinct in all descendant lineages. This assumption allows us to separate the duplication-loss process from the multilocus coalescent.

Duplicate and deletion extinction

Here, we explain some of the complex scenarios that can result due to hemiplasy of duplications and losses. Although these are difficult events to model in an inference algorithm, we can at this time define them easily in a generative process.

Consider again the gene family in Figure 2, except this time let the duplicate fix only in species C (p = 1) while it fails to fix and goes extinct (p = 0) sometime before reaching species B (Fig. 2B). Interestingly, the duplication event is ancestral to the divergence of species B and C, but only species C has the duplicate. A pure dup-loss model would explain this by an independent loss (i.e., gene deletion) of the duplicate in the branch leading to species B, but in this case, it is not a deletion or independent; it is simply the failure of the previous duplication to fix, leading to hemiplasy of the duplication (Avise and Robinson 2008). Although this term has been mainly used for point mutations, there is nothing to exclude larger mutations such as segmental or gene duplications from undergoing hemiplasy. There are likely real cases of this effect in human and primate evolution (Marques-Bonet et al. 2009). Failure to model this effect may lead to the overestimation of gene losses (deletions) following gene duplication events. While it is reasonable for duplicates to have relaxed selection and a potentially increased deletion rate, this is a distinct event from gene extinction. Distinguishing between accelerated event rates and duplication hemiplasy will be important for understanding the true rate and character of gene duplication within various genomes. Also note that by the same reasoning, gene losses can also exhibit hemiplasy.

To evaluate the prevalence of duplication and loss hemiplasy, we implemented a program that simulates duplication and loss allele sweeps under a neutral model at varying population sizes and duplication/loss rates (Supplemental Section 3.4). We find that 5% of simulated fly gene trees show hemiplasy for N = 10⁶ (Charlesworth 2009) and λ = μ = 0.0012 (Hahn et al. 2007b). This provides a bound on how often our hemiplasy assumption holds.

A new reconciliation method

Using the DLCoal model, we can now develop new methods for understanding gene family evolution in the presence of gene duplication, loss, and coalescence. We have used the model to develop a new reconciliation algorithm called DLCoalRecon, which addresses the long-standing problem of inferring duplications and losses while not being misled by ILS. The reconciliation problem is to determine the evolutionary events necessary for explaining a given gene tree topology T^G and species tree 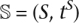(Goodman et al. 1979; Page 1994). The gene tree topology can be obtained using any existing phylogenetic method (e.g., ML, Bayesian, Neighbor-joining, etc.) and a previously determined species tree. Our method differs from previous methods in that we also require species divergence times, gene duplication-loss rates, and estimated population sizes, all of which can be estimated by other means (see Results). Using this information, we can estimate the maximum posterior locus tree from which we can infer gene duplications and losses. For more details, see Methods.

Results

Evaluating reconciliation of simulated gene trees

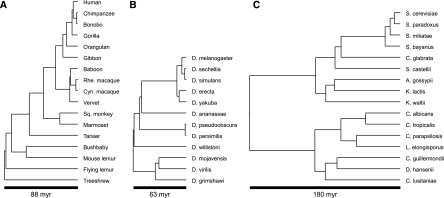
To evaluate the performance of our new reconciliation method, we compared it with the usual maximum parsimony reconciliation (MPR) algorithm (Page 1994) on several simulated data sets using parameters estimated for two clades of species: the 12 Drosophila species and 17 primates and other mammals (Fig. 4A,B). Data sets are simulated using a new simulation program based on our model (Supplemental Section 3).

Figure 4.

Species trees used in evaluation. (A,B) For our simulation evaluations, we used a data set of 15 primates (including two outgroup species) and 12 Drosophila species. (C) For our evaluation on real data, we used 16 species of fungi.

For our Drosophila data set, we used the same species tree used by the Drosophila 12 Genomes Consortium (2007) with divergence times estimated by Tamura et al. (2004). We used gene duplication and loss rates of 0.0012 events/gene per million years (Hahn et al. 2007b) and assumed 10 generations/yr (Sawyer and Hartl 1992; Pollard et al. 2006). For effective population size N_e, we used a wide range of 1–500 million individuals. Drosophila melanogaster is estimated to have an effective population size of ~1.15 million (Charlesworth 2009). We also used a range of duplication-loss rates from the estimated real rate (1×), to rates that are twice (2×) and four times (4×) as fast.

For our primate data set, we used the species tree and divergence times presented in Siepel (2009), a gene duplication and loss rate of 0.0017 events/gene per million years (Hahn et al. 2007a), and assumed a generation time of 20 yr. Primates have been estimated to have effective population sizes ranging from 10,000 to 25,000 (Charlesworth 2009). As with the Drosophila data set, we used a range of duplication-loss rates (1×, 2×, and 4×).

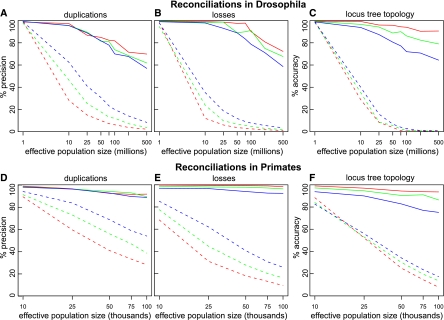
For the Drosophila data set with an effective population size of 25 million and a duplication-loss rate of 0.0012 events/gene per million years (1×), our 500 simulated gene trees contained 232 duplications, 216 losses, and 33,182 pairs of orthologous genes. At this population size, a large number of ILS events occur, and these are confused as duplication events by the standard MPR algorithm. In fact, MPR infers 1241 duplications followed by 3495 losses, corresponding to a precision of 15.0% and 6.0%, respectively. In contrast, DLCoalRecon finds many fewer events and with much higher precision, specifically 242 duplications (86.8%) and 216 losses (98.6%). In terms of ortholog pair accuracy, DLCoalRecon gains in sensitivity, since fewer of the ortholog pair relations are disrupted by erroneously inferred duplication nodes. DLCoalRecon recovers 99.7% of ortholog pairs, whereas MPR only recovers 64.5%. These trends hold for a variety of population sizes and duplication-loss rates (Fig. 5A,B,D,E). In general, higher population sizes are more difficult for both methods due to increased ILS rate, and an increase in duplication-loss rate is more difficult for the DLCoalRecon method.

Figure 5.

Increased performance of DLCoalRecon in simulated fly and primate gene trees. DLCoalRecon (solid) and MPR (dashed) were used to reconcile 500 fly and 500 primate simulated gene trees. Duplications and losses were simulated at rates that were the same as (1×, red), twice (2×, green), and four times (4×, blue) the rate estimated in real data. Increased performance is seen both in the precision of inferring duplications and losses (A,B,D,E) as well as the accuracy of reconstructing the locus tree topology (C,F).

We also asked how often the correct locus tree is recovered. DLCoalRecon correctly recovers >80% of locus tree topologies for primates and 100% for all fly population sizes <100 million (Fig. 5C,E). Although the MPR method does not explicitly reconstruct the locus tree, it does assume that it is congruent with the gene tree. However, we find that the accuracy of this assumption decreases rapidly with increasing population sizes (Fig. 5C,E, dashed lines).

The errors that DLCoalRecon commits could be due to either a limit in the power of the model to identify the correct reconciliation or limitations in our present implementation of the heuristic search. To evaluate the performance of the search, we additionally ran DLCoalRecon with the search initialized on the correct locus tree. On the simulated flies data set (N = 2.5 × 10⁶, λ,μ = 0.0012 events/gene per million years), we find an increased duplication precision of 97.4% and locus accuracy of 99.2%, suggesting that some of our present errors are likely attributable to insufficient search and that better search heuristics could lead to greater performance increases.

For this evaluation, we used the true duplication-loss rates and population sizes used in the simulations. In practice, these parameters will need to be estimated from genome-wide data using other existing methods (Rannala and Yang 2003; Hahn et al. 2005).

Evaluating reconciliation of 16 fungal genomes

We have also assessed the feasibility of using DLCoalRecon to infer duplication-loss events on a real data set. In previous work, we presented a new gene tree reconstruction method SPIMAP and compared it against several other algorithms—SYNERGY (Wapinski et al. 2007), PrIME-GSR (Åkerborg et al. 2009), PhyML (Guindon and Gascuel 2003), RAxML (Stamatakis et al. 2005), BIONJ (Gascuel 1997), and MrBayes (Ronquist and Huelsenbeck 2003)—in order to evaluate their accuracy for reconstructing gene trees and inferring duplication-loss events (Rasmussen and Kellis 2011). Several of these methods (SPIMAP, SYNERGY, PrIME-GSR) are “species-aware,” in that they reconstruct gene trees and perform reconciliation simultaneously, and in general this technique gives them a significant advantage over methods that perform these two steps separately. In that analysis, we combined each of the “species-unaware” methods (RAxML, PhyML, BIONJ, MrBayes) with the standard MPR algorithm for reconciliation. If ILS is present among these species, then the decreased accuracy of the species-unaware methods may be due to MPR's poor reconciliation. To test this, we combined the PhyML algorithm, a maximum likelihood method, with our DLCoalRecon method and assessed its performance on 5351 gene families using our previously used metrics (Rasmussen and Kellis 2011).

For this comparison, we used the same 16 fungal genomes as Rasmussen and Kellis (2011), which have a previously estimated species tree with divergence times (Fig. 4C; Butler et al. 2009). For an effective population size, we used a constant size of 1 × 10⁷ throughout the species tree, which has been estimated for Saccharomyces paradoxus (Tsai et al. 2008). Given this population size, we determined a reasonable generation time by performing simulations of one-to-one orthologous gene families with various generation times (0.1–1.5 yr/generation). The level of ILS was measured for each simulation using the PhyloNet software package (Than et al. 2008) to count the total number of “extra lineages” present in each gene tree. In a real data set of 739 one-to-one orthologs (Rasmussen and Kellis 2011), we found ~3.76 extra lineages per gene tree, which was closest to a simulation using 0.9 yr/generation. Although the effective population size and generation time are likely variable across these species, these approximations serve as reasonable average estimates. Of course, as better estimates of these parameters become available for species across this phylogeny, the DLCoal framework can make use of them.

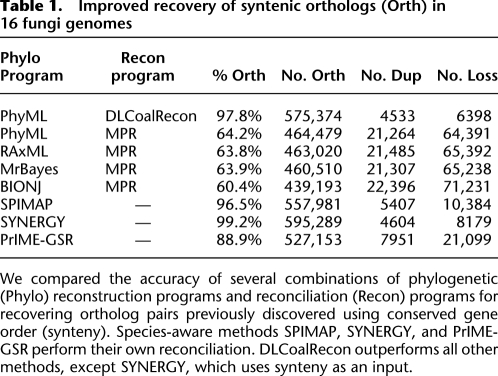
Using these parameters, we reconstructed 5351 gene trees with PhyML, reconciled them using DLCoalRecon, and then compared the inferred locus trees and events against the other methods (Table 1). As with any real data set, the truth is not known, but several informative metrics provide a sense of the performance of the different methods.

Table 1.

Improved recovery of syntenic orthologs (Orth) in 16 fungi genomes

The first metric we analyzed was the recovery of syntenic orthologs (one-to-one homologous gene pairs with conserved gene order). We find that DLCoalRecon recovers 97.8% of syntenic orthologs (Table 1), which is a dramatic improvement over methods using MPR (<64.2%) and is even higher than several “species-aware” methods, such as SPIMAP (96.5%) and PrIME-GSR (88.9%). We also find that DLCoalRecon finds significantly fewer duplication and loss events than all other methods, suggesting that ILS results in spurious duplication and loss events in each of the other methods.

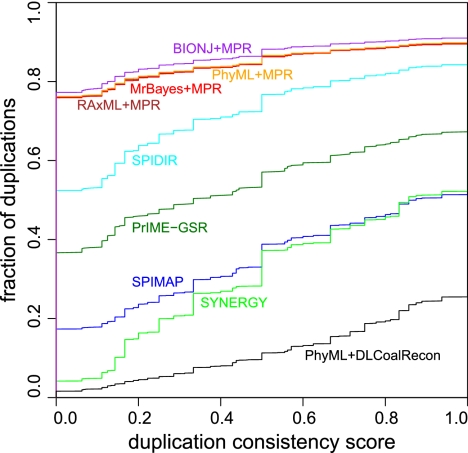
For our second metric, we used the duplication consistency score (Vilella et al. 2009), which is a measure of the plausibility of the duplication events inferred. The consistency of a duplication node is defined as |L ∩ R|/|L ∪ R|, where L and R are the sets of species present in descendants left and right of the duplication node, respectively. The consistency score often tends toward zero for erroneous duplications, since they are often followed by many compensating losses (Hahn 2007; Vilella et al. 2009) and result in low species overlap |L ∩ R|. Using this score, we find that 74.5% of duplications inferred by DLCoalRecon have a consistency score of one and only 1.6% have a score of zero. By comparison, 48.6% (17.4%) of duplications inferred by SPIMAP have a score of one (zero) and SYNERGY has 47.8% (4.2%) duplications with a score of one (zero). The improvement in scores is even greater over the MPR methods, which have a score of one (zero) for 10.2% (76.2%) of their duplications. In general, the score distribution for DLCoalRecon is consistently higher than all other methods, both species-aware and species-unaware (Fig. 6).

Figure 6.

Cumulative distribution of duplication consistency scores. Each gene tree reconstruction program was used genome-wide to infer the duplications present in 16 fungi species. For each duplication, we computed the consistency score. Among all of the programs, the combination of PhyML+DLCoalRecon infers the fewest duplications with a score of zero (1.6%) and the most duplications with a score of one (74.5%).

Lastly, in Rasmussen and Kellis (2011), we introduced a test involving the ability to recover more recent duplications due to gene conversion events. This test is especially difficult for species-aware methods that overpenalize duplications. However, we find that DLCoalRecon performs well on this test by recovering 86.5% of the recent gene-converted paralogs, which is comparable to SPIMAP (83.8%), PrIME-GSR (89.2%), and other species-unaware methods (85.15%). This indicates that although DLCoalRecon infers fewer duplications and losses, it is still sensitive enough to recover such events if the sequence data provide strong evidence for their existence.

Gene duplications increase the frequency of ILS

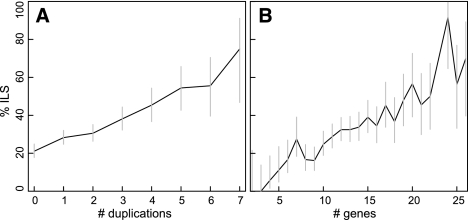
Using our DLCoal model, we can also investigate how duplications, losses, and coalescence interact with one another. For example, notice that duplications break up branches in the locus tree into segments with smaller units of time (Fig. 2A). Therefore, there is an increased chance of two lineages in the gene tree coalescing deeper than their first opportunity (ILS). To understand how great this effect could be, we used our simulation program to generate gene trees with duplications, losses, and coalescence (Supplemental Section 3). Using a species tree determined for 12 Drosophila species (Drosophila 12 Genomes Consortium 2007), an effective population size of 5 million, duplication and loss rates of λ = μ = 0.0048 events/gene per million years, and 10 generations/yr (Pollard et al. 2006), we simulated 2000 gene trees. By binning gene trees based on the number of duplications present, we do indeed find that ILS increases significantly as more duplications occur (Fig. 7). Therefore, even if ILS is rare for orthologous gene families (i.e., one gene per species) in a particular set of species, the duplicated families may have a fairly high frequency of ILS that could complicate analyses that assume ILS is negligible.

Figure 7.

Duplications increase the rate of incomplete lineage sorting (ILS). Using the DLCoal model, we simulated 2000 gene trees for the 12 flies phylogeny, using an effective population size of N = 5 × 10⁶, duplication-loss rates of λ = μ = 0.0048 events/gene per million years, and 10 generations/yr. (A) As more gene duplications occur in a gene tree, the probability of ILS increases. (B) Overall, larger gene families tend to have increased ILS frequency. Error bars indicate 95% confidence intervals.

Discussion

One challenge in developing a model that combines both the coalescent and dup-loss processes is that these two models currently use the term gene tree in very different ways. For example, the number of gene branches present in one time slice in a species branch in the coalescent model (Fig. 1D) represents the number of chromosomes that are ancestral to the extant sequences. However, the same time slice in the dup-loss model (Fig. 1E) represents how many loci exist within the ancestral genome at that time.

We resolved these incompatible definitions by introducing a third tree, the locus tree, but what does it really represent? Instead of representing the history of a particular DNA sequence like the gene tree, the locus tree represents the history of a pool or set of sequences, namely, all of the sequences in a population that belong to the same species and the same locus. This pool of sequences is important to represent because given our model assumptions (no migration and no gene conversion), only sequences within the same pool can coalesce. It is these restrictions that allow us to think of the gene tree as evolving “inside” of the locus tree. In our model, there are two ways this pool can change over time. Either the pool splits because the species speciates or because the locus duplicates. These events can be represented using a tree data structure, and each of the internal nodes can be labeled with either a speciation or a duplication event. Therefore, the locus tree behaves very similar to the “gene tree” from dup-loss models. In turn, the structure of the locus tree is restricted by the species tree, since the locus tree must speciate whenever the species tree does. The DLCoalRecon algorithm illustrates one way of recovering a locus tree by taking into account the restrictions placed on it by the gene tree and species tree.

With this in mind, our DLCoal model can be viewed as a generalization of the two popular models for gene family evolution: the multispecies coalescent and the dup-loss model. In particular, the additional assumptions of these models are really assumptions about the congruence of the locus tree with either the species tree or gene tree, respectively. For example, when coalescent analyses discard gene families that contain paralogs, this is equivalent in our model to requiring that the locus tree be congruent to the species tree (Fig. 3B). Note that when these two trees are congruent, the only remaining process is the multilocus coalescent (MLC), and since no duplications are present, this process simplifies to the usual multispecies coalescent (see Methods). Conversely, in applications of pure dup-loss models, it is often assumed that no incomplete lineage sorting (ILS) occurs. In our model, this translates into requiring congruence between the gene tree and locus tree, and therefore the only remaining process is the dup-loss process (Fig. 3C).

Using the DLCoalRecon reconciliation algorithm, one can infer duplications, losses, and ILS simultaneously. We envision this method being used in a larger phylogenetic pipeline, where one can build a phylogenetic tree for a gene family of interest using their preferred method (e.g., maximum likelihood, Bayesian, Neighbor-joining, etc.) and reconcile it to a known species tree using DLCoalRecon. This will not only infer the events more accurately, but it will also construct a locus tree, which in most applications will likely be the most relevant tree to the user, since the gene tree in this case is a nuisance variable. This is because only the locus tree can unambiguously describe the history of duplication and loss events.

In this study, we made several assumptions in order to make reconciliation of duplicated gene families spanning dozens of species feasible. Similar to most reconciliation algorithms, we have currently assumed a model that ignores gene conversion. However, it may be possible to expand the DLCoal model to incorporate these events. For example, gene conversion could be modeled as migration of gene lineages between branches in the locus tree. We also made the common assumption of no recombination within the gene locus. Relaxing this assumption may be desirable in some cases, but would greatly increase the complexity of the model by essentially replacing the gene tree with an ancestral recombination graph (ARG) (Griffiths and Marjoram 1996). We have also assumed that many of our model parameters, such as duplication-loss rates and effective population sizes, have been estimated by other methods before application of our method. In most cases, these existing methods (Rannala and Yang 2003; Hahn et al. 2005) and parameters estimates should suffice, since DLCoalRecon's main strength is to use the genome-wide and population-wide parameters to reconstruct the history of a particular gene family. Lastly, the reconciliation method could be expanded to incorporate uncertainty in the gene tree or to model hemiplasy of the duplication and loss events. It should also be possible to extend this method to use Markov chain Monte Carlo (MCMC) in order to estimate the full posterior distribution of the locus tree, such that the uncertainty of the reconciliation can be represented.

Going forward, we are optimistic about increased understanding of gene evolution. This work is only one step in a series of recent developments that unify many important aspects of gene family evolution. There has been work on combining models of sequence evolution and duplication-loss (Arvestad et al. 2004; Dubb 2005; Vilella et al. 2009), incorporating substitution rate variation (Rasmussen and Kellis 2007; Åkerborg et al. 2009; Rasmussen and Kellis 2011), considering conserved gene order (Wapinski et al. 2007), handling multifurcating gene trees and species trees (Chang and Eulenstein 2006; Vernot et al. 2008), merging models with horizontal transfer (Doyon et al. 2010; David and Alm 2011; Tofigh et al. 2011), and others. From these models, one can derive new methods for reconciliation (Arvestad et al. 2003; Vernot et al. 2008), gene tree reconstruction (Wapinski et al. 2007; Åkerborg et al. 2009; Rasmussen and Kellis 2011), species tree reconstruction (Liu and Pearl 2007), or estimation of population statistics (Rannala and Yang 2003).

Methods

DLCoal model details

To complete our description of the DLCoal model, we define a stochastic process, called the multilocus coalescent, which we describe by building on several smaller processes.

The bounded coalescent

Let a bounded coalescent be a process in which we have a mutation creating a new allele at a known time t*, and we are given k lineages at time t = 0 that also have the new allele. For our purposes, the new allele represents the presence of a new duplicate, and the old allele represent its absence. In addition, we have no knowledge of the frequency of the allele at any other time. Let the coalescent times of the k lineages be described by a new process called the bounded coalescent. This situation is similar to the conditional coalescent, except that the mutation time t* is given and all k lineages descend from the mutation (Wiuf and Donnelly 1999).

We can derive the distribution of the coalescent times in the bounded coalescent by making the following observation. Requiring that all k lineages have the new allele implies that the k lineages must be descendants of the first individual with a new allele at t*, and only coalescent trees whose most recent common ancestor (MRCA) has a time t_MRCA more recent than t* satisfy this condition. Furthermore, given that a coalescent tree has t_MRCA < t*, there is a 1/2N probability that the root of the tree has the new allele. Notice that this probability is independent of the tree's topology and branch lengths. Therefore, a coalescent process conditioned on t_MRCA < t* is an equivalent definition of the bounded coalescent. The probability density of the time t of the next coalescent between k lineages in the bounded coalescent process is then:

where P(t|k, N) is the probability density of the coalescent time within the usual unbounded coalescent, namely:

The bounded multispecies coalescent (BMC)

Continuing to define our model, we can now consider the coalescent process of lineages descended from a duplication further up in a species tree (Fig. 2A). Using the same arguments, we can model these gene lineages as a multispecies coalescent with the condition that the age of their MRCA τ(r) is more recent than the time of the duplication t*. We call this conditioned process the bounded multispecies coalescent (BMC).

Let r be the root (MRCA) of the gene tree 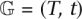with topology T and branch lengths t. Let n be a vector of gene counts for each extant species, such that n_u = |{v: R(v) = u,v ∈ L(T)}| for u ∈ L(S). Typically n_u = 1, unless multiple extant individuals are present per species in the data. The probability distribution of the gene tree is then:

Fortunately, the numerator is the probability of a gene tree in the multispecies coalescent, which has been derived by Rannala and Yang (2003), and the denominator has also been derived by Efromovich and Kubatko (2008). For additional details, see Supplemental Section 2.4.

The multilocus coalescent (MLC)

The process that generates a gene tree from a locus tree in our model is called the multilocus coalescent (MLC). The MLC process is a multispecies coalescent conditioned such that each daughter edge has complete coalescence, that is, only one gene lineage is present at the top of each daughter edge.

This process is equivalent to partitioning the locus tree T^L at every daughter edge e(v) into the mother subtree (locus 1) and a series of daughter subtrees T^L,v. Let each daughter subtree T^L,v take ownership of the branch e(v). For each daughter subtree T^L,v, a BMC process generates the coalescent tree T^G,v. For the mother subtree, an unbounded multispecies coalescent generates subtree T^L,v, where r = root(T^L). The resulting trees T^G,v are then joined to create a single gene tree T^G. For example, in Figure 2A, a BMC is used to generate the portion of the gene tree in locus 2, and a multispecies coalescent is used to generate the remaining portion of the gene tree in locus 1. This concludes the description of the DLCoal process.

Deriving the DLCoalRecon algorithm

The algorithm takes as input a gene tree topology T^G, a species tree topology S, species branch lengths t^S, effective population sizes N, and gene duplication-loss rates λ and μ. As output it returns a maximum a posteriori reconciliation R. Usually, a reconciliation is defined as a mapping from vertices in the gene tree to vertices and edges in the species tree; however, in the DLCoal model, the reconciliation ℝ is instead defined as a tuple, ℝ = (T^L, R^G, R^L, δ^L), where T^L is the locus tree, R^G is a mapping from the gene tree to the locus tree, R^L is a mapping from the locus tree to the species tree S, and δ^L is a set of daughter nodes. Given our model parameters, θ = (t^S, N, λ, μ), our goal is to compute the maximum a posteriori reconciliation,

Note that maximizing the posterior is the same as maximizing the joint probability when T^G is given. We currently assume that the gene tree times t^G are unknown, since in practice they are not directly known without a molecular clock assumption. By introducing the locus tree branch lengths t^L, we can now separate the variables for the gene tree and locus tree. Furthermore, we can factor the locus tree (see Supplemental Section 2.7) into a probability for its daughter nodes, and topology, branch lengths:

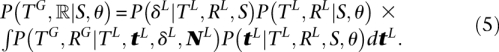The term P(T^L, R^L|S, θ) has been derived (Arvestad et al. 2003; 2009) and for the daughters set δ^L, we have:

where dup(T^L, R^L, S) gives the number of duplications in the locus tree. This probability represents the fact that there are two ways to choose a daughter node for each duplication in the locus tree. We perform the integration using Monte Carlo as in Arvestad et al. (2004) and Rasmussen and Kellis (2011). The remaining probability to define is the probability of the gene tree topology T^G in the MLC process, which is derived in Supplemental Section 2.7.

Reconciliation search

Using the results of the previous section, we can compute the joint probability of any proposed reconciliation. To estimate the maximum a posteriori reconciliation, we presently use a heuristic hill-climbing search. We initialize the search with a reconciliation ℝ that has a locus tree topology T^L congruent with the gene tree T^G, mappings R^G and R^L that are Least Common Ancestor (LCA) mappings (Page 1994), and randomly chosen daughter nodes δ^L. Next, we propose new reconciliations by performing one of the following: rearranging one of the mappings (Doyon et al. 2012), rearranging the locus tree using subtree pruning and regrafting (SPR), or choosing new daughter nodes. The search continues for a user-specified number of iterations, and the algorithm outputs the proposed reconciliation that obtained the highest posterior probability.

Data access

The DLCoalRecon software as well as supplemental data are freely available for download at http://compbio.mit.edu/dlcoal.