Estimation of Spatial Scale across the Visual Field Using Sinusoidal Stimuli

In this study, spatial scale was assessed across the central visual field to gain a better understanding of psychophysical contrast sensitivity to sinusoidal stimuli and how sensitivity relates to ganglion cell density.

Abstract

Purpose.

To characterize contrast sensitivity for sinusoidal stimuli across the central visual field and help bridge the gap between perimetry and visual psychophysics by developing a contrast-sensitivity template for spatial scale (experiment 1) and testing it on a new dataset (experiment 2).

Methods.

In experiment 1, 40 subjects free of eye disease, ages 43 to 84 years, had one eye tested. Twenty-three locations along the horizontal and vertical meridians were tested with sinusoidal stimuli having peak spatial frequencies of 0.5, 1.0, and 2.0 cpd and a spatial bandwidth of 1.0 octave. Contrast sensitivity functions were fit with a low-pass template slid horizontally on a log–log plot by a spatial scale factor. In experiment 2, 29 of the original subjects had one eye tested. Twenty-six locations in grid form were tested with sinusoidal stimuli having peak spatial frequencies of 0.375, 0.53, 0.75, and 1.5 cpd. Spatial scale values were predicted using the 0.375 cpd data and template and compared to empirical values determined from the remaining data.

Results.

In experiment 1, the change in spatial scale alone fit the mean sensitivities well (residual sum of squares = 0.01 log unit). Spatial scale increased with eccentricity except for horizontal nasal displacements between 3° and 15°. In experiment 2, differences between empirical and predicted spatial scale values were within ±0.1 log unit (mean and SEM: 0.00 ± 0.01 log unit).

Conclusions.

Spatial scale characterized the visual field tested in perimetry well and can contribute to further linkage between clinical perimetry and basic vision science.

Automated perimetry is one of the most widely used clinical psychophysical tests for detecting and monitoring visual defects in patients with a range of eye diseases and is the standard of care for monitoring patients with glaucoma. The most common form in clinical use is conventional automated perimetry (CAP), which assesses the differential light threshold for sharp-edged circular luminance increments presented at 54 to 72 locations within ±30° from fixation using optical systems with shutters and movable mirrors.¹ The stimuli used for CAP were based on psychophysical methods and principles of the first half of the 20th century and stimulus design was guided by Weber's law, Ricco's law, and Bloch's law.²

A decade after CAP stimuli were standardized as circular increments, new display systems were used to produce a different type of stimulus: sinusoidal grating stimuli with little or no increment in mean luminance.³ Grating stimuli became widely used in spatial vision research, with both psychophysical and electrophysiological studies using grating stimuli rather than luminance increments. The Fourier transform of the CAP stimulus has a significant DC component (the increment in luminance) but also has components at a range of spatial frequencies (due to the edge), so a wide range of cortical spatial mechanisms could mediate detection.⁴ Grating stimuli can be used to eliminate the luminance increment and target a single spatial frequency, although the window through which the grating is viewed will add additional spatial frequency components. Several researchers used these stimuli to make systematic measurements at different locations in the visual field, each study extensively examining only two or three subjects.^5–7 As spatial vision models became more sophisticated, it became clear that optimal stimuli had two-dimensional windows, such as sinusoidal gratings windowed by two-dimensional Gaussian windows^8–10; these have become a standard stimulus in spatial vision and are commonly referred to as “Gabor patches.”^11,12 However, to date only a few studies have used Gabor patches for perimetry.^11,13–15 The present study used Gabor patches to assess variation in contrast sensitivity across the central visual field.

The purpose of the current manuscript is to contribute to further linkage between perimetry and spatial vision by performing perimetry with modern stimuli and applying the method of “spatial scale” to the central visual field tested by CAP. Spatial scale corresponds to magnification or minification of a stimulus required to equate contrast sensitivity at different locations in the visual field. Watson⁸ noted the advantages of using a fixed spatial bandwidth for Gabor patches when assessing spatial scale, since the window size decreases as spatial frequency increases, so that change in spatial scale will magnify the stimulus as it is moved away from the fovea. Previous studies had potential bias because the stimulus window was varied with eccentricity based on prior assumptions rather than as simple magnification. We used Watson's method as an assumption-free means of assessing the scaling factor.

Perimetric sensitivity for CAP declines more slowly with eccentricity than does ganglion cell density¹⁶ or cortical magnification,^17,18 and for eccentricities from 4° to 30° variation in sensitivity with test location can be accounted for by a change in spatial scale with little or no change in overall sensitivity.¹⁹ Our goal was to develop an empirical model for variation in spatial scale across the normal visual field, and use this model to predict perimetric sensitivities for a range of stimuli, based on sensitivity to a single stimulus. A successful model would allow the choice of stimuli for perimetry to be based on predictable effects of stimulus parameters.

Methods

Participants

Forty subjects free of eye disease, ages 43 to 84 years (mean ± SD, 63 ± 11 years), were recruited from a longitudinal study of contrast sensitivity perimetry at the Indiana University School of Optometry. Analysis of data from experiment 1 led to predictions that were tested in experiment 2. Twenty-nine subjects from experiment 1 were successfully recruited for experiment 2. The research for this study adhered to the tenets of the Declaration of Helsinki and was approved by the Indiana University institutional review board. Informed consent was obtained from each participant after explanation of the procedures and goals of the study, before testing began.

The preferred eye of each person was tested, and data collected from the left eyes were converted to right-eye format by multiplying x-values for all locations by −1. Inclusion criteria were absence of known eye disease during a comprehensive eye examination within 2 years, best corrected visual acuity of 20/20 or better, spherical correction within ±6 D, cylinder correction <3 D, clear ocular media, and IOP < 22 mm Hg. Exclusion criteria were an ocular or systemic disease known to affect the visual field, a first-degree relative with glaucoma, usage of medications known to affect vision, and inability to produce consistent data. Four subjects were excluded from the study: two had chronic migraines, one dropped out of the study before a complete data set was gathered, and one was excluded due to inability to produce consistent data. An additional subject's data were removed from experiment 2 only, because of an eyelid artifact. In perimetry, “eyelid artifact” refers to reduced sensitivity and increased variability, due to lowered eyelids obscuring the stimuli and has the largest effect at stimulus locations with the greatest vertical eccentricity. Only areas along the horizontal and vertical meridians were tested for experiment 1, making these data less likely to be affected by an eyelid artifact than in experiment 2, which had twice as many locations at the greatest vertical eccentricity.

Equipment

A custom testing station was built using a visual stimulus generator (ViSaGe; Cambridge Research Systems, Ltd., Cambridge, UK). A photometer and calibration software (Opti-Cal; Cambridge Research Systems Ltd.) were used to measure luminance versus voltage values for each phosphor, calculate transfer functions, and produce red-green-blue (RGB) gamma correction look-up tables. Each subject was asked to place his or her head in a chin rest with the forehead against a bar so that the eye was 40 cm from a fixation target displayed on a 21-in. monitor (Diamond Pro 2070SB; Mitsubishi Digital Electronics America, Inc., Irvine, CA) that subtended 42° × 35° of visual angle. The resolution of the monitor was 800 × 600 pixels with a frame rate of 140 Hz.

Stimuli

Stimuli were two-dimensional Gabor sinusoids, horizontal sinusoidal gratings windowed with circular two-dimensional Gaussians. The space constant was set to 0.5625 divided by peak spatial frequency, so that the spatial bandwidth was 1.0 octave. The stimuli were presented with a temporal Gaussian envelope having an SD of 100 ms, so that 68% of the energy was in the central 200 ms. The mean luminance was 50 cd/m².

For experiment 1, 23 locations at ±3° alongside the horizontal and vertical meridians of the visual field were tested with three Gabor stimuli having nominal peak spatial frequencies of 0.5, 1.0, and 2.0 cyc/deg, based on a fixed number of pixels per degree. For all analyses, the actual spatial frequency was computed for each eccentricity accounting for the use of a flat screen rather than a dome. The two locations nearest to the center of the blind spot were not used in the analysis. The furthest eccentricities tested in the visual field spanned ±21° and ±15° along the horizontal and vertical meridians. One of the locations in the superior meridian at 15° eccentricity was tested with two sets of staircases, which allowed determination of within-test variability; for the primary analysis, the results from both staircases at this location were averaged. For experiment 2, 26 locations in the visual field used by Hot et al.¹³ were tested with four Gabor stimuli having peak spatial frequencies in steps of one half or one octave: 0.375, 0.53, 0.75, and 1.5 cyc/deg (magnification corrected for use of a flat screen).

Threshold Algorithm

Contrast sensitivity across the central visual field was measured by having the subject fixate a target in the center of the CRT screen and respond to stimuli presented at a range of locations in visual space. The subject was asked to click a button whenever the stimulus was seen; the interstimulus interval averaged 1700 ms, with a variable foreperiod. A one-down, one-up staircase method with four reversals was used to determine the subject's contrast threshold at each location. For each staircase a stimulus with 25% contrast was presented first. Contrast of the stimulus was decreased by 0.3 log unit if responded to, or else increased by 0.3 log unit if not responded to, until a reversal (change in response/no-response) occurred. This was considered the first of four reversals. Then the stimulus contrast was either increased (if not responded to) or decreased (if responded to), by 0.3 log unit again for the second reversal. After the second reversal, the staircase used steps of 0.15 log unit. The average of the log contrasts for the last two reversals was taken as an estimate of contrast threshold.

In addition to the trials used in the staircases, other trials (∼15% of total trials) were used to assess rates for fixation loss, false positives, and false negatives, as described in detail in Hot et al.¹³ Briefly, fixation loss trials were presentations of the stimulus in the center of the blind spot, at maximum contrast; false-positive trials were those in which no stimulus was presented at the end of an interstimulus interval, and a false positive was scored if there was a response during the following interstimulus interval before the next stimulus was presented. False-negative trials were trials at which the stimulus was set to a contrast 0.6 log unit above the ongoing threshold estimate. The rates for fixation loss and false positives were computed as fractions of responses to the two types of trials. After the experiment was finished, maximum likelihood estimation was performed to estimate threshold, slope and false-negative rate at each location, and the average of false-negative rates across all locations was used as the false-negative rate for that experiment.

When there was no response to the stimulus for a presentation at maximum contrast, it was scored as a “reversal” at that location, and the maximum stimulus was presented again the next time that location was tested. When there was never a response to a stimulus at a given location, the location was scored as “not seen” for that test. Because our subjects were free of eye disease, “not seen” was taken as an indication that: the stimulus spatial frequency was higher than the subject could detect at that location, the location was within the physiological blind spot, or the location was obscured by eyelid ptosis (eyelid artifact). Because there were four reversals and starting contrast was 25%, a score of not seen means that there was no response at that location to six stimuli with contrasts presented in the sequence 25%, 50%, 100%, 100%, 100%, and 100%. With typical psychometric slopes for this study, the likelihood function for this set of stimulus contrasts and subject responses has an asymptotic plateau starting near a log contrast sensitivity of −0.15, which was assigned for nonseeing locations. Across subjects, frequency, and locations the value −0.15 log contrast sensitivity was assigned a total of 50 times (0.9%). Nonseeing locations occurred more often at peripheral locations and with higher spatial frequencies. Percentage of locations not seen with maximum contrast were 3%, 2%, 0.5%, and 0.1% for the 2.0, 1.5, 1.0, and 0.5 cpd spatial frequency stimuli respectively. There were no nonseeing locations for the other spatial frequencies.

Protocol

Fixation was monitored using a closed-circuit video system and the Heijl-Krakau method.²⁰ With this technique, a suprathreshold stimulus is presented periodically at the blind spot, and if the subject responds to the stimulus, then it is assumed that either the subject is not fixating properly or else is responding without seeing a stimulus (false positive). Only one eye was tested, and the other was covered with a translucent occluder. Test glasses with spherical equivalent for the 40 cm viewing distance (in steps of 1 D) were used if necessary. Each subject was refracted, and near correction was determined by taking age, distance correction, and viewing distance into account. The spherical refractive error ranged from −4.00 to +3.00 D, with a median of 0 and interquartile interval from −0.25 to +0.50 D. Cylindrical error ranged from 0.00 to −2.25 D with a median of −0.75 and interquartile interval of −1.00 to 0.00 D; visual acuity of at least 20/25 on a near vision card placed at 40 cm was required before testing began.

For each subject, the center of the blind spot was mapped before the initial visual field test, by projecting a low-luminance increment in the region of the mean normal blind spot. The blind spot stimulus had a diameter of 0.5° and was presented at maximum contrast (900% Weber contrast) on a 10-cd/m² background. The first location tested was 6° temporal and 1° below the horizontal midline, and after the subject responded, the stimulus moved temporally in 1° increments until the subject stopped responding for a number of trials and then began responding on the other side of the blind spot. The locations where the subject did not respond were used to approximate the horizontal extent and midpoint of the blind spot. Stimuli were then presented in a similar manner along a vertical line intersecting the horizontal midpoint of the blind spot, giving an estimation of the center of the blind spot. The blind spot was remapped if the subject responded to stimuli presented in the estimated blind spot during subsequent testing.

Experiment 1

Contrast sensitivity was averaged (in log units) across subjects for each spatial frequency, meridian, and eccentricity. These means were plotted versus spatial frequency and were fit by sliding a single low-pass contrast sensitivity template (equation 1) horizontally on the log-spatial-frequency axis, using only one free parameter: S, the log spatial scale factor:

where f is spatial frequency and CS is contrast sensitivity. Before equation 1 was used to estimate variations in spatial scale with visual field location, fixed parameters a, b, and c were first empirically determined by analyzing data at the two innermost and outermost eccentricities along the nasal meridian. The data at the farther eccentricity were slid horizontally to higher spatial frequencies with a scaling factor that aligned the two data sets. This alignment was determined by eye. A second-order polynomial fit these data well, with a = 0.89, b = −0.86, and c = −0.32. These parameters were then fixed for all further analyses (all calculations made using Igor Pro, ver. 5.05A; WaveMetrics, Inc., Portland, OR).

Results

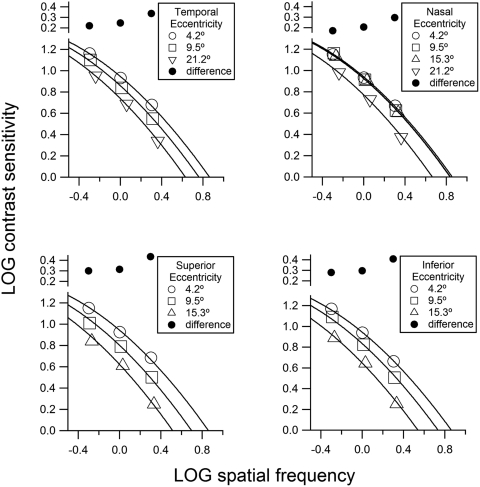
The template gave good fits to the averaged data with a simple change in spatial scale (Fig. 1, residual sum of squares = 0.01 log unit). The spatial scale changed more dramatically along the vertical meridians than the nasal meridian. The change in spatial scale from 3° to 15° was approximately 0.05 log unit for the nasal meridian and greater than 0.34 log unit for the vertical meridians. In addition, change in spatial scale from 3° to 9° was less than 0.04 log unit along the nasal meridian and approximately 0.12 log unit along the temporal meridian. This nasal-temporal asymmetry was further investigated in analysis of data from experiment 2.

Figure 1.

Spatial contrast sensitivity functions for locations offset by 3° from the horizontal and vertical meridians, fit with the empirical template (equation 1). The size of the symbols was selected to represent approximately ±1 SEM. Filled circles at the top of each graph represent the difference between contrast sensitivities at the innermost and outermost eccentricities for each spatial frequency, to demonstrate the effects of the horizontal shift of the template. In all four graphs, the circles show that the difference increases with spatial frequency in a manner consistent with a horizontal, but not vertical, shift of the template.

Experiment 2

Analysis and Statistical Design: Part 1.

The reasonable fits obtained with the low-pass contrast-sensitivity template using only a change in spatial scale led to an additional question: Using the template created in experiment 1, can the spatial scale value at any given location be predicted from contrast sensitivity for a single spatial frequency?

Data collected with a peak spatial frequency of 0.375 cpd were used to make spatial scale predictions. Log contrast sensitivity was averaged across all the subjects at each of the 26 locations. Using equation 2, spatial scale values were determined for each location from the average change in contrast sensitivity at 0.375 cpd. Equation 2 was derived from equation 1, using the quadratic formula and the values of a, b, and c fixed in experiment 1:

where S is the log spatial scale factor and logCS is log contrast sensitivity at 0.375 cpd.

Next, empirical spatial scale values were determined from the 0.53-, 0.75-, and 1.5-cpd data using the contrast sensitivity template created in experiment 1. Each subject's data were fit individually with equation 1, and the spatial scale values at each location were averaged across subjects. These empirical values were then compared to the predicted spatial scale values from equation 2.

Analysis and Statistical Design: Part 2.

To further assess the apparent nasotemporal spatial scale asymmetry in experiment 1, we asked the question: Is spatial scale significantly smaller in the nasal visual field than in the temporal field out to ±15° horizontally?

Data collected for stimuli with peak spatial frequencies of 0.375, 0.53, 0.75, and 1.5 cpd were used to address this question. The null hypothesis was that spatial scale is not significantly different between the nasal and temporal visual field. To test this hypothesis, the template from experiment 1 was used to calculate spatial scale for each subject at four nasal and four temporal locations. Each nasal location had a corresponding temporal location that was equal in vertical distance and eccentricity from the point of fixation. There were a limited number of corresponding nasal and temporal locations because the data analyzed were from an ongoing study that had chosen these locations to assess glaucomatous defects and not to test hypotheses concerning nasal–temporal asymmetry. Therefore, locations were chosen along horizontal lines that allowed the greatest number of corresponding points. Corresponding superior and inferior locations were averaged. Two one-tailed within-subject t-tests were used to compare spatial scale along the two directions at the corresponding eccentricities. Significance was set at P < 0.025, using the Bonferroni correction to account for repeated tests.

Results

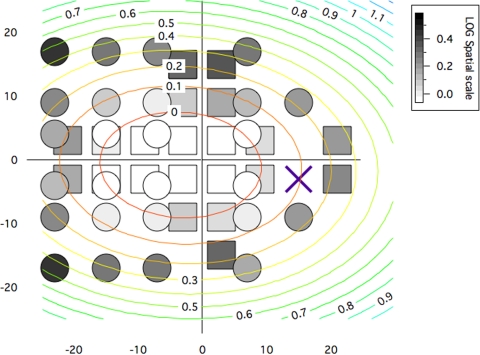
Spatial scale values throughout the visual field from experiment 2 appear to have similar features as those along horizontal and vertical meridians in experiment 1. A gray-scale map representing spatial scale values averaged across all the same subjects for both experiments is shown in Figure 2. From this map, a relatively small change in spatial scale is apparent for horizontal nasal displacement from 3° to 15° compared to all other directions of change in the map. A two-dimensional parabola was fit to the spatial scale values and shows nasal displacement.

Figure 2.

Gray-scale map of spatial scale values derived by fitting equation 1 to data from experiments 1 and 2. The map is in right-eye format, so nasal visual field locations have negative x-values and temporal locations have positive x-values. Squares represent values derived from experiment 1, and circles represent values derived from experiment 2. The concentric ellipses illustrate a two-dimensional parabolic fit to the spatial scale values, with each ellipse having constant spatial scale, in steps of 0.1 log unit from 0.0 to 1.1.

Part 1

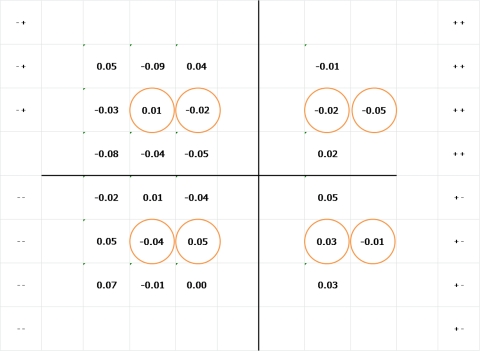
The differences between the empirical and predicted spatial scale values in log units are shown in Figure 3. All differences were within ± 0.1 log unit and the mean (± SEM) for the differences was 0.00 (± 0.01) log unit.

Figure 3.

Map of the differences between empirical and predicted spatial scale values in log units. A positive value indicates that the empirical scale factor was larger than predicted. Empirical values were derived by fitting equation 1 to all the data at that location, and predicted values were derived using equation 2 to compute scale from contrast sensitivity at 0.375 cpd. Circled locations represent the locations used for the analysis in part 2 of experiment 2.

Part 2

The two t-tests found that the changes in spatial scale factors in the nasal field were significantly smaller than the changes in spatial scale factors in the temporal field at both the inner locations (t = −2.75; P = 0.005) and outer locations (t = −6.2; P < 0.0001).

Eleven subjects dropped out of the study between experiments 1 and 2; in order to detect possible bias, we compared mean contrast sensitivities and spatial scale at each location for the 29 subjects who continued in experiment 2 with those for all the subjects from experiment 1. The mean difference across locations was less than 0.01 log unit for both contrast sensitivity and spatial scale (SD 0.02 and 0.01 log unit, respectively).

Discussion

The purpose of this study was to characterize perimetric sensitivity for Gabor patches across the central visual field, as tested clinically with perimetry, using Watson's method for estimating spatial scale⁸ to help bridge the gap between perimetry and basic visual psychophysics. We derived a contrast sensitivity template that allowed us to predict spatial scale based on contrast sensitivity to a single spatial frequency and found that spatial scale changed at different rates along vertical and horizontal directions. At any tested vertical distance above and below the horizontal midline, spatial scale and contrast sensitivity remained relatively constant along the horizontal direction from 3° to 15° nasally. For all other directions, spatial scale and contrast sensitivity decreased systematically with eccentricity.

Our finding on nasal/temporal differences was consistent with findings from a study of peripheral spatial resolution,²¹ and with five of six nasal–temporal comparisons in a recent study.²² The one discrepancy was for a stimulus that is quite susceptible to window artifacts: a 10° × 10° square window for a 3.5-cyc/deg grating. We used Gabor stimuli with one-octave bandwidths to avoid window artifacts, which may also explain why we found that the nasal and temporal spatial scales were similar at 21°, whereas a study of resolution acuity in the periphery²³ found acuity to be much greater in the temporal field than the nasal field at eccentricities of 20° and 25°. In that study, a grating stimulus was used that introduces artifacts with spatial frequency content well below the nominal spatial frequency of the grating. A histologic study of human eyes²⁴ found similar densities of retinal ganglion cells at 21° nasal and temporal, consistent with our 21° data but not the resolution acuity data. A study of nasotemporal asymmetry in the near and far periphery²⁵ found no nasotemporal difference at 11° eccentricity for Gabor stimuli and for a flickering stimulus. These differences led us to question whether our findings of asymmetry for the nasotemporal spatial scale are unique to our stimulus and population.

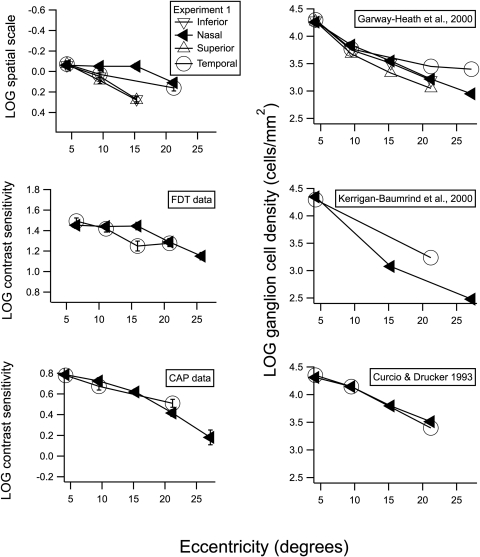
Previously collected FDT data from our population show very similar behavior along the nasal meridian (Fig. 4, middle left). At 15° eccentricity, contrast sensitivity for the nasal visual field was higher than for the temporal visual field. This trend was also apparent in the CAP data previously collected from our population (Fig. 4, bottom left). However the asymmetry between nasal and temporal sensitivity is not as prominent in the CAP data, and the small difference may not be significant. Overall, the decrease in contrast sensitivity with eccentricity was steeper for the CAP data, which we attribute to the different type of stimulus used.

Figure 4.

Spatial scale, contrast sensitivity, and ganglion cell density as a function of eccentricity in degrees of visual angle. (◀) Results for nasal visual field and temporal retina; (○) results for the temporal visual field and nasal retina. For our perimetric data in the graphs on the left, the size of the symbols was selected to represent approximately ±1 SEM. The top graphs include additional data on spatial scale and ganglion cells for superior visual field (inferior retina) and for the inferior visual field (superior retina). The graphs on the right show change in ganglion cell density with eccentricity for three human studies.^24,26,27

To determine whether this difference between the nasal and temporal fields was unique to our population, we compared our mean FDT and CAP sensitivities to the means in other studies. The normative database for FDT perimetry²⁸ shows the same asymmetry we found for our FDT data. Means for perimetric data from Heijl et al.²⁹ showed a pattern similar to that of our CAP data. The CAP critical diameters estimated by Pan and Swanson¹⁹ based on Latham et al.¹⁶ also appear to show a more shallow decrease in contrast sensitivity along the 165° (nasal) meridian out to approximately 15°. These similarities across studies indicate that the trend found in our data is not a characteristic solely of our population.

The spatial scale values in Figure 2 form a visual streak, as illustrated by an elliptical contour map for a two-dimensional parabola fit to the spatial scale values. The fact that these ellipses have longer horizontal axes than vertical axes is consistent with prior psychophysical studies and also with ganglion cell density maps. However, the ellipses are displaced nasally, whereas ganglion cell densities do not show a corresponding displacement. We suggest that cortical factors underlie this nasal displacement of the visual streak.

The asymmetrical spatial scaling along the meridians that we found in our data adds a new perspective to other researchers' interpretations of ganglion cell density findings. In several studies researchers have discussed correlations between ganglion cell density and contrast sensitivity,^16,25,30 and other studies have designed quantitative models that can predict ganglion cell density from perimetric sensitivity.^26,31,32 Although these studies showed that ganglion cell density and ganglion cell loss relate to perimetric sensitivity, we conclude that other factors in addition to ganglion cell density may be useful to consider. In the present study, we found a difference between spatial scale in the nasal and temporal visual field that cannot be readily explained by ganglion cell density. Declines in ganglion cell density with eccentricity for three human studies are shown in graphs on the right side of Figure 4.^24,26,27 Two datasets (upper and lower graphs) show nasal and temporal locations with similar densities from 4° to 15°, and two datasets (upper and middle graphs) show higher density for the temporal visual field beyond 20°.

The spatial scale values in Figure 4 are from data gathered by perimetric methods, which do not have the same control over observer criterion as conventional psychophysical methods, such as two-alternative, forced-choice testing. Therefore, changes in observer criterion with visual field location and/or stimulus spatial frequency could affect our results. However, the impact of subject criterion in healthy eyes is reduced by perimetric methods due to steep psychometric functions,³³ which provide good test–retest variability, despite the limited number of trials at each location required for perimetry. For example, perimetric studies in macaques, where control of criterion is more stringent than in humans, obtain results that are very consistent with human perimetric data.³¹ Perimetry is different from conventional psychophysical tasks in that sensitivities are assessed at many different locations in one testing session, yielding high uncertainty as to when and where the stimulus will occur. In subjects free of eye disease, psychometric functions for perimetry are relatively steep,³³ consistent with the expected effects of the subject's high level of uncertainty.³⁴ For these reasons, it seems unlikely that our results could be explained by systematic changes in observer criterion across visual field locations and stimulus spatial frequencies.

In conclusion, we performed perimetry with sinusoidal stimuli in control subjects free of eye disease, to help bridge the gap between perimetry and basic visual psychophysics. We derived a template for predicting contrast sensitivity for a two-octave range of spatial frequencies at any location in the central visual field, based on contrast sensitivity at that location for a single spatial frequency. We found an asymmetry in contrast sensitivity between the nasal and temporal visual field and conclude that there are factors in addition to ganglion cell density affecting perimetric contrast sensitivity. We suggest that methods for relating ganglion cell density to perimetric sensitivity may be improved by investigating these factors.