Volumetric Medical Image Coding: An Object-based, Lossy-to-lossless and Fully Scalable Approach

Abstract

In this article, an object-based, highly scalable, lossy-to-lossless 3D wavelet coding approach for volumetric medical image data (e.g., magnetic resonance (MR) and computed tomography (CT)) is proposed. The new method, called 3DOBHS-SPIHT, is based on the well-known set partitioning in the hierarchical trees (SPIHT) algorithm and supports both quality and resolution scalability. The 3D input data is grouped into groups of slices (GOS) and each GOS is encoded and decoded as a separate unit. The symmetric tree definition of the original 3DSPIHT is improved by introducing a new asymmetric tree structure. While preserving the compression efficiency, the new tree structure allows for a small size of each GOS, which not only reduces memory consumption during the encoding and decoding processes, but also facilitates more efficient random access to certain segments of slices. To achieve more compression efficiency, the algorithm only encodes the main object of interest in each 3D data set, which can have any arbitrary shape, and ignores the unnecessary background. The experimental results on some MR data sets show the good performance of the 3DOBHS-SPIHT algorithm for multi-resolution lossy-to-lossless coding. The compression efficiency, full scalability, and object-based features of the proposed approach, beside its lossy-to-lossless coding support, make it a very attractive candidate for volumetric medical image information archiving and transmission applications.

INTRODUCTION

Due to the rapid advances in digital imaging technology, medical images are nowadays almost taken/gathered in digital format. This not only facilitates an easy and efficient way of storage and transmission for clinical picture archiving and communication systems (CPACS), but also makes it possible to conduct a digital process on the image information, which is required in computer-aided diagnosis (CAD) schemes.

From the coding point of view the main features required for efficient medical image information archiving and a transmission system can be highlighted as follows:

Lossy-to-lossless coding: Medical image coding should support lossy-to-lossless coding functionality in order to enable the provision of appropriate services for different applications according to their sensitivity to the image quality in the diagnosis process. In lossless compression, the reconstructed image is exactly identical to the original image, while lossy compression aims to achieve a higher compression ratio by allowing some degradation in the image quality. As lossless compression does not degrade the image, it facilitates more accurate diagnosis, of course at the expense of lower compression ratios (i.e., higher bit rates). Discarding small image details that might be an indication of pathology could alter diagnosis, causing severe human and legal consequences. However, lossy compression is required to significantly reduce transmission and storage costs where the loss is not diagnostically significant. During the past years, many lossless and lossy compression techniques have been proposed for natural images, which resulted in several international standards such as: JPEG (for lossy image coding),[1] JPEG-LS (for lossless image coding),[2] and JPEG-2000 (the latest standard for lossy-to-lossless image coding).[3]

Object-based coding: Often there are regions inside a medical image that contain the main information relevant to medical diagnostic purposes. For an efficient CPACS system, an object-based coding is desirable to enable the coding of such regions, which can have any arbitrary shape, separately from the other parts of the image. This feature helps to achieve a very high compression ratio by focusing only on the important regions in the image and discarding the unimportant background that usually takes up a large area of the medical images, or by encoding the background at a lower precision with a lossy image coder.[4–7] The region-of-interest (ROI) coding feature in the JPEG-2000 standard considers the whole image for coding, but applies a higher coding precision to the ROI.[8,9] On the other hand, an object-based coding makes it possible to encode the region (with any shape, not only rectangular shape as is the case in most ROI coding techniques) as a separate object, regardless of the rest of the image.

Scalability: This feature refers to the potential in the coded bitstream that allows the decoder to usefully decode from only parts of the bitstream in order to meet a certain quality and/or a spatial resolution requirement. In this article, scalability is always seen in conjunction with embedded (progressive) coding. A scalable coded bitstream consists of a set of embedded parts that offer an increasingly better signal-to-noise ratio (SNR) (known as SNR scalability or quality scalability) or higher spatial resolution (referred to as spatial scalability).[10] A highly scalable coding approach that supports both SNR and spatial scalability is an important requirement for the efficient archiving of medical images. It enables the hierarchical search of a medical database from low resolution/quality images to high resolution/quality, images, which can effectively speed up the search for a specific image or a group of images, by discarding a considerable number of images at the early low resolution/quality search stages. For telemedicine applications, especially over heterogeneous networks such as the Internet, the scalability functionality enables a wide range of end-users with different processing and network access bandwidths, to be serviced from one embedded bitstream. Adding the scalability feature to an object-based coding enables the low performance end-users in a telemedicine network to receive the unimportant regions of medical images at low resolution and/or quality and to spend their coding budget on receiving the important regions at a high quality and resolution, which are crucial for correct diagnosis. Moreover, scalability supports a better error-protection mechanism. This is due to the fact that partitioning of the information into different parts makes it possible to provide better protection for the more important parts.

Volumetric medical images (e.g., MR and CT) are 3D data sets that consist of a sequence of 2D data slices. For efficient archiving and transmission of such vast amounts of data, a high degree of compression is required. A straightforward method is to apply a 2D coding scheme successively, to encode each slice independent from the other slices. Although this method is simple, it ignores the high correlation that generally exists between the consecutive slices. 3D coding approaches, on the other hand, try to exploit the interslice dependency to achieve a higher compression ratio. For this, contiguous slices are often organized in groups, and each group of slices (GOS) is encoded as a 3D data set. More details on this type of 3D coding will be given below.

Over the past decade, wavelet-based image compression schemes have become increasingly important and gained widespread acceptance. An example is the JPEG2000 still image compression standard.[3,11] Due to the multi-resolution signal representation offered by the wavelet transform, wavelet-based coding schemes have a great potential to support the scalability features. Among the state-of-the-art embedded wavelet coding approaches the Set Partitioning in Hierarchical Trees (SPIHT) algorithm[12] is well known, as a bench- mark for its compression efficiency, full SNR scalability support, and very low complexity. These features have made SPIHT very attractive for medical image coding as well.[4,13–14] As shown in,[4] an object-based version of SPIHT (OB-SPIHT) exhibits a very competitive peak signal-to-noise ratio (PSNR) performance for the compression of digital mammography. On the other hand, the research conducted by Pearlman[15] showed a very significant complexity reduction of SPIHT over JPEG2000.

Three-dimensional extensions of SPIHT have been reported in the literature for video coding[16–18] as well as for volumetric medical image compression.[13,14] Other 3D wavelet-based techniques for coding of volumetric medical data sets have also been reported in literature (e.g.,[19–21] ). The research conducted in[14] on lossless CT and MR coding, with an improved version of 3D SPIHT, showed that SPIHT is quite efficient, in comparison to other 2D and 3D coders, for lossless volumetric medical image coding.

The current literature on volumetric medical image coding is mainly focused on compression. The SPIHT bitstream is tailored for full SNR scalability, but it does not support spatial scalability. For an efficient medical image archiving and transmission system, however, a fully scalable coder is greatly required. Such a coder must provide a bitstream that can be parsed for multi-resolution decoding at different rates, by different clients, with different capabilities, and it must also provide other important features such as object-based access and coding.

This research proposes an object-based volumetric medical image coding system based on the highly scalable set partitioning in hierarchical trees (HS-SPIHT) algorithm. The HS-SPIHT, introduced by the authors in their previous studies,[22,23] is a modification of the SPIHT algorithm[12] that adds spatial scalability features to the SPIHT algorithm without sacrificing the interesting features of the original algorithm. The coding system proposed in this article, called 3DOBHS-SPIHT, extends the 2D HS-SPIHT algorithm to 3D and further modifies it for object-based coding. A new asymmetric tree structure for the 3D wavelet coefficients is introduced to allow a small size for the GOSs, for efficient random access to the slices in the decoding process. The 3DOBHS-SPIHT algorithm fulfills all of the highlighted requirements for medical image information, archiving, and transmission systems mentioned earlier in this section.

The rest of this article is organized as follows. First we explain the whole 3DOBHS-SPIHT coding system in four subsections. Then, simulations of the coding system are given in detail. After that we present some experimental results for multi-resolution lossy and lossless coding by the proposed coding system, and finally, we conclude the article.

3D OBJECT-BASED HS-SPIHT SYSTEM

In this section first an overview of the 3DOBHS-SPIHT coding system is given, then an asymmetric tree structure for the 3D coding is introduced, and subsequently the 3DOBHS-SPIHT coding algorithm is explained. Finally the scalable structure of the 3DOBHS-SPIHT bitstream is presented.

System Overview

The proposed 3DOBHS-SPIHT coding system is depicted in Figure 1. The system input is a volumetric medical image set that is divided into GOS. On the encoder side, the input GOS is first segmented in order to extract the medical object of interest from the background. Each voxel in the data set is considered either inside or outside the object. The GOS object is decomposed by a 3D shape-adaptive integer DWT (3DSA-IDWT) approach, which maps the integer object voxels to the integer wavelet coefficients. Details on the segmentation process and the DWT will be given in In the next section.

Figure 1.

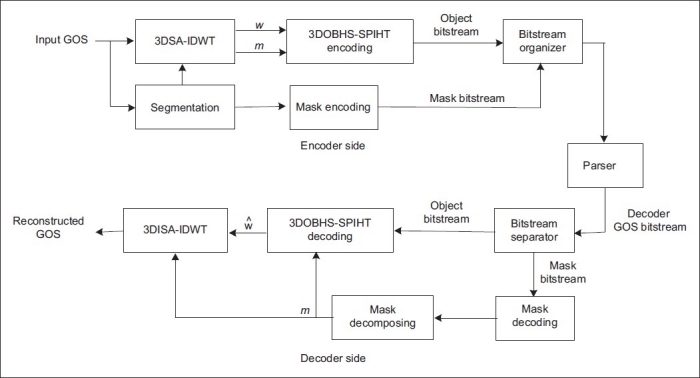
Block diagram of the 3DOBHS-SPIHT coding system; w denotes the wavelet coefficients and m the decomposed mask

The decomposed object coefficients, denoted as w, and the decomposed shape mask, denoted as m, are then consigned to the 3DOBHS-SPIHT encoder. The encoder only encodes the coefficients that belong to the decomposed object. To recognize these coefficients it uses the decomposed shape mask. The bitstreams from the shape coding and object coding algorithms are assembled in the bitstream organizer to generate the final encoder output bitstream for the GOS.

In a customization stage, the encoded bitstream is reordered and truncated by a parser, which provides proper bitstreams for multiscale lossy-to-lossless decoding. On the decoder side, the bitstream separator first extracts the mask and the object bitstreams from the parsed bitstream. The shape mask is then reconstructed by decoding the shape bitstream. The decomposed mask, which is required by the 3DOHS-SPIHT decoder, is provided by applying the same level of decomposition as that used by the encoder to the shape mask. The 3DOHS-SPIHT decoder then decodes the object bitstream, and the inverse 3DSA-IDWT is applied to the decoded wavelet coefficients to reconstruct the GOS object at the requested rate and resolution.

Asymmetric Tree Structure

Figure 2 depicts the parent-offspring relationship in a 2D tree of wavelet coefficients defined in the SPIHT algorithm. A straightforward symmetric extension of this 2D tree is used in[13] for lossless volumetric MR and CT image coding by a 3DSPIHT. Figure 3a shows the symmetric 3D extension of the 2D tree structure for the 3D wavelet packet decomposition of a GOS, after applying two levels of axial decomposition, followed by two levels of transaxial decomposition, resulting in 21 sub-bands. This 3D tree structure was introduced in[17] for 3DSPIHT video coding. In this structure the coefficients in the lowest transaxial-axial sub-band are grouped into 2×2×2 adjacent coefficients that are known as tree roots [Figure 3a]. Thus, it is always required to have an even number of slices (at least two) in the lowest axial band. On the other hand, in a 3D coding of volumetric medical images, in order to provide efficient random access to individual slices in a data set, for search and retrieval purposes, it is necessary to have the coding units (i.e., the GOS) as small as possible. A smaller GOS size is also favorable for the encoder, parser, and decoder, as it consumes less memory. Choosing a small GOS size, however, limits the number of axial wavelet decomposition levels, which has a negative impact on the compression gain. For example to be able to apply two levels of axial decomposition, the GOS size needs to be at least eight. To overcome this problem, we have modified the 3D parent-offspring relationship in the decomposed GOS and have introduced an asymmetric tree structure. Figure 3b shows the new asymmetric tree structure. In the lowest transaxial-axial sub-band, the coefficients, which are known as roots, are grouped into 2×2 elements rather than 2×2×2 elements. In each slice, the parent-offspring relationship is the same as defined in 2DSPIHT. The coefficients in the lowest transaxial sub-band (the roots of 2D trees in each slice) establish the tree structure in the axial direction as shown in Figure 4. Therefore, in each slice, each root has two offsprings in the next higher axial domain (except for the roots in the lowest axial band (t-L₂), which has one offspring in the t-H₂ band, and for the roots in the highest axial band (t-H₁), which are leaves and do not have any offspring in the axial direction) and four offsprings in the next transaxial band, in the same slice. Note that this is the same as for 2DSPIHT, where one coefficient in each 2×2 element, marked by * in Figure 2, has no transaxial offspring. The new tree structure is called asymmetric, because unlike the symmetric tree [Figure 3a], in which each coefficient has eight offsprings, the number of offsprings in the new tree structure is different and depends on the location of the parent coefficient in the decomposed GOS sub-bands. Algorithm 1 shows the details of the parent-offspring relationship for the new tree structure.

Figure 2.

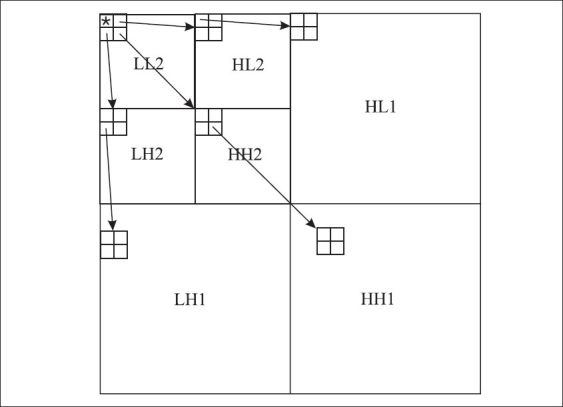
2D SPIHT parent-children dependency across wavelet sub-bands in each slice

Figure 3.

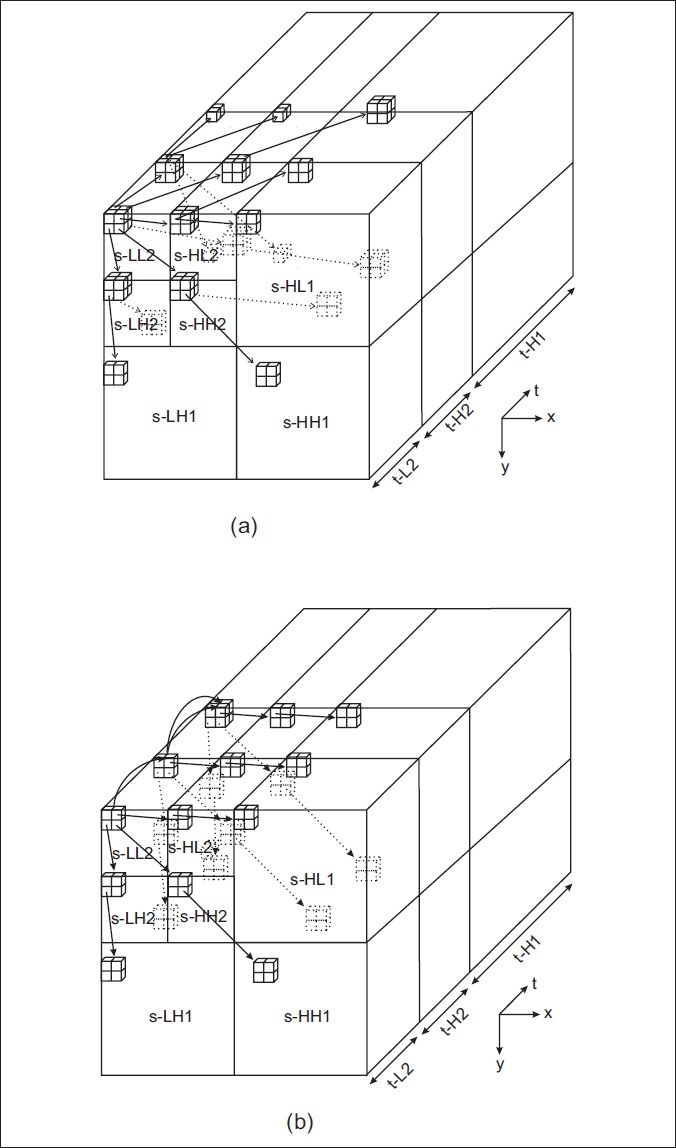
3D tree structures. (a) The structure used in 3D SPIHT[17] after two levels of wavelet packet decomposition of a GOS; (b) The asymmetric 3D tree structure used in the proposed algorithm in this article after two levels of wavelet packet decomposition of a GOS

Figure 4.

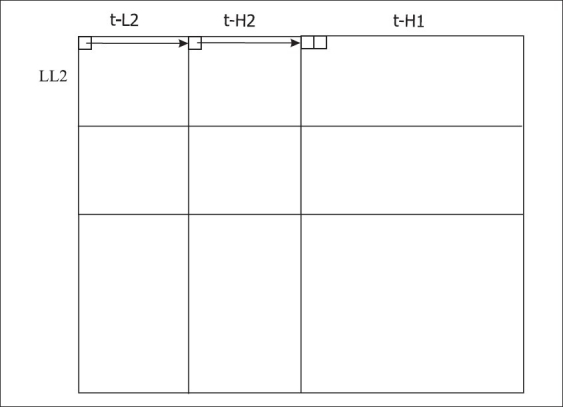
1D interslice dependency in a 3D wavelet decomposed GOS (only defined for the coefficients in the lowest spatial sub-band in each slice)

Algorithm 1: Parent-offspring relationship for the 3D asymmetric tree structure

• if (the coefficient is in the lowest transaxial sub-band)

• if (the coefficient is in the lowest axial sub-band) it has five offsprings (one in the next axial sub-band [Figure 4] and four in the next transaxial sub-band [Figure 2], except for the coefficient marked by *, which has only one offspring in the next axial sub-band.

• else, if (this coefficient is in the highest axial sub-band) it has four offsprings in the next transaxial sub-band [Figure 2], except for the coefficient marked by FNx01, which has no offspring.

• else, it has six offsprings (two in the next axial sub-band [Figure 4] and four in the next transaxial sub-band [Figure 2].

• else, if (the coefficient is in the highest transaxial sub-band) it has no offspring.

• else, it has four offspring in the next transaxial sub-band [Figure 2].

The 3D OBHS-SPIHT Algorithm

The 3DSPIHT algorithm of[17] considers sets of coefficients that are related through the parent-offspring dependency depicted in Figure 3a. In its bitplane coding process, the algorithm deals with the wavelet coefficients as either members of insignificant sets, individual insignificant pixels, or significant pixels. It sorts these coefficients into three ordered lists: the list of insignificant sets (LIS), the list of insignificant pixels (LIP), and the list of significant pixels (LSP). The main concept of the algorithm is managing these lists in order to efficiently extract insignificant sets in a hierarchical structure and identify significant coefficients, which is the core of its high compression performance. The 3DSPIHT algorithm provides a progressive (by quality) bitstream, which is fully SNR scalable, however, its bitstream does not support spatial scalability.

In[22,23] we proposed a scalable modification of 2DSPIHT for image coding, called highly scalable SPIHT (HS-SPIHT), through the introduction of multiple resolution-dependent lists and a resolution-dependent sorting pass.

In the present study, the HS-SPIHT algorithm is first extended to 3D (3DHS-SPIHT), to be able to use it for volumetric coding and then further improved to be object-based (3DOBHS-SPIHT) for coding of objects with any shape.

In a 3D (2D+1D) wavelet-decomposed GOS, the number of spatial resolution levels depends on the number of 2D spatial wavelet decomposition levels applied to the slices. In general, by applying Ns levels of a 2D wavelet transform to each slice, at most, the Ns+1 levels of different spatial resolution will be provided. We denote the lowest spatial resolution level as level Ns+1. The original sequence that has slices with the full spatial resolution is then known as level 1. The assigned spatial resolution to level k is 1/2^k-1 of the spatial resolution of the original data set. The three transaxial sub-bands (HL_k, LH_k, HH_k in all axial sub-bands) that need to be added to the spatial resolution Level k+1 to increase its resolution to Level k are grouped and called spatial sub-band set level k and referred to as B_k [Figure 5].

Figure 5.

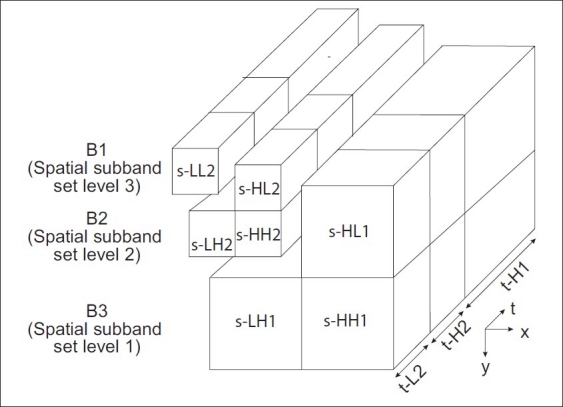
Different levels of spatial sub-band sets related to different spatial resolutions in a 3D wavelet packet decomposition

To provide full spatial scalability, the 3DOBHS-SPIHT algorithm encodes the different resolution sub-band sets separately, allowing a transcoder or a decoder to directly access the data needed for reconstruction of a desired spatial resolution and/or quality. To improve the algorithm to be used for coding of volumetric medical images, which contain 3D objects with arbitrary shape, we only consider and process those coefficients that belong to the decomposed object [Figure 6] and those sets that are at least partially located inside the decomposed object, similar to the SA-SPIHT algorithms in.[24,25]

Figure 6.

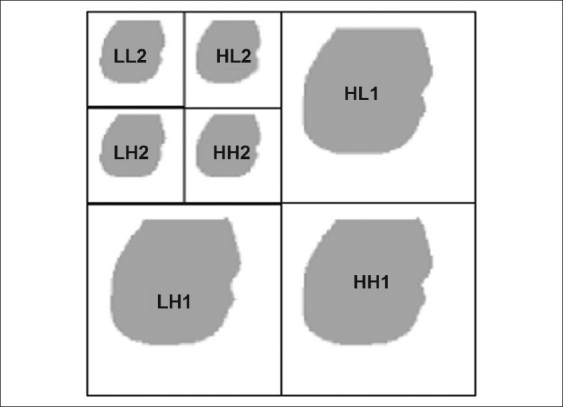
Example of a 2D decomposed mask of an arbitrarily shaped object

The 3DOBHS-SPIHT algorithm uses the asymmetric tree structure defined in the previous subsection.

To manage the scalable coding process, for each resolution sub-band set, the algorithm defines a set of LIV, LSV, and LIS, which refer to a list of insignificant voxels, list of significant voxels, and list of insignificant sets, respectively. Therefore there are LIV_k, LSV_k, and LIS_k for k=s_max, s_max-1,..., 1 where smax is the maximum number of spatial resolution levels supported by the encoder (s_max≤Ns+1). Similar to 3DSPIHT, 3DOBHS-SPIHT transmits bitplane by bitplane, but it uses multiple lists for handling different resolution levels, similar to.[22,26] In each bitplane, the 3DOBHS- SPIHT coder starts encoding from the maximum resolution level (s_max) and proceeds to the lowest level (level 1). During its resolution-dependent sorting pass for the lists that belong to level s, the algorithm first does the sorting for the coefficients in the LIV_s, in the same manner as 3DSPIHT, to find and output significance bits for all list entries, and then processes the LIS_s. In the LIS_s sorting pass, all entries of the list are processed in order. Sets that are at least partially located in the resolution level are tested for significance and those that completely fall outside the resolution level are moved to the LIS_s-1. Once a set is tested for significance, it stays in the LIS_s. If it is insignificant a ‘0’ is placed in the bitstream. If significant, a ‘1’ goes to the bitstream, and the set is partitioned into its offspring voxels and descendant subsets and will be removed from the LIS_s. The offspring voxels will be tested for significance and moved to the end of LIV_s if insignificant and LSV_s if significant. The new subsets will then be added to the end of LIS_s-1. After completing the sorting pass for LIV_s and LIS_s, the refinement pass will be done for all entries of LSV_s according to the current threshold. Then the threshold is lowered for the next bitplane coding stage and the procedure will be repeated. After the algorithm completes the sorting and the refinement passes to resolution level s it will repeat the same procedure for the next lower level until the full-resolution stage (level 1) is completed. The total number of bits belonging to a particular bitplane for 3DOBHS-SPIHT is the same as for 3DSPIHT, but 3DOBHS-SPIHT arranges them according to their spatial resolution dependency. Note that the total storage requirement for LIV_s, LSV_s, and LIS_s, for all resolutions, is the same as for LIS, LIP, and LSP used by the 3DSPIHT algorithm.

Bitstream Structure

Figure 7 shows the structure of the bitstream generated by the 3DOBHS-SPIHT encoder for a GOS. The GOS bitstream contains the mask and object bitstreams. The scalable object bitstream is constructed with different codeparts (Pⁿ), where each part belongs to a bitplane level. Inside each bitplane codepart, the bits belong to different spatial sub-band sets, P_kⁿ, separable. To support bitstream parsing, some markers are put into the bitstream, to provide the information required for identifying the different resolution and bitplane codeparts in the parsing process.

Figure 7.

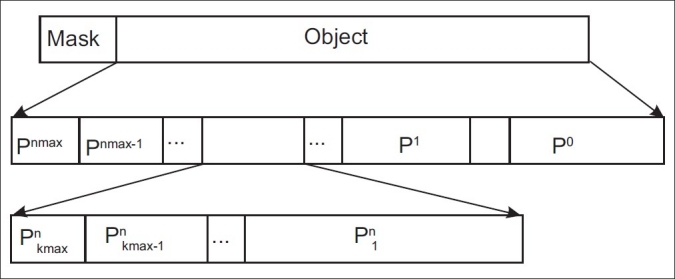
Structure of the 3DOBHS-SPIHT encoder bitstream for a GOS. Pⁿ_k is related to the codepart of spatial sub-band set level k (B_k) at bitplane level n

The encoder needs to encode the input 3D object only once at a lossless rate (covering all biplane coding levels from the maximum bitplane level to bitplane level 0). Different bitstreams for different spatial resolutions can be easily generated from the encoded bitstream by selecting the related resolution codeparts. For example, to provide a bitstream for resolution level r, in each bitplane codepart, only the resolution parts that belong to the spatial resolution levels greater or equal to r are kept, and all other parts are removed. The parsing process is a simple reordering of the original bitstream codepart and can be carried out by a server that stores the encoded medical data sets or by an individual parser as a part of an active network. The parser does not need to decode any part of the bitstream. As a distinct feature, the reordered bitstreams for each spatial resolution are completely rate-embedded (fine granular at the bit level) and can be truncated at any point up to the level of a perfect lossless reconstruction. Note that the markers in the main bitstream are only used by the parser and do not need to be sent to the decoder.

The decoder required for decoding the reordered bitstreams follows the encoder exactly, similar to the original SPIHT algorithm. It needs to keep track of the various lists only for spatial resolution levels greater or equal to the required one. Thus, the proposed algorithm naturally provides computational scalability as well.

SIMULATION DETAILS

As volumetric medical data we have chosen the four gray-scale (eight bits per voxel) MR data sets that were also used in.[13,14,27] These data sets are available online for downloading at.[28] A description of the MR sets is given in Table 1. In each slice, to extract objects from the unimportant, very low magnitude background voxels and a two-stage threshold-based segmentation scheme were applied. In the first stage, each MR set was compared with a threshold and all voxels that exceeded the threshold were considered to belong to the object. In the second stage, all the background areas that were surrounded by the object were reclassified to belong to the object. Similarly, small object regions not connected with the main object were removed and classified as the background. The threshold chosen was small enough to make sure that the extracted region in each slice completely covered the true object. Note that the main contribution of this article does not include object segmentation and the segmentation process mentioned here is only to have a rough mask, which covers the whole area of the object (to make sure that the main object is completely inside the mask) to enable us to provide results for object-based coding cases and show this functionality of the proposed coding algorithm. The first slices of the MR test sets and their appropriate segmentation masks are shown in Figures 8 and 9, respectively.

Table 1.

Description of the MR data sets used as test volumetric medical images in this article

Figure 8.

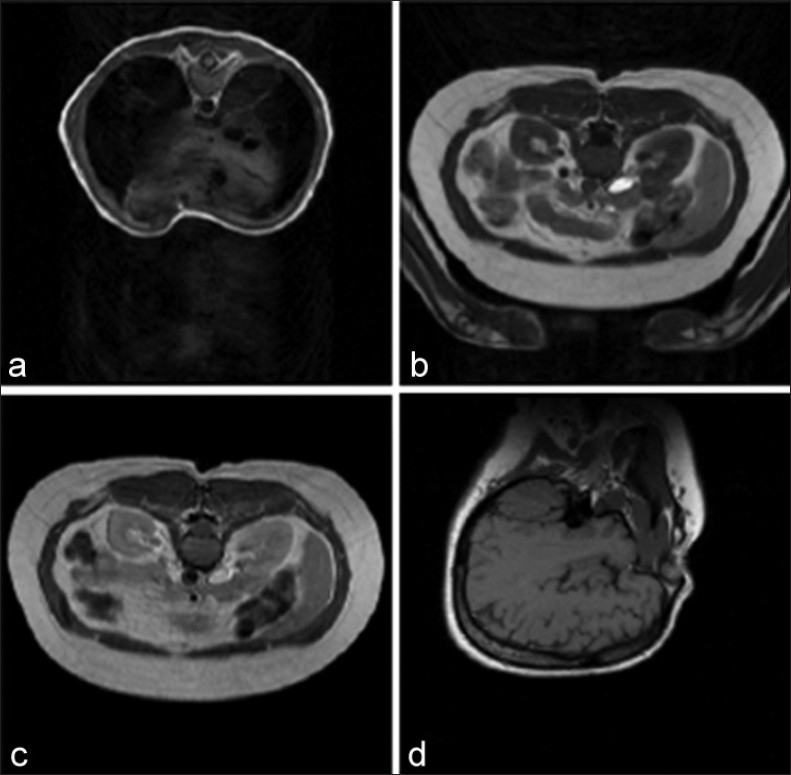
The first slice of each volumetric MR data set. (a) MR ped chest; (b) MR liver t1; (c) MR liver t2e1; (d) MR sag head

Figure 9.

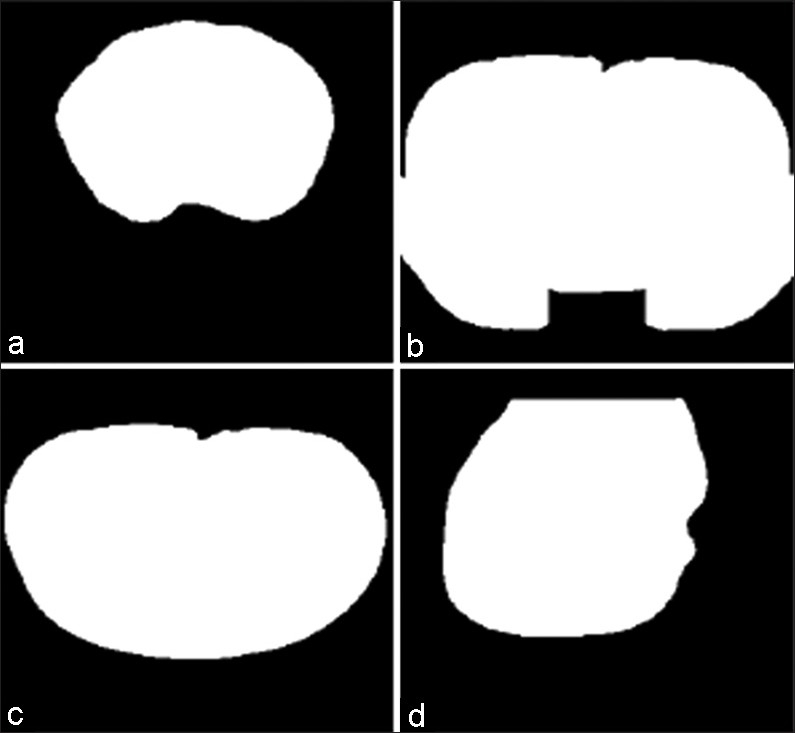
Segmentation masks for the first slice of each volumetric MR data set. (a) MR ped chest; (b) MR liver t1; (c) MR liver t2e1; (d) MR sag head

For object-based wavelet decomposition, an efficient, non-expansive SA-DWT approach, based on the method introduced in[29] was implemented. The GOS size was set to 4. Note that, as mentioned before, a small GOS size is favorable for easy and fast random access to certain slices in the data set bitstream. Two levels of 1D decomposition in the axial domain were first applied to the input GOS followed by three levels of 2D decomposition in the transaxial (spatial) domain. The integer I(2,2) wavelet filter bank[30] was implemented in a lifting scheme and used for both axial and transaxial decompositions, with symmetric extension at the boundaries of the GOS object.

For lossy decoding, the wavelet transform should be unitary or near-unitary, so that the distortion in the transform domain can be directly related to the distortion in the voxel domain.

As the reversible integer transform was not unitary, the 2D sub-band weighting scheme used in[31] was extended to 3D, and applied, to make the transform approximately unitary.

The 3DOBHS-SPIHT encoder was set to progressively encode the decomposed objects of all GOSs, of each MR test set, to the lossless stage (i.e., coding from the maximum required bitplane to bitplane zero), with three levels of spatial scalability support. As the last GOS of each MR data set contains less than four slices, some blank slices were added to the end in order to fix the GOS size to four. The flexibility of the 3D coding of data sets with any number of slices is provided by the object-based functionality of both the transform and the coding process. The binary GOS mask information was encoded by an arithmetic binary coding scheme.[32]

After encoding, the 3DOBHS-SPIHT bitstream was fed into a parser to produce progressive (by quality) bitstreams for multi-resolution lossy-to-lossless decoding. Reference slices for the lower spatial resolutions were defined by taking the lowest resolution sub-band after applying appropriate levels of 2D SA-IDWT to the slices. In the original GOS, and the fidelity was measured by the PSNR defined as

PSNR=10log10(PEAK²/MSE) dB      (1)

where MSE is the mean squared error between the original reference and the reconstructed data, and PEAK is the maximum possible magnitude for a voxel, which is 255 for the MR test sets. The bit rates (bits per voxel) for all resolutions were calculated according to the total number of voxels in the original full resolution GOS.

RESULTS AND DISCUSSION

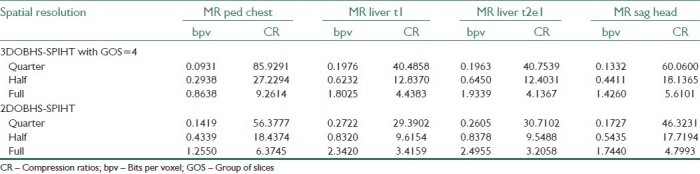
Table 2 provides the average bits per voxel (bpv) and compression ratios (CR) obtained by 3DOBHS-SPIHT for multi-resolution lossless coding of the four MR object sets. For comparison, results of the same cases obtained by a 2DOBHS-SPIHT coding approach, which encodes each slice separately, are also provided in this table. For all the three spatial resolutions (quarter, half, and full) specified in Table 2, the 3DOBHS-SPIHT method significantly outperforms the 2DOBHS-SPIHT method. As the results show for both methods, a lossless version of the lower resolutions can be obtained at very small rates. Note that the rate consumed for coding of the binary mask information of the MR sets was between 0.011 bpv and 0.014 bpv, and therefore ignorable, compared to the rate spent for coding of the object texture.

Table 2.

Average bits per voxel and compression ratios obtained for lossless encoding of the MR data sets

In Table 3, the 3DOBHS-SPIHT results for lossless coding at full resolution are compared with some other coding approaches.

Table 3.

Comparison results for average bits per voxel and compression ratios obtained for lossless encoding of the MR data sets at full resolution with different coding methods

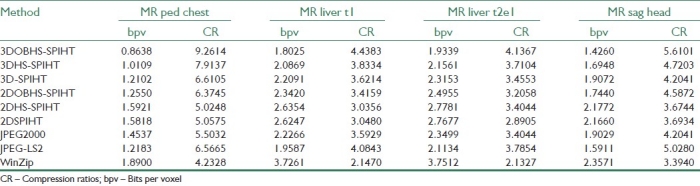
For the 3DHS-SPIHT, 3D-SPIHT, 2DHS-SPIHT, 2DSPIHT, JPEG2000, JPEG-LS, and WinZip cases, which are not object-based, the object background in all slices was set to zero before encoding. This results in better compression efficiency, and therefore, it is a fair comparison with object-based coding cases (i.e., 2DOBHS-SPIHT and 3DOBHS-SPIHT). A very small difference between the lossless compression rates of 2DHS-SPIHT and 2DSPIHT is due to the extra budget consumed by 2DHS-SPIHT for the markers put into the bitstream, which are required for the parsing process. The 3DHS-SPIHT approach is a 3D extension of the 2DHS-SPIHT approach and uses the asymmetric tree structure, but unlike 3DOBHS-SPIHT, does not support the object-based coding functionality. To show the efficiency of the asymmetric tree structure, results for 3D-SPIHT, which use the symmetric tree structure, are also provided in this table.

The results show a better performance for 3DHS-SPIHT than 3D-SPIHT. Among the 2D coding algorithms in Table 3, JPEG-LS, which is especially tailored for lossless coding, shows a slightly better compression efficiency than 2DOB-SPIHT, however, it does not support the spatial scalability feature. The proposed 3DOBHS-SPIHT algorithm shows a significantly better performance than all other coding approaches in the table. To show the effect of GOS size on the 3DOBHS-SPIHT coding performance, Table 4 provides the lossless coding results at a full spatial resolution for three different GOS sizes. As expected, by increasing the GOS size, the coding performance was increased.

Table 4.

Results obtained for lossless encoding of the MR data sets at full resolution with different GOS sizes by 3DOBHS-SPIHT

It should be mentioned that all results reported here for SPIHT and HS-SPIHT, for both object-based and non-object-based, the 2D and 3D coding cases were obtained without extra arithmetic coding of the encoder output bitstreams. As shown in,[12] an improved coding performance for SPIHT and consequently for HS-SPIHT can be achieved by further compressing the binary bitstreams with an arithmetic coder.

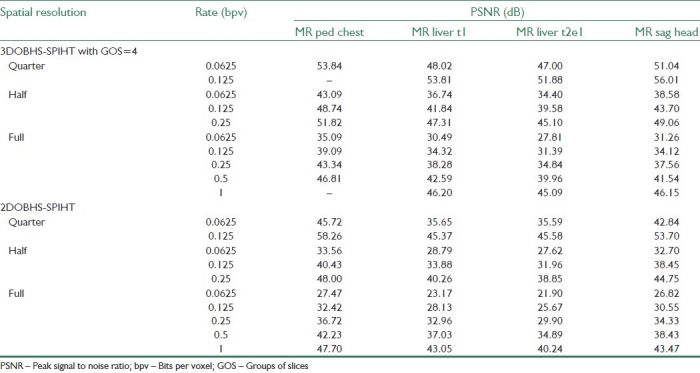
To show the full scalability of 3DOBHS-SPIHT, Table 5 presents some numerical results for multi-resolution decoding of the MR test sets at a wide range of bit rates. This is based on a scenario of one-time-encoding and multiple-times-decoding, and by parsing the encoder bitstream for various resolutions and rates. The parsed bitstream was decoded by the 3DOBHS-SPIHT decoder and the fidelity was measured by the PSNR. For comparison purposes, the results for the same resolutions and rates obtained from the 2DOB-SPIHT algorithm are also provided in the table. As the results clearly show, the 3D coding significantly outperforms the 2D coding for all resolutions and rates. For all resolutions, as the rate decreases, the difference between the 3D and 2D PSNRs increases. Thus, the 3D case benefits more from the better compaction of the GOS energy in the lower wavelet sub-bands provided by the 3D wavelet decomposition.

Table 5.

PSNR results for lossy decoding of the lossless bitstreams at different spatial resolutions and rates

To give a visual impression, slice 9 of the MR sag head data set was decoded at three different spatial resolutions (full, half, and quarter).

Figure 10 shows the original slice 9. Figures 11 and 12 give visual results for scalable decoding, reconstructed by the 3DOBHS-SPIHT and 2DOBHS-SPIHT decoders at 0.05 bpv, 0.1 bpv, and 0.2 bpv, respectively. As one can see, 3D-OBHS-SPIHT not only has a higher PSNR, but also a much better visual quality than 2DOBHS-SPIHT. The same holds for all other scalable decoders mentioned earlier.

Figure 10.

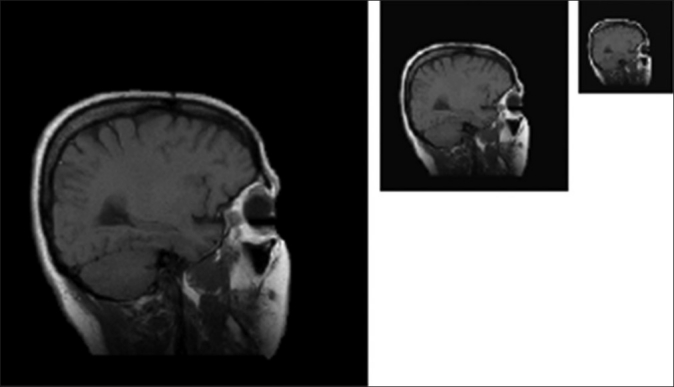
Original slice 9 of MR sag head at full, half, and quarter resolution

Figure 11.

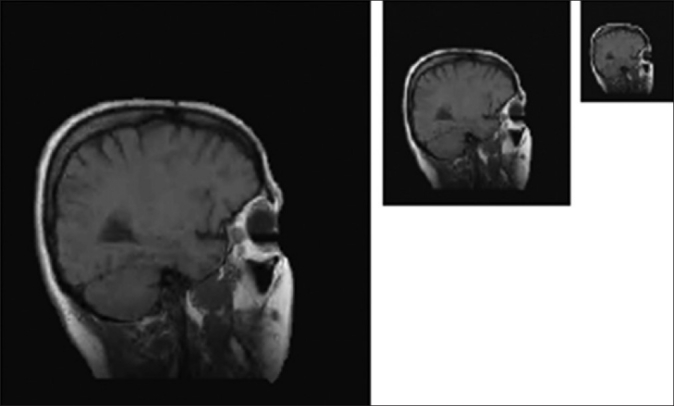
Scalable lossy reconstruction of slice 9 of MR sag head by 3DOBHS-SPIHT. Left: full resolution, bpv=0.2, PSNR=36.63dB. Middle: half resolution, bpv=0.1, PSNR=41.37dB. Right: quarter resolution, bpv=0.05, PSNR=48.76dB

Figure 12.

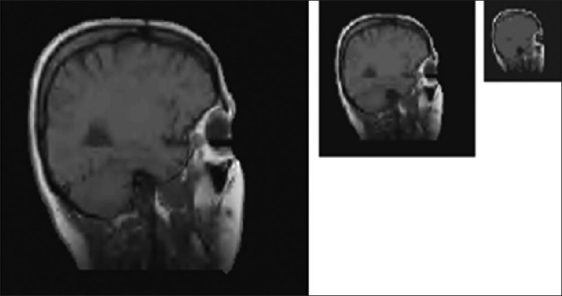
Scalable lossy reconstruction of slice 9 of MR sag head by 2DOBHS-SPIHT. Left: full resolution, bpv=0.2, PSNR=33.33dB. Middle: half resolution, bpv=0.1, PSNR=35.90dB. Right: quarter resolution, bpv=0.05, PSNR=37.07dB

CONCLUSIONS

An object-based, highly scalable 3D wavelet coding system, 3DOBHS-SPIHT, for lossy-to-lossless coding of volumetric medical images was presented. The 3D medical data set was first organized in groups of slices (GOS) and the objects of interest were segmented from the background in each slice. A 3D (1D axial+2D transaxial) reversible shape-adaptive integer DWT was used to decompose the input GOS. The 3DSPIHT algorithm was modified to support spatial scalability. The symmetric tree definition of the original 3DSPIHT algorithm was improved to an asymmetric structure, which allowed small GOS sizes, which not only facilitated more efficient random access to the slices, but also required less memory from the coding system. The 3DOBHS-SPIHT bitstream was fully scalable and easily re-orderable by a simple parser for multi-resolution decoding at lossy-to-lossless rates. For the parsing process, the parser did not need to decode the main bitstream. The experimental results on some MR data sets provided for both lossy and lossless coding, at various spatial resolution levels, showed excellent performance of the proposed 3DOBHS-SPIHT algorithm. Even at the lossless stage, the proposed coder significantly outperformed other known non-scalable coders. Possessing important features, such as, arbitrarily shaped object coding, resolution scalability functionality, and progressive lossy-to-lossless coding made the proposed approach attractive for volumetric medical image information archiving and transmission systems.

BIOGRAPHIES

Habibiollah Danyali received the B.Sc. and M.Sc. degrees in Electrical Engineering respectively from the Isfahan University of Technology, Isfahan, Iran, in 1991 and the Tarbiat Modarres University, Tehran, Iran, in 1993. From 1994 to 2000, he was with the Department of Electrical Engineering, University of Kurdistan, Sanandaj, Iran, as a lecturer. In 2004, he received his PhD degree in Computer Engineering from the University of Wollongong, Australia. After finishing his PhD, he continued his academic work with University of Kurdistan as an assistant professor. As of September 2009, he is with the Department of Telecommunication Engineering, Shiraz University of Technology, Shiraz, Iran. He is a Member of the IEEE. His research interests include data hiding, scalable image and video coding, medical image processing and biometrics.

Alfred Mertins received the Dipl.-Ing. degree in Electrical Engineering from the University of Paderborn, Germany, in 1984, the Dr.-Ing. degree in Electrical Engineering and the Dr.-Ing. habil. degree in Telecommunications from the Hamburg University of Technology, Germany, in 1991 and 1994, respectively. From 1986 to 1991, he was with the Hamburg University of Technology, Germany, from 1991 to 1995 with the Microelectronics Applications Center Hamburg, Germany, from 1996 to 1997 with the University of Kiel, Germany, from 1997 to 1998 with the University of Western Australia, and from 1998 to 2003 with the University of Wollongong, Australia. From April 2003 to October 2006, he was with the University of Oldenburg, Germany. In November 2006 he joined the University of Lübeck, Germany, as a Professor of Computer Science and director of the Institute for Signal Processing. He is a Senior Member of the IEEE. His research interests include speech, audio, image and video processing, wavelets and filter banks, and digital communications