Predicting protein flexibility through the prediction of local structures

Abstract

Protein structures are valuable tools for understanding protein function. However, protein dynamics is also considered a key element in protein function. Therefore, in addition to structural analysis, fully understanding protein function at the molecular level now requires accounting for flexibility. However, experimental techniques that produce both types of information simultaneously are still limited. Prediction approaches are useful alternative tools for obtaining otherwise unavailable data.

It has been shown that protein structure can be described by a limited set of recurring local structures. In this context, we previously established a library composed of 120 overlapping long structural prototypes (LSPs) representing fragments of 11 residues in length and covering all known local protein structures. Based on the close sequence-structure relationship observed in LSPs, we developed a novel prediction method that proposes structural candidates in terms of LSPs along a given sequence. The prediction accuracy rate was high given the number of structural classes. In this study, we utilise this methodology to predict protein flexibility. We first examine flexibility according two different descriptors, the B-factor and root mean square fluctuations from molecular dynamics simulations. We then show the relevance of using both descriptors together. We define three flexibility classes and propose a method based on the LSP prediction method for predicting flexibility along the sequence. The prediction rate reaches 49.6%. This method competes rather efficiently with the most recent, cutting-edge methods based on true flexibility data learning with sophisticated algorithms, Accordingly, flexibility information should be taken into account in structural prediction assessments.

Introduction

Knowledge on protein 3D structures is essential for better understanding protein functions. In the case of enzymes, determination of 3D structures has helped elucidate why residues far apart in the sequence are involved in a given catalytic reaction. When proteins are implicated in disease mechanisms, structures of targeted proteins are especially useful for designing new drugs. Drug design has become extremely challenging due to the necessity for high-throughput screening of new target proteins and to the emergence of drug resistance ^1–3. Although essential, structural information does not suffice to fully understand protein function. Protein function is frequently associated with conformational changes that can cover a large range of amplitude scales. Protein dynamics has proved to be at the heart of catalysis processes as it is involved in the regulation of turnover rates, in ligand/target recognition and binding and in product release. Protein dynamics are strongly implicated in allosteric regulation ^4–6 and more generally in molecular recognition processes ^7–9 and protein stability. Conformational changes are also the basis of misfolding and aggregation, both of which are responsible for neurodegenerative disorders ¹⁰. Therefore, information on protein flexibility is as crucial as protein structure to elucidate protein function and to enhance drug design ^{6, 7}.

Regarding the importance of protein dynamics for elucidating protein function, an interesting hypothesis has been proposed ⁴ whereby it is postulated that protein evolution has led to the potential for multiple conformations —critical for function — rather than a single, optimal folded state. Therefore, understanding relationships between structure, energy landscapes, dynamics and function is now a major challenge. Consequently, the classic paradigm of the sequence-structure-function relationship is now considered as an oversimplified view and dynamics should be included in a new paradigm of protein function that entails the sequence-structure-dynamics-function relationship.

Moreover, the recent discovery of the importance of intrinsically disordered proteins in the last decade has strongly reinforced interest in studying protein flexibility ¹¹. These proteins are mostly associated with essential biological functions such as regulation and signalling ^{9, 12}. However, the term “disorder” hides a wide variety of processes. It can involve random coil, associated with rapidly interchanging conformations, as well as molten globules, showing highly ordered secondary structures but without stabilisation by tertiary contacts ¹³. Hence, the extent of disorder can be extremely variable, involving short or long unfolded regions or the entire protein. Interestingly, intrinsic disorder and flexibility seem to be differentially encoded in the primary sequence ^{14, 15}.

In comparison to the extensive and challenging studies on disorder, very few approaches have been truly dedicated to the analysis and prediction of flexibility of ordered proteins, ^{9, 16}, apart important works that rely on 3D structures for predicting dynamics (for a review see ref. 17 and 18) Accordingly, tools for predicting the flexibility properties from sequence of ordered proteins would be a tremendous improvement¹⁹. As for the disorder concept, flexibility encompasses many different features. Different flexibility properties can be observed depending on observation timescale ⁶. Moreover, depending on the type of motion and the extent of the region involved, two main classes of flexibility can be distinguished. The first one is related to local motions involving few residues. This kind of flexibility restricted mainly to the residue scale, is related to the capacity of a local structure (a small set of atoms) to deform or to change conformation.. In this case, the concept of “deformability” can be introduced. The second class involves motions of longer fragments and long-range conformational changes, such as loop motions and even domain motions. In this case, the motions of different residues in a sequence are highly inter-correlated. This observation has led to the emergence of the concept of mobility ²⁰. Mobility and deformability are complementary but not necessarily associated, e.g., hinge regions can undergo local conformational modifications without fluctuating, whereas regions undergoing rigid-body movements can present large-amplitude fluctuations without becoming deformed.

Flexibility prediction methods generally define flexibility through α-carbon B-factor values obtained from X-ray experiments. These so-called “temperature” factors reflect atom mobility due to thermal vibration and static disorder. Furthermore, correlation between B-factors and disorder predictor outputs has recently been explored ²¹. Most flexibility prediction methods, developed so far and based on sequence information alone, exploit evolutionary information, predicted secondary structures and/or accessibility ²² coupled with elaborate regression methods such as logistic regression ¹⁴, support vector regression (SVR) ^{23, 24}, or neural networks ²⁵. Other methods, such as the CamP method, use alternative descriptors of flexibility such as protection factor values obtained by equilibrium hydrogen exchange experiments ²⁶. These descriptors seem to explore larger amplitude fluctuations than B-factors. The Wiggle series approach focuses on functional large-scale fluctuations extracted from Gaussian network modelling ²⁷. A few methods which focus on the deformability concept are also available. FlexRP ²⁸ is based on the analysis of multiple experimental structures in the Protein Data Bank (PDB, ²⁹). Based on a novel sequence representation and feature selection coupled to machine learning, the FlexRP method predicts flexible/non-flexible regions. Finally, the continuum secondary structure prediction method ³⁰ is based on DSSPcont ³¹ and predicts regions undergoing conformational modifications as observed in the comprehensive Database of Macromolecular Movements (MolMovDB) ³².

These studies all show that flexibility is closely related to structural properties that, in turn, depend on sequence. This relationship may influence the success of structural prediction, i.e., some predicted conformations considered as incorrect, may actually reflect the structural flexibility through alternative conformational states. In the present study, we explore this hypothesis and propose a novel and simple approach to predict flexibility. We take advantage of the method we previously elaborated to predict local protein structures. We have described global protein structures using a limited set of recurring local structures ^33–36: a library of 120 overlapping representative fragments of 11 amino acids in length named long structural prototypes (LSP) is now available (see supplementary data I). These LSPs encompass all known local protein structures and ensure good quality 3D local approximation ³⁷. The length of representative fragments makes it possible to account for long-range interactions and correlations. Using the sequence-structure relationships deduced from this library, prediction methods in terms of LSPs can now be elaborated ^{37, 38}. The prediction method is based on evolutionary information coupled with an efficient learning method called support vector machines (SVM). This method provides a list of five possible structural candidates for a target sequence. The prediction rate reaches 63.1%, a rather high value given the high number of structural classes. Finally, the index that we developed can evaluate the structural “predictability” of a sequence, a property that may be related to “structural plasticity” ³⁸.

In the present paper, we first analyse the flexibility of fragments in representative datasets. We examine protein flexibility using two different approaches, X-ray experiments and in silico simulations. Different in silico strategies can be envisaged. For instance, normal mode analysis could be chosen, in particular using elastic network model (ENM) or GNM. Motions described by ENM or GNM low-frequencies modes are generally highly collective, i.e. a large set of atoms moves concertedly. These motions are much more related to mobility rather than flexibility. Alternatively, molecular dynamics (MD) simulations performed in a realistic environment have been shown to be well adapted for depicting protein dynamics and for describing deformation of local regions³⁹, i.e. deformability, generally associated with high(er) frequency modes of motions. Consequently, results of MD simulations were used in the present rather than normal mode analysis because the present study focuses on more local conformational changes.

We consider two descriptors for quantifying protein dynamics. The first one is the most commonly used descriptor, X-ray B-factors ^{10, 25, 39, 40} and the second one, frequently used in MD, is the root mean square fluctuation (RMSF) that measures the amplitude of atom motions during simulation. We then combine both descriptors to define flexibility classes and examine the flexibility classes of LSPs. Finally we evaluate the usefulness of using local structure prediction for deciphering the putative flexible zones of a structure from its sequence. This method turns out to be rather efficient compared to the most commonly used ones, based on the true learning of flexibility with sophisticated strategies. We also propose a confidence index for predicting the quality of the flexibility prediction rate.

Materials and Methods

Protein structure datasets

A dataset of 172 X-ray high-resolution (≤ 1.5 Å) globular protein structures was extracted from the Protein Data Bank (PDB) using the PDB-REPREDB database web service ⁴¹. In this dataset, the proteins shared less than 10% sequence identity and differed by at least 10 Å Cα root mean square deviation (Cα RMSD). A second filter was applied: selected protein structures were 70 to 200 residues long (as in ³⁰), composed of a single domain and were not involved in a protein complex, and did not have extensive number of contacts with ligands. A final dataset of 43 protein structures was obtained. The structures included in this dataset covered the distribution of known folds described by the SCOP classification: 5 all-α, 10 all-β, 6 α/β and 22 α+β proteins ⁴². Moreover, the secondary structures contained in the dataset according to the DSSP method was representative of known protein structures⁴³: 35.1 % of residues were in α-helix, 27.4% in β-strand, 19.7% in turn and 17.8% in coil. In a larger, non-redundant databank composed of 1421 X-ray structures with resolution higher than 1.5 Å, sequence identity smaller than 30% and Cα RMSDs larger than 10 Å (selected using PDB-REPRDB), the distribution of secondary structures was 37.8, 21.4, 20.9 and 19.9%, respectively.

Protein structures in the dataset were then analysed in terms of overlapping fragments of 11 residues long. Each fragment was assigned to one of the 120 long structure prototypes (LSPs) according to our previous definition ³⁷ (see supplementary data I). The assignment was based on a minimal Cα RMSD criterion between the fragment under consideration and the representative LSP. In other words, it consisted in computing Cα RMSDs between each protein fragment and each of the 120 prototypes. The LSP assigned to the fragment corresponded to the LSP with the lowest RMSD..

For validation purposes, we considered a second, independent and larger dataset (hereafter called the ‘Validation set’), and previously defined as Set 3 in ref. 37, 38). This set was composed of 259 protein structures with resolution higher than 2 Å, pairwise sequence identity lower than 30%, Cα RMSDs higher than 10 Å. The set included 64,229 fragments, also assigned to LSPs.

Extraction of experimental B-factors

We extracted Cα B-factors from the PDB files of the protein structures dataset. For purposes of comparison, the raw values were normalized for each protein using the method in ref. 40. After removing outliers detected statistically with a median-based approach, the normalized B-factors were calculated as B-factor_Norm = (B-factor_Raw−μ)/σ where μ and σ stand for the mean and the standard deviation of the Cα B-factor, respectively. Flexibility of each 11-residue long, overlapping fragment in the dataset was characterised by the B-factor_Norm associated with its central Cα.

Molecular dynamics simulations

Molecular dynamics (MD) simulations were performed for all protein structures with GROMACS 3.3.1 software ⁴⁴, using GROMOS96 43A1 force field ⁴⁵ and simple point charge (SPC) explicit water model ⁴⁶. Each protein structure was immersed in a periodic water box neutralised with Na⁺ or Cl⁻ counter ions. The system was then energy-minimised with a steepest-descent algorithm for 1000 steps. The MD simulations were performed in isotherm-isobar thermodynamics ensemble, with temperature and pressure kept fixed at 300 K and 1 bar, respectively using the Berendsen algorithm ⁴⁷. The coupling time constants were τ_T=0.1 ps and τ_P=0.5 ps for temperature and pressure, respectively. Bond lengths were constrained with LINCS ⁴⁸, which allowed an integration step of 2 fs, The generalized reaction field algorithm ⁴⁹ was used for long-range electrostatic interactions using a dielectric constant of 54 and a cut-off of 1.4 nm for non-bonded interactions. For each system, a short MD simulation (100 ps) in which protein atom positions were constrained but water molecules and ions were free was first performed, then the system was fully relaxed for 5 ns. Structures were recorded every 1 ps during this unrestrained phase. The analyses were conducted on the production phase, i.e., the phase beginning when the Cα RMSD reached a plateau with respect to the starting structure. For each protein, we checked that the secondary structures were generally conserved and that the snapshots not too far from the initial structure (Cα RMSD < 3 Å). Based on these criteria, we discarded three protein structures. Finally, 40 proteins cumulating nearly 150 ns, were further analysed. This set corresponds to 4,942 fragments of 11 residues in length.

Simulations were extended to 10 more nanoseconds for 37 proteins. The starting conformation and the starting velocities corresponded to the final conformation and final velocities of the 5-ns simulation detailed above. However, the forces having not been kept, the 10ns-simulations cannot be considered as a simple continuation of the 5 ns ones. Consequently, these simulations allowed evaluating the effect of the simulation duration and sampling a slightly different conformational space.

Flexibility measurements from MD simulations

Cα root mean square fluctuation (Cα RMSF) was calculated using GROMACS tools ⁴⁴ after superimposing snapshot structures on the initial conformation. Cα RMSF gives the mean amplitude of each Cα movement compared to a mean reference position: ${\mathit{RMSF}}_{\mathit{Norm}}^i=\sqrt{\frac{1}{T}{\displaystyle \sum _{t-0}^T}{({\stackrel{\text{r}}{R}}_t^i-{\stackrel{\text{r}}{R}}_{\mathit{ave}}^i)}^2}$ where T is the production time expressed in snapshot number, ${\stackrel{\text{r}}{R}}_t^i$ the coordinates of Cα atom i of structure at time t and ${\stackrel{\text{r}}{R}}_{\mathit{ave}}^i$, average coordinates of Cα atom i over production time. Raw RMSF values were normalized for each protein. The RMSF_Norm associated with the central Cα of each 11-residue fragment characterised the flexibility using MD.

Three flexibility classes from two descriptors of protein dynamics

Both experimental B-factor_Norm and RMSF_Norm values were used to analyse protein flexibility. We chose to define three flexibility classes (see Figure 1). Consequently, two threshold pairs were required to separate the three classes. The first threshold pair (τ_B1, τ_F1) separated rigid residues from intermediate residues and the second threshold pair (τ_B2, τ_F2) separated intermediate residues from flexible residues (τ_B and τ_F refer to B-factor_Norm and RMSF_Norm thresholds, respectively). The three classes thus defined were indexed 1, 2 and 3 from the most rigid to the most flexible.

Figure 1. Normalised B-factor values according to normalized RMSF values as determined from molecular dynamics simulations.

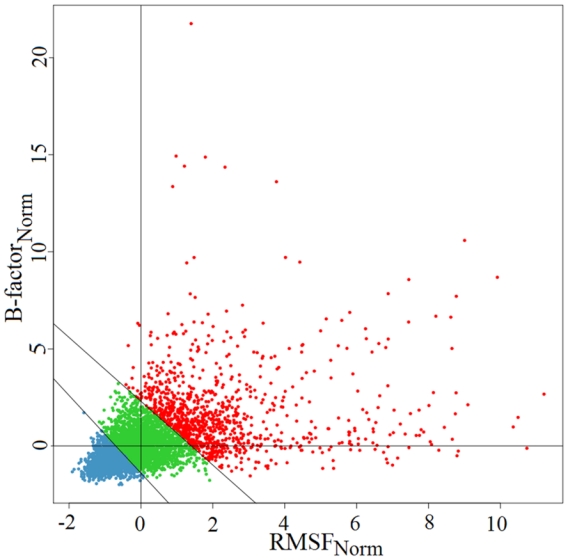
The two diagonal lines delimit the three flexibility classes defined by the quadruplet (τ_B1, τ_F1, τ_B2, τ_F2) = (−1.5, −0.5, 2.2, 1.1)

Each Cα of the dataset was then assigned to classified in one of the three flexibility classes according to its observed B-factor_Norm and RMSF_Norm values. Hence, each 11-residue long fragment was assigned to the flexibility class of its central residue. These assigned classes are referred to as the observed flexibility classes of fragments.

Characterisation of local structure flexibility

We characterised the flexibility of each LSP in the abovementioned library ³⁷. We calculated the propensity of fragments belonging to an LSP, noted LSP_s, to be associated with flexibility class f, noted C_f, as

$${\text{P}}_{C_f}^{{\mathit{LSP}}_s}=\frac{\text{Probability}(C_f/{\mathit{LSP}}_s)}{\text{Probability}(C_f)}=\frac{\frac{{\text{n}}_{C_f}^{{\mathit{LSP}}_s}}{{\text{n}}^{{\mathit{LSP}}_s}}}{\frac{{\text{n}}_{C_f}}{N}}=\frac{\frac{{\text{n}}_{C_f}^{{\mathit{LSP}}_s}}{{\text{n}}_{C_f}}}{\frac{{\text{n}}^{{\mathit{LSP}}_s}}{N}}$$

where ${\text{n}}_{C_f}^{{\mathit{LSP}}_s}$ is the number of fragments in LSP_s assigned to flexibility class C_f, n^LSP_s the total number of fragments in LSP_s, n_Cf the total number of fragments in flexibility class C_f, and N the total number of fragments (subscript s ranges from 1 to 120 and subscript f from 1 to 3). Consequently, ${\text{P}}_{C_f}^{{\mathit{LSP}}_s}$ measures the strength with which LSP_s fragments belongs to a C_f class, compared to random assignment. Finally, the flexibility class C_f maximizing ${\text{P}}_{C_f}^{{\mathit{LSP}}_s}$ was assigned to the corresponding LSP_s. Each LSP_s class was also characterized by an average B-factor_Norm and RMSF_Norm, respectively noted m_B and m_F. The corresponding values were obtained by averaging B-factor values (or RMSF values) over the fragments corresponding to a given LSP.

Deducing dynamics from local structure prediction features

Protein sequences were extracted from the protein structure dataset, parsed into overlapping 11-residue long fragments and used for local structure prediction. For each 11-residue long sequence fragment, the LSP was predicted using the strategy developed in ref. 38. We also considered longer 21-residue sequence windows to account for a long-range effect. The method provided the five top-scoring LSP candidates for each target fragment sequence. Then, for each of the five predicted LSPs, the corresponding flexibility class C_f was assigned. The final, unique flexibility class value for the target sequence fragment was simply the rounded average of the five flexibility classes. We also predicted B-factor_Norm (respectively RMSF_Norm) values for each fragment sequence by computing the average m_B (m_F) characterising the five LSP candidates.

To assess the whole prediction strategy and avoid introducing any bias, (i) we checked that protein structures in the present dataset were not included the training set used for developing our LSP prediction method; (ii) we used a jackknife procedure for selecting the optimal (τ_B1, τ_F1, τ_B2, τ_F2) quadruplet and evaluating the related prediction (see Assessment section below) and (iii) we also carefully checked that the LSP prediction rate for the current dataset was similar to the prediction rate previously obtained ³⁸. Whatever the evaluation scheme, based on classical Q₁₂₀ or a geometrical criterion, the values were consistent with our previous results (35.7 and a 61.3% prediction rate, respectively).

Assessment of flexibility predictability from local structure prediction

Two evaluation schemes were used to evaluate flexibility predictability from local structure. First, assessment of the flexibility class prediction was done by calculating the prediction rate Q₃ = TP/N where TP (true positive) is the number of fragments correctly predicted and N the number of fragments. As in ref. 25, we also computed the F-measure, combining accuracy (ACC) and coverage (COV) using a harmonic mean: $F=2\frac{\mathit{ACC}·\mathit{COV}}{\mathit{ACC}+\mathit{COV}}$. Second, B-factor_Norm and RMSF_Norm value predictions were evaluated by calculating the Pearson correlation coefficient between real observed (R) and predicted (P) values. Moreover, as proposed in ref. 21, R values were clustered into 23 groups and the correlation was computed between the mean R of all groups and the corresponding mean P.

Determining thresholds for flexibility classes

The delimitation of flexibility classes was rather arbitrary and all the more difficult because we considered two descriptors jointly. The quadruplet values that delimit the three flexibility classes were chosen according to a scoring procedure, which primarily aims at optimising the overall flexibility prediction rate while maintaining a well-balanced prediction rate for each flexibility class. A grid search was performed where the flexibility prediction rate was computed for each quadruplet. The grid search obeyed the following rules: (a) the thresholds τ_B1, τ_B2, τ_F1 and τ_F2 took all possible values in [−2; −0.5][0.5; 5] by steps of 0.1, and (b) a class should include at least 15% of fragments. On average, 71,255 quadruplets were tested. The scoring procedure consisted in the following steps: (i) the procedure was initialised by a null score S; (ii) quadruplets guaranteeing flexibility classes populated by more than 10% of LSPs won one point (S=S+1); (iii) quadruplets associated with the best 25% average Q₃ won an additional point (S=S+1); (iv) quadruplet for which the prediction rate is among the 25% best balanced for the three classes won one more point.

At this step, two supplementary indices specially designed for evaluating the relevance of a multiclass prediction were introduced: the squared correlation coefficient, R²(X,Y), which measures the non-linear dependence between observed (X) and predicted (Y) states, and N_eq(Y/X) which is the conditional equivalent number of predicted states Y given the observed states X ⁵⁰. Quadruplets that resulted in one of the 25% highest R²(X,Y) values won an additional point and finally quadruplets that led to one of the 25% lowest N_eq(Y/X) values obtained a supplementary point. At this stage, the procedure was re-iterated from step (ii) if several quadruplets were identical for the highest scores S, until only one quadruplet was kept. The grid search was performed on the MD dataset using all 40 proteins except one to assess the true performance using a jackknife procedure. With this procedure, a threshold quadruplet was selected for each one of the 40 rounds of jackknife (one round per protein). Finally, the selected quadruplet corresponded to the mean over the 40 rounds.

Prediction quality was quite stable for similar quadruplets. Each step of selection was very strict and many quadruplets were eliminated. Only 1.5 % of quadruplets obtained a score of 4 and the highest scores, i.e., from 5 to 9 were associated with 0.41% of quadruplets (see supplementary data II).

We also tested different ranges of threshold values for grids and different quadruplet selection methods. The described algorithm led to the best results. The procedure was also applied to the large validation dataset with similar results.

The procedure can be tested at the following url: http://www.dsimb.inserm.fr/dsimb_tools/predyflexy. The web site is still under development and due to limited computer resources, the number of jobs is restricted.

Results

In this section, we present our results on the two main questions addressed in this paper: (i) the definition of flexibility classes and (ii) the prediction of flexibility from sequence through the prediction of local structures.

Defining and quantifying flexibility

Flexibility descriptors

We studied protein dynamics using two different descriptors, B-factors determined from crystallography experiments and root mean square fluctuations (RMSF) computed from molecular dynamic simulations. The first index is a classical descriptor used in most approaches of flexibility prediction. It has the advantage that it can be deduced from X-ray diffraction experimental data. The second index is less frequently used and is obtained from simulation data. It has the advantage of representing protein dynamics behaviour in solution, as in NMR experiments. For both descriptors, we focused on the properties of the alpha carbons (Cα).

A comparison of raw B-factor values with raw RMSF values led to a 0.29 Pearson correlation coefficient, which is rather low. After normalising these values for each protein, the correlation between B-factors (B-factor_Norm) and RMSFs (RMSF_Norm) increased to 0.46 leading to 0.50 on average on a per-protein basis (a value named ρ in the following) with a standard deviation of 0.20 (see Figure 1), This result is weakly sensitive to the length of the simulations. Indeed, when the simulations were extended for ten more ns (i.e. 15ns in total), ρ value equalled 0.48 instead of 0.50 (data not shown). In addition, when larger proteins (size > 200 residues) were examined, the corresponding average value reached 0.58 (data not shown)..

We also considered ENM results and noticed that the relationship between X-Ray B-factors and ENM-RMSF was stronger on average than with MD-RMSF (ρ = 0.68). An identical ρ (0.68) was obtained between ENM-B-Factors and MD-RMSF. Surprisingly, the value decreased with longer simulations (ρ=0.57) (see supplementary data III).

Clearly, the two descriptors were related but far from identical: some residues were considered as flexible according to B-factor_Norm but rigid according to MD RMSF_Norm and vice versa. Hence, a single descriptor combining both descriptors would be helpful to better qualify and quantify flexibility properties (see below)

Flexibility of local structure prototypes

The results described above do not take into account any specific location or (local) structures of the residues in the protein. Here, we analysed protein flexibility with respect to local structures in a library that we previously developed ³⁷. This library contains 120 long structure prototypes (LSPs) and encompasses the structures of all 11-residue fragments observable in known protein 3D structures. All 120 LSPs are necessary to characterise the whole set of 3D protein structures. Nevertheless, for purposes of presentation, we roughly grouped LSPs into four categories according to their secondary structure content, i.e., helical, extended core, extended edges and connection structures grouping 16, 13, 40 and 51 LSPs, respectively ³⁷. Apart from their important role in structural description, LSPs were a key element for predicting sequence flexibility in the present study (see below).

LSP flexibility properties were described by normalised B-factors (and normalised RMSFs) associated with the central α carbon of the LSP (sixth residue). Figure 2 shows the relation between the mean B-factor_Norm m_B and the mean RMSF_Norm m_F calculated for each LSP category. In contrast to what was presented above for the whole set of protein fragments, a high Pearson correlation coefficient of 0.77 was observed between the two descriptors. According to B-factor_Norm, the three most rigid LSPs were LSP 9, 10 and 107. They all belonged to the extended core local structures category. The most flexible LSPs were LSP 89, 87 and 55. The first two LSPs are connection structures whereas the third one corresponds to an extended edge structure. According to RMSF_Norm, the three most rigid structural prototypes were LSP 9, 10 and 97 but LSP 107 was classified as the 6^th most rigid LSP. As observed with B-factor_Norm, these rigid LSPs correspond to extended core structures. The three most flexible LSPs were the connection structures 85, 113 and 103. Thus, using LSPs, both descriptors provided a very similar description of flexibility, despite some minor discrepancies.

Figure 2. Relationship between the mean B-factor_Norm m_B and the mean RMSF_Norm m_F per LSP class.

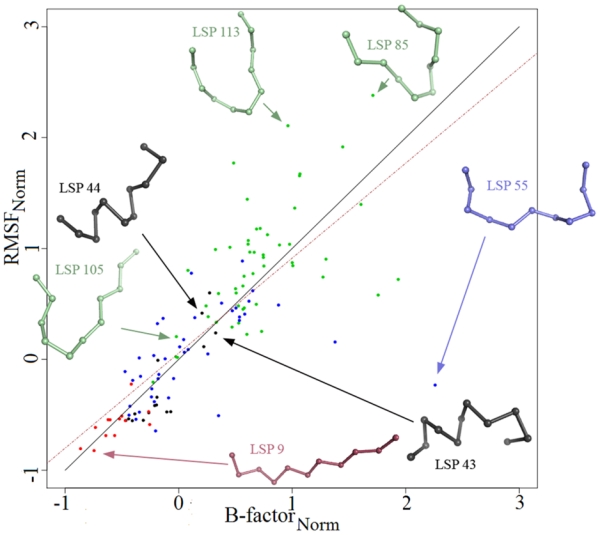
Dot colour represents the secondary structure LSP category, with helical, extended core, connection and extended edge LSPs in black, red, green and blue, respectively. The black line is the first bisector. The brown dashed line gives the regression line.

Flexibility classes

To define flexibility classes, two main issues were addressed: (i) the number of flexibility classes and (ii) the limits between these classes. Defining these classes is rather arbitrary and it is difficult to delimit them ²⁵. Most approaches developed thus far consider only two flexibility classes (Boolean classes). We decided to go one step further and considered three flexibility classes (rigid, intermediate and flexible); more importantly, we used both descriptors, B-factor_Norm and RMSF_Norm. Two thresholds were thus required to separate (i) rigid from intermediate residues (τ_B1, τ_F1) and (ii) intermediate residues from flexible residues (τ_B2, τ_F2), where τ_B and τ_F refer to Bfactor and RMSF descriptors, respectively (see Figure 1). To define these thresholds, the best parameters were selected so as to optimally discern the sequence specificities of each class and thereby maximize their predictability. The optimal quadruplet (one pair of index values for each threshold) was obtained after a grid search coupled with a selection procedure (see Materials and Methods and supplementary data II). The rigid and intermediate flexibility classes were similarly populated with 40.4% and 36.7% of protein fragments, respectively, whereas only 22.9% were classified in the most flexible class. Standard deviation values increased with the flexibility index averages as shown in Figure 1 (see red dots).

LSPs and flexibility classes

We also examined the distribution of the 120 LSPs in each flexibility class defined above. We found that 35.8% of LSPs were assigned to the rigid class (see Materials and Methods), while 25.0 and 39.2% LSPs were assigned to the intermediate and the flexible classes, respectively. Using secondary structure content as categories, we observed that the rigid class was comprised of 23.3% of helical LSPs, 30.2% of extended core structures and 46.5% of extended edges (see Table 1). Interestingly, the rigid class included all the extended core LSPs but was devoid of connection LSPs. The intermediate flexibility class contained 13.3, 43.3 and 43.3% of helical, connection and extended edge LSPs, respectively. The flexible class had 4.3% of helical LSPs, 80.9% of connection LSPs and 14.9% of extended edge LSPs. In contrast to extended core structures, helical LSPs were observed in all three flexibility classes. Of the 16 helical LSPs, two (LSP 43 and 44) were observed in the flexible class.

Table I.

Confusion matrix between LSPs and assigned flexibility classes for the MD dataset.

		LSPs (%)				Sum
		Helix	Extended Core	Extended Edge	Connection
Flexibility classes (%)	Rigid	23.3	30.2	46.5	Ø	100.0
	Intermediate	13.3	Ø	43.3	43.3	100.0
	Flexible	4.3	Ø	14.9	80.9	100.0

As suggested by a reviewer, we examined end-to-end distance (EToE) of each LSP and their associated B-factors (or RMSF) or flexibility class (see Supplementary data IV). The most extended LSPs with the largest EToE values had the lowest B-factors (rigid class) while the most compact ones with the shortest EToE showed the largest B-factors (flexible class). However, this criterion was not accurate enough to finely classify the LSPs in flexibility classes. Indeed, LSPs with similar EToE distances were distributed in the three classes of flexibility. Nevertheless, beyond EToE measure, the shape of LSPs could be a powerful indicator of the flexibility but a better description of the shape is required, with additional parameters to consider.

Predicting flexibility through prediction of local structure

In contrast to most classical flexibility prediction methods based on sequence information, our new approach takes advantage of the relationship between LPSs and flexibility classes. We applied the previously developed LSP-SVM_PSSM method ³⁸, which yields an ordered list of five LSP candidates. For each LSP candidate in the list, the corresponding flexibility class value (1, 2 or 3 for rigid, intermediate or flexible, respectively) based on the above results was predicted. The final flexibility class prediction corresponds to the rounded average of the five values and its value was applied to the central residue of the sequence. No training was performed on the flexibility datasets: for a given target sequence, flexibility was inferred uniquely on the basis of flexibility characteristics of the predicted LSP candidates.

Inferring a flexibility class for each residue in a sequence

The LSP-SVM_PSSM method led to an average, very well-balanced prediction rate of 49.4% for the three defined flexibility classes. The score remained relatively low due to a poor prediction rate for the intermediate flexibility class (see Table 2). Table 2 shows that 86.5% of rigid protein fragments were predicted to be rigid or intermediate. Likewise, 94.2% of flexible fragments were predicted to belong to an intermediate or flexible class. In contrast, confusion between flexible and rigid classes was very low. Less than 13.5% of fragments observed in the rigid class were predicted to be flexible, whereas only 6.0% of fragments observed in the flexible class were predicted to be rigid. More importantly, this prediction rate was considerably higher than a random prediction rate. A random prediction would have given 36.0%, with only 8.5 and 13.8% of rigid and flexible fragments correctly predicted.

Table II.

Confusion matrix between assigned and predicted flexibility classes for the MD dataset.

		Predicted flexibility classes
		1	2	3	Σ
Assigned Flexibility classes	1	47.4	39.1	13.5	100.00
	2	20.2	48.3	31.5	100.00
	3	5.8	39.2	55.0	100.00

Predicting LSP flexibility

A detailed analysis of flexibility prediction shows different prediction rates for each LSP. To illustrate our results as clearly as possible, we give the prediction rates for each LSP as a function of RMSF_Norm (see Figure 3). Very similar results were obtained with Bfactor_Norm, thereby confirming the similarity of the two descriptors when using the LSP dataset. A significant correlation coefficient (r = −0.71) between prediction rates and mean RMSF_Norm, was obtained. Considering the categories of the four secondary structures described above, we observed that helical and extended core LSPs often had better prediction rates compared to the two other categories. As mentioned above, helical and extended core LSPs are generally associated with low flexibility. Accordingly, 100% of extended core LSPs and 62.5% of helical LSPs were assigned to the rigid flexibility class. In contrast, connection LSPs and extended edge LSPs were the most difficult to predict. This result is presumably related to a lower structural prediction rate for the connection LSP category, which could in turn affect the flexibility prediction rate ³⁸. The connection LSP category was also mainly associated with the highest flexibility index, (74.5% connection LSPs) and none to the most rigid class (see also Figure 2). The extended edge category, the second most difficult structural category to predict, also showed high flexibility properties with 17.5% of extended edge LSPs assigned to the most flexible class and 32.5% to the intermediate class.

Figure 3. Relationship between observed flexibility and prediction rate for each LSP class.

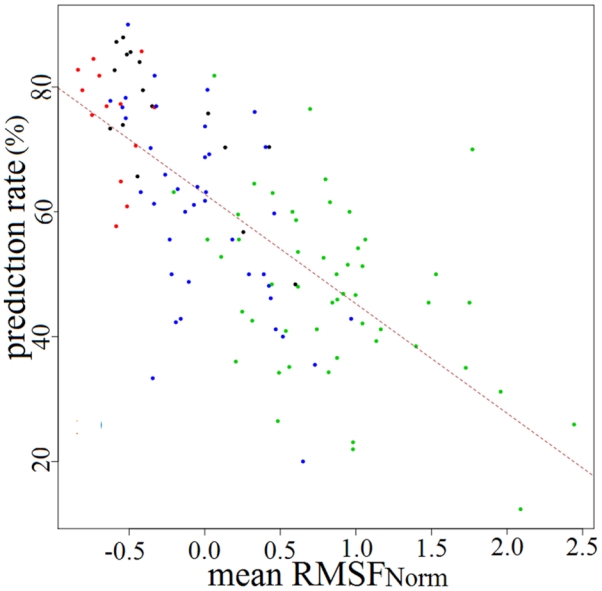
Flexibility was measured by the mean RMSF_Norm m_F. Dot colour represents the secondary structure LSP category, with helical, extended, connection and extended edge LSPs in black, red, green and blue, respectively. The brown dashed line gives regression line.

Hence, the difficulty of structural prediction seems to be closely related to highly dynamic properties.

Inferring flexibility profiles for proteins from sequence

To explore further, we considered predicted Bfactor_Norm and RMSF_Norm descriptors separately for each position along protein sequences. For each position, values were simply obtained by averaging the m_b (m_f for RMSF_Norm) of the five predicted LSP candidates. Considering the values in 23 flexibility bins as was done in ref. 21, the correlation between observed and predicted values reached 0.71 and 0.69 for Bfactor_Norm and RMSF_Norm, respectively. When outliers were excluded, correlations were 0.94 and 0.96, respectively. This correlation is slightly better than the best correlation value obtained by the PONDR VSL1 prediction methods in CASP6 ⁵¹.

As an illustration, we give the detailed results obtained for the rat intestinal fatty acid-binding protein sequence ⁵² for which the structure (PDB code 1FIC) has been solved at high resolution (1.2 Å). Figures 4 and 5 illustrate the predicted flexibility profiles defined by Bfactor_Norm and RMSF_Norm, respectively. Based on raw values, the correlation coefficient was 0.43 and 0.60 for Bfactor_Norm and RMSF_Norm, respectively, and 0.53 and 0.67 when outliers were excluded. Considering the 23 categories, the correlation coefficients for this protein reached 0.67 and 0.61 for Bfactor_Norm and RMSF_Norm profiles, respectively.

Figure 4. Flexibility prediction on the rat intestinal fatty acid-binding protein.

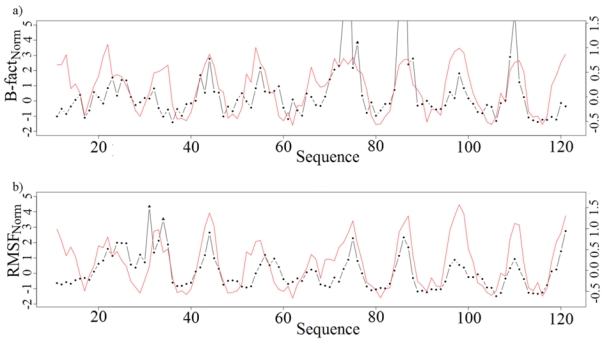
(PDB code 1IFC, 131 residues). Top: observed and predicted B-factor_Norm values, bottom: observed and predicted RMSF_Norm values. Black dotted lines indicated observed values and red lines indicate predicted values. Outlier values are symbolised by triangles.

Figure 5. Observed and predicted flexibility descriptors mapped on the rat intestinal fatty acid-binding protein structure.

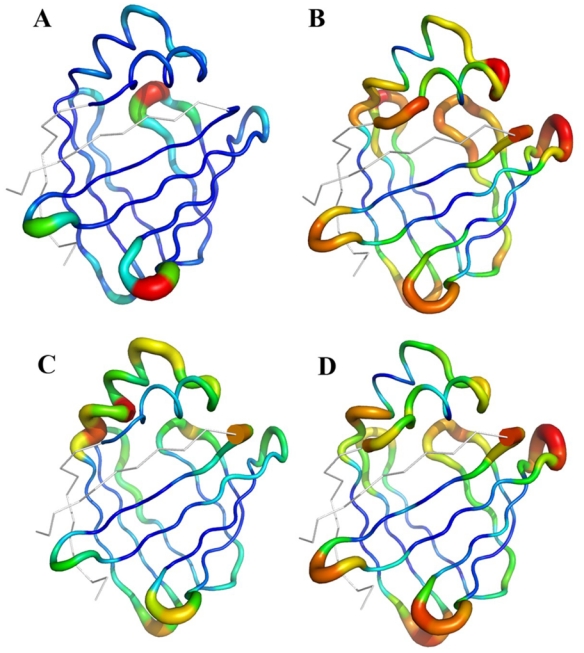
(PDB code 1IFC). A. Normalized B-factors, B. Predicted B-factors, C. Normalized RMSF from molecular dynamics simulations, D. Predicted RMSF.

This example is also representative of different situations that arise when measuring flexibility and assessing prediction. For example, residues 20 to 22 of the protein were assigned to the flexible class with RMSF_Norm and to a lesser extent with Bfactor_Norm,. Both predictions thus identified these residues as flexible ones. Moreover, the local structure prediction of these fragments centred on positions 20 to 22 was quite accurate. For the three positions, the top four predicted LSPs were indeed the observed ones (connection LSPs 30, 31, 32) and other candidates were also quite consistent. Surprisingly, NMR order parameters, S², ⁵³ indicate a rigid region, the S² values being 0.92, 0.55 and 0.90, for the three positions, respectively. This discrepancy between predicted and observed values is difficult to explain insofar as NMR experiments are deemed to be appropriate for measuring flexibility. This last example illustrates the fact that different factors, such as environment, long-range interactions can affect flexibility descriptors.

Similarly, residues 33 to 35 were observed to belong to the flexible class with RMSF_Norm but not with Bfactor_Norm. Predicted profiles indicated these residues as flexible. Interestingly, these residues belong to the small helical region that has been proposed to be a “portal” for ligands toward a buried cavity within the core of the protein ^{52, 54}. In addition, NMR experiments ⁵³ have shown that the region from V26 to N35 is characterized by very low order parameters in the apo-form of the protein, but not in the holo-form. Therefore, the dynamic properties of these residues may facilitate the entry of the ligand into the binding cavity. These NMR results match our predictions, showing a high flexibility for these residues that X-ray B-factors do not depict. Although the mechanism of entry of the fatty acids into the protein cavity is not yet fully understood ⁵⁴, these residues seem to be very important for protein function.

Overall, these promising results suggest that relevant information can be gleaned from this type of analysis on other proteins.

Defining a confidence index for flexibility prediction

The methodology proposed here can supply structural information but also information on flexibility properties. Moreover, it provides an additional means to assess the quality of the prediction. With LSP prediction, we defined a confidence index (CI), based on the discriminative power of the SVM classifiers. This index, graded from 1 to 19, was shown to directly estimate the quality of prediction for each predicted fragment sequence. It thus identifies easy-to-predict regions (high confidence index) and regions more difficult to predict (low confidence index) ³⁸.

The results are illustrated in Figure 6, where the flexibility prediction rate is represented as a function of the local structure prediction confidence index (CI). Overall, the flexibility prediction rate was very stable whatever the CI value. However, there were differences, depending on the flexibility class considered. For rigid fragments, the flexibility prediction rate increased with the local structure prediction CI. For low CI (<6), the prediction rate was quite poor (9.52%) but for high CI (>13) the prediction rate reached 59.9%. Importantly, 61.0% of rigid fragments were associated with high CI whereas only 5.3% were found in the low CI zones. For flexible fragments, the situation was inversed, but the flexibility prediction rate was less sensitive to the local structure prediction CI categories. The prediction rate was high (68.3%) for low CI and decreased (48.5%) for high CI. The distribution of flexible fragments was more similar between these two extremes, i.e., 23.5 and 28.4% fragments were found in low CI and high CI categories, respectively. Low sequence informativity for structural prediction was informative for predicting flexibility and inversely, high sequence informativity for structural prediction for predicting rigidity.

Figure 6. Flexibility and prediction rate according to the local structure prediction confidence index (CI).

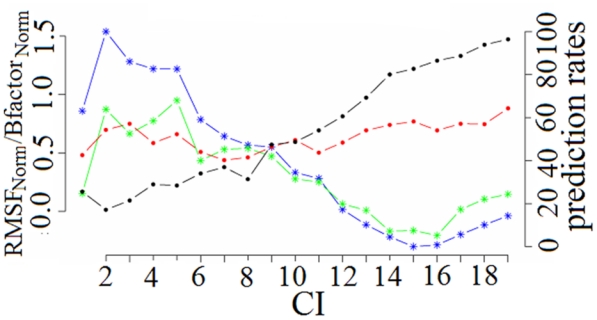
Flexibility descriptors are given on the left y-axis. RMSF_Norm and B-factor_Norm averages according to CI categories are indicated by blue and green lines, respectively. Prediction rates are given on the right y-axis. Local structure prediction rates according to CI are indicated in black and flexibility prediction rates obtained with the quadruplet defined on the whole dataset are in red.

Discussion

Choice of descriptors

For comparison purposes, we analysed the flexibility classes obtained using B-factor_Norm or RMSF_Norm, separately. The flexibility classes were consequently delimited by new optimised parameters τ, the only constraint being to maintain a similar distribution of fragments as previously observed in each class. Table 3 quantifies the confusion between the three classes defined with B-factor_Norm and the three classes obtained with RMSF_Norm. The values were normalised by the total number of fragments. Off diagonal values were rather similar, with differences between the same pairs of classes below 1%. Consequently, fragments were generally determined to be flexible (or rigid) using either experimental B-factors or with RMSF values. Hence, since the distribution of fragments was conserved, we did not observe any systematic bias due to the selected descriptor.

Table III.

Confusion matrix between normalised B-factors and normalised RMSF values from MD dataset for the three flexibility classes.

		RMSFNorm
		1	2	3	Σ
B-factorNorm	1	26.47	11.19	2.79	40.45
	2	11.88	16.03	8.78	36.69
	3	2.10	9.47	11.29	22.87
	Σ	40.45	36.69	22.87	100.00

Given the limitations of MD simulations, i.e., limited simulation time, approximations in force field and differences in environmental representation, the prediction similarity of both descriptors result may appear to be rather surprising. However, B-factors also include some approximations. B-factors are obtained as a result of a theoretical model fitted to experimental data and their accuracy strongly depends on crystal resolution. Moreover, the crystal environment also influences atomic fluctuations ⁵⁵. All together, both descriptors provide accurate information on flexibility and are valuable for defining flexibility classes.

Interestingly, molecular dynamics simulations provide additional information that cannot be captured with a unique crystal structure, namely transitions between different structural states. A preliminary analysis shows for instance, that 5.6% of fragments assigned to a connection LSP in PDB structures changed assignment in the earliest steps of the MD simulation. Assignment changes were usually to another connection LSP (98.7%). Moreover, these fragments visited on average 3.6 other LSP classes during the MD simulation. The extended edge category also exhibited interesting dynamical properties, with 6.7% of extended edge fragments changing assignment in the first MD steps: 4.8% changed to another extended edge LSP, 1.4% to a connection LSP and 0.5% to an extended core LSP. During MDs, fragments assigned to extended edge LSPs in X-ray structures visited on average 4.6 other assignments.

NMR data would be an interesting alternative for describing flexibility ⁵⁶. NMR experiments can monitor protein motions on a broad range of timescales. In particular, order parameters S² are powerful descriptors for characterising fast dynamic sites. Slow protein dynamics frequently associated with large conformational changes can be described by spin-spin relaxation data (R₂). Recent advances in the characterisation of protein-backbone motions from residual dipolar couplings (RDCs) also provide quantitative internal motional modes and amplitudes from experimental data alone ⁵⁷. However, despite these important advances, NMR experiments are limited by protein size.

Prediction errors

The prediction rates obtained in this study are rather promising given the simplicity of the procedure. The prediction rate can be improved yet further. Prediction failures can be attributed to (i) an incorrect structural prediction and/or (ii) different flexibility properties of fragments coded by the same LSPs. In any case, long-range interactions play a major role and are presumably partially responsible for the observed discrepancies. The case of the prokaryotic phospholipase A2 (PDB code 1LWB, chain A) is a clear illustration of this type of discrepancy. This protein has two long-range disulfide bridges (C45-C61, C97-C107) that stabilise the 3D structure. A 21-residue loop is predicted as highly flexible, but it is actually highly rigid due to the cystine residues in the loop. One solution is to couple our method with a method that predicts disulfide bridges.

The number of occurrences of each structural group also influences the capacity to decipher the sequence-structure relationship. Therefore, overlapping properties of LSPs may play a significant role. LSP length (11 residues) accounts for long-range interactions, but only partially. One solution is to lengthen LSPs. Unfortunately, the number of fragments in a given structural class rapidly decreases with length. As a consequence, this may weaken the sequence-structure relationship.

Comparison with sophisticated flexibility prediction methods

Finally, we assessed our method by comparing our results to those of recently developed, sophisticated methods. The PROFbval ²⁵ method carries out a two-class prediction (rigid/flexible) on normalised B-factor values. Flexibility classes are defined according to a strict and a non-strict threshold, i.e., 0.03 and −0.3, respectively. Based on this method, we modified our flexibility classes by using only Bfactor_Norm and considering only two classes defined based on PROFbval thresholds. We performed the prediction and its evaluation on the MD dataset. We also used our larger, independent Validation dataset (see Materials and Methods) that contains longer proteins and is more similar to the assessment set used for PROFbval. Table 4 shows that F-measures of 48.1 and 72.0% were obtained for strict and non-strict thresholds, respectively, on the MD dataset. On our Validation set, the results were 44.9 and 69.7%, respectively, whereas PROFbval method obtained 53.3 and 71.9% (Table 4). Results using our method are extremely encouraging given the fact that the parameters used in this method were not the optimal ones. The similarity of the results obtained with a non-strict threshold confirms that our method is rather efficient compared to other more sophisticated methods in the field, which are based on a true learning of the flexibility data.

Table IV.

Comparison of our flexibility prediction results with those using the PROFbval method.

	Datasets	This study, adapted for comparison			PROFbval	PredBF
		MD dataset	MD dataset	Large dataset	MD Dataset	MD Dataset
		(a)-B-factorNorm and RMSFNorm	(b)B-factorNorm only	(b)B-factorNorm only	(b)B-factorNorm only	(c)B-factorNorm only
Strict	threshold value(s)	2.3±0.4; 1.4±0.5	0.03	0.03	0.03	2.3
	% of rigid fragments	78.76	57.80	58.20	57.80	48.0
	% of flexible fragments	21.24	42.20	41.80	42.20	52.0
	ACC COV F-measure	38.73 55.03 45.46	59.30 40.43 48.08	55.30 37.81 44.91	63.1 46.2 53.3	61.1 45.8 52.9
Non-Strict	threshold value(s)	−1.4±0.3; −0.7±0.2	−0.3	−0.3	−0.3	−1.4
	% of rigid fragments	35.09	44.33	45.64	44.33	37.0
	% of flexible fragments	64.91	55.67	54.36	55.67	63.0
	ACC COV F-measure	74.84 84.54 79.39	61.23 87.35 71.99	58.49 86.16 69.68	70.1 73.9 71.9	62.4 75.5 68.3

^(a)for this study. two combined criteria, B-factor_Norm and a RMSF_Norm were used. The values correspond to the intercepts with x and y axes of figure 1 respectively.

^(b)for comparison purpose with ProFbval, only B-factor_Norm threshold was used and was chosen equal to ProFbVal threshold.

^(c)using Bfact_Norm thresholds defined in our procedure.

We also assessed a two-class prediction based on the two descriptors defined in the present study. We evaluated the results with a non-strict threshold that separates the intermediate class and the flexible class. This choice conserves a distribution of the residues in each group similar to the one observed with PROFbval thresholds (see Table 4). The results obtained using our method are slightly better than PROFbval ones, with 74.8% accuracy, 84.5% coverage and an F-measure of 79.4%. This confirms that LSP description is truly useful for addressing flexibility prediction.

We performed a similar comparison with the method recently developed by Pan & Shen [24]. The results were obtained with the procedure implemented on the PredBF web server. The corresponding results for the MD dataset are reported in Table 4 (PredBF column). We first observed that the distribution of PredBF B-factor values was quite different from Schlessinger’s values or ours for the MD dataset. Consequently, using our strict B-factor threshold (2.3), the rigid class appeared less populated than the flexible residues in the strict ensemble. The PROFbval threshold (0.03) would presumably tend to reinforce this effect. Hence, the efficiency was difficult to compare although the values seem similar to PROFbVal results. In contrast, using our non-strict B-factor threshold (−1.4), the distribution of flexible and rigid fragments appeared similar to our corresponding distribution. The prediction rates for Acc, Cov and F were quite comparable even slightly better with our approach.

Conclusion

Here, we presented an original approach that studies and predicts sequence flexibility in protein structures. The systematic exploration of dynamics associated with the 120 LSPs led to the characterisation of differential local structure behaviours. Aside from the well-known behaviour of loops with generally higher flexibility compared to that of repetitive secondary structures, we demonstrated subtle interdependence between defined local protein structures and flexibility properties. Accordingly, some motifs can be more mobile than others. We also show that sequence information contained in local protein structures can also be used to predict flexibility characteristics. The flexibility prediction strategy we propose here is directly derived from our local structure prediction method. The results of this successful proof of concept are as efficient as recently developed, elaborate methods without requiring any sophisticated training procedures. In addition, our results suggest that some discrepancies between predicted and observed local structures may actually be due to alternative, accessible local structures when dynamics are taken into account. This observation further enhances the usefulness of our local structure prediction method, which proposes several structural candidates for a target sequence. We showed here that LSP prediction is in itself very informative of protein flexibility properties. Finally, due to the simplicity of the procedure, further improvements can be easily implemented. Thus, using the LSP flexibility information content coupled with an appropriate learning process should greatly improve predictions of protein flexibility.