Thermodynamic Coupling of Protonation and Conformational Equilibria in Proteins: Theory and Simulation

Abstract

Ionization-coupled conformational phenomena are ubiquitous in biology. However, quantitative characterization of the underlying thermodynamic cycle comprised of protonation and conformational equilibria has remained an elusive goal. Here we use theory and continuous constant pH molecular dynamics (CpHMD) simulations to provide a thermodynamic description for the coupling of proton titration and conformational exchange between two distinct states of a protein. CpHMD simulations with a hybrid-solvent scheme and the pH-based replica-exchange (REX) protocol are applied to obtain the equilibrium constants and atomic details of the ionization-coupled conformational exchange between open and closed states of an engineered mutant of staphylococcal nuclease. Although the coupling of protonation and conformational equilibria is not exact in the simulation, the results are encouraging. They demonstrate that REX-CpHMD simulations can be used to study thermodynamics of ionization-coupled conformational processes—which has not possible using present experimental techniques or traditional simulations based on fixed protonation states.

Introduction

Ionization-coupled conformational transitions are ubiquitous in biology (e.g., protein folding and misfolding, catalysis, and bioenergy transduction). To understand such phenomena, it is necessary to characterize the protonation equilibria and details of the conformational events. The former can be accomplished through determination of the pK_a values of titratable groups. For surface groups (which comprise the majority of titratable sites in proteins), because ionization-induced conformational changes are negligible, the pK_a values can be accurately determined by NMR titration (1) or quantitatively predicted using traditional electrostatic calculations (2). However, for deeply buried groups, protonation/deprotonation often results in large conformational changes, i.e., partial or complete unfolding, which makes direct measurement difficult or impossible (3). Also, traditional electrostatic calculations can break down because of the inability to model large conformational changes that accompany protonation/deprotonation (4,5). Thus, characterization of ionization-coupled conformational transitions has remained an elusive goal.

Toward this goal, we explore protonation equilibrium that is coupled to the exchange of two very distinctive conformational states (Fig. 1). As in most biological events, the conformational transition occurs at a much slower timescale than the protonation reaction. Our model system is the engineered mutant N100K of the hyperstable variant Δ+PHS of staphylococcal nuclease (SNase), referred to as Δ+PHS/N100K in what follows (see Fig. 2). We consider the protonation equilibrium of residue Lys¹⁰⁰, which, according to experimental evidence and our simulations, is coupled to the conformational exchange between closed and open states. By analogy to the wild-type residue Asn¹⁰⁰, Lys¹⁰⁰ is deeply buried in the hydrophobic core of the protein. Its amine nitrogen is 5 Å from the center of mass of the protein, in contrast to other surface titratable residues that are ∼14 Å away from the mass center. Furthermore, Lys¹⁰⁰ is separated by at least 7 Å from other titratable groups. Deeply buried ionizable residues without charge compensation are expected to have very large pK_a shifts relative to the model (or solution) value because the neutral form is significantly stabilized relative to the charged form. Thus, it is puzzling that analysis of the pH-dependent stability data gave a pK_a value of 8.6 ± 0.2 (6,7) corresponding to a shift of <2 units relative to the model value of 10.4. In fact, the pK_a of N100K is arguably the most challenging case in the recent efforts of blind pK_a predictions (2). Most structure-based electrostatic calculations either severely underestimated or failed to predict the value. Our calculation, based on continuous constant pH molecular dynamics (CpHMD) with the generalized-Born implicit-solvent model, underpredicted the pK_a by 5 units, which was the largest deviation in the data set of 87 blind targets (8).

Figure 1.

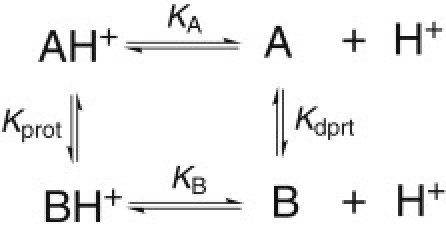
Coupling between protonation equilibria and conformational exchanges. In regard to Δ+PHS/N100K, A and B refer to the open and closed states, respectively.

Figure 2.

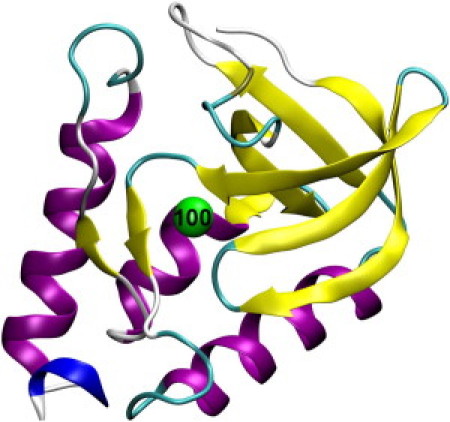
X-ray crystal structure of the wild-type Δ+PHS SNase (PDB ID: 3BDC). Residue Asn¹⁰⁰ is indicated.

This article is organized as follows. We will first apply analytical theory to consider the general case of the protonation equilibrium coupled to conformational exchange between two states. We will then make use of the recent development of the CpHMD technique in explicit solvent to characterize the coupled protonation equilibrium of Lys¹⁰⁰ in Δ+PHS/N100K and the conformational exchange between the closed and open states. Simulations of proton titration coupled to conformational dynamics allow us to obtain the equilibrium constants that completely specify the underlying thermodynamic cycle.

Theory

Coupled protonation and conformation equilibria

We consider a titratable molecule M existing in two conformational states, A and B, which can interconvert in a pH-dependent manner. Thus, the protonation equilibrium of the molecule, MH ⇔ M + H⁺, can be microscopically described as the protonation equilibria involving AH and BH that are coupled to the conformational equilibria involving the protonated and deprotonated forms of A and B (Fig. 1). The equilibrium constants for the deprotonation reactions of states A and B are given as

$$K_{\text{A}}=\frac{\left[\text{A}\right]\left[{\text{H}}^{+}\right]}{\left[\text{AH}\right]}\text{and}{K}_{\text{B}}=\frac{\left[\text{B}\right]\left[{\text{H}}^{+}\right]}{\left[\text{BH}\right]}.$$ (1)

Thus,

$$K_{\text{A}}\left[\text{AH}\right]+K_{\text{B}}\left[\text{BH}\right]=\left(\left[\text{A}\right]+\left[\text{B}\right]\right)\left[{\text{H}}^{+}\right].$$ (2)

Dividing both sides of Eq. 2 by the total concentration of the protonated species, [AH] + [BH], gives

$$\frac{K_{\text{A}}\left[\text{AH}\right]+K_{\text{B}}\left[\text{BH}\right]}{\left[\text{AH}\right]+\left[\text{BH}\right]}=\frac{\left[\text{A}\right]+\left[\text{B}\right]}{\left[\text{AH}\right]+\left[\text{BH}\right]}\left[{\text{H}}^{+}\right].$$ (3)

To simplify the above equation we denote the fractions of state A and B in the protonated species as

$$f_{\text{AH}}=\frac{\left[\text{AH}\right]}{\left[\text{AH}\right]+\left[\text{BH}\right]}\text{and}{f}_{\text{BH}}=\frac{\left[\text{BH}\right]}{\left[\text{AH}\right]+\left[\text{BH}\right]},$$ (4)

and we denote the total concentration of the protonated and deprotonated species as

$$\left[\text{MH}\right]=\left[\text{AH}\right]+\left[\text{BH}\right]\text{and}\left[\text{M}\right]=\left[\text{A}\right]+\left[\text{B}\right].$$ (5)

Substituting Eqs. 4 and 5 into Eq. 3 leads to

$$f_{\text{AH}}{K}_{\text{A}}+f_{\text{BH}}{K}_{\text{B}}=\frac{\left[\text{M}\right]}{\left[\text{MH}\right]}\left[{\text{H}}^{+}\right].$$ (6)

Equation 6 is analogous to the Henderson-Hasselbalch (HH) equation in that the left side of the equation represents the equilibrium constant of the macroscopic deprotonation reaction. The associated pK_a is the apparent pK_a for the molecule. We note that, because the exchange between AH and BH is at equilibrium, f_AH and f_BH are constants, i.e., are not dependent upon pH. In fact, we can express them in terms of the equilibrium constant of the exchange reaction,

$$K_{\text{prot}}=\frac{\left[\text{BH}\right]}{\left[\text{AH}\right]},$$ (7)

as

$$f_{\text{AH}}=\frac{1}{K_{\text{prot}}+1};\text{and}{f}_{\text{BH}}=1-f_{\text{AH}}.$$ (8)

Taking logarithm of both sides of Eq. 6 and making use of the definitions for pH, pH = −log[H⁺], we obtain

$$\text{pH}=-log\left(f_{\text{AH}}{K}_{\text{A}}+f_{\text{BH}}{K}_{\text{B}}\right)+log\frac{\left[\text{M}\right]}{\left[\text{MH}\right]}.$$ (9)

Thus, the macroscopic or apparent pK_a of the molecule is

$$\text{p}{K}_a\left(\text{M}\right)=-log\left(f_{\text{AH}}{K}_{\text{A}}+f_{\text{BH}}{K}_{\text{B}}\right).$$ (10)

Evidently, pK_a(M) encapsulates the microscopic pK_a values associated with conformations A and B as well as the ratio between the two populations. From Eq. 10 it can be seen that if K_A and K_B are very similar, as in the case of surface residues, where the dielectric environment in the two conformational states is similar, pK_a(M) ≈ pK_a(A) ≈ pK_a(B). However, if K_A and K_B are very different, as in the case of a deeply buried residue that can explore both buried and exposed positions, the calculation of pK_a(M) requires knowledge of the microscopic pK_a values as well as the relative population of the two states.

Coupled equilibria involving a deeply buried residue

We consider the protonation equilibrium of a deeply buried residue, which can become exposed to solvent upon ionization. Later we will see that this is the case for the titration of Lys¹⁰⁰ in Δ+PHS/N100K. In the open conformation (A), because of the solvent exposure, lysine has a pK_a close to the model value, whereas in the closed conformation (B) its pK_a is downshifted. If K_B(closed) is much larger than K_A(open) and assuming that f_BH is nonnegligible, the term f_AH K_A can be dropped in Eq. 10. So the apparent pK_a value can be approximated as

$$\text{p}{K}_a\left(\text{M}\right)\approx -log\left(f_{\text{BH}}{K}_{\text{B}}\right)=\text{p}{K}_a\left(\text{B}\right)-log{f}_{\text{BH}}.$$ (11)

Equation 11 shows that the apparent pK_a is mainly determined by the pK_a of the closed state with a correction that shifts the pK_a up (because f_BH is <1). The smaller the f_BH value, the larger the shift.

Thermodynamic cycle

At equilibrium the reactions of protonation/deprotonation and conformational exchange form a thermodynamic cycle. Thus,

$$\Delta G\left(\text{AH}\to \text{A}\right)-\Delta G\left(\text{BH}\to \text{B}\right)=\Delta G\left(\text{AH}\to \text{BH}\right)-\Delta G\left(\text{A}\to \text{B}\right).$$ (12)

This is equivalent to stating that

$$\text{p}{K}_a\left(\text{A}\right)-\text{p}{K}_a\left(\text{B}\right)=-log{K}_{\text{prot}}+log{K}_{\text{dprt}},$$ (13)

where K_prot and K_dprt can be determined, respectively, from the fraction of AH in the exchange with BH and the fraction of B in the exchange with A,

$$\begin{array}{c}{K}_{\text{prot}}=1/f_{\text{AH}}-1,\\ K_{\text{dprt}}=\frac{1}{1/f_{\text{B}}-1}.\end{array}$$ (14)

Methods

REX-CpHMD titration simulations

Our study employed the newly developed hybrid-solvent based continuous constant pH molecular dynamics (CpHMD) technique with the pH-based replica-exchange (REX) sampling protocol (9). Briefly, a set of titration coordinates with fictitious mass is propagated simultaneously with the atomic coordinates in the CpHMD simulation (10) via an extended Hamiltonian as in the λ-dynamics approach (11). In the hybrid-solvent-based CpHMD method, the effect of solvation on the titration coordinates is implicitly included using a generalized Born model, GBSW (12), whereas that on the conformational dynamics is explicitly included using the explicit-solvent model. The pH-based REX protocol provides a means to enhance sampling of coupled protonation and conformational dynamics. Details of the hybrid-solvent-based CpHMD method as well as benchmark titrations for proteins can be found elsewhere (9,13,14).

Structure preparation

The initial structure of Δ+PHS/N100K was prepared by mutating residue Asn¹⁰⁰ to lysine based on the x-ray crystal structure of the Δ+PHS variant of staphylococcal nuclease (PDB ID: 3BDC) (15) using the MOLDEN program (16). (See also Fig. 2.) The sequence was acetylated at the N-terminus and amidated at the C-terminus. Hydrogens were added using the HBUILD facility of CHARMM (17). To remove potential steric clashes involving hydrogen atoms, energy minimization was performed using 100 steps of steepest descent followed by 50 steps of adopted basis Newton-Raphson method with all heavy atoms restrained by a harmonic potential with the force constant of 50 kcal/(mol·Å). The energy-minimized structure was then solvated in a truncated octahedral box containing ∼7300 water molecules. The distance between the protein and edges of the water box is at least 10 Å and water molecules within 2.8 Å of the heavy atoms of the protein were removed. Further energy minimization was performed to allow adjustment of water molecules using 100 steps of steepest descent followed by 50 steps of adopted basis Newton-Raphson method with all heavy atoms in the protein fixed. A second round of minimization was conducted with a harmonic restraint of 100 kcal/(mol·Å) applied on the heavy atoms of the protein. Counterions were not added to the system because the total net charge at different pH conditions is different, and changes during the titration simulation. Our previous study using highly charged test proteins demonstrated that it is not necessary to include neutralizing ions in relatively short titration simulations for obtaining accurate pK_a values (9).

Simulation protocol

The simulation was conducted using a developmental version of CHARMM (c35b3), where the hybrid-solvent CpHMD method was implemented (9) and the MMTSB toolset (18), where the pH-REX protocol was implemented. The protein was represented by CHARMM22 force field (19) with the CMAP potential for backbone conformational correction (20). Water molecules were represented by the TIP3P water model (21). Molecular dynamics was performed under an isobaric-isothermal (NPT) condition at a pressure of 1 atm and temperature of 298 K. The pressure was controlled using the Langevin piston method with a collision frequency of 20 per ps (22). The temperature was controlled using the Hoover thermostat (23). The SHAKE algorithm (24) was applied to all bonds and angles involving hydrogen atoms to allow an integration timestep of 2 fs. Nonbonded electrostatic interactions were calculated using the particle-mesh Ewald summation with a charge correction to reduce pressure and energy artifacts for systems with a net charge (25).

In the GB calculation, the Debye-Hückel model was used to account for salt-screening effects with an ionic strength of 0.1 M in accord with the experimental condition (6,7). The input radii for the GBSW model was taken from Chen et al. (26). All other input parameters were identical to the previous work (9,14). In the pH-REX protocol, 13 replicas were placed at pH values between 4 and 10 with an interval of 0.5 units. In the first stage, each pH replica was subjected to a 5-ps equilibration run where a harmonic potential with the force constant of 10 kcal/(mol·Å) was applied to all solute heavy atoms. In the second stage, the restraint was released and pH exchanges between adjacent replicas were attempted every 500 steps (1 ps) and continued to 2 ns per replica. In the final stage, randomly selected conformations were placed at pH 4–10 and the simulation continued to another 2 ns per replica. The pH exchange success ratio was at least 20% and the average was 50%. The last 1.5 ns of the simulation (per replica) was used for analysis. During the pH-REX simulation, all Asp, Glu, and Lys residues were allowed to titrate. The model pK_a values are 4.0, 4.4, and 10.4, respectively. To verify convergence of the protonation-state sampling, the time series of the unprotonated fractions was examined (see Supporting Material).

Simulation Results

Titration simulations of Δ+PHS/N100K

We applied the hybrid-solvent based CpHMD technique (9) with the pH-based replica-exchange (REX) sampling protocol to explore the protonation equilibrium of Lys¹⁰⁰ in Δ+PHS/N100K. A preliminary REX-CpHMD simulation was carried out with 13 replicas (pH 4–10). After 2 ns (per replica) of simulation, the buried site of Lys¹⁰⁰ opened up at very low pH conditions. Nevertheless, the unprotonated fractions at different pH did not plateau even after the simulation was extended to 10 ns/replica. Close examination revealed that the open states did not walk through the pH space to reach high pH conditions. To promote the exchange between replicas and hence sampling convergence, we therefore initiated five independent runs of REX-CpHMD simulations using the representative snapshots of the open and closed states from the preliminary simulation as starting structures. At the beginning of these simulations, the open and closed conformations were randomly placed at different pH replicas. After 2 ns/replica, the unprotonated fractions were converged in all five runs (see Fig. S1 in the Supporting Material).

Protonation equilibrium of Lys¹⁰⁰ in the closed and open conformations

Fitting the unprotonated fractions of Lys¹⁰⁰ at pH 4–10 to the Hill equation gave an apparent pK_a value ranging from 6.1 to 7.9 based on the five runs (Fig. 3 and Table 1). Next, we investigated the microscopic protonation equilibria of the closed and open states. We computed the solvent-accessible surface area (SASA) of the lysine side chain, which varies from 0 (completely buried) to nearly 50 Å² (completely exposed) when combining all pH conditions (Fig. 4 A). The bimodal distribution of SASA allows us to separate the buried (closed) from exposed (open) conformations based on a cutoff of 5.0 Å². To examine the titration of the two states, we calculated the unprotonated fractions at all pH (Fig. 4 B). It can be seen that for the open states the unprotonated fraction remains low in the entire pH range, which shows that the pK_a for the open states is near or >10. In contrast, the closed states are mostly unprotonated at high pH and become protonated at low pH. Based on these data, we calculated the microscopic pK_a values for the closed and open states (Table 1). The pK_a value for the closed state is low, ranging from 5.3 to 6.4 in the five independent simulation runs. The fitting to the Hill equation is very good except for one run. The pK_a value for the open state ranges from 9.4 to 12. The large spread and incomplete titration indicate that sampling of the open state is not sufficient and the end-point pH condition may not be high enough to accurately determine the pK_a value.

Figure 3.

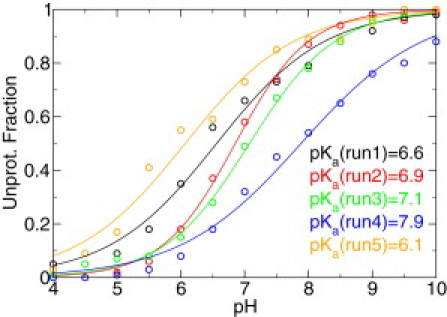
Simulated titration data for residue Lys¹⁰⁰ in Δ+PHS/N100K. The unprotonated fractions were fit to the Hill equation. The results are shown as fitting curves and pK_a values.

Table 1.

Thermodynamic characterization of the coupled ionization and conformational equilibria of Lys¹⁰⁰ in Δ+PHS/N100K

Run	pKa (apparent)	pKa (open)	pKa (closed)	−logKeq(prot)	−logKeq(dprt)
1	6.6	12.0	5.3	1.0	−2.3
2	6.9	9.6	5.9	0.8	−2.2
3	7.1	9.4	5.8	1.0	−1.9
4	7.9	10.1	6.4	1.0	−1.1
5	6.1	—∗	5.6∗	0.7	−2.7
Avg/SD†	6.9 ± 0.7	10.3 ± 1.2	5.8 ± 0.4	0.9 ± 0.15	−2.0 ± 0.59
Expt‡	8.6 ± 0.2
Difference§		4.5		2.9

Apparent pK_a was obtained from fitting the simulated titration data to the Hill equation (Fig. 3). The fitting error in the pK_a calculation in runs 1–4 is estimated to be <0.3 units (see Fig. S2 and related discussion in the Supporting Material). K_eq represents the equilibrium constant for the conformational exchange.

^∗Fitting for the closed states is poor. The pK_a value could not be estimated because the unprotonated fraction is too low under all pH conditions (see Fig. 4).

^†Standard deviation is the spread of the values from the five simulation runs.

^‡Experimental data derived from the pH dependence of the thermodynamic stabilities of Δ+PHS and N100K mutant (see main text).

^§This row lists the values for pK_a(open) − pK_a(closed) and −logK(prot) + logK(dprt).

Figure 4.

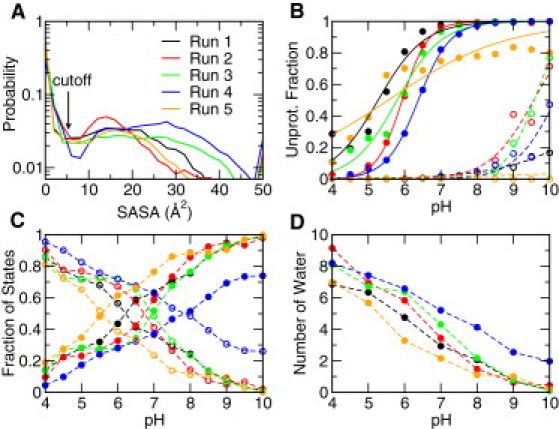
Proton titration and pH-dependent population shift involving residue Lys¹⁰⁰ in Δ+PHS/N100K. (A) Probability distribution of the solvent-accessible surface area (SASA) of the lysine side chain combining all pH conditions. The cutoff for defining the open and closed states is indicated. (B) Unprotonated fraction for the open and closed states at different values of pH. (C) Fraction of the open and closed states at different values of pH. (D) Number of water molecules within 5 Å from the amine nitrogen of Lys¹⁰⁰ at different values of pH. (In panels B and C, the open and closed states are shown as open and solid circles, respectively. Different simulation runs are indicated by color.)

To examine the conformational equilibrium between the closed and open states, we calculated the fractions of the two states (in both protonated and deprotonated forms) at each pH (Fig. 4C). It can be seen that the closed and open conformations dominate at high and low pH, respectively, and the crossover takes place at intermediate pH where the population of the two states becomes equal. Because pK_a(open) is at least three units higher than pK_a(closed), according to the theoretical consideration (Eq. 11 and related discussion), the apparent pK_a is mainly determined by pK_a(closed). The presence of a small fraction of the protonated closed conformations (f_BH of 0.1) makes 1-unit correction to the apparent pK_a that is in agreement with the difference between the calculated apparent pK_a and pK_a(closed).

Thermodynamic coupling of protonation equilibria and conformational exchanges

As noted earlier, the relative population of open versus closed states should remain constant if conformational equilibrium is reached. To test this, we calculated the fraction of protonated open states in exchange with protonated closed states, f_AH, at all pH conditions (Table 2). We also calculated the fraction of deprotonated closed states that are in exchange with deprotonated open states, f_B (Table 2). In five runs, the average f_AH over all pH conditions ranges from 0.84 to 0.91, while the standard deviation is 0.07–0.11. The average f_B ranges from 0.92 to 1.0 with the standard deviation <0.01. The large values for f_AH and f_B are expected, because protonation favors the open conformations whereas deprotonation favors the closed conformations. Somewhat surprisingly, the standard deviation is small (0.09 or 10%), suggesting that sampling of the exchange between the open and closed states is nearly converged, which we attribute to the use of the pH-based replica-exchange protocol that accelerates the rate of crossing the barrier between the two local minima (9). We note that the establishment of a quasi-equilibrium between the open and closed states does not mean that sampling of the ensemble of substates is fully converged (for more information, see Discussion).

Table 2.

The fractions of open and closed conformations

Run	fAH	fB
1	0.91 ± 0.07	0.99 ± 0.00
2	0.87 ± 0.10	0.99 ± 0.01
3	0.91 ± 0.08	0.99 ± 0.01
4	0.91 ± 0.08	0.92 ± 0.08
5	0.84 ± 0.11	1.00 ± 0.00
Avg/SD∗	0.89 ± 0.09	0.99 ± 0.02

Column f_AH lists the average and standard deviation of the fraction of the open conformations in the protonated species at all pH conditions. Column f_B lists the average and standard deviation of the fraction of the closed conformations in the deprotonated species at all pH conditions.

^∗Standard deviation refers to the spread of the values from the five simulation runs.

Based on the values of f_AH and f_B and Eq. 14, we obtained the equilibrium constants (in the form of −logK_eq) for the conformational exchanges (vertical processes in Fig. 1). Together with the pK_a values for the open and closed conformations (horizontal processes in Fig. 1), which represent the equilibrium constants for the deprotonation reactions, they allow us to examine the thermodynamic coupling between protonation and conformational transitions. If the simulation results were exact, the four processes should form a “closed” thermodynamic cycle, resulting in pK_a(open) − pK_a(closed) being identical to −logK_eq(prot) + logK_eq(dprt). However, in our simulations the former was calculated to be 1.6 units larger than the latter (Table 1), which indicates that the thermodynamic cycle is not completely closed. We will come back to this point in Discussion.

Details of the pH-dependent population shift

We hypothesized that the shift from the closed to the open conformations as pH is lowered is linked to ionization-induced water penetration into the hydrophobic site, a mechanism previously suggested for the neutral form of V66E in the PHS variant of SNase based on the cryogenic crystal structure (27) although not confirmed with the room-temperature crystal structure or magnetic relaxation dispersion data (28). Several molecular dynamics studies examining the pK_a shifts in mutants of SNase also have demonstrated water penetration concomitant with ionization-induced conformational relaxation (5,29). To test this hypothesis, we calculated the average number of water molecules within a radius of 5 Å from the amine nitrogen of N100K under all pH conditions (Fig. 4 D). As pH is lowered from 10 to 4, the average number of waters increases from zero to 7–9 in the five simulation runs. The number of water molecules follows the trend in the fraction of open conformations as a function of pH. Further analysis reveals that as water molecules enter, the side chain of Lys¹⁰⁰ becomes extended and the hydrophobic pocket opens up (Fig. 5).

Figure 5.

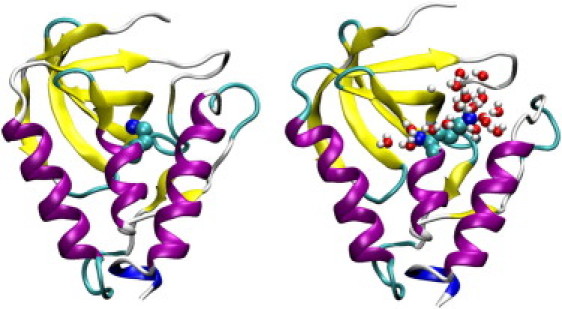
Snapshot of Δ+PHS/N100K at pH 10 (left) and pH 4 (right). Lys¹⁰⁰ and water molecules are explicitly shown.

Discussion

The REX-CpHMD simulations presented here reveal that Δ+PHS/N100K exists in both open and closed conformations, whose relative population depends on the pH condition (Fig. 6). At very low pH, Δ+PHS/N100K is mainly in the open conformation with Lys¹⁰⁰ being charged, whereas at very high pH, it is mainly in the closed conformation with Lys¹⁰⁰ being neutral. At intermediate pH, 6–7, both closed and open conformations are populated, where in the former state Lys¹⁰⁰ can be neutral or charged, whereas in the latter state Lys¹⁰⁰ is charged. The coexistence of open and closed states at intermediate pH is consistent with line broadening in the NMR spectrum of Δ+PHS/N100K at neutral pH, which is indicative of a fast exchange between the native state and other conformation(s) (personal communication with B. García-Moreno E, The Johns Hopkins University, 2011). However, the additional state(s) cannot be the unfolded state because the secondary structure is intact according to the circular dichroism spectra and the folding is first-order according to the equilibrium unfolding data (6).

Figure 6.

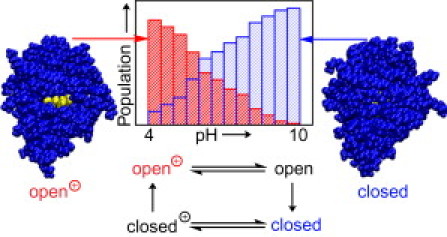
(Upper) pH-dependent population shift between the open and closed conformations of Δ+PHS/N100K. (Lower) Transition between the open and closed states must traverse the charged, closed and neutral, open forms.

It is encouraging and somewhat surprising that despite the limited simulation time, the spread in the calculated fractions of open and closed states over the entire pH range is <10% (Table 2), which indicates that the barrier crossing events between the two local minima are adequately sampled such that an equilibrium (or quasi-equilibrium) between the open and closed states in the protonated and deprotonated forms were established in the simulation. Combined with the data that demonstrate the convergence of protonation-state sampling (see Fig. S1), it suggests that all four processes comprising the underlying thermodynamic cycle as shown in Fig. 1 reached equilibrium (or quasi-equilibrium). However, the calculated value for pK_a(open) − pK_a(closed) is 1.6 units higher than the value for −logK_eq(prot) + logK_eq(dprt), revealing that the protonation/deprotonation of the open and closed states are not completely coupled in the simulation. In terms of free energy, the difference means that the deprotonation of the open versus closed state is 2.2 kcal/mol less favorable compared to the transition from the open to closed state in the protonated versus deprotonated form. Interestingly, this difference coincides with the deviation between our calculated apparent pK_a (6.9 ± 0.7) and experiment (8.6 ± 0.2), which may suggest that the simulation overestimated the value for pK_a(open) − pK_a(closed) by ∼1.7 units, assuming the calculation for −logK_eq(prot) + logK_eq(dprt) to be relatively accurate. The latter assumption is reasonable because the accuracy for the explicit-solvent based conformational sampling is likely higher than the pK_a calculation based on the hybrid-solvent scheme.

We consider the accuracy of the calculated pK_a values. Based on the theoretical consideration, the apparent pK_a can be approximated as the closed-state pK_a with a correction −logf_BH accounting for the presence of the energetically unfavorable states that are closed and protonated (Eq. 11). Using the spread in the simulated value of f_BH, the maximum random error in the correction term is estimated to be ∼0.3, which is negligible compared to the deviation between the calculated apparent pK_a and experiment. Although a systematic error is likely present in the estimated value of f_BH, we believe that it is much smaller than the error in the closed-state pK_a value. Increasing it by 1.7 unit would not only eliminate the discrepancy between the calculated and experimental pK_a values but also completely couple the titration and conformational processes. Thus, we suggest that the closed-state pK_a (5.8 ± 0.4) is underestimated. One source of error is the hybrid-solvent scheme. The GB electrostatic calculation cannot accurately capture the effect of a few nearby water molecules on the dielectric environment of a buried site. Concerning the calculated pK_a value of 10.3 ± 1.2 for the open state, we believe that the average is a reasonable estimate given the pK_a of 10.4 for the model lysine in solution. The large uncertainty is mainly due to the limited sampling time. Although water penetration and protrusion of the lysine side chain were observed upon protonation, significantly longer simulation may be required to fully capture the ionization-induced conformational change.

Equation 9 shows that the macroscopic titration of Lys¹⁰⁰ can be described by a monophasic model in analogy to the Henderson-Hasselbalch (HH) equation. This is because the protonation equilibria of the open and closed states are coupled through conformational exchanges, giving rise to a thermodynamic linkage. However, as discussed earlier, our numerical simulations do not give an exact cycle. As a result, the two protonation equilibria are not completely linked, giving rise to a titration curve that significantly deviates from the HH equation and can be better described using a linear combination of two monophasic models (Fig. 3). The deviation from the monophasic or HH behavior cannot be attributed to the coupling with other titratable residues, as Lys¹⁰⁰ remains far (at least 7 Å) away from the nearest titratable residue at all pH conditions. We also note that this type of deviation does not occur in the titration of model compounds where the perfect HH behavior is expected. Interestingly, it occurs in the titration of a single surfactant in a micelle that has extensive shape fluctuation (30). Similar to Lys¹⁰⁰, the titrating surfactant samples both buried and exposed states that have very different dielectric environment. By contrast, in more rigid micelles, where the ionization-induced change in the dielectric environment is not as drastic, titration data fit well to the HH equation (30).

We suggest that the hybrid-solvent scheme employed in our simulation may be a major source for the inexact closure of the thermodynamic cycle. Because the forces on the titration coordinates are evaluated using the GB model but conformational dynamics is propagated using the explicit-solvent model, the free energies calculated for the protonation processes may not exactly match those for the conformational processes. This is a limitation of the current CpHMD method, which will be addressed in the future. Another source for the inexact cycle is limited sampling. The timescale for conformational exchanges may be orders-of-magnitude slower than protonation/deprotonation. To more accurately estimate thermodynamic parameters for both processes, extensive sampling is required for all four energy minima and the transitions between them, which may become more challenging if a fully explicit-solvent-based CpHMD is used.

Finally, we make some remarks on the experimental pK_a of Lys¹⁰⁰. Because direct pK_a determination by NMR was not possible due to line broadening at or below neutral pH (personal communication with B. García-Moreno E, The Johns Hopkins University, 2011), the given value was obtained from analyzing the pH-dependent stability data (6,7). In this approach, the difference in the thermodynamic stability of the parent protein and the mutant N100K relative to a common reference pH condition is fit to the equation (31)

$$\Delta \Delta G_{\text{wt}}^o-\Delta \Delta G_{\text{mt}}^o=RTln\frac{1+{10}^{p{K}_a^{\text{N}}-\text{pH}}}{1+{10}^{p{K}_a^{\text{D}}-\text{pH}}},$$ (15)

to give $p{K}_a^{\text{N}}$ and $p{K}_a^{\text{D}}$ as the native- and denatured-state pK_a values, respectively. The above equation bears the assumption that the mutation does not affect the pK_a values of other residues such that their contributions in the parent protein and mutant cancel. However, because of the aforementioned evidence of local unfolding in N100K, this assumption may not be true. Our previous work shows that a correction can be made to account for the perturbation in the pK_a values due to mutation (32).

Conclusion

We have provided a theoretical framework for understanding the thermodynamics of coupled protonation and conformational equilibria. We then applied REX-CpHMD simulations to investigate the titration of Lys¹⁰⁰ and the associated conformational exchange between open and closed states of Δ+PHS/N100K. Simulations allowed, to the best of our knowledge, the first quantitative characterization of the underlying thermodynamic cycle, and details of the conformational interconversion, which cannot be yet accessed by experimental techniques. The pH-dependent population shift in Δ+PHS/N100K provides a paradigm for understanding ionization-coupled conformational transitions that are ubiquitous in biology. The ionization state of Lys¹⁰⁰ is exploited to enable a switch between open and closed conformations via two intermediates, the deprotonated open state and the protonated closed state (Fig. 6, lower). Although the inexact closure of the thermodynamic cycle points out a limitation of our CpHMD technique, this study demonstrates that REX-CpHMD simulations offer a quantitative tool for elucidating thermodynamics of ionization-coupled conformational processes that play important roles in biology.