Membrane Dynamics Correlate with Formation of Signaling Clusters during Cell Spreading

Abstract

The morphology and duration of contacts between cells and adhesive surfaces play a key role in several biological processes, such as cell migration, cell differentiation, and the immune response. The interaction of receptors on the cell membrane with ligands on the adhesive surface leads to triggering of signaling pathways, which allow cytoskeletal rearrangement, and large-scale deformation of the cell membrane, which allows the cell to spread over the substrate. Despite numerous studies of cell spreading, the nanometer-scale dynamics of the membrane during formation of contacts, spreading, and initiation of signaling are not well understood. Using interference reflection microscopy, we study the kinetics of cell spreading at the micron scale, as well as the topography and fluctuations of the membrane at the nanometer scale during spreading of Jurkat T cells on antibody-coated substrates. We observed two modes of spreading, which were characterized by dramatic differences in membrane dynamics and topography. Formation of signaling clusters was closely related to the movement and morphology of the membrane in contact with the activating surface. Our results suggest that cell membrane morphology may be a critical constraint on signaling at the cell-substrate interface.

Introduction

Cell adhesion is mediated by the specific interactions between receptors on the cell membrane and substrate-bound ligands. The contact between a cell and an adhesive surface triggers a variety of events that are vital for cellular functions such as the distinction of self and foreign in immune responses, differentiation and migration during formation of tissues, or the formation of neuronal synapses (1). Cell-substrate interactions are of particular relevance in the immune response, which involves binding of cell-surface receptors to antigen peptides displayed on antigen-presenting cells (APCs) (2).

The formation of contacts between a cell and another surface is driven by deformations occurring at multiple length scales. Large-scale deformations of the cell membrane, driven by cytoskeletal reorganization, allow the formation of cellular contacts over micrometer length scales (3–8). The cell-substrate contact area, together with the spatial pattern of receptor-ligand bonds, determines the signaling efficiency and fate of the cell. Recent work has devoted considerable attention to cell adhesion and spreading during the first few minutes of cell-substrate contact (3,4,8–11). In particular, theoretical and experimental studies have focused on the kinetics of spreading. An emerging consensus view is that cell spreading occurs in phases, where the growth of spread area (or contact) follows a power law in time with distinct exponents (4,8,9) or other distinct functional forms (3,12).

In many cell types, the engagement of receptors to surface ligands leads to the accumulation of signaling proteins that drive cytoskeletal remodeling and the activation of transcriptional programs. This is likely facilitated by nanometer-scale fluctuations of the membrane that allow binding and unbinding of receptors to ligands on another surface. Spontaneous fluctuations generated thermally or by active consumption of ATP are typical for soft interfaces, such as membranes, whose bending stiffness is comparable to k_BT (13). Transverse oscillations of up to 20–30 nm in amplitude and of frequency 1–30 Hz have been observed in many nucleated cells, such as fibroblasts, lymphocytes, and monocytes (14). These transverse fluctuations may be important in initiating adhesive linkages by potentially controlling the formation, breakage, and lifetime of receptor-ligand bonds (15). These nanoscale contacts allow activation of signaling cascades that typically lead to cytoskeletal reorganization and larger-scale membrane deformations (2,16). Despite extensive study of cell contacts, it remains unclear how membrane topography and dynamics modulate receptor-ligand interactions, the signaling function of cells, and subsequent cytoskeletal rearrangement leading to cell spreading.

We have used interference reflection microscopy (IRM) and simultaneous total internal reflection fluorescence (TIRF) microscopy to analyze the dynamics of the cell periphery, the topography of the cell-substrate contact and the formation of signaling clusters during the early stages of T cell spreading, using Jurkat cells as a model system. We found that the contact area of spreading cells is characterized by a common function of time with a characteristic timescale, which is determined in part by signaling from the receptor to the actin cytoskeleton and the dynamics of the actomyosin cytoskeleton but is largely insensitive to ligand density and substrate adhesivity. We found two distinct modes of cell spreading with similar kinetics but striking differences in membrane topography and dynamics, paralleled by a difference in the spatiotemporal development of signaling clusters. Our observations suggest that spreading kinetics are robust to environmental perturbations with an intrinsic cellular timescale designed to achieve maximal signaling within a minute or two of contact initiation. Furthermore, our studies indicate a potential link between membrane topography and the formation of signaling domains.

Materials and Methods

Cell culture and reagents

E6-1 Jurkat T cells were cultured using standard protocol (16,17). Briefly, cells were grown in RPMI medium at 37°C in a CO₂ incubator. Before imaging, 1 ml of cells was centrifuged at 240 × g for 5 min. The supernatant was removed and the cells were resuspended in imaging buffer (RPMI medium without Phenol red containing 25 mM Hepes or L-15 CO₂-independent medium, Invitrogen, Carlsbad, CA). For experiments with serum, 10% fetal bovine serum (FBS) (Invitrogen) was added to the imaging buffer. For drug inhibitions and treatments, the appropriate amount of reagent—latrunculin-A, blebbistatin, Y27632, or lysophosphatidic acid (LPA) (all purchased from Sigma-Aldrich, St. Louis, MO)—was added to the imaging buffer. Cells were incubated at 37°C for 15 min before imaging.

Substrate preparation and imaging

Chambered coverslips (LabTek) were cleaned with 1 M HCl and 70% ethanol for 30 min and dried at 37°C for 1 h. Chambers were treated for 10 min with 0.01% (weight/volume) poly-L-lysine solution (Sigma-Aldrich), drained, and dried for 1 h at 37°C. Chambers were coated with 10 μg/ml anti-CD3 antibody (Hit-3a, eBiosciences, San Diego, CA) for 2 h at 37°C. Excess antibody was removed by extensive washing with phosphate-buffered saline. Physabsorption maintains the functionality of antibodies as verified by the binding of soluble T-cell-receptor (TCR) zeta-chain fragments to the substrate (18). To test the effect of substrate coverage on spreading kinetics, the solution antibody concentration was varied over 0.01–10 μg/ml. Over this concentration range, the adsorption of antibodies on glass is in the linear part of the Langmuir isotherm, and accordingly, the amount of soluble TCR-zeta-chain fragments that bind to the substrate increases linearly (18,19). This suggests that the surface antibody density is not saturating over the applied concentration range. At ligand concentrations of 1 μg/ml of anti-CD3, there are ∼300 binding sites/μm², which is matched to the total TCRs on the cell surface (19). For coating with integrin ligands, vascular cell adhesion molecule (VCAM) and fibronectin were added to the dish at the indicated concentrations after antibody coating was completed. Cells were seeded onto chambers in the appropriate imaging medium. Fluorescence and IRM images were collected using an inverted microscope (TE2000 PFS, Nikon, Melville, NY) with a cooled CCD camera (Coolsnap HQ2, Photometrics, Tucson, AZ). TIRF imaging was done with a 60× 1.49 NA objective lens and a 491 nm laser (100 mW, Andor, South Windsor, CT) for yellow fluorescent protein (YFP) excitation.

Image analysis

Histograms of IRM image intensities of adherent cells are typically characterized by a prominent peak corresponding to the background, as well as a small peak corresponding to the adhered zones and a broad tail corresponding to the rest of the cell. Images were first low-pass filtered to remove shot noise. Two thresholds were identified by visual inspection to mark the adhered and background pixels. An expectation-maximization algorithm using the thresholds as starting points was used to fit log-concave probability distributions to the background and dark pixels and mark the regions of the image as belonging to the background or the cell (dark and bright pixels, respectively). Dilation operations were used to close the image and obtain a final binary image from which the contour and cell area were extracted. For analysis of ZAP70 clusters, the image was denoised using Wiener filtering, and clusters were isolated using the a trous wavelet algorithm (20). First, the intensity-weighted moments were computed by calculating the cell centroid from the fluorescence images, and then the mean-squared distance of each pixel belonging to a cluster from the centroid, weighted by its intensity, was calculated.

The analysis of the IRM intensity fluctuations followed a procedure described previously (13,21,22). Eighty IRM images were collected at 8 frames/s (fps) for a fully spread cell. After background subtraction and Wiener filtering, the maximum and minimum intensities (across the stack) were extracted and images were normalized. The time-averaged normalized intensity and standard deviation of intensity fluctuations at each pixel were calculated from the last 25 frames. Since intensity fluctuations due to shot noise—$\mathit{\eta }=c\sqrt{I}\mathit{\eta }=c\sqrt{I},$ where I is the mean pixel intensity and c is a camera-dependent constant—depend on the mean intensity, the apparent fluctuations for brighter regions are higher than for darker regions. To correct for this, we normalized the measured fluctuations by that expected for shot noise alone (21) to derive a relative fluctuation amplitude of $\hat{u}=(I\left(t\right)-\langle I\rangle )/\sqrt{\langle I\rangle }$ for each pixel. Pure shot noise yields $\hat{u}=1$, while deviations from unity denote interfacial fluctuations. IRM intensities can be used to construct relative height maps using $h=(\mathit{\lambda }/4\mathit{\pi }){\cos }^{-1}(2I-{\mathit{I}}_{\mathit{m}}-I_M)/({\mathit{I}}_{\mathit{m}}-I_M)$, where λ is the excitation wavelength (545 nm), and I_m and I_M are the maximum and minimum intensities across the image series. Since the relation between intensity and height in IRM is sinusoidal, the phase is known only up to modulo π. To determine the branch of the sinusoid, we can use the expressions in Limozin and Sengupta (23). Assuming the refractive index of our medium to be 1.34–1.36 (slightly larger than that of phosphate-buffered saline to account for dissolved proteins) and taking the refractive index of cytosol to be ∼1.384 (24), we calculate the height offset to be ∼10 nm. Even allowing for variations in these estimates (as well as thickness of the lipid bilayer or accumulated proteins), this height offset is likely 15–20 nm, which is below our minimum calculated height (∼20 nm). This suggests that the first branch of the sinusoid can be used and that the intensity-height relation is monotonic. In support of this, we do not find a dark rim surrounding the adhered zone, as would be expected for the 0th branch of the sinusoid (23). Despite the uncertainties in the absolute height, the height fluctuations are confined to a single branch, and hence the intensity fluctuations can be related to membrane height fluctuations.

Results

Kinetics of cell spreading

To examine the biophysical factors that determine spreading kinetics and the role of membrane dynamics in signaling we studied the spreading of Jurkat cells on glass substrates coated with anti-CD3 antibodies. Antibody binding to CD3 leads to induction of signaling and activation of actin polymerization. This model system has been shown to induce robust spreading of T cells, recapitulating many aspects of T-cell signaling and activation (16,17,19,25,26) while facilitating multimodal imaging of the cell-substrate interface. Cells were allowed to contact an antibody-coated glass substrate in serum-free media and imaged with bright-field microscopy and IRM. Within seconds of incubation, cells started forming contacts with the coated substrate. The contacts appeared as fluctuating light and dark IRM patterns and interference rings. After initial contact, the cells started spreading and rapidly increased their contact area (Fig. 1 a). The contact zone of a spreading cell appeared as a predominantly dark gray patch that increased in size isotropically, with the cell boundary being relatively smooth and circular, until the spread area saturated in 2–3 min (Fig. 1 a and Movie S1 in the Supporting Material). Cells displayed limited spreading on poly-L-lysine coated glass or plain glass, suggesting that T cell spreading requires specific adhesion.

Figure 1.

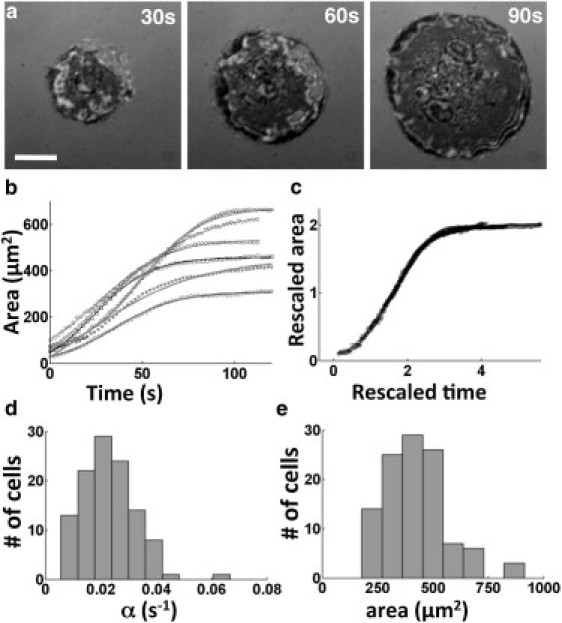
Spreading of Jurkat T lymphocytes on antibody-coated substrates. (a) Time-lapse IRM images showing the increasing contact zone as the cell spreads out. Scale bar, 5 μm. (b) Contact area as a function of time for six representative cells. The smooth lines are fits to a tanh function, A(t) ∼ A₀ tanh(αt). (c) Rescaled graphs showing that the spreading of all cells can be described by a common spreading function. (d) Histogram of the spreading rate, α (n = 88). (e) Histogram of the final spread area A₀.

We found that the cell-substrate contact area showed a rapid growth after a small initial lag period, and eventually saturated (Fig. 1 b). The overall time course of the spread area supports a model recently proposed by Chamaraux et al. (3,12). This model predicts that growth of the contact area as a function of time follows a tanh function and highlights the requirement of actin polymerization to drive spreading. Accordingly, we found that the area was well fit by a hyperbolic tangent function, A(t) ∼ A₀ tanh(αt) (Fig. 1 b), as indicated by the fit residuals. This allowed us to extract a characteristic timescale of spreading to saturation, as well as the asymptotic spread area. Upon rescaling the area of each cell with the final area A₀, and the time by α, all the data from the cells fell on a single universal curve (Fig. 1 c) showing that a common mechanism likely underlies the spreading of all these cells. From the fits, we obtained a typical spreading rate of α ∼ 0.02 ± 0.01 s⁻¹ and a final spread area of A₀ ∼ 430 ± 160 μm². Both these parameters showed some degree of heterogeneity across the cell population (Fig. 1 d).

The model of active spreading by Chamaraux et al. (12) predicts that the spreading rate should be independent or weakly dependent on the density of adhesive ligands on the substrate. To test this for T cell spreading, we examined the effect of the antibody coating density by changing the antibody concentration in solution from 0.01 μg/ml to 10 μg/ml. At concentrations >0.2 μg/ml, cell spreading was similar to that at 10 μg/ml (the control concentration), with similar spreading rates and final areas (Fig. S1, a and b). At concentrations <0.2 μg/ml, cells established adhesive patches but did not spread. However, for the small fraction of cells that did spread, the mean α value was the same as that of control cells. These observations suggest that the spreading kinetics is not rate-limited by receptor diffusion into the contact zone, in contrast to predictions (11). Similar behavior has been observed for the spreading of vesicles on adhesive substrates, which is suggestive of a first-order phase transition between a state with ligand-receptor bonds and a state with no bonds (27,28). To determine the effect of substrate adhesivity on spreading, we coated coverslips with the ligands VCAM-1, which binds to the α₄β₁ integrin, VLA-4, and fibronectin, which binds to α₅β₁ receptors on the T-cell surface. These are known to act as costimulatory factors for lymphocyte activation and to facilitate initial T-cell attachment to antigen-presenting cells in vivo and spreading in vitro (19,29). The addition of either VCAM-1 (1 μg/ml) or fibronectin (10 μg/ml) to anti-CD3 coated substrates did not affect the spreading kinetics or final spread areas (Fig. S2, c and d). Thus, spreading kinetics of T cells are robust, with a characteristic timescale that does not change over a range of antibody density and substrate adhesion.

Role of the actomyosin cytoskeleton on cell spreading

Previous work has shown that the binding of TCRs to anti-CD3 antibodies on the substrate leads to the activation of signaling cascades that regulate actin polymerization (16,17,30–32). Cells treated with very high doses (500 nM and higher) of actin polymerization inhibitor Latrunculin-A (Lat-A) do not spread. At 100 nM Lat-A, cells can spread but with lower spreading rates and final areas as compared to the control population (Fig. 2, a and b). At even lower concentrations of Lat-A (10 nM), the final areas of spread cells were similar to those for control cells, but spreading occurred with significantly slower rates (Fig. 2, a and b). The dose-dependent effect of Lat-A on spreading rate indicates that the rate of spreading is largely determined by actin polymerization kinetics, and distinguishes it from the passive spreading described by Cuvelier et al. (4). Previous studies have shown that nonmuscle myosin II (NMMII) regulates the rate of cell spreading in fibroblasts (33,34). In T cells, NMMII (specifically the IIA isoform) knockdown or inhibition alters signaling in the immune synapse (35). However, its role in the initial spreading of T cells has not been investigated. Cells treated with blebbistatin (a specific inhibitor of the ATPase action of NMMII) were able to spread, and the contact area growth over time followed a tanh function, as in the case of control cells. For low concentrations of blebbistatin (≤20 μM), the rate of spreading was only weakly reduced and the maximal spread area showed no significant change (Fig. 2, c and d). In 50 μM blebbistatin, the spreading rate was reduced compared to the control case, but the maximal areas were largely unaffected (Fig. 2, c and d). To assess the roles of distinct signaling pathways that might control the activity of NMMII, we investigated the role of the Rho-associated protein kinase (ROCK), which is essential for phosphorylation of myosin light chain (MLC), in turn essential for NMMII activity. We found that the ROCK inhibitor Y27632 (100 μM) significantly reduced the spreading rate of cells but not their final area.

Figure 2.

Cells with compromised actin polymerization do not spread efficiently. (a) Spreading rate (α) decreases as the concentration of Lat-A increases (p < 0.01, t-test). (b) The final spread area is unaffected for small concentrations of Lat-A, but is much smaller for higher concentrations (p < 0.05, t-test). (c) Spreading rate is diminished upon inhibition of the activity of NMMII or Rho kinase (ROCK). (d) Final spread area is not affected by inhibition of NMMII or ROCK. The number of cells analyzed was >18 in all conditions.

Effect of serum on cell spreading

In the experiments described so far, cells were cultured in growth medium, and then withdrawn from serum 15 min before imaging. These conditions are used routinely to study T-cell activation and signaling (30,31). To test whether TCR-mediated spreading behavior depends on the presence of serum, a more physiological condition, we imaged cell spreading in medium supplemented with 10% FBS. As in serum-free medium, cells in medium with 10% FBS rapidly established contact with the substrate and started spreading (Fig. 3 a and Movie S2). The growth of contact area as a function of time for a spreading cell could be well fit by a tanh function, similar to the case for serum-free conditions. However, the kinetics were characterized by an irregular growth of the projected cell area (Fig. 3 b). The spreading rate, α, for cell populations was the same in the presence and absence of serum (Fig. 3 c) (p > 0.1, t-test, n = 88 serum-free, n = 45 with serum), although the final spread area, A₀, was lower in the serum-supplemented than in the serum-free case (p < 0.05). However, there was a remarkable difference in the nature of spreading. Kymographs of the cell edge (Fig. 3 d) showed that the cell-substrate contacts were highly dynamic, with the cell edge undergoing repeated protrusions and retractions during spreading. In contrast, cells spreading in the absence of serum showed a smooth movement of the cell periphery (Fig. 3 e). Across the population, in the presence of serum, most cells showed an irregular anisotropic pattern of spreading (>75%), whereas nearly all cells in serum-free medium (>95%) showed smooth isotropic spreading.

Figure 3.

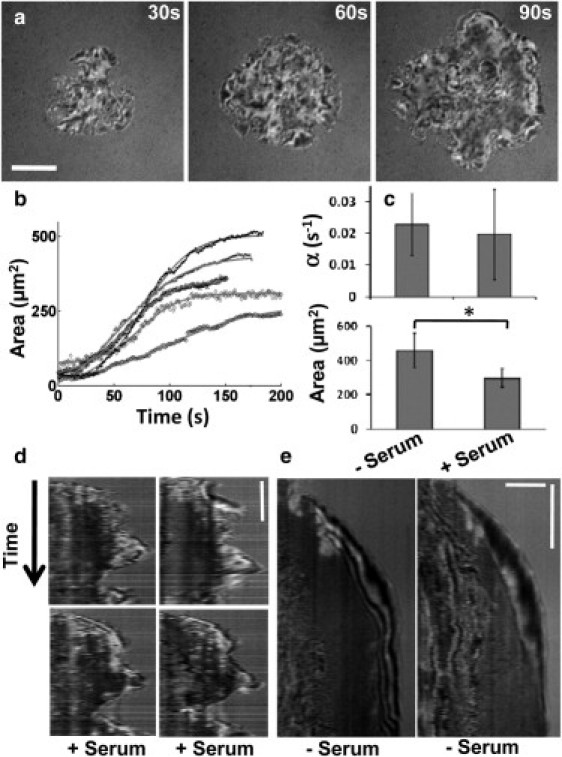
Spreading in the presence of serum is qualitatively different. (a) Time-lapse IRM images of a T cell spreading on antibody-coated glass substrate in the presence of serum. Scale bar, 5 μm. (b) Contact area of the cell as a function of time. Each graph corresponds to a different cell. The solid gray lines show a fit to a hyperbolic tangent function. (c) Comparison of spreading rate, α, and final spread area, A₀, for serum and serum-free cases shows that these parameters are very similar in the two conditions. (d) Kymographs of four representative sections in serum. (e) Kymographs of two representative sections in serum-free conditions (scale bars, 3 μm, 30 s).

Membrane topography and fluctuations

The geometrical constraints imposed by the dynamics and topography of the ventral membrane are likely to influence receptor-ligand interactions. The morphology of the cell-substrate contact can be studied using images that are formed by interference between the light reflected from the top surface of the substrate and the bottom surface of the cell, as done using IRM imaging. The resulting intensity distribution is related to the height of the cell membrane above the substrate, with different intensities in the IRM images corresponding to a variation in membrane height above the substrate (7,13,23). We found that the IRM images of the cell-substrate contact were different with and without serum. In the absence of serum, the IRM image of the contact zone was a smooth dark gray and slowly increased in size without significant changes in the pattern, indicative of a membrane that is closely and uniformly adhered to the substrate (Fig. 4 a). In contrast, cells spreading in serum-supplemented medium displayed large spatial variations in IRM intensity, indicating convoluted membrane topography in the contact zone (Fig. 4 b).

Figure 4.

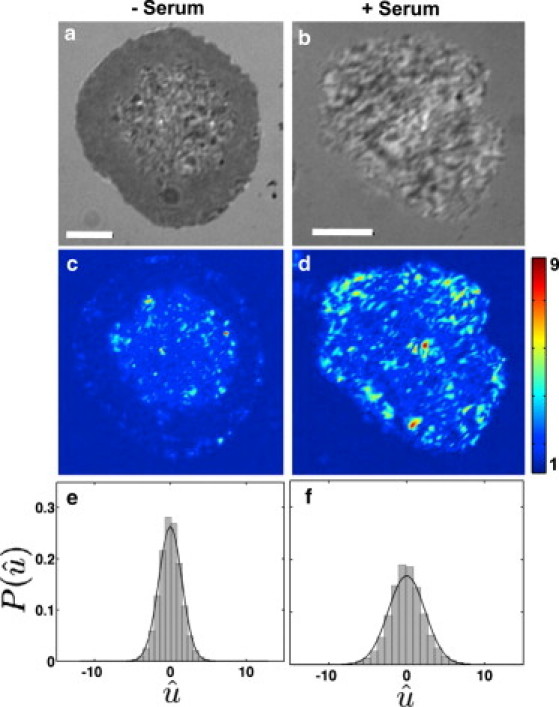
Cell-contact topography is different in the two spreading modes. (a) Denoised IRM images for cells in serum-free media, and (b) in serum containing media. (c) Heat map showing intensity fluctuations relative to shot noise for cells in serum-free media. (d) Heat map showing intensity fluctuations relative to shot noise for cells in serum containing media. (e) Population histograms of relative fluctuation amplitudes, $\stackrel{⌢}{u}$, in serum-free and (f) in serum. Note: The color bars in both cases represent fluctuation amplitudes relative to shot noise. Scale bars, 5 μm; n = 15 for each condition.

To quantify the dynamic nature of the cell-substrate interface, we performed rapid IRM imaging (8 Hz) on fully spread cells to calculate the variability of relative height fluctuations over time (21). We found that in the absence of serum, the height of the membrane in the cell-substrate contact zone fluctuated very little, with intensity values varying over a range expected from shot noise (Fig. 4 c), which denotes strongly adhered regions. In contrast, the membrane height was very dynamic for cells spreading in serum-supplemented medium, and exhibited large fluctuations (Fig. 4 d). Across the population, these fluctuations have a narrower distribution (F-test, p < 0.001) in the serum-free case (Fig. 4 e) compared to the serum-supplemented case (Fig. 4 f). Our results suggest that in the absence of serum, cells spread with a smooth progression of the periphery while making a tight attachment to the substrate. In the presence of serum, the membrane appears to be loosely attached to the substrate, with larger vertical fluctuations of the membrane height, as well as larger excursions of the edge in the horizontal plane.

To determine the factors in serum that may be responsible for the enhanced dynamics of the membrane, we studied the effect of lysophosphatidic acid (LPA), a serum component that acts through G-protein coupled receptors to activate Rho-GTPase pathways. Previous studies have shown that LPA leads to changes in membrane topography and dynamics, possibly through the modulation of ezrin-radixin-moesin (ERM) phosphorylation (37–40). These proteins are known to be expressed in T cells and are critical for proper immune synapse formation (41). We incubated cells in serum-free medium supplemented with 10 μM LPA, allowed them to spread, and imaged membrane fluctuations in spread cells. We found that the addition of LPA to serum-free medium resulted in enhanced membrane fluctuations, similar to the effect seen with the addition of serum (Fig. S2). Addition of 100 nM Lat-A to fully spread cells in serum resulted in a decrease of the fluctuation amplitude (p < 0.0001, F-test). However, fluctuation amplitudes were higher overall than those observed in serum-free conditions. These results suggest that the enhanced fluctuations in serum require an intact actin cytoskeleton.

Signaling clusters colocalize with strongly adhered regions

Antigen binding to the TCR complex in Jurkat cells results in the phosphorylation of CD3ζ chains on the TCR. These serve as binding sites for a variety of kinases and scaffold proteins, which then accumulate in microclusters nucleated by activated TCR (17,26,42–44). ZAP70 is one such kinase, which is recruited to phosphorylated CD3ζ and subsequently phosphorylates a number of downstream targets. As visualizing phosphorylated TCR is difficult in a living cell, fluorescently tagged ZAP70 has been used as a marker for sites of initial signaling (25). Even though signaling microclusters have been observed consistently upon cell activation (42,44), the principles governing their formation or distribution are not well understood. We conjectured that the morphology and dynamics of the membrane close to the antibody-coated surface might determine contact formation and govern the lifetime of bonds, thus influencing the formation of signaling clusters.

We examined the formation of ZAP70 clusters and membrane morphology during T cell spreading by TIRF microscopy of YFP-ZAP70-expressing cells and IRM imaging, respectively. Signaling clusters formed only in cells spreading on antibody-coated substrates. Substrates coated with poly-L-lysine with no antibody failed to initiate cluster formation (Fig. S3). Regions of high fluorescence intensity of YFP-ZAP70 correspond to locations of activated TCRs in the membrane. Similar to previous studies (17,44), ZAP70 accumulated in a punctate manner throughout the cell-substrate contact zone (Fig. 5 a, left). The normalized intensity map of the contact zone of the same cell was generated from IRM images (Fig. 5 a, middle), which are related to the membrane height above the substrate up to an additive constant (see Materials and Methods). Clusters were localized from the fluorescence images, and the cluster boundaries were traced and superimposed on the intensity map. Our results show that ZAP70 clusters were colocalized with regions of the membrane that are topographically similar, corresponding to similar IRM intensity (Fig. 5 a, right).

Figure 5.

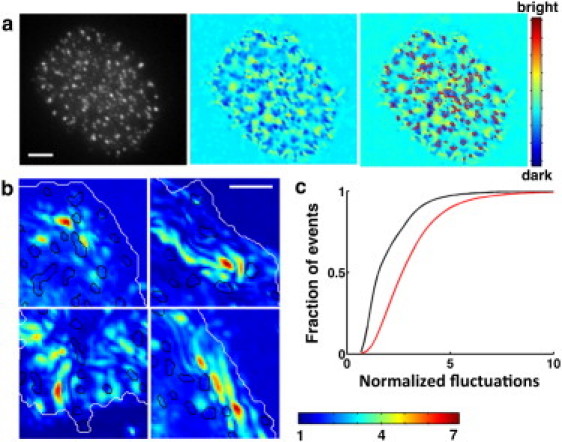
Membrane topography and dynamics of contact are correlated with signaling. (a) Left: TIRF image showing ZAP70 clusters; middle: denoised IRM intensity map showing relative membrane height; right: contours in red show ZAP70 clusters superimposed on the height map. Scale bar, 5 μm. (b) ZAP70 clusters (contours in black) superimposed on regions of low fluctuation, shown in four typical zoomed-in sections of the contact zone from four different cells in serum-supplemented medium. Scale bar, 2 μm. (c) Cumulative histogram of the normalized height fluctuations (black, serum-free; red, serum-supplelmented) for pixels belonging to ZAP70 clusters (10 cells for each condition).

We further reasoned that the fluctuations of the membrane might influence the location and dynamics of signaling clusters. We characterized the spatial correlations between the fluctuation map and the location of signaling clusters in spread cells. Fig. 5 b shows the superposition of cluster boundaries with the fluctuation map for small regions from four representative cells in serum. We found that in the presence of serum, clusters formed in regions of lower fluctuation (median value relative to background intensity fluctuations of 2.5, n = 20). In the serum-free case as well, the locations of ZAP70 clusters were strongly correlated with areas of lowest fluctuation (median value relative to background intensity fluctuations of 1.8, n = 20), as shown in the cumulative histogram of fluctuation values (Fig. 5 c). Consistent with our observations of overall larger fluctuations in the presence of serum, the fluctuation values associated with ZAP70 clusters were higher in the presence of serum than in its absence.

Spatiotemporal distribution of clusters is different in the two modes of spreading

Given our observations of differences in the dynamics of the cell edge and membrane fluctuations in the presence and absence of serum, we reasoned that the temporal development and distribution of signaling clusters would show distinctions in the two modes of spreading. In the serum-free case, where the cell boundary shows steady isotropic expansion, ZAP70 clusters formed upon initial contact and continued to form as the cell spread, covering the entire contact zone (Fig. 6 a and Movie S3). New clusters mainly formed at the periphery, increasing in number as the cell spread. The distance between the periphery of the clustered zone at any given time point (Fig. 6 a, cyan line) and the final cell periphery (Fig. 6 a, red line) steadily decreased, demonstrating the smooth outward progression of the clustered zone. In the presence of serum, where cells showed considerable oscillations of the boundary, clusters appeared initially over a large area, which slowly filled in with more clusters (Fig. 6 b and Movie S4). Furthermore, the spatial distribution of ZAP70 was distinct in the two cases. In the serum case, the ZAP70 clusters were sharply punctate and randomly distributed over the contact zone (Fig. 6 c). In contrast, without serum, ZAP70 fluorescence appeared diffusely distributed and concentrated at the periphery (Fig. 6 d). This was reflected in a comparison of the second spatial moment (intensity-weighted moment of inertia) of the ZAP70 fluorescence distribution across the two populations (Fig. 6 e). To examine the effect of NMMII activity on the formation of ZAP70 clusters, we imaged cells in the presence of Y27632 for both serum and serum-free conditions. The IRM patterns and the distribution of clusters were similar to the control case (data not shown). Thus, although inhibition of ROCK slows down spreading, it does not change the morphology of the cell-substrate interface and cluster formation, suggesting that ZAP70 cluster formation is determined more by the membrane morphology than by the speed of spreading.

Figure 6.

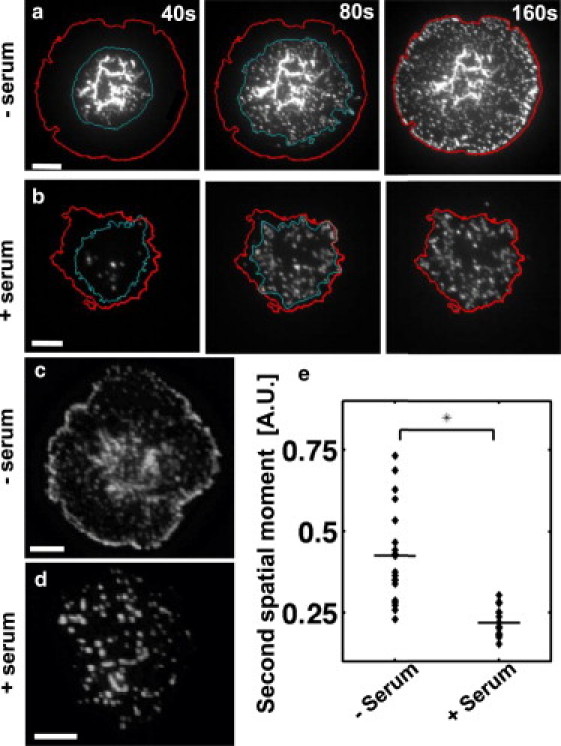
Dynamics and spatial distribution of ZAP70 clusters is distinct in the two modes of spreading. (a) Time-lapse TIRF image of T cells expressing YFP-ZAP70 spreading on an antibody-coated glass substrate in serum-free media. The cyan (inner) line represents the boundary of the clustered zone at any given time point. The red (outer) line denotes the final boundary of the fully spread cell. (b) Time-lapse TIRF image of T cells spreading in serum. To facilitate comparison, the three time-lapse images shown are at 40 s, 80 s, and 160 s (corresponding to rescaled times of 1, 2, and 4). (c) TIRF image of a typical YFP-ZAP70 cell in serum-free media. (d) TIRF image of a typical YFP-ZAP70 cell in serum containing media. Scale bars, 5 μm. (e) Intensity-weighted second spatial moment of fluorescent clusters show that ZAP70 clusters are more peripheral in serum-free conditions but uniformly distributed in serum (p < 0.001, Wilcoxon rank test).

Discussion

The initial attachment of cell membranes to a surface plays a key role in the formation of receptor-ligand bonds during cell-cell and cell-substrate junction formation. We have investigated the topography and fluctuations of the cell membrane during contact formation with a ligand-coated surface and the formation of signaling microdomains. We found that the morphology of the membrane is directly linked to formation of signaling clusters during Jurkat T cell spreading. We identified two modes of spreading that are characterized by marked differences in the dynamics of the cell edge, consistent with previous observations in spreading fibroblasts (5). In addition, we found that membrane topography and fluctuations were very different in the two modes. Whereas the spreading rate was similar in both modes, the spatiotemporal characteristics of signaling, as assessed by the accumulation of the kinase ZAP70 in microclusters, were distinct. These signaling microclusters of ZAP70 preferentially formed in regions of low fluctuations and strong adhesions between the cell and the substrate.

Models of spreading and role of physical parameters

We found that the contact area of spreading Jurkat T cells on antibody-coated substrates was well described by a hyperbolic tangent function, with a characteristic timescale of ∼45 s. This is similar to the time over which the initial signaling peaks (45). Our results are consistent with a recent model of cell spreading, which predicts that the spread area grows as tanh(αt) (3). Previous studies have described the kinetics of spreading in different cells as power laws (3–6,8,9,46). A recent hydrodynamic model of spreading that balances the polymerization stress by the stress due to membrane deformation results in a power-law growth of cell area (exponent ∼1) over a timescale of a few minutes (10). We note that the early phase of spreading in our observations, after the initial lag period, is compatible with models suggesting linear growth of cell area (since at early times a tanh function is linear). Perturbing the actin cytoskeleton using Lat-A in a dose-dependent manner leads to slower spreading, as predicted by these models. This shows that actin polymerization is essential for spreading and controls its timescale.

Our observations, in combination with current literature, suggest the following mechanistic model for spreading. The initial contacts between the cell and the substrate lead to formation of receptor-antibody bonds, a critical number of which might be required to trigger downstream signaling events (this would lead to the slight lag observed in the very early stages of spreading). TCR engagement triggers signaling events, including the dephosphorylation of ERM proteins, which loosens the plasma membrane from the underlying actin cortex (39). Signaling also leads to actin polymerization via activation of various downstream pathways (16,17,31,32). The polymerization of actin against the detached membrane leads to the rapid advance of the cell edge, thereby increasing the contact area and bringing additional receptors into contact with the antibody-coated substrate. These newly engaged receptors initiate signaling pathways, and the cycle continues. The actin-generated force is opposed by the stress due to membrane tension and bending of the membrane-cytoskeleton composite, slowing down spreading and leading to saturation in the contact area.

The role of NMMII in determining the early spreading kinetics in T lymphocytes is not known. Our experiments showed that inhibition of NMMII and ROCK activity slowed down spreading kinetics without significantly altering the maximal spread area. This is in contrast to observations in fibroblasts, where spreading is enhanced by the inhibition of NMMII (33,34), presumably due to the loss of contractile activity of the actomyosin network that applies an inward tension to cells. This suggests that the actomyosin network may not function similarly in the early stages of T cell spreading. It is possible that the contraction of the actomyosin network applies a force that squeezes the lamellipodia outward (47). Inhibition of myosin would then slow down the outward movement of the cell edge, as we observed. This alternate hypothesis has been postulated before for leukocyte and lymphocyte motility and could also presumably be functional during the spreading of T cells (47).

Significance of membrane topography and dynamics for signaling

We found that the topography of the interface between the cell membrane and the activating substrate was smooth in the absence of serum and characterized by small fluctuations of the IRM intensity. In contrast, the membrane at the interface was highly undulating and rough in the presence of serum, as indicated by a nonuniform IRM pattern and larger height fluctuations. The T-cell surface is known to be convoluted with membrane wrinkles (48,49), which likely corresponds to the rough IRM pattern that we observe. This uneven membrane topography likely leads to zones of low and high adhesion between the cell membrane and the substrate, with increased fluctuations in regions of lower adhesion. These membrane wrinkles are believed to be stabilized by ERM-mediated actin-membrane linkages (48). Serum withdrawal may lead to global dephosphorylation of ERM and the dissolution of folds, resulting in a flatter cell-substrate interface and lower fluctuations. In support of this, we find that addition of LPA, a serum factor implicated in ERM phosphorylation and the control of membrane morphology (37,38), to serum-free medium leads to an enhancement of fluctuations. Furthermore, addition of Lat-A to cells spread in serum leads to decreased fluctuations and more regions of stronger adhesion, likely due to the partial dissolution of folds upon actin depolymerization. In addition, some serum components might act as repellers that inhibit adhesion. As has been shown for vesicle adhesion, repellers could serve to hinder specific adhesion, thereby leading to regions of the membrane that are more loosely in contact with the surface and free to fluctuate more (15,23). We expect that both active signaling downstream of LPA, and possibly other factors, as well as modulation of adhesion due to serum factors, work in concert to result in the observed membrane topography and dynamics. Active myosin contraction may not be the driver of the fluctuations that we observe, since myosin inhibition did not affect the fluctuations.

The duration and topography of intercellular contacts is thought to play a key role in influencing signaling in immune cells (50), a view reinforced by observations of dynamic membrane protrusions such as ruffles and filopodia at the synapse between NK cells and target cells (51). Membrane topography can influence activation of signaling cascades in various ways (14). First, regions of high local curvature on the plasma membrane might facilitate the formation of clusters of signaling proteins (52). Second, forces exerted on receptor-ligand pairs due to fluctuations might enhance clustering by causing conformational changes of receptors, leading to phosphorylation and activation of signaling cascades. Third, membrane topography and fluctuations might influence the accessibility of cell-surface proteins for binding and their association/dissociation kinetics, thereby influencing the formation of signaling domains (21,28). In support of this, we found that the location of clusters of ZAP70 correlated well with domains of low fluctuation or strong adhesion, indicating that the topography of the contact is important for determining the location of signaling assemblies.

The spreading and membrane dynamics that we observe may be relevant to the events that occur during the activation of T cells. Activation requires physical interaction of T cells with antigen-presenting cells (29,54), which display fragments derived from foreign and self proteins on their surface where they bind to specialized receptors (TCRs). Receptor engagement leads to the reorganization of actin filaments, enabling the T cell to spread over the surface of the APC (16,17). Antigen recognition and activation depends on two main aspects of T cell spreading. The timescale of spreading determines the time over which a maximal area is available for the receptors on the T cell to sample antigens on the APC and initiate sustained signaling. As signaling events, which ultimately determine the cellular response, are initiated within a minute of contact (55), the rapid increase in contact area during early spreading is critical for the immune response. Further, the local morphology and duration of intercellular contacts at the interface between two cells affects the spatiotemporal patterns of signaling (50). Despite sustained attention to protein rearrangements during formation of contacts between T cells and APC (26,29,44) and the biochemical aspects of signaling (43), the biophysical constraints that shape the initial spreading process and kinetics of contact formation are largely unknown. We have provided, for the first time to our knowledge, a view of the membrane topography during early events in T cell signaling and shown that this is correlated with the formation of signaling clusters. Our observations suggest that the cellular membrane morphology may be a critical constraint on signaling at the cell substrate interface.