Highly Perturbed pK_a Values in the Unfolded State of Hen Egg White Lysozyme

Abstract

The majority of pK_a values in protein unfolded states are close to the amino acid model pK_a values, thus reflecting the weak intramolecular interactions present in the unfolded ensemble of most proteins. We have carried out thermal denaturation measurements on the WT and eight mutants of HEWL from pH 1.5 to pH 11.0 to examine the unfolded state pK_a values and the pH dependence of protein stability for this enzyme. The availability of accurate pK_a values for the folded state of HEWL and separate measurements of mutant-induced effects on the folded state pK_a values, allows us to estimate the pK_a values of seven acidic residues in the unfolded state of HEWL. Asp-48 and Asp-66 display pK_a values of 2.9 and 3.1 in our analysis, thus representing the most depressed unfolded state pK_a values observed to date. We observe a strong correlation between the folded state pK_a values and the unfolded state pK_a values of HEWL, thus suggesting that the unfolded state of HEWL possesses a large degree of native state characteristics.

Introduction

A good understanding of the determinants of protein stability remains an essential requirement for the successful design of novel biocatalysts and protein-based therapeutics. Our present understanding of protein stability derives mostly from extensive studies of the folded state of proteins as observed in x-ray structures combined with experimental measurements of ΔΔG_fold values. Such studies have yielded valuable information on the strength of e.g., hydrogen bond interactions and van der Waal's forces, and have been used to construct numerous algorithms (e.g. (1–4).) for predicting mutant-induced changes in protein stability. These algorithms have been constructed on the premise that the unfolded state consists mostly of weak local interactions and play no particular part in determining the stability of a protein. However, in recent years there is a growing awareness that the mutant-induced changes in the energy of the unfolded state are important. Aune et al. (5) early noted that several proteins contained residual structure in the acid- and heat-denatured states, and studies on the ovomucoid third domain (6), barnase (7), RNase SA (8), N-terminal domain of the ribosomal protein L9 (9) and CI2 (10) pointed to perturbed unfolded state pK_a values. NMR studies have shown significant residual structure in unfolded states and a growing body of evidence points to the presence of significant interactions in protein unfolded states (11–15). Electrostatic interactions play a particularly interesting role in protein stability due to their long-range nature and their role in determining protein pK_a values and thereby the pH dependence of protein stability (16). The latter is of significant interest in both academic studies (17–20) and in industrial applications that often take place at unphysiological pH values (21,22). The pH dependence of protein stability is determined by the difference in pK_a values between the folded and unfolded states of the protein (see later), and a detailed understanding of protein pH-stability profiles therefore necessitates the measurement of site-specific protein pK_a values.

Site-specific pK_a values can be measured in the folded state of proteins using a number of techniques, but the method of choice is NMR spectroscopy (23). Folded state pK_a values have been found to be significantly shifted compared to the so-called model pK_a values for amino acid side chains that approximate the pK_a value of the amino acid side chain in solution (24–26). Several research groups have identified shifted pK_a values in the unfolded states of proteins (7,10,27,28) using NMR spectroscopy or denaturation experiments of mutant proteins. Typically, these experiments have found unfolded pK_a values for acidic residues to be slightly lowered compared to their model compound pK_a values, thus indicating the existence of stabilizing electrostatic interactions in the unfolded state. However, presently known pK_a values for unfolded states are relatively unperturbed compared to their model pK_a values as shown by an average absolute perturbation of 0.17 pK_a units for currently known pK_a values in the unfolded states of proteins (data not shown). The corresponding value for the folded state pK_a values of the same residues is 0.36 units, and the average absolute perturbation of pK_a values in the PPD (24) is 0.84 units, thus amounting to a significant difference in the average perturbation of folded and unfolded pK_a values. We hypothesize that the lower average pK_a perturbation reflects the small size and relative disorder of the unfolded states of the proteins studied until now, and we therefore set out to examine if titratable groups with significantly perturbed pK_a values in the unfolded state could be found in proteins with more constrained unfolded state ensembles.

In this work, we use the detailed knowledge of the pK_a values of the folded state of HEWL ((23,29) and B. M. Tynan-Connolly, H. Webb, F. O'Meara, J. E. Nielsen, unpublished) in combination with site-directed mutagenesis and CD temperature-denaturation measurements to determine pK_a values of seven acidic residues in the unfolded state of the protein. We examine the pK_a values in terms of their similarity to the pK_a values in the folded state of HEWL, and we examine the ability of an MD/PBE-based protocol to reproduce the unfolded state pK_a values.

Understanding the pH dependence of HEWL stability

The pH dependence of HEWL stability was studied extensively in the 1960s with several landmark works in the field (31,32), and its heat-denatured state was found to contain significant amounts of residual structure (5). Furthermore, the denaturation process was found to be essentially reversible and two-state, and although the latter contradicts with the more high-resolution work on HEWL folding (33) the former conclusion can easily be confirmed with a simple reheating experiment in a CD spectropolarimeter (Fig. S1 in the Supporting Material). The heat-denatured state of HEWL is thus a logical place to look for significantly shifted pK_a values due to its compactness, which presumably is induced by the four disulfide bonds that stabilize the protein. Earlier work (31) has speculated on the existence of perturbed pK_a values in the unfolded states, but to our knowledge these hypotheses have never been confirmed.

The pH-dependent stability of proteins has been an active area of research for several decades following the seminal work of Linderstrøm-Lang (34). Theoretical investigations center on the framework derived by Tanford and Wyman (16,35) that describes the pH-dependent stability of reversibly folding proteins as being a function of the difference between the net charge of the folded and unfolded states:

$$\Delta \Delta G_{fold}=\ln \left(10\right)RT\underset{\mathrm{p}{\mathrm{H}}_{start}}{\overset{\mathrm{pH}}{\int }}\Delta Qd\mathrm{pH},$$ (1)

where ΔG_fold is the free energy of folding, R is the gas constant, T is the temperature, and ΔQ = Z_F – Z_u with Z_F and Z_U being the net charge in the folded and unfolded states, respectively. Studies that exploit mutation-induced differences in pH-stability profiles have been used to examine and determine pK_a values in the folded and unfolded states of proteins (7,36–38) and have generally been of great use in explaining the pH-stability profiles of proteins. Recently, NMR studies have started to provide pK_a values for unfolded states of proteins under native conditions (27,39–41), thus significantly expanding our understanding of the unfolded ensembles of proteins.

Materials and Methods

Construction of mutants

HEWL mutants were constructed using Escherichia coli/Pichia pastoris shuttle vector, pPic9 (Invitrogen) using the QuikChange site-directed mutagenesis kit (Agilent Technologies). Mutagenic primers were designed using the DNATool component of PEATDB (42) and incorporated a silent mutation to introduce a unique restriction site. After initial transformation into E. coli XL-1 blue supercompotent cells (Agilent Technologies) mutant clones were identified by colony polymerase chain reaction and restriction digests.

E. coli colonies displaying the correct restriction digest pattern for the mutant DNA sequence were used for plasmid extraction. Plasmid extraction was performed using a QIAprep Spin Miniprep Kit (Qiagen) and 2 mL cultures of LB-ampicillin, (100 μg/mL), incubated overnight at 37°C, 200 rpm. Purified plasmid was eluted in 20 μL of sterile MilliQ water and stored at −20°C.

Plasmids were linearized using Pme1, (2 h at 37°C), before transformation into the methylotrophic yeast strain P. pastoris. Newly made transformants were incubated at 30°C in 250 μL NZY broth, without shaking, before aliquoting 25 μL of cells onto minimal dextrose agar plates for incubation at 30°C, 48 h. The identity of all mutants was confirmed by sequencing the entire hewl gene to ascertain that only the desired mutations were present.

Fermentation

WT and mutant strains of P. pastoris were cultured using a 2 L bioflo-110 bio-reactor unit (New Brunswick Scientific). The Pichia strain was used to inoculate an MD plate and incubated at 30°C for 48 h. A single colony from this was used to inoculate 2 mL of buffered minimal dextrose, BMD, (60 mL deionized water, 10 mL dextrose (10% w/v), 10 mL ammonium sulfate (15% w/v), 10 mL yeast nitrogen base (13.4% w/v), 10 mL of 1.0 M potassium phosphate buffer, 0.2 mL biotin (20% w/v)), and incubated at 30°C for 18 h, at 225 rpm.

This 2 mL culture was then used to inoculate a further 98 mL of BMD, and incubated at 30°C, 225 rpm for an additional 18 h. This 100 mL BMD culture was used to inoculate 800 mL sterile basal salts media (calcium sulfate dihydrate (0.00028% w/v), magnesium sulfate heptahydrate, (0.0046% w/v), phosphoric acid (0.0084% v/v), adjusted to pH 3.0 with KOH, and 140 mL of nutrients solution (40 mL dextrose (10% w/v), 90 mL ammonium sulfate (15% w/v), 5 mL biotin (20% w/v), 5 mL Pichia trace metals).

The culture was maintained at pH 5.0 throughout the fermentation using 2 M KOH. The temperature was maintained at 30°C using a heater blanket, and dissolved oxygen levels were maintained at 30% via automatic agitation.

Induction was initiated 24 h after inoculation by the addition of 50 mL of 7% (v/v) methanol, to a final concentration of 0.05% v/v. Methanol levels were maintained at 0.05% by the further addition of methanol solution over the course of 72 h until cells were harvested by centrifugation.

To harvest, cells were separated from the media by centrifugation at 10,000 × g for 20 min in an F-10 fixed angle rotator at 4−C. Supernatant was kept, and filtered using Whatman microfiber filters, 0.47 μm, and durapore membranes; 0.45 μm. Filtered supernatant was stored at 4°C until purification could be achieved.

Protein purification

Initial purification was performed using IEX-FPLC (UPC-900 Amersham Biosciences) and 50 mL of Source 30S anion exchange resin (GE Healthcare). The column was equilibrated with six column volumes of loading buffer, (50 mM Tris-Base, pH 7.5) before loading the supernatant. After loading, the column was washed with three column volumes of loading buffer to remove any unbound protein. Purification of lysozyme was obtained by the application of a salt gradient provided by the elution buffer (50 mM Tris-Base with 1 M NaCl, pH 7.5). A gradient of between 0% and 40% elution buffer was applied over six column volumes, with HEWL eluting from the column at ∼22% elution buffer, or 220 mM NaCl.

Individual fractions from this purification were pooled and diluted 1:5 with MilliQ water to perform a second round of purification, this time using 30 mL of Source 15S anion exchange resin (GE Healthcare). Sample loading, washing, and elution steps were as described previously. Purified fractions were pooled and stored at 4°C.

CD temperature denaturation scans

The temperature-induced denaturation of WT and mutant HEWL proteins was determined at pH 1.5, 2.0, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 10.5, and 11.0 in a 50 mM Britton-Robinson buffer (50 mM Na₃PO₄, 50 mM H₃BO₃, and 50 mM acetic acid) adjusted by KOH or HCl to the appropriate pH. CD spectropolarimetry was performed using a Jasco J-810 equipped with a Peltier element for sample temperature control. A volume of 650 μL HEWL (0.1 mg/mL) was heated from 10 to 95°C in a 2 mm quartz cuvette. We used a scanrate of 1.0°C/min and followed the change in ellipticity at 222 nm. Changes in the ellipticity signal were measured for every 0.1°C increases in temperature. The bandwidth for the incident light was 1 nm.

Fitting thermal denaturation data

Ellipticity as a function of temperature was converted to fraction folded using the relationship:

$$f_u=\frac{Y_0-\left(Y_{\mathrm{N}}-m_{\mathrm{N}}T\right)}{\left(Y_{\mathrm{U}}-m_{\mathrm{U}}T\right)-\left(Y_{\mathrm{N}}+m_{\mathrm{N}}T\right)},$$ (2)

where f_U is the fraction unfolded, Y₀ is the signal obtained from the CD, Y_N is the y-axis intercept for the native baseline, Y_U is the y-axis intercept for the unfolded baseline, m_N and m_U are the slopes of the native and unfolded baselines, respectively.

After conversion of ellipticity into fraction unfolded, the data were analyzed using the van't Hoff equation:

$$\ln \left(K\right)=\frac{\Delta S^{\circ }}{R}-\frac{\Delta H^{\circ }}{R}\frac{1}{T},$$ (3)

to determine T_m, ΔS°, and ΔH° for each protein. These values are given for all proteins and pH values in the Supporting Material.

Conversion of T_m values to ΔΔG°_fold values

ΔΔG_fold for all proteins (mutants and the WT) at each pH value was determined using the T_m for WT HEWL at pH 1.5 and the Schellman equation: ΔΔG = ΔS°_mΔT_m (43). Because there is a significant amount of variation in the ΔS°_m values as determined by the van't Hoff analysis, we used a range of ΔS°_m values to properly assess the uncertainty of the ΔΔG°_fold values (see Supporting Material).

Fitting pH-stability profiles

pH-stability profiles were fitted using the well-known equation derived by Tanford (16) relating the pH-dependent stability of a protein to the difference in charge between its folded and unfolded states:

$$G_{fold}\left(\mathrm{pH}\right)=\ln \left(10\right)RT\underset{\mathrm{p}{\mathrm{H}}_{start}}{\overset{\mathrm{pH}}{\int }}\Delta Qd\mathrm{pH},$$ (4)

where R is the gas constant, T is the temperature, and ΔQ is the difference in charge between the folded and unfolded states:

$$\Delta Q=Z_{\mathrm{F}}-Z_{\mathrm{U}}.$$ (5)

If we assume that all titratable groups behave as perfect Henderson-Hasselbalch groups, the charge of a given state can then be calculated using a simple summation using the Henderson-Hasselbalch equation:

$$Z_X=\sum _{i=1}^{\mathit{N}}\frac{z_i}{{10}^{z_i\left(\mathrm{pH}-\mathrm{p}{\mathrm{K}}_{a,i}\right)}+1},$$ (6)

where Z_X is the charge of the protein in state X, z_i is +1 for a base and −1 for an acid and pK_a,I is the pK_a of group i in state X. N is the number of titratable groups in the protein.

The insertion of Eqs. 5 and 6 into Eq. 4 leads to Eq. 7 relating the pK_a values of the folded and unfolded states of the protein directly to its pH-stability profile:

$$\Delta G_{fold}\left(\mathrm{pH}\right)=\ln \left(10\right)RT\underset{\mathrm{p}{\mathrm{H}}_{start}}{\overset{\mathrm{pH}}{\int }}\sum _{i=1}^N\frac{z_i}{{10}^{z_i\left(\mathrm{pH}-{\mathrm{pK}}_{\mathrm{a}i,\mathrm{F}}\right)}+1}-\frac{z_i}{{10}^{z_i\left(\mathrm{pH}-{\mathrm{pK}}_{\text{a}}\text{U}\right)}+1}.$$ (7)

In this work we fit this equation to the pH-stability profiles and the differences between WT and mutant pH-stability profiles using the simplex nonlinear fitting routines as implemented in SciPy (http://www.scipy.org) toolkit for python (http://www.python.org).

Because we have measurements for almost all of the pK_a values in the folded state of HEWL, the only unknowns in Eq. 7 are the pK_a values of the titratable groups in the unfolded form of the protein.

Fitting mutant-induced differences in pH-stability profiles

The mutation of a titratable group to a nontitratable group (or the introduction of a titratable group) will change both the pH-independent and the pH-dependent stability of the protein. The pH-dependent changes (i.e., the differential pH-stability profile) will reflect the difference in the ΔQ (change in charge) between the folded and unfolded states of both the mutant and WT proteins, whereas the pH-independent changes (ΔΔG_fold,I in Eq. 8) will shift the entire pH-stability profile.

If we assume that the mutation does not change any other pK_a values in the protein (i.e., in neither the folded nor the unfolded state of the protein), then both the unfolded and folded pK_a value of the mutated titratable group can be determined directly from the differential pH-stability profile by fitting to Eq. 8c where we consider only the pK_a value of the titratable group that has been mutated:

$$\begin{array}{l}\Delta \Delta G_{fold}\left(\mathrm{pH}\right)=\Delta \Delta G_{fold,i}+\Delta \Delta G_{fold}\left(\mathrm{pH}\right)\hfill \\ \Downarrow \hfill \\ \Delta \Delta G_{fold}\left(\mathrm{pH}\right)=\Delta \Delta G_{fold,i}+\left(\Delta G_{fold,mut}\left(\mathrm{pH}\right)-\Delta G_{fold,\mathrm{WT}}\left(\mathrm{pH}\right)\right)\hfill \\ \Downarrow \hfill \\ \Delta \Delta G_{fold}\left(\mathrm{pH}\right)=\Delta \Delta G_{fold,i}+\left(-\ln \left(10\right)RT\underset{\mathrm{p}{\mathrm{H}}_{start}}{\overset{\mathrm{pH}}{\int }}\frac{z_i}{{10}^{z_i\left(\mathrm{pH}-{\mathrm{pK}}_{\mathrm{a}i,\mathrm{F}}\right)}}-\frac{z_i}{{10}^{z_i\left(\mathrm{pH}-{\mathrm{pK}}_{\mathrm{a}i,\mathrm{U}}\right)}}\right).\hfill \end{array}$$ (8a, 8b, 8c)

However, because even conservative point mutations quite often introduce pK_a value shifts in the folded states of proteins, the assumption is not justified for the folded state. Luckily, because we have knowledge of the mutant-induced ΔpK_a values in HEWL for mutations of the residues considered here, we can expand Eq. 8c to include the titratable groups whose pK_a values change, and then use the expanded Eq. 8c to fit the differential pH-stability profiles.

Specifically, this means that we explicitly evaluate Eq. 7 for both the WT and the mutant protein to account for the pK_a shifts observed in the folded state.

In all cases we assume that the mutations do not affect the pK_a values of the unfolded state.

Assessing the error on the derived pK_a values

The uncertainty of each pK_a value was determined by randomly varying the observed ΔΔG°_fold values using a Gaussian distribution (mean 0 kJ/mol, standard deviation by 1 kJ/mol) and refitting to Eq. 7. In addition to varying the experimental energies in this way, the starting values of all free pK_a values were varied around the model pK_a value of the residue using a Gaussian distribution with a standard deviation of 2 pK_a units, mean 0.0 pK_a units.

The refitting procedure was repeated 100 times to obtain the average pK_a values and their standard deviations.

In addition to this exercise we also used a range of values for ΔS°_m to properly reflect the uncertainty in the experimental data and these results are shown in Table S4.

Calculation of the contact order

The contact order of a residue is calculated using the equation $CO=1/N\sum \Delta S_{i,j}$, where N is the total number of contacts, ΔS_i,j is the sequence separation of contacting residues i and j. The sum is over all pairs of contacting residues. Two residues are in contact if they have heavy atoms with 6Å of each other.

Calculating pK_a values for the unfolded ensemble

A 10 ps MD simulation in vacuo was carried out with Yasara (http://www.yasara.com) at 700 K using the WT HEWL structure with PDB ID 2LZT to produce a starting point for constructing the unfolded ensemble. The last frame of the 700 K MD simulation was solvated, and subjected to steepest descents energy minimization with Gromacs (44). This was followed by a restrained MD simulation at 360 K for 50 ps to allow for water relaxation. Finally, the unfolded ensemble was constructed by simulating for 500 ps at 360 K using standard Gromacs settings with particle-mesh Ewald summation and a Berendsen temperature and pressure coupling.

One hundred evenly spaced snapshots from the last 400 ps of the simulation were used for pK_a calculations with the WHAT IF pK_a calculation suite (45) using a uniform protein dielectric constant of 8. A dielectric constant of 80 was used for the solvent and the ionic strength was set to 0.144 M. The WHAT IF pK_a calculation routines use DelPhi II (46) to solve the PBE and employs a hydrogen-bond optimization algorithm (47) to achieve realistic modeling of protonation states.

pK_a values for the unfolded ensemble were calculated by simple averaging of the pK_a values from the 100 snapshots.

Results and Discussion

We investigate the determinants of HEWL pH-dependent stability by measuring the T_m using CD spectropolarimetry at 13 pH values for the WT protein and 8 mutant proteins. Specifically, we mutate Asp-18, Asp-48, Glu-35, Asp-52, Asp-66, Asp-87, Asp-101, and Asp-119. In the following we measure site-specific pK_a values for the temperature-denatured disulfide-intact unfolded state of HEWL using analysis of single mutant thermal denaturation scans. We use the information on mutant-induced ΔpK_a values in the folded state from separate NMR titration experiments (B. M. Tynan-Connolly, H. Webb, F. O'Meara, J. E. Nielsen, unpublished) in combination with the mutant-induced changes in the pH dependence of ΔG_fold calculated from the thermal denaturation analysis. In this way we indirectly determine the pK_a values of seven titratable groups in the unfolded state. We continue to investigate the structural features determining the pK_a values in the unfolded state using MD simulations and structure-based pK_a calculations.

Rationalizing the WT HEWL pH-stability profile

HEWL displays an irregular pH-stability profile with its thermal stability being maximal at pH 4–5 (Fig. 1). HEWL consists of 32 titratable groups (7 Asp, 2 Glu, 1 His, 6 Lys, 11 Arg, 3 Tyr, and 2 termini), carries a strong net positive charge (+8) at pH 7.0, and has a pI of 11.0. We currently have direct or indirect experimental measurements of 21 of the pK_a values of the folded state of HEWL. This leaves only the pK_a values of the Arginine residues unknown in the folded state. In the following we assume that the pK_a values of Arg in both the folded and denatured states of HEWL are >12.0 and that they therefore do not contribute to the pH-stability profiles we have measured here. This assumption is justified because a deprotonated Arg, to our knowledge, never has been observed in a biomolecules between pH 0 and pH 12.

Figure 1.

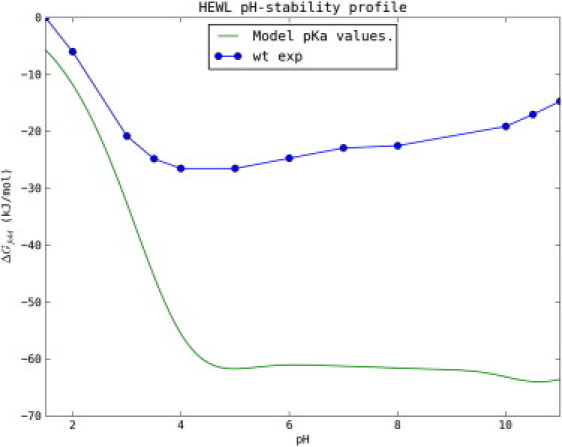
Experimentally measured pH-stability profile of WT HEWL (blue) and the calculated pH-stability profile assuming nonperturbed model pK_a values for the unfolded state (green). The large discrepancy illustrates that the pK_a values for the unfolded groups are highly perturbed from their model values.

We thus have knowledge of all 32 pK_a values in the folded state of HEWL, and furthermore assume that we know the pK_a values of the 11 Arginines in the unfolded state. This leaves 21 undetermined pK_a values in the HEWL unfolded state, which can be fitted to obtain agreement between the observed pH-stability profile of HEWL and that calculated using Eq. 7.

A first approximation is to assume that all pK_a values in the unfolded state are unperturbed compared to their model compound pK_a values. The green line in Fig. 1 shows the pH dependence of ΔG_fold calculated assuming model pK_a values for the unfolded state, and clearly illustrates that this assumption does not hold for HEWL.

We therefore adopt a mutational strategy to estimate the pK_a values of the acidic residues in the unfolded state to gain a better understanding of the structural features that determine pK_a values in the unfolded states of proteins.

Fitting mutant-induced differences in the HEWL pH-stability profile

We constructed nine single mutants (D18A, E35Q, D48A, D52N, D52A, D66A, D87A, D101A, and D119A) to probe the unfolded state pK_a values of HEWL. D87A could not be expressed in sufficient amounts for thermal denaturation analysis and we were consequently left with eight mutants that were subjected to CD-temperature denaturation scans at 13 pH values.

Fig. 2 shows the pH dependence of ΔG_fold for WT HEWL and the mutants determined using CD-monitored temperature denaturation experiments with the Schellman equation as detailed in the Materials and Methods. Of the eight mutants, only D101A and D52N are more stable than the WT across the pH range (for D52N this is true except for pH 3.0), whereas D48A, D66A, D119A, and D18A are destabilizing over the entire pH range. Mutants E35Q and D52A are destabilizing at low pH values, but become stabilizing above pH 4–5.

Figure 2.

Raw (A) and differential (B) pH-stability profiles for the single mutants examined in this study. The ΔG_fold values were determined from CD temperature-denaturation experiments as described in the Materials and Methods.

It is immediately clear that the differential pH-stability curves of the HEWL mutants are much more complicated than those recently reported in the elegant SNase experiments (37), and that we therefore cannot assume that folded state pK_a values do not change upon the introduction of mutations. Consequently, we cannot determine reliable pK_a values for both the folded and unfolded states from the pH-stability profiles alone. However, because we in parallel have measured folded state mutant-induced ΔpK_a values for a similar set of mutants using ¹⁵N NMR pH-titrations (Table 1 and B. M. Tynan-Connolly, H. Webb, F. O'Meara, J. E. Nielsen, unpublished), we use these data to supply the folded state pK_a values for the mutant proteins and in this way determine the pK_a values in the unfolded state. Using this approach it is possible to achieve reasonable fits of the majority of the differential pH-stability curves and thus determine reliable pK_a values for the unfolded state of HEWL (Table 2). Upon examination of Fig. 2 B, a number of mutant-induced changes to the pH-stability profile above pH 8 are visible. In the current analysis we ignore these changes and use experimental data <= pH 8.0 because we are interested only in determining pK_a,U values for the acidic residues in HEWL. In the following we briefly comment on the fitting of each differential pH-stability profile before performing a structural analysis of the data.

Table 1.

Known and assumed pK_a values in the folded state of HEWL used in this study

Titratable group	WT	D48N/D48A	D52N/D52A	D66N/D66A	E35A
N-term	7.9
Lys-1	10.1
Arg-5	>10.0∗
Glu-7	2.6
Lys-13	9.9
Arg-14	>10.0∗
His-15	5.5
Asp-18	2.8
Tyr-20	10.3
Arg-21	>10.0∗
Tyr-23	9.8
Lys-33	9.9
Glu-35	6.2	5.8/5.8∗	5.0/5.0∗	5.8/5.8∗	–
Arg-45	>10.0∗
Asp-48	1.4	-
Asp-52	3.6	3.3/3.3∗	–	3.1/3.1∗	3.4
Tyr-53	12.1
Arg-61	>10.0∗
Asp-66	1.2			-
Arg-68	>10.0∗
Arg-73	>10.0∗
Asp-87	2.2
Lys-96	10.2
Lys-97	9.6
Asp-101	4.5
Arg-112	>10.0∗
Arg-114	>10.0∗
Lys-116	9.8
Asp-119	3.5
Arg-125	>10.0∗
Arg-128	>10.0∗
C-term	2.7

Data are compiled from Webb et al. (23). Assumed (i.e., nonmeasured) pK_a values are marked with an asterisk. For the mutant proteins, only changed pK_a values are shown.

Table 2.

pK_a values for the folded and unfolded states of HEWL with RMSD values from differential pH-activity profile fits for all mutant proteins

Mutant	RMSD (kJ/mol)	ΔΔGfold,i (kJ/mol)	pKa,U	ΔpKa,U,	pKa,N	ΔpKa,N	ΔpKaU→N
D18A	0.7 (0.1)	0.0 (0.7)	3.4 (0.2)	−0.6	2.8	−1.2	−0.6
E35Q	1.1 (0.2)	5.3 (0.7)	5.0 (0.2)	+0.6	6.1	+1.7	+1.1
D48A	0.9 (0.1)	1.0 (1.2)	2.9 (0.3)	−1.1	1.4	−2.6	−1.5
D52A	1.1 (0.2)	1.8 (0.8)	4.0 (0.2)	0.0	3.6	−0.4	−0.4
D52N	1.0 (0.2)	−1.5 (0.7)	4.1 (0.2)	+0.1	3.6	−0.4	−0.5
D66A	1.3 (0.2)	−0.8 (0.7)	3.1 (0.1)	−0.9	1.2	−2.8	−1.9
D101A	1.0 (0.2)	−1.1 (0.7)	4.4 (0.2)	+0.4	4.5	+0.5	+0.1
D119A	0.9 (0.2)	2.7 (1.0)	3.6 (0.2)	−0.4	3.5	−0.5	−0.2

pK_a values for the unfolded state are fitted and reported as averages of the fitted solutions with RMSDs <= two times the lowest RMSD from a total of 100 fits. Values in parentheses indicate standard deviations. RMSD, RMSD between experimental and fitted ΔΔG_fold values; ΔΔG_i, pH-independent effect of mutation; pK_a,U, fitted value for the pK_a value in the unfolded state. ΔpK_a,U→N indicate the pK_a change produced by the reversible folding of HEWL (transition between the U and N states). ΔpK_a,U and ΔpK_a,N indicate the difference between the model compound pK_a value (Asp-4.0 and Glu-4.4) (45) and the pK_a values for the unfolded and folded states, respectively. Note that the errors in this table only reflect the fitting errors, and thus do not include errors that stem from the determination of ΔG using the Schellman equation (see Table S5).

D18A

The differential pH-stability profile of D18A displays a single transition with a decrease in stability of ∼3.5 kJ/mol from pH 1.5 to 7. This curve is fit satisfactorily with a ΔΔG of 0.0 ± 0.7 kJ/mol and a pK_aU of 3.4 (0.2). Note that although the variation in ΔΔG_i is quite large, the pK_a of the unfolded state can still be fit with a high accuracy.

E35Q

Glu-35 is the catalytic proton donor in HEWL, and has an elevated pK_a value of 6.1–6.2 according to NMR pH-titration data (23). The differential pH-stability profile of E35Q clearly describes the large destabilizing effect that the elevated pK_a value of Glu-35 has on HEWL by undergoing a stabilizing effect of 8 kJ/mol from pH 1.5 to pH 7 equivalent to a change in pK_a of 1.4 units. Fits to Eq. 7 yield an optimal agreement with experimental data with a pK_a,U of 5.0 thus giving a ΔpK_a,_U→F value upon folding of 1.1–1.2 units.

D48A

Asp-48 is situated in the β-domain of HEWL close to Asp-66 and Asp-52, and plays an important role in maintaining the hydrogen bond network around Asp-52. The mutation of Asp-48 induces changes in the pK_a values of Asp-52 and Glu-35 (Table 1) that allow for a good fit of the differential pH-stability profile. The pK_a of Asp-48 in the unfolded state is measured to be 2.9, thus showing a very large drop compared to its model pK_a value.

D52N/D52A

Aspartic acid 52 is situated in the active site cleft of HEWL, and has a relatively unperturbed pK_a value compared to the Asp model compound pK_a value. Despite this, the differential pH-stability profiles of D52N and D52A display large changes. Both profiles are characterized by a decrease in stability at low pH (pH < 4.0) of ∼3 kJ/mol (D52A) and 0.7 kJ/mol (D52N). This decrease in stability is followed by a large increase in stability (>5.0 kJ/mol for D52A, and ∼4.0 kJ/mol for D52N) at pH 4–8. Comparison of ¹⁵N NMR titration curves from WT HEWL and D52N reveal that the pK_a value of Glu-35 drops by 1.1 units, thus agreeing with the increase in stability (a 1.1 unit decrease in an acidic pK_a value stabilizes a protein by 6.3 kJ/mol). The decrease in stability of ∼3 kJ/mol at low pH is presumed to arise from the loss of the favorable interactions that D52 makes with its neighbors, In WT HEWL Asp-52 accepts hydrogen bonds from the side chains of Asn-44 and Gln-59 and therefore has a slightly lowered pK_a value accounting for the destabilization when this residue is mutated. However, Asp-52 is part of a complex hydrogen bond network involving Asn-44, Gln-59, Ser-50, Asn-46, Asp-48, and Arg-61, and the mutation of Asp-52 is therefore likely to affect the pK_a value of Asp-48, the structure of this part of the HEWL β-domain, and thereby possibly the pK_a value of Asp-66.

Comparisons of the ¹⁵N titration curves of Asp-48, Asp-66, Ser-50, and Asn-44 reveal changes in the titrational behavior of Asp-48 and Asp-66, and the mutations therefore induce local structural changes that affect the pH-stability profile. This is clearly observed in the fits of the differential pH-stability profiles of D52N and D52A (Fig. S1), which have difficulty reproducing the position of the destabilizing peak assuming unaltered pK_a values for Asp-48 and Asp-66. This is especially pronounced for D52N, where only the adjustment of the pK_a values of Asp-48 and Asp-52 in the folded state yields a fit with a satisfying error.

D66A

The differential stability profile of D66A displays a large decrease in stability of 7 kJ/mol accumulating from pH 1.5 to 4.0, followed by a modest increase in stability from pH 6 to 8. This difference is fit well using ΔpK_a values of −0.3 and −0.5 for Glu-35 and Asp-52, respectively, and these are supported by ¹⁵N titration curves of WT and D52N HEWL that display ΔpK_a values of −0.2 and −0.25 for these two residues. The difference between the two sets of pK_a values is well within the uncertainty of the methods applied. The pK_a value of Asp-66 in the unfolded state is found to be 3.1, thus displaying a significant drop compared to its model pK_a value.

D101A and D119A

The differential pH-stability profiles of D101A and D119A are fairly flat with no distinctive titrations evident at low pH. The noise in these pH-stability profiles therefore is of the same magnitude as the signal, and consequently the fitted solutions are tentative and give pK_a values for the unfolded state of 4.4 ± 0.2 and 3.6 ± 0.2, respectively. However, due to the absence of any large pH-dependent changes in protein stability we can safely assume that the pK_a values of these two residues are relatively unperturbed compared to the folded state.

Fitting global pH-stability profiles

The determination of the pK_a values of the six aspartic acid residues and Glu-35 in the unfolded state leads to new possibilities for fitting the global pH-stability profile of HEWL using a progressive fitting strategy. In the following we assume model pK_a values for any unknown pK_a values, and examine the size of the pK_a shifts that would be needed to reproduce the HEWL pH-stability profile.

We start by noting that the only remaining groups with an unfolded pK_a value likely to be lower than 5.0 are Glu-7, Asp-87, and the C-terminus. A fit of the WT pH-stability profile data up to pH 5.0 with three free parameters gives a good solution with pK_a values of 1.6, 3.3, and 3.3. Because we do not perform the fitting in a structural context, it is not possible to rigorously assign these pK_a values to specific residues, but we tentatively speculate that the C-terminus has the most depressed pK_a value in the unfolded state due to its sequence-proximity to Arg-128 and Arg-125.

Assigning these pK_a values to Glu-7, Asp-87, and the C-terminus allows for a fit of the pK_a value of His-15 using the data from pH 5.0 to pH 8.0 yielding an essentially unchanged pK_a value (5.6) compared to the native state.

We speculate that the next group to titrate in the unfolded state is the N-terminal, but it is not possible to obtain a good fit of the overall pH-stability profile by adjusting only the unfolded state pK_a value of the N-terminus. Instead, fitting the unfolded pK_a value of any of the lysines and the pK_aU of the N-terminus shows that slightly shifted pK_a values for such two groups can reproduce the pH-stability profile fairly well (Fig. S3). However, we would like to emphasize that the previous pK_aU values inferred from fits of the global pH-stability profile are very speculative, and represent merely one scenario that is able to reproduce the pH-stability profile of HEWL fairly well.

Rationalization of unfolded state pK_a values

Fig. 3 plots the difference between the observed pK_a value and the model compound pK_a value for both the folded and the unfolded states. The R² between these two ΔpK_a values (ΔpK_aN and ΔpK_aU) is 0.91 with a slope of 0.39, thus suggesting that the HEWL unfolded state retains some of its native state characteristics in accordance with the expectation that the HEWL thermally denatured state contains residual structure. Calculation of a residue-specific contact order reveals that most of the mutated residues make native state contacts with residues close in sequence (Table 3). The exception to this is Glu-35 whose contacts are predominantly long range in sequence space (contact order 10.1). It is striking that the largest disulfide bond-induced reduction in contact order occurs for Glu-35 and one might speculate that a possible role for disulfide bonds is to reduce the contact order of residues with unfavorable ΔpK_as so as to minimize the energetic costs incurred upon folding. The low contact order for the majority of the mutated residues means that the contacts affecting their pK_a values will also be close by in the unfolded state. Thus, providing a tentative explanation for the perturbed pK_a values in the HEWL unfolded state.

Figure 3.

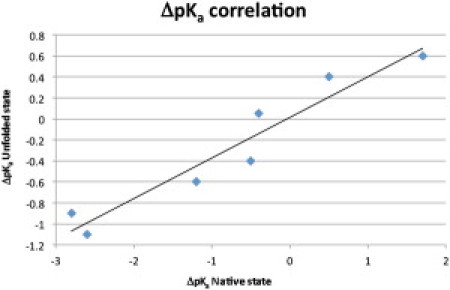
Correlation between ΔpK_a values in the folded and unfolded states for the seven residues examined here. The R² value is 0.93 and the slope of the regression line is 0.39.

Table 3.

Effect of disulfide bonds on the absolute contact order of the titratable groups studied in this work

Residue	CO no disulfides	CO disulfides present	Difference
Asp-18	4.3	3.9	−0.4
Glu-35	26.0	10.1	−15.9
Asp-48	4.1	4.1	0.0
Asp-52	4.9	4.9	0.0
Asp-66	5.2	4.2	−1.0
Asp-101	7.6	4.0	−3.6
Asp-119	2.1	2.1	−3.2

Overall the contact order is very low for all titratable groups, thus indicating that their pK_a values are determined mostly by sequence-local interaction. Strikingly, the largest disulfide bond-induced decrease in contact order is observed for Glu-35.

Calculation of unfolded pK_a values from an unfolded ensemble

It is of interest to investigate if structure-based calculations can reproduce the pK_a values in the HEWL unfolded state. To this end we produced temperature-denatured structures of HEWL using MD simulations as detailed in the Materials and Methods, and calculated the pK_a values for 100 unfolded structures using a standard PBE-based pK_a calculation algorithm. Table 4 shows the pK_a values calculated for the seven residues using this approach and yield and a root mean-square deviation (RMSD) to the experimental values of 1.7 pK_a units, which is not able to beat the null model (RMSD 0.7 units).

Table 4.

pK_a values from MD simulations of the unfolded state compared to the experimentally measured pK_a values and to the null model

Group	pKaU,exp	pKasim 360K	pKasim 460K	Null model
Asp-18	3.4	3.3 (0.3)	2.4 (0.9)	4.0
Glu-35	5.0	4.4 (0.2)	3.8 (0.6)	4.4
Asp-48	2.9	4.0 (0.1)	2.7 (0.9)	4.0
Asp-52	4.05	3.9 (0.3)	3.4 (0.4)	4.0
Asp-66	3.1	3.2 (0.9)	2.3 (1.1)	4.0
Asp-101	4.4	1.6 (0.7)	2.7 (1.1)	4.0
Asp-119	3.6	0.8 (0.6)	1.8 (0.9)	4.0
RMSD	−	1.6	1.2	0.7

Discussion

The work presented here shows that estimates of unfolded state pK_a values can be determined using a combination of NMR spectroscopy and CD-monitored thermal denaturation. The interpretation of the data is challenging, the noise in the measurements is substantial, and it is important to stress that we do not measure unfolded state pK_a values directly. However, despite this it is possible to derive estimates of pK_a values for the acidic residues in the unfolded state of HEWL.

It is remarkable that the pK_a,U values of Asp-18, Asp-48, and Asp-66 are shifted downward by more than half a pK_a unit. We speculate that sequence-local contacts (Lys-13, Arg-14, His-15, and Arg-21 for Asp-18, Arg-45, Thr-47, and Ser-50 for Asp-48, and Asn-65, Arg-68, and Thr-69 for Asp-66) are responsible for these shifts. Indeed, the strong correlation between folded state and unfolded state ΔpK_a values suggests that native contacts are responsible for perturbing the pK_a values in the unfolded state of HEWL. The low contact order observed for all the groups except Glu-35 is a further indication that sequence-local contacts can produce a stable structure, thus further supporting the role of local interactions.

The results are subject to the assumption that the titratable groups titrate independently in the unfolded state and that their pK_a values in the unfolded state therefore are not affected by the point mutations we construct. It is not possible to test the validity of this assumption with the present experimental data, but we consider it more likely that interactions in the unfolded state are provided by residues that are close in sequence. The residual structure of the unfolded state of HEWL makes it plausible that some of the acidic titratable groups could interact at longer distances, but this is a less likely scenario. The most obvious candidates for unfolded state interactions between titratable groups are Glu-35-Lys-33 (2 residues apart), His-15-Asp-18 (3 residues apart), Lys-116-Asp-119 (3 residues apart), and Asp-48-Asp-52 (4 residues apart), whereas all other residue pairs are more distant. We note that only interactions between pairs of residues that both have pK_a values <8.0 will have an effect on the validity of our analysis because we only consider pH values from 1.5 to 8.0. The effect of interactions between acidic residues in the unfolded state would be to artificially decrease the difference between folded state and unfolded state pK_a values and thus make the unfolded state pK_a values appear more shifted toward their folded state values. We cannot rule out that our results partly are a product of this effect, but we consider it highly unlikely that the much shifted pK_a values in our data set result exclusively from strong interactions between titratable groups in the unfolded state.

MD simulations indicate that local contacts can indeed influence the pK_a values in the unfolded state as evidenced by the pK_a values calculated with a PBE-based pK_a calculation routine. However, serious discrepancies were found between the calculated and experimentally measured pK_a values, thus suggesting that more extensive simulations are needed before reliable pK_a values can be obtained using an MD-based strategy as the one outlined here.

Conclusion

In this work we have demonstrated that several of the pK_a values in the heat-denatured state of HEWL are significantly shifted from their model pK_a values. We find a strong correlation between folded state pK_a values and unfolded state pK_a values thus indicating that the heat-denatured state of HEWL is likely to be quite compact. Using a progressive fitting strategy, we are able to arrive at approximate pK_a values for a number of additional groups, and show that the full pH-stability profile of HEWL can be explained by adjusting only a few additional pK_a,U values.

Furthermore, we investigated the use of structure-based pK_a calculations to predict unfolded state pK_a values when applied to an unfolded structural ensemble produced by a simplistic MD protocol. We observe a good agreement for approximately half of the titratable groups, and find the predictions for two groups (Asp-101 and Asp-119) to be seriously wrong due to the persistence of salt bridge interactions in the MD simulations.