Excitable Actin Dynamics in Lamellipodial Protrusion and Retraction

Abstract

Many animal cells initiate crawling by protruding lamellipodia, consisting of a dense network of actin filaments, at their leading edge. We imaged XTC cells that exhibit flat lamellipodia on poly-L-lysine-coated coverslips. Using active contours, we tracked the leading edge and measured the total amount of F-actin by summing the pixel intensities within a 5-μm band. We observed protrusion and retraction with period 130–200 s and local wavelike features. Positive (negative) velocities correlated with minimum (maximum) integrated actin concentration. Approximately constant retrograde flow indicated that protrusions and retractions were driven by fluctuations of the actin polymerization rate. We present a model of these actin dynamics as an excitable system in which a diffusive, autocatalytic activator causes actin polymerization; F-actin accumulation in turn inhibits further activator accumulation. Simulations of the model reproduced the pattern of actin polymerization seen in experiments. To explore the model's assumption of an autocatalytic activation mechanism, we imaged cells expressing markers for both F-actin and the p21 subunit of the Arp2/3 complex. We found that integrated Arp2/3-complex concentrations spike several seconds before spikes of F-actin concentration. This suggests that the Arp2/3 complex participates in an activation mechanism that includes additional diffuse components. Response of cells to stimulation by fetal calf serum could be reproduced by the model, further supporting the proposed dynamical picture.

Introduction

Crawling cells typically move over substrates by a combination of actin-based protrusions at the leading edge, adhesion to the substrate, and myosin-based contraction at the rear (1–4). Dictyostelium discoideum amoebas extend actin-based protrusions (pseudopodia) to guide motion toward one another upon starvation (5). Tissue cells move to repair wounds through the use of a thin lamellipodium at the leading edge (1–4). During embryonic development, neurons extend actin-based neuronal growth cones to locate their synaptic targets (6). Cancer cells utilize actin-based motility to spread throughout the tissue, often resulting in metastasis (7). Because all these types of motile cells must respond quickly and efficiently to a changing environment, the structure and regulation actin structures at the leading edge is highly dynamic and regulated by multiple factors.

In lamellipodia, activation of the Arp2/3 complex nucleates new filaments off the side of preexisting actin filaments (F-actin). The barbed ends of the actin filaments in this dendritic network push against the membrane at the leading edge and generate protrusive force by polymerization (3,8–10). Frequent filament severing catalyzes actin filament disassembly into monomers that recycle back to filaments by polymerization. The whole actin meshwork in the lamellipodium undergoes retrograde flow away from the leading edge, aided by myosin contraction.

To gain insight into the control of actin assembly at the leading edge, we focus on periodic lamellipodial protrusion and retraction patterns, the subject of recent experimental work (11–17). Upon adsorption onto a surface, most cells undergo isotropic spreading, maintaining a near-circular shape. After ∼40 min, spreading cells begin to exhibit noticeable fluctuations of the leading edge, characterized by periodic extensions and retractions (12,16), as also observed in other eukaryotic cell types and polarized cells (11–17). In some cells, protrusion waves propagate along the leading edge (11,14,15,17–21).

The regularity of protrusion and retraction during spreading indicates a process that can be described by a coarse-grained mathematical model. Searching for such a model, we examined protrusion dynamics and associated concentration changes of F-actin at the leading edge of XTC cells (3). These cells exhibit flat lamellipodia and are ideal for quantitative analysis, allowing accurate averaging and calculations of correlations among different components. Motivated by the data analysis, we propose a model of actin assembly as an excitable system, which has important mechanistic differences to previous studies (22–24).

Results

Protrusion and retraction patterns along the leading edge of XTC cells suggest an excitable system

To visualize actin dynamics at the leading edge, we used XTC cells expressing LifeAct-mCherry (25). LifeAct attaches to filamentous actin transiently (see Movie S1 in the Supporting Material), with observed fluorescence-recovery-after-photobleaching recovery times <0.2 s (25). Within 30 min after introducing the cells onto a poly-L-lysine substrate, the cells spread and many adopt a circular shape (see Fig. 1 A). For the next ∼250 min, the cells exhibit continuous protrusions and retractions along the cell circumference, resembling the Phase 2 (12) and V states (14) previously reported in different cells systems (see Fig. 1 B and Movie S2). At longer times, the cells develop stress fibers and become quiescent.

Figure 1.

Leading-edge velocities and LifeAct intensity measured by fitting active contours to the leading edge. (A) XTC cell expressing LifeAct-mCherry. (B) Kymograph of leading edge (10 s intervals) for indicated section in panel A. (C) XTC cell expressing EGFP-actin in low concentration. (D) Actin speckles within 5 μm of the leading edge of the cell in panel C exhibit small variations in retrograde flow rate compared to variations in leading-edge speed. Bars indicate mean ± SE. (E) Polar coordinate system indicating the leading edge and the inner boundary of a 4-μm-wide band of lamellipodium. (F) 4-μm-wide bands of lamellipodium, mapped from a two-dimensional ribbon of lamellipodium. The lines indicate the inside and outside of the cell as in panel E. (G) Section of XTC cell expressing LifeAct-mCherry with superimposed active contour. Cell has been on the substrate for 40 min. (H) Normal leading-edge velocity (with respect to fixed substrate) versus angle and time, for cell in panel G. Positive (negative) velocities indicate protrusion (retraction). The retrograde flow speed for this cell (74 ± 3 nm/s, n = 15 measurements of bright features in kymographs) did not vary noticeably during observation. (I) Total LifeAct-mCherry intensity versus angle and time. LifeAct-mCherry intensity was summed over a 5-μm ribbon of lamellipodium of cell in panel G for each time point.

To determine whether changes in retrograde flow underlie leading-edge motion, we used single-molecule imaging to measure retrograde flow rates for EGFP-actin (Fig. 1, C and D, and see Fig. S1 in the Supporting Material) and EGFP-p21, a component of the Arp2/3 complex (see Fig. S2) (26,27). Retrograde flow was approximately constant throughout each extension cycle (Fig. 1 D, and see Fig. S1 C, and Fig. S2, B and C), with smaller variations compared to studies of migrating epithelial cells (28,29). This is also evident in bright features that present as diagonal lines of approximately constant slope in kymographs (Fig. 1 B). Thus, we hypothesize that fluctuation in actin polymerization underlies the observed protrusions and retractions, similar to filopodia in growth cones (30).

To quantify the protrusion and retraction pattern and its relationship to actin polymerization, we tracked leading-edge position over time (11–14,17,31) using active contours (32). The fit also allowed us to measure local LifeAct-mCherry intensity as a function of angle and time, by summing the intensity of pixels within a ribbon around the edge (Fig. 1, E and F). Because filopodia protrusions were typically short (Fig. 1 A), the smooth active contour captured the leading-edge dynamics. In cases of long filopodia, the active contour cut through them (Fig. 1 G). To achieve better spatial resolution and reduce photodamage we imaged small sections of cells, as in Fig. 1 G (see Movie S3).

Tracking of the leading edge allowed measurement of the local normal leading-edge velocity as a function of angle and time. We observed a relatively regular sequence of protrusion and retraction events with a period of 130–200 s and typical protrusion velocities of the order of tens of nm/s (Fig. 1 H). Some of the protrusions and retractions propagated locally as waves along the cell circumference (Fig. 1 H), in both clockwise and counterclockwise orientations. This pattern was reproducible, with small variations in period, amplitude, and retrograde flow rates among cells (n = 7).

The dynamics of the LifeAct intensity (integrated over 5 μm) versus angle and time in Fig. 1 I followed the pattern of the velocity in Fig. 1 H, displaying periodic increases and decreases in density, as well as wavelike propagation. Large (small) amount of F-actin correlated with negative (positive) leading-edge velocities. Intensity values in Fig. 1 I indicate that the total amount of F-actin approximately doubles during a protrusion cycle. These measurements reflect the total amount of F-actin and do not address finer features such as dependence on distance from the leading edge. Kymographs such as in Fig. 1 B reveal that F-actin starts to accumulate close to the leading edge during protrusion.

To quantify the results in Fig. 1, correlation analysis was performed on the leading-edge velocity and the integrated LifeAct-mCherry intensity (Fig. 2 and see Fig. S3). In Fig. 2 A we plot the autocorrelation of leading-edge velocity, LifeAct-mCherry intensity, and the cross correlation of velocity and LifeAct-mCherry, at the same position (arc-length = 0 in Fig. S3). The oscillatory shape confirms the periodicity of the protrusion and F-actin assembly. The peaks of the velocity autocorrelation are sharper than those of the LifeAct-mCherry, likely as a result of less noise in the signal (measurement or intrinsic). Thus, the position of the velocity autocorrelation peaks is a slightly more accurate measurement of the period (∼130 s in this cell). The cross-correlation function in Fig. 2 A shows that the two signals are almost exactly out of phase, with an offset ∼10 s. Thus, larger speeds correspond to smaller than average total F-actin amount and vice versa. Fig. 2 B shows the correlations as a function of arc length, at zero time offset. These autocorrelation curves indicate that the lateral width with coordinated protrusion, retraction, and F-actin density is ∼5 μm (full width at half-maximum in the figure). The diagonal stripe patterns in two-dimensional correlation functions in Fig. S3 reflect the wavelike propagation.

Figure 2.

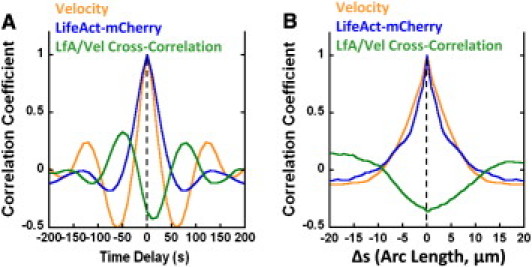
Correlation functions of leading-edge velocity and LifeAct-mCherry intensity (for cell in Fig. 1G). (A) Average correlation coefficients for leading-edge velocity autocorrelation, LifeAct-mCherry autocorrelation, and LifeAct-mCherry-velocity cross correlation, versus time and with no positional offset. (B) Same as Fig. 1D, versus arc length and no time offset. Arc-length is calculated by multiplying angular positions in Fig. 1G by cell radius.

Diffuse-activator, delayed-local-inhibition model with noise-induced excitations

The observed dynamics are suggestive of excitations driven by noise (i.e., stochastic concentration fluctuations): Figs. 1 and 2 show cycles of bursts of actin polymerization in a random pattern around the cell, lateral propagation, followed by disassembly. Excitability typically involves the interaction between an activator and an inhibitor: in an excitation, an activator species self-recruits rapidly; this activator in turn recruits an inhibitor that causes the activator to slowly dissipate (33). We speculate that the anticorrelation of leading-edge velocity with total actin intensity suggests that F-actin acts as an inhibitor. Likely mechanisms for this inhibition include the formation of actomyosin bundles (34) and adhesions (35,36) and accumulation of mechanical tension (4,28). Many molecules are activator candidates: actin polymerization can be triggered by the Scar/WAVE and WASp proteins that self-recruit on the cell membrane to activate the Arp2/3 complex (37–39). Once activated, the Arp2/3 complex generates new barbed ends as branches off preexisting filaments, thought to lead to autocatalytic dendritic nucleation (8,9). Severing of growing filaments could also contribute to diffusive autocatalytic generation of barbed ends (26,40) through transient association of diffuse cofilin and AIP1 with F-actin (41). Formin-mediated nucleation of new filaments is another possible activation mechanism (42,43).

In our model, we calculate the concentrations of a diffusible activator, A(x,t), free barbed ends, B(x,t), and F-actin, F(x,t), at different positions x along the leading edge over time (Fig. 3 A). The lamellipodium is modeled in one dimension, each coordinate representing a slice along the arc length of the leading edge. We assume that protrusions and retractions stem from underlying concentration fluctuations in the local actin network and do not explicitly consider cell membrane displacement. Denoting rate constants by k and ρ, the equations governing the concentrations are

$$\frac{\partial A}{\partial t}=\left({\rho }_0+{\rho }_2{A}^2\right)e^{-F/F_s}-k_A^{-}A+D_A{\nabla }^2\text{A}+\sigma \left(x,t\right),$$ (1)

$$\frac{\partial B}{\partial t}=k_B^{+}A-k_B^{-}B,$$ (2)

$$\frac{\partial F}{\partial t}=k_F^{+}B-k_F^{-}F.$$ (3)

The first term on the right-hand side of Eq. 1 allows for spontaneous accumulation as well as nonlinear self-recruitment of the activator. We chose a simple quadratic dependence on A (see Section S2.1 of the Supporting Material). When F-actin exceeds saturation concentration, F_s, the activator on-rate is reduced. This is the negative feedback in Fig. 3 B. The second term on the right-hand side in Eq. 1 represents deactivation. Diffusion of the activator (third term on the right-hand side) along the membrane couples neighboring sites and allows propagation of actin dynamics along the leading edge. The last term in Eq. 1 is white noise,

$$\langle \sigma \left(x,t\right)\sigma \left(x^{\prime },t^{\prime }\right)\rangle ={\sigma }_0^2\delta \left(t-t^{\prime }\right)\delta \left(x-x^{\prime }\right),$$

and represents concentration fluctuations (23,24) that generate excitations by perturbing the system out of its stable state (see Section S2 of the Supporting Material). Equation 2 describes accumulation of free barbed ends as a result of the activation process. Rate constant k_B⁺ describes how fast the activator generates new barbed ends. Rate constant k_B⁻ ≈ 0.4–8 s⁻¹ is the rate of free barbed end loss through capping by capping protein (37). Equation 3 describes change of F-actin as a result of polymerization at free barbed ends and spontaneous disassembly.

Figure 3.

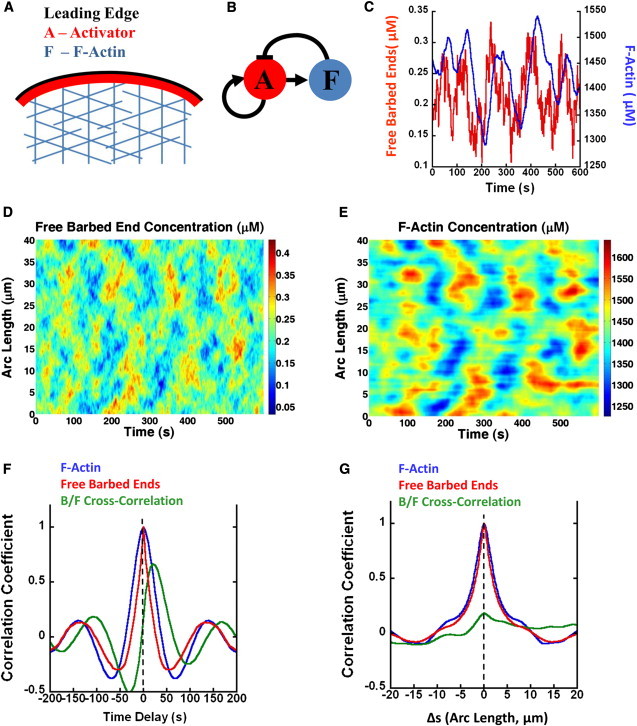
Results of model of leading-edge actin dynamics. (A) The model includes F-actin, F, activator A, and free barbed ends, B, as functions of position along the arc-length of the membrane. (B) Reaction network diagram. Assembly of F promoted by autocatalytic activator A that generates free barbed ends. Accumulation of F inhibits A recruitment. (C) F-actin and free barbed end concentrations at a fixed point along the model membrane as a function of time. (D) Free barbed end concentration versus arc length and time. (E) Same as panel D, for F-actin. (F) Correlation coefficients versus time and with no positional offset for free barbed end autocorrelation, F-actin autocorrelation, and the cross correlation between panel B and F-actin. (G) Same as panel F, but as a function of arc length and no time offset.

Because the capping rate k_B⁻ is much faster than the frequency of the protrusion and retraction events, generation of barbed ends must be fast enough such that B responds to changes in A quickly. This leads to B ≈ k⁺_BA/k⁻_B and allows us to rewrite Eq. 1 as

$$\frac{\partial B}{\partial t}=\left(r_0+r_2{B}^2\right)e^{-F/F_s}-k_A^{-}B+D_A{\nabla }^{2}B+s\left(x,t\right).$$ (4)

Here, unknown rate constant k_B⁺ is absorbed into the new rate constants r₀ and r₂ and into the amplitude of the noise that is now s₀. Equations 3 and 4 form a closed system in terms of B and F. Details on selecting model parameters are given in Section S2 and Table S1 in the Supporting Material.

Numerical integration of the equations produces spikes of free barbed end concentration, followed by spikes in local F-actin concentration (Fig. 3 C). In space, point excitations propagate laterally along the membrane (see Fig. S9). As noise excites actin randomly along the membrane, excitations coordinate into structures similar to those seen in experiment: Fig. 3, D and E, shows that the model captures the wavelike propagation across sections of the membrane's arc length as well as the magnitude and timescale of the actin fluctuations of Fig. 1 I.

We calculated the space-independent and time-independent autocorrelation and cross-correlation function of B and F in Fig. 3, F and G, for comparison to Fig. 2, A and B. The model reproduces the main features of the experiment, including the period of F-actin autocorrelation (Fig. 3 F) and width of spatial correlations (Fig. 3 G). A characteristic feature is the fact that spikes of B precede those of F. Fig. 3 F shows this leading behavior, demonstrated by the positive shift of the cross-correlation peak to the right of the origin by ∼25 s. The shapes of the time-independent autocorrelation functions in Fig. 3 G are similar for both B and F. Interestingly, the cross correlation between these two signals (green curve) is flat by comparison: at a fixed point in time, there is little coupling between activator and F-actin concentrations at any arc-length difference. The two-dimensional correlation functions of B and F in Fig. S4 exhibit periodic diagonal patterns, similar to those in the F-actin autocorrelations of Fig. S3 B.

The Arp2/3 complex may participate in the proposed activation mechanism

The Arp2/3 complex generates free barbed ends via branching of preexisting filaments (37,38). Thus, its concentration at the leading edge could reflect the dynamics of the model's activator. We tagged the p21 subunit of the complex with EGFP and imaged cells expressing both p21-EGFP and LifeAct-mCherry (Fig. 4 A, and see Movie S4). The amount of p21-EGFP varied discernibly at the leading edge over time (Fig. 4 A, right). p21-EGFP localized to the leading edge during protrusion and dissipated during retraction. Spikes of p21 accumulation preceded those of F-actin, similarly to the activator dynamics in the model. A similar pattern was observed when we tagged the p41 subunit of the Arp2/3 complex and actin with RFP.

Figure 4.

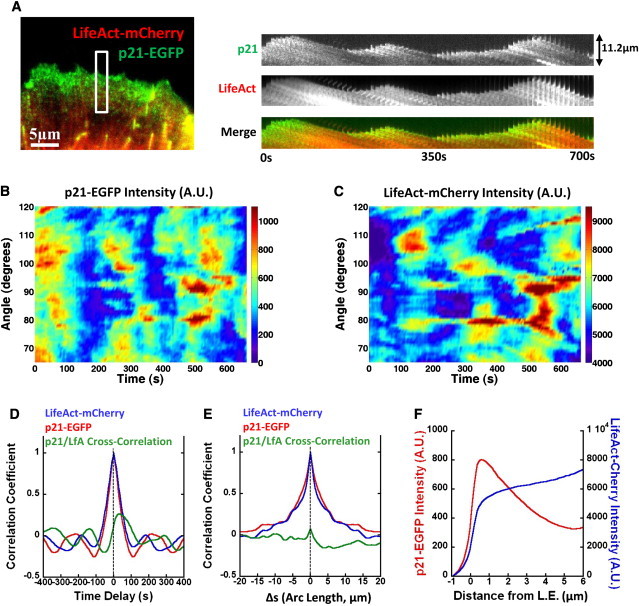
p21-EGFP/LifeAct-mCherry measurements indicate that Arp2/3 complex accumulation precedes F-actin accumulation. (A) XTC cell expressing p21-EGFP and LifeAct-mCherry. (Right panels) Montage of a indicated section of the leading edge over time (frames are 10 s apart). p21-EGFP accumulates at the leading edge during protrusion and dissipates during retraction, preceding F-actin. Retrograde flow remains unchanged, 48 ± 1 nm/s (n = 15 measurements of bright features). (B) Total p21-EGFP intensity versus angle and time, over a 5-μm-wide band of lamellipodium. (C) Same as panel B, for LifeAct-mCherry. Protracted horizontal patterns are due to filopodia. (D) Average correlation coefficients versus time and with no positional offset for p21-EGFP autocorrelation, LifeAct-mCherry autocorrelation, and cross correlation of p21-EGFP with LifeAct-mCherry. (E) Same as panel D, but as a function of arc length and no time offset. (F) Average intensity of p21-EGFP and LifeAct-mCherry versus distance from the leading edge.

Measured integrated p21-EGFP and LifeAct-mCherry intensities exhibit periodic and wavelike behavior similar to the activator in Fig. S4 A (Fig. 4, B and C). p21-EGFP accumulation occurs at approximately the same locations along the membrane as F-actin. Because the cell in Fig. 4 has been on a substrate for 180 min, the period is slightly longer than the cell of Fig. 1 E that had been on the substrate for 40 min. This cell also has more bundled F-actin structures and so the wave features of actin are less pronounced.

Fig. 4, D and E, and Fig. S5 show correlation functions for p21-EGFP and LifeAct-mCherry intensities that are similar to those of the model in Fig. 3. The p21-EGFP autocorrelation has a period ∼180 s (Fig. 4 D). The peak of the cross-correlation function is offset from the origin, indicating that Arp2/3 complex spikes lead those of F-actin by 35 s on average. The cross correlation as a function of space alone, with no temporal offset (Fig. 4 E), indicates little coupling between amount of F-actin and Arp2/3 at neighboring sites along the membrane, similar to the model in Fig. 3 G.

In summary, we find that Arp2/3 complex accumulates in bursts along the leading edge. These bursts precede maxima of total F-actin amount, indicating a possible role for the Arp2/3 complex in the activation process proposed by the model in Fig. 3. Measurement of the p21-EGFP and LifeAct-mCherry intensities as a function of distance from the leading edge (Fig. 4 F) confirms that the Arp2/3 complex localizes in a narrower region away from the leading edge as compared to F-actin. This observation is also consistent with an Arp2/3-complex-dependent activation mechanism that starts within 5 μm of the leading edge.

Response of cells to stimulation by fetal calf serum

We explored the ability of the model to capture response to chemical stimulants. Introduction of fetal calf serum (FCS) in quiescent cells that have been on slides for hours revives the protrusion and retraction of earlier times (41). We hypothesize that this transition may be captured within our model by changing the parameters to guide the system from a nonexcitable to an excitable state (see Section S3 of the Supporting Material).

We imaged quiescent cells expressing p41-EGFP, a marker for the Arp2/3 complex that behaves similarly to p21-EGFP (26,27), and LifeAct-mCherry (see Movie S4). Fig. 5 A shows a montage of the leading-edge cell stimulated at 200 s. After stimulation, a dramatic increase in both p41-EGFP and LifeAct-mCherry intensities was observed along the whole lamellipodium (Fig. 5 B). After the increase, both exhibit periodic oscillations, with peaks in p41-EGFP preceding those of LifeAct-mCherry by ∼40 s, similar to the timing difference in cells not exposed to a stimulus (Fig. 4 D).

Figure 5.

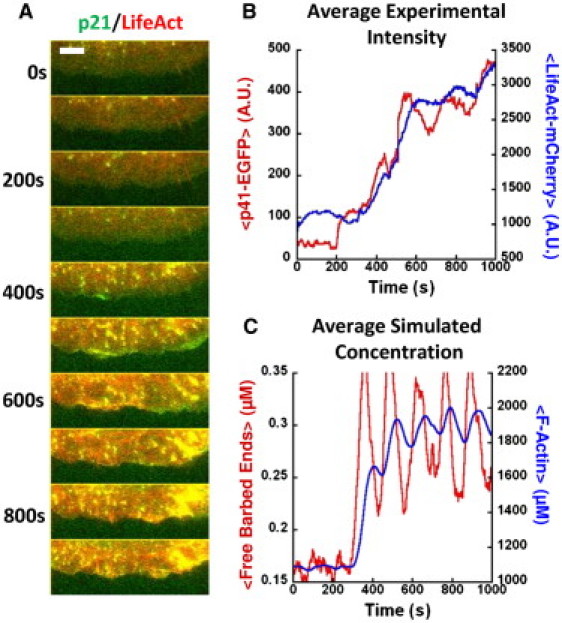
XTC cell response to FCS and comparison to model. (A) Montages of leading edge of cell expressing p41-EGFP and LifeAct-mCherry stimulated by FCS at 200 s. The cell had been plated for 4 h. Intensity increases are evident after stimulation. Bar: 5 μm. (B) Intensities of p41-EGFP and LifeAct-mCherry averaged over all angles versus time. (C) Results of model showing concentrations of the free barbed end and F-actin concentrations, averaged over arc length. Rate constants were functions of time: r₀(t) = 1 μM s⁻¹ + 24 μM s⁻¹H(t), r₂(t) = 1 μM⁻¹ s⁻¹ + 624 μM⁻¹ s⁻¹H(t). Here H(t) = Θ(t – 250 s)t³/(T³ + t³), where T = 220 s and Θ is the step function.

The model can capture the FCS response by allowing the linear and autocatalytic free barbed end on-rates, r₀ and r₂, to increase in response to FCS (see Fig. 5 C). This change reproduces the behavior observed experimentally, most notably the out-of-phase transient oscillations in Arp2/3 complex and F-actin at late times after stimulation. Dictyostelium response to cAMP has also been interpreted as an indication of excitability (23). However, Dictyostelium undergoes cringing and global polarization, followed by adaptation, whereas application of FCS to our cells leads to long-lived changes in leading-edge dynamics without immediate cell-shape changes.

Discussion

In this article we developed a model that is complex enough to capture the main experimental observations, yet simple enough to allow an in-depth mathematical study. We predict how F-actin dynamics respond to model parameter changes, which may be implemented experimentally by stimulation (Fig. 5) or via biochemical treatments. We modeled the integrated concentrations over a 5-μm ribbon near the leading edge, a first step for future work to study concentrations as a function of distance from leading edge. In the Supporting Material, we discuss the relation of our model to other theoretical studies (22–24,36,44–46; and see 57,58).

Our approach is most similar with parts of the LEGI model of Xiong et al (23) and the FitzHugh-Nagumo model of Hecht et al. (24) for pseudopodia formation in Dictyostelium, in support of common features existing in very different cell types. Unlike these studies, however, we do not assume a fast-diffusing global inhibitor. Fast inhibitor diffusion in these studies suppressed pseudopodia away from those few regions that get excited after stimulation. Our system exhibits a spatially extended, fluctuating pattern of protrusion and retraction so we suggest that inhibition is local and related to local growth of the actin cytoskeleton and focal adhesions. The wave patterns are instead caused by a diffuse activator as proposed by Weiner et al. (47), Doubrovinski and Kruse (48), and Carlsson (49) for cortical actin waves.

Our study can also provide insight into the I and V protrusion and retraction patterns observed in PtK1, epithelial cells, and MEFs adhered to a substrate (14). I-states exhibited synchronous protrusion and retraction events along the cell edge, whereas V-states exhibited transverse propagation of protrusion along the cell edge. The protrusions and retractions of the XTC cell in Fig. 1 H are reminiscent of the V patterns, though the V shapes are less pronounced as compared to Machacek and Danuser (14). Similarly to Enculescu et al. (22), we suggest that these two patterns correspond to the lamellipodium system existing in different dynamical regimes (see the Supporting Material).

Dendritic growth is autocatalytic: Arp2/3-complex-nucleated branches act as nuclei for further branches. Could the Arp2/3 complex be the only activator species of the model, as in a model by Carlsson (49) for cortical actin waves? We find this to be unlikely because lateral spreading of Arp2/3 complex-mediated branching would be too slow to cause the observed traveling waves of protrusion: the effective diffusion coefficient calculated by a branching mechanism is ∼10 times smaller (D = 0.01 μm²/s (49)) than the value for the activator species in Table S1. This is in agreement with Döbereiner et al. (15), who estimate a minimum D = 0.1 μm²/s. These numbers support the involvement of diffuse proteins such as Rho GTPases and Scar/WAVE and WASp (37–39), severing by cofilin (26,40,41) and de novo filament nucleation (42). However, although the Arp2/3 complex may not be the only activator species involved, it likely contributes to self-amplification locally (see Section S3 of the Supporting Material). Interestingly, the measured time delay between the peak of protrusion rate and Arp2/3 complex concentration depends on the distance to the leading edge (see Fig. S11). Thus, early stages of protrusion may be assisted by Arp2/3 complex-mediated branching. This initial actin network could continue to change and grow by branching and later by other factors and internal network remodeling, as the network undergoes retrograde flow.

What is the role of myosin contraction in generating protrusions and retractions? Previous work (14,29,50) suggested that oscillatory dynamics do not require varying myosin activity. However, in many previous studies, retraction was coupled to sudden increase in retrograde flow (11,28,29). Here, we did not observe significant changes in retrograde flow, suggesting a process driven primarily by actin polymerization/depolymerization (though we did not exclude a contributing role of myosin in the negative feedback). It is possible that myosin contraction acts as an additional mechanism in some cells to cause rapid collapse of protrusion events. This indicates another instance where different combinations of the polymerization and contraction activities can both contribute to motility.

To illustrate the sequence of events in a protrusion and retraction cycle, in Fig. 6 we show the results of the model after a perturbation, but with noise removed from the equations. Without the driving noise, the system reequilibrates after a few cycles (unlike the real system that is inherently noisy and is constantly excited). In Fig. 6 we also plot the expected protrusion rate from our observation of anticorrelation between protrusion rate and total F-actin amount in Fig. 2. In the figure, a peak in the protrusion rate is followed by a peak in barbed end concentration, a peak in the Arp2/3 complex concentration, and finally a peak in the F-actin concentration. These values represent integrated concentrations over a 5-μm band.

Figure 6.

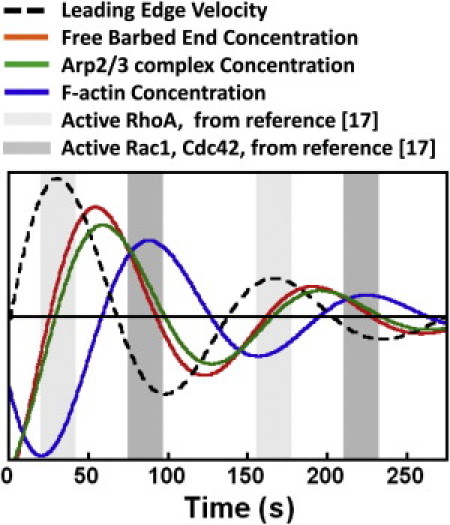
Temporal coordination of leading-edge velocity, with free barbed end, Arp2/3 complex, and F-actin concentrations (integrated over a 5-μm band). Curves for free barbed ends and F-actin were generated from the model by perturbing the system from its steady state and allowing it to relax without noise. Perturbations without noise result in underdamped oscillations with period τ = 135 s. Spikes in free barbed end concentration lead spikes in F-actin by 33 s. Leading-edge velocity and Arp2/3 complex concentration signals were manually added at the appropriate temporal offset with respect to F-actin (in Fig. 2A, the leading-edge velocity is 0.85 τ out of phase with F-actin; in Fig. 4 spikes in Arp2/3 complex concentration precede spikes in F-actin concentration by ∼0.2 τ). Previous measurements (17) suggest that a peak in RhoA activation accompanies peaks in leading-edge velocity (light-shaded background). The same study found that peaks in Rac1 and Cdc42 activation occurred at ∼0.4 τ after the RhoA activation peak (17) (dark-shaded background).

Experiments provided evidence for all of the timings in Fig. 6, except for the concentration of barbed ends, B, which peaks ∼30 s after the maximum of the protrusion rate. This timing is consistent with Ji et al. (28), who reported that the polymerization rate of epithelial cells spikes ∼20 s after the maximum of the protrusion rate (as measured by fluorescence speckle microscopy). The polymerization rate in our model is k⁺_FB and we assumed that the polymerization rate per filament, k⁺_F, is constant. Fluctuations in G-actin concentration (42) and force-induced reduction of the polymerization rate (10) may cause k⁺_F to vary. We expect, however, that inclusion of these effects will still require a timing of the barbed end concentration peak similar to Fig. 6: force or depletion of monomer pool should result in k⁺_F being at a minimum when the lamellipodium is near maximum extension (see also Ji et al. (28)) and at a maximum when the lamellipodium is near maximum retraction; such a behavior would be almost out of phase with the change of the polymerization rate suggested in Fig. 6 (and in Ji et al. (28)). Thus, we expect that the free barbed end concentration peaks in between the maxima of protrusion rate and total F-actin amount. This is consistent with the suggestion of Ji et al. (28) that the morphology of the actin meshwork changes during the protrusion and retraction cycle, with different fractions of actin filament growth converted to forward motion at different stages of the cycle. Fig. 6 shows a small offset between peaks of B and Arp2/3 complex. This offset is smaller than the 20 s offset in the cross-correlation peak between local actin assembly rate and Arp2/3 complex concentration measured in lamellipodia in Ponti et al. (51) (in that study, however, the overall variation in the correlation coefficient was small).

Fig. 6 also compares our findings to the results of Machacek et al. (17) who measured Rho GTPase activation in migrating mouse embryonic fibroblasts. The peak of RhoA activity (light-shaded background) occurs early in the protrusion cycle and its timing is close to the spike of the activator A in the model (that is approximately proportional to barbed end concentration). Active Cdc42 and Rac1 signals spike at about the same time as F-actin (dark-shaded background) (17). Perhaps F-actin growth and the resulting formation of focal adhesions trigger signaling pathways that result in the removal of activator molecules such as RhoA, as suggested by recent work (52). This would justify our choice of associating F-actin growth with inhibition and would be consistent with the observation that Cdc42 and Rac1 peak at a distance 1.8 μm away from the leading edge (17), indicating the involvement of adhesions. We note, however, that Rho proteins have multiple effectors and regulators, and that different signaling pathways may apply during spreading and cell crawling, so their role in leading-edge protrusion and retraction could be complex. For example, Fig. 6 suggests that the concentration of the Arp2/3 complex peaks before the peak of active Cdc42, which indirectly activates the Arp2/3 complex (39). When we looked at the timing of Arp2/3 complex activation as a function of distance from the leading edge, we did not find evidence that the Arp2/3 complex concentration first spikes away from the leading edge as was found for Cdc42 in Machacek et al. (17) (see Fig. S11). Perhaps Cdc42 plays multiple roles in the lamellipodium so its Arp2/3-complex-activating component in Machacek et al. (17) was dominated by Cdc42 participation in other processes.

A growing body of work describes actin as an excitable system that provides cells with an adaptable and rapidly responding system for motility and polarization. This includes cortical waves in Dictyostelium (19,47,53,54), cortical oscillations (55), and actin ring closure in wound repair (56). Further studies could identify common underlying molecular mechanisms. Mechanical forces (44), membrane curvature (46), hydrostatic pressure (57,58), and biochemical processes can all contribute. Quantitative approaches, combining experiment with analysis and modeling, should help distinguish among these possibilities.