Recognition of Human Tumor Necrosis Factor α (TNF-α) by Therapeutic Antibody Fragment

Background: Human TNF-α is a cytokine involved in many disease-related cellular processes.

Results: High affinity binding of therapeutic antibody (inhibitor) to native and molten globule-like TNF-α conformation is driven by specific noncovalent interactions.

Conclusion: Binding-coupled conformational changes are crucial for antibody-TNF-α recognition.

Significance: This work helps learn which forces drive unfolding of TNF-α and its recognition by monoclonal antibodies and how they affect TNF-α activity regulation.

Abstract

Human tumor necrosis factor α (TNF-α) exists in its functional state as a homotrimeric protein and is involved in inflammation processes and immune response of a human organism. Overproduction of TNF-α results in the development of chronic autoimmune diseases that can be successfully treated by inhibitors such as monoclonal antibodies. However, the nature of antibody-TNF-α recognition remains elusive due to insufficient understanding of its molecular driving forces. Therefore, we studied the energetics of binding of a therapeutic antibody fragment (Fab) to the native and non-native forms of TNF-α by employing calorimetric and spectroscopic methods. Global thermodynamic analysis of data obtained from the corresponding binding and urea-induced denaturation experiments has been supported by structural modeling. We demonstrate that the observed high affinity binding of Fab to TNF-α is an enthalpy-driven process due mainly to specific noncovalent interactions taking place at the TNF-α-Fab binding interface. It is coupled to entropically unfavorable conformational changes and accompanied by entropically favorable solvation contributions. Moreover, the three-state model analysis of TNF-α unfolding shows that at physiological concentrations, TNF-α may exist not only as a biologically active trimer but also as an inactive monomer. It further suggests that even small changes of TNF-α concentration could have a considerable effect on the TNF-α activity. We believe that this study sets the energetic basis for understanding of TNF-α inhibition by antibodies and its unfolding linked with the concentration-dependent activity regulation.

Introduction

Human tumor necrosis factor α (TNF-α) is an important cytokine involved in many diverse and complex functions in human organism, particularly in inflammation and cellular immune response (1–3). Its wide role in biological processes and observations of its ability to trigger regression of tumors makes the TNF-α one of the most intensively investigated proteins over past decades, although cytotoxicity prevents its extensive clinical use (1, 4). The crystal structure determined in 1989 (PDB code 1TNF) suggests that TNF-α consists of three identical 17.35-kDa poly-peptide chains. Each of them is packed into an antiparallel β-sandwich structure. Subunits are held together by noncovalent interactions and form a compact bell-shaped trimer characterized by a 3-fold axis of symmetry (5, 6). Biologically active TNF-α is a homotrimer (7–10), which may dissociate to monomers in the solution at physiological concentrations (10, 11). This regulatory feature has been suggested to be a part of a mechanism essential for maintenance of optimal biological activity of TNF-α (10, 11).

Overproduction of TNF-α in tissues results in development of chronic autoimmune diseases such as rheumatoid arthritis, multiple sclerosis, psoriasis, and Crohn disease (12, 13). Currently, the availability of certain biopharmaceuticals to bind TNF-α and consequently block its binding to receptors enables successful treatment of these pathologies. Such TNF-α inhibitors are in most cases monoclonal antibodies, e.g. infliximab, adalimumab, golimumab; however, some other approaches to TNF-α inhibition are effective as well (14). Approval of the first TNF-α inhibitors that successfully treat the pathologies associated with elevated TNF-α level has induced over the past decades an intensive search for more effective and safe inhibitors of TNF-α. Presently used therapeutics are efficient in therapy; however, they still induce a number of undesired side effects. To solve this problem, extensive research focusing on the design of new and better inhibitors is going on in several pharmaceutical companies. Unfortunately, despite all these efforts, the molecular basis of forces that drive recognition of TNF-α by its inhibitors (15) remains poorly understood. Therefore, we decided to study energetics of recognition (stabilization) of native and non-native forms of TNF-α by adalimumab, which is the first commercially available therapeutic human antibody. It has been shown that mixing of solutions of adalimumab and TNF-α results in a heterogeneous mixture of TNF-α-adalimumab complexes (16). Because quantitative thermodynamic analysis and structural modeling of binding events in such a complex interacting system are not possible, we simplified the process by using a fragment of adalimumab (Fab) instead of the full-length antibody.

Binding of Fab to TNF-α at nondenaturing conditions was monitored by isothermal titration calorimetry (ITC)³ and by circular dichroism (CD) spectroscopy. In addition, the stabilization of TNF-α by Fab at denaturing conditions was investigated via urea-induced unfolding of the TNF-α-Fab complex, unbound TNF-α, and unbound Fab by CD and fluorescence spectroscopy. Thermodynamic parameters obtained from global analysis of experimental data measured at various conditions (temperature, protein concentration, and urea concentration) are discussed in terms of structural alterations that accompany the observed binding and unfolding processes. In addition, we designed a structural model of the TNF-α-Fab complex that was, in the absence of its three-dimensional structure, used in molecular interpretation of the obtained thermodynamic parameters of binding (Fig. 1).

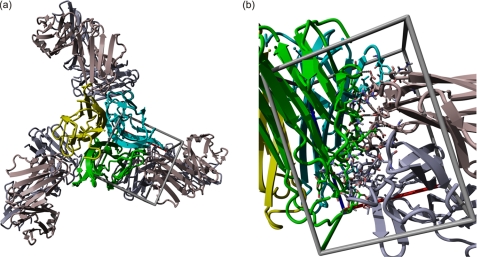
FIGURE 1.

Structural model of TNF-α-Fab complex. a, TNF-α subunits are presented in green, blue, and yellow. Three Fab fragments (in gray) are bound on the TNF-α surface at the contact of the TNF-α subunits. b, closer view of the binding site in a different orientation.

EXPERIMENTAL PROCEDURES

Preparation of Protein Solutions

The preparation and purification of human TNF-α has been described elsewhere (17). Monoclonal antibody adalimumab was purchased from Abbott Laboratories Ltd. Its digestion was performed by papain immobilized on an agarose beads, and Fab fragments were isolated from the digestion mixture by protein A affinity chromatography. Immobilized papain, protein A affinity column, and Fab fragment preparation protocols were obtained from Pierce and Thermo Fisher Scientific. SDS-PAGE electrophoresis under reducing and nonreducing conditions shows that the Fab fragment is present in solution in a form of polypeptide chains linked with disulfide bond. The amino acid sequence of the Fab fragment and SDS-PAGE data are available in the supplemental material.

Prior to calorimetric and spectroscopic measurements, solutions of proteins were dialyzed extensively against phosphate buffer (0.02 m sodium phosphate, 0.14 m NaCl, pH 7.4). All of the samples for the urea denaturation experiments were prepared by mixing 10 m urea and protein stock solution to a final urea concentration between 0 and 8 m. The pH value of all solutions was checked and adjusted to 7.4 by the addition of NaOH. The protein concentration was determined spectrophotometrically from the absorbance measured at 278 nm in 6 m guanidine HCl at 25 °C using extinction coefficients obtained by the method introduced by Gill and von Hippel (18) (see the supplemental material).

Isothermal Titration Calorimetry

Experiments were performed between 5 and 54 °C in an iTC₂₀₀ calorimeter from MicroCal Inc. (Northampton, MA). Before each experiment, the protein solutions were degassed for 10 min. A solution of Fab was titrated into a solution of TNF-α. The enthalpy of interaction (ΔH_T) was obtained by integration of the raw signal, corrected for the corresponding heat of dilution, and expressed per mole of Fab fragment added per injection.

CD Spectroscopy

CD spectroscopy measurements were performed with an AVIV model 62A DS spectropolarimeter (Aviv Associates) at different temperatures lower than the one at which the proteins start to denature irreversibly. Changes in secondary structure at increasing urea concentrations (0–8 m) were followed by measuring the ellipticity (ϴ) of the protein solutions at several wavelengths. Ellipticities of Fab solutions were measured at 234 nm in a 1-mm cuvette and at protein concentration of ∼43 μm. Ellipticities of the TNF-α solutions were measured at 224 nm in 1- and 10-mm cuvettes at protein concentrations of ∼17 and ∼1.8 μm, respectively. Measurements of TNF-α-Fab complex solutions were performed at 222 and 234 nm in 1- and 10-mm cuvettes at the complex concentrations of ∼7 and ∼0.3 μm, respectively. The reversibility of the urea-induced transitions was checked by diluting the protein solutions from the post-transition to the pre-transition urea concentrations. By comparing the CD spectra measured for these diluted solutions with those obtained for the sample solutions prepared directly from urea and buffer solutions, we estimated the extent of reversibility of the observed transitions to be higher than 80%.

Molar ellipticities ([ϴ], 10⁵ degrees cm² dmol⁻¹) presented in this study were obtained from raw data (ellipticities ϴ) by subtracting the corresponding ϴ of the buffer solution and taking into account the molar concentration of protein (c) and optical path length (l) through the relation [ϴ] = ϴ/(c·l).

Fluorescence Spectroscopy

Fluorescence emission spectra were recorded using a PerkinElmer Life Sciences LS 50 luminescence spectrometer equipped with thermally controlled cell holder and a cuvette with a 1-cm path length. All measurements were performed at 25.0 ± 0.1 °C. Concentration of TNF-α in solutions was ∼2.2 μm, whereas concentration of the TNF-α-Fab complex was ∼0.45 μm. Fluorescence spectra accompanying urea-induced denaturation were measured in the presence of 15 μm 1-anilino-8-naphthalene sulfonate (ANS), a hydrophobic probe frequently used as an indicator of the molten globule-like protein states (19). The ANS emission spectra were measured between 400 and 580 nm with excitation at 380 nm.

Molecular Modeling

Molecular modeling of the TNF-α-Fab complex was started with building and refining a homology model of Fab using YASARA Structure (20, 21). Protein-protein docking software Hex 6.0 (22–24) was used to obtain an ensemble of representative complexes between TNF-α and Fab. 25 complexes with the lowest docking score were saved for further modeling and analysis. The complexes were then refined using short 10-ps molecular dynamics (YASARA Structure, Yamber2 FF) in vacuum followed by energy minimization in water (Convergence 0.05 kJ/mol per atom during 200 steps) (25). Finally, FoldX (26) (as a YASARA plugin) was used for the final refinement and calculation of interaction energy between Fab and TNF-α. NACCESS (27) was used for the analysis of protein surfaces.

RESULTS

Binding of Fab to TNF-α Monitored by ITC and CD Spectroscopy

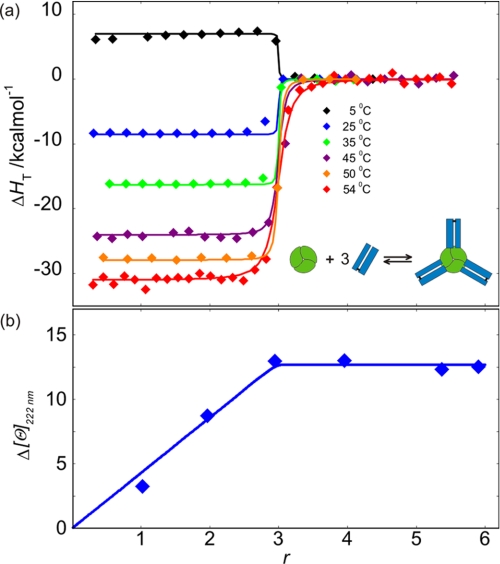
The calorimetric biding isotherms accompanying association of Fab to TNF-α exhibit the characteristics of a 3:1 association process (Fig. 2). This observation is confirmed by a very good fitting of the family of the ITC curves measured at different T with the corresponding model function based on the binding model that assumes the existence of three equivalent independent Fab binding sites on the TNF-α molecule (Fig. 2; see the supplemental material for details). Therefore, the obtained model-based thermodynamic parameters (Table 1) may be considered as appropriate descriptors of the binding process. In line with the ITC data are the results of the CD spectroscopic measurements, which clearly indicate that the association of TNF-α with Fab is accompanied by significant rearrangements of Fab and/or TNF-α structure (Fig. 2).

FIGURE 2.

Binding of Fab to TNF-α monitored by ITC and CD spectroscopy. a, enthalpies of Fab binding to TNF-α at various Fab/TNF-α molar ratios (r) and temperatures monitored by ITC. Lines represent the best global fit of the model (see the supplemental material; overall binding event schematically presented as an inset) from which the corresponding thermodynamic parameters were extracted (Table 1 and Fig. 6). b, changes in secondary structure upon Fab binding to TNF-α at various Fab/TNF-α molar ratios (r) monitored by CD spectroscopy at 222 nm and 25 °C. Δ[ϴ] was calculated by subtracting molar ellipticities of (unbound) TNF-α and Fab at 222 nm from the measured ellipticities of the TNF-α-Fab complex normalized to TNF-α molar concentration and optical path length of 1 cm (Δ[ϴ] = [ϴ]_exp − [ϴ]_TNF-α − r[ϴ]_Fab). The blue line represents the model function calculated from best fit binding parameters obtained from the analysis of ITC measurements.

TABLE 1.

Thermodynamic parameters at T_o = 37 °C obtained from global fitting of the model functions (see supplemental material) to the ITC binding data (Fig. 2) and urea denaturation data (Figs. 3 and 5)

Process		Parametera/unit
		ΔG(To)o/kcal mol−1	ΔH(To)o/kcal mol−1	ΔCPo/kcal mol−1 K−1	m/kcal mol−1m−1
Fab binding to the binding site of TNF-α		−13.1 (±0.07)b	−17.8 (±0.1)	−0.78 (±0.01)
Urea unfolding of
Fab	F ↔ FD	23.8 (±0.7)	38.8 (±1.5)	0.8 (±0.1)	3.6 (±0.1)
TNF-α	T3 ↔ I3	5.5 (±0.4)	8.2 (±0.2)	1.5 (±0.3)	1.1 (±0.1)
	I3 ↔ 3TD	21.8 (±0.4)	6.5 (±1.5)	−0.5 (±0.2)	2.1 (±0.05)
TNF-α-Fab complex	T3F3 ↔ ITF	12.1 (±0.5)	18.5 (±1.5)	0.3 (±0.1)	1.9 (±0.1)
	ITF ↔ 3TD + 3FD	126 (±2)	166 (±5)	5.6 (±0.4)	12.8 (±0.1)

^a ± values represent standard deviations estimated from diagonal elements of the corresponding variance-covariance matrixes.

^b The corresponding value of the binding constant calculated as K_(To) = exp(−ΔG_(To)^o/RT) = 1.7 (±0.3) × 10⁹ m⁻¹.

To test whether protonation or deprotonation of the proteins is coupled to their binding, we also performed the same ITC experiments in Tris buffer (0.02 m Tris, 0.14 m NaCl, pH = 7.4, T = 35 °C), which has about 10 times higher ionization enthalpy than the phosphate buffer (28). Because the titration curves observed in Tris are very similar to those observed in phosphate, we concluded that no protonation or deprotonation is involved in association of Fab with TNF-α.

Urea-induced Unfolding Monitored by CD and Fluorescence Spectroscopy

Because of the irreversibility of the thermal denaturation of Fab, TNF-α, and the TNF-α-Fab complex, we attempted to investigate the thermodynamics of their unfolding transitions via the reversible urea denaturation (see Figs. 3 and 5). The quantitative thermodynamic analysis of such denaturation processes has been discussed extensively elsewhere (29–31), and therefore, the details of its application to our systems are discussed in supplemental material.

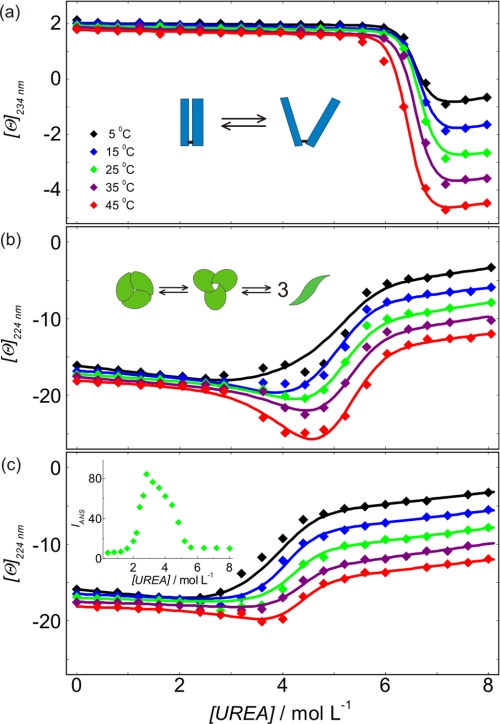
FIGURE 3.

Modeling urea-induced denaturation transitions of Fab and TNF-α. a–c, molar ellipticities measured as a function of urea concentration for Fab (a) and TNF-α at high (17 μm) (b) and low (1.8 μm) (c) concentration and various temperatures. Lines represent the best global fit of the denaturation models (see the supplemental material; schematically presented as insets in a and b) to the experimental denaturation curves. In c, the inset shows ANS emission fluorescence of TNF-α at 2.2 μm protein concentration and 15 μm ANS concentration measured at 458 nm and 25 °C.

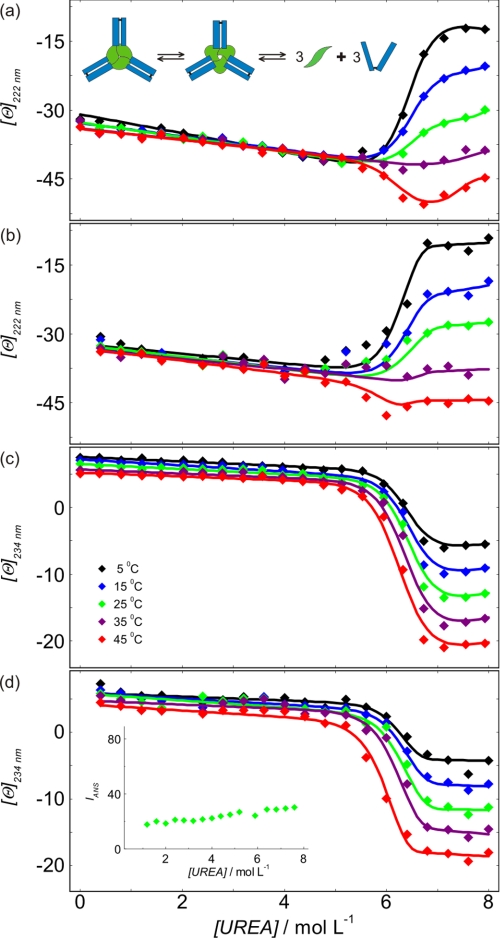
FIGURE 5.

Modeling urea-induced denaturation transitions of TNF-α-Fab complex. a and b, molar ellipticities of the TNF-α-Fab complex measured as a function of urea concentration at 222 nm at high (7 μm) (a) and low (0.3 μm) (b) concentration of the complex. c and d, molar ellipticities of the TNF-α-Fab complex measured as a function of urea concentration at 234 nm at high (7 μm) (c) and low (0.3 μm) (d) concentration of the complex. Lines represent the best global fit of the denaturation model (see the supplemental material). In a, the inset shows a schematic presentation of the TNF-α-Fab complex denaturation. In d, the inset shows ANS emission fluorescence of the TNF-α-Fab complex recorded at 0.45 μm complex and 15 μm ANS concentration measured at 458 nm and 25 °C.

Fab

SDS-PAGE electrophoresis (see the supplemental material) shows that the Fab molecule is composed of two polypeptide chains linked by a disulfide bond. Therefore, Fab (F) urea-induced unfolding can be treated as a monomolecular transition. A very good global fit is obtained for the two-state transition model expressed as: F(native) ↔ F^D(denatured) with the family of CD denaturation curves measured at various temperatures (Fig. 3a). This suggests that the model is appropriate and gives reliable thermodynamic parameters of Fab unfolding (Table 1).

TNF-α

A brief examination of CD denaturation curves (Fig. 3, b and c) suggests that between 0 and 8 m urea TNF-α may populate three conformational states. At 0–2.5 m urea, TNF-α predominantly exists as a native trimer. The intermediate state of TNF-α is discernible mainly from CD denaturation curves measured from 25 to 45 °C at 2.5–6 m urea and high TNF-α concentration. Observation of the corresponding ANS fluorescence spectra suggests that TNF-α in the intermediate state binds a known molten globule-specific fluorescence probe ANS (Fig. 3c, inset). CD spectra measured in 8 m urea (Fig. 4) indicate that in its urea-denatured state, TNF-α still contains a considerable amount of secondary structure. Careful comparison of CD denaturation curves measured at high and low TNF-α concentration (Fig. 3, b and c) suggests that the transition from the native to the intermediate state is concentration-independent (monomolecular), whereas the transition from the intermediate state to the denatured state is concentration-dependent (non-monomolecular). Based on these qualitative findings, previously reported results on TNF-α folding (32), and known TNF-α structural features (5, 8, 9), we assumed that TNF-α (T₃) unfolding may be described by the following three-state transition model: T₃(native) ↔ I₃(intermediate) ↔ 3T^D(denatured). Global fitting of the model resulted in its good agreement with the family of TNF-α CD denaturation curves measured at different T and different TNF-α concentration (Fig. 3). The corresponding thermodynamic parameters are presented in Table 1.

FIGURE 4.

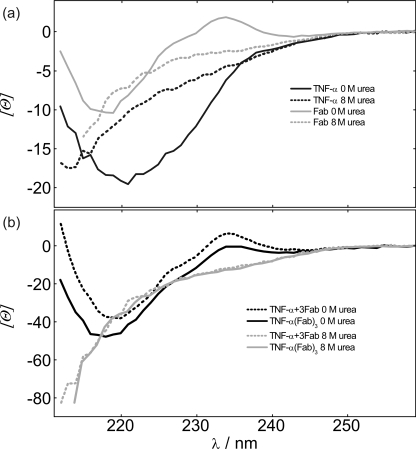
CD spectra of TNF-α, Fab, and TNF-α-Fab complex. a, far-UV CD spectra of TNF-α and Fab in 0 and 8 m urea at 25 °C. b, far-UV CD spectra of the TNF-α-Fab complex in 0 and 8 m urea at 25 °C in comparison with the corresponding sum of spectra of unbound TNF-α and Fab.

TNF-α-Fab Complex

Analysis of ITC and CD binding experiments and molecular modeling of TNF-α-Fab formation suggest that the TNF-α-Fab complex is a heterohexamer consisting of three Fab molecules bound on a TNF-α trimer (T₃F₃). Denaturation curves of the TNF-α-Fab complex were measured at various temperatures and two concentrations of the complex. CD spectra in 0 m urea show local maximum at about 234 nm in the case of Fab and TNF-α-Fab complex but not in the case of the unbound TNF-α (Fig. 4). Because molar ellipticities of TNF-α at 234 nm in 0 and 8 m urea are practically the same, it may be assumed that denaturation curves of the TNF-α-Fab complex measured at 234 nm reflect mostly changes in the secondary structure of Fab. On the other hand, at 222 nm, both proteins contribute to the measured signal. The complexity of denaturation curves measured at 222 nm suggests that denaturation of the TNF-α-Fab complex should be considered at least as a three-state process. In contrast to TNF-α, solutions of the TNF-α-Fab complex exhibit no induced ANS fluorescence between 0 and 8 m urea, suggesting that in the intermediate state, Fab is strongly bound to the binding sites of ANS (Fig. 5). Moreover, concentration dependence of urea unfolding curves suggests that the overall process of denaturation of the complex is not a monomolecular process. Based on these findings and known TNF-α unfolding features, we assumed that TNF-α-Fab complex (T₃F₃) unfolding may be described as: T₃F₃(native) ↔ I_TF(intermediate) ↔ 3T^D + 3F^D. Global fitting of the model resulted in good agreement of the corresponding model function with the family of TNF-α-Fab CD denaturation curves measured at different T and TNF-α-Fab complex concentrations. The corresponding thermodynamic parameters are presented in Table 1. It should be mentioned that in contrast to the model analysis of Fab and TNF-α unfolding curves that resulted in reasonably reliable and uniform thermodynamic descriptors, TNF-α-Fab complex unfolding curves could be equally well described by various sets of thermodynamic parameters. Because all these parameters are state functions, the problem of their high correlation was solved in the following way. The overall parameters of the TNF-α-Fab complex unfolding were calculated independently from parameters describing Fab (Fig. 3a) and TNF-α (Fig. 3, b and c) unfolding and Fab binding to TNF-α (Fig. 2) and further used in the fitting procedure as fixed parameters. The validity of this approach was justified experimentally by measuring CD spectra of Fab, TNF-α, and their complex in 8 m urea. Namely, it can be seen in Fig. 4 that CD spectrum (physical property) corresponding to the denatured TNF-α-Fab complex is equal to the corresponding sum of spectra (physical properties) of the individual denatured proteins.

DISCUSSION

Driving Forces of TNF-α Recognition by Fab

Very good agreement of the proposed model with the experimental ITC data measured at various temperatures suggests that each TNF-α binds three Fab molecules. The thermodynamic parameters of binding of Fab to TNF-α (Table 1) obtained by model analysis of ITC data show that the binding of Fab to TNF-α is an enthalpy-driven process accompanied by an unfavorable entropy contribution (Fig. 6). The measured large negative heat capacity change suggests that hydrophobic effect is an important driving force of the observed binding event. Standard thermodynamic parameters of binding, ΔF^o, can be dissected into contributions coming from conformational changes, ΔF_CONF^o, of Fab and/or TNF-α (experimentally observed by CD spectroscopy; Fig. 2) and from the rigid body association, ΔF_BIND^o, of the prestructured Fab and TNF-α

where G, H, S, and C_P represent Gibbs free energy, enthalpy, entropy, and heat capacity, respectively. ΔF^o values were obtained from model analysis of ITC experiments (Table 1; see the supplemental material), whereas the ΔF_BIND^o contributions were estimated using empirical parameterization that is mainly based on changes in polar and nonpolar solvent-accessible surface areas. The solvent-accessible surface area values were calculated from the structural model of the TNF-α-Fab complex (Fig. 1; see the supplemental material). Finally, the contributions of structural changes were estimated as ΔF_CONF^o = ΔF^o − ΔF_BIND^o. Fig. 6 shows that the main driving force of TNF-α recognition by Fab is the very large negative ΔH_BIND^o, suggesting that a large number of strong intermolecular contacts are formed upon binding of the prestructured Fab and TNF-α. This is in accordance with our structural model that predicts the formation of about 20 H-bonds (per binding site) and several van der Waals contacts in the TNF-α-Fab binding interface (Fig. 1). Moreover, the molecular recognition is to a large extent driven by favorable solvation entropy contributions (ΔC_P,BIND^o < 0 and ΔC_P,CONF^o < 0) arising mainly from desolvation of a relatively large nonpolar surface area (ΔA_N,BIND ≈ ΔA_N,CONF ≈ −1400 Ų; see the supplemental material). The calculated significantly positive ΔG_CONF^o is in accordance with the experimental observation that the prestructured Fab and TNF-α conformations are not present in the unbound state at given experimental conditions and thus supports the validity of the presented parsing of thermodynamic parameters. ΔG_CONF^o > 0 may be associated with a large loss of configurational entropy that overcompensates the corresponding small favorable enthalpy and large favorable solvation entropy contribution. An estimate of configurational entropy loss upon folding ((Number of residues) × 4.3 cal K⁻¹ (mol residue)⁻¹) (33) suggests that the observed binding-coupled conformational transition involves about 10 residues most likely located on the hypervariable loops in the Fab binding region. Structural rearrangements of this region are expected in light of the inhibition of TNF-α activity, which requires tight fitting of Fab into the narrow groove formed in the contact of two TNF-α subunits (location of TNF-α receptor epitope).

FIGURE 6.

Dissection of binding parameters. Standard thermodynamic quantities of Fab binding to TNF-α (Exp.) at 37 °C obtained by global analysis of ITC data (Table 1) were dissected into the contributions of rigid body binding (Bind.) and conformational change (Conf.) (see Equation 1 and the corresponding discussion). Rigid body binding parameters were calculated from the structural model (Fig. 1), whereas conformational change parameters were estimated as Conf. = Exp. − Bind.

High binding affinity and specificity of inhibitors are of particular importance in the development of efficient therapeutics. In this light, our approach of dissecting the thermodynamics of inhibitor binding to TNF-α may be used as a general methodology for uncoupling the specificity and affinity factors. Namely, binding specificity is predominantly determined by the ability of inhibitor to form energetically favorable interactions with its target. Because highly specific binding results in highly negative ΔH_BIND^o, this parameter, which can be estimated on the basis of structural data (Fig. 6; see the supplemental material), may be used as a criterion of the binding specificity. Often, ΔH_BIND^o predominantly contributes to the overall ΔH^o of binding. In such cases, the measured ΔH^o itself could be used as a valuable specificity criterion. Therefore, ΔH^o and/or ΔH_BIND^o can complement the affinity data that, in the process of development of new, improved versions of inhibitors, usually characterize the therapeutic candidates (34).

Thermodynamic Stability of TNF-α and Regulation of Its Activity

Inspection of thermodynamic parameters in Table 1 suggests that the folding of Fab (F^D → F), TNF-α (3T^D → T₃), and TNF-α-Fab complex (3T^D + 3F^D → T₃F₃) in the corresponding standard states at physiological temperatures is an enthalpy-driven process that is a general feature of globular proteins (35, 36). To estimate the degree of unfolding of TNF-α and Fab in the denatured state, the observed overall heat capacities of unfolding were compared with the corresponding averages over a large set of proteins presented by Robertson and Murphy (37). The expected average ΔC_p^o values were calculated from the linear relation between the number of residues in the cooperatively unfolding unit of the protein and the heat capacity change. In the case of TNF-α, the experimentally obtained ΔC_p^o is only 15% of the expected average value, and in the case of Fab, it is only 14% of the expected average value, which is in agreement with CD spectra showing a significant amount of residual protein structure even in 8 m urea (Fig. 4).

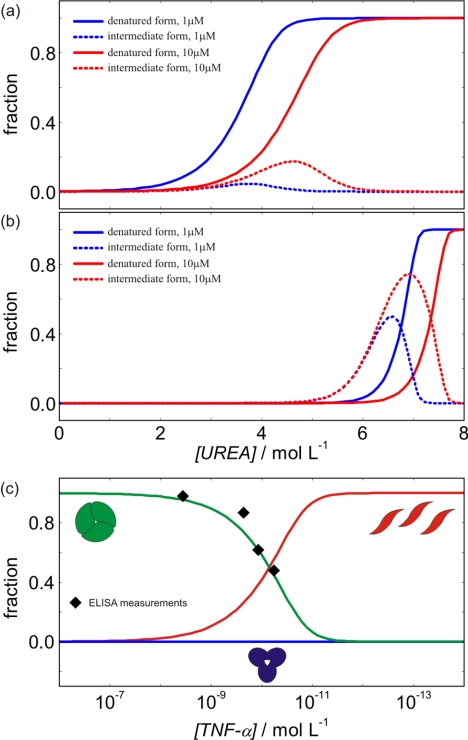
We used thermodynamics to determine the mechanism and driving forces of TNF-α unfolding and binding to Fab. Namely, it enables prediction of TNF-α behavior at different conditions (temperature, urea concentration, TNF-α concentration, and Fab concentration). In this context, speciation diagrams (Fig. 7) indicate that Fab significantly protects the TNF-α native and intermediate form against urea denaturation. Moreover, the population of states in the presence and in the absence of urea (Fig. 7) is significantly affected by changes in TNF-α concentration. In the absence of urea, the changes of populations of TNF-α native, intermediate, and denatured forms (Fig. 7c) may be important for regulation of TNF-α activity. Namely, at physiological concentrations (38) (picomolar range), TNF-α not only exists as a native (biologically active cytotoxic) trimer, but a considerable fraction of monomeric (inactive noncytotoxic) TNF-α may be present as well (11). Our model of TNF-α denaturation predicts that in the absence of urea, decreasing TNF-α concentration for an order of magnitude (e.g. from 100 to 10 pm) may result in about 100 times lower concentration of its active form and in the complete absence of the intermediate form. It follows that at such conditions, even small changes of TNF-α concentration could have a considerable effect on TNF-α activity. The predictions of our model are in very good agreement with the corresponding data measured by ELISA (11).

FIGURE 7.

Population of different TNF-α and TNF-α-Fab complex forms at various conditions at 37 °C. a and b, population of TNF-α forms (a) and population of the TNF-α-Fab complex forms (b) at different urea and protein concentrations. c, population of different forms of TNF-α in the absence of urea as a function of TNF-α concentration. Black diamonds represent the values measured by ELISA (Corti et. al. (11)).

Taking these data together, we believe that the measured energetics of the protein-protein binding and protein unfolding together with the corresponding molecular interpretation will improve our understanding of forces that drive recognition of TNF-α by monoclonal antibody fragments and understanding of molecular mechanism of TNF-α activity regulation in general. Moreover, because many new monoclonal antibodies and their fragment-based therapeutics are in different stages of preclinical and clinical development, we believe that the thermodynamic approach presented in this work can be successfully used in the more rapid design, development, stability assessment, and production of more efficient and safer drugs.