Abstract
We propose in this work a patch-based image labeling method relying on a label propagation framework. Based on image intensity similarities between the input image and an anatomy textbook, an original strategy which does not require any non-rigid registration is presented. Following recent developments in non-local image denoising, the similarity between images is represented by a weighted graph computed from an intensity-based distance between patches. Experiments on simulated and in-vivo MR images show that the proposed method is very successful in providing automated human brain labeling.
Index Terms: brain MRI, image segmentation, non-local approach, label propagation
I. Introduction
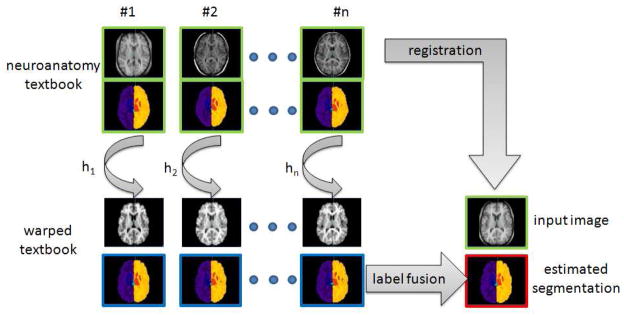
Automated brain labeling [28], [7], [24], [23] is a crucial step in neuroimaging studies since it provides a segmentation map of contiguous meaningful brain regions. Label propagation (also called label fusion) is a way to segment an image and it is usually performed by registering one or several labeled images to the image to be segmented. The labels are then mapped and fused using classification rules to produce a new label map of the input image [30], [15], [3], [2], [16], [8], [33], [35], [26], [38], [34], [25], [19]. The principle of such registration-based labeling approach is shown in Figure 1. This segmentation approach is highly versatile since the main prerequisite is an anatomy textbook, i.e. a set of measured images (such as Magnetic Resonance (MR) imaging or Computerized Tomography (CT)) and the corresponding label maps. The use of label propagation has been extensively investigated for automatic brain MR segmentation, especially for structures such as hippocampus, caudate, putamen, amygdala, etc., and cortex areas. The keypoints of registration-based label propagation approaches concern the accuracy of the non-rigid registration, the fusion rules [11], [30], [36], [15], [3], the selection of the labeled images [37], [2], [35] and the labeling errors in primary manual segmentation.
Fig. 1.
Principle of registration-based label propagation methods. The input data (shown with green borders) are an anatomy textbook (i.e. a set of N anatomical images with the corresponding label maps), and one anatomical image I. The set of anatomical images of the textbook is (non-linearly) registered to the input image I, and each label map is deformed with respect to the estimated transformation Hi. The final image segmentation (shown with red borders) is then obtained by fusing all the deformed label maps (shown with blue borders).
Because of the use of a registration algorithm, one makes the implicit (and strong) assumption that there exists a one-to-one mapping between the input image and all the anatomical images of the textbook. In the case where no one-to-one mapping is possible, a registration-based labeling framework propagates incorrect labels. Moreover, local incorrect matching due to inherent registration errors can also lead to segmentation errors. Finally, as shown in a recent evaluation study [22], there is a non-negligible discrepancy in term of quality of matching between non-rigid registration techniques. Thus, even if several algorithms are now freely available, the non-rigid registration procedure remains a complex step to setup and it is usually quite CPU time consuming.
In this work, following recent developments in non-local image denoising [6], [17], we propose an alternate strategy for label propagation which does not require any non-rigid registration. The proposed algorithm makes use of local similarities between the image to be labeled and the images contained in the anatomy textbook. The key idea is similar to a fuzzy block matching approach which avoids the constraint of a strict one-to-one mapping. The method described in this article has been developed irrespective of a similar patch-based approach recently proposed by Coupé et al. [10]. The contributions of our work can be summarized as follows: 1) a patch-based framework for automated image labeling, 2) investigation of several patch aggregation strategies (pair-wise vs group-wise labeling and pointwise vs multipoint estimation), 3) comparison of fusion rules (majority voting rule vs STAPLE [36]), 4) application to human brain labeling using publicly available simulated (Brainweb) and in-vivo (IBSR and NA0-NIREP) datasets, 5) comparison with a non-rigid registration-based technique.
II. Patch-based Label Propagation
A. Patch-based Principle
Recently, Buades et al. [6] have proposed a very efficient denoising algorithm relying on a non-local framework. Since then, this non-local strategy has been studied and applied in several image processing applications such as non-local regularization functionals in the context of inverse problems [20], [27], [14], [29], [31] or medical image synthesis [32].
Let us consider, over the image domain Ω, a weighted graph w that links together the voxels of the input image I with a weight w(x, y), (x, y) ∈ Ω2. This weighted graph w is a representation of non-local similarities in the input image I.
In [6], the non-local graph w is used for denoising purpose using a neighborhood averaging strategy (called non-local means (NLM)):
| (1) |
where w is the graph of self-similarity computed on the noisy image I, I(y) is the gray level value of the image I at the voxel y and Inlm is a denoised version of I.
The weighted graph reflects the similarities between voxels of the same image. It can be computed using a intensity-based distance between patches [9]:
| (2) |
where PI(x) is a 3D patch of the image I centered at voxel x; f is a kernel function (f(x) = e−x in [6]), N is the number of voxels of a 3D patch; σ is the standard deviation of the noise and β is a smoothing parameter. With the assumption of Gaussian noise in images, β can be set to 1 (see [6] for theoretical justifications) and the standard deviation of noise σ is estimated via pseudo-residuals as defined in [13].
B. Label Propagation
In this work, we propose to investigate the use of such a non-local patch-based approach for label propagation. Let
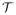 be an anatomy textbook containing a set of T1-weighted MR images
be an anatomy textbook containing a set of T1-weighted MR images
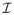 and the corresponding label maps
and the corresponding label maps
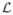 :
:
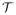 = {(
= {(
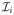 ,
,
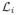 ), i = 1, ···, n}.
), i = 1, ···, n}.
1) Weighted Graph and Label Propagation
Let us consider, over the image domain Ω, a weighted graph wi that links together voxels x of the input image I and voxels y of the image
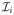 with a weight wi(x, y), (x, y) ∈ Ω2. wi is computed as follows:
with a weight wi(x, y), (x, y) ∈ Ω2. wi is computed as follows:
| (3) |
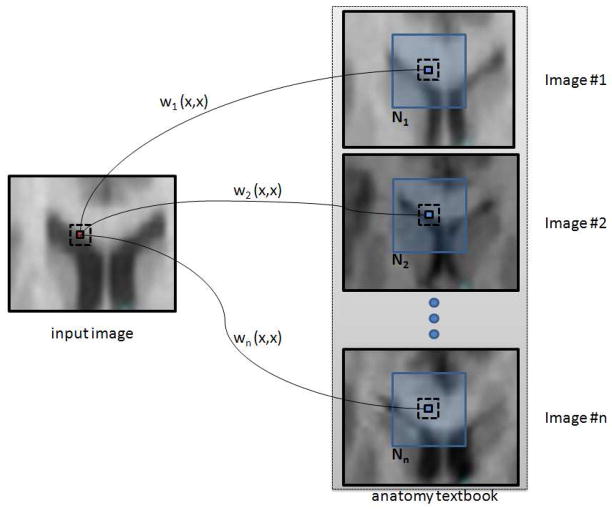
This weighted graph wi is a representation of non-local similarities between the input image I and the image
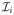 of the textbook (see Figure 2).
of the textbook (see Figure 2).
Fig. 2.
Weighted graph building. The set of graphs {wi}i=1, ···,
n is a representation of non-local interactions between the input image I and the images {
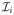 }i=1, ···,
n of the textbook.
}i=1, ···,
n of the textbook.
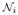 (x) is the neighborhood of the voxel x in the image
(x) is the neighborhood of the voxel x in the image
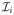 .
.
The assumption on which the proposed method relies is the following one: if patches of the input image I are locally similar to patches of the anatomy textbook, they should have a similar label. The label propagation procedure is then performed using the set of graphs {wi}i=1, ···,
n which reflects the local similarities between I and {
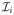 }i=1, ···,
n.
}i=1, ···,
n.
In the context of denoising [6], Buades et al. assume that every patch in a natural image has many similar patches in the same image. Thus, the graph w is computed between each voxel of the input image (which has led to the term “non-local” algorithm):w = {w(x, y), ∀(x, y) ∈ Ω2}. This is because of the assumption that similarities can be found in the entire image I. However, in the context of human brain labeling, the location of the brain structures is not highly variable and it is then not desirable to go through the entire image domain Ω to find good examples for the segmentation of a specific part of a brain. In this work, the graph is computed using a limited number of neighbors: w = {w(x, y), ∀x ∈ Ω, y ∈
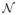 (x)}, where
(x)}, where
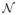 (x) is the neighborhood of the voxel x. The size of the considered neighborhood
(x) is the neighborhood of the voxel x. The size of the considered neighborhood
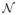 is directly related to the brain variability. The influence of this parameter is evaluated in the Section III-B.
is directly related to the brain variability. The influence of this parameter is evaluated in the Section III-B.
2) Pair-wise Label Propagation
For clarity sake, let start with an input image I and a textbook
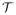 which contains only one anatomical image and the corresponding labeled image:
which contains only one anatomical image and the corresponding labeled image:
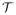 = (
= (
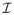 ,
,
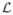 ) (this is the basis of pair-wise label propagation techniques). Using the patch-based approach described previously, the image I can be labeled using the following equation:
) (this is the basis of pair-wise label propagation techniques). Using the patch-based approach described previously, the image I can be labeled using the following equation:
| (4) |
where
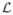 (y) is a vector of [0, 1]M (M is the total number of labels) representing the proportions for each label at the voxel y in the image
(y) is a vector of [0, 1]M (M is the total number of labels) representing the proportions for each label at the voxel y in the image
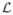 (this notation unifies the case where the anatomy textbook contains hard or fuzzy label maps). Thus, L(x) = (l1(x), l2(x), ···, lM (x)) are the membership ratios of the voxel x with respect to the M labels, such that Σk lk (x) = 1 and lk(x) ∈ [0, 1], ∀k ∈ [[1, M]]. Then, for each voxel x of I, the equation (4) leads to a fuzzy labeling of the input image I since L(x) ∈ [0, 1]M. A hard segmentation H of the image I can be obtained by taking the component of L(x) with the highest value. The hardening of the fuzzy label vector L(x) to get a binary label vector H(x) is done as follows:
(this notation unifies the case where the anatomy textbook contains hard or fuzzy label maps). Thus, L(x) = (l1(x), l2(x), ···, lM (x)) are the membership ratios of the voxel x with respect to the M labels, such that Σk lk (x) = 1 and lk(x) ∈ [0, 1], ∀k ∈ [[1, M]]. Then, for each voxel x of I, the equation (4) leads to a fuzzy labeling of the input image I since L(x) ∈ [0, 1]M. A hard segmentation H of the image I can be obtained by taking the component of L(x) with the highest value. The hardening of the fuzzy label vector L(x) to get a binary label vector H(x) is done as follows:
| (5) |
Now, let us consider a textbook
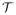 containing n pairs of images:
containing n pairs of images:
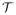 = {(
= {(
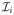 ,
,
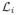 ), i = 1, ···, n}. The most straightforward approach is to perform n times the pair-wise procedure previously described, leading to n fuzzy segmentations {Li(x)}i=1, ···,
n (or n hard segmentations {Hi(x)}i=1, ···,
n). Then, these n label maps can be fused using a classifier combination strategy [21]. Thus, for instance, under the assumption of equal priors and by hardening the fuzzy label maps Li to get a set of hard segmentations {Hi}i=1, ···,
n, the final labeling Λ(x) at the voxel x can be obtained by applying the majority voting (MV) rule:
), i = 1, ···, n}. The most straightforward approach is to perform n times the pair-wise procedure previously described, leading to n fuzzy segmentations {Li(x)}i=1, ···,
n (or n hard segmentations {Hi(x)}i=1, ···,
n). Then, these n label maps can be fused using a classifier combination strategy [21]. Thus, for instance, under the assumption of equal priors and by hardening the fuzzy label maps Li to get a set of hard segmentations {Hi}i=1, ···,
n, the final labeling Λ(x) at the voxel x can be obtained by applying the majority voting (MV) rule:
| (6) |
where hij is a binary value corresponding to the label j of the image i at the voxel x and Λ(x) = (λ1(x), λ2(x), ···, λM (x)).
The pair-wise labeling approach using the majority voting rule to fuse the labels is described in Algorithm 1. A version of this pair-wise technique using STAPLE as the final label fusion is also evaluated in the Section III.
Algorithm 1.
Pair-wise labeling method using the majority voting rule
inputs: an image I and an anatomy textbook
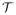 = {( = {(
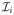 , ,
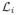 ), i = 1, ···, n} ), i = 1, ···, n} |
| ouput: a label image Λ |
| for all x ∈ Ω do |
| for i = 1 to n do |
| Compute Li(x) using Equation (4) |
| Compute Hi(x) using Equation (5) |
| end for |
| Compute Λ(x) by aggregating the set of labels {Hi}i=1, ···, n (Equation (6)) |
| end for |
3) Group-wise Label Propagation
We propose to study a group-wise combination strategy which takes all the images of the textbook to produce a fuzzy labeling. Indeed, the Equation (4) can be applied for an arbitrary number of labeled images:
| (7) |
Again, this leads to a fuzzy labeling which can be thresholded to obtain a hard labeling by taking the maximum of each vector L(x):
| (8) |
In this case, the final segmentation Λ can be set to L (resp. H) if a final fuzzy (resp. hard) labeling is desired. Unlike the pair-wise approach, the weight of each label map
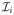 is automatically set by using the local patch-based similarity measure (see Equation (3)) with the input image I. There is no need to apply a classifier combination strategy. This is described in Algorithm 2.
is automatically set by using the local patch-based similarity measure (see Equation (3)) with the input image I. There is no need to apply a classifier combination strategy. This is described in Algorithm 2.
Algorithm 2.
Group-wise labeling method
inputs: an image I and an anatomy textbook
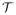 = {( = {(
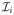 , ,
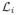 ), i = 1, ···, n} ), i = 1, ···, n} |
| ouput: a label image Λ |
| for all x ∈ Ω do |
| Compute L(x) using Equation (7) |
| Compute H(x) using Equation (8) |
| Λ(x) ← H(x) |
| end for |
C. Pointwise and Multipoint Estimation
In the previous section, according to the classification proposed by Katkovnik et al. in [17], the patch-based labeling techniques (both pair-wise and group-wise) provide pointwise estimates (Equations (4) and (7)). This means that the pairwise and group-wise methods estimate one label vector L for every voxel x. However, since the patch-based similarity measure is the core of the proposed labeling methods, one can obtain a label patch estimate at each considered voxel. This is called a multipoint label estimator. In contrast to the pointwise estimator, a multipoint estimator gives the estimate for a set of points (in our case, a patch).
For instance, a multipoint estimate for the group-wise labeling method is given by:
| (9) |
where P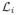 (y) is a 3D patch of the label map
(y) is a 3D patch of the label map
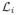 centered at the voxel y, and PL(x) is one multipoint label estimate centered at the voxel x. Thus, by going through the entire image domain Ω, one label patch estimate is obtain for each voxel. Since there is an overlap between all these label patches (each containing N voxels), for every voxel x ∈ Ω, we have N label estimates. Indeed, the label patch estimate of each voxel y which belongs to the patch P(x) contributes to the final label estimate of the voxel x. These N estimates can then be aggregated using a combination classifier. In this work, we have used the majority voting rule to fuse these N estimates.
centered at the voxel y, and PL(x) is one multipoint label estimate centered at the voxel x. Thus, by going through the entire image domain Ω, one label patch estimate is obtain for each voxel. Since there is an overlap between all these label patches (each containing N voxels), for every voxel x ∈ Ω, we have N label estimates. Indeed, the label patch estimate of each voxel y which belongs to the patch P(x) contributes to the final label estimate of the voxel x. These N estimates can then be aggregated using a combination classifier. In this work, we have used the majority voting rule to fuse these N estimates.
As suggested in [9], it is possible to speed-up the algorithm by considering a subset Ω★ of the image domain Ω with the constraint that there is at least one label estimate for each voxel. For instance, by using patches of size 3 × 3 × 3 voxels, one can consider only voxels with even spatial index (in each dimension) which leads to a speed-up of 8. Such an approach (denoted as fast multipoint in this article) is evaluated in the Section III. Moreover, for pointwise and multipoint estimation, based on the mean and variance of patches [9], a voxel preselection can be used to avoid useless computation.
Finally, several patch-based label propagation algorithms can be derived from the proposed framework depending of the following choices: pair-wise (PW) vs group-wise (GW), point-wise vs (possibly fast) multipoint estimates, majority voting (MV) rule vs STAPLE.
III. Experiments
A. Evaluation Framework
In this work, experiments have been carried out on three publicly available image datasets: Brainweb [4], the Internet Brain Segmentation Repository (IBSR) database and the NA0 database developed for the Non-rigid Image Registration Evaluation Project (NIREP). These three complementary image datasets provide different challenges for label propagation techniques: Brainweb dataset is used to mainly evaluate the separation power between 2 principal brain structures (white matter and gray matter), IBSR is a well known dataset for segmentation algorithms evaluation since it contains 32 brain structures (white matter, cortex, internal gray structures such as hippocampus, caudate, thalamus, putamen, etc.), and the NA0 dataset which has been originally created for registration evaluation purpose, provide also a good evaluation framework for cortical parcellation algorithms.
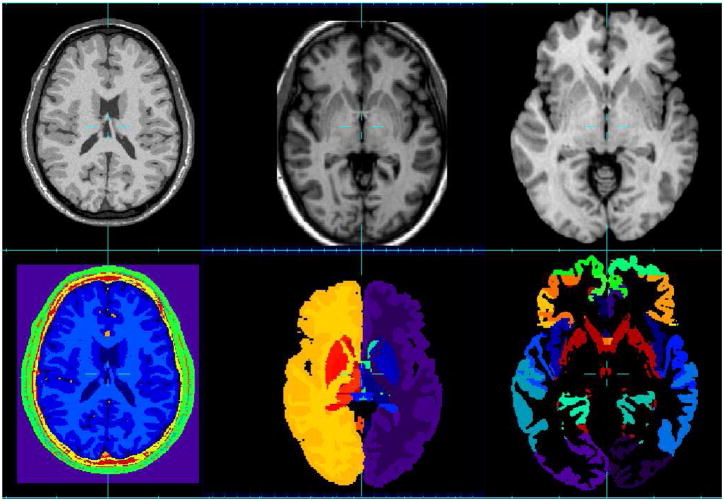
The Brainweb dataset1 is a set of 20 T1-weighted simulated data with these specific parameters: SFLASH (spoiled FLASH) sequence with TR=22ms, TE=9.2ms, flip angle=30 deg and 1 mm isotropic voxel size. Each anatomical model consists of a set of 3-dimensional tissue membership volumes, one for each tissue class: background, cerebro-spinal fluid (CSF), gray matter (GM), white matter (WM), fat, muscle, muscle/skin, skull, blood vessels, connective (region around fat), dura matter and bone marrow. Example images from the Brainweb dataset are shown in Figure 3 (first column).
Fig. 3.
MR image datasets used for the evaluation and the corresponding segmentation. First column: Brainweb database, second column: IBSR database, third column: NA0-NIREP database.
For the IBSR dataset2, the MR brain data sets and their manual segmentations are provided by the Center for Morphometric Analysis at Massachusetts General Hospital. It contains 18 images of healthy brains and the corresponding segmentation of the whole brain into 32 structures. Example images from the IBSR dataset are shown in Figure 3 (second column). The following pre-processing has been applied on IBSR images: 1) N3-based bias field correction using MIPAV3, 2) ITK-based histogram matching using 3DSlicer4, 3) affine registration using ANTs5 [5]. For each image to segment, all the images of the anatomy textbook are registered to this current image. Then, the label maps are also transformed (using a nearest neighbor interpolation). A total of 18*17 affine registrations have been performed.
The evaluation database NA06 consists of a population of 16 annotated 3D MR image volumes corresponding to 8 normal adult males and 8 females. The 16 MR data sets have been segmented into 32 gray matter regions of interest (ROIs) (see Figure 3 (third column). MR images were obtained in a General Electric Signa scanner operating at 1.5 Tesla, using the following protocol: SPGR/50, TR 24, TE 7, NEX 1 matrix 256 × 192, FOV 24 cm. 124 contiguous coronal slices were obtained, with 1.5 or 1.6 mm thick, and with an interpixel distance of 0.94 mm. Three data sets were obtained for each brain during each imaging session. These were coregistered and averaged post hoc using Automated Image Registration (AIR 3.03, UCLA)7. The final data volumes had anisotropic voxels with an interpixel spacing of 0.7 mm and interslice spacing of 1.5 – 1.6mm. All brains were reconstructed in three dimensions using Brainvox8. Before tracing ROIs, brains were realigned along a plane running through the anterior and posterior commissures (i.e., the AC-PC line); this ensured that coronal slices in all subjects were perpendicular to a uniformly and anatomically defined axis of the brain. The following preprocessing has been applied on NA0 images: 1) N3-based bias field correction using MIPAV, 2) ITK-based histogram matching using 3DSlicer.
As it is usually used for label propagation method evaluation, for each aforementioned dataset, a leave-one-out study is performed. Each image is separately selected as the image to be segmented. Using the provided segmentations of the remaining images as the anatomy textbook, label propagation is performed to obtain a segmentation of the considered image. In all cases, the Dice Index (DI) overlap is used as a segmentation quality measure:
| (10) |
where TP is the number of true positives, FP is the number of false positives and FN, the number of false negatives. The Dice index is computed for hard segmentations.
B. Neighborhood
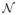 , Patch P and β
, Patch P and β
Experiments were carried out on the Brainweb dataset to determine the influence of the size of the neighborhood
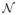 (which can be viewed as a local search area for similar patches), the size of the patches P and the smoothing parameter β (Equation 2). A pair-wise label propagation approach with the MV rule to fuse label maps has been used to determine the optimal parameter set. We found that the highest overlap value for both gray matter and white matter is obtained with the smallest size of patches (i.e. 3 × 3 × 3 voxels), the lower value of β (0.5) and large neighborhood
(which can be viewed as a local search area for similar patches), the size of the patches P and the smoothing parameter β (Equation 2). A pair-wise label propagation approach with the MV rule to fuse label maps has been used to determine the optimal parameter set. We found that the highest overlap value for both gray matter and white matter is obtained with the smallest size of patches (i.e. 3 × 3 × 3 voxels), the lower value of β (0.5) and large neighborhood
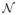 (the dice index stabilizes at a neighborhood size of 11 × 11 × 11 voxels). These findings are similar to some results obtained for image denoising [9] or image reconstruction [31]. β is a noise level dependent parameter. While the lowest value of β provides the best overlap results on Brainweb images (which are almost noiseless), we have found that a value of 1 is more appropriate for in-vivo brain MR images. In the next sections, the following setting has been used: a patch size of 3 × 3 × 3 voxels, a neighborhood size of 11 × 11 × 11 voxels, and β = 1.
(the dice index stabilizes at a neighborhood size of 11 × 11 × 11 voxels). These findings are similar to some results obtained for image denoising [9] or image reconstruction [31]. β is a noise level dependent parameter. While the lowest value of β provides the best overlap results on Brainweb images (which are almost noiseless), we have found that a value of 1 is more appropriate for in-vivo brain MR images. In the next sections, the following setting has been used: a patch size of 3 × 3 × 3 voxels, a neighborhood size of 11 × 11 × 11 voxels, and β = 1.
C. Influence of the size of the anatomy textbook
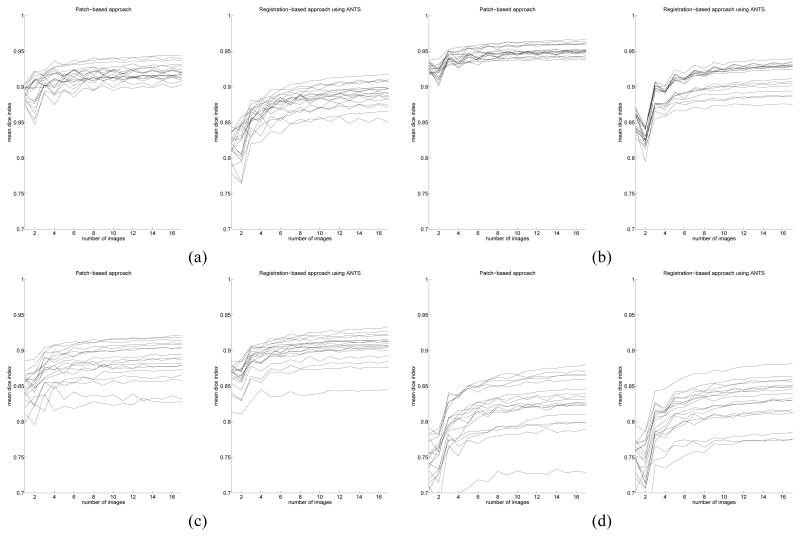
The evolution of the mean Dice index with respect to the size of the anatomy textbook has also been studied. This experiment has been carried out on the IBSR dataset, using up to 30 image permutations for each image to label. The behavior of the fast multipoint patch-based approach is compared with a non-rigid registration-based method (using ANTs [5], with the following command line: ANTS 3 -m PR[target.nii, source.nii, 1, 2] -i 100×100×10 -o output.nii -t SyN[0.25] -r Gauss[3,0] and the majority voting rule as label fusion strategy). In both cases, it has been found that increasing the size of the anatomy textbook provides higher overlap values (which stabilize quickly around 8 images). Figure 4 shows the evolution of the mean Dice index with respect to the number of images contained in the anatomy textbook. For all the results shown in the next sections, the maximum number of images has been used.
Fig. 4.
Mean dice index with respect to the number of images used for label propagation Left: patch-based approach, right: registration-based approach using ANTS (using, for each case, majority voting to fuse labels). (a): left white matter, (b): left cortex, (c): left thalamus, (d): left hyppocampus.
D. Pointwise vs blockwise
Comparison of pair-wise (using the majority voting rule for label fusion) vs group-wise approaches is shown in Table I for the Brainweb images, in Table II for IBSR and in Table VI for NA0-NIREP. We have also compared three types of estimators: pointwise vs multipoint vs fast multipoint. As mentioned in [17] (“in multipoint image estimation a weighted average of a few sparse estimates is better than single sparse estimate alone”), the results obtained on the three datasets suggest that the use of a multipoint estimator leads to the best segmentation (i.e. the highest overlap measures). Finally, the pair-wise approach and the group-wise approach lead to very similar results.
TABLE I.
Comparison (using the mean Dice index) of several possible combinations of patch-based approaches (using optimal global parameter setting) on the Brainweb dataset. For the pair-wise results, labels have been fused using the majority voting rule. Highest overlap rates are shown in bold.
| brain structure | pair-wise | group-wise | ||||
|---|---|---|---|---|---|---|
| pointwise | multipoint | fast multipoint | pointwise | multipoint | fast multipoint | |
|
| ||||||
| CSF | 0.87 | 0.88 | 0.87 | 0.87 | 0.86 | 0.86 |
| Gray Matter | 0.95 | 0.95 | 0.94 | 0.95 | 0.93 | 0.94 |
| White Matter | 0.95 | 0.95 | 0.94 | 0.95 | 0.94 | 0.94 |
| Fat | 0.83 | 0.87 | 0.85 | 0.83 | 0.85 | 0.84 |
| Muscle | 0.66 | 0.70 | 0.67 | 0.66 | 0.67 | 0.66 |
| Muscle/Skin | 0.93 | 0.94 | 0.93 | 0.93 | 0.93 | 0.93 |
| Skull | 0.92 | 0.93 | 0.91 | 0.92 | 0.92 | 0.92 |
| vessels | 0.61 | 0.59 | 0.56 | 0.61 | 0.56 | 0.57 |
| around fat | 0.37 | 0.36 | 0.30 | 0.37 | 0.34 | 0.36 |
| dura matter | 0.51 | 0.53 | 0.47 | 0.51 | 0.49 | 0.50 |
| bone marrow | 0.81 | 0.83 | 0.79 | 0.81 | 0.81 | 0.80 |
TABLE II.
Comparison (using the mean Dice index) of several possible combination of patch-based approaches (using optimal global parameter setting) on the IBSR dataset. When structures are separated into left/right, two overlap scores are reported. For the pair-wise results, labels have been fused using the majority voting rule. Highest overlap rates are shown in bold.
| brain structure | pair-wise | group-wise | ||||
|---|---|---|---|---|---|---|
| pointwise | multipoint | fast multipoint | pointwise | multipoint | fast multipoint | |
|
| ||||||
| Cerebral WM | 0.92 - 0.92 | 0.92 - 0.92 | 0.92 - 0.91 | 0.92 - 0.91 | 0.93 - 0.92 | 0.92 - 0.92 |
| Cerebral Cortex | 0.94 - 0.93 | 0.95 - 0.95 | 0.94 - 0.94 | 0.93 - 0.93 | 0.95 - 0.95 | 0.94 - 0.94 |
| Lateral Ventricle | 0.92 - 0.91 | 0.93 - 0.92 | 0.92 - 0.91 | 0.90 - 0.89 | 0.93 - 0.92 | 0.91 - 0.91 |
| Inferior Lat Vent | 0.58 - 0.53 | 0.61 - 0.56 | 0.58 - 0.55 | 0.50 - 0.49 | 0.60 - 0.56 | 0.56 - 0.54 |
| Cerebellum WM | 0.87 - 0.87 | 0.88 - 0.88 | 0.88 - 0.87 | 0.87 - 0.87 | 0.88 - 0.88 | 0.88 - 0.88 |
| Cerebellum Cortex | 0.93 - 0.94 | 0.95 - 0.95 | 0.94 - 0.94 | 0.93 - 0.93 | 0.95 - 0.95 | 0.94 - 0.94 |
| Thalamus | 0.88 - 0.87 | 0.89 - 0.88 | 0.88 - 0.88 | 0.89 - 0.89 | 0.89 - 0.89 | 0.89 - 0.89 |
| Caudate | 0.87 - 0.87 | 0.87 - 0.87 | 0.86 - 0.86 | 0.87 - 0.87 | 0.88 - 0.89 | 0.88 - 0.88 |
| Putamen | 0.87 - 0.86 | 0.88 - 0.87 | 0.87 - 0.87 | 0.88 - 0.88 | 0.89 - 0.89 | 0.88 - 0.88 |
| Pallidum | 0.69 - 0.66 | 0.71 - 0.69 | 0.66 - 0.63 | 0.77 - 0.77 | 0.79 - 0.79 | 0.78 - 0.79 |
| 3rd Ventricle | 0.79 | 0.81 | 0.79 | 0.74 | 0.80 | 0.77 |
| 4th Ventricle | 0.83 | 0.85 | 0.84 | 0.80 | 0.84 | 0.82 |
| Brain Stem | 0.92 | 0.94 | 0.93 | 0.92 | 0.93 | 0.92 |
| Hippocampus | 0.80 - 0.81 | 0.83 - 0.83 | 0.81 - 0.81 | 0.79 - 0.79 | 0.83 - 0.83 | 0.81 - 0.81 |
| Amygdala | 0.73 - 0.71 | 0.76 - 0.74 | 0.73 - 0.70 | 0.71 - 0.70 | 0.75 - 0.75 | 0.73 - 0.72 |
| CSF | 0.66 | 0.69 | 0.65 | 0.64 | 0.68 | 0.66 |
| Accumbens area | 0.63 - 0.61 | 0.66 - 0.63 | 0.58 - 0.56 | 0.66 - 0.65 | 0.68 - 0.66 | 0.67 - 0.65 |
| Ventral DC | 0.79 - 0.79 | 0.82 - 0.82 | 0.79 - 0.78 | 0.79 - 0.80 | 0.82 - 0.82 | 0.80 - 0.81 |
TABLE VI.
Comparison (using the mean Dice index) of several possible combination of patch-based approaches (using optimal global parameter setting) on the NA0-NIREP dataset. When structures are separated into left/right, two overlap scores are reported. For the pair-wise results, labels have been fused using the majority voting rule. Highest overlap rates are shown in bold.
| brain structure (left/right) | pair-wise | group-wise | ||||
|---|---|---|---|---|---|---|
| pointwise | multipoint | fast multipoint | pointwise | multipoint | fast multipoint | |
|
| ||||||
| Occipital Lobe | 0.74 - 0.77 | 0.79 - 0.81 | 0.76 - 0.78 | 0.74 - 0.77 | 0.78 - 0.80 | 0.76 - 0.78 |
| Cingulate Gyrus | 0.73 - 0.76 | 0.77 - 0.80 | 0.76 - 0.77 | 0.73 - 0.76 | 0.76 - 0.79 | 0.75 - 0.77 |
| Insula Gyrus | 0.82 - 0.85 | 0.85 - 0.88 | 0.83 - 0.86 | 0.82 - 0.85 | 0.84 - 0.87 | 0.83 - 0.86 |
| Temporal Pole | 0.80 - 0.84 | 0.83 - 0.87 | 0.81 - 0.85 | 0.80 - 0.84 | 0.82 - 0.86 | 0.81 - 0.85 |
| Superior Temporal Gyrus | 0.71 - 0.70 | 0.75 - 0.74 | 0.73 - 0.71 | 0.71 - 0.70 | 0.74 - 0.73 | 0.73 - 0.71 |
| Infero Temporal Region | 0.80 - 0.81 | 0.84 - 0.84 | 0.81 - 0.82 | 0.80 - 0.81 | 0.83 - 0.83 | 0.82 - 0.82 |
| Parahippocampal Gyrus | 0.79 - 0.81 | 0.82 - 0.84 | 0.80 - 0.82 | 0.79 - 0.81 | 0.81 - 0.83 | 0.80 - 0.82 |
| Frontal Pole | 0.78 - 0.77 | 0.82 - 0.82 | 0.80 - 0.79 | 0.78 - 0.77 | 0.81 - 0.80 | 0.79 - 0.78 |
| Superior Frontal Gyrus | 0.77 - 0.77 | 0.80 - 0.81 | 0.78 - 0.78 | 0.77 - 0.77 | 0.80 - 0.80 | 0.79 - 0.79 |
| Middle Frontal Gyrus | 0.75 - 0.73 | 0.78 - 0.77 | 0.76 - 0.74 | 0.75 - 0.73 | 0.78 - 0.76 | 0.76 - 0.75 |
| Inferior Gyrus | 0.65 - 0.71 | 0.70 - 0.75 | 0.67 - 0.72 | 0.65 - 0.71 | 0.69 - 0.74 | 0.67 - 0.72 |
| Orbital Frontal Gyrus | 0.80 - 0.80 | 0.84 - 0.84 | 0.81 - 0.81 | 0.80 - 0.80 | 0.83 - 0.83 | 0.81 - 0.81 |
| Precentral Gyrus | 0.72 - 0.69 | 0.76 - 0.74 | 0.73 - 0.70 | 0.72 - 0.69 | 0.75 - 0.73 | 0.73 - 0.71 |
| Superior Parietal Lobule | 0.71 - 0.69 | 0.75 - 0.73 | 0.73 - 0.70 | 0.71 - 0.69 | 0.74 - 0.72 | 0.72 - 0.70 |
| Inferior Parietal Lobule | 0.74 - 0.70 | 0.78 - 0.74 | 0.75 - 0.71 | 0.74 - 0.70 | 0.77 - 0.73 | 0.75 - 0.72 |
| Postcentral Gyrus | 0.65 - 0.60 | 0.70 - 0.65 | 0.65 - 0.60 | 0.65 - 0.60 | 0.69 - 0.63 | 0.67 - 0.61 |
E. Aggregation strategy
For the label fusion step, the majority voting rule is compared to the simultaneous truth and performance level estimation (STAPLE) [36]. STAPLE estimates the performance of each classifier iteratively and weights it accordingly, relying on an expectation-maximization (EM) optimization approach. We used the implementation provided by T. Rohlfing9. As already reported in [3], STAPLE based fusion rule does not necessary lead to higher Dice coefficients compared to the majority voting rule.
F. Comparison with previously reported results
The results obtained on the IBSR dataset are reported in Table V (highest Dice coefficients are in bold). In this table are also shown results reported in the literature, including non-rigid registration-based approaches and segmentation techniques. This experiment clearly shows that the proposed patch-based framework is very competitive with respect to recently published methods.
TABLE V.
Comparison (using the mean Dice index) of the group-wise multipoint patch-based approach with other segmentation methods. “Patch-based” denotes multipoint group-wise patch-based approach. Highest Dice coefficients are in bold.
| brain structure (left/right when available) | Patch-based | LWV-MSD 2009 [3] | Fischl et al. 2002 [12] | Khan et al. 2009 [18] | MA-IDMIN+ 2010 [26] | Sdika 2010 [34] | Akselrod 2007 [1] |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Cerebral WM | 0.93 - 0.92 | 0.78 - 0.78 | - | - | - | 0.91 | 0.87 |
| Cerebral Cortex | 0.95 - 0.95 | 0.81 - 0.81 | - | - | - | 0.94 | 0.86 |
| Lateral Ventricle | 0.93 - 0.92 | 0.83 - 0.82 | 0.78 | 0.85 | - | 0.90 | - |
| Inferior Lat Vent | 0.60 - 0.56 | 0.22 - 0.22 | - | - | - | 0.44 | - |
| Cerebellum WM | 0.88 - 0.88 | 0.79 - 0.79 | - | - | - | 0.86 | - |
| Cerebellum Cortex | 0.95 - 0.95 | 0.86 - 0.86 | - | - | - | 0.95 | - |
| Thalamus | 0.89 - 0.89 | 0.87 - 0.88 | 0.86 | 0.89 | 0.89 | 0.89 | 0.84 |
| Caudate | 0.88 - 0.89 | 0.83 - 0.83 | 0.82 | 0.83 | 0.85 | 0.86 | 0.80 |
| Putamen | 0.89 - 0.89 | 0.86 - 0.86 | 0.81 | 0.87 | 0.90 | 0.88 | 0.79 |
| Pallidum | 0.79 - 0.79 | 0.78 - 0.79 | 0.71 | 0.72 | 0.83 | 0.79 | 0.74 |
| 3rd Ventricle | 0.80 | 0.74 | - | - | - | 0.77 | - |
| 4th Ventricle | 0.84 | 0.77 | - | - | - | 0.81 | - |
| Brain Stem | 0.93 | 0.91 | - | - | - | 0.93 | 0.84 |
| Hippocampus | 0.83 - 0.83 | 0.74 - 0.76 | 0.75 | 0.76 | 0.80 | 0.81 | 0.69 |
| Amygdala | 0.75 - 0.75 | 0.72 - 0.72 | 0.68 | 0.66 | 0.75 | 0.74 | 0.63 |
| CSF | 0.68 | 0.61 | - | - | - | 0.70 | 0.83 |
| Accumbens area | 0.68 - 0.66 | 0.67 - 0.67 | 0.58 | 0.61 | - | 0.72 | - |
| Ventral DC | 0.82 - 0.82 | 0.82 - 0.82 | - | - | - | 0.85 | 0.76 |
G. Computational Time
Table VII shows the comparison of the computational time for a non-rigid registration-based approach (using ANTs [5]) and the proposed patch-based techniques. We choose ANTs as it has been ranked as one of the best among fourteen non-rigid registration algorithms [22]. The use of pointwise or multipoint estimator leads to higher computational time than using non-rigid registration. However, the fast multipoint approach provides a very time efficient algorithm. Moreover, the multi-threading of the proposed label propagation method is particularly adapted due its blockwise nature. As eight processors were used for our experiments, the computational time with multi-threading is about 8 times smaller. In this case, the propagation of one label image with the fast multipoint estimator can be performed in about 1mn.
TABLE VII.
Approximate mean computational time (in minutes) using an Intel Xeon E5420 2.5GHz. The time per image corresponds to the label propagation using one example. Total time stands for the image segmentation process using the entire textbook (the Brainweb textbook contains 19 images with 11 labels, the IBSR textbook contains 17 images with 32 labels and the NA0-NIREP textbook contains 15 with 33 labels).
| data | method | 1 core | 8 cores | ||
|---|---|---|---|---|---|
| time per image | total time | time per image | total time | ||
|
| |||||
| Brainweb | non-rigid registration (using ANTs [5]) | 50 | 950 | - | - |
| pointwise/multipoint | 67 | 1200 | 9 | 170 | |
| fast multipoint | 10 | 185 | 1.3 | 25 | |
|
| |||||
| IBSR | non-rigid registration (using ANTs [5]) | 40 | 680 | - | - |
| pointwise/multipoint | 60 | 1000 | 8 | 130 | |
| fast multipoint | 10 | 165 | 1.2 | 22 | |
|
| |||||
| NIREP | non-rigid registration (using ANTs [5]) | 78 | 1170 | - | - |
| pointwise/multipoint | 58 | 840 | 7.5 | 110 | |
| fast multipoint | 10 | 145 | 1.3 | 19 | |
H. Visual Evaluation
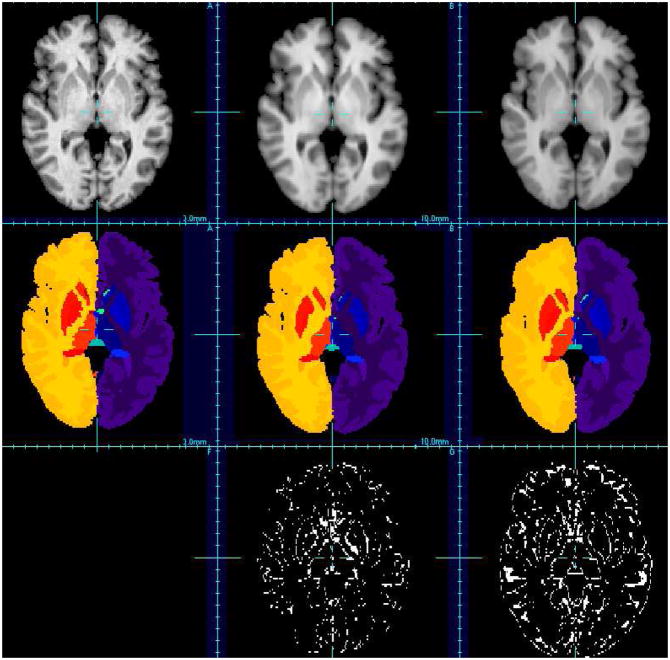
Figures 5 and 6 show visual comparison between the proposed patch-based approach with a non-rigid registration-based approach (ANTs + majority voting). The first row of this figure corresponds to the mean image obtained using the T1-weighted MR images of the anatomy textbook. Such mean image is one way of visual evaluation used for non-rigid registration algorithms. The proposed patch-based method can also provided such mean image by simply using intensities (instead of labels) of the images contained in the textbook. The second row corresponds to obtained brain segmentation. This figure illustrates well the fact that the proposed technique allows one to get a better delineation of brain structures (and especially the cortex for instance).
Fig. 5.
Visual evaluation of brain segmentation results (IBSR, image #7). First row: T1-weighted images, second row: corresponding segmentation, third row: misclassified voxels. Left: ground-truth, middle: patch-based technique, right: non-rigid registration-based approach (using ANTs).
Fig. 6.
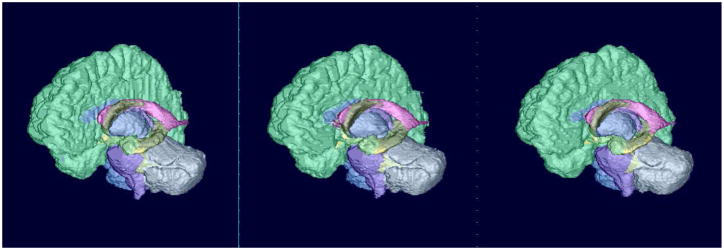
Surface rendering of segmentation results (IBSR, image #7). Left: ground-truth, middle: patch-based technique, right: non-rigid registration-based approach (using ANTs).
I. Combining patch-based strategies and registration-based techniques
The main purpose of the proposed patch-based method is to avoid long time computation due to non-rigid registration. However, one can wonder if the two techniques should cooperate to reach better results. To one side, one of the advantages of the patch-based approach is to possibly consider multiple examples within the same image of the anatomy textbook. The consequence of the local search windows use is to relax the one-to-one constraint usually involved in non-rigid registration-based label propagation approaches. Experiments on the IBSR dataset have clearly shown that the use of the patch-based approach leads to very satisfactory segmentation results for brain structures with sharp contrast. On the other side, the use of one-to-one constraint leads to a topologically regularized segmentation. We have experimentally observed that this aspect is important for cortex parcellation. Indeed, the delineation of cortical areas does not rely on intensity contrast within the cortex. It appears then that the intensity similarity assumption which the patch-based approach relies on is not sufficient to provide the highest quality cortical parcellation.
Table VIII shows the mean Dice index obtained on the NA0-NIREP dataset using the multipoint pair-wise patch-based approach, a non-rigid registration-based technique using ANTs (using majority voting or STAPLE as fusion rule) and the mixed approach. This latter technique simply consists in fusing the labeling obtained with a non-rigid registration algorithm, with the hard cortical mask obtained with a patch-based technique. The mixed approach clearly leads to higher Dice index compared to the two other techniques (which provide similar overlap scores separately). It is also interesting to note that in the combining approach, STAPLE seems to provide a better label fusion framework than the majority voting rule. Figure 7 presents a cortex parcellation result using the combined approach with STAPLE.
TABLE VIII.
Complementarity between patch-based strategies and registration-based techniques on the NA0-NIREP dataset, using a multipoint estimation approach. When structures are separated into left/right, two overlap scores are reported. Highest overlap rates are shown in bold.
| brain structure (left/right when available) | pair-wise patch + MV | ANTs + MV | ANTs + STAPLE | Combination (MV) | Combination (STAPLE) |
|---|---|---|---|---|---|
|
| |||||
| Occipital Lobe | 0.79 - 0.81 | 0.80 - 0.81 | 0.70 - 0.72 | 0.81 - 0.83 | 0.83 - 0.86 |
| Cingulate Gyrus | 0.77 - 0.80 | 0.81 - 0.81 | 0.78 - 0.78 | 0.81 - 0.82 | 0.82 - 0.84 |
| Insula Gyrus | 0.85 - 0.88 | 0.85 - 0.87 | 0.82 - 0.84 | 0.86 - 0.88 | 0.86 - 0.89 |
| Temporal Pole | 0.83 - 0.87 | 0.83 - 0.85 | 0.79 - 0.82 | 0.84 - 0.86 | 0.84 - 0.87 |
| Superior Temporal Gyrus | 0.75 - 0.74 | 0.78 - 0.77 | 0.73 - 0.73 | 0.79 - 0.78 | 0.80 - 0.79 |
| Infero Temporal Region | 0.84 - 0.84 | 0.84 - 0.84 | 0.79 - 0.79 | 0.86 - 0.85 | 0.86 - 0.86 |
| Parahippocampal Gyrus | 0.82 - 0.84 | 0.83 - 0.85 | 0.80 - 0.82 | 0.84 - 0.86 | 0.84 - 0.86 |
| Frontal Pole | 0.82 - 0.82 | 0.82 - 0.80 | 0.77 - 0.75 | 0.84 - 0.82 | 0.85 - 0.84 |
| Superior Frontal Gyrus | 0.80 - 0.81 | 0.80 - 0.80 | 0.75 - 0.75 | 0.82 - 0.81 | 0.82 - 0.83 |
| Middle Frontal Gyrus | 0.78 - 0.77 | 0.79 - 0.76 | 0.73 - 0.68 | 0.81 - 0.78 | 0.82 - 0.80 |
| Inferior Gyrus | 0.70 - 0.75 | 0.75 - 0.75 | 0.70 - 0.69 | 0.76 - 0.76 | 0.78 - 0.78 |
| Orbital Frontal Gyrus | 0.84 - 0.84 | 0.84 - 0.83 | 0.81 - 0.80 | 0.85 - 0.84 | 0.86 - 0.85 |
| Precentral Gyrus | 0.76 - 0.74 | 0.77 - 0.75 | 0.71 - 0.69 | 0.78 - 0.76 | 0.80 - 0.79 |
| Superior Parietal Lobule | 0.75 - 0.73 | 0.75 - 0.75 | 0.65 - 0.64 | 0.77 - 0.76 | 0.80 - 0.80 |
| Inferior Parietal Lobule | 0.78 - 0.74 | 0.76 - 0.75 | 0.69 - 0.67 | 0.78 - 0.77 | 0.80 - 0.79 |
| Postcentral Gyrus | 0.70 - 0.65 | 0.72 - 0.70 | 0.67 - 0.62 | 0.73 - 0.70 | 0.76 - 0.74 |
Fig. 7.
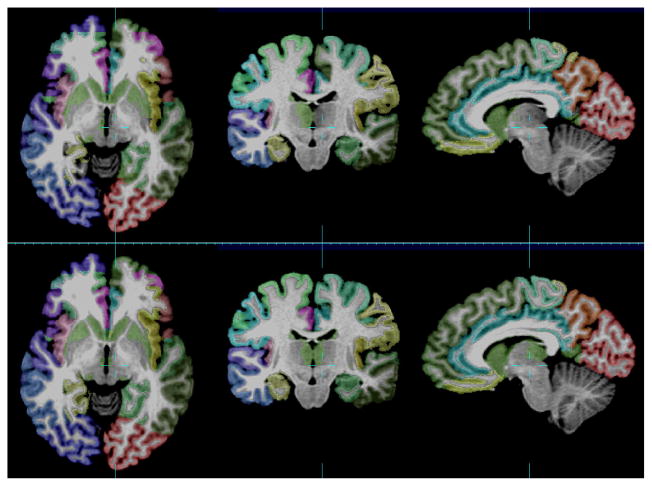
Visual evaluation of cortex parcellation results (NA0-NIREP, image #6). First row: ground truth, second row: combination technique (ANTs + patch + STAPLE).
IV. Discussion
Label propagation is a versatile image segmentation technique which can be applied to a large variety of images. In this work, we focus on the development of a new label propagation framework applied to automated human brain labeling. A patch-based label propagation has been proposed whose purpose is to relax the one-to-one constraint existing in non-rigid registration-based techniques. Indeed, this image similarity-based approach can be seen as a one-to-many block matching technique. It allows the use of several good candidates (i.e. the most similar patches) to estimate label patches. Several patch-based algorithms have been derived depending on the patch aggregation strategies and the label fusion rules (if needed). Comparison with previously proposed non-rigid registration-based methods on publicly available in-vivo MR brain images has shown a great potential of this method.
The proposed approach is also related to supervised learning methods which try to learn the link between image intensity patches and label patches. In our work, instead of learning the link between image intensity and labels, the label estimation relies on a weighted graph which represents directly the similarity between intensity of the input image and intensity of the anatomy textbook images. As mentioned in the Introduction, the work presented in this article shares similarities with the one done by Coupé et al. [10]. Indeed, they have proposed a patch-based strategy relying on a group-wise technique for label fusion. The main methodological differences concern the smoothing parameter in the definition of patch weights and the voxel pre-selection. About validation, they have investigated one aggregation strategy (group-wise) on two regions of interest: hippocampus and lateral ventricles (on a non-publicly available dataset).
The experiments on three freely available T1-weighted MR image datasets (Brainweb, IBSR, NA0-NIREP) have shown that the proposed framework can lead to high quality segmentation of a large number of brain structures. It has been shown that CPU time consuming non-rigid registration steps can be avoided. The proposed patch-based technique does not require an accurate correspondence between the input image and the anatomy textbook. The usual assumption of one-to-one mapping is relaxed by using local search windows. Further work may investigate the use of more complex similar patch search steps. For instance, using a rotation-invariant patch match is one of the possible extensions of the proposed method (in particular when considering large patches), while keeping in mind that it might increase the CPU time. However, the results obtained with translation-based patch match are already very competitive with respect to existing methods. Some possible methodological extensions are local adaptivity of patch size and search window size, choice of kernel function f and the use of graph operators.
As the algorithm relies on the assumption of similar intensities between the input image and the anatomy textbook, the segmentation accuracy may depend on the contrast of the structure to segment or intensity variations (such as intensity bias). Intensity variations might disturb the search process of similar patches, which would lead to a final labeling obtained with less relevant patch examples. The sensitivity of intensity variations can be captured by the smoothing factor beta. However, using a fixed global value of β in conjunction with common correction techniques such as intensity bias correction and histogram matching, the proposed algorithm provides very satisfactory results. Also for the IBSR data, it can be noticed that the segmentation of the pallidum is not as good as the segmentation of other brain structures. The reason for failure is that this structure has no clear contrasted boundaries in MR T1-weighted images. Thus, contrary to registration-based techniques which can propagate spatial relations of the structures, a pure intensity-based method such as the one proposed in this work cannot provide a satisfactory delineation of the pallidum. This assertion is corroborated by the experiments performed on the NA0-NIREP dataset. Because of the key assumption of intensity similarity, a non-rigid registration-based label propagation approach outperforms the proposed patch-based method. In this context of cortex parcellation, we have shown that these two techniques can be complementary. In particular, the joint use of non-rigid registration and patch-based strategy can significantly improve the segmentation result. Thus, further work may explore the incorporation of a regularization term and prior information such as spatial relations or a topological atlas into the patch-based framework.
Contrary to registration-based techniques, especially for the group-wise approach using a patch selection, if there is no correspondence between the input and the anatomy textbook (i.e. the image similarity is lower than the threshold used in the patch selection step), no label is propagated. This prevents an incorrect label being introduced in the estimation of the final label image. Thus, further work is to evaluate the robustness of this label propagation method to images which contain lesions or tumors, and to use this patch-based technique to potentially detect these pathological patterns. Another research direction concerns the use of a database of images as IBSR to segment pathological images. Such a “cross-site” study will analyze the robustness of the method in the presence of large anatomical variability, including the initial affine registration, intensity and shape variations, and the research of examples in the anatomy textbook.
Finally, as mentioned in other works [37], [2], [35] and as shown in the experiments performed on the Brainweb dataset, the label image can be estimated using a subset of the anatomy textbook (the observed convergence rate is about 10 example images). This remark leads to the issue of atlas selection, i.e. identifying a subset of representative examples in the textbook with respect to the input image. This can be particularly important when using a large anatomy textbook to avoid useless heavy computational burden.
Fig. 8.
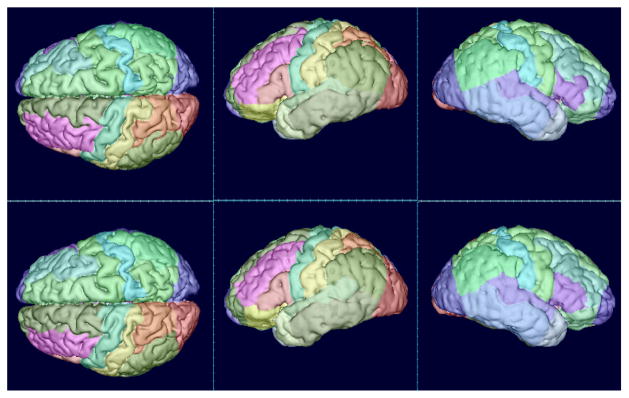
Surface rendering of cortex parcellation results (NA0-NIREP, image #6). First row: ground truth, second row: combination technique (ANTs + patch + STAPLE).
TABLE III.
Comparison (using the mean Dice index) of aggregation strategies (majority voting vs STAPLE) on the IBSR dataset, using a multipoint estimation approach. When structures are separated into left/right, two overlap scores are reported. Highest overlap rates are shown in bold.
| brain structure (left/right) | pair-wise patch + MV | pair-wise patch + STAPLE | group-wise patch |
|---|---|---|---|
|
| |||
| Cerebral WM | 0.92 - 0.92 | 0.92 - 0.92 | 0.93 - 0.92 |
| Cerebral Cortex | 0.95 - 0.95 | 0.95 - 0.95 | 0.95 - 0.95 |
| Lateral Ventricle | 0.93 - 0.92 | 0.92 - 0.91 | 0.93 - 0.92 |
| Inferior Lat Vent | 0.61 - 0.56 | 0.53 - 0.51 | 0.60 - 0.56 |
| Cerebellum WM | 0.88 - 0.88 | 0.88 - 0.88 | 0.88 - 0.88 |
| Cerebellum Cortex | 0.95 - 0.95 | 0.95 - 0.95 | 0.95 - 0.95 |
| Thalamus | 0.89 - 0.89 | 0.88 - 0.88 | 0.89 - 0.89 |
| Caudate | 0.87 - 0.87 | 0.86 - 0.86 | 0.88 - 0.89 |
| Putamen | 0.88 - 0.87 | 0.86 - 0.85 | 0.89 - 0.89 |
| Pallidum | 0.71 - 0.69 | 0.70 - 0.68 | 0.79 - 0.79 |
| 3rd Ventricle | 0.81 | 0.80 | 0.80 |
| 4th Ventricle | 0.85 | 0.78 | 0.84 |
| Brain Stem | 0.94 | 0.94 | 0.93 |
| Hippocampus | 0.83 - 0.83 | 0.79 - 0.80 | 0.83 - 0.83 |
| Amygdala | 0.76 - 0.74 | 0.72 - 0.70 | 0.75 - 0.75 |
| CSF | 0.69 | 0.66 | 0.68 |
| Accumbens area | 0.66 - 0.63 | 0.65 - 0.63 | 0.68 - 0.66 |
| Ventral DC | 0.82 - 0.82 | 0.83 - 0.83 | 0.82 - 0.82 |
TABLE IV.
Comparison (using the mean Dice index) of aggregation strategies (majority voting vs STAPLE) on the NA0-NIREP dataset, using a multipoint estimation approach. When structures are separated into left/right, two overlap scores are reported. Highest overlap rates are shown in bold.
| brain structure (left/right) | pair-wise patch + MV | pair-wise patch + STAPLE | group-wise patch |
|---|---|---|---|
|
| |||
| Occipital Lobe | 0.79 - 0.81 | 0.75 - 0.74 | 0.78 - 0.80 |
| Cingulate Gyrus | 0.77 - 0.80 | 0.77 - 0.78 | 0.76 - 0.79 |
| Insula Gyrus | 0.85 - 0.88 | 0.84 - 0.87 | 0.84 - 0.87 |
| Temporal Pole | 0.83 - 0.87 | 0.81 - 0.86 | 0.82 - 0.86 |
| Superior Temporal Gyrus | 0.75 - 0.74 | 0.75 - 0.74 | 0.74 - 0.73 |
| Infero Temporal Region | 0.84 - 0.84 | 0.82 - 0.81 | 0.83 - 0.83 |
| Parahippocampal Gyrus | 0.82 - 0.84 | 0.80 - 0.83 | 0.81 - 0.83 |
| Frontal Pole | 0.82 - 0.82 | 0.81 - 0.81 | 0.81 - 0.80 |
| Superior Frontal Gyrus | 0.80 - 0.81 | 0.79 - 0.80 | 0.80 - 0.80 |
| Middle Frontal Gyrus | 0.78 - 0.77 | 0.78 - 0.76 | 0.78 - 0.76 |
| Inferior Gyrus | 0.70 - 0.75 | 0.70 - 0.74 | 0.69 - 0.74 |
| Orbital Frontal Gyrus | 0.84 - 0.84 | 0.83 - 0.83 | 0.83 - 0.83 |
| Precentral Gyrus | 0.76 - 0.74 | 0.74 - 0.73 | 0.75 - 0.73 |
| Superior Parietal Lobule | 0.75 - 0.73 | 0.74 - 0.73 | 0.74 - 0.72 |
| Inferior Parietal Lobule | 0.78 - 0.74 | 0.77 - 0.74 | 0.77 - 0.73 |
| Postcentral Gyrus | 0.70 - 0.65 | 0.64 - 0.59 | 0.69 - 0.63 |
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Communitys Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 207667). This work is also funded by NIH/NINDS Grant R01 NS 055064.
Footnotes
Contributor Information
François Rousseau, Email: rousseau@unistra.fr, Laboratoire des Sciences de l’Image, de l’Informatique et de la Télédétection (LSIIT), UMR 7005 CNRS-University of Strasbourg, 67412 Illkirch, France.
Piotr A. Habas, Biomedical Image Computing Group, University of Washington, Seattle, WA 98195, USA
Colin Studholme, Biomedical Image Computing Group, University of Washington, Seattle, WA 98195, USA.
References
- 1.Akselrod-Ballin A, Galun M, Gomori JM, Brandt A, Basri R. Prior knowledge driven multiscale segmentation of brain MRI. Medical Image Computing and Computer-Assisted Intervention: MICCAI. 2007;10(Pt 2):118–126. doi: 10.1007/978-3-540-75759-7_15. [DOI] [PubMed] [Google Scholar]
- 2.Aljabar P, Heckemann RA, Hammers A, Hajnal JV, Rueckert D. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy. NeuroImage. 2009 Jul;46(3):726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- 3.Artaechevarria X, Munoz-Barrutia A, Ortiz-de-Solorzano C. Combination strategies in multi-atlas image segmentation: application to brain MR data. IEEE Transactions on Medical Imaging. 2009 Aug;28(8):1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
- 4.Aubert-Broche B, Evans AC, Collins L. A new improved version of the realistic digital brain phantom. Neuroimage. 2006 Aug;32(1):138145. doi: 10.1016/j.neuroimage.2006.03.052. [DOI] [PubMed] [Google Scholar]
- 5.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008 Feb;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Buades A, Coll B, Morel JM. A review of image denoising algorithms, with a new one. Multiscale Modeling & Simulation. 2005 Jan;4(2):490–530. [Google Scholar]
- 7.Collins DL, Holmes CJ, Peters TM, Evans AC. Automatic 3-D model-based neuroanatomical segmentation. Human Brain Mapping. 1995;3(3):190–208. [Google Scholar]
- 8.Collins DL, Pruessner Jens C. Towards accurate, automatic segmentation of the hippocampus and amygdala from MRI by augmenting ANIMAL with a template library and label fusion. NeuroImage. 2010 Oct;52(4):1355–1366. doi: 10.1016/j.neuroimage.2010.04.193. [DOI] [PubMed] [Google Scholar]
- 9.Coupé P, Yger P, Prima S, Hellier P, Kervrann C, Barillot C. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Transactions on Medical Imaging. 2008 Apr;27(4):425–441. doi: 10.1109/TMI.2007.906087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Coupé P, Manjón JV, Fonov V, Pruessner J, Robles M, Collins DL. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. NeuroImage. 2011 Jan;54(2):940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- 11.Duda RO, Hart PE, Stork DG. Pattern Classification. 2. Wiley-Interscience; Oct, 2000. [Google Scholar]
- 12.Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002 Jan;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 13.Gasser T, Sroka L, Jennen-Steimetz C. Residual variance and residual pattern in nonlinear regression. Biometrika. 1986 Dec;73(3):625–633. [Google Scholar]
- 14.Gilboa G, Osher S. Nonlocal operators with applications to image processing. Multiscale Modeling & Simulation. 2008 Jan;7(3):1005–1028. [Google Scholar]
- 15.Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006 Oct;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- 16.Isgum I, Staring M, Rutten A, Prokop M, Viergever MA, van Ginneken B. Multi-atlas-based segmentation with local decision fusion–application to cardiac and aortic segmentation in CT scans. IEEE Transactions on Medical Imaging. 2009 Jul;28(7):1000–1010. doi: 10.1109/TMI.2008.2011480. [DOI] [PubMed] [Google Scholar]
- 17.Katkovnik V, Foi A, Egiazarian K, Astola J. From local kernel to nonlocal Multiple-Model image denoising. Int J Comput Vision. 2010;86(1):1–32. [Google Scholar]
- 18.Khan AR, Chung MK, Beg MF. Robust atlas-based brain segmentation using multi-structure confidence-weighted registration. Medical Image Computing and Computer-Assisted Intervention: MICCAI. 2009;12(Pt 2):549–557. doi: 10.1007/978-3-642-04271-3_67. [DOI] [PubMed] [Google Scholar]
- 19.Khan AR, Cherbuin N, Wen W, nstey KJ, Sachdev P, Beg MF. Optimal weights for local multi-atlas fusion using supervised learning and dynamic information (SuperDyn): Validation on hippocampus segmentation. Neuroimage. 2011;56(1):126–139. doi: 10.1016/j.neuroimage.2011.01.078. [DOI] [PubMed] [Google Scholar]
- 20.Kindermann S, Osher S, Jones PW. Deblurring and denoising of images by nonlocal functionals. Multiscale Modeling & Simulation. 2005 Jan;4(4):1091–1115. [Google Scholar]
- 21.Kittler J, Hatef M, Duin RPW, Matas J. On combining classifiers. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1998;20(3):226–239. [Google Scholar]
- 22.Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang M-C, Christensen GE, Collins DL, Gee J, Hellier P, Song JH, Jenkinson M, Lepage C, Rueckert D, Thompson P, Vercauteren T, Woods RP, Mann JJ, Parsey RV. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009 Jul;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klein A, Hirsch J. Mindboggle: a scatterbrained approach to automate brain labeling. NeuroImage. 2005 Jan;24(2):261–280. doi: 10.1016/j.neuroimage.2004.09.016. [DOI] [PubMed] [Google Scholar]
- 24.Lancaster JL, Rainey LH, Summerlin JL, Freitas CS, Fox PT, Evans AC, Toga AW, Mazziotta JC. Automated labeling of the human brain: A preliminary report on the development and evaluation of a forward-transform method. Human Brain Mapping. 1997;5(4):238–242. doi: 10.1002/(SICI)1097-0193(1997)5:4<238::AID-HBM6>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Langerak T, van der Heide U, Kotte A, Viergever M, van Vulpen M, Pluim J. Label fusion in Atlas-Based segmentation using a selective and iterative method for performance level estimation (SIMPLE) IEEE Transactions on Medical Imaging. 2010 Jul; doi: 10.1109/TMI.2010.2057442. [DOI] [PubMed] [Google Scholar]
- 26.Lötjönen JM, Wolz R, Koikkalainen JR, Thurfjell L, Waldemar G, Soininen H, Rueckert D. Fast and robust multi-atlas segmentation of brain magnetic resonance images. NeuroImage. 2010 Feb;49(3):2352–2365. doi: 10.1016/j.neuroimage.2009.10.026. [DOI] [PubMed] [Google Scholar]
- 27.Mignotte M. A non-local regularization strategy for image deconvolution. Pattern Recogn Lett. 2008;29(16):2206–2212. [Google Scholar]
- 28.Miller MI, Christensen GE, Amit Y, Grenander U. Mathematical textbook of deformable neuroanatomies. Proceedings of the National Academy of Sciences of the United States of America. 1993 Dec;90(24):11944–11948. doi: 10.1073/pnas.90.24.11944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Peyré G, Bougleux S, Cohen L. Non-local regularization of inverse problems. Proceedings of the 10th European Conference on Computer Vision: Part III; Marseille, France. Springer-Verlag; 2008. pp. 57–68. [Google Scholar]
- 30.Rohlfing T, Russakoff DB, Maurer CR. Performance-based classifier combination in atlas-based image segmentation using expectation-maximization parameter estimation. IEEE Transactions on Medical Imaging. 2004 Aug;23(8):983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
- 31.Rousseau F. A non-local approach for image super-resolution using intermodality priors. Medical Image Analysis. 2010 Aug;14(4):594–605. doi: 10.1016/j.media.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roy S, Carass A, Shiee N, Pham DL, Prince J. MR contrast synthesis for lesion segmentation. Proc IEEE Int Symp Biomed Imaging. 2010 Jun;:932–935. doi: 10.1109/ISBI.2010.5490140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sabuncu M, Yeo BT, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Transactions on Medical Imaging. 2010 Jun; doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sdika M. Combining atlas based segmentation and intensity classification with nearest neighbor transform and accuracy weighted vote. Medical Image Analysis. 2010 Apr;14(2):219–226. doi: 10.1016/j.media.2009.12.004. [DOI] [PubMed] [Google Scholar]
- 35.van Rikxoort EM, Isgum I, Arzhaeva Y, Staring M, Klein S, Viergever MA, Pluim JPW, van Ginneken B. Adaptive local multi-atlas segmentation: application to the heart and the caudate nucleus. Medical Image Analysis. 2010 Feb;14(1):39–49. doi: 10.1016/j.media.2009.10.001. [DOI] [PubMed] [Google Scholar]
- 36.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging. 2004 Jul;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wu M, Rosano C, Lopez-Garcia P, Carter CS, Aizenstein HJ. Optimum template selection for atlas-based segmentation. NeuroImage. 2007 Feb;34(4):1612–1618. doi: 10.1016/j.neuroimage.2006.07.050. [DOI] [PubMed] [Google Scholar]
- 38.Yushkevich PA, Wang H, Pluta J, Das SR, Craige C, Avants BB, Weiner MW, Mueller S. Nearly automatic segmentation of hippocampal subfields in in vivo focal t2-weighted MRI. NeuroImage. 2010 Dec;53(4):1208–1224. doi: 10.1016/j.neuroimage.2010.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]