Evaluating the consistency and specificity of neuroimaging data using meta-analysis

Abstract

Making sense of a neuroimaging literature that is growing in scope and complexity will require increasingly sophisticated tools for synthesizing findings across studies. Meta-analysis of neuroimaging studies fills a unique niche in this process: It can be used to evaluate the consistency of findings across different laboratories and task variants, and it can be used to evaluate the specificity of findings in brain regions or networks to particular task types. This review discusses examples, implementation, and considerations when choosing meta-analytic techniques. It focuses on the multilevel kernel density analysis (MKDA) framework, which has been used in recent studies to evaluate consistency and specificity of regional activation, identify distributed functional networks from patterns of co-activation, and test hypotheses about functional cortical-subcortical pathways in healthy individuals and patients with mental disorders. Several tests of consistency and specificity are described.

Introduction

Recent years have seen a rapid increase in the number and variety of investigations of the human brain using neuroimaging techniques. Studies using functional magnetic resonance imaging (fMRI) or positron emission tomography (PET) have emerged as a major methodology for investigating function in the intact and disordered human brain. Psychological processes under investigation are as diverse as psychology itself, and nearly every major domain of psychology is represented in this growing body of work. Many popular domains–such as cognitive control, working memory, decision-making, language, emotion, and disorders such as attention deficit disorder, schizophrenia, and depression–have been the subject of a large number of neuroimaging studies, whose results can be synthesized and interpreted in the context of data from lesion studies, electrophysiology, behavioral studies, and related methodologies.

This burgeoning literature places increasing demands on scientists to understand, integrate, and evaluate the neuroimaging work that has been performed in each of these areas. One important set of questions relates to the consistency, or replicability across laboratories, scanners, and task variants, of activated regions¹. Which brain regions are consistently associated with domains such as working memory, decision-making, emotional experience, and so on? And where are the boundaries between functional regions that identify studies that do and do not replicate?

Another important set of questions relates to synthesis across areas of study, and in particular the specificity of particular activation patterns for particular psychological processes. Is a region typically related to working memory load unique to this domain, or is it shared by a broader set of cognitive demands? For example, some brain regions, such as the left inferior frontal gyrus, are characterized variously as “working memory regions,” “language regions,” “emotion regulation regions,” or “decision making regions”, depending on the functional domain being investigated. Before positing hypotheses about common underlying functions, it is important to establish whether these different researchers are discussing the same region, or whether nearby activations in different task domains can be reliably discriminated.

Why use meta-analysis? Establishing activation consistency

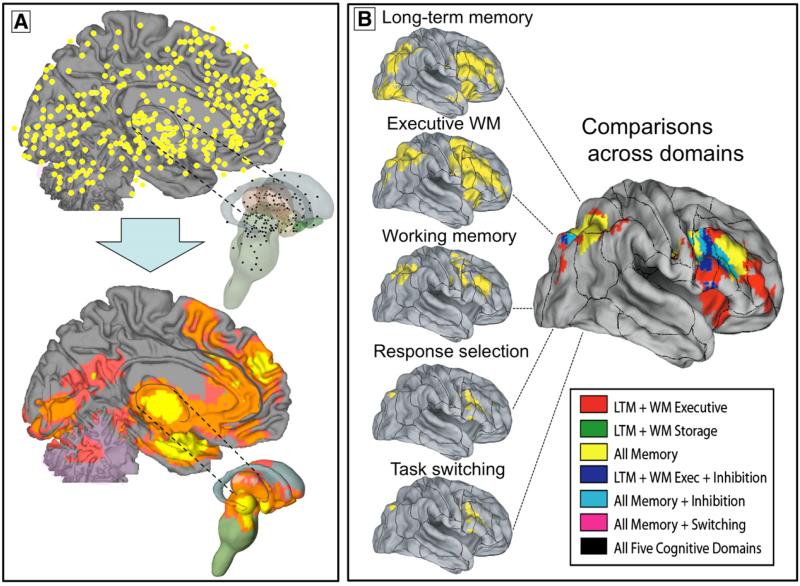
Meta-analysis fills a unique role in the neuroimaging literature because many of the important, fundamental questions posed above are difficult or impossible to address within individual studies. Therefore, a major use for meta-analysis in imaging is to identify the consistently activated regions across a set of studies. In Fig. 1A, for example, a number of reported activation peaks from many studies (top panel) are summarized in a meta-analysis of consistently reported regions (bottom panel).

Fig. 1.

Examples of results from multilevel kernel density analysis (MKDA). (A) Top panel: Peak activation coordinates from 437 study comparison maps (SCMs; from 163 studies) plotted on medial and subcortical brain surfaces (Wager et al., 2008). Peak locations within 12 mm from the SCM are averaged. Bottom panel: Summary of consistently activated regions across SCMs in the MKDA analysis. Yellow indicates a significant density of SCMs in a local neighborhood, and orange and pink indicate significant density using extent-based thresholding at primary thresholds of 0.001 and 0.01, respectively (see text for details). All results are family-wise error rate corrected at p<.05 for search across brain voxels. (B) MKDA results from five published meta-analyses of executive function mapped onto the PALS-B12 atlas (Van Essen, 2005) using Caret software, and the overlap in activations across the five types of executive function, from Van Snellenberg and Wager (in press). The results illustrate how meta-analysis can inform about common and differential activations across a variety of psychological processes.

Evaluating consistency is important because false positive rates in neuroimaging studies are likely to be higher than in many fields (somewhere in the range of 10–40%; see below). Thus, some of the reported activated locations shown in Fig. 1A are likely to be false positives, and it is important to assess which findings have been replicated and have a higher probability of being real activations.

Inflated false positive rates are a byproduct of the commonly used strategy of making statistical brain maps composed of many tests (“voxel-wise” mapping), combined with the use of small sample sizes (usually 8–25 participants) due to the considerable expense of neuroimaging. Although there is a trend towards larger sample sizes and more rigorous multiple comparisons correction, until recently most studies have not corrected for multiple comparisons because they were too under-powered (Nichols and Hayasaka, 2003; Wager et al., 2007a). Many studies that have used corrections used methods whose assumptions are likely to be violated, or ad hoc methods that do not control the false positive rate at the nominally specified level (Wager et al., 2007b). Gene arrays in genetic research have the same problem, for the same reasons—though in both fields, the benefits of making whole-brain or whole-genome maps make them preferred choices for many researchers.

Data that illustrate these issues are shown in Table 1, which summarizes the results of four meta-analyses on a total of 415 studies involving 4,856 participants. The meta-analyses were all performed using the same method, multi-level kernel density analysis (MKDA; Kober et al., 2008; Wager et al., 2008; data from Wager and Smith, 2003, was also reanalyzed using MKDA). The median sample size from the included studies range from N=10 to N=12 across studies of working memory, long-term memory, and emotion. A basic power calculation (see Fig. 12 in Wager et al., in press) shows that with a standard effect size of d=1 (Cohen's d, an effect divided by its standard deviation), approximately 45 participants are required to achieve 80% power using Bonferroni correction in a typical whole brain, voxel-wise analysis. Correction methods such as those based on Gaussian Random Field Theory are often just as conservative, but nonparametric correction improves power substantially (Nichols and Hayasaka, 2003). With nonparametric correction, approximately only 30 participants are needed for 80% power (Wager et al., in press), though this sample size is still larger than all but the largest studies in our samples². Thus, performing proper correction is impractical without relatively large sample sizes, but failing to make appropriate corrections leads to increased false positive rates.

Table 1.

Database	Studies	Sample size (N)				Reported peaks
		Total	Median	Min	Max	Total	In	Out	% “replicated”
WM storage	26	305	12	5	21	377	225	152	60
Executive WM	60	664	10	5	28	1086	867	219	80
Emotion	163	2010	11	4	40	2478	2198	280	89
Long term memory	166	1877	11	5	33	3265	2950	315	90

“In” refers to peaks within 10 mm of the significant meta-analysis area, and “Out” refers to peaks further than 10 mm from the significant meta-analysis area. WM: Working memory “Replicated” peaks are within a consistently activated area in the meta-analysis.

The MKDA results can also be used to provide a rough estimate of false positive rates. For each meta-analysis in Table 1, we calculated the number and proportion of peaks reported near (within 10 mm) one of the regions identified as consistently activated in the meta-analysis. The proportion of peaks outside of the consensus regions provides a rough estimate of false positive rates across studies. Table 1 shows an estimated false positive rate around 10% for the larger databases, and 20%–40% for the smaller meta-analyses, which may have been underpowered and therefore failed to find more truly activated regions. Of course, there are a number of reasons why this figure is imprecise; false-positives could contribute to consistently-activated regions, and heterogeneity among studies could result in true positives outside those regions found to be significant in meta-analyses. However, even if imprecise, this figure provides a rough estimate of how big the false-positive problem may be. Using another method based on examining the estimated search space, thresholds, and image smoothness, we previously estimated a false positive rate of roughly 17% (Wager et al., 2007a,b). In sum, there is a need to integrate and validate results across studies.

The simplest goal of a meta-analysis is to provide summaries of the consistency of regional brain activation for a set of studies of a particular task type, providing a consensus about which regions are likely to be truly activated by a given task. In addition, meta-analysis can also be used to extend beyond regional activation to identify groups of consistently co-activated regions that may form spatially distributed functional networks in the brain. We have used this approach to identify distributed groups of functionally related brain regions in emotion (Kober et al., 2008) and anxiety-related disorders (Etkin and Wager, 2007), and other groups have used similar approaches to identifying large-scale functional networks organized around particular cognitive processes (Neumann et al., 2005), or functional co-activation with target brain structures across many tasks (Postuma and Dagher, 2006). Identifying co-activated networks can provide the basis for testing them as units of analysis in individual studies, and can lead to the development of testable hypotheses about functional connectivity in specific tasks.

Why use meta-analysis? Evaluating functional specificity

In addition to establishing consistent activation in one task type, meta-analysis can be used to evaluate the specificity of activation (in regions or ‘networks’) to one type of task among a set of different tasks. For example, one might identify a set of regions consistently activated by self-referential processes (Northoff et al., 2006), and then ask whether activity in these regions is specific to self-referential processes—that is, that they are not activated by other tasks that do not involve self-reference. This information is critical to using measures of brain activity to predict psychological processes (i.e., making a “reverse inference” that activity in some region implies the involvement of a given psychological process; Poldrack, 2006; Sarter et al., 1996).

Specificity can only be examined across a range of tested alternative tasks: A region that is specific for faces compared with houses may not be specific for faces compared with tools. Likewise, a region that discriminates self-referential word judgments from non-self-referential ones does not imply that the region discriminates self-referential processes from retrieval of semantic knowledge from long-term memory. Unfortunately, different psychological domains are usually studied in isolation, and it is virtually impossible compare a wide range of tasks in a single study. However, meta-analysis provides tools for doing exactly that: Activation patterns can be compared across the entire range of tasks studied using neuroimaging techniques, providing a unique way to evaluate activation specificity across functional domains.

The simplest kind of specificity analysis compares activation patterns among two or more task types, such as positive vs. negative emotion (Phan et al., 2002; Wager et al., 2003), high-conflict vs. low-conflict conditions in cognitive control tasks (Nee et al., 2007), or various types of executive demand in working memory tasks (Wager and Smith, 2003). Many more examples appear in the growing meta-analysis literature, some of which is referenced in Table 2.

Table 2.

A sampling of neuroimaging meta analyses

Authors	Year	Method	Psychological focus
Cognitive control/executive function
Chein et al.	2002	Density (Gaussian)	Verbal working memory
Wager et al.	2003	Clustering of peaks, chi-square	Working memory
Wager et al.	2004	KDA, spatial MANOVA	Attention/task switching
Buchsbaum et al.	2005	ALE	Wisconsin card sorting
Chein and Schneider	2005	Density (Gaussian)	Practice effects in cognitive control
Laird et al.	2005	ALE	Stroop interference
Neumann et al.	2005	ALE, co-activation “replicator dynamics”	Stroop interference
Costafreda et al.	2006	Spatial location	Verbal fluency in left IFG
Gilbert et al.	2006	Spatial location/Chi-square/classifier	Episodic memory, multitasking mentalizing in BA 10
Nee et al.	2007	KDA, logistic regression	Cognitive control/interference
Van Snellenberg and Wager	in pressa	MKDA/KDA	Cognitive control and memory
Emotion and motivation
Phan et al.	2002	Chi-square within regions	Emotion
Murphy et al.	2003	Spatial location (K–S test)	Emotion
Wager et al.	2003	KDA, Chi-square	Emotion
Kringelbach and Rolls	2004	Spatial location	Reinforcers in OFC
Phan et al.	2004	Qualitative	Emotion
Baas et al.	2004	Chi-square	Amygdala lateralization
Northoff et al.	2006	Clustering of peaks	Self-referential processes
Krain et al.	2006	ALE	Decision-making
Wager et al.	2008	MKDA, Chi-square	Emotion
Kober et al.	2008a	MKDA, co-activation	Emotion
Disorder
Zakzanis et al.	2000	Effect sizes	Schizophrenia
Zakzanis et al.	2003	Effect sizes	Alzheimer's disease
Whiteside et al.	2004	Effect sizes	Obsessive–compulsive disorder
Glahn et al.	2005	ALE	Working memory in schizophrenia
Fitzgerald et al.	2006	ALE	Depression, DLPFC
Dickstein et al.	2006	ALE	ADHD
Van Snellenberg et al.	2006	Effect sizes	Schizophrenia and working memory
Steele et al.	2007	Spatial location (“unwarped”)	Depression, frontal cortex
Valera et al.	2007	Effect sizes	Brain structure in ADHD
Etkin and Wager	2007	MKDA, Co-activation	Anxiety disorder
Hoekert et al.	2007	Effect sizes	Emotional prosody in schizophrenia
Language
Turkeltaub et al.	2002	ALE	Single-word reading
Jobard et al.	2003	Clustering of peaks	Word reading
Brown et al.	2005	ALE	Speech production
Vigneau et al.	2006	Clustering peaks	Language, left cortical hemisphere
Ferstl et al.	2008	ALE, Co-activation “replicator dynamics”	Text comprehension
Others
Joseph	2001	Spatial location	Object recognition: category specificity
Grèzes and Decety	2001	Qualitative	Action
Kosslyn and Thompson	2003	Logistic regression	Visual imagery
Nielsen et al.	2004	Kernel density/multivariate	Cognitive function
Gottfried and Zald	2005	Spatial location	Olfaction in OFC
Nickel and Seitz	2005	Clustering of peaks	Parietal cortex
Petacchi et al.	2005	ALE	Auditory function, cerebellum
Lewis	2006	Average maps in CARET	Tool use
Postuma and Dagher	2006	Co-activation	Basal ganglia
Zacks	2008		Mental rotation

A sample of published neuroimaging meta-analyses. See text for abbreviations.

^aResults discussed in relative detail in this paper.

However, it is also possible to compare the results of meta-analysis from a number of functional domains, such as the results across 5 different task types shown in Fig. 1. In a recent chapter (Van Snellenberg and Wager, in press) we examined the overlap in meta-analytic results among studies that isolated cognitive control processes (e.g. task switching and speeded response selection) and studies that involved maintenance of information in working memory (WM), including WM storage, the subtraction of [Executive WM–WM storage], and long-term memory encoding and retrieval. Our working hypothesis was that the more complex memory maintenance and manipulation tasks would involve task switching and response selection, and so would activate a super-set of the areas involved in more elementary cognitive control processes. The illustration in Fig. 1B supports this notion, showing that the inferior frontal junction and pre-supplementary motor area are consistently activated across studies within each task type, but that more rostral portions of the prefrontal cortex were only consistently activated when WM was involved. The most anterior prefrontal regions were activated only when manipulation of information in memory was required.

Whereas the results in Fig. 1 present a qualitative comparison across five task types that summarize commonalities and differences across types, quantitative analyses of specificity can also be performed using several other methods discussed below. These methods include χ² (chi-square) and approximations to multinomial exact tests, analysis of reported peak density differences, and pattern classifier systems. In each analysis, formal predictions can be made about task types given patterns of brain activity. For example, in a particularly interesting application using meta-analytic data, Gilbert et al. (2006) used classifier analyses to identify regions within the medial and orbitofrontal cortices that discriminated different cognitive functions of the anterior frontal cortex. This study is an example of how formal predictions about psychological states can be tested across diverse kinds of studies using meta-analysis.

Coordinate-based meta-analysis and its many varieties

There are now a number of quantitative meta-analyses of neuroimaging data in the literature, as evidenced by the partial list in Table 2. The vast majority use reported peak coordinates from published studies, which are readily available in published papers and stored electronically in databases such as Brainmap (http://brainmap.org/). We refer to this as the “coordinate-based meta-analysis” approach. Alternatively, full statistic maps for each study could be used and effect sizes aggregated at each voxel (Lewis, 2006). Though we consider this to be a “gold standard” approach, and advocate its development in future meta-analytic work, this approach is complicated by the lack of readily-available statistic images.

Collectively, the coordinate-based meta-analysis literature to date covers a cornucopia of innovative techniques. Some meta-analyses evaluate consistency by combining effect size data (Van Snellenberg et al., 2006) or analyzing the frequencies of reported peaks (Phan et al., 2002) within anatomically defined regions of interest. Variants on this theme use multiple logistic regression (Kosslyn and Thompson, 2003; Nee et al., 2007) or summarize co-activations among regions (Etkin and Wager, 2007; Nielsen et al., 2004). A popular approach to examining specificity has been to analyze the locations of coordinates in stereotaxic space, testing for functional gradients or spatial distinctions (Gottfried and Zald, 2005; Joseph, 2001), and sometimes extending these analyses to perform space-based classification of study types using MANOVA (Joseph, 2001; Wager et al., 2004) or cluster analyses using χ² tests (Nickel and Seitz, 2005; Northoff et al., 2006; Wager and Smith, 2003).

While the procedures above refer to analyses carried out on pre-defined anatomical areas, the most popular approaches for summarizing reported coordinates from neuroimaging studies involve so-called “voxel-wise” analyses, or the construction of statistical maps summarizing peak coordinates in a neighborhood around each voxel in a standard brain (Chein et al., 2002; Fox et al., 1999). At their heart, these kernel-based methods are related to kernel-based methods for analyzing the multivariate distributions of sparse data, and essentially summarize the evidence for activation in a local neighborhood around each voxel in a standard atlas brain. They are popular because they provide ways of summarizing activations across the brain without imposing rigid prior constraints based on anatomical boundaries, which are currently difficult to specify precisely.

Our goal in the remainder of this paper is to describe recent advances and applications using this kernel-based approach. We focus in particular on MKDA, a recently developed extension of voxel-wise meta-analysis approaches, for example activation likelihood estimation (ALE; Laird et al., 2005; Turkeltaub et al., 2002) and kernel density analysis (KDA; Wager et al., 2007b). The essence of the approach is to reconstruct a map of significant regions for each study (or statistical contrast map within study), and analyze the consistency and specificity across studies in the neighborhood of each voxel.

In Section 1, we describe how MKDA can be used to evaluate the consistency of activations. We consider issues of level of analysis (peak vs. study contrast map), weighting, thresholding, and multiple comparisons, and show the results of simulations comparing ALE, KDA, and MKDA methods. We also show how this approach lends itself to the construction of analogues to some meta-analysis plots in the traditional meta-analytic literature, in particular logistic funnel plots. In Section 2, we consider how MKDA can be used to analyze specificity. We consider a) density difference maps to compare activations in two types of studies, and b) A multinomial permutation test–an alternative to the χ² test with several desirable properties–for comparing two or more study types. Finally, in Section 3, we describe extensions of the MKDA approach to analyze co-activations across regions, including clustering and mediation analysis on co-activation data to develop models of functional pathways.

Methods

Section I. The MKDA approach

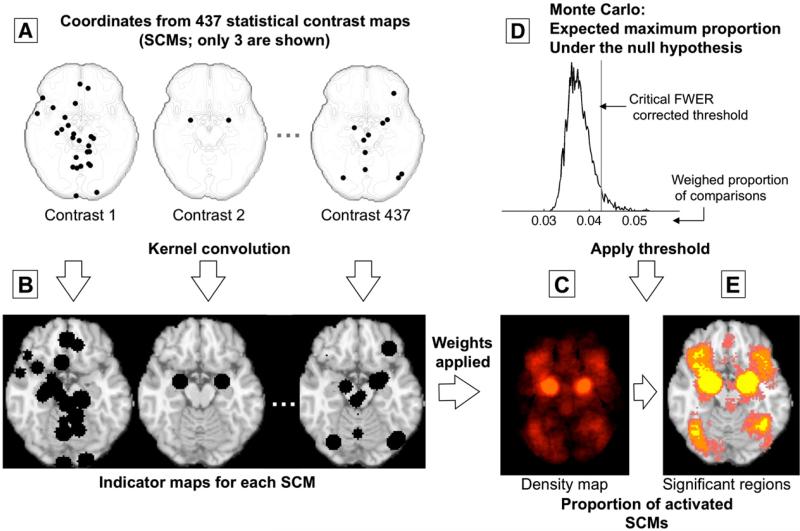
The MKDA method analyzes the distribution of peak coordinates from published studies across the brain. The technique, used in several recent published analyses (Etkin and Wager, 2007; Kober et al., 2008; Wager et al., 2008, 2007b) is summarized in Fig. 2. Essentially, the reported x (left–right), y (posterior–anterior), and z (inferior–superior) coordinates in a standard stereotaxic space (i.e., Montreal Neurological Institute space) are treated as a sparse representation of activated locations. In the literature, peak coordinates are reported in reference to a particular statistical contrast map (SCM); for example, a study might compare high memory load vs. low memory load. Studies may report results from multiple contrast maps (e.g., load effects for verbal stimuli and load effects for object stimuli), so we refer to the maps as SCMs rather than as study maps.

Fig 2.

Example procedures for multilevel kernel density analysis (MKDA). (Adapted from Wager et al. (2007), Fig. 3). (A) Peak coordinates of three of the 437 comparison maps included in a meta-analysis of emotion. Peak coordinates of each map are separately convolved with the kernel, generating (B) indicator maps for each study contrast map (SCM). (C) The weighted average of the indicator maps is compared with (D) the maximum proportion of activated comparison maps expected under the null hypothesis in a Monte Carlo simulation and (E) thresholded to produce a map of significant results. Color key is as in Fig. 1.

To integrate peaks across space, the peaks obtained from each SCM are convolved with a spherical kernel of radius r, which is user-defined, and thresholded at a maximum value of 1 so that multiple nearby peaks are not counted as multiple activations (left side of Fig. 2). Formally, this amounts to the construction of an indicator map for each SCM, where a voxel value of 1 indicates a peak in the neighborhood, while 0 indicates the absence of a peak, i.e. for each voxel k:

$$I_k=\{\begin{array}{cc}1\hfill & \text{if}\sqrt{\sum {({\overrightarrow{v}}_k-\overrightarrow{x})}^2}\le \mathrm{r}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (1)

where ${\overrightarrow{v}}_k$ is the $[\overrightarrow{x},y,z]$ triplet in mm for voxel k's location in MNI space, and x̄ is the [x, y, z] triplet for the nearest reported peak. The choice of r is somewhat arbitrary, but should be related to the degree of consistency found across studies. Better inter-study consistency would allow for meaningful neighborhood summaries using smaller values of r and would thus allow for higher-resolution meta-analytic results. In practice, r=10 mm is commonly used, which provides a good balance between sensitivity and spatial resolution (Wager et al., 2004).

A weighted average of the resulting indicator maps provides a summary map with an interpretable metric: The (weighted) number of nominally independent SCM indicator maps that activate in the neighborhood of each voxel. The weights relate to measures of study quality and are described below. The convenient interpretation of the statistic (an SCM activation count) motivates the use of the spherical kernel, though in principle other kernels (such as a Gaussian kernel) could be used. Information about the extent and shape of the activation summarized by each peak could be incorporated as well, but in practice, inconsistency in reporting this information across studies has prevented it from being used.

The final step is to establish a statistical threshold for determining what constitutes a significant number of activating SCMs in a local area. The threshold is determined using a Monte Carlo procedure, and a natural null hypothesis is that the ‘activated’ regions in the SCM indicator maps are not spatially consistent; that is, they are distributed randomly throughout the brain. The procedure is described in detail below.

Thus, in MKDA, the peak locations are not analyzed directly. Rather, indicator maps for each SCM are constructed, and the SCM is treated as the unit of analysis. Thus, the metric used to summarize consistency is not directly related to how many peaks were reported near a voxel–after all, the peaks could all have come from one study–but rather, is related to how many SCMs activated near a voxel.

This is the primary difference between MKDA and previously used “voxel-wise” approaches, including KDA and ALE (Fox et al., 1998; Laird et al., 2005; Nielsen et al., 2005; Wager et al., 2003, 2004). The latter methods also summarize peak coordinates using a kernel-based approach, but they do not take into account which SCM or study the peaks came from. Thus, the KDA an ALE measures do not summarize consistency across studies; rather, they summarize consistencies across peak coordinates. Interpreting these methods as reflecting consistency across studies requires the implicit assumption that there are no true inter-study differences in number and location of peaks, smoothness, false positive rates, and statistical power. This assumption is clearly violated in most meta-analyses that integrate data from many laboratories, and the consequence is that a significant KDA or ALE ‘meta-analytic’ result can be driven by a single study. Thus, one cannot conclude from a significant KDA/ALE p-value that a new study on the same topic would be likely to activate similar regions. This issue is analogous to the fixed versus random-effects model issue in individual functional imaging studies, in which fixed-effects models treat observations (time points) as the unit of analysis and ignore inter-subject variability, while random-effects models account for this variability by treating subjects as the unit of analysis. The fixed-effects issue has also received considerable discussion in the traditional meta-analysis literature, and Monte Carlo simulations have demonstrated that when there is true between-study variability, fixed-effects models have inflated Type I error rates, particularly for meta-analysis of a small number of studies (Hedges and Vevea, 1998).

An analogy to a standard clinical study may help clarify this point. Not modeling SCM as a level of analysis is akin to ignoring the fact that different observations in a clinical study came from different participants; thus, the analysis and inference procedures would be identical whether the observations came from a group of participants or only a single participant. For example, examine the peaks in Fig. 2A, which are 3 representative contrast maps from a set of 437 used in recent meta-analyses of emotion (Kober et al., 2008; Wager et al., 2008). Imagine that we performed a meta-analysis only on the plotted peaks from these three studies. Because study is ignored in the ALE/KDA analysis, information about which study contributed each of the peaks is not preserved, and all the peaks are combined. Contrast 1 contributes 26 peaks, many of them very close together, whereas Contrast 2 contributes only two. When the KDA map is generated and thresholded in this example, three peaks within 10 mm are required to achieve significance in the meta-analysis. Study 1 has enough peaks near the amygdala to generate significant results by itself. This is quite a plausible scenario due to differences in scanning, analysis, and reporting procedures across studies; and, in fact, the data shown are real.

This example illustrates some of the advantages to treating SCM or study, rather than peak, as the unit of analysis. A study may report peaks either very densely or sparsely, depending on reporting standards and the smoothness of statistical images. Smaller studies tend to produce rougher (less smooth) statistic images, because they average over fewer subjects. Rougher statistic images produce a topography consisting of many local peaks; thus, there is a tendency for smaller studies to report more local peaks! Clearly, it is disadvantageous to consider each peak as an independent observation.

In summary, the MKDA procedure has several important advantages over previously used voxel-wise meta-analysis approaches. First, other approaches have typically analyzed the peak locations from a set of studies, ignoring the nesting of peaks within contrasts. MKDA takes account of the multi-level nature of the data. Second, the MKDA statistic has a straightforward interpretation: the proportion of contrasts (P) activating within r mm of each voxel. Third, contrast maps are weighted based on sample size and study quality. And finally, the procedure controls the family-wise error rate (FWE), or the chance of observing a false positive anywhere in a meta-analytic brain map, and so each significant MKDA result can be interpreted. We elaborate on these latter points of comparison below.

Weighting of study contrast maps and peaks

Weighting by sample size and/or study quality is typical in meta-analysis across fields (DerSimonian and Laird, 1986), and incorporating sample size into the meta-analysis is a key feature of standard meta-analytic methods, because the precision of a study's estimates (1/standard error) are proportional to the square root of the study's sample size. Weighting in meta-analysis ensures that larger and more rigorously performed studies exert more influence on the meta-analytic results. However, there are several choices to be made in deciding how to weight activation peaks from neuroimaging studies. One choice is whether to weight individual peaks by their reliability (i.e., Z-scores), individual SCMs, or both. Weighting peaks by their Z-scores may seem like a good idea at first glance, but there are significant disadvantages. First, Z-scores from different studies may not be comparable because of the different analysis methods used. For example, some (mostly older) studies treat subjects as a fixed effect, whereas others treat it as a random effect. “Fixed effects” analyses do not appropriately model inter-subject variance and therefore do not allow for inferences about a population—a critical part of scientific inference. Z-scores from fixed-effects studies are systematically higher than those from random-effects studies. Second, the massive multiple testing framework employed in most neuroimaging studies creates a situation in which peaks with the highest Z-scores may have occurred by chance. For an analogy, consider the survivors from the Titanic. On average, those who survived were better swimmers, but another major component was luck. Here, reported significant voxels in a study are the “survivors.” This situation causes the well-known phenomenon of regression to the mean: Z-scores corresponding to these peaks regress toward their true values in a replication. Thus, it may not be safe to assume that Z-scores from a group of studies are comparable.

Rather than weighting Z-scores, the current version of MKDA weights by the square root of the sample size for each SCM. In addition, we down-weight studies using fixed effects analyses by a factor of 0.75, an arbitrary value that reduces the impact of fixed-effects studies. These factors are combined into the following weighting equation:

$$P=\sum _c{I}_c\left(\frac{{\delta }_c\sqrt{N_c}}{\sum _c{\delta }_c\sqrt{N_c}}\right)$$ (2)

where P is the weighted proportion of activated comparisons (SCM indicators), c indexes comparison maps I, δ is the fixed effects discounting factor, and N is the sample size. This approach could potentially be expanded to weight peaks within study by their relative activation strength within the study, and thereafter weight studies in proportion to their sample size. In addition, this weighting scheme could be used to weight by other study quality measures developed by the analyst, such as diagnostic criteria or sample-matching procedures employed in studies of psychiatric or medical populations. While the precise weight values assigned for various study characteristics are necessarily somewhat arbitrary, assigning higher weights to higher-quality studies is generally preferable to ignoring differences in study quality or excluding some studies altogether. However, because weighting by study quality involves choices by the analyst that can be somewhat arbitrary, it is common in the traditional meta-analysis literature to additionally report the results of an unweighted analysis (Rosenthal and DiMatteo, 2001) so that the influence of the weighting procedure on the results can be assessed.

Thresholding and multiple comparisons

The null hypothesis in MKDA, like KDA and ALE analyses, is a “global” null hypothesis stating that there is no coherent spatial consistency across SCMs (or reported peaks, for KDA and ALE). Rejecting the null technically implies that there are one or more neighborhoods (regions) with consistent reports. However, the test still provides a test with strong control of FWE, in the sense that under the null hypothesis, the chances of a false positive anywhere in the brain is α (e.g., p<.05, corrected for search across the brain). Considering an alternative null conditional on one or more consistent regions, it can be shown that the required density to achieve FWE control for remaining regions is lower than the required density for the global null. Thus, the test is over-conservative, and KDA analysis incorporated a step-down test (Wager et al., 2004) that has not yet been implemented in MKDA.

In practice, MKDA uses a threshold derived from Monte Carlo simulation of the global null. Contiguous clusters of activated voxels are identified for each SCM, and the cluster centers are randomized within gray-matter (plus an 8 mm border) in the standard brain. For each iteration (although results typically stabilize after about 2000 iterations, we typically use 10,000), the maximum MKDA statistic (P in Eq. (2)) over the whole brain is saved. As with other nonparametric FWE correction methods, the (1–α)th percentile of the distribution of maxima provides a critical statistic value.

An advantage to randomizing cluster locations, rather than peak locations, is that the density of peaks in a particular study will not have an undue influence on the null hypothesis values in the Monte Carlo simulation. Even if peaks are reported very densely, the MKDA Monte Carlo threshold will not be influenced as long as peaks are reported within the same activated area. This is not true for peak-coordinate based Monte Carlo simulations (i.e., KDA and ALE), and thus dense peak reporting will lead to higher thresholds for reporting significant meta-analytic results and less power.

In addition, in MKDA an ‘extent-based’ thresholding can be used (Wager et al., 2008), paralleling methods available in the popular Statistical Parametric Mapping software (Friston et al., 1996). In our MKDA implementation, we have established primary thresholds at the average uncorrected (1–α)th percentile of the MKDA statistic across the brain (with permuted blobs, i.e., under null hypothesis conditions), where α is by default .001, .01, and .05. The maximum extent of contiguous voxels at this threshold is saved for each iteration of the Monte Carlo simulation, and the critical number of contiguous voxels is calculated from the resulting distribution of maximum null-hypothesis spatial extents. For example, the yellow regions in Figs. 1A and 2 are significant at p<.05 MKDA-height corrected, whereas orange and pink regions are significant at p<.05 cluster-extent corrected with primary thresholds of .001 and .01, respectively.

Meta-analysis diagnostic plots

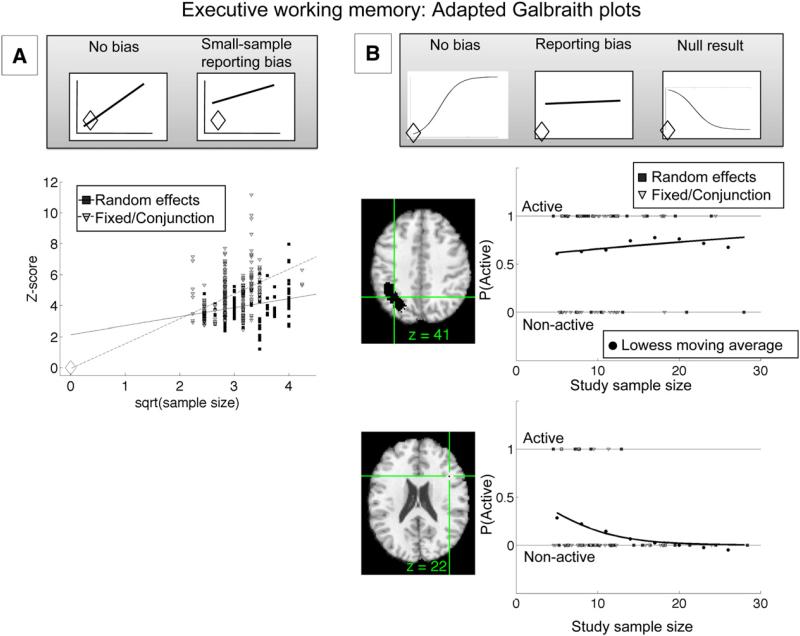
Traditional meta-analyses often make extensive use of diagnostic plots to illustrate the sensibility (or lack thereof) of results across a group of studies. For example, the Galbraith plot shows the relationship between effect size (e.g., Z-scores, y-axis) and study precision (x-axis) (Egger et al., 1997). Precision is equal to 1/standard error for each study, which is related to the residual standard deviation and square root of the study sample size (N). Simple regression is used to analyze the relationship between precision and effect size. A reliable non-zero effect across studies should have a positive slope in the Galbraith plot, because the more precise studies (with lower standard errors) should have higher Z-scores. This plot can be used to detect bias of several types. If there is no bias, the intercept of the plot should pass through the origin: With a precision of zero (e.g., zero sample size), the predicted effect size should be zero. A positive intercept indicates small-sample bias.

An example is shown in Fig. 3. Panel A shows an adapted Galbraith plot; √N is plotted on the x-axis for studies of executive working memory, as the full standard error is not generally available from published neuroimaging papers. The slope will thus be different from the standard Galbraith plot, but the expected intercept is still zero in the absence of bias. Z-scores from the subset of available studies within the significant regions in the MKDA analysis for [Executive WM–Storage] (Fig. 1) are shown. As Fig. 3A shows, Z-scores for fixed-effects studies (light-colored triangles) pass through the intercept (unfilled diamond), but those from random-effects studies (dark squares) do not. Thus, there is evidence for bias in the random-effects studies. One plausible type of bias is the well-known “file drawer” problem. Smaller studies that did not find effects in these regions may be unpublished, and thus Z-scores from published studies with small sample sizes would be inflated relative to the true effect size across all studies. This problem is exacerbated because small-sample studies have very little power in a random-effects framework, and thus those that end up being published are those that happen to have particularly large Z-scores (either by chance or because of some real difference in effect magnitude). Fixed-effects studies do not show apparent bias, perhaps because these studies tend to be older and were publishable even with relatively low effect sizes. In addition, fixed-effects analysis is substantially more liberal than random-effects analysis, resulting in higher Z-scores overall, and thus studies using fixed-effects analyses are more likely to yield Z-scores high enough to meet publication standards even with small samples. One issue with these plots is that Z-score values are not independent from one another, and thus the statistical significance of the Galbraith plot regression is difficult to interpret.

Fig. 3.

Adapted Galbraith plots illustrating application to meta-analysis. (A) Plot of Z-scores from available peaks from the executive working-memory (WM) vs. WM storage comparison of a published meta-analysis (Wager and Smith, 2003). Z-scores within significant regions in the multilevel kernel density analysis (MKDA; y-axis) are plotted against the square root of sample size (x-axis). In the absence of bias, the regression line should pass through the intercept (unfilled diamond). This condition holds for fixed-effects studies (light gray triangles), but not for random-effects studies (dark gray squares), indicating small-sample bias in the random-effects studies. See text for additional details. (B) Adapted Galbraith-style graph plotting activations for each study contrast map (SCM; y-axis) as a function of sample size (x-axis) within regions of interest from the MKDA analysis. Individual SCMs are plotted as points (1=active, 0=not active), and the solid regression line shows logistic regression fits for the proportion of activated SCMs (P(active), y-axis) as a function of sample size. The gray circles show estimates of P(active) using loess smoothing (λ=.75) and can be used to assess the quality of logistic regression fits. In the absence of bias, the logistic fit should pass through the intercept (see text). The upper plot shows results from a parietal region indicating some small-sample bias. The lower plot shows a small white-matter region in the frontal cortex. Activation was significantly consistent in the MKDA analysis, but the plot shows that it was driven entirely by the small-sample studies, suggesting a lack of true responses to executive WM in this region.

Fig. 3B shows an analogous plot, but shows the probability of a nominally independent SCM activating (y-axis) vs. N (x-axis). Individual studies are plotted with y-axis values of either 1 (active) or 0 (non-active), and logistic regression is used to create a best-fit prediction (solid black lines) of the probability of activation (P(active)) as a function of N. The gray circles show smoothed averages of P (active) vs. N estimated using loess smoothing, and can be used to assess the logistic regression model fit. As with the standard Galbraith plot, if a region is truly activated by the task (executive WM in Fig. 4) and there is no bias, P(active) should increase with increasing sample size and should pass through the origin (P(active)=0 when N=0). Bias in small-sample studies is indicated by a non-zero intercept. Finally, a negative regression slope would indicate that an effect is driven predominantly by the small studies, and that P(active) converges on zero as N increases; thus, it is evidence that a region does not respond to the task studied. Plots are shown for two regions of contiguous voxels that were significant in the MKDA analysis shown in Fig. 1. The first, a region in the left parietal cortex commonly activated in executive WM tasks, which shows evidence for both a positive slope and a non-zero intercept, indicating a true effect and a tendency to over-report by small studies. This bias could be related to the use of lowered thresholds, or other factors discussed above. The second region, a small region in white matter in the lateral frontal cortex, shows evidence for a null result: The consistent activation is produced exclusively by the small-sample studies, resulting in a negative regression slope. (We are not arguing here against a role of lateral prefrontal cortex in executive WM: Other lateral prefrontal regions showed more well-behaved data). These results illustrate the usefulness of meta-analytic plots, above and beyond localizing significant regions using MKDA or a similar analysis.

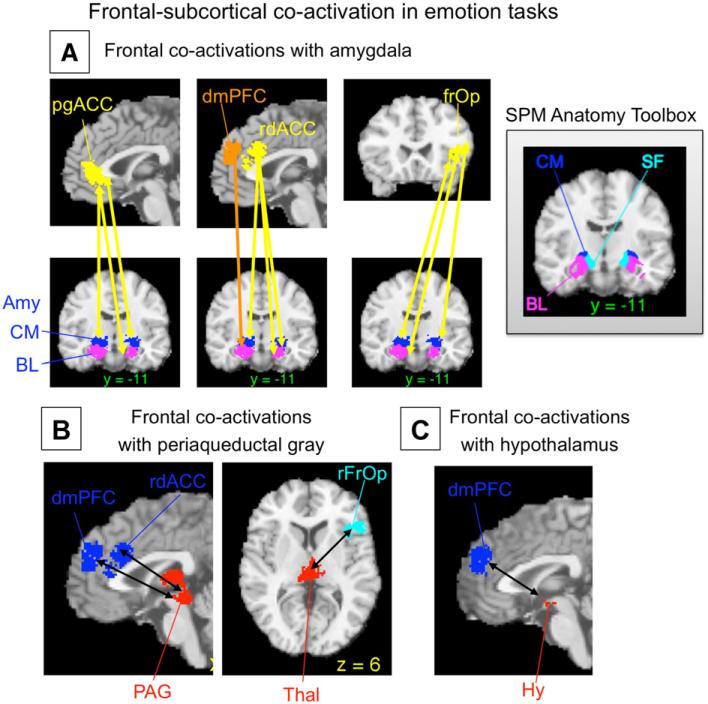
Fig. 4.

Example of co-activation analyses from a recent meta-analysis of emotion Adapted from Kober et al. (2008), Figs. 8–9). Co-activated regions show a significant tendency to be activated in the same study contrast maps (SCMs), as assessed with Kendall's tau-b. Arrows show significant co-activation. (A) Frontal regions (yellow/orange) co-activated with amygdala subregions (blue/purple) are a surprisingly circumscribed set of regions limited to the medial prefrontal cortex (mPFC) and the right ventrolateral PFC/frontal operculum. The inset shows regions from the SPM Anatomy Toolbox (V15; (Eickhoff, Heim, Zilles, and Amunts, 2006; Eickhoff et al., 2005). Amy, amygdala; BL, basolateral complex; CM, centromedial complex; dmPFC, dorsomedial prefrontal cortex; pgACC, pregenual anterior cingulate; rdACC, rostral dorsal anterior cingulate; rfrOp, right frontal operculum; SF, superficial amygdala. (B) Frontal regions co-activated with midbrain periaqueductal gray (red, shown including a contiguous region in the thalamus) include a subset of the same frontal regions. (C) The only frontal region co-activated with hypothalamus (red) was the dmPFC. These results suggest locations for functional frontal-limbic and frontal-brainstem pathways related to emotional experience that can be tested in future neuroimaging and lesion studies.

Section II: Analyzing activation specificity

Meta-analysis is perhaps the only way to compare neuroimaging results across a wide variety of tasks, as shown in the example in Fig. 1B Van Snellenberg and Wager (in press). This unique advantage can be captured quantitatively in analyses that examine the specificity of regional activation to particular task types.

The most basic type of between-task comparison is between two conditions (e.g., positive and negative emotion, or executive WM vs. simple storage). An early approach counted the number of peaks or studies activating within a pre-specified anatomical area, and used a χ² test to determine whether the proportions of peaks inside vs. outside the area differed by task type (Phan et al., 2002; Wager et al., 2003; Wager and Smith, 2003). This analysis controls for the marginal counts of overall peaks within the area and overall frequency of peaks for each task type, and is valid for comparisons of two or more task types. However, it has several drawbacks. First, anatomical boundaries currently cannot be precisely specified. Second, counting peaks suffers from the same fixed-effects issues discussed above, thereby limiting generalizability, but study counts are often too low to perform a valid χ² test on studies or SCMs. This is because the χ² test is a large-sample approximation and is not valid if expected counts in any cell in the contingency table fall below 5 or so. Therefore, large numbers of studies and large regions are needed.

In addition, it is important to note one other consideration. The Phan et al. χ² test provides estimates of relative activation frequency: if one area is very dense with peak/study activations, it will influence the overall marginal frequencies of peaks used in tests in every other region. We return to this issue in more detail below.

In recent work, we have employed an alternative to the χ² test, a multinomial permutation test (MPT), which addresses some of these issues. The MPT is very similar in principle to the χ² test, and in fact uses the χ² statistic as a summary statistic; however, it is a permutation-based procedure that approximates the multinomial exact test (Agresti, 2002). Like the χ² test, it can be used to make whole-brain maps of areas showing task-type differences in each local neighborhood around the brain. For the local area around each voxel, a “yes/no” by task type contingency table is constructed, where “yes” and “no” refers to whether the SCM activated within r mm of the voxel. Exact p-values can be obtained for 2×2 tables using Fisher's exact test or for larger tables using the multinomial exact test (MET), but both of these are extremely computationally demanding, and the MET for even a single voxel of a moderately sized meta-analysis (e.g., 80 maps) is not feasible with current commonly available computing resources. However, permutation methods can be used to approximate the MET with much lower computational cost. We permute the “yes/no” activation indicator, providing a sample from the set of null-hypothesis tables with the same marginal distributions of activation counts and task-type counts, as suggested in Agresti (2002, p. 98). We use the χ² statistic as a convenient summary of asymmetries between activation and task type, and threshold the distribution of χ² statistics from permuted tables at 1-α. In practice, 5000 permutations at each voxel provides stable results, is computationally feasible (2–3 days for a whole-brain map with a large sample of >400 SCMs), and is substantially faster than Fisher's exact test for large (i.e., 80 or more) numbers of SCMs.

In this way, the other problematic issues raised above are addressed as well. To avoid ambiguities with imprecisely defined ROIs, we perform the test voxel-by-voxel over the whole brain (or a volume of interest). To avoid the complications related to making inferences about peaks without considering which study they came from, SCMs rather than individual peaks are counted and analyzed. This test is different from the χ² test described above in another way as well: It analyzes only the distribution of activating vs. non-activating SCMs within a given brain region. Therefore, it provides a direct test of differences among tasks in the probability of activating a single region, independent of activation frequencies in other regions. This test is implemented in the current version of the MKDA software.

Comparing two task types using MKDA

Another means of comparing two conditions uses voxel-wise analysis within the ALE/KDA/MKDA framework. In this approach, separate maps are constructed for each of two task types and subtracted to yield difference maps. The same procedure is employed in the course of the Monte Carlo randomization: The locations of contiguous activation blobs (peaks in ALE/KDA) are randomized, providing simulated null-hypothesis conditions from which we establish a threshold for significant differences.

Like the Phan et al. χ² test, the Monte Carlo ALE/KDA/MKDA difference maps test the relative frequency of activating in a given region, compared with the overall frequencies in the rest of the brain. Thus, a very reliable concentration of peaks in one area for one task type will shift (increase) the marginal activation frequencies for that task, which will affect the null-hypothesis difference in the Monte Carlo simulations. Thus, for task types with relatively few peaks, there need not be a greater absolute probability of activating a region to achieve a significant density for that region relative to other task types. Consider the following example: Studies of positive and negative emotion activate the ventral medial prefrontal cortex (vmPFC) with about equal frequencies. The MPT test would reveal no differences. However, negative emotions more reliably activate the amygdala and many other regions (Wager et al., 2008), resulting in a greater frequency of activation across the brain. With enough studies, either the Phan et al. χ² test or density-difference analyses will produce a significant positive > negative effect in vmPFC, even though the absolute proportion of activating studies is roughly equal for positive and negative emotion. This is not necessarily a flaw, as a relative concentration of activity in a condition that produces few activations in general can convey meaningful information. For example, vmPFC activity may indeed be diagnostic of positive emotion. However, it is important to keep these issues in mind when interpreting results from these analyses.

Section III: Testing connectivity

Meta-analysis can also be used to reveal patterns of co-activated regions. If two regions are co-activated, studies that activate one region are more likely to activate the other region as well. Co-activation is thus a meta-analytic analogue to functional connectivity analyses in individual neuroimaging studies, and can provide converging evidence on functionally connected regions and hypotheses that can be tested in subsequent studies.

As with summaries of consistency, a natural level of analysis is the SCM (Etkin and Wager, 2007; Kober et al., 2008). In the MKDA-based approach, the data is an n×v indicator matrix of which of the n SCMs activated in the neighborhood of each of the v voxels in the brain. The resulting connectivity profiles across voxels can be simplified into connectivity among a smaller set of structurally or functionally defined regions (groups of voxels). Hypothesis tests can be performed on connectivity, and relationships among multiple regions can be summarized and visualized.

There are several potential measures of association for bivariate, binomial data, including Kruskal's Gamma, Kendall's Tau, Fisher's exact test, and other recent measures of association for binomial data developed within the neuroimaging literature (Neumann et al., 2005; Patel et al., 2006; Postuma and Dagher, 2006). We have used Kendall's Tau-b (τ) because it is appropriate for binomial data and has a clearly interpretable metric (Gibbons, 1993; Gibbons et al., 2003).

Co-activation measures can be used for a number of purposes. First, they can be used to test for specific relationships among brain areas of interest. For example, we used a database of 437 SCMs from emotion tasks to test which frontal regions were co-activated with the amygdala, periaqueductal gray (PAG), and hypothalamus, three key subcortical nuclear complexes involved in emotion (Kober et al., 2008). Only four specific frontal areas showed positive co-activation with these areas (see Fig. 4). They included several specific regions in the medial prefrontal cortex (mPFC)–including pregenual anterior cingulate, rostral dorsal cingulate, and dorsomedial prefrontal cortex– and one area in the right frontal operculum. These results reveal a relatively specific pattern of frontal connectivity with these important subcortical regions. They correspond well with animal studies showing direct projections to amygdala and PAG mainly from the MPFC (An et al., 1998; McDonald et al., 1996). In addition, the homologies between rat or primate and human mPFC are not currently well understood, and this kind of information in humans helps to establish homologous regions.

Another use for co-activation measures is in functional parcellation of the brain (Flandin et al., 2002; Thirion et al., 2006), or the establishment of groups of contiguous voxels that show similar functional characteristics and may be treated as units of analysis in future studies. In the Kober et al. study, it would have been computationally unwieldy to examine co-activation between thousands of voxels in the frontal cortex and thousands of voxels in subcortical regions of interest. Instead, we calculated co-activation among parcels: We first used singular value decomposition on a 437 (SCMs)×18,489 (voxels) matrix of significant voxels from the MKDA analysis and identified groups of contiguous voxels that loaded most highly on the same component. These regions were taken as parcels, and a new SCM indicator for each parcel was constructed, which indicated whether each SCM activated in the neighborhood of the parcel. These parcels corresponded well in many cases with the locations of known anatomical regions. For example, in Fig. 4, sub-regions of the amygdala derived from parcellation of the meta-analysis are shown in comparison with those derived from cytoarchitectural analysis of post-mortem brains (Eickhoff et al., 2005).

The parcel indicators were subjected to two iterations of non-metric multidimensional scaling and clustering to identify functional regions and large-scale networks. The details of this procedure are beyond the scope of this brief discussion, but the end result is that parcels of functionally related brain activity, and networks of co-activated regions at several spatial scales, can be identified and used to guide interpretation and a priori testing in future studies.

Co-activation measures can also be used to characterize differences among groups of individuals, including those with psychiatric and neurological disorders. For example, Etkin and Wager (2007), compared frontal-amygdala and frontal-insula co-activation in studies of three types of anxiety-related disorders: Post-traumatic stress disorder, social anxiety disorder, and specific phobias. We tested the hypothesis that medial frontal increases would be consistently associated with a lower incidence of amygdala and insula activity across studies. Co-activation analyses supported this view (See Fig. 4), and we found that this co-activation was driven by studies of PTSD specifically. This is one example of how meta-analysis can be used to test the consistency of functional relationships among brain regions, and also compare functional relationships across different functional domains (in this case, anxiety-related disorders).

Section IV: Future directions

There is tremendous potential for development of meta-analytic techniques and applications to advance the cumulative science of brain imaging. One avenue for development involves increasing integration of meta-analysis results with brain atlases and databases (Dickson, Drury, and Van Essen, 2001; Van Essen et al., 2001) so that consensus results will be immediately available to researchers. Another is the aggregation and analysis of full summary statistic images from each study, rather than analysis of the reported peaks. This would allow effect-size based meta-analyses with full information across the brain, and would greatly enhance the value of meta-analytic maps.

Whether full statistic images or reported coordinates are analyzed, there is ample room for the development and application of both new and traditional meta-analysis techniques. Here we have presented an initial use of graphical meta-analysis plots, which could be very useful in detecting and quantifying bias in future meta-analyses. New applications of techniques for parcellating and evaluating co-activation based on data across studies can provide increasingly precise maps of large-scale functional regions, which can in turn inform increasingly precise anatomical hypotheses in new studies.

In addition, other avenues require development: One is how to model SCMs, which are currently treated as independent, but which are often nested within studies, and whose cohorts sometimes share individuals even if they come from different studies. Another is the application of logistic regression techniques appropriate for low-frequency responses, to analyze task specificity while controlling for confounding variables. The tests for specificity described above analyze activation frequencies as a function of a single psychological variable (e.g., spatial vs. verbal vs. object WM). However, such variables may be correlated with other confounding variables: for example, PET vs. fMRI studies, storage and manipulation vs. pure storage in WM, or other factors may be asymmetrically distributed across levels of WM Content Type. This raises the potential for multi-colinearity and, in some cases, for Simpson's Paradox to occur. For example, spatial WM may activate more frequently that object WM overall, but the reverse may be true when comparing within categories of PET and fMRI studies. Only a few meta-analyses have used logistic regression to control for confounding variables because coverage of the possible combinations of variables is too sparse. This approach will become more feasible as the number of studies increases and samples of studies can be collected that are relatively balanced across levels of potentially confounding factors.

Finally, developing meta-analysis based applications of classifier techniques is a particularly important future direction, as meta-analysis affords a unique opportunity to make quantitative brainpsychology inferences across many task domains. This approach can be extended beyond simple classification to testing functional ontologies. Because many different kinds of task labeling schemes can be applied to study contrasts, meta-analysis provides the means to pit alternative psychological categorization schemes against one another and ask which maps most cleanly onto brain activity. This approach may turn out to be a unique and valuable way of establishing links between psychological and biological levels of analysis.