Modeling the Hemodynamic Response Function in fMRI: Efficiency, Bias and Mis-modeling

Abstract

Most brain research to date has focused on studying the amplitude of evoked fMRI responses, though there has recently been an increased interest in measuring onset, peak latency and duration of the responses as well. A number of modeling procedures provide measures of the latency and duration of fMRI responses. In this work we compare several techniques that vary in their assumptions, model complexity, and interpretation. For each method, we introduce methods for estimating amplitude, peak latency, and duration and for performing inference in a multi-subject fMRI setting. We then assess the techniques’ relative sensitivity and their propensity for mis-attributing task effects on one parameter (e.g., duration) to another (e.g., amplitude). Finally, we introduce methods for quantifying model misspecification and assessing bias and power-loss related to the choice of model. Overall, the results show that it is surprisingly difficult to accurately recover true task-evoked changes in BOLD signal and that there are substantial differences among models in terms of power, bias and parameter confusability. Because virtually all fMRI studies in cognitive and affective neuroscience employ these models, the results bear on the interpretation of hemodynamic response estimates across a wide variety of psychological and neuroscientific studies.

INTRODUCTION

Functional magnetic resonance imaging (fMRI) is based on studying the vascular response in the brain to neuronal activity and can be used to study mental activity. It is most commonly performed using blood oxygenation level-dependent (BOLD) contrast (Ogawa, Tank, Menon, Ellerman, Kim, Merkle and Ugurbil (1992)) to study local changes in deoxyhemoglobin concentration in the brain. The primary goal of fMRI research is to use information provided by the BOLD signal to make conclusions about the underlying unobserved neuronal activation. Therefore, the ability to accurately model the evoked hemodynamic response to a neural event plays an important role in the analysis of fMRI data. When analyzing the shape of the estimated hemodynamic response function (HRF), summary measures of psychological interest (e.g., amplitude, delay, and duration) can be extracted and used to infer information regarding the intensity, onset latency, and duration of the underlying brain metabolic activity.

To date most fMRI studies have been primarily focused on estimating the amplitude of evoked HRFs across different tasks. However, there is a growing interest in studying the time-to-peak and duration of activation as well (Bellgowan, Saad, & Bandettini, 2003; Formisano & Goebel, 2003; Richter et al., 2000). The onset and peak latencies of the HRF can provide information about the timing of activation for various brain areas and the width provides information about the duration of activation. However, questions remain regarding which methods for obtaining estimates of these parameters are most efficient while giving rise to the least amount of bias and misspecification.

In this paper, we focus on estimation of response amplitude/height (H), time-to-peak (T), and full-width at half-max (W) in the HRF as potential measures of response magnitude, latency and duration of neuronal activity. Ideally, the parameters of the HRF should be directly interpretable in terms of changes in neuronal activity, and should be estimated so that statistical power is maximized. An accurate estimate of the HRF shape may help prevent both false positive and negative results from arising due to ill-fitting constrained statistical models, as even minor amounts of mis-modeling can lead to severe loss in power and validity (Lindquist & Wager, 2007; Loh, Lindquist and Wager 2008).

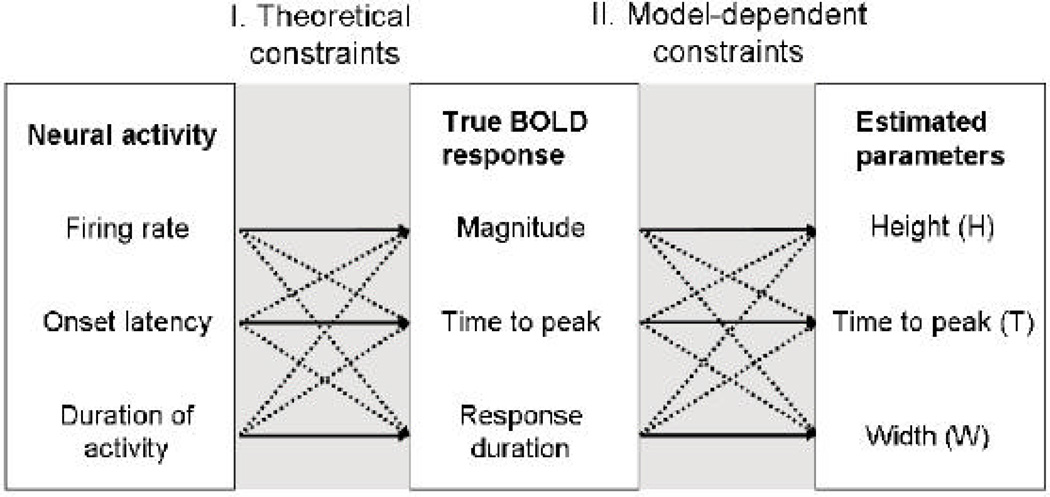
The issue of interpretability is complex, and the problem can be divided into two parts, shown in Figure 1. The first relates to whether changes in physiological, metabolic-level parameters (e.g. magnitude, delay, and duration of evoked changes in neuronal/glial activity) directly translate into changes in corresponding parameters of the HRF, such as H, T, and W. These physiological parameters are often assumed to be neural in origin as they have been shown to correlate highly with measures of extracellular post-synaptic activity (Logothetis, 2003), but they also have glial components (Schummers, Yu, & Sur, 2008). However, this part of the problem is complicated for several reasons. First, the neural response to a given stimulus is complex, task-dependent, and is not constant over time (Logothetis, 2003). Second, the hemodynamic response is sluggish (i.e., there is hysteresis) and, when it does reflect neuronal/glial activity, it integrates this activity across time. Thus, an increase in the duration of neuronal activity could result in increases in both the amplitude (H) and duration (W) of the evoked BOLD response. Third, the BOLD response is itself a nonlinear integrator, as the vascular response saturates over time (Friston, Mechelli, Turner, & Price, 2000; Vazquez et al., 2006; Wager, Vazquez, Hernandez, & Noll, 2005), further complicating matters. In sum, there is not always a clear relationship between neuronal/glial activity changes and parameters of the evoked BOLD response.

Figure 1.

The relationship between neural activity, evoked changes in the BOLD response, and estimated parameters. Solid lines indicate expected relationships, and dashed lines indicate relationships that complicate interpretation of the estimated parameters. As an example, for task-induced changes in estimated time-to-peak to be interpretable in terms of the latency of neural firing, the estimated time-to-peak must vary only as a function of changes in neural firing onsets, not firing rate or duration. The relationship between neural activity and true BOLD responses determines theoretical limits on how interpretable the parameter estimates are. The relationship between true and estimated BOLD changes introduces additional model-dependent constraints on the interpretability of parameter estimates.

The second part of the problem depicted in Figure 1 is whether the statistical model of the HRF recovers the true magnitude, time to peak, and width of the response. That is, do changes in the estimate of the height correspond to equivalent changes in the true magnitude of the BOLD response? While the second issue may seem easy to resolve, as we show here, both the use of multiple regression models and presentation of stimuli rapidly enough to evoke overlapping fMRI responses lead to the potential for mis-modeling and incorrect inference.

In spite of these challenges, well over a thousand studies have to date demonstrated relationships between task-evoked changes in brain metabolic activity and measured BOLD responses. These studies treat the evoked BOLD response as the signal of interest, without attempting to make a direct quantitative link to neuronal activity. Early studies presented events with large separation in time (e.g., visual stimuli every 20–30 sec), so that task-evoked average BOLD responses could be recovered, and H, T, and W estimated directly. However, this design is highly inefficient, as very few stimuli can be presented in a session, and it has become common practice to present events rapidly enough so that the BOLD responses to different events overlap. The dominant analysis strategy is to assume that BOLD responses to events add linearly (Boynton, Engel, Glover, & Heeger, 1996) and use a set of smooth functions to model the underlying HRF.

Choices of HRF models range from the use of a single canonical HRF, the use of a basis set of smooth functions (Friston, Fletcher et al., 1998), the use of flexible basis sets such as finite impulse response models (Glover, 1999; Goutte, Nielsen, & Hansen, 2000; Ollinger, Shulman, & Corbetta, 2001), and nonlinear estimation of smooth reference functions with multiple parameters (Kruggel & von Cramon, 1999; Kruggel et al., 2000; Lindquist & Wager, 2007; Miezin et al., 2000). These models all involve a simplified estimation of the BOLD HRF, which gives rise to the second problem identified at the right side of Figure 1. Not all models are equally good at capturing evoked changes in the true H, T, and W of the BOLD response. Evaluating the performance of these models is the focus of the current paper.

Thus, in sum, the nature of the underlying BOLD physiology limits the ultimate interpretability of the parameter estimates in terms of neuronal and metabolic function, but modeling task-evoked BOLD responses is useful, and is in fact critical for inference in virtually all neuroscientific fMRI studies. Because of the complexity in the relationship between neural activity and BOLD, we do not attempt to relate BOLD signal directly to underlying neuronal activity in this work. Instead, we concentrate on the second issue in Figure 1 and treat the evoked HRF as the signal of interest, and determine the ability of different statistical models to recover true differences in the height, time-to-peak, and width of the true BOLD response.

In previous work (Lindquist & Wager, 2007) we showed that with virtually all models of evoked BOLD responses, true changes in one parameter (e.g. T) can be mistaken for changes in others (e.g. H and W). This problem is independent from the issue of how neuronal activity actually leads to the BOLD response. The goal of this paper is to expand on our previous work assessing the validity and power of various hemodynamic modeling techniques by introducing techniques for performing inference on estimated H, T and W parameters in a multi-subject fMRI setting, as well as methods for quantifying the amount of mis-modeling each model gives rise to. We consider a number of BOLD response models, which vary significantly in their assumptions, model complexity and interpretation, under a range of different conditions, including variations in true BOLD amplitude, latency, and duration. Overall, the results reported here show that it is surprisingly difficult to accurately recover true task-evoked changes in BOLD H, T, and W parameters, and there are substantial differences among models in power, bias and parameter confusability. Because virtually all fMRI studies in cognitive and affective neuroscience employ these models, the results bear on the way HRFs are estimated in hundreds of neuroscientific studies published per year. Thus, the current results can inform the choice of BOLD response models used in these studies, until it becomes practical to incorporate more complete models of BOLD hemodynamics (including nonlinear neuro-vascular coupling) on a voxel-by-voxel basis in cognitive studies.

METHODS

Modeling the Hemodynamic Response Function

The relationship between the stimulus and BOLD response is typically modeled using a linear time invariant (LTI) system, where the signal at time t, y(t), is modeled as the convolution of a stimulus function s(t) and the hemodynamic response h(t), i.e.

$$y(t)=(s*h)(t).$$ (1)

In many studies h(t) is assumed to take a fixed canonical shape. However, to increase the flexibility of the approach, h(t) is often modeled as a linear combination of B basis functions g_i(t), where i = 1,….B. We can then write

$$h(t)={\displaystyle \sum _{i=1}^B}{\beta }_i{g}_i(t)$$ (2)

where the β_i are unknown model parameters. Typically the vectors (s * g_i)(t) are collated into the columns of a design matrix, X, and the model is expressed

$$\mathbf{Y}=\mathbf{X}\mathbf{\beta }+\mathbf{e}$$ (3)

where β is a vector of regression coefficients, Y is a vector containing the observed data, and e is a vector of unexplained error values.

For most statistical analysis the use of a LTI system is considered a reasonable assumption that provides for valid statistical inference. Therefore, in this work we assume an LTI system, and our main focus will be finding flexible models for the impulse function in the LTI system, i.e. the HRF. A number of models, varying greatly in their flexibility, have been suggested in the literature. In the most rigid model, the shape of the HRF is completely fixed and the height (i.e., amplitude) of the response alone is allowed to vary (Worsley & Friston, 1995). By contrast, one of the most flexible models, a finite impulse response (FIR) basis set, contains one free parameter for every time-point within a given window of time following stimulation in every cognitive event type modeled (Glover, 1999; Goutte et al., 2000; Ollinger et al., 2001). Thus, the model is able to estimate an HRF of arbitrary shape for each event type in every voxel of the brain. There are a number of models that fall somewhere between these two extremes. A popular choice is to use a combination of the canonical HRF and its derivatives with respect to time and dispersion (Friston, Josephs, Rees, & Turner, 1998; Henson, Price, Rugg, Turner, & Friston, 2002). Other approaches include the use of basis sets composed of principal components (Aguirre, Zarahn, & D'Esposito, 1998; Woolrich, Behrens, & Smith, 2004), cosine functions (Zarahn, 2002), radial basis functions (Riera et al., 2004), spline basis sets, a Gaussian model (Rajapakse et al., 1998) and spectral basis functions (Liao et al., 2002). Also, a number of researchers have used nonlinear fitting of a canonical function with free parameters for magnitude and onset/peak delay (Kruggel & von Cramon, 1999; Kruggel et al., 2000; Lindquist & Wager, 2007; Miezin et al., 2000).

In general, the more basis functions used in a linear model or the more free parameters in a nonlinear one, the more flexible the model is in measuring the parameters of interest. However, including more parameters also means more potential for error in estimating them, fewer degrees of freedom, and decreased power and validity if regressors are collinear. It is also easier and statistically more powerful to interpret differences between task conditions on a single parameter such as height than it is to test for differences in multiple parameters — conditional, of course, on the interpretability of those parameter estimates. Together these problems suggest using a single, canonical HRF and it does in fact offer optimal power if the shape is specified exactly correctly. However, the shape of the HRF varies as a function of both task and brain region, and any fixed model will be misspecified for much of the brain (Birn, Saad, & Bandettini, 2001; Handwerker, Ollinger, & D'Esposito, 2004; Marrelec et al., 2003; Wager et al., 2005). If the model is incorrectly specified, statistical power will decrease, and the results may be invalid and biased. In addition, using a single canonical HRF does not provide a way to assess latency and duration—in fact, differences between conditions in response latency will be confused for differences in amplitude (Calhoun, Stevens, Pearlson, & Kiehl, 2004; Lindquist & Wager, 2007).

HRF Models

In this work we study seven HRF models in a series of simulation studies and an application to real data. We briefly introduce each model below, but leave a more detailed description for Section A of the Appendix. The first model under consideration is SPMs canonical HRF (Here denoted GAM), which consists of a linear combination of two Gamma functions (Eq. A1 in the Appendix). To increase its ability to fit responses that are shifted in time or have extended activation durations, we also consider models using the canonical HRF plus its temporal derivative (TD) and the canonical HRF plus its temporal and dispersion derivatives (DD). The next class of models is based on the use of the finite impulse response (FIR) basis set, which is the most flexible basis set that can be applied directly in a linear regression framework. In this work, we study both the standard FIR model and a semi-parametric smooth FIR model (sFIR). Finally, we also consider two models fit using non-linear techniques. These include one with the same functional form as the canonical HRF but with 6 variable parameters (NL) and the inverse logit model (IL), which consists of the superposition of three separate inverse logit functions.

Estimating parameters

After modeling the HRF we seek to estimate its height (H), time-to-peak (T) and width (W). Several of the models have closed form solutions describing the fits (e.g., the Gamma based models & IL), and hence estimates of H, T and W can be derived analytically. A lack of closed form solution (e.g., for FIR models) does not preclude estimating values from the fitted HRFs, and procedures for doing so are described in Section B of the Appendix. However, when possible we use the parameter estimates to calculate H, T and W. Estimates for IL have been derived in Lindquist & Wager (2007). When using models that include the canonical HRF and its derivatives it is common to only use the non-derivative term as an estimate of the HRF amplitude. However, this solution will be biased and therefore for TD and DD we use a “derivative boost” to counteract anticipated delay-induced negative amplitude bias (Calhoun et al., 2004). For TD this estimate is

$$H=\mathit{\text{sign}}({\widehat{\beta }}_1)\sqrt{{\widehat{\beta }}_1^2+{\widehat{\beta }}_2^2}$$ (4)

where β̂₁ and β̂₂ are the regression parameters for the canonical HRF and first derivative term respectively. For DD it is

$$H=\mathit{\text{sign}}({\widehat{\beta }}_1)\sqrt{{\widehat{\beta }}_1^2+{\widehat{\beta }}_2^2+{\widehat{\beta }}_3^2}$$ (5)

where β̂₃ is the regression parameter corresponding to the second derivative term.

Inference

We also seek to compare several techniques for performing population inference on the estimated amplitude. Let H_i be the estimated amplitude for subject i, i=1,….M, defined for hypothesis testing purposes to be the global extreme point for the HRF, i.e. either a minimum or a maximum. The goal is to test whether H significantly differs from 0 in the population. In this work we compare three statistical techniques: the standard summary statistics approach (Holmes & Friston, 1998), a bootstrap procedure (Efron & Tibshirani, 1993) and a sign permutation test (Nichols & Holmes, 2002). Each of these methods has received extensive attention in the neuroimaging literature, and is described in detail in Section C of the Appendix.

Detecting Model Misspecification

Each of the models presented in this paper differ in their ability to handle unexpected HRF shapes. Using an ill-fitting model will violate the assumptions (e.g., mean 0 noise) required for valid inference and even a small amount of mis-modeling can result in severe power loss and inflate the false positive rate beyond the nominal value. Due to the massive amount of data, performing model diagnostics is challenging, and only limited attention has been given to this problem (e.g., (Luo & Nichols, 2003)). We have recently introduced a procedure (Loh, Lindquist & Wager, 2008) that uses model residuals to identify voxels where model misfit (e.g. mis-specification of onset, duration, or response shape) may be present. The key idea is that residuals will be systematically larger in mis-modeled segments of the time series.

Suppose r(i), i=1,…T are the whitened residuals and K(t) a kernel function. Let,

$$Z_w(t)={\displaystyle \sum _{i=t}^{t+w-1}}r(i)K(t-i)$$ (6)

be the moving average of w consecutive observations, starting at time t. Under the null hypothesis that the model is correct, Z_w is mean 0 for all values of t. Thus a large value of Z_w indicates that model mis-fit might be present and the statistic S max Z_w (t) = measures the strongest evidence against the null hypothesis. Using a Gaussian kernel allows Gaussian random field theory to be used to determine the p-value (Worsley, Evans, Marrett, & Neelin, 1992; Worsley, Marrett, Neelin, Vandal et al., 1996). The results can be used to detect population wide mis-modeling in a voxel, by calculating the test statistic $Q=-2{\displaystyle \sum _{i=1}^M}\text{log}(p_i)$, where p_i is the p-value for subject i. Under the null hypothesis of no effect, Q follows a chi-square distribution with 2M degrees of freedom.

As a follow-up we have proposed techniques for determining whether there is task-related signal remaining in the residuals and for quantifying the amount of power-loss and bias directly attributable to model misspecification. Estimates of bias and power-loss can be computed from the residuals for each voxel, and bias and power loss maps can be constructed. The details of this procedure are beyond the scope of this paper, and we refer the interested reader to Loh, Lindquist and Wager (2008).

Comparing HRF models: Simulation studies

The simulations described below were designed to compare the performance of the HRF modeling methods, specifically with respect to the ability to model variations in stimulus onset and duration relative to the assumed experimental reference (“neuronal”) signal (Eq. 1). We also assess the validity and power of each method using different types of inference: the summary statistic, the bootstrap test, and the sign permutation test.

Creation of “ground truth” data for simulation

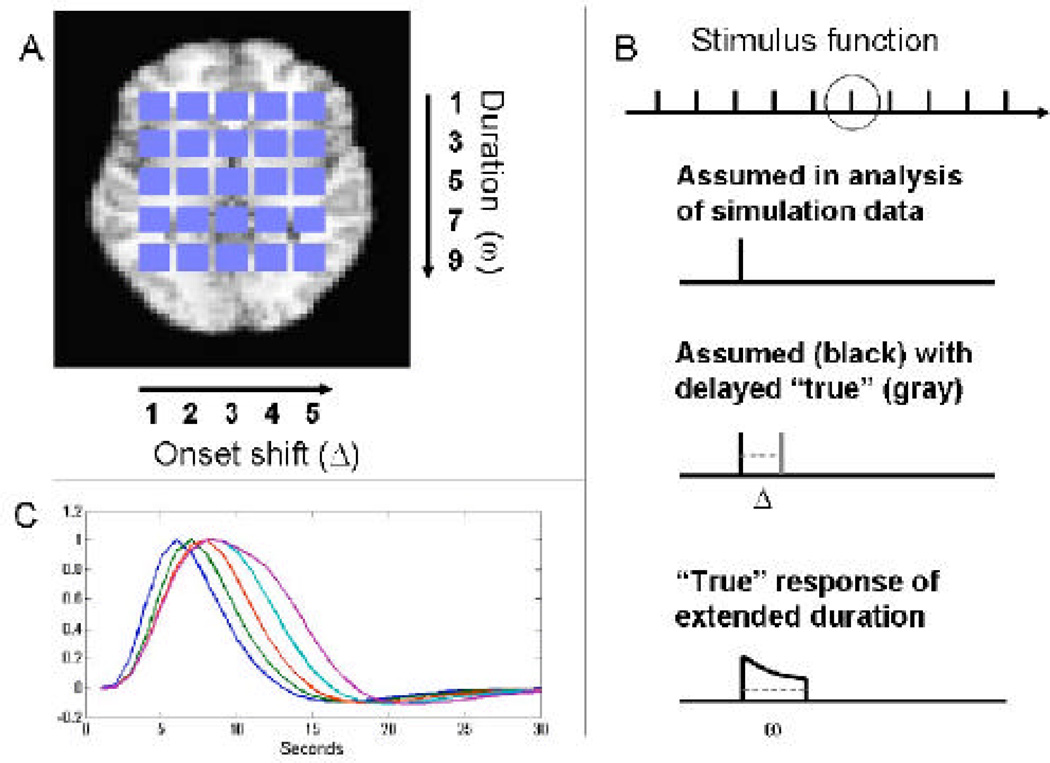
As shown in Fig. 2A, inside a static brain volume of size 51×40, a set of 25 squares of size 4×4 were placed to represent regions of interest. In each square, we created “true” simulated BOLD signals based on different stimulus functions, which varied systematically across the squares in their onset and duration of their neuronal activation as outlined in Figure 2. From left to right the onset of activation varied between the squares from the first to the fifth TR (i.e. Δ=1,…5 in Fig. 2B, third row). From top to bottom, the duration of activation varied from one to nine TR in steps of two (i.e. ω=1, 3, 5, 7, 9 in Fig. 2B, fourth row). To create the “true” response, we convolved the stimulus function in each square with SPMs canonical HRF; however, we used a modified nonlinear convolution that includes an exponential decay to account for refractory effects with stimulation across time, with the net result that the BOLD response saturates with sustained activity in a manner consistent with observed BOLD responses (Wager et al., 2005). The TR was assumed to be 1s long and the inter-stimulus interval was 30s. This simulated activation pattern was repeated to simulate 10 epochs. Fig. 2C shows differences in the activation profiles across one column of squares. To simulate a sample of subjects and simulate group “random effects” analysis, we generated 15 subject datasets for each simulation, which consisted of the “true” BOLD time series at each voxel plus white noise, creating a plausible effect size (Cohen’s d = 0.5) based on observed effect sizes in the visual and motor cortex (Wager et al., 2005). This basic data set of size 51×40×300 was used in two separate simulation studies. The first studied bias and mis-modeling in the estimates of H, W and T. The second studied the ability to perform multi-subject inference using the estimated values of H.

Figure 2.

Illustration of “ground truth” data used in the simulations. (A) A set of 25 squares were placed within a static brain slice to represent regions of interest. BOLD signals were created based on different stimulus functions which varied systematically across the squares in their onset and duration of neuronal activation. From left to right the onset of activation varied between the squares from the first to the fifth TR (i.e. Δ=1,…5). From top to bottom, the duration of activation varied from one to nine TR in steps of two (i.e. ω=1, 3, 5, 7, 9). (B) An illustration of the assumed stimulus (second row) and the true stimulus corresponding to different values of Δ and ω (third and fourth rows). The stimulus was repeated for 10 epochs (top row) with an inter-stimulus interval of 30s. The TR was assumed to be 1s long. (C) The convolution of the five stimulus functions with varying duration (ω) with a canonical HRF. The plot illustrates differences in time-to-peak and width attributable to changes in duration.

Simulation 1

An event-related stimulus function with a single spike (see Fig. 2B, second row) repeated every 30s was used for fitting the 7 HRF models to the data set described above. This implies that the square in the upper left-hand corner of Fig 2A is correctly specified while the remaining squares have activation profiles that are mis-specified to various degrees. After fitting each model, estimates of H, T and W were obtained. The average values across the 15 subjects were compared with the true values of H, T and W to assess model dependent bias in the estimates. A Gaussian kernel (4 s FWHM) was used to calculate the misspecification statistic S, and p-values were calculated for each subject using 1D Gaussian random field theory and combined across subjects to obtain population level p-values for each voxel. Finally, the distribution of H in non-active voxels (i.e. for voxels inside of the brain, but outside of the 25 squares) was used to find the distribution of H when the null hypothesis that the amplitude is equal to 0 is true. This was done to determine the validity of the summary statistics approach.

Simulation 2

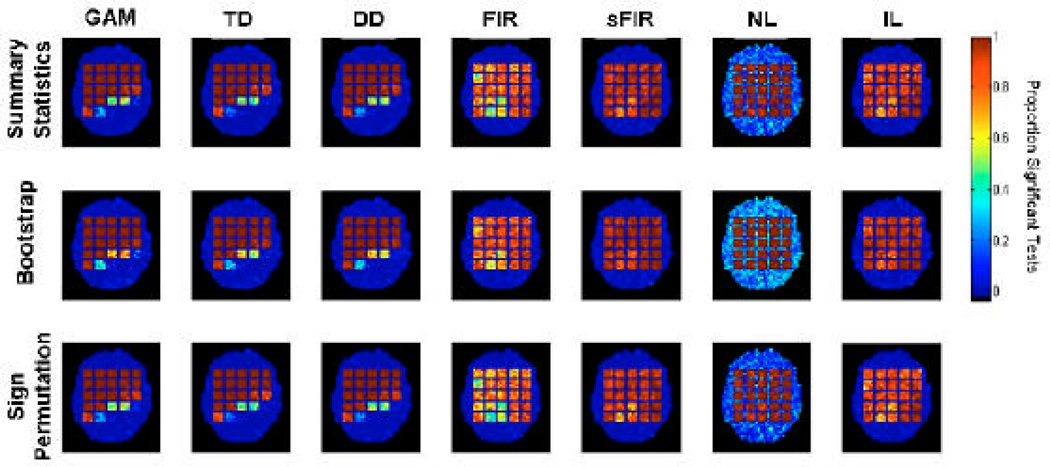
Data were simulated for 15 subjects in the same manner as in Simulation 1. After fitting each of the 7 methods, the value of H was estimated for each voxel and subject. Population inference was performed using the three testing procedures to determine whether the population height differed significantly from zero. The whole procedure was repeated 30 times and the number of times each voxel was deemed significant at the α=0.001 level was recorded.

Experimental procedures: Thermal Pain

Participants (n = 20) provided informed consent and all procedures were approved by the Columbia University IRB. During fMRI scanning, 48 thermal stimuli, 12 at each of 4 temperatures, were delivered to the left forearm. Temperatures were calibrated individually for each participant before scanning to be warm, mildly painful, moderately painful, and near tolerance. Heat stimuli, preceded by a 2 s warning cue and 6 s anticipation period, lasted 10 s in duration followed by a 30 s inter-trial interval. Functional T2*-weighted EPI-BOLD images (TR = 2 s, 3.5 × 3.5 × 4 mm voxels) were collected during functional runs of length 6 min. 8s. Gradient artifacts were removed from reconstructed images prior to preprocessing. Images were slice-time corrected and adjusted for head motion using SPM5 software (http://www.fil.ion.ucl.ac.uk/spm/). A high-resolution anatomical image (T1-weighted spoiled-GRASS [SPGR] sequence, 1 × 1 × 1 mm voxels, TR = 19 ms) was coregistered to the mean functional image using a mutual information cost function, and segmented and warped to the MNI template. Warps were also applied to functional images, which were smoothed with a 6 mm-FWHM Gaussian kernel, high-pass filtered with a 120s (.0083 Hz) discrete cosine basis set, and Winsorized at 3 standard deviations prior to analysis. Each of the 7 models were fit to data voxel-wise in a single axial slice (z = −22 mm) covering several pain-related regions of interest, including the anterior cingulate cortex. Separate HRFs were estimated for stimuli of each temperature, though we focus on the responses to the highest heat level in the results. The misspecification statistic was calculated using a Gaussian kernel (8 s FWHM) and p-values determined using Gaussian random field theory.

RESULTS

Simulation Studies

Simulation 1

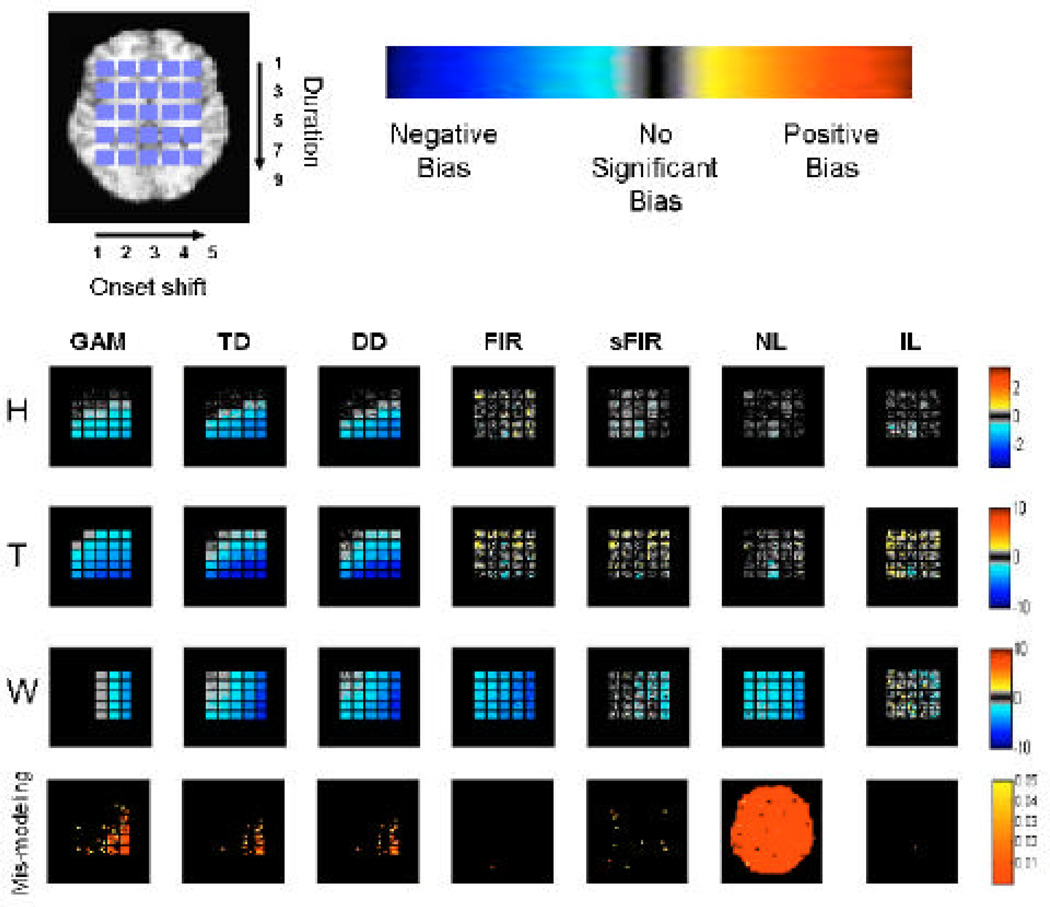
The results of Simulation 1 are summarized in Figures 3 and 4. Figure 3 shows maps of bias and mis-modeling for each of the 7 methods. In each square, black indicates a lack of bias/mismodeling, gray indicates some bias, and blue/yellow-red indicate negative or positive bias, respectively. Colors in the bottom row of Fig. 3 show p-values for the test for mis-modeling, where significance (colored in plots) indicates severe detectable mis-specification of the HRF. Note that substantial bias and power loss may exist before the mis-modeling test statistic reaches a significant p-value.

Figure 3.

Results of Simulation 1. The first three rows illustrate the average bias in the estimates of H, T and W across the brain for each of the 7 fitting methods. The last row shows voxels with significant model misspecification (p-value < 0.05).

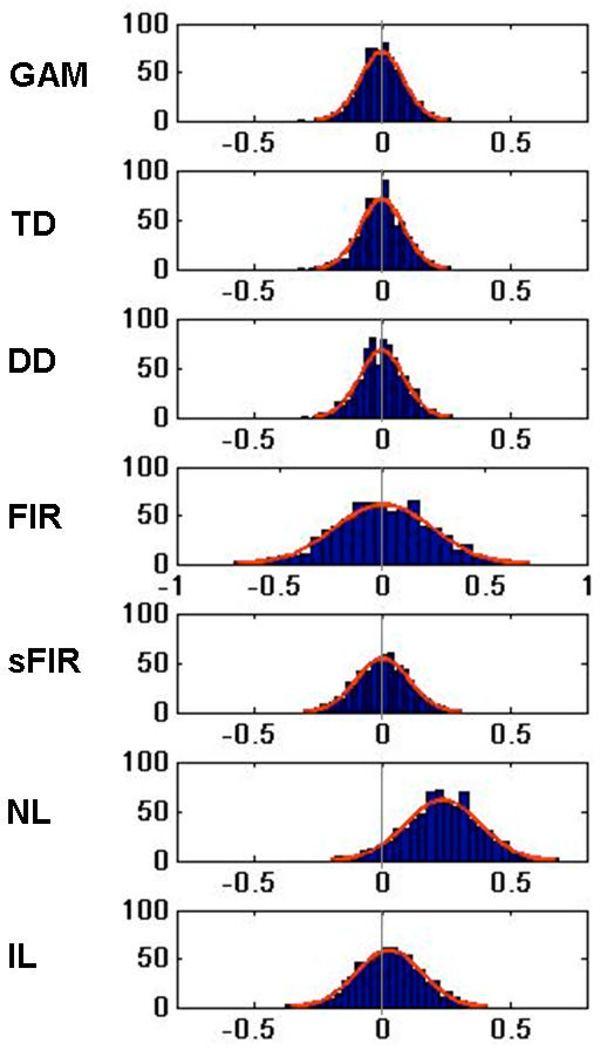
Figure 4.

Histograms depicting estimates of H in non-active voxels (inside the brain, but outside of the 25 squares). They illustrate the shape and location of the null hypothesis distributions needed for hypothesis testing. Normal curves are superimposed for reference purposes.

The GAM model (first column) gives reasonable results for delayed onsets within 3 s and widths up to 3 s (squares in the upper left-hand corner), but under-estimates amplitude dramatically as onset and duration increase. This is natural as the GAM model is correctly specified for the square in the upper left-hand corner (and thus optimal), but not well equipped to handle a large amount of model misspecification. Of special interest is the fact that there is no bias in the squares contained in the first two columns of the W map. This is true because in these cases the fixed width of the canonical HRF exactly coincides with the width of the simulated data. The same is true for the square in the upper left-hand corner of the T map. However, studying the results in the bottom row indicates severe mis-modeling present for voxels in the lower right-hand corner.

The second and third column show equivalent results for TD and DD, which show that the inclusion of derivative terms provide a slight improvement over GAM for squares where there is a minor amount of mis-modeling of the onset and duration. However, there is again a drastic decrease in model fit with delayed onsets greater than about 3 s or extended durations greater than 3 s. Interestingly enough, there appear to be only minor differences between the results for DD and TD, which indicates that the inclusion of the dispersion derivative does not lead to an improvement in the model robustness across onset and duration shifts. Also it is interesting to note that for each of the gamma-based models (GAM, TD and DD) there is a consistent negative bias in the estimates of T and W (all voxels are blue). The estimation procedure was repeated using only the non-derivative term as an estimate of the HRF amplitude as is the common practice in the field. The results (not presented here) showed that the “derivative boost” resulted in a slight decrease in reported bias.

Both models based on the use of FIR basis sets (FIR and sFIR) give rise to some bias in all three model parameters, with estimates tending to be negatively biased (e.g., shrunk towards zero for positive activations). The results for sFIR are consistent with similar simulations performed in Lindquist & Wager (2007). Of special interest is that for FIR, the W map shows a strong, systematic negative bias (all squares are blue), because the full response width is almost never captured due to the roughness of the FIR estimates. The sFIR model performs substantially better in estimating width, with substantial bias only with 4–5 s onset shifts, at a small cost in under-estimating H. This cost is likely due to the fact that the Gaussian prior term leads to shrinkage of the amplitude of the fitted HRF. Both methods showed some bias in estimates of T, but without a clear, consistent directionality. Finally, it appears that the sFIR model has some minor (occasional) problems with model mis-specification, while the FIR shows no significant model misspecification.

The NL model shows reasonable results with respect to bias, except for a strong tendency to under-estimate duration, but shows severe problems with model mis-specification. This can further be seen in Figure 4, which shows the null hypothesis data for NL is biased away from zero. Hence, it appears that the NL model is not appropriate for fitting noisy data and should only be used on regions where it is known that there is signal present. Finally, the IL model shows very little bias in H, with some unsystematic bias in T and W. In each of the maps there is a seemingly random scattering of positive and negative bias (yellow and cyan) indicating that there is no systematic bias present in the estimation of H, T and W. T appears to be the most difficult parameter to estimate accurately, with performance comparable to the FIR and sFIR models. In addition, there is no significant model mis-specification.

Figure 4 shows summary results for non-active voxels (inside the brain, but outside of the active squares) that provide information about bias and estimation efficiency under the null hypothesis. Histograms for the estimates of H from each model are shown. These can be used to assess some assumptions required for standard parametric inference (e.g., obtaining p-values using the summary statistics approach to group analysis). In each case the results look roughly normal, indicating the normality assumption is met. However, it appears that the estimates obtained using NL are biased (non-zero under the null); thus, it appears that this model will give rise to many false positives. Some of this bias is undoubtedly implementation-specific and depends on the optimization algorithm and choices; however, as the methods we used are standard choices implemented in Matlab R2007b software, these results suggest that caution and validation is in order when using these models.

Simulation 2

Simulation 2 assessed two nonparametric alternatives to the standard parametric summary statistics approach. The results are summarized in Figure 5, in the same basic format as in Figure 3. Color indicates the proportion of the 30 tests in each voxel that were significant; Thus, higher values within the squares indicate higher true positive rates (TPR), and higher values outside the squares but within the brain outline indicate higher false positive rates (FPRs). Black indicates no significant tests, blue hues indicate ~.01–.4 positive test rates, and yellow-red indicates ~0.6 – 1 positive test rates.

Figure 5.

Results of Simulation 2. Population inference was performed using three different testing procedures (summary statistic, bootstrap and sign permutation tests) to test for significant non-zero amplitude (p-value < 0.001). The procedure was repeated 30 times and the proportion of times each voxel was deemed significant is summarized in maps for each statistical test and fitting technique.

In summary, the results are consistent across the three inference techniques (each shown in one row in Figure 5), with no obvious differences in sensitivity. This is natural as the simulated data conformed to the assumptions of the summary statistics approach, and assumptions checked from the model estimates appeared valid for all models but the NL model. Due to bias in the null hypothesis data for NL, it suffers from a radically inflated FPR, shown by bright blue areas in the null-hypothesis regions, reaching an average value of roughly 30%. These results are consistent with those of Simulation 1 (Figure 4). We note that some differences in sensitivity may exist, as the parametric approach is thought to be the most sensitive one if all model assumptions are met.

From Fig. 5 it is clear that each of the Gamma based models provide excellent control of the true positive rate (TPR) when only minor amounts of model misspecification are present (e.g. squares in the upper left hand corner), but the TPR quickly decreases as the amount of model misspecification increases (e.g. squares in the lower right hand corner). In contrast, the sFIR and IL models provide uniform control of the true positive rate (TPR) across each of the 25 squares. While, the TPR is slightly lower than the Gamma based models in squares with minor model misspecification, both of these methods provide a clear improvement with increasing model misspecification.

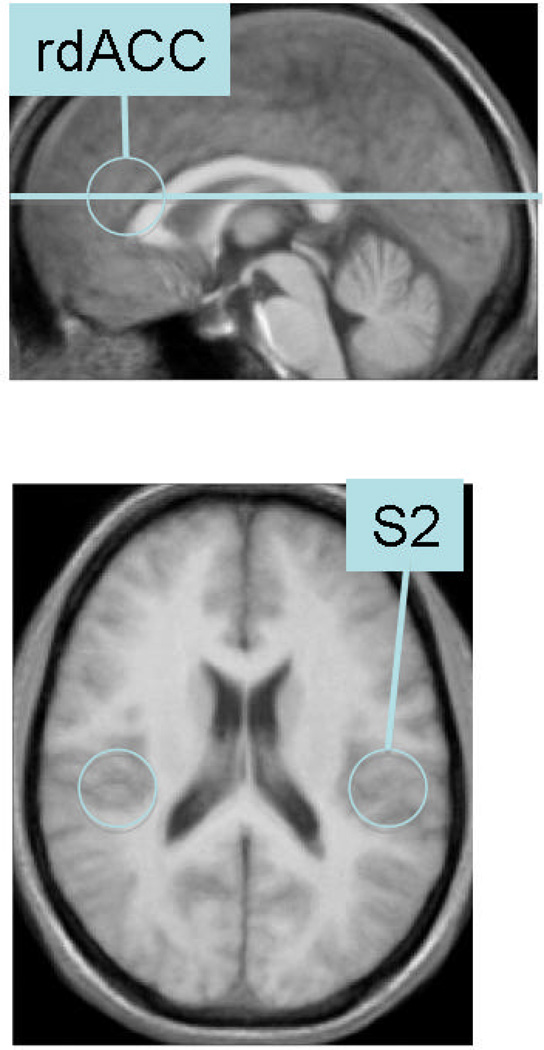
Experiment

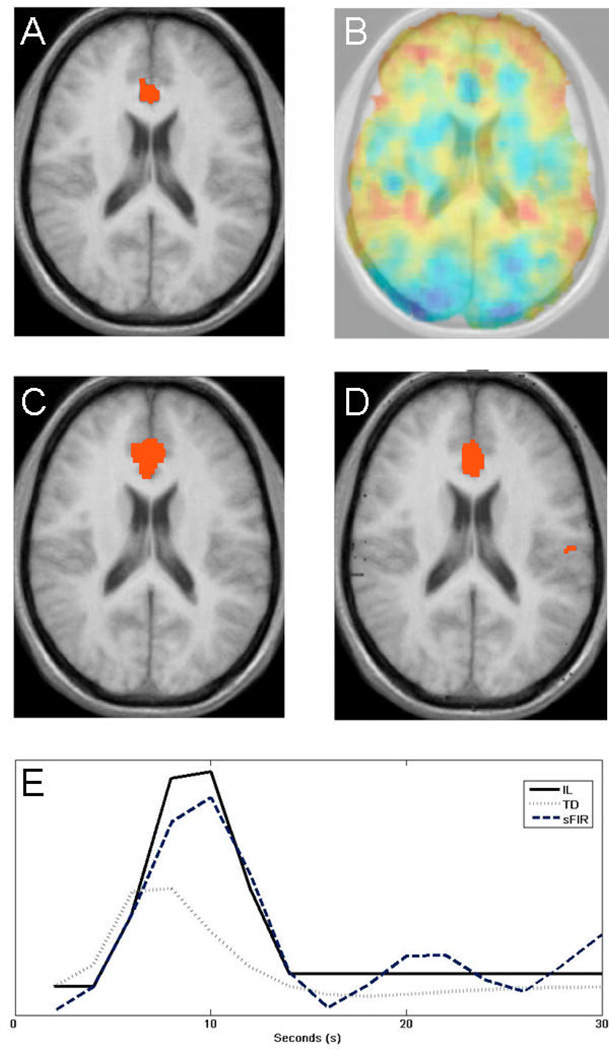
The results of the pain experiment are summarized in Figures 6–7. The location of the slice used and an illustration of areas of interest (rdACC and S2, two brain regions known to process pain intensity (Ferretti et al., 2003; Peyron, Laurent, & Garcia-Larrea, 2000) are shown in Fig. 6. In Fig. 7A, we show results obtained after estimating the height parameter on the 12 high-pain trials for each participant using the TD model, and testing for a population effect using the summary statistics approach (p < 0.01). In addition, we show a map of model misspecification in Fig. 7B. Here red corresponds to values with increased mis-modeling. In particular note the relatively large amount of mis-modeling present in the regions corresponding to S2. Figs. 7C–D shows results obtained after fitting the height parameter using the sFIR and IL models, and testing for a population effect using the summary statistics approach. The IL model is the only model that shows significant activation in S2 contralateral to noxious stimulation. Figure 7E shows the estimated HRFs from the rdACC obtained using each of the three models described above. Note the relative similarity between the estimates obtained using sFIR and IL, while TD peaks at an earlier time point. In general the estimates obtained using TD peak earlier (on average after 7 s) and are narrower (W is on average equal to 6 s), than for sFIR (10 and 8 s, respectively) and the IL model (9 and 8 s, respectively).

Figure 6.

The location of the slice used in the experiment and an illustration of areas of interest. Both rdACC and S2 are regions known to process pain intensity.

Figure 7.

(A) A statistical map obtained using the summary statistics approach and the TD model. (B) A map of model misspecification, with red indicating areas with a higher degree of mis-modeling. In particular note mis-modeling present in areas corresponding to S2. (C) A statistical map obtained using the summary statistics approach and the smooth FIR model. (D) Same results using the IL model. (E) Estimates of the HRF over the rdACC obtained using the TD, sFIR and IL models.

DISCUSSION

Though most brain research to date has focused on studying the amplitude of evoked activation, the onset and peak latencies of the HRF can provide information about the timing of activation for various brain areas and the width of the HRF provides information about the duration of activation. However, the independence of these parameter estimates has not been properly assessed, as it appears that even if basis functions are independent (or a nonlinear fitting procedure provides nominally independent estimates), the parameter estimates from real data may not be independent. The present study extends work originally presented in Lindquist & Wager (2007) that seeks to bridge this gap in the literature. To assess independence, we determine the amount of confusability between estimates of height (H), time-to-peak (T) and full-width at half-maximum (W) and actual manipulations in the amplitude, time-to-peak and duration of the stimulus. This was investigated using a simulation study that compares model fits across a variety of popular methods. Even models that attempt to account for delay such as a gamma function with nonlinear fitting (e.g., Miezin et al., 2000) or temporal and dispersion derivatives (e.g., Calhoun et al., 2004; Friston et al., 1998) showed dramatic biases if the true HRF differed in onset or duration from the canonical gamma function by more than a few seconds. As might be expected, the derivative models and related methods (e.g., Liao et al., 2002; Henson et al., 2002) may be quite accurate for very short shifts in latency (< 1 s) but become progressively less accurate as the shift increases. The IL model and the smooth FIR model did not show large biases, and the IL model showed by far the least amount of confusability of all the models that were examined. Both these methods are clearly able to handle even large amounts of model misspecification and uncertainty about the exact timing of the onset and duration of activation. However, for situations when the exact timing and duration of activation are not known a priori (e.g. certain studies of emotion and stress) we recommend using alternative methods based on change-point analysis (Lindquist & Wager, 2008; Lindquist, Waugh, & Wager, 2007).

In this work we also introduce procedures for performing inference on the estimated summary statistics. In our simulations we find that “nonparametric” bootstrap and sign permutation tests perform adequately with each model, and are roughly comparable in sensitivity to the standard parametric model when model assumptions hold. Use of these models may be advantageous when testing effects that do not have clear parametric p-values, such as the distribution of maxima used in multiple comparisons correction (Nichols & Holmes, 2002), or for which parametric p-values are insensitive (such as mediation tests; (Shrout & Bolger, 2002)).

A key point of this paper is that model misspecification can result in bias in addition to loss in power. This bias may inflate the Type I error rate beyond the nominal a level, so that p-values for the test are inaccurate. For example, a statistical parametric map thresholded at p < .001 may actually only control the false positive rate at, for example, p < .004. We find that even relatively minor model mis-specification can result in substantial power loss. In light of our results, it seems important for studies that use a single canonical HRF or a highly constrained basis set to construct maps of bias and power loss, so that regions with low sensitivity or increased false positive rates may be identified. We discuss a procedure for detecting deviations in fMRI time series residuals. Using these ideas, it is possible to construct whole-brain bias and power loss maps due to systematic mis-modeling. Matlab implementations of the IL model and a mis-modeling toolbox can be obtained by contacting the authors.

APPENDIX

A. Overview of the Models

In this section we give a detailed overview of the seven models included in our simulation study. The models under consideration are the canonical HRF (SPMs double gamma function – Here denoted GAM), the canonical HRF plus its temporal derivative (TD), the canonical HRF plus its temporal and dispersion derivatives (DD), a finite impulse response (FIR) filter, a smooth FIR filter (sFIR), a gamma function fit using nonlinear fitting techniques (NL) and the inverse logit (IL) model. Each model is described in greater detail below.

(i) Models using the Canonical HRF and its derivatives – (GAM, TD & DD)

The canonical HRF used in SPM consists of a linear combination of two Gamma functions, i.e.

$$h(t)=A(\frac{t^{{\alpha }_1-1}{\beta }_1^{{\alpha }_1}{e}^{-{\beta }_{1}t}}{\mathrm{\Gamma }({\alpha }_1)}-c\frac{t^{{\alpha }_2-1}{\beta }_2^{{\alpha }_2}{e}^{-{\beta }_{2}t}}{\mathrm{\Gamma }({\alpha }_2)})$$ (A1)

where t references time, α₁ = 6, α₂ = 16, β₁ = β₂ = 1 and c = 1/6. Here Γ represents the gamma function, which acts as a normalizing parameter, and the only unknown parameter in the model is the amplitude A. This function is convolved with the stimulus function to obtain a task related regressor to include in the design matrix. This model is attractive due to its simplicity, but inflexible. To increase its ability to fit responses that are shifted in time or have extended activation durations, it is common practice to include either the temporal derivative of h(t) or the dispersion derivative (Friston et al., 2002; Friston, Josephs et al., 1998) as additional regressors in the model. Ultimately, the number of unknown parameters depends on the number of basis sets included in the model as there is one unknown amplitude parameter for each regressor.

Heuristically, the temporal derivative allows the response to be shifted slightly (< 1 s or so) in time, while the dispersion derivative provides some capacity to model prolonged activation. Intuition for the inclusion of the temporal derivative term can be seen by assuming that the actual response, y(t), is equal to the canonical hrf, h(t), shifted in time by a small amount Δ. We can write this as y(t)=αh(t+Δ). Taking the first order Taylor expansion of y(t), we can re-express this as y(t) = α(h(t) +Δh'(t)), which illustrates that a simple linear equation can be used to model small shifts in the onset of activation.

(ii) Finite Impulse Response models - (FIR & sFIR)

The FIR basis set is the most flexible basis set that can be applied directly in a linear regression framework. In this work, we use both the standard FIR model (Glover, 1999) and a semi-parametric smooth FIR model (Goutte et al., 2000). In general, the FIR basis set contains one free parameter for every time point within a window of time following stimulation in every cognitive event type modeled. Assuming that x(t) is a n-dimensional vector of stimulus inputs, which is equal to 1 at time t if a stimuli is present at that time point and 0 otherwise, we can define the design matrix corresponding to the FIR filter of order d as,

$$\mathbf{X}=\left[\begin{array}{cccc}\hfill x(1)& \hfill 0\hfill & \hfill \mathrm{\Lambda }\hfill & \hfill 0\hfill \\ \hfill x(2)& \hfill x(1)\hfill & \hfill \mathrm{\Lambda }\hfill & \hfill 0\hfill \\ \hfill \mathrm{M}& \hfill \mathrm{M}\hfill & \hfill \mathrm{O}\hfill & \hfill \mathrm{M}\hfill \\ \hfill x(d)& \hfill x(d-1)\hfill & \hfill \mathrm{\Lambda }\hfill & \hfill x(1)\hfill \\ \hfill \mathrm{M}& \hfill \mathrm{M}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill x(n)& \hfill x(n-1)\hfill & \hfill \mathrm{\Lambda }\hfill & \hfill x(n-d+1)\hfill \end{array}\right]$$ (A2)

Further, if we assume Y is the vector of measurements, the FIR solution can be obtained using a standard general linear model:

$${\widehat{\beta }}_{\mathit{\text{FIR}}}={({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T\mathbf{Y}$$ (A3)

Without high-quality data this solution tends to be very noisy, as many separate parameters are estimated. To constrain the fit to be smoother (but otherwise of arbitrary shape), a Gaussian prior can be placed on β The resulting a posteriori estimate is then:

$${\widehat{\beta }}_{\mathit{\text{sFIR}}}={({\mathbf{X}}^T\mathbf{X}+{\sigma }^2{\mathrm{\Sigma }}^{-1})}^{-1}{\mathbf{X}}^T\mathbf{Y}$$ (A4)

where the elements of Σ are given by

$$S_{\mathit{\text{ij}}}=\nu \text{ exp}(-\frac{h}{2}{(i-j)}^2).$$ (A5)

(defined below). This is equivalent to the solution of the least square problem with a penalty function, i.e., β_sFIR is the solution to the problem:

$$\text{max}\{{(\mathbf{y}-\mathbf{X}\beta )}^T(\mathbf{y}-\mathbf{X}\beta )+{\sigma }^2{\displaystyle \sum }{s}_{\mathit{\text{ij}}}{\beta }_i{\beta }_j\}$$ (A6)

where s_ij is the (i, j)^th component of the matrix Σ⁻¹.

Compared to the standard FIR model, the smoothed version has three additional parameters h, ν and σ. The parameter h controls the smoothness of the filter and its value is set a priori to be:

$$h={\left(\frac{1}{7/\mathit{\text{TR}}}\right)}^2.$$ (A7)

In estimating β̂_sFIR, only the ratio of the parameters ν and σ is of interest and it is determined empirically that the ratio:

$$\frac{{\sigma }^2}{\nu }=10$$ (A8)

typically gives rise to adequately smooth FIR estimates, without significant bias due to shrinkage (Goutte et al., 2000; Lindquist & Wager, 2007).

(iii) Non-Linear fit on two Gamma functions – (NL)

This model takes the same functional form as the canonical HRF, i.e.

$$h(t)=A(\frac{t^{{\alpha }_1-1}{\beta }_1^{{\alpha }_1}{e}^{-{\beta }_{1}t}}{\mathrm{\Gamma }({\alpha }_1)}-c\frac{t^{{\alpha }_2-1}{\beta }_2^{{\alpha }_2}{e}^{-{\beta }_{2}t}}{\mathrm{\Gamma }({\alpha }_2)})$$ (A9)

where A controls the amplitude, α and β control the shape and scale, respectively, and c determines the ratio of the response to undershoot. In this model each of the 6 parameters are assumed to be unknown and they are fit using the Levenberg-Marquardt algorithm. The starting values for the algorithm are set to coincide with those of the canonical HRF.

(iv) Inverse Logit (IL) Model

The inverse logit function, defined as L(x) = (1+e^−x)⁻¹, is an increasing function of x taking values 0 and 1 in the limits. To derive a model for the HRF that can efficiently capture details inherent in the function (e.g. the positive rise and the post-activation undershoot), we use a superposition of three separate inverse logit functions (Lindquist & Wager, 2007). The first describes the rise following activation, the second the subsequent decrease and undershoot, while the third describes the stabilization of the HRF (i.e., return to baseline). Our model of the hemodynamic response function, h(t), can be written:

$$h(t|\theta )={\alpha }_{1}L((t-T_1)/D_1)+{\alpha }_{2}L((t-T_2)/D_2)+{\alpha }_{3}L((t-T_3)/D_3).$$ (A10)

Here the α parameters control the direction and amplitude of the curve. If α_i is positive, α_i · L(x)will be an increasing function that takes values between 0 and α_i. The parameter T_i is used to shift the center of the function T_i time units. Finally the parameter D_i controls the angle of the slope of the curve, and works as a scaling parameter.

In our implementation we constrain the values of α₂ and α₃ so that the fitted response begins at zero at the time point t = 0 and ends at magnitude 0. This leads to a model with 7 variable parameters that can be fit either using a stochastic (e.g., simulated annealing, which we use here) or a gradient descent solution. See Lindquist and Wager (2007) for further details.

B. Estimating parameters

When H, T, and W cannot be calculated directly using a closed form solution, we use the following procedure to estimate them from fitted HRF estimates. Estimates of H and T are calculated by taking the derivative of the HRF estimate h(t) and setting it equal to 0. In order to ensure that this is a maximum, we check that the second derivative is less than 0. If two or more peaks exist, we choose the first one. Hence, our estimate of time-to-peak is T = min {t | h'(t) = 0 & h"(t) < 0}, where t indicates time and h'(t) and h"(t) denote first and second derivatives of the HRF h(t). To estimate the peak we use H = h(T) .

For hypothesis testing purposes, our goal is typically to determine whether H significantly differs from 0. To ensure the estimate of H is mean-zero under the null hypothesis, T is in this situation defined based on the largest absolute deviation (either positive or negative). This can be obtained with minor modifications of the procedure outlined above.

Finally, to estimate the width we perform the following steps¹:

1. Find the earliest time point t_u such that t_u > T and h(t_u) < H /2, i.e. the first point after the peak that lies below half maximum.

2. Find the latest time point t_l such that t_l < T and h(t_l) < H / 2, i.e. the last point before the peak that lies below half maximum.

3. As both t_u and t_l take values below 0.5H, the distance d = t_u − t_l overestimates the width. Similarly, both t_u−1 and t_l+1 take values above 0.5H, so the distance d = t_u−1 −t_l+1 underestimates the width. We use linear interpolation to get a better approximation of the time points between (t_l, t_l+1) and (t_u−1, t_u) where h(t) is equal to 0.5H. According to this reasoning, we find that

   $$W=(t_{u-1}+{\mathrm{\Delta }}_u)-(t_{l+1}-{\mathrm{\Delta }}_l)$$ (B1)

   where

   $${\mathrm{\Delta }}_l=\frac{h(t_{l+1})-0.5H}{h(t_{l+1})-h(t_l)}$$ (B2)

   and

   $${\mathrm{\Delta }}_u=\frac{h(t_{u-1})-0.5H}{h(t_{u-1})-h(t_u)}.$$ (B3)

For high-quality HRFs this procedure suffices, but if the HRF estimates begin substantially above or below 0 (the session mean), then it may be desirable to calculate local HRF deflections by calculating H relative to the average of the first one or two estimates.

C. Inference

Let H_i be the estimated amplitude for subject i, i=1,….M. Note for hypothesis testing purposes, we define H_i to be the global extreme point for the HRF, i.e. either a minimum or a maximum. These values can be obtained using the procedure outlined in the previous section. Our goal is to test whether H significantly differs from 0 in the population. Here we will discuss three simple statistical techniques: the standard summary statistics approach, a bootstrap procedure and a sign permutation test.

(i) Summary statistics approach

Our first inference technique is the classic single-summary-statistic approach (Holmes & Friston, 1998) commonly used in neuroimaging. Here we assume that H̅ is the sample mean and s_H the sample standard deviation of the M amplitude estimates (H₁, H₂, Κ H_M). Using these values we calculate the test statistic:

$$t=\frac{\overline{H}}{s_H/\sqrt{M}}$$ (C1)

P-values are obtained by comparing the results with a t-distribution with M-1 degrees of freedom.

There are a few important issues to keep in mind when applying the summary statistic approach. First, the method assumes constant within-subject variation of the height estimates across subjects, though this assumption can be relaxed in a manner similar to that outlined by Beckman et al. (Beckmann, Jenkinson, & Smith, 2003). However, in this work we simply discuss the classic summary statistics approach with the caveat that the conclusions are only valid if the within-subject variance is homogenous across subjects. A second issue is that p-values are only valid when the H_i are normally distributed. This will typically be true when performing inference directly on the β values obtained from least-squares (canonical HRF term only or FIR basis set). However, when using the derivative boost, sFIR, NL or IL approach assuming that the amplitudes follow a normal distribution may not necessarily be reasonable.

(ii) Bootstrap

The bootstrap procedure (Efron & Tibshirani, 1993) provides a non-parametric alternative to the summary statistics approach. Due to its non-parametric nature, it is valid for each of the models under consideration and no additional assumptions need to be made regarding the distribution of the H_i. Our testing procedure can be described as follows:

1. Select B (e.g. 5,000–10,000) independent bootstrap samples, each consisting of M data values sampled with replacement from the set (H₁, H₂, Κ H_M).

2. Calculate the sample mean for each bootstrap sample.

3. Compute the bootstrap distribution for the sample mean using the B replications.

4. Construct 100 (1-α)% confidence intervals and determine whether they contain 0.

For small sample sizes there may be problems with the accuracy of the bootstrap confidence intervals. Therefore we suggest the use of the bootstrap bias-corrected accelerated (BCa) interval as a modification that adjusts the percentiles to correct for bias and skewness. For more details we refer the interested reader to Efron & Tibshirani (1998). It is important to note that the bootstrap procedure is designed to estimate the sample standard error of a statistic and can therefore be used to construct confidence intervals. The bootstrap distribution is not calculated with a specific null hypothesis in mind and for this we need to use a permutation test. Also, for the specific problem of FWE-control using the max distribution of a large number of tests with small M, it has been shown (Troendle, Korn, & McShane, 2004) that the Bootstrap can be unstable and permutation tests are to be preferred.

(iii) Sign Permutation Test

The final method, the sign permutation procedure (Nichols & Holmes, 2002), is another non-parametric test that is valid for each of the models under consideration. The testing procedure can be described as follows:

1. Randomly permute the sign of each value of H_i, i.e. take a resample (x₁, x₂, Κ x_M) where

   $$x_i=\{\begin{array}{c}{H}_i\text{ with probabiltity }0.5\hfill \\ -H_i\text{ with probabiltity }0.5\hfill \end{array}$$

2. Calculate the sample mean x̄ for each resample.

3. Repeat steps 1 and 2 a total of B (e.g. 5,000–10,000) times and use the collection of sample means to construct the permutation distribution.

4. Use the permutation distribution to calculate the p-value. The p-value for the one-sided test of H₀: H=0 is given by

   $$\mathrm{p}-\text{value}=\frac{\#\{\overline{x}>\overline{H}\}}{N}$$

   If our data consists of M different values of H_i there are a total of 2^M possible permutations of signed values. If M is reasonably small, an exact p-value can be obtained by using each possible permutation rather than by taking a random subset.