Abstract
This study quantified normal age-related changes to the photoreceptor axons in the central macula using the birefringent properties of the Henle fiber layer. A scanning laser polarimeter was used to acquire 15 × 15 deg macular images in 120 clinically normal subjects, ranging in age from the third decade to the eighth. Raw image data of the macular cross were used to compute phase retardation maps associated with Henle fiber layer. Annular regions of interest ranging from 0.25 to 3 deg eccentricity and centered on the fovea were used to generate intensity profiles from the phase retardation data, which were then analyzed using sine curve fitting and Fast Fourier Transform (FFT). The amplitude of a 2f sine curve was used as a measure of macular phase retardation magnitude. For FFT analysis, the 2f amplitude, as well as the 4f, were normalized by the remaining FFT components. The amplitude component of the 2f curve fit and the normalized 2f FFT component decreased as a function of age, while the eccentricity of the maximum value for the normalized 2f FFT component increased. The phase retardation changes in the central macula indicate structural alterations in the cone photoreceptor axons near the fovea as a function of age. These changes result in either fewer cone photoreceptors in the central macula, or a change in the orientation of their axons. This large sample size demonstrates systematic changes to the central cone photoreceptor morphology using scanning laser polarimetry.
Keywords: Henle fiber layer, polarimetry, phase retardation, birefringence, fovea, aging, cones
1. Introduction
As the population ages, and as individuals have greater life expectancies, the importance of understanding aging changes in the retina is increasingly important. Differentiating between normal aging changes and disease processes is fundamentally important for the purposes of separating pathology from normal morphology and in staging disease for management and treatment.
The normal retina has a high degree of structural regularity, and this regularity causes the retina to possess form birefringence (van Blokland, 1985; Brink & van Blokland, 1988; Huang, & Knighton, 2003), a measure of phase retardation per unit distance. Thus, polarization sensitive imaging can use the presence or absence of phase retardation as a biomarker for particular types of tissue specific changes. This approach has allowed retinal structures to be more accurately characterized and visualized with improved contrast both in en face imaging (Weber et al., 2004; Bueno & Vohnsen, 2005; Tweitmeyer et al., 2008; Song et al., 2008) and in cross sectional imaging using polarization sensitive optical coherence tomography (PSOCT) (Cense et al., 2004; Yamanari et al., 2008; Götzinger et al., 2008; Götzinger et al., 2009; Ahlers et al., 2010). Improved contrast has also improved the ability to delineate pathological features in diseases such as epiretinal membranes (Miura et al., 2007); drusen (Burns et. al., 2003); changes near the optic nerve head (Mellem-Kairala et al., 2005); exudative age-related macular degeneration (Elsner et al., 2007; Miura et al., 2008; Weber et al., 2007); and central serous chorioretinopathy (Miura et al., 2005).
One of the most striking components emphasized by polarization sensitive imaging is the macular cross seen at the fovea, which is the result of the interaction of the corneal phase retardation with the phase retardation from the Henle fiber layer (Brink & van Blokland, 1988; Elsner at al., 2008; Knighton, Huang & Cavuto, 2008). The photoreceptor outer segments in the fovea are perpendicular to the retinal surface, but their axons are oriented in a radially symmetric pattern nearly parallel to the retinal surface. Known as the Henle fiber layer, these axons reach up to nearly 700 μm in length (Drasdo et al., 2007) and exhibit behavior analogous to a uniaxial crystal with a slow axis radially oriented with respect to the fovea (van Blokland, 1985). The interaction of the phase retardation of the Henle fiber layer with polarized light has been modeled (Brink & van Blokland, 1988). This macular cross pattern has been used qualitatively to localize the fovea in normal subjects (VanNasdale et al., 2009); monitor fixation and eye tracking in infants and young subjects (Gramatikov et al., 2006; Gramatikov et al., 2007; Hunter et al., 2004; Hunter et al., 1999; Hunter et al., 2003; Nassif et al., 2003); and characterize damage due to age-related macular degeneration (Elsner et al., 2007; Weber et al., 2007); and central serous chorioretinopathy (Miura et al., 2005).
The intensity distribution of the macular cross pattern can also be used to quantitatively model the foveal structure, providing specific information about the cone photoreceptor density and distribution in the central macula (Elsner et al., 2008). The radially symmetric pattern of the axons leads to the systematic variation of phase retardation along a ring concentric with the fovea with modulation that is described by a sine function, but with twice the frequency of the ring. As a result, curve fitting using a 2f sine function has been used for quantitative analysis of pixel intensity profiles of these rings. Within regions of interest that are concentric rings at increasing eccentricities from the fovea, the Henle fiber layer contains a cumulatively larger numbers of cone photoreceptor axons that are relatively perpendicular to the incident light. The increasing number of birefringent photoreceptor axons leads to a thickness-dependent increase in phase retardation. One exception is the very central fovea, where little phase retardation is expected, due to the photoreceptor cell bodies being displaced eccentrically. At a few degrees eccentricity from the fovea, the retinal cells are no longer displaced laterally and the photoreceptor axons become oriented more parallel to the incident light. At this location, the orientation of the photoreceptors does not generate phase retardation along the optical path of incident light and any phase retardation at these eccentricities becomes dominated by other features, such as the retinal nerve fiber layer.
The phase retardation of the Henle fiber layer is seen with polarized light; however depolarization is also an important characteristic of light tissue interactions in the retina. A proportion of the incident light will not retain its polarization characteristics as it interacts with normal and diseased tissue. This light becomes randomly polarized and does not modulate with changes in the input polarization conditions, i.e. the degree of polarization in the measured light decreases. A decrease with increasing age for the degree of polarization has been reported for annular regions surrounding the optic nerve head and the fovea (Naoun, et al., 2005; Bueno et al., 2009; Bueno, 2004). The amount of light that has become randomly polarized can be used to quantify scattering related to not only aging changes in the anterior segment, but also to altered or irregular structures and deeper retinal layers. Additionally, changes associated with diseases like age-related macular degeneration (AMD) can introduce phase retardation associated with pathological features that disrupt the radial symmetry of the phase retardation in the central macula (Elsner et al., 2007; Weber et al., 2007).
Quantification of the Henle fiber layer may provide a global measure of cone photoreceptor density and distribution in the central macula, by using phase retardation as measured with scanning laser polarimetry (SLP). The Henle fiber layer phase retardation could potentially act as a surrogate marker for cone photoreceptor axon density in the fovea. The amount and distribution of phase retardation in and around the fovea should be directly proportional to the density and thickness of the photoreceptor axons constituting the Henle fiber layer, as well as the orientation of the Henle fibers with respect to the measurement beam. The shape of the foveal pit also depends upon these factors. The phase retardation measure differs from an increase of thickness with aging of a combined outer plexiform layer and Henle fiber layer, reported recently (Curcio et al., 2011), since to date only the phase retardation of axons, rather than the additional neural elements and support cells, has been hypothesized as the source of the phase retardation. In this study, we examined the distribution of the macular cross pattern as a surrogate marker for photoreceptor density or orientation and modeled this characteristic pattern using two analysis methods for concentric rings as regions of interest centered on the macula: the previously used 2f sine analysis (Elsner et al., 2008) and a normalized metric from the 2f and 4f components of the Fast Fourier Transform (FFT) by the other frequency components above 2f to remove the influence of corneal polarization. Based on previous findings using imaging techniques of an average decrease of cone photopigment and macular pigment in the central fovea of older subjects (Elsner et al., 1998), along with complementary findings with psychophysical techniques (Eisner et al., 1987; Burns & Elsner, 1989; Swanson & Fish, 1996), we hypothesize that we will find an age-dependent decrease for the magnitude of these two metrics at a fixed distance from the center of the fovea. Similarly, we hypothesize an increase in the eccentricity of the maximum relative phase retardation if the cones in the central macula are disproportionately affected.
2. Methods
2.1 Subjects
Images were evaluated for 120 eyes (63 right eyes, 57 left eyes) in 120 subjects, incorporating 10 males and 10 females from each decade from the third decade through the eighth. This careful age-matching allowed us to uncover any potential gender effects. Study participants were considered eligible for enrollment if a complete ophthalmologic examination had been completed within the past year including dilated fundus examination and refraction, with no signs of ocular pathology. Subjects with systemic diseases that carry a high likelihood of ocular manifestations were excluded. Subjects were included if they exhibited normal lens opacification that did not result in visual acuities worse than 20/25. There was no difference in refractive error among the age groups categorized by decade (ANOVA, p = 0.431). The mean refractive error spherical equivalent was −1.59 diopters with a standard deviation of 2.46, so that the effects of high refractive error or axial length would be sufficiently limited to allow us to study aging effects. All but 2 subjects had refractive error spherical equivalents within +/− 6 diopters. One subject, age 41, had a refractive error spherical equivalent of −6.25, the other, age 67, had a refractive error spherical equivalent of −8.125. Additionally, there were 4 subjects that were pseudophakic in the tested eye, all in the 8th decade (70, 72, 75, and 78 years old). All procedures conformed to the Declaration of Helsinki and subjects were recruited following an approved human subjects protocol from Indiana University.
2.2 Instrumentation and Imaging
A confocal scanning laser polarimeter (GDx, Laser Diagnostic Technologies/Carl Zeiss Meditec; Dublin, CA) was used to acquire images of the central macula using the acquisition and analysis method described previously (Burns et al., 2003; Elsner et al., 2007; Mellem-Kairala et al., 2005; VanNasdale et al., 2009; Weber et al., 2004; Weber et al., 2007). The GDx uses a 780-nm linearly polarized near infrared light source to scan a 15 × 15 deg raster pattern on the retina. For this study, the element used to compensate for corneal phase retardation was removed enabling a full interaction between the phase retardation of the cornea and that of the Henle fiber layer, resulting in a distinct macular cross pattern. The modulation of phase retardation in the macular cross pattern is influenced by the retardation introduced by the cornea, however the age of subjects is not correlated with either the corneal axis or retardance (Knighton & Huang, 2002).
The GDx has a linearly polarized illumination beam that passes though a rotating half wave plate to vary input polarization to the eye. The GDx has 2 detectors collecting data simultaneously, a parallel detector collecting light with the same polarization as the input polarization; and a crossed detector, collecting light with polarization that is 90 deg from the input polarization. Each detector produces an image at each of 20 input polarization conditions, for a total of 40 images per image series. Each image has 256 × 256 resolution with 8-bit grayscale. The image series has an acquisition time of approximately 0.9 seconds and is performed non-invasively without mydriasis. Three data sets per eye were acquired for each subject, and the best one chosen for analysis, to ensure images that were well-focused, adequately and evenly illuminated, and without movement artifacts.
2.3 Image Processing and Analysis
Raw image data were processed using custom Matlab routines (Matlab, Mathworks, Natick, MA) (Burns et al., 2003; Mellem-Kairalla et al., 2005; Elsner et al., 2007; Elsner et al., 2008). For each pixel, the intensity modulation across the 20 input polarization conditions in the crossed detector was used to determine phase retardation for that pixel location. Intensity changes at each pixel were low pass filtered using a Fast Fourier Transform (FFT). The amplitude of that smoothed curve was plotted pixel by pixel to produce a 256 × 256 grayscale phase retardation map. The GDx has a high intensity central reflection artifact inherent in the system. This artifact was manually removed, and replaced column-by-column, with the average of the first pixel above the reflection artifact and the first pixel below the reflection artifact. During image acquisition, subjects were instructed to fixate so the fovea was not obscured by the reflection artifact, and to ensure the artifact was not located within the region of interest used for analysis.
2.4 Data Analysis and Modeling
The center of the macular cross pattern was designated as the foveal center and used as the center of regions of interest for further processing. The processing was performed in concentric rings ranging continuously in 1 pixel radius increments from 0.25 to 3.0 deg eccentricity from the fovea. To reduce noise, each region of interest was the average of pixel intensities of the specific eccentricity averaged with the pixel intensities of immediately adjoining inner and outer rings. We used two complementary techniques to model the phase retardation associated with the Henle fiber layer. One method was to fit a 2f sine curve to the intensity profiles, or changes in pixel intensity in the phase retardation maps along the circular regions of interest (Elsner et al., 2008). The amplitude of the 2f phase retardation, y, was modeled with the following equation:
| (1) |
where coefficient a is the scalar constant representing the amplitude of the intensity profile, b is the phase offset, and c is the generalized offset term. Coefficient a is an indicator of systematic phase retardation magnitude corresponding to the Henle fiber layer distribution at different eccentricities. An additional variable of interest was a goodness of fit parameter, the RMS error.
Additionally, we assessed each region of interest using a Fast Fourier Transform (FFT) and evaluated the individual frequency components. Several normal subjects demonstrate a 4f macular cross pattern, instead of the more typical 2f pattern, which we took into consideration for any evaluations of the Henle fiber radial symmetry. FFT analysis of concentric regions of interest at increasing eccentricities from the fovea can be used to evaluate different sinusoidal components independently or in specific combinations. This analysis can be used to find locations where the 2f and 4f FFT components dominate, indicating a high degree of radial symmetry and highest density of photoreceptor axons associated with the Henle fiber layer.
We computed a normalized 2f component as the sum of the 2f and 4f components that corresponds to interaction of the cornea and the Henle fiber layer to the sum of the 1f, 3f, 5f and higher components that corresponds to phase retardation from other sources.
| (2) |
where N 2f Component is the Normalized 2f Component and ai is the amplitude of each frequency component. This method minimizes variations in amplitude due to instrumentation fluctuation, corneal phase retardation, ocular filters, and light lost due to intraocular scatter. This normalization reduces artifact from the DC level, which could be affected by inter-subject characteristics like retinal pigmentation and pupil size.
2.5 Polarization Modeling Parameters
2.5.1 Coefficient a at 1.25 deg
For each subject, we determined the coefficient a and the RMS for the 2f curve fitting at 1.25 deg eccentricity. This specific eccentricity was chosen because the 2f component remains twice as large as the 1f component for the majority of normal individuals at this eccentricity, and the 2f component dominates the 1f component for all eccentricities around 1 deg (Elsner et al., 2008). To examine whether foveal phase retardation decreased with age, we performed linear regression as a function of age on the coefficient a.
2.5.2 Eccentricity of the maximum of the normalized 2f component
We examined the hypothesis that foveal structure changes with age, resulting in a decreased cone density or configuration change in the central fovea compared to the parafovea in older subjects. This implies that the maximum phase retardation would occur at greater eccentricities in older subjects. For each subject, we determined the eccentricity corresponding to the maximum of the normalized 2f component from the FFT, indicating the location of maximum phase retardation attributed to the Henle fiber layer. To examine whether the eccentricity of the phase retardation increased with age, we performed linear regression on the eccentricity of the maximum of the normalized 2f as a function of age.
2.5.3 RMS error at 1.25 deg compared to RMS at eccentricity of the maximum of the normalized 2f
To determine whether age or eccentricity affected the goodness of fit for the 2f sine curve fitting, we obtained the RMS error for each subject from the fit of the data to equation 1 at 1.25 deg eccentricity. Similarly, we obtained the RMS error for each subject at their eccentricity of the maximum of the normalized 2f. We categorized subjects by decade and performed a 2-way analysis of variance (ANOVA), testing the main effects of decade, RMS at the two eccentricities, and the interaction of the two.
2.5.4 Normalized 2f component averaged between 1 and 1.25 deg eccentricity
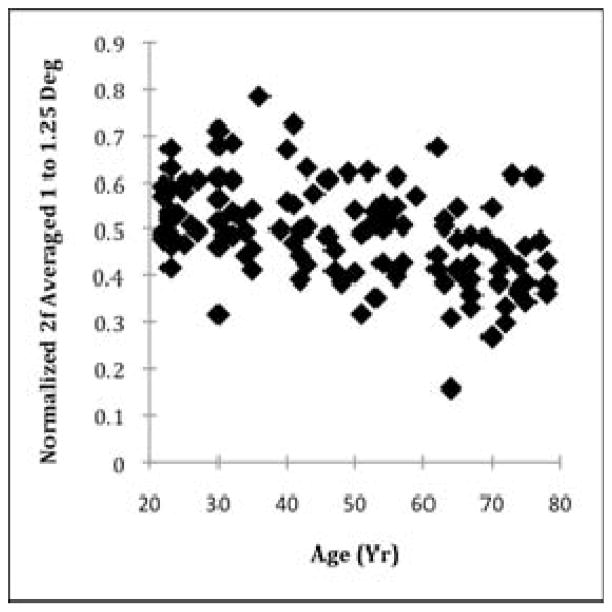
To reduce the unwanted influence of variables not corresponding to the Henle fiber layer, and also the random variations in the data, we plotted the normalized 2f component averaged from 1 to 1.25 deg eccentricity as a function of age and performed a linear regression.
2.5.5 Area under curve of the normalized 2f FFT component
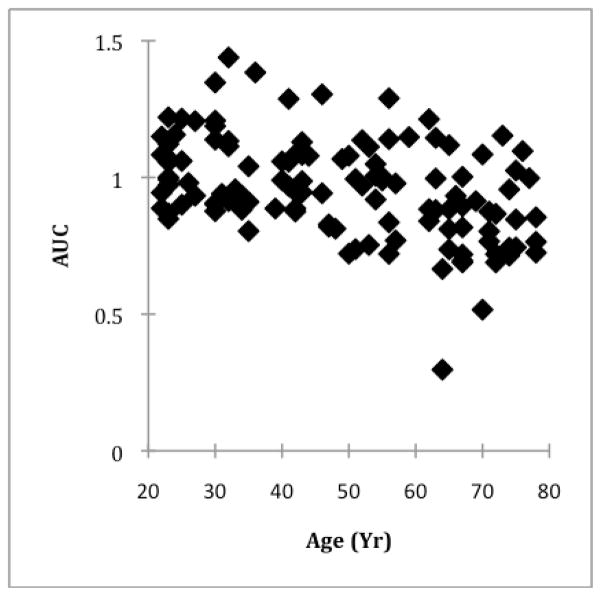
To develop a comparative measure of overall phase retardation between individuals within the central 0.5 to 2.5 deg of the macula, we took the area under the curve (AUC) for of the normalized 2f component of the FFT analysis to perform a linear regression as a function of age. We selected this region because eccentricities less than 0.5 deg provide low phase retardation signals and are thus noisy, and eccentricities over 2.5 deg begin to incorporate increasing amounts of phase retardation from other retinal structures such as the nerve fiber layer.
3. Results
3.1 Image Processing and Analysis
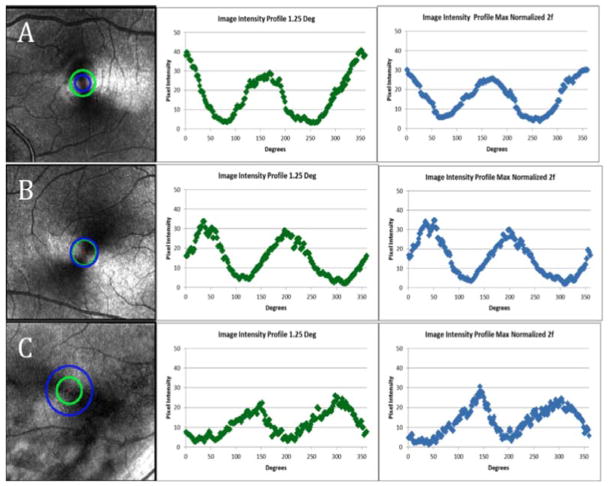
All subjects demonstrated an intact macular cross pattern with measurable phase retardation for the 2f component, ranging from 0.25 to 3 deg eccentricity. Gender effects were not evident in any of our primary analyses. There was considerable overlap between males and females in the data, for instance for the mean slope of coefficient a at 1.25 deg was the same for both males and females, the RMS of the 2f curve fitting at 1.25 deg (p = 0.352), and the AUC of the normalized 2f from 0.50 to 2.50 deg eccentricity (p = 0.427). Figure 1 illustrates the overall results by showing 3 individual data sets, comparing results for subjects from the third, sixth, and eighth decade age groups. For the phase retardation maps for each subject, a green ring indicates the region of interest at 1.25 deg eccentricity. A blue ring indicates the maximum of the normalized 2f component eccentricity. The pixel intensities associated with these regions of interest demonstrate that modulation is well-modeled by a 2f sine function. This figure illustrates the systematic changes seen with aging. First, the amplitude of the 2f component as measured at 1.25 deg eccentricity decreases with increasing age. Second, a greater eccentricity for the maximum of the normalized 2f component is seen for the older subject, compared with the two younger subjects.
Fig. 1.
Examples of grayscale phase retardation maps and accompanying intensity profiles at the 2 eccentricities used for analysis. Left Column- Phase retardation maps marked with sampled locations for the center and right columns in a 24 year old subject (A), 52 year old subject (B), and 72 year old subject (C). Eccentricities are marked on the images corresponding to 1.25 deg (green circle) as well as the location of the maximum of the normalized 2f component (blue circles). Center Column- Intensity profiles at 1.25 deg eccentricity shown in green (A,B,C). Right Column- Intensity profiles at the eccentricity of the maximum of the normalized 2f component shown in blue (A,B,C). The sharp peaks seen in the intensity profiles in the 52 and 72 year old subjects are not typical of increasing age.
3.2 Results of Polarization Modeling Parameters
3.2.1 Coefficient a at 1.25 deg
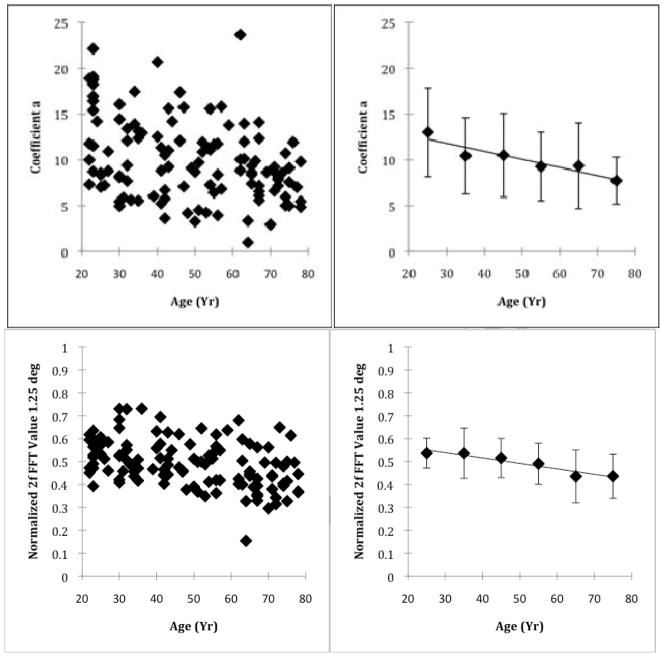
When the entire sample was analyzed, the amplitude of the phase retardation decreased as a function of age at 1.25 deg eccentricity (Fig 2). Linear regression indicated an average decrease of 0.086 gray scale units per year, (p<0.001, R2 = 0.121). A similar trend was also seen at this eccentricity with the normalized 2f component.
Fig. 2.
Individual and grouped data showing the decrease with age of phase retardation at 1.25 deg. Top Left Panel- Foveal phase retardation at 1.25 deg eccentricity quantified as Coefficient a, which is the amplitude of the 2f phase retardation, plotted as a function of age. Top Right Panel- Data grouped by decade with mean and 1 standard deviation error bars. Bottom Left Panel- Foveal phase retardation at 1.25 deg eccentricity quantified as the normalized 2f FFT component. Bottom Right Panel- Data grouped by decade with mean and 1 standard deviation error bars.
3.2.2 Eccentricity of the maximum of the normalized 2f component
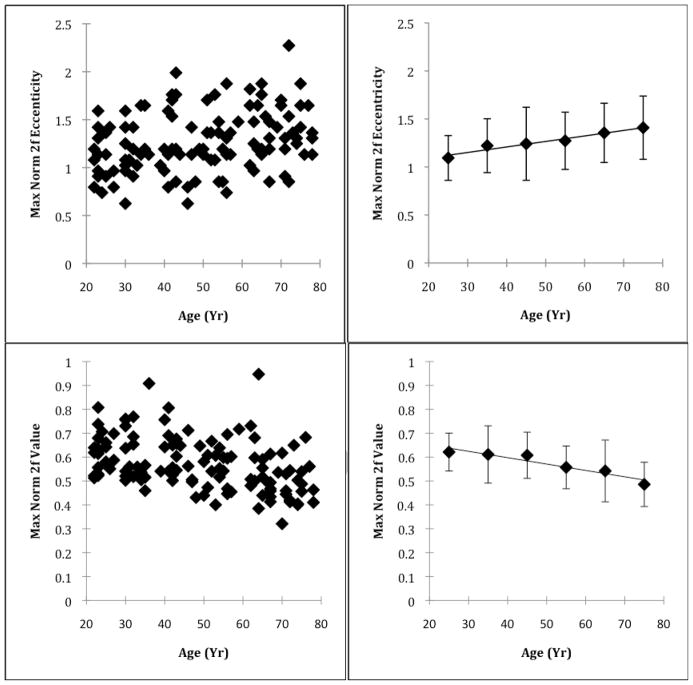
The eccentricity of the maximum of the normalized 2f component increased slightly as a function of age (Fig 3). Linear regression indicated an increased eccentricity of 0.005 degrees per year (p = 0.005, R2 = 0.066). The mean eccentricity of the maximum of the normalized 2fcomponent was 1.09 deg for subjects from the third decade and increasing to 1.41 for subjects from the eighth.
Fig 3.
Individual and grouped data showing the effect of age on the eccentricity of the maximum normalized 2f FFT component and the corresponding value. Top Left Panel- Location of peak foveal phase retardation, quantified as the eccentricity of the maximum normalized 2f FFT component, plotted as a function of age. Top Right Panel- Data grouped by decade with mean and 1 standard deviation error bars. Bottom Left Panel- Maximum value of the normalized 2f FFT component for each subject plotted as a function of age. Bottom Right Panel- Data grouped by decade with mean and 1 standard deviation error bars. The peak foveal phase retardation moves outward and the maximum value decreases with increasing age.
3.2.3 RMS error at 1.25 deg compared to RMS at the maximum of the normalized 2f eccentricity
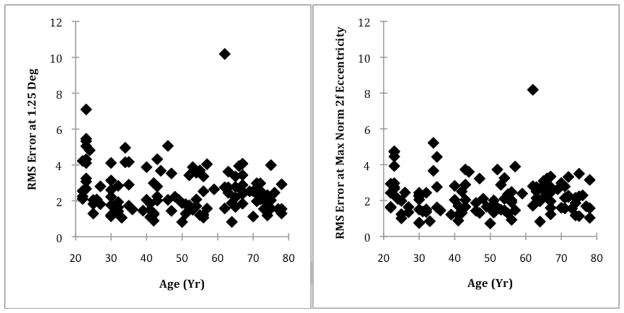
The RMS error at 1.25 deg was greater than the RMS error at the eccentricity of the maximum normalized 2f component (Fig. 4), indicating poorer 2f curve fitting when limited to just the 1.25 deg eccentricity. For all subjects, the mean RMS error for the 2f curve fitting at 1.25 deg, and the eccentricity of the maximum of the normalized 2f component were 2.60 and 2.26 grayscale units, respectively.
Fig. 4.
Regularity of macular phase retardation, as measured by the RMS of the 2f curve fitting at 1.25 deg (Left Panel) and at the eccentricity of the maximum normalized 2f component (Right Panel). The RMS of the 2f bow tie pattern decreases with age, indicating a more regular 2f pattern.
In the 2 way ANOVA comparing the RMS error values from the 2f fits, the RMS error was significantly higher at the 1.25 deg eccentricity than at the eccentricity of the maximum of the normalized 2f component (p < 0.001). The combined RMS error at the two eccentricities was not significantly different among the different age groups categorized by decade (p = 0.05). The interaction of RMS error difference*decade was significant (p = 0.045), with older subjects having a lower RMS error at the eccentricity of the maximum of 2f component than at 1.25 deg eccentricity, and younger subjects having more similar RMS errors at the two eccentricities. There was one subject with significantly higher RMS values at both the 1.25 deg eccentricity and at the eccentricity of the maximum of the normalized 2f component. This subject also had the highest coefficient a at both eccentricities. The statistics were re-evaluated after excluding this subject. The only resulting statistical change was a significant difference in the combined RMS error at the two eccentricities among the different age groups categorized by decade (p=0.032 instead of p=0.05), with older subjects having smaller RMS errors, on average.
3.2.4 Normalized 2f averaged between 1 and 1.25 deg eccentricity
Consistent with the aging effect for coefficient a at 1.25 deg eccentricity, the normalized 2f FFT component averaged between 1 and 1.25 deg eccentricity decreased as a function of age (Fig. 5). Linear regression indicated an overall decrease of 0.003 gray scale units per year (p < 0.001, R2 = 0.213). We found similar results without the averaging, which are not shown.
Fig. 5.
Foveal phase retardation between 1 and 1.25 deg eccentricity, quantified by the normalized 2f amplitude averaged between 1 and 1.25 deg eccentricity. The data indicate an overall decrease in phase retardation with increasing age.
3.2.5 AUC of the normalized 2f FFT component
The AUC of the normalized 2f FFT component from 0.25 to 2.5 deg eccentricity, used as an overall indication of phase retardation, also decreased as a function of age (Fig. 6). Linear regression indicated an overall decrease of 0.004 gray scale units per year (p < 0.001, R2 = 0.179).
Fig. 6.
The total amount of phase retardation, quantified as the area under the curve (AUC) of the normalized 2f component from 0.25 to 2.5 deg, plotted as a function of age. The data indicate an overall decrease in total phase retardation between 0.25 and 2.5 deg with increasing age.
4. Discussion
4.1 Aging changes in foveal phase retardation
Using polarization sensitive imaging, we found systematic and systematic age-related changes to the structural properties of the central macula. This imaging technique is particularly sensitive to the Henle fiber layer, which produces the dominant phase retardation signal at that location. We found that phase retardation profiles, when sampled from concentric rings centered on the fovea, change with age for both 2f curve fitting and FFT analysis. All subjects demonstrated a strong 2f or 4f macular cross pattern, consistent with the location and radial structure of the Henle fiber layer. Our findings support and further the previous modeling that was restricted to a young age group, demonstrating a systematic phase retardation pattern with a maximum 2f component within 3 deg eccentricity from the fovea (Elsner et al., 2008). The excellent agreement between the curve fitting and FFT models is consistent with a retention of the radial symmetry of the Henle fiber layer over a wide age range. The increase in phase retardation as a function of eccentricity from the central fovea outward demonstrates the thickness-dependent nature of accumulating photoreceptor axons
Constraints on modeling the changes with age in foveal phase retardation are placed by the age-dependence of all of the following: the amplitude of coefficient a of the sine curve fitting function, the normalized 2f signal from the FFT analysis, the eccentricity of the maximum normalized 2f component, the AUC of the normalized 2f FFT component, and the RMS errors of our curve fitting method. Specifically, the amplitude of the normalized 2f component, the coefficient a at 1.25 deg eccentricity, and the AUC of the normalized 2f FFT component all decreased with age, while the eccentricity of the maximum of the normalized 2f component increased with age. In addition to the decrease in phase retardation at the foveal center, the area under the curve data implies an overall decrease with age in phase retardation across the foveal region that is related to the radially symmetric Henle fibers. These results can be distinguished from mere tissue disruption leading to increased noise in the curve fitting. First, both an increase in random noise or a decrease in radial symmetry due to selective loss of cones in one location are inconsistent with lower RMS errors in older subjects than in young. For example, increased scatter, although expected in the older eyes, would lead to worse fits to the model, and larger RMS errors, but we found less phase retardation in older eyes without worse fits. Further, a random loss or rearrangement of cones, or a loss in one radial segment compared with another, would not have led to the finding for older subjects of greater phase retardation at greater eccentricities compared with locations nearer to the fovea that were associated with the highest phase retardation in younger eyes. Similarly, a systematic decrease in corneal phase retardation, depending on the phase, would lead to less overall phase retardation. There would be no change for our findings with either of the normalized metrics: the greater eccentricity for older subjects of in the peak phase retardation, nor the better fits to the model. A model incorporating only linear birefringence could potentially have no impact of corneal birefringence on the amplitude of coefficient a, but would have an effect on the phase parameter b and the offset parameter c in equation 1 (Bueno, 2004). This model cannot be fully tested using our data because we do not have an independent measure of corneal birefringence, but our previous measurements agree with the magnitude of diattenuation being relatively small (Tweitmeyer et al., 2008). Thus, regardless of the source of noise, the RMS curve fitting finding at both eccentricities, 1.25 deg and the eccentricity producing the maximum normalized 2f component, help establish that the decrease in phase retardation with age is not solely due to intrusion from other model components or noise from scattered light.
The age-dependent alterations to the birefringent properties of the central macula likely occur through two mechanisms: morphological alterations to the foveal architecture, changes in the cone photoreceptor density, or some combination of the two. Our finding could be explained by an alteration in the orientation of photoreceptor axons in the center of the macula. A more parallel alignment of the photoreceptor axons with respect to the imaging light would result in a reduction of phase retardation along that axis. A reduction in the lateral displacement of these central photoreceptor axons would cause an age-associated shallowing of the foveal pit, as demonstrated with reflectivity maps of the foveal depression (Gorrand & Delori, 1999). Changes of this nature would also be expected to cause a decrease in the centerpoint macular thickness, also consistent with recent findings of macular thinning with age (Song et al., 2010), although changes with age in macular thickness are inconsistent among laboratories. There is, on average, less photopigment in the central region of older eyes, as compared to a sharper peak found in younger ones (Eisner et al., 1987; Burns & Elsner, 1989; Swanson & Fish, 1996; Marcos et al., 1997; Elsner et al., 1998). In older subjects macular pigment, as well as cone photopigment, can decrease in density in the central fovea, as compared with adjacent but more eccentric locations. Some older subjects have annular distributions, with the central decrease consistent with the photopigment distribution, that is the decreased central area of macular pigment being slightly larger in diameter or more eccentric (Elsner et al., 1998). Macular pigment distributions can also be annular, or have a decrease in the foveal center (Elsner et al., 1998; Berendschot & van Norren, 2006; Delori et al, 2006; Kirby et al., 2010). These changes are consistent with axons being displaced outward from the fovea. These combined results imply that a disproportionate decrease in the photoreceptors in the central fovea occurs with normal aging. A reconfiguration of the fovea with aging must be consistent with not only a shallower pit but also a decrease in the photopigment and macular pigment in the central fovea and less fovea phase retardation.
This density change could occur through photoreceptor loss or through migration of the central cone photoreceptors to a slightly more peripheral location. Previous histological findings with donor tissue have concluded that there is a stable cone photoreceptor density in the central macula as a function of age, (Gao & Hollyfield, 1992; Curcio et al., 1993). However, there is a high degree of inter-individual variability in these studies, along with small sample sizes. Further, the histology data mapped the cone density with a coarser scale, compared with the retinal densitometry data for photopigment and macular pigment optical density.
The histological studies do not take into consideration axial length, which has been shown to correlate with photoreceptor density in high-resolution imaging studies, such as when using an Adaptive Optics Scanning Laser Ophthalmoscope (AOSLO) (Chui, Song, & Burns, 2008b; Li, Tiruveedhula, & Roorda, 2010). Our subject sample was not expected to have extensive variability due to axial length, since nearly all subjects were within a restricted range of refractive error, thereby allowing inter-individual differences from other sources to become evident.
A recent paper with histologically determined thicknesses of retinal layers is consistent with our finding of increasing thickness of the Henle fiber layer from the central fovea outward to about 1 mm, although this study also included the outer plexiform layer (Curcio et al., 2011). There is partial support for our finding of the Henle fiber layer having its greatest thickness at a greater eccentricity than in young subjects, although the thicknesses of the histological tissue includes neural and support elements that have to date not been assumed to contribute to phase retardation.
Focal disruptions to the smooth distribution of photopigment are macular pigment are found even in younger subjects (Elsner et al., 1998; Elsner et al., 2000). The decrease in optical density in younger, healthy subjects is more subtle and occurs prior to the ages found for early age-related macular degeneration (Elsner, Burns, & Weiter, 2002). Focal disruptions of photoreceptors or photopigment in the younger eyes would lead to poorer fits to the systematic components in the FFT analysis, consistent with our findings that younger subjects had more phase retardation on average in the central fovea, but poorer fits.
4.2 Implications of the comparison with other techniques for studying foveal cone photoreceptors
Changes with age and disease processes of cone structure and function have been studied with a variety of methods. Different techniques rely on different assumptions and probe different portions of photoreceptors, such as cone outer segment or photopigment as opposed to cell bodies or axons. In this paper, we used foveal phase retardation in the Henle fiber layer to demonstrate changes in the cone axon distribution with age. The Henle fiber layer has also been visualized in retinal cross sections in a limited number of individuals by means of intensity images in Optical Coherence Tomography (Lujan et al., 2010; Otani, Yamaguchi & Kishi, 2011), in an effort to improve layer segmentation for the outer nuclear layer. The Henle fiber layer has further been visualized with Polarization Sensitive Optical Coherence Tomography (Miura et al., 2008; Cense et al., 2009), but aging data are not yet available with either technique. SLP uses the entire foveal region to improve signal-to-noise ratio, reducing the potential to detect focal changes but providing a much larger signal than a single cross section, thereby allow quantification.
Histological studies yield mixed photoreceptor density results associated with normal aging. Two studies find no age-associated change in foveal cone density (Gao & Hollyfield, 1992; Curcio et al., 1993), although these studies included a relatively small cohort, and variability in photoreceptor density exhibits large inter-individual variability (Gao & Hollyfield, 1992; Curcio et al., 1990). In contrast, one histological study examining extrafoveal cones in a larger sample found an age-dependent loss of 0.18% per year (Panda-Jonas, Jonas, & Jakobczyk-Zmija, 1995).
When the photopigment in the cone outer segments is quantified in healthy subjects, central foveal cones of older subjects have reduced photopigment (Eisner et al., 1987; Burns & Elsner, 1989; Swanson & Fish, 1996; Elsner et al., 1998). Photopigment quantified by imaging techniques have sufficiently fine resolution to clearly demarcate focal defects and foveal peaks or lack thereof. Cones at the foveal edge have photopigment similar in optical density but different in bleaching and regeneration timecourse (Elsner et al., 1988).
In histological assessment of eyes from patients with age-related maculopathy, cone densities were concluded to be similar to that of age-matched controls (Curcio, Medeiros, & Millican, 1996; Curcio, 2001; Jackson, Owsley & Curcio, 2002). In contrast, the optical density of cone photopigment measured in eyes of living patients with early age-related macular degeneration is greatly reduced compared to that of age-matched controls (Elsner et al., 1998; Elsner et al., 2002).
Cone outer segments are the target of measurements of photoreceptor density performed with high resolution imaging techniques, such as with AOSLO. Cone outer and inner segments must guide sufficient light to be visualized and then counted. It is challenging to image the narrow central foveal cones (Chui, Song, & Burns, 2008a; Li, Tiruveedhula, & Roorda, 2010; Zou, Qi & Burns, 2011), particularly since the optical correction necessary for high resolution imaging can also be affected by aging changes that increase scattering and ocular aberrations from both anterior and posterior ocular structures (McLellan, Marcos & Burns, 2001).
Phase retardation measurements with SLO and cone density measures with AOSLO typically use near infrared light, which minimized the effects of absorption of the aging lens. Despite the use of near infrared light, AOSLO methods may still require pupil dilation to take advantage of reducing aberrations over a wide pupil to reduce the illumination level. Similarly, cone photopigment measurements can be limited to the use of long wavelength visible light, which is minimally impacted by changes to the aging lens when using measures based on differences between two eccentricities or bleached vs. fully regenerated photopigment concentrations (Elsner et al., 1988; Elsner et al., 1998). However, measurements of macular pigment or rod photoreceptors that use short wavelength light are impacted by large individual differences in the absorption of aging human lens.
While idiosyncratic differences in foveal architecture may alter the measured foveal phase retardation, SLP is unaffected by several factors that vary over time and that can be outside of experimental control and not necessarily related to aging or disease mechanisms. For instance, macular pigment density can vary with dietary supplementation (Connolly et al., 2010). Photopigment density varies with individual differences in photopigment action spectra (Elsner, Burns, & Webb, 1993; Elsner, Burns, & Weiter, 2002). AOSLO cone density measurements may be negatively impacted by media problems such as tear film and cataract that may have less effect on other techniques.
The data in our study showed inter-individual variability, as demonstrated in the linear regression models. This is consistent with both histology and high resolution imaging, which have demonstrated large inter-individual variability in cone photoreceptor density (Gao & Hollyfield, 1992; Curcio et al., 1990; Curcio et al., 1993; Li, Tiruveedhula, & Roorda, 2010). Further, the differences among aging studies and normative values in macular thickness as measured with OCT may be related to these individual differences (Song et al., 2010). The changes with aging found in foveal morphology from foveal phase retardation, cone photopigment optical density, and macular pigment all point towards differences in macular thickness or light sensitivity with aging that depend upon the exact eccentricities measured.
Foveal phase retardation may be particularly useful in separating normal aging changes in the macula from sub-clinical changes and has the potential to be particularly useful in patients with cone photoreceptor dystrophies and degenerations, where symptoms may precede early clinical signs in the central macula. However, with the decrease with normative aging in the central most fovea indicates that studies should include a somewhat larger or more eccentric region of interest to avoid confounding aging changes with those due to disease.
Foveal phase retardation was modeled using curve fitting and FFT analysis
There are normal, polarization sensitive, age-dependent changes in the macula
Overall phase retardation in the central macula decreases as a function of age
Maximum foveal phase retardation becomes more peripheral as a function of age
We have developed a normative database of polarization sensitive macular changes
Acknowledgments
This project described was support by Grant Numbers K23-EY017886 (DAV), RO1-EY007624 (AEE), RO1-EB002346 (AEE), and P30-EY019008 (SAB) from the National Eye Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Eye Institute or the National Institutes of Health. The authors would also like to acknowledge Ms. Anne Hasiuk for her assistance in preparation of this manuscript, and Mr. Joel Papay for his technical assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Dean A. VanNasdale, Email: dvannasd@indiana.edu, Indiana University, School of Optometry.
Ann E. Elsner, Email: aeelsner@indiana.edu, Indiana University, School of Optometry.
Timothy Hobbs, Email: timhobbs@indiana.edu, Indiana University, School of Optometry.
Stephen A. Burns, Email: staburns@indiana.edu, Indiana University, School of Optometry.
References
- Ahlers C, Götzinger E, Pircher M, Golbaz I, Prager F, Schütze C, Bauman B, Hitzenberger CK, Schmidt Erfurth U. Imaging of the retinal pigment epithelium in age-related macular degeneration using polarization-sensitive optical coherence tomography. Invest Ophthalmol Vis Sci. 2010;51:2149–2157. doi: 10.1167/iovs.09-3817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendschot TT, van Norren D. Macular pigment shows ringlike structures. Invest Ophthalmol Vis Sci. 2006;47:709–714. doi: 10.1167/iovs.05-0663. [DOI] [PubMed] [Google Scholar]
- Brink HB, van Blokland GJ. Birefringence of the human foveal area assessed in vivo with Mueller-matrix ellipsometry. J Opt Soc Am A. 1988;5:49–57. doi: 10.1364/josaa.5.000049. [DOI] [PubMed] [Google Scholar]
- Bueno JM. The influence of depolarization and corneal birefringence on ocular polarization. J Opt A: Pure Appl Opt. 2004;6:S91–S99. [Google Scholar]
- Bueno JM, Vohnsen B. Polarimetric high-resolution confocal scanning laser ophthalmoscope. Vision Res. 2005;45:3526–3524. doi: 10.1016/j.visres.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Bueno JM, Cookson CJ, Hunter JJ, Kisilak ML, Campbell MC. Depolarization properties of the optic nerve head: the effect of age. Ophthalmic Physiol Opt. 2009;29:247–255. doi: 10.1111/j.1475-1313.2009.00644.x. [DOI] [PubMed] [Google Scholar]
- Burns SA, Elsner AE. Localizing color vision deficiencies in eye disease. In: Drum B, Verriest G, editors. Docum Ophthal Proc Series. Kluwer Academic Publishers; Dordecht: pp. 1989pp. 167–180. [Google Scholar]
- Burns SA, Elsner AE, Mellem-Kairala MB, Simmons RB. Improved contrast of subretinal structures using polarization analysis. Invest Ophthalmol Vis Sci. 2003;44:4061–4068. doi: 10.1167/iovs.03-0124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cense B, Chen TC, Park BH, Pierce MC, de Boer JF. Thickness and birefringence of healthy retinal nerve fiber layer tissue measured with polarization sensitive optical coherence tomography. Invest Ophthalmol Vis Sci. 2004;45:2606–2612. doi: 10.1167/iovs.03-1160. [DOI] [PubMed] [Google Scholar]
- Cense B, Gao W, Brown JM, Jones SM, Jonnal RS, Muja M, Park BH, de Boer JF, Miller DT. Retinal imaging with polarization-sensitive optical coherence tomography and adaptive optics. Opt Express. 2009;17:21634–21651. doi: 10.1364/OE.17.021634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chui TY, Song H, Burns SA. Adaptive-optics imaging of human cone photoreceptor distribution. J Opt Soc Am A, Opt Image Sci Vis. 2008a;25:3021–3029. doi: 10.1364/josaa.25.003021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chui TY, Song H, Burns SA. Individual variations in human cone photoreceptor packing density: variations with refractive error. Invest Ophthalmol Vis Sci. 2008b;49:4679–4687. doi: 10.1167/iovs.08-2135. Erratum in 2009: Invest Ophthalmol Vis Sci 50, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly EE, Beatty S, Thurnham DI, Loughman J, Howard JN, Stack J, Nolan JM. Augmentation of macular pigment following supplementation with all three macular carotenoids: an exploratory study. Curr Eye Res. 2010;35:335–351. doi: 10.3109/02713680903521951. [DOI] [PubMed] [Google Scholar]
- Curcio CA. Photoreceptor topography in ageing and age-related maculopathy. Eye (Lond) 2001;15:376–383. doi: 10.1038/eye.2001.140. [DOI] [PubMed] [Google Scholar]
- Curcio CA, Medeiros NE, Millican CL. Photoreceptor loss in age-related macular degeneration. Invest Ophthalmol Vis Sci. 1996;37:1236–49. [PubMed] [Google Scholar]
- Curcio CA, Messinger JD, Sloan KR, Mitra A, McGwin G, Spaide RF. Human chorioretinal layer thicknesses measured using macula-wide high resolution histological sections. Invest Ophthalmol Vis Sci. 2011 Mar 18; doi: 10.1167/iovs.10-6377. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curcio CA, Millican CL, Allen KA, Kalina RE. Aging of the human photoreceptor mosaic: evidence for selective vulnerability of rods in central retina. Invest Ophthalmol Vis Sci. 1993;34:3278–3296. [PubMed] [Google Scholar]
- Curcio CA, Sloan KR, Kalina RE, Hendrickson AE. Human photoreceptor topography. J Comp Neurol. 1990;292:497–523. doi: 10.1002/cne.902920402. [DOI] [PubMed] [Google Scholar]
- Delori FC, Goger DG, Keilhauer C, Salvetti P, Staurenghi G. Bimodal spatial distribution of macular pigment: evidence of a gender relationship. J Opt Soc Am A Opt Image Sci Vis. 2006;23:521–538. doi: 10.1364/josaa.23.000521. [DOI] [PubMed] [Google Scholar]
- Drasdo N, Millican CL, Katholi CR, Curcio CA. The length of Henle fibers in the human retina and a model of ganglion receptive field density in the visual field. Vision Res. 2007;47:2901–2911. doi: 10.1016/j.visres.2007.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisner A, Fleming SA, Klein ML, Mauldin WM. Sensitivities in older eyes with good acuity: cross-sectional norms. Invest Ophthalmol Vis Sci. 1987;28:1824–1831. [PubMed] [Google Scholar]
- Elsner AE, Berk L, Burns SA, Rosenberg PR. Aging and human cone photopigments. J Opt Soc Am A. 1988;5:2106–2112. doi: 10.1364/josaa.5.002106. [DOI] [PubMed] [Google Scholar]
- Elsner AE, Burns SA, Beausencourt E, Weiter JJ. Foveal cone photopigment distribution: small alterations associated with macular pigment distribution. Invest Ophthalmol Vis Sci. 1998;39:2394–2404. [PubMed] [Google Scholar]
- Elsner AE, Burns SA, Webb RH. Mapping cone photopigment optical density. J Opt Soc Am A Opt Image Sci Vis. 1993;10:52–58. doi: 10.1364/josaa.10.000052. [DOI] [PubMed] [Google Scholar]
- Elsner A, Moraes L, Beausencourt E, Remky A, Weiter J, Walker J, Wing G, Burns S, Raskauskas P, Kelley L. Scanning laser reflectometry of retinal and subretinal tissues. Opt Express. 2000;6:243–250. doi: 10.1364/oe.6.000243. [DOI] [PubMed] [Google Scholar]
- Elsner AE, Burns SA, Weiter JJ. Cone photopigment in older subjects: decreased optical density in early age-related macular degeneration. J Opt Soc Am A Opt Image Sci Vis. 2002;19:215–222. doi: 10.1364/josaa.19.000215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsner AE, Weber A, Cheney MC, VanNasdale DA. Spatial distribution of macular birefringence associated with the Henle fibers. Vision Res. 2008;48:2578–2585. doi: 10.1016/j.visres.2008.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsner AE, Weber A, Cheney MC, VanNasdale DA, Miura M. Imaging polarimetry in patients with neovascular age-related macular degeneration. J Opt Soc Am A Opt Image Sci Vis. 2007;24:1468–1480. doi: 10.1364/josaa.24.001468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao H, Hollyfield JG. Aging of the human retina: differential loss of neurons and retinal pigment epithelial cells. Invest Ophthalmol Vis Sci. 1992;33:1–17. [PubMed] [Google Scholar]
- Gorrand JM, Delori FC. Reflectance and curvature of the inner limiting membrane at the foveola. J Opt Soc Am A Opt Image Sci Vis. 1999;16:1229–1237. doi: 10.1364/josaa.16.001229. [DOI] [PubMed] [Google Scholar]
- Götzinger E, Pircher M, Geitzenauer W, Ahlers C, Baumann B, Michels S, Schmidt-Erfurth U, Hitzenberger CK. Retinal pigment epithelium segmentation by polarization sensitive optical coherence tomography. Opt Express. 2008;16:16410–16422. doi: 10.1364/oe.16.016410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Götzinger E, Pircher M, Baumann B, Ahlers C, Geitzenauer W, Schmidt-Erfurth U, Hitzenberger CK. Three-dimensional polarization sensitive OCT imaging and interactive display of the human retina. Opt Express. 2009;17:4151–4165. doi: 10.1364/oe.17.004151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramatikov BI, Zalloum OH, Wu YK, Hunter DG, Guyton DL. Birefringence-based eye fixation monitor with no moving parts. J Biomed Opt. 2006;11:34025. doi: 10.1117/1.2209003. [DOI] [PubMed] [Google Scholar]
- Gramatikov BI, Zalloum OH, Wu YK, Hunter DG, Guyton DL. Directional eye fixation sensor using birefringence-based foveal detection. Appl Opt. 2007;46:1809–1818. doi: 10.1364/ao.46.001809. [DOI] [PubMed] [Google Scholar]
- Huang XR, Knighton RW. Theoretical model of the polarization properties of the retinal nerve fiber layer in reflection. Appl Opt. 2003;42:5726–5736. doi: 10.1364/ao.42.005726. [DOI] [PubMed] [Google Scholar]
- Hunter DG, Nassif DS, Piskun NV, Winsor R, Gramatikov BI, Guyton DL. Pediatric Vision Screener 1: instrument design and operation. J Biomed Opt. 2004;9:1363–1368. doi: 10.1117/1.1805560. [DOI] [PubMed] [Google Scholar]
- Hunter DG, Sandruck JC, Sau S, Nassif D, Guyton DL. Mathematical modeling of retinal birefringence scanning. J Opt Soc Am A Opt Image Sci Vis. 1999;16:2103–2111. doi: 10.1364/josaa.16.002103. [DOI] [PubMed] [Google Scholar]
- Hunter DG, Shah AS, Sau S, Nassif D, Guyton DL. Automated detection of ocular alignment with binocular retinal birefringence scanning. Appl Opt. 2003;42:3047–3053. doi: 10.1364/ao.42.003047. [DOI] [PubMed] [Google Scholar]
- Jackson GR, Owsley C, Curcio CA. Photoreceptor degeneration and dysfunction in aging and age-related maculopathy. Ageing Res Rev. 2002;1:381–396. doi: 10.1016/s1568-1637(02)00007-7. [DOI] [PubMed] [Google Scholar]
- Kirby ML, Beatty S, Loane E, Akkali MC, Connolly EE, Stack J, Nolan JM. A central dip in the macular pigment spatial profile is associated with age and smoking. Invest Ophthalmol Vis Sci. 2010;51:6722–6728. doi: 10.1167/iovs.10-5344. [DOI] [PubMed] [Google Scholar]
- Knighton RW, Huang XR. Linear birefringence of the central human cornea. Invest Ophthalmol Vis Sci. 2002;43:82–86. [PubMed] [Google Scholar]
- Knighton RW, Huang XR, Cavuoto LA. Corneal birefringence mapped by scanning laser polarimetry. Opt Express. 2008;16:13738–13751. doi: 10.1364/oe.16.013738. [DOI] [PubMed] [Google Scholar]
- Li KY, Tiruveedhula P, Roorda A. Intersubject variability of foveal cone photoreceptor density in relation to eye length. Invest Ophthalmol Vis Sci. 2010;51:6858–6867. doi: 10.1167/iovs.10-5499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lujan BJ, Roorda A, Knighton RW, Carroll J. Revealing Henle's fiber layer using Spectral Domain Optical Coherence tomography. Invest Ophthalmol Vis Sci. 2010;52:1486–1492. doi: 10.1167/iovs.10-5946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcos S, Tornow RP, Elsner AE, Navarro R. Foveal cone spacing and cone photopigment density difference: objective measurements in the same subjects. Vision Res. 1997;37:1909–15. doi: 10.1016/s0042-6989(96)00295-7. [DOI] [PubMed] [Google Scholar]
- McLellan JS, Marcos S, Burns SA. Age-related changes in monochromatic wave aberrations of the human eye. Invest Ophthalmol Vis Sci. 2001;42:1390–1395. [PubMed] [Google Scholar]
- Mellem-Kairala MB, Elsner AE, Weber A, Simmons RB, Burns SA. Improved contrast of peripapillary hyperpigmentation using polarization analysis. Invest Ophthalmol Vis Sci. 2005;46:1099–1106. doi: 10.1167/iovs.04-0574. [DOI] [PubMed] [Google Scholar]
- Miura M, Elsner AE, Weber A, Cheney MC, Osako M, Usui M, Iwasaki T. Imaging polarimetry in central serous chorioretinopathy. Am J Ophthalmol. 2005;140:1014–1019. doi: 10.1016/j.ajo.2005.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura M, Elsner AE, Cheney MC, Usui M, Iwasaki T. Imaging polarimetry and retinal blood vessel quantification at the epiretinal membrane. J Opt Soc Am A Opt Image Sci Vis. 2007;24:1431–1437. doi: 10.1364/josaa.24.001431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura M, Yamanari M, Iwasaki T, Elsner AE, Makita S, Yatagai T, Yasuno Y. Imaging polarimetry in age-related macular degeneration. Invest Ophthalmol Vis Sci. 2008;49:2661–2667. doi: 10.1167/iovs.07-0501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naoun OK, Dorr VL, Allé P, Sablon JC, Benoit AM. Exploration of the retinal nerve fiber layer thickness by measurement of the linear dichroism. Appl Optics. 2005;44:7074–7082. doi: 10.1364/ao.44.007074. [DOI] [PubMed] [Google Scholar]
- Nassif D, Gramatikov B, Guyton D, Hunter D. Society of Photo-optical Instrumentation Engineers. Pediatric vision screening using binocular retinal birefringence scanning. In: Manns F, Soderberg PG, Ho A, editors. Ophthalmic technologies; 25–26 January 2003; San Jose, California. Proceedings of SPIE; 4951. SPIE; Bellingham, Wash: 2003. pp. 9–20. [Google Scholar]
- Otani T, Yamaguchi Y, Kishi S. Improved visualization of Henle fiber layer by changing the measurement beam angle on optical coherence tomography. Retina. 2011;31:497–501. doi: 10.1097/IAE.0b013e3181ed8dae. [DOI] [PubMed] [Google Scholar]
- Panda-Jonas S, Jonas JB, Jakobczyk-Zmija M. Retinal photoreceptor density decreases with age. Ophthalmology. 1995;102:1853–1859. doi: 10.1016/s0161-6420(95)30784-1. [DOI] [PubMed] [Google Scholar]
- Song H, Zhao Y, Qi X, Chui YT, Burns SA. Stokes vector analysis of adaptive optics images of the retina. Opt Lett. 2008;33:137–139. doi: 10.1364/ol.33.000137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song WK, Lee SC, Lee ES, Kim CY, Kim SS. Macular thickness variations with sex, age, and axial length in healthy subjects: a spectral domain-optical coherence tomography study. Invest Ophthalmol Vis Sci. 2010;51:3913–3918. doi: 10.1167/iovs.09-4189. [DOI] [PubMed] [Google Scholar]
- Swanson WH, Fish GE. Age-related changes in the color-match-area effect. Vision Res. 1996;36:2079–2085. doi: 10.1016/0042-6989(95)00280-4. [DOI] [PubMed] [Google Scholar]
- Twietmeyer KM, Chipman RA, Elsner AE, Zhao Y, VanNasdale D. Mueller matrix retinal imager with optimized polarization conditions. Opt Express. 2008;16:21339–21354. doi: 10.1364/oe.16.021339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Blokland GJ. Ellipsometry of the human retina in vivo: preservation of polarization. J Opt Soc Am A. 1985;2:72–75. doi: 10.1364/josaa.2.000072. [DOI] [PubMed] [Google Scholar]
- VanNasdale DA, Elsner AE, Weber A, Miura M, Haggerty BP. Determination of foveal location using scanning laser polarimetry. J Vis. 2009;9:21.1–17. doi: 10.1167/9.3.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber A, Cheney M, Smithwick Q, Elsner AE. Polarimetric imaging and blood vessel quantification. Opt Express. 2004;12:5178–5190. doi: 10.1364/opex.12.005178. [DOI] [PubMed] [Google Scholar]
- Weber A, Elsner AE, Miura M, Kompa S, Cheney MC. Relationship between foveal birefringence and visual acuity in neovascular age-related macular degeneration. Eye (Lond) 2007;21:353–361. doi: 10.1038/sj.eye.6702203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamanari M, Miura M, Makita S, Yatagai T, Yasuno Y. Phase retardation measurement of retinal nerve fiber layer by polarization-sensitive spectral-domain optical coherence tomography and scanning laser polarimetry. J Biomed Opt. 2008;13:014013. doi: 10.1117/1.2841024. [DOI] [PubMed] [Google Scholar]
- Zou W, Qi X, Burns SA. Woofer-tweeter adaptive optics scanning laser ophthalmoscopic imaging based on Lagrange-multiplier damped least-squares algorithm. Biomedical Optics Express. 2011;2:1986–2004. doi: 10.1364/BOE.2.001986. [DOI] [PMC free article] [PubMed] [Google Scholar]