Abstract
This paper describes the use of magnetic levitation (MagLev) to measure the association of proteins and ligands. The method starts with diamagnetic gel beads that are functionalized covalently with small molecules (putative ligands). Binding of protein to the ligands within the bead causes a change in the density of the bead. When these beads are suspended in a paramagnetic aqueous buffer and placed between the poles of two NbFeB magnets with like poles facing, the changes in the density of the bead on binding of protein result in changes in the levitation height of the bead that can be used to quantify the amount of protein bound. This paper uses a reaction-diffusion model to examine the physical principles that determine the values of rate and equilibrium constants measured by this system, using the well-defined model system of carbonic anhydrase and aryl sulfonamides. By tuning the experimental protocol, the method is capable of quantifying either the concentration of protein in a solution, or the binding affinities of a protein to several resin-bound small molecules simultaneously. Since this method requires no electricity and only a single piece of inexpensive equipment, it may find use in situations where portability and low cost are important, such as in bioanalysis in resource-limited settings, point-of-care diagnosis, veterinary medicine, and plant pathology. It still has several practical disadvantages. Most notably, the method requires relatively long assay times and cannot be applied to large proteins (> 70 kDa), including antibodies. The design and synthesis of beads with improved characteristics (e.g., larger pore size) has the potential to resolve these problems.
INTRODUCTION
Bioassays that involve the binding of proteins to resin-bound small molecules are often used to screen for inhibitors of proteins, and to identify cellular targets of bioactive small molecules.1 On-bead binding assays are also used to determine the concentrations of specific proteins in solutions.2 Current methods for on-bead binding assays often use fluorescent or radioactive labels to quantify the binding of a receptor to its ligand.3 The installation and measurement of these labels requires access to relatively expensive equipment and materials. While these methods are very broadly useful, we believe that a low-cost, label-free alternative would be valuable for specific applications (for example, in point-of-care diagnosis, especially in resource-limited environments).4
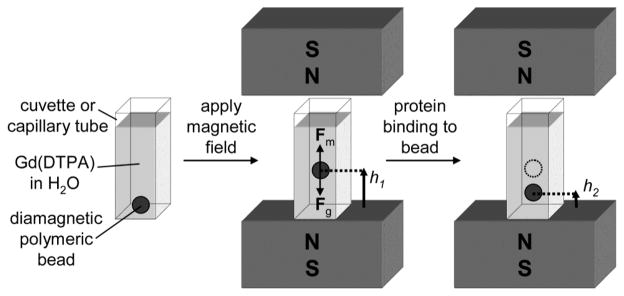
This article describes a method for measuring the association of proteins and ligands that uses magnetic levitation (MagLev).5 The method employs porous diamagnetic beads that are functionalized with covalently bound small molecules (putative ligands). We suspend these diamagnetic beads in a paramagnetic aqueous solution, which is placed in a cuvette between two permanent NdFeB magnets oriented with like poles facing each other (Figure 1). The balance of gravitational and magnetic forces acting on the diamagnetic bead causes beads within a range of densities to levitate; the density of the bead determines its equilibrium position in the magnetic field.6 With an appropriate choice of bead, binding of protein to ligands within the bead causes a change in the overall density of the bead, and results in a change in the position at which it levitates.6a
Figure 1.
Schematic representation of the device and method based on MagLev for detecting proteins binding to small molecules immobilized on a diamagnetic bead. The device consists of two 0.4 T NdFeB magnets oriented with like poles facing each other. A diamagnetic bead suspended in a paramagnetic solution levitates in the presence of the magnetic field when the gravitational force (Fg) acting on the bead is balanced by the magnetic force (Fm). Binding of protein to the bead alters its density, and thus its vertical position within the device.
This analytical method has the potential to be simple operationally. The underlying physical chemistry is, however, more complicated: it requires partitioning of protein from solution into the bead, diffusion of protein within the bead, and binding of the protein to the immobilized ligands.7 To examine the fundamental principles that determine rates and equilibrium constants as measured by this system, we have developed a model that enables us to explore all of these characteristics. This model generates data in the form of density of the bead as a function of time. We use this model to define the range of physical parameters (e.g., concentration of protein, and dissociation constant of the protein-ligand complex) over which we expect the assay to work. Detailed experimental work using a model system supports the validity of this analysis and leads to predictions about how the system may be improved.
The objective of this paper is to use physical-organic strategies to characterize a MagLev-based analytical tool for detecting protein and analyzing protein-ligand interactions, rather than to prove the generality and limits of this method in practical analysis. This study is thus aimed at describing the fundamental processes by which the system operates, and building an analytical model for it, with the goal of constructing the physical-chemical foundation for future use in bioanalysis.
Our model system consists of poly[acryloylated O,O′-bis(2-aminopropyl) polyethylene glycol] (PEGA) beads that are covalently labeled with known inhibitors of bovine carbonic anhydrase (BCA; E.C. 4.2.1.1). We levitate these beads in solutions of BCA and monitor the change in levitation height – and hence the change in density of the beads – over time, as protein binds to the beads. We explain the observed kinetics using a reaction-diffusion model, and validate this model by using it to explain the effects of varying several experimental parameters (the concentration of protein, the concentration of immobilized ligand, the protein-ligand binding constant, and the size of the beads) on the rate of protein binding to the beads and the total amount of protein that binds to the beads.
This Maglev-based technique has six attributes that make it an attractive approach for detecting protein-ligand binding events: (i) It is inexpensive (requiring only a capillary tube or a cuvette filled with a paramagnetic solution, and two NdFeB magnets that cost ~$5 – 20 each). (ii) It is easy to use: the results can be visualized with the unaided eye. (iii) It is sensitive: association or dissociation of pmoles of protein to or from an appropriate bead results in an easily measurable change in its levitation height. (iv) It is quantitative: with the correct orientation and separation of magnets, the amount of protein bound per bead correlates linearly with the levitation height of the bead. (v) It can be multiplexed, and offers a method for comparing binding constants of different ligands. (vi) It enables monitoring of association and dissociation of proteins to and from beads in real time.
The technique, however, has at least five characteristics that are either of uncertain value, or are limitations: (i) The detection is carried out in non-physiological medium containing a non-natural ion at moderate ionic strength (e.g., 300 mM chelated gadolinium, 6 mM phosphate, pH 7.4).8 (ii) The assay requires at least one ligand (with Kd < 1 mM) that can be attached covalently to the diamagnetic bead. (iii) The bead must be different in density from the protein, so that the association of protein and ligand in the bead results in a change in the average density of the bead. (iv) Mass transport (i.e., diffusion) of protein through the gel-based bead is rate-limiting; measurement of protein-ligand on- and off-rates is, therefore, not possible. (v) The effective pore size of the gel must be sufficiently large to allow protein in solution to partition into the bead to a concentration that produces a perceptible change in density.
Other techniques may also be used to detect protein binding to solid supports directly (e.g., quartz microbalances,9 cantilevers,10 force transduction,11 conductance modification,12 surface plasmon resonance,13 and other optical methods). These techniques, however, certainly require electricity, and also often require sophisticated laboratory equipment. We believe that using MagLev to monitor protein-ligand binding may, after further development, find use in several situations requiring biochemical analysis, including: (i) in the developing world, where access to electricity is not guaranteed, (ii) in point-of-care settings, where a small and simple solution is desirable, and (iii) in applications for other in-the-field settings where simplicity may be important (e.g., veterinary or plant pathology, forensics, food quality, and other types of chemical analysis). MagLev-based binding assays may also find use in protein-ligand binding assays in drug development and biochemistry, where resin-bound small molecules are often used to identify inhibitors of proteins, or as a research tool to aid in identifying the cellular targets of small molecules.
EXPERIMENTAL DESIGN
Design of the Device
We used a device we described previously; it consists of two commercial NdFeB magnets (50 × 50 × 25 mm) positioned with like poles facing towards each other, 45 mm apart.6 In this configuration of magnets, Eqn. 1 describes the vertical position of the levitating bead (h), and indicates that the position correlates linearly with the density of the bead (ρbead).
| (1) |
In this equation, ρbead and ρm, (both kg·m−3) and χbead and χm (both unitless) are the densities and the magnetic susceptibilities of the bead and the paramagnetic medium, respectively; g is the acceleration due to gravity (m·s−2), μ0 is the magnetic permeability of free space (N·A−2), d is the distance between the magnets (m), and B0 is the magnitude of the magnetic field at the surface of the magnets (T).
Choice of the Paramagnetic Fluid
We chose to use buffered aqueous solutions of disodium gadolinium (III) diethyl-lenetriaminepentaacetic acid (2Na+·Gd(DTPA)2−) as the medium for levitation. Gd(DTPA) is a relatively low-cost ($μ/g), commercially available, water-soluble MRI contrast agent with high magnetic susceptibility. The complex is non-denaturing to many proteins, and has a stability constant of 1017.7 M−1 in aqueous solutions at pH 7.4.14,15 Adjusting the concentration of the paramagnetic ion tunes the dynamic range and sensitivity of the assay. Higher concentrations of the paramagnetic ion increase the dynamic range of the assay; lower concentrations increase the sensitivity.6c The absolute range can also be adjusted by addition of a diamagnetic material with higher or lower density than the solution (e.g., sucrose or ethanol, respectively).6c
The experiments described in this paper can be conveniently performed in 300-mM solutions of Gd(DTPA) in phosphate-buffered saline (1100 mOsm·kg−1). We quantified the magnetic susceptibility (|χbead − χm| ≅ χm = 8.400·10−5) and density (ρm = 1.099 g·mL−1) of this levitation buffer using density standard beads (see Supporting Information).6c We used two magnets separated by 45 mm in an anti-Helmholtz configuration. In this configuration the magnetic field strength was 0.38 T at the surface of the magnets; this value provided a dynamic range in density of 1.056 – 1.143 g·mL−1.
We used a ruler with a millimeter scale to measure the distance from the bottom magnet to a levitating bead (i.e., the levitation height of the bead). Using a digital camera outfitted with a macro lens, we could measure this distance with an uncertainty of ±0.1 mm; measuring the levitation height with the unaided eye increased this uncertainty to ±0.3 mm. In this study, the greatest source of uncertainty in calculating the density of a bead from the levitation height of that bead is the measurement of its levitation height. Using a camera, we could, therefore, measure the change in density of a bead with an uncertainty of ±0.0002 g·cm−3; without the camera the uncertainty increased to ±0.0006 g·cm−3.
Choice of Model Protein-Ligand System
We defined the basic biophysical chemistry of protein binding using bovine carbonic anhydrase (BCA) as a model system16 because: (i) BCA is inexpensive and commercially available. (ii) Numerous inhibitors of BCA are known; many are commercially available, and have well-characterized binding constants. Many inhibitors of CA contain aryl sulfonamides, which bind to the active site Zn(II) ion as anionic ligands, and several of the reported inhibitors can be covalently attached to the polymeric support using standard coupling chemistry. (iii) BCA is a small protein (~ 30 kDa) and will diffuse in and out of the PEGA beads (vide supra) used in this study. (iv) BCA has an exceptionally stable tertiary structure,16 and is not adversely affected by the levitation media. (v) There is extensive background on the use of carbonic anhydrase in physical organic studies of protein binding.16 In particular values of Kd, kon, and koff, are known for a number of ligands.
Choice of Solid Support (Resin)
We used commercially available poly[acryloylated O,O′-bis(2-aminopropyl) polyethylene glycol] (PEGA) beads for this study (300–500 μm diameter in water).17 This resin is synthesized from 1900 MW PEG. These beads present amine functionality (0.2 mmol·g−1); this functional group makes chemical modification straightforward. In addition, previous studies have demonstrated that PEGA beads resist non-specific adsorption of proteins.18–21 This combination of properties has resulted in their widespread use for applications including: the identification of target proteins of resin-bound small molecules;18 the screening of libraries of inhibitors;19 the synthesis of peptides;20 and the covalent immobilization of proteins.21
The density of PEGA beads (ρPEGA ≈ 1.07 g·cm−3) is significantly different from the density of the protein (ρprotein ≈ 1.3–1.5 g·cm−3).22 This difference in density is required if binding of protein to the bead is to cause a usefully quantifiable change in the overall density of the bead.23
The main disadvantage of these commercial PEGA beads is that their small pores (as a cross-linked acrylamide gel) slow the mass transport of proteins into and through the interior of the bead, and excludes proteins with molecular weight greater than ~ 40–70 kDa.24 We used fluorescein-labeled BCA (FITC-BCA) to estimate both the diffusion coefficient of BCA in PEGA beads (Dbead ~ 5 × 10−13 m2·s−1) and the partition coefficient of BCA between the beads and solution (Kbead/sol ~ 0.4, see the supporting information). This value for the diffusion coefficient of BCA within the bead agrees well with data from the literature,25 and is approximately two orders of magnitude slower than the diffusion coefficient in water (~ 9 × 10−11 m2·s−1).26
Unmodified PEGA beads are also difficult to visualize during levitation because their refractive index is close to that of the solution. To improve the visibility of these beads, we functionalized a small portion of the amines on them with dyes (e.g., by reaction with the isothiocyanates of rhodamine, malachite green, and 7-dimethylamino-4-methylcoumarin). These modifications make the beads easily visible under ambient or UV light.
Model for Quantifying the Amount of Protein Bound Per Bead with MagLev
Using Eqn. 1, we derived Eqn. 2 to correlate changes in the amount of protein bound to the beads and changes in the levitation height of the bead (Δh, m).
| (2) |
The change in density, ρbead,p − ρbead, is proportional to the difference in the amount of protein present in the bead, after displacing an equivalent volume of the buffer solution out of the bead (Eqn. 3). Here, [P] is the concentration of protein within the bead (M), MWprotein (g·mol−1) and Vprotein (m3) are the molecular weight and volume of a protein molecule, NA (mol−1) is the Avogadro constant, and ρsol (kg·m−3) is the density of the solution. Using this relationship, Δh can be expressed linearly in terms of [P] (Eqn. 4).
| (3) |
| (4) |
BCA has a molecular weight of 29.1 kg·mol−1 and a volume of 3 × 10−26 m3 (the protein is assumed to be a sphere with radius ~ 20 Å).27 Eqn. 4, therefore, predicts that, under our standard levitation conditions, a 1-mM increase in the concentration of protein within a bead will result in a 5-mm decrease in levitation height. Experimentally, we obtained a similar value (Δh/[P] = −8.6 mm/mM, see Supporting Information); the difference between these experimental and theoretical values is likely due to a discrepancy between the assumed and actual volume of the protein, Vprotein, and/or to inaccuracies in measurements of the volume of the beads.
Model for Kinetic Analysis of Binding
MagLev enables the detection of a change in density that occurs when a soluble protein associates with or dissociates from a ligand that is covalently immobilized on a gel or solid support (provided that there is a difference in density between the protein and the gel/solid support). We model the binding of protein to ligands immobilized in a gel matrix by a three-step process (Figure 2A): (i) partitioning of the protein from solution to the gel (thereby displacing an equivalent volume of buffer solution from the bead into the bulk solution), (ii) diffusion of protein within the gel, (iii) binding and unbinding of protein to the ligands immobilized in the gel.
Figure 2.
Reaction-diffusion model describing the binding of protein from solution to ligands immobilized in a gel bead. (A) The model consists of three distinct steps: (i) partitioning of the protein into the bead, (ii) diffusion within the bead, and (iii) binding of protein to the ligand immobilized on the bead. (B) In a diffusion-limited process (fast/instantaneous reaction), reaction only occurs at the propagating front, lF, when the flux of protein (before the front) encounters the unconsumed ligands at the front. This approximation of the diffusion-limited process allows us to derive a simplified characteristic time, τ, for the reaction-diffusion process.
Before each experiment, the gel beads are first equilibrated with a buffered solution of Gd(DTPA). Using a magnetic susceptibility balance, we found that the magnetic susceptibility of these equilibrated beads is similar to the magnetic susceptibility of the buffer; this observation indicates that the concentration of Gd(DTPA) in solution is approximately the same both inside and outside the bead (see Supporting Information). At the beginning of each experiment (t = 0), the beads are transferred to a solution of protein dissolved in the same Gd(DTPA) buffer. The process that follows, involving protein diffusing into the beads and binding to the ligands immobilized there, can be described mathematically as follows.
Sulfonamide 1, when bound to resin, is expected to bind tightly to BCA (the Kd of an analogous ligand in solution is 0.7 μM, see Supporting Information). Sulfonamide 2 should not associate measurably with BCA;16 this functionalized bead serves as a control. The PEGA beads we used have a density of amine groups of 0.2 mmol·g−1 (when dry); this value gives a final concentration of ligand within the bead of 1 – 10 mM (when swollen in water).
The partitioning of the protein between the bead and the solution is described by the partition coefficient, Kbead/sol (Eqn. 5), where denotes the concentration of proteins at the external boundary of the bead and [P]sol denotes the concentration of protein in the bulk solution. Once inside the bead, the protein, Pbead, diffuses toward the center of the bead, reacting with the immobilized ligands, *L, to form protein-ligand complexes, *PL, according to Eqn. 6 (throughout this text, * is used to indicate a species immobilized on the gel).
| (5) |
| (6) |
Together, the dynamics of all these three steps can be expressed mathematically in terms of a system of reaction-diffusion equations (Eqns. 7, 8).28 In these equations, r is the radial coordinate of the bead, t is time, and Dbead is the diffusion coefficient of the protein in the bead.
| (7) |
| (8) |
The initial parameters (at t = 0) are defined as follows: (i) The concentration of ligand within the bead, [*L], is defined as [*L]0. (ii) The concentration of protein in solution ([P]sol) is equal to [P]0,sol. (iii) There is no protein within the bead ([P]bead = 0). (iv) At the external boundary of the bead, the concentration of protein is described by the partition coefficient and the concentration of protein in solution (Eqn. 9).
| (9) |
The volume of the bead is assumed to be constant; therefore [*PL] = [*L]0 − [*L].29 Eqn. 10 describes the process of penetration of protein into the bead at its external boundary. In this equation, A is the surface area of the bead, r is the radial coordinate, Vsol is the volume of solution and NB is the number of beads used.
| (10) |
To correspond with our experiments, we used the following parameters for our calculations: (i) The radius of each bead, R, is 170 μm. (ii) There are 15 beads in each experiment (NB). (iii) The volume of the solution, Vsol, is 0.6 mL. (iv) The initial concentration of ligand within the bead, [*L]0 is 3.2 mM. (v) The partition coefficient, Kbead/sol, is 0.4. (vi) The diffusion coefficient, Dbead, is ~10–12 m2·s−1, as observed in a previous study and confirmed experimentally by us (see Supporting Information).25 Solving this system of equations using a finite-difference method30 in spherical coordinates (implemented in Matlab), gives the concentration profiles of protein, ligand and bound protein-ligand complex with respect to both space and time. Integrating the concentration profile of bound protein-ligand throughout the bead gives the total amount of protein-ligand complex in the bead, nPL (Eqn. 11).31
| (11) |
Experimentally, we determined that the change in levitation height, Δh (mm), is proportional to nPL (mmol) and inversely proportional to the volume of the bead, Vbead (L) according to the relationship Δh = −8.6nPL/Vbead (see Supporting Information; Eqn. 4 provides a theoretical approximation of this relationship).
The Characteristic Time, τ, of the Reaction-Diffusion Process
We describe here our derivation of a characteristic time parameter, τ, which describes the time required for the reaction-diffusion process to reach equilibrium; we begin by proving that this process is diffusion-limited. Eqn. 12 describes the characteristic time for the binding of protein to ligands within a bead, τrxn. In this expression, kon (M−1s−1) is the reaction rate constant and [P]bead is a characteristic concentration of protein in the bead; this concentration can be represented by the product of the partition coefficient, Kbead/sol, and the initial concentration of protein in the solution, [P]0,sol. Based on the known values of kon (~ 105 M−1s−1)16, Kbead/sol (0.4), and [P]0,sol (~100 μM), the characteristic time (τrxn) for the forward reaction is, therefore, ~ 0.25 s. Eqn. 13 describes the characteristic time for diffusion of the protein within the bead (τdiff).
| (12) |
| (13) |
Given the diffusion coefficient of the protein in the bead, Dbead ~ 10−12 m2·s−1, and a bead of radius R (~170 μm), we estimate τdiff to be on the order of 8 hours. Since τdiff ≫ τrxn (8 hrs ≫ 0.25 s), the reaction-diffusion process is diffusion-limited. We, therefore, make the following two assumptions in order to derive a simple, analytical expression for the characteristic time of the reaction-diffusion process: (i) the reaction to form the protein-ligand complex is instantaneous in comparison to the rate of diffusion, and (ii) once formed, the protein-ligand complex, *PL, does not dissociate (the rate of dissociation is typically much slower than the rate of association). Given these assumptions, there exists a propagation front of the protein (Figure 2B), that is a boundary where the concentration of diffusive protein penetrating into the bead is zero. At the propagation front, the incoming flux of protein is immediately consumed to form the protein-ligand complex (Eqn. 6) according to Eqn. 14.
| (14a) |
| (14b) |
In this equation, r is the radial coordinate, AF is the cross-sectional area of the front, lF is the radial position of the front, and dlF/dt is the velocity of the propagating front. We derive an estimate of the term ∂[P]bead/∂r by considering the region before the propagating front, where the incoming protein is subject only to diffusion. In this region, we can apply a pseu-do-steady approximation to the concentration profile of diffusing protein (Eqn. 15).
| (15) |
This approximation assumes that the concentration profile of diffusing protein is established much more rapidly than the propagating front moves (this approximation is reasonable when [P]0,solKbead/sol/[*L]0 ≪ 1, as is the case in our system).32 We derive the average value <1/∂ P]bead/∂r|lF>r across the bead by solving Eqn. 15 using the following boundary conditions: at r = R, [P]bead = [P]0,solKbead/sol, and at r = lF, [P]bead = 0 (Eqn. 16).
| (16) |
For the system we describe here, the characteristic time τ of the reaction-diffusion process is proportional to the radius of the bead R over the average velocity of the propagating front, dlF/dt (Eqn. 17).32 Finally, combining Eqns. 14, 16, and 17 yields an expression that describes the characteristic time τ as a function of a number of experimental variables (Eqn. 18).
| (17) |
| (18) |
This expression indicates that the time required for the system to reach steady-state is proportional to the square of the radius of the beads, R2, the initial concentration of the ligands in the bead, [*L]0, and is inversely proportional to the diffusion coefficient, Dbead, the initial concentration of protein in solution, P0,sol and the partition coefficient, Kbead/sol. These mathematical relationships agree well with experiment (vide supra). In practice, the characteristic time τ can be derived from a plot of levitation height (h) versus time (t) by fitting the data to a first-order exponential equation (Eqn. 19), where hf and h0 are the final and initial levitation heights, respectively.
| (19) |
RESULTS AND DISCUSSION
This section outlines a detailed physical-organic study of a MagLev-based analytical tool that can be used for (i) quantifying the amount of protein bound to beads, and (ii) monitoring the kinetics and thermodynamics of association of proteins with resin-bound small molecules. We use this physical-organic study to identify the parameters that ultimately influence the function and practicality of this tool.
Unless specified otherwise, all MagLev measurements were performed in a solution of 300 mM Gd(DTPA), and 0.05% polysorbate 20, dissolved in 6-mM phosphate buffer and adjusted to pH 7.4 using sodium hydroxide (referred to throughout this text as the “standard levitation buffer”). This composition provided a buffer with an approximate match in density to that of the PEGA beads. The chosen concentration of gadolinium(III) provided a useful compromise between sensitivity and dynamic range of detection by MagLev. Addition of the non-denaturing surfactant, polysorbate 20, reduced non-specific binding of proteins to the PEGA beads, and prevented the beads from adhering to the cuvette.
MagLev provides a spectroscopy-free method of measuring the binding of protein to ligand-functionalized PEGA beads
Initially, we verified that protein would adsorb to PEGA beads only when these beads were functionalized with a small-molecule ligand that bound specifically to that protein. We reasoned that the binding of most proteins (average density ≈ 1.3–1.5 g·cm−3) to PEGA beads (density ≈ 1.07 g·cm−3) should increase the density of the beads, and result in quantifiable changes in levitation height between bound and unbound states.
Throughout these studies, we used a well-characterized system of proteins and ligands: bovine carbonic anhydrase (BCA) and derivatives of benzenesulfonamide.16 We immobilized 4-carboxybenzene sulfonamides 1 and 2 on Rhodamine-dyed PEGA beads using standard coupling chemistry (Eqn. 20, EDC = N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide, NHS = N-hydroxysuccinimide, see Supporting Information for more information).
At least one hour before each experiment, the PEGA beads were placed in a solution of the standard levitation buffer in order to insure that they equilibrated completely with this buffer. We then transferred seven to ten beads functionalized with either sulfonamide 1 or 2 into a microcuvette containing 0.6 mL of a solution of BCA in the standard levitation buffer. We observed only a very small decrease (< 0.1 mm) in the levitation height of beads functionalized with 4-dimethylsulfamoylbenzoic acid 2 after incubation with 0.33 mM BCA for 7 days. In contrast, we observed a time- and concentration-dependent change in the levitation height of beads functionalized with sulfonamide 1.
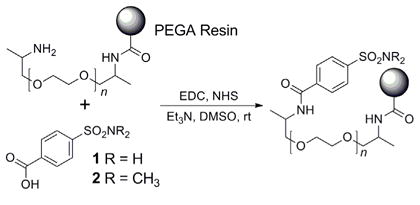 |
(20) |
We plotted the change in levitation height of beads functionalized with sulfonamide 1 (Δh, in millimeters) versus time (t, in hours) for each concentration of BCA and fit these data to our model of the reaction-diffusion process (Eqns. 7, 8). The comparison demonstrates good agreement (Figure 3A).33 We estimate the dissociation constant from the model to be Kd ~ 1.5 μM. We note that since the process of protein binding to ligands within the beads is diffusion-limited (see the Section on characteristic time for further discussion), we can only determine Kd, and not the on and off rates (koff and kon).
Figure 3.
Monitoring the association of bovine carbonic anhydrase (BCA) with 4-carboxybenzene sulfonamide (1) immobilized on PEGA beads. We levitated functionalized PEGA beads in cuvettes in the standard levitation buffer. (A) Adding BCA to the levitation media resulted in a change in levitation height (h) that depended on time, and on the concentration of protein. The figure shows the fit of the experimental plots to the estimates from the reaction-diffusion model. The reaction-diffusion model predicts that the time to reach equilibrium should be proportional to the protein concentration (equilibration is predicted be faster with higher protein concentrations). (B) We illustrate the effect of the ligand concentration within the bead on the rate of change in levitation height. The data confirm that the time to reach equilibrium is inversely proportional to the ligand concentration, as predicted by the reaction-diffusion model.
Eqn. 21 presents an alternative method of calculating the dissociation constant using the equilibrium conditions of the reaction summarized in Eqn. 6, and assuming that protein is in excess.
| (21) |
Experimentally we found that with [P]0,sol = 100 μM, [*L]0 = 3.2 mM and Kbead/sol = 0.4, the final change in height of the beads is 26.5 mm; this value indicates that the [*PL]eq is 3.08 mM (Eqn. 4). Substituting these values into Eqn. 21 gives a dissociation constant, Kd, of 1.5 μM.
These results demonstrate that this MagLev-based method provides reasonable estimates of binding constants for BCA with benzenesulfonamides, without the need for spectroscopy. The small difference between the measurements using MagLev and more conventional spectroscopic methods may be due to an increase in the protein-ligand dissociation constant as a result of immobilization of the ligand. We previously found that the observed dissociation constants of BCA with ligands in solution are ~ 10 times lower than the dissociation constants of the corresponding ligands presented on the surface of a monolayer.34
The system reaches a state of equilibrium more rapidly when higher concentrations of protein in solution and/or lower concentrations of ligand within the beads are used
Based on our derivation of the characteristic time, τ, we inferred that both increasing the concentration of protein in solution, and decreasing the concentration of ligand within the bead, should increase the rate at which the bead would reach an equilibrium concentration of protein and protein-ligand complex (τ ~ [L]0/[P]0,sol, Eqn. 18). In addition to decreasing the assay time, experimenting with these parameters would also allow us to test the validity of our model. To vary the concentration of ligand within the beads, we combined benzene sulfonamides 1 and 2 in molar ratios of 1:0, 1:2, 1:8, 1:26, and 1:80. We used these mixtures to synthesize batches of PEGA beads containing different concentrations (3.2 – 0.040 mM) of benzene sulfonamide (Eqn. 22).
 |
(22) |
We placed seven to ten of each batch of beads in a microcuvette containing a solution of 100-μM bovine carbonic anhydrase (BCA) dissolved in the standard levitation buffer, and plotted the change in levitation height (Δh, in millimeters) versus time (t, in hours) for each concentration of ligand (Figure 3B). Fitting these data to our reaction-diffusion numerical integration model (Eqns. 3, 10) revealed the expected correlations: lower concentrations of ligand within the bead resulted in smaller changes in levitation height (Δh = h0 − hf); the equilibration time was, however, inversely proportional to the concentration of ligand in the bead.
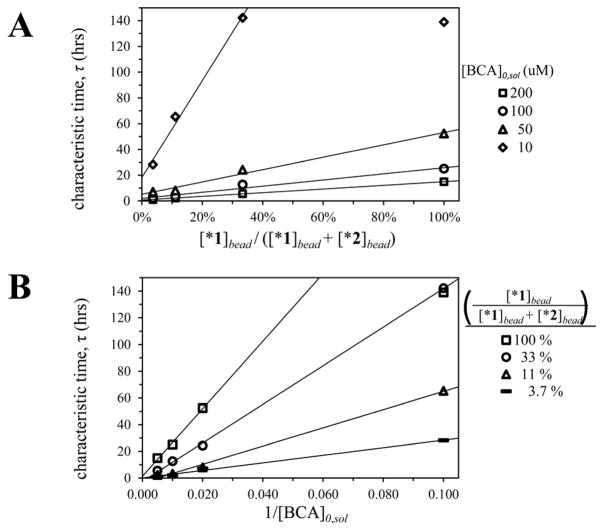
In order to verify these results further, we repeated the same experiment with several different concentrations of BCA. Each plot was fit to a first-order exponential curve (Eqn. 19) from which we derived the calculated characteristic times τ. Figure 4 illustrates the expected mathematical relationships. In Figure 4A, we plot characteristic time against the concentration of ligand 1 within the bead (τ versus [*1]bead); the data demonstrate the expected linear relationship, with the exception of the datum at 100% concentration of sulfonamide 1 and 10-μM protein.35 Similarly, Figure 4B reveals the linear relationship between the characteristic time and the inverse of the concentration of protein in solution, (1/[BCA]0,sol; again with exclusion of the datum at 100% concentration of 1 and 10-μM protein). Thus, equilibration is much faster with lower concentrations of ligand within the bead ([*L]0), and with higher concentrations of protein in solution ([P]0,sol), as predicted by both the reaction-diffusion model and our derivation of the characteristic time τ (Eqns. 10, 18).
Figure 4.
Effect of the concentration of protein in solution, and the ligand concentration within the beads, on rates of equilibration. We calculated each characteristic time, τ, by fitting a plot of levitation height versus time to Eqn. 18. The combined data substantiate our derivation of the characteristic time (Eqn. 17) by illustrating the predicted linear relationships between (A) the characteristic time τ and the concentration of ligand within the bead (expressed as the percentage of the bead functionalized with sulfonamide 1), and (B) the characteristic time τ and the reciprocal of the concentration of protein in solution (1/[BCA]0,sol).
The rate of equilibration is faster for smaller beads
PEGA beads, as supplied commercially, span a range of sizes. For our studies, beads purchased from Polymer Laboratories were reported to range in diameter from 300 – 500 microns (when swollen in water). To quantify the effect of bead size on the rate of binding of protein to ligands within the bead, we isolated the largest and smallest beads by filtering through several sizes of mesh (see Supporting Information).
We levitated eight large beads (average radius of 166 ± 5 microns) and eight small beads (average radius of 136 ± 7 microns) in a solution of 130-μM BCA dissolved in the standard levitation buffer. Figure 5 shows the comparison of the change in levitation height (Δh, in millimeters) versus time (t, in hours) for each batch of beads. When these data were fit to first-order exponential curves (Eqn. 19), the calculated characteristic times, τ, were 14.6 ± 2.7 hours for the small beads, and 26.9 ± 2.1 hours for the large beads. This ratio is in accord with our prediction of the relationship between the radius of the bead (R) and τ (τ ~ R2, Eqn. 18).
Figure 5.

Effect of the radius of the bead on the rate of binding of BCA to ligand-functionalized beads. We levitated functionalized PEGA beads in cuvettes in the presence of 130 μM BCA dissolved in the standard levitation buffer. We plot the average levitation height for eight large beads (<R> = 166 ± 5 μm), and eight small beads (<R> = 136 ± 7 μm) versus time, and show the predictions of the reaction diffusion model (the dotted and dashed lines).
MagLev enables multiple binding interactions to be monitored simultaneously
MagLev provides the basis for an on-bead assay that can measure the affinity of multiple different resin-bound small molecules for the same protein. To make it possible to differentiate resin-bound inhibitors visually, we functionalized a small portion of the available amines on PEGA beads with one of five different dyes (isothiocyanates of rhodamine, fluorescein, malachite green, eosin and 7-dimethylamino-4-methylcoumarin). Using standard coupling chemistry, we attached five different ligands (4-carboxybenzene sulfonamide, 4-(isothiocyanatomethyl) benzenesulfonamide 3-carboxybenzene sulfonamide, 3-carboxy-4-methoxybenzene sulfonamide, and 4-dimethylsulfamoylbenzoic acid) of carbonic anhydrase to the differently colored beads.
We then suspended these five color-coded beads, each functionalized with a different inhibitor of BCA, (~15 beads per inhibitor) in a microcuvette containing a solution of 100-μM BCA dissolved in the standard levitation buffer. Initially, the beads all levitate at nearly the same height (Figure 6).36 In the presence of BCA, the beads begin to sink, and begin to segregate based on binding affinities. The relative levitation height of the beads represents the relative differences in binding affinities of the ligands attached to the beads; the bead containing the ligand with the lowest dissociation constant for BCA levitates at the lowest value of h because it has more protein bound to it than the other two beads. Using Eqn. 21, we calculated the dissociation constants of the immobilized ligands from BCA. We also measured the dissociation constants of analogous ligands in solution using fluorescence (see Supporting Information). A comparison of the values measured using both methods demonstrates good agreement (Figure 6).
Figure 6.
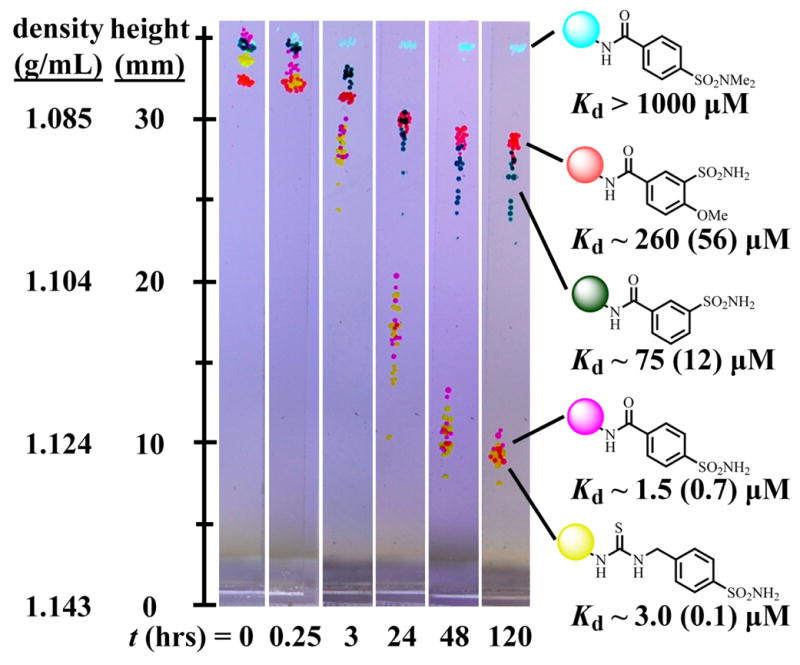
Using MagLev to measure the binding of BCA to several immobilized ligands. This figure presents a series of photographs showing changes in levitation height over time that result from incubating PEGA beads functionalized with five different inhibitors of BCA in the presence of 100-μM BCA dissolved in the standard levitation buffer. We used Eqn. 21 to calculate the dissociation constants of the immobilized ligands from BCA; also shown, in parentheses, are the dissociation constants of analogous ligands in solution from BCA (see Supporting Information).
At the beginning of the experiment, the beads form relatively tight clusters because they have equal densities. As the beads approach 50% equilibration, however, they become increasingly disperse. We hypothesize that this dispersion results from differences in the percentage of ligands that are bound to protein as a result of differences in the size of the beads or the size of the pores in the beads.6b As the beads approach their final levitation height, their dispersion in levitation heights decreases because each bead contains the same concentration of ligand, and the final equilibrium levitation height ultimately depends only on the density of the bead, not on its radius.
MagLev is a useful tool for quantifying the concentration of a specific protein
Methods for the detection of small amounts (nmol – fmol) of protein have revolutionized biotech-nology, and comprise some of the most heavily used methods for the diagnosis of disease.37 In order to adapt the MagLev-based methods described in this paper to the detection of small amounts of protein, we utilize a semi-kinetic approach. We begin by incubating a single bead in a solution of a target protein. To provide optimal detection of small amounts of protein, we fully functionalize this bead with a ligand that binds tightly to the target protein. Specifically, we use PEGA beads functionalized with sulfonamide 1 to detect BCA.
With the goal of detecting low concentrations of protein, it is beneficial to maximize the sensitivity of the system to changes in the density of the bead by performing measurements of levitation height using the lowest practical concentration of paramagnetic salt. For these measurements, we, therefore, utilize a lower concentration of Gd(DTPA) than what is present in the standard levitation buffer: 150 mM Gd(DTPA) provides a practical compromise between sensitivity and equilibration time. With this concentration of Gd(DTPA), the beads reach their equilibrium levitation height in ~ 30 minutes and we are able to differentiate between differences in density of ± 0.0004 g·cm−3. With lower concentrations of Gd(DTPA), sensitivity is increased, but the beads take significantly longer to reach their equilibrium levitation height.6c Future studies will focus on increasing the rate of adsorption of protein by using smaller beads, lower concentrations of ligand within the beads, or beads with larger pore volumes.
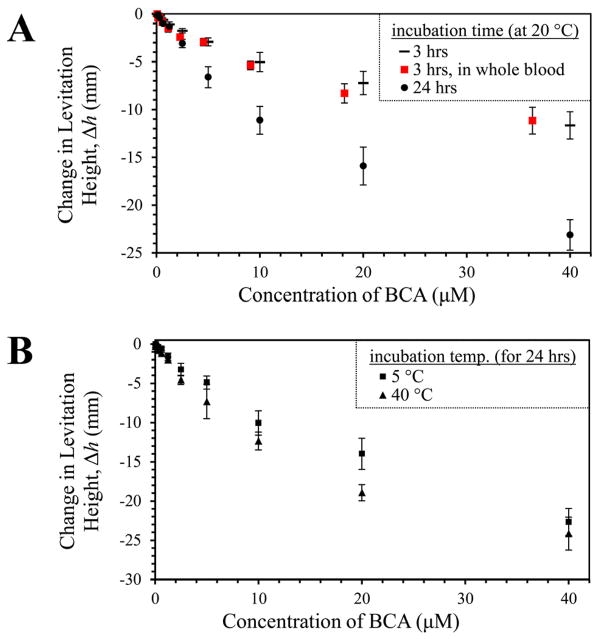
Reaching an equilibrium state at low concentrations of protein requires an impractically long time (for example, a bead functionalized with sulfonamide 1 requires more than one thousand hours to equilibrate fully with a 10-μM solution of BCA). A calibration curve, however, can easily be generated to relate the change in levitation height after a given period of time to the concentration of protein in the sample. Figure 7 demonstrates this relationship.38
Figure 7.
Detecting BCA using MagLev. For these experiments, beads were levitated in the high sensitivity levitation buffer. (A) We incubated individual beads, functionalized with sulfonamide 1, in solutions (20 μL) of BCA (40 nM – 40 μM) dissolved in 1 × PBS at room temperature (20 °C), for either 3 or 24 hours. After incubation, we transferred the beads into microcuvettes containing the high-sensitivity levitation buffer, and measured their levitation heights (in comparison to a bead that had been incubated in a solution free of BCA). We then repeated this experiment, changing the incubation media to whole blood (the beads were filtered and washed before levitation). The error bars show one standard deviation (n = 7). (B) We examined the temperature dependence of the protein detection process. Over a 24-hour period, beads that were incubated at 5 °C absorbed slightly less protein than beads that were incubated at 40 °C.
To generate the data in Figure 7A, we incubated individual beads, functionalized with sulfonamide 1, in solutions (20 μL) of BCA (40 nM – 40 μM) dissolved in 10 mM PBS at room temperature (20 °C), for either 3 or 24 hours. We then transferred these beads into a microcuvette containing a solution of 150-mM Gd(DTPA) and 200-mM sucrose dissolved in 6-mM phosphate buffer and adjusted to pH 7.4 with NaOH (referred to hereafter as the ‘high sensitivity levitation buffer’), and measured their levitation height (in comparison to the levitation height of a bead that had been incubated in a solution free of BCA). After three hours, beads that have been incubated in a 600-nM solution of BCA can be distinguished from beads that have been incubated in a solution free of BCA; after 24 hours the detection limit is lowered to 300 nM. Notably, this method requires only 20 μL of sample (the volume of blood in a typical finger prick).
The initial rate of protein absorption correlates linearly with the concentration of protein in solution (τ ~ 1/[P]0,sol, Eqn. 18); as the ligands become saturated with protein, however, the rate of net protein diffusion into the beads decreases. The result is that at short incubation times, there is an approximately linear relationship between the concentration of protein in the incubation solution and the amount of protein adsorbed on the bead, while at longer incubation times this simple correlation no longer holds true (at very long incubation times the system approaches equilibrium, where binding is described by Eqn. 21).
MagLev can be used to detect BCA in blood
This short study was intended to determine if MagLev could operate successfully starting with samples as complex as blood and serum. We incubated individual beads, functionalized with sulfonamide 1, in 20 μL aliquots of whole blood containing 2-fold dilutions of BCA (40 nM – 40 μM). After 3 hours we separated these beads from the blood by filtration through a fine mesh and rinsed them with levitation buffer. We then transferred the beads into a microcuvette containing the high sensitivity levitation buffer (described above), and measured their levitation heights (in comparison to the levitation height of a bead that had been incubated in whole blood containing no added BCA; Figure 7A). These results indicate that this method is capable of detecting a specific protein in a complex biological medium such as blood without the need for initial separation or purification steps.
The temperature of incubation has only a small influence on the reaction-diffusion process
We also examined the temperature dependence of this method of detecting protein (Figure 7B). We incubated PEGA beads, functionalized with sulfonamide 1, in solutions of BCA (40 nM – 40 μM) at two different temperatures (5 °C, 40 °C) for 24 hours. Only slightly more protein was absorbed into the beads that were incubated at the warmer temperature. The difference between the levitation heights of the beads that were incubated at these two temperatures is predicted by the inverse relationship between the characteristic time, τ, of the reaction-diffusion process and the diffusion coefficient of the protein within the bead (τ ~1/Dbead, Eqn. 18). The dependence of the diffusion coefficient, D, on temperature, T, can be approximated by the Stokes–Einstein equation (Eqn. 23), where kB is Boltzmann’s constant, η is the dynamic viscosity of the levitation media inside the bead, and R is the hydrodynamic radius of the protein inside the bead. We assume that the levitation media has a dynamic viscosity similar to that of water (η5°C = 1.519, η40°C = 0.653), and that R is independent of temperature; the ratio of Dbead,40°C and Dbead,5°C is, therefore, ~ 2.1. This value agrees qualitatively with the increased rate of the reaction-diffusion process at higher temperatures.
| (23) |
CONCLUSION
MagLev provides a new way to detect and measure specific protein-ligand interactions. Its simplicity and independence of electricity and infrastructure suggest that, with development, it has the potential to be useful in resource-limited environments. In this method, the binding of protein to ligands immobilized within a gel bead results in a change in the density of the bead. MagLev allows the density of the bead to be monitored in real time with high accuracy, and therefore provides a direct readout of the amount of protein bound to the bead.
We have developed a mathematical model of the reaction-diffusion processes that result in the binding of protein to ligands immobilized within the bead. This model provides good quantitative agreement between theory and experiment. The magnitude of the change in levitation height as a function of time depends on a number of controllable parameters including: (i) the concentration of protein in solution, (ii) the structure, concentration, and binding constant of the ligand immobilized in the bead, and (iii) the size of the bead. The rate of change in levitation height also depends on a number of factors that are more difficult to manipulate, such as: (i) the partition coefficient of the protein between the bead and the bulk solution, and (ii) the diffusion coefficient of protein within the bead. We developed Eqn. 17, which describes the dependence of the characteristic time, τ, for protein binding to ligands immobilized within gel beads, on all of the reaction parameters. This equation, therefore, allows the performance of the system to be predicted, under a variety of conditions.
Overall, the MagLev-based method for detecting protein-ligand binding has a number of significant advantages: (i) This method requires no electricity, and only a single piece of equipment. It may, therefore, find use in situations where portability and low cost are a high priority; for example, in point-of-care diagnosis, especially in resource-limited, military, and home environments, or in veterinary medicine, plant pathology, and food safety. (ii) It is easy to use; results can be visualized with the naked eye. (iii) It has the capability to monitor binding accurately in real time. This attribute provides a quantitative means of determining the concentration of a specific protein in solution. (iv) It can qualitatively distinguish the binding affinities of a protein to several resin-bound small molecules simultaneously. Using analogous procedures, MagLev should also be capable of measuring the binding of multiple proteins simultaneously to an array of resin-bound small molecules. This property should allow for the ready design of multiplexed binding assays. (v) Protein-ligand binding directly results in a change in levitation height. This method, therefore, does not require intermediate reagents, such as enzyme-linked secondary antibodies.
In its present form, this method also has several disadvantages; we summarize them briefly, but note that there are clear development paths to reduce or eliminate them. These disadvantages include: (i) The kinetics of protein-ligand binding are relatively slow (on the order of several days). This problem may potentially be resolved through the design and synthesis of beads with improved characteristics (e.g., larger pore size). (ii) This method is only applicable to ligands that are amenable to chemical immobilization on a gel support; this limitation, however, is inherent to most detection methods that occur on solid support. (iii) This method is currently not applicable to large proteins, most notably antibodies, due to the restricted pore size of the PEGA beads we used. (iv) For detection of proteins in blood or other biological samples, the gel beads must be separated from this sample (e.g. by filtration) before analysis using Maglev; this process adds time and complexity to the method.
Supplementary Material
Acknowledgments
This work was partially supported by the Bill & Melinda Gates Foundation (no. 51308), the Wyss Institute of Biologically Inspired Engineering, the U.S. Department of Energy (no. DE-FG02-00ER45852, funding used for the development of the multiplexed assays), and postdoctoral fellowships from the Damon Runyon Cancer Research Foundation (STP) and NIH (STP and NDS).
ABBREVIATIONS
- MagLev
Magnetic Levitation
- BCA
bovine carbonic anhydrase
- EDC
N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide
- NHS
N-hydroxysuccinimide
- PEGA
poly[acryloylated O,O′-bis(2-aminopropyl) polyethylene glycol]
Footnotes
ASSOCIATED CONTENT
Supporting Information Available: General methods and additional experimental information. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.(a) Cuatrecasas P. J Biol Chem. 1970;245:3059. [PubMed] [Google Scholar]; (b) Lam KS, Lebl M, Krchňák V. Chem Rev. 1997;97:411. doi: 10.1021/cr9600114. [DOI] [PubMed] [Google Scholar]; (c) Rademann J, Jung G. Science. 2000;287:1947. doi: 10.1126/science.287.5460.1947. [DOI] [PubMed] [Google Scholar]; (d) Salisbury CM, Maly DJ, Ellman JA. J Am Chem Soc. 2002;124:14868. doi: 10.1021/ja027477q. [DOI] [PubMed] [Google Scholar]; (e) Vegas A, Fuller J, Koehler AN. Chem Soc Rev. 2008;37:1385. doi: 10.1039/b703568n. [DOI] [PMC free article] [PubMed] [Google Scholar]; (f) Gault VA, McClenaghan NH. Understanding Bioanalytical Chemistry: Principles and Applications. John Wiley & Sons, Ltd; West Sussex, UK: 2009. [Google Scholar]
- 2.(a) Venn RF. Principles and Practice of Bioanalysis. Taylor & Francis; London, UK: 2000. [Google Scholar]; (b) Walker JM, Rapley R, editors. Molecular Biomethods Handbook. Humana Press; Totowa, NJ: 2008. [Google Scholar]
- 3.Stockwell BR. Nature. 2004;432:846. doi: 10.1038/nature03196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.(a) Ahn CH, Choi JW, Beaucage G, Nevin JH, Lee JB, Puntambek A, Lee JY. Proc IEEE. 2004;92:154. [Google Scholar]; (b) White-sides GM. Nature. 2006;442:368. [Google Scholar]; (c) Yager P, Edwards T, Fu E, Helton K, Nelson K, Tam MR, Weigl BH. Nature. 2006;442:412. doi: 10.1038/nature05064. [DOI] [PubMed] [Google Scholar]; (d) Chin CD, Linder V, Sia SK. Lab Chip. 2007;7:41. doi: 10.1039/b611455e. [DOI] [PubMed] [Google Scholar]; (e) Yager P, Domingo G, Gerdes J. Annu Rev Biomed Eng. 2008;10:107. doi: 10.1146/annurev.bioeng.10.061807.160524. [DOI] [PubMed] [Google Scholar]; (f) Konry T, Walt DR. J Am Chem Soc. 2009;131:13232. doi: 10.1021/ja905125b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.(a) Beaugnon E, Tournier R. Nature. 1991;349:470. [Google Scholar]; (b) Catherall AT, Eaves L, King PJ, Booth SR. Nature. 2003;422:579. doi: 10.1038/422579a. [DOI] [PubMed] [Google Scholar]; (c) Ikezoe Y, Hirota N, Nakagawa J, Kitazawa K. Nature. 1998;393:749. [Google Scholar]; (d) Kimura T, Mamada S, Yamato M. Chem Lett. 2000:1294. [Google Scholar]
- 6.(a) Winkleman A, Perez-Castillejos R, Gudiksen KL, Phillips ST, Prentiss M, Whitesides GM. Anal Chem. 2007;79:6542. doi: 10.1021/ac070500b. [DOI] [PubMed] [Google Scholar]; (b) Mirica KA, Phillips ST, Shevkoplyas SS, White-sides GM. J Am Chem Soc. 2008;130:17678. doi: 10.1021/ja8074727. [DOI] [PubMed] [Google Scholar]; (c) Mirica KA, Shevkoplyas SS, Phillips ST, Gupta M, Whitesides GM. J Am Chem Soc. 2009;131:10049. doi: 10.1021/ja900920s. [DOI] [PubMed] [Google Scholar]; (d) Mirica KA, Phillips ST, Mace CR, Whitesides GM. J Agric Food Chem. 2010;58:6565. doi: 10.1021/jf100377n. [DOI] [PubMed] [Google Scholar]; (e) Mirica KA, Ilievski F, Ellerbee AK, Shevkoplyas SS, Whitesides GM. Adv Mater. 2011;23:4134. doi: 10.1002/adma.201101917. [DOI] [PubMed] [Google Scholar]
- 7.(a) Halling PJ, Ulijn RV, Flitsch SL. Curr Opin Biotechnol. 2005;16:385. doi: 10.1016/j.copbio.2005.06.006. [DOI] [PubMed] [Google Scholar]; (b) Laurent N, Haddoub R, Flitsch SL. Trends Biotechnol. 2008;26:328. doi: 10.1016/j.tibtech.2008.03.003. [DOI] [PubMed] [Google Scholar]; (c) Schuck P, Zhao H. Methods Mol Biol. 2010;627:15. doi: 10.1007/978-1-60761-670-2_2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mammalian cells typically have intracellular ionic strengths on the order of 200–300 mM, and contain ~200 mg/mL protein, see: Storey KB. Functional Metabolism: Regulation and Adaptation. John Wiley & Sons; Hoboken, NJ: 2004. p. 403.
- 9.(a) Ebersole RC, Ward MD. J Am Chem Soc. 1988;110:8623. [Google Scholar]; (b) Rickert J, Brecht A, Gopel W. Biosens Bioelectron. 1997;12:567. doi: 10.1016/s0956-5663(96)00077-2. [DOI] [PubMed] [Google Scholar]; (c) Nishino H, Murakawa A, Mori T, Okahata Y. J Am Chem Soc. 2004;126:2264. doi: 10.1021/ja0361805. [DOI] [PubMed] [Google Scholar]; (d) Su X, Zhang J. Sens Actuators B. 2004;100:309. [Google Scholar]; (e) Muratsugu M, Ohta F, Miya Y, Hosokawa T, Kurosawa S, Kamo N, Ikeda H. Anal Chem. 1993;65:2933. doi: 10.1021/ac00068a036. [DOI] [PubMed] [Google Scholar]
- 10.(a) Fritz J, Baller MK, Lang HP, Rothuizen H, Vettiger P, Meyer E, Güntherodt H-J, Gerber Ch, Gimzewski JK. Science. 2000;288:316. doi: 10.1126/science.288.5464.316. [DOI] [PubMed] [Google Scholar]; (b) Savran CA, Knudsen SM, Ellington AD, Manalis SR. Anal Chem. 2004;76:3194. doi: 10.1021/ac049859f. [DOI] [PubMed] [Google Scholar]; (c) Burg TP, Godin M, Knudsen SM, Shen W, Carlson G, Foster JS, Babcock K, Manalis SR. Nature. 2007;446:1066. doi: 10.1038/nature05741. [DOI] [PubMed] [Google Scholar]; (d) Goeders KM, Colton JS, Bottomley LA. Chem Rev. 2008;108:522. doi: 10.1021/cr0681041. [DOI] [PubMed] [Google Scholar]; (e) Datar R, Kim S, Jeon S, Hesketh P, Manalis S, Boisen A, Thundat T. MRS Bull. 2009;34:449. [Google Scholar]
- 11.Ndieyira JW, Watari M, Barrera AD, Zhou D, Vogtli M, Batchelor M, Cooper MA, Strunz T, Horton MA, Abell C, Rayment T, Aeppli G, Mckendry RA. Nat Nanotechnol. 2008;3:691. doi: 10.1038/nnano.2008.275. [DOI] [PubMed] [Google Scholar]
- 12.Chua JH, Chee RE, Agarwal A, Wong SM, Zhang GJ. Anal Chem. 2009;81:6266. doi: 10.1021/ac901157x. [DOI] [PubMed] [Google Scholar]
- 13.(a) Schasfoort RB, Tudos AJ, editors. Handbook of Surface Plasmon Resonance. Royal Society of Chemistry; Cambridge, UK: 2008. [Google Scholar]; (b) Homola J. Chem Rev. 2008;108:462. doi: 10.1021/cr068107d. [DOI] [PubMed] [Google Scholar]; (c) Stewart ME, Anderton CR, Thompson LB, Maria J, Gray SK, Rogers JA, Nuzzo RG. Chem Rev. 2008;108:494. doi: 10.1021/cr068126n. [DOI] [PubMed] [Google Scholar]; (d) Mayer KM, Hafner JH. Chem Rev. 2011;111:3828. doi: 10.1021/cr100313v. [DOI] [PubMed] [Google Scholar]
- 14.Weinmann HJ, Brasch RC, Press WR, Wesbey GE. Am J Roentgenol. 1984;142:619. doi: 10.2214/ajr.142.3.619. [DOI] [PubMed] [Google Scholar]
- 15.Caravan P, Ellison JJ, McMurry TJ, Lauffer RB. Chem Rev. 1999;99:2293. doi: 10.1021/cr980440x. [DOI] [PubMed] [Google Scholar]
- 16.Krishnamurthy VM, Kaufman GK, Urbach AR, Gitlin I, Gudiksen KL, Weibel DB, Whitesides GM. Chem Rev. 2008;108:946. doi: 10.1021/cr050262p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.(a) Auzanneau FI, Meldal M, Bock K. J Pept Sci. 1995;1:31. doi: 10.1002/psc.310010106. [DOI] [PubMed] [Google Scholar]; (b) Renil M, Ferreras M, Delaisse JM, Foged NT, Meldal M. J Pept Sci. 1998;4:195. doi: 10.1002/(SICI)1099-1387(199805)4:3%3C195::AID-PSC141%3E3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 18.Kuramochi K, Miyano Y, Enomoto Y, Takeuchi R, Ishi K, Takakusagi Y, Saitoh T, Fukudome K, Manita D, Takeda Y, Kobayashi S, Sakaguchi K, Sugawara F. Bioconjugate Chem. 2008;19:2417. doi: 10.1021/bc8002716. [DOI] [PubMed] [Google Scholar]
- 19.(a) Meldal M, Svendsen I, Breddam K, Auzanneau FI. Proc Natl Acad Sci U S A. 1994;91:3314. doi: 10.1073/pnas.91.8.3314. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Meldal M, Svendsen I. J Chem Soc Perkin Trans 1. 1995:1591. [Google Scholar]
- 20.(a) Meldal M, Auzanneau FI, Hindsgaul O, Palcic MM. J Chem Soc, Chem Commun. 1994:1849. [Google Scholar]; (b) Renil M, Meldal M. Tetrahedron Lett. 1995;36:4647. [Google Scholar]; (c) Haddoub R, Dauner M, Stefanowicz FA, Barattini V, Laurent N, Flitsch SL. Org Biomol Chem. 2009;7:665. doi: 10.1039/b816847d. [DOI] [PubMed] [Google Scholar]
- 21.Wong LS, Thirlway J, Micklefield J. J Am Chem Soc. 2008;130:12456. doi: 10.1021/ja8030278. [DOI] [PubMed] [Google Scholar]
- 22.(a) Chick H, Martin CJ. Biochem J. 1913;7:92. doi: 10.1042/bj0070092. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Quillin ML, Matthews BW. Acta Cryst. 2000;56:791. doi: 10.1107/s090744490000679x. [DOI] [PubMed] [Google Scholar]; (c) Fischer H, Polikarpov I, Craievich AF. Protein Sci. 2004;13:2825. doi: 10.1110/ps.04688204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.It would also be possible to use beads with density greater than the density of protein. This experimental design, however, would require that the levitation media contain a diamagnetic cosolute of high density in order to match the density of the levitation media (ρm) with the density of the bead.
- 24.(a) Kress J, Zanaletti R, Amour A, Ladlow M, Frey JG, Bradley M. Chem Eur J. 2002;8:3769. doi: 10.1002/1521-3765(20020816)8:16<3769::AID-CHEM3769>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]; (b) Auzanneau FI, Meldal M, Bock K. J Pept Sci. 1995;1:31. doi: 10.1002/psc.310010106. [DOI] [PubMed] [Google Scholar]
- 25.(a) Thornton PD, McConnell G, Ulijn RV. Chem Commun. 2005:5913. doi: 10.1039/b511005j. [DOI] [PubMed] [Google Scholar]; (b) Bosma AY, Ulijn RV, McConnell G, Girkin J, Halling PJ, Flitsch SL. Chem Commun. 2003:2790. doi: 10.1039/b308078a. [DOI] [PubMed] [Google Scholar]
- 26.Tyn MT, Gusek TW. Biotech Bioeng. 1990;35:327. doi: 10.1002/bit.260350402. [DOI] [PubMed] [Google Scholar]
- 27.Gao J, Whitesides GM. Anal Chem. 1997;69:575. doi: 10.1021/ac9608073. [DOI] [PubMed] [Google Scholar]
- 28.Wei Y, Wesson PJ, Kourkine I, Grzybowski BA. Anal Chem. 2010;82:8780. doi: 10.1021/ac102055a. [DOI] [PubMed] [Google Scholar]
- 29.Previous studies have demonstrated that protein binding to PEGA beads does not significantly change the volume of the beads, see ref 25.
- 30.Morton KW, Mayers DF. Numerical Solution of Partial Differential Equations: An Introduction. Cambridge University Press; Cambridge, UK: 2005. [Google Scholar]
- 31.Although both bound and unbound protein increase the density of the bead, the influence of the unbound protein is negligible because its concentration is significantly lower than the concentration of the bound protein.
- 32.Deen WM. Analysis of Transport Phenomena. Oxford University Press; New York, NY: 1998. [Google Scholar]
- 33.The plots shown in Figure 3 are also presented in the supporting information with error bars.
- 34.Mrksich M, Grunwell JR, Whitesides GM. J Am Chem Soc. 1995;117:12009. [Google Scholar]
- 35.We monitored the levitation height of beads functionalized with 100% sulfonamide 1 in the presence of 10-μM BCA for more than 500 hours (3 weeks). Even after this extended period of time, protein-ligand binding had not yet reached its equilibrium state. This fact hindered our ability to calculate accurately the characteristic time for this system; as a result, we have excluded this datum point from further analysis.
- 36.The small variations in the initial levitation heights of the color-coded beads are likely due to differences in the densities of the beads resulting from differences in the densities of the covalently immobilized ligands, see ref 6b.
- 37.(a) Wild D, editor. The Immunoassay Handbook. Macmillan Press; Basingstoke, UK: 1994. [Google Scholar]; (b) Lost GJ. Principles & Practice of Point-of-Care Testing. Lippincott Williams & Wilkins; Philadelphia, PA: 2002. [Google Scholar]
- 38.The plot shown in Figure 7A is also presented in the supporting information with a logarithmic concentration axis.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.