Population Based Analysis of Directional Information in Serial Deformation Tensor Morphometry

Abstract

Deformation morphometry provides a sensitive approach to detecting and mapping subtle volume changes in the brain. Population based analyses of this data have been used successfully to detect characteristic changes in different neurodegenerative conditions. However, most studies have been limited to statistical mapping of the scalar volume change at each point in the brain, by evaluating the determinant of the Jacobian of the deformation field. In this paper we describe an approach to spatial normalisation and analysis of the full deformation tensor. The approach employs a spatial relocation and reorientation of tensors of each subject. Using the assumption of small changes, we use a linear modeling of effects of clinical variables on each deformation tensor component across a population. We illustrate the use of this approach by examining the pattern of significance and orientation of the volume change effects in recovery from alcohol abuse. Results show new local structure which was not apparent in the analysis of scalar volume changes.

1 Introduction

Repeated structural magnetic resonance imaging (MRI) of the brain [1], when combined with image analysis tools, is an increasingly useful tool in the study of neurodegenerative conditions [2–8, 17]. In particular, non-rigid registration based methods have been developed to map subtle geometric changes in brain anatomy, and separate true volume changes from local tissue displacements [17]. This is important in both brain development and degeneration where volume change is a key physical property of interest, whereas displacements of tissue may only be a secondary surrogate marker of tissue integrity change and collapse. In this paper we are interested in studying common patterns of volume change across a population by using accurate spatial normalisation to bring individual volume change maps into a common space. Previous studies have focused on examining the determinant of the deformation tensor at each point, which provides a scalar measure summarizing change. Such scalar data can be evaluated using univariate voxelwise statistical parametric mapping [10] to examine the relationship between local atrophy rate and variables of interest (such as diagnosis) together with other confounding variables (such as age).

Critically, these studies cannot reveal orientation specific characteristics in the pattern of volume changes and their relationship to clinical variables. For example: whether contractions associated with a particular anatomical region in a clinical condition are predominantly anterior-posterior or medial-lateral. Such characteristics may reveal changes that are related to underlying tissue properties, and on a more basic level, they may be important from a purely signal detection view point. For example: in regions where volume changes at a given point in anatomy are only well defined in one axis and are poorly defined in other directions, the determinant of the deformation tensor may be corrupted by the noise from the poorly defined directions. This may reduce the strength of the statistical relationship with clinical variables of interest. Thus, looking at modeling specific orientation components of the deformation tensor may provide a more sensitive correlation with clinical variables of interest.

In this paper we describe the basic steps used to form a multivariate linear model of the elements of the deformation tensor of anatomical change, and their relationship to clinical variables across a population of subjects. This analysis includes the process of re-orienting each subject’s deformation change tensor into a common space and then building a statistical model of the relationship between clinical variables and the elements of the deformation tensor matrix at each voxel.

2 Method

2.1 The Deformation Tensor of Anatomical Change

Given a pair of images of a subject n, using a fluid registration algorithm, we can estimate a transformation T_Δn(x_n) = x + u(x_n) that captures the anatomical changes from the earlier to the later time point. The volume changes at a given location can then be characterized by the deformation tensor [11–13]:

$${\mathbf{J}}_{\mathrm{\Delta }n}({\mathbf{x}}_n={[x_n,y_n,z_n]}^T)=\left[\frac{\partial {\mathbf{T}}_{\mathrm{\Delta }n}({\mathbf{x}}_n)}{\partial {\mathbf{x}}_n}\right]=\left[\begin{array}{ccc}\frac{\partial x_{\mathrm{\Delta }n}}{\partial x_n}& \frac{\partial x_{\mathrm{\Delta }n}}{\partial y_n}& \frac{\partial x_{\mathrm{\Delta }n}}{\partial z_n}\\ \frac{\partial y_{\mathrm{\Delta }n}}{\partial x_n}& \frac{\partial y_{\mathrm{\Delta }n}}{\partial y_n}& \frac{\partial y_{\mathrm{\Delta }n}}{\partial z_n}\\ \frac{\partial z_{\mathrm{\Delta }n}}{\partial x_n}& \frac{\partial z_{\mathrm{\Delta }n}}{\partial y_n}& \frac{\partial z_{\mathrm{\Delta }n}}{\partial z_n}\end{array}\right],$$ (1)

where the transformed coordinates at the second time point are:

$${\mathbf{x}}_{\mathrm{\Delta }n}={[x_{\mathrm{\Delta }n},y_{\mathrm{\Delta }n},z_{\mathrm{\Delta }n}]}^T={\mathbf{T}}_{\mathrm{\Delta }n}({\mathbf{x}}_n).$$ (2)

This Jacobian can be normalised by the scan interval $\frac{1}{\mathrm{\Delta }{t}_{\mathit{scan}}}$ to give the rate of deformation over time in studies where the interval varies between subjects. For a population of subjects, we can also estimate a transformation T_Rn(x_R) which maps from a location x_R in a reference anatomy to the first time point for each subject, as illustrated in figure 1. To analyze the deformation tensor matrix (1) describing the change in individual subjects in a common reference coordinate system, we need to both spatially relocate and reorient J_Δn(x_n into the reference coordinate system. Reorientation of the tensor from a locally affine transformation is achieved by using information provided by the deformation tensor of the spatially normalizing transformation, T_Rn, denoted by ${\mathbf{J}}_{Rn}({\mathbf{x}}_R)=\left[\frac{\partial {\mathbf{T}}_{Rn}({\mathbf{x}}_r)}{\partial {\mathbf{x}}_r}\right]$. We can follow a similar approach to the analysis of diffusion tensor image data [14] and apply a normalisation transformation matrix S to the subject change tensor J_Δn(x_n):

$${\mathbf{J}}_{\mathrm{\Delta }n}{({\mathbf{x}}_n)}^{\prime }=\mathbf{S}{\mathbf{J}}_{\mathrm{\Delta }n}({\mathbf{x}}_n){\mathbf{S}}^T$$ (3)

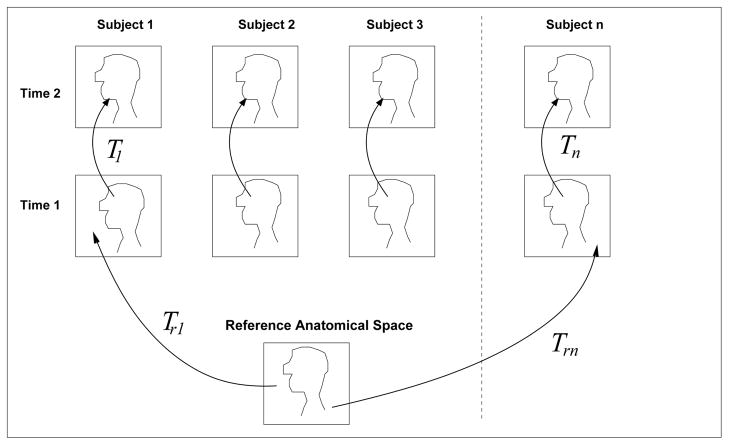
Fig. 1.

Using non-rigid registration to capture local shape differences between subjects from the transformations T_Rn. To examine common patterns across subjects, maps of shape measures derived from these transformations may be transformed and compared in the common anatomical space.

The required form of this normalisation transformation is influenced by our interests in analyzing the pointwise volume change rate across subjects. If S is a full affine transformation, then it will account for changes in the relative size and shape of this element of anatomy when mapping from reference to subject space. Thus, for a subject with a temporal lobe which is twice a big as another subject, their atrophy rate will be increased by a factor of two when mapping the change deformations into the reference space. Here we are interested only in the pointwise rate of change of a given tissue. i.e. we are investigating the equivalent rate of expansion of a tissue element at x_R across different subjects. We thus use the rigid components of the local deformation given by the decomposition [15]:

$$\mathbf{R}={({\mathbf{J}}_{Rn}{\mathbf{J}}_{Rn}^T)}^{-1/2}{\mathbf{J}}_{Rn}$$ (4)

This locally describes the reorientation of an element of tissue from the reference coordinates to the subject coordinates, without changing its local shape or size. To bring the subject change tensor back into the coordinate system of the reference anatomy we therefore set S(x_R) = R(x_R)⁻¹ and apply equation (3). In terms of common reference anatomy coordinates x_R, the deformation matrix J_Δn for subject n, in reference coordinates is then:

$${\mathbf{J}}_{\mathrm{\Delta }n}{({\mathbf{x}}_R)}^{\prime }=\mathbf{S}{\mathbf{J}}_{\mathrm{\Delta }n}({\mathbf{T}}_{Rn}({\mathbf{x}}_R)){\mathbf{S}}^T$$ (5)

2.2 Modeling of Differences in the Deformation Tensor Components

After spatial normalisation, we have a set of maps of deformation tensor matrices, the elements of which describe the rates of contraction or expansion of points of tissue in each of the three axes with respect to the three axes in the reference anatomy. We want to examine whether there is a relationship between one or more of these directions of volume change and variables of interest related to each subject (such as age or clinical criteria). This can be explored using a multivariate general linear model such that at a given voxel:

$$\mathbf{Y}({\mathbf{x}}_R)=\mathbf{XB}({\mathbf{x}}_R)+\mathbf{U}({\mathbf{x}}_R),$$ (6)

where Y(x_R) are the deformation parameters at each voxel, X_R are the clinical variables associated with each subject, B(x_R) are the parameters to be estimated, determining the strength of the linear relationships, and U are the errors. Here, in general, there are n subjects, 9 deformation variables at each voxel (the elements of the 3 × 3 deformation tensor) and p numbers of parameters to estimate. We form matrix Y from the elements of the spatially normalized Jacobian matrix, from each subject. The right hand side of the equation is conventionally divided into the variable of interest and the p′ = p − 1 confounding variables such that:

$$\begin{array}{rrrr}\hfill \mathbf{Y}({\mathbf{x}}_R)=& \hfill {\mathbf{X}}_1{\mathbf{B}}_1({\mathbf{x}}_R)+& \hfill {\mathbf{X}}_2{\mathbf{B}}_2({\mathbf{x}}_R)+& \hfill \mathbf{U}({\mathbf{x}}_R)\\ \hfill (n\times [3\times 3])& \hfill (n\times 1)(1\times [3\times 3])& \hfill (n\times p^{\prime })(p^{\prime }\times [3\times 3])& \hfill (n\times [3\times 3])\end{array}$$ (7)

Standard linear least squares methods are used to solve for B(x_R) of the full model and B₂x_R of the reduced model. Statistical inference on B is obtained by computing the Wilks Λ test statistic, where Λ is the determinant of the error sum of squares and products of the full model divided by determinant of the error sum of squares and products of the reduced model [13]. Significance and p-values are based on transforming Λ to an approximate F statistics using Rao’s approximation [16].

The final estimated model B for each voxel consists of matrix for each model parameter (age, grouping and offset). Each of these matrices holds the estimate of the increase or decrease of the rate of contraction or expansion, in elements of (1) associated with a subject variable X.

2.3 Implementation and Reduction of Spatial Normalisation Variance

For this work we have used a robust fluid based non rigid registration to map changes over time in each subject dataset [17]. The derivatives of this deformation field were then evaluated using finite differences in the coordinate system of each subject’s first time point. We then employed a fine scale B-Spline based spatial normalisation [18] regularized to prevent folding, to estimate a mapping between a single subject reference brain and the first time point scans of each individual. This deformation field, parameterized using a 1.8mm regular B-Spline lattice, was converted to a voxel displacement field and local derivatives of this were then evaluated using finite differences. One of the key factors in the population based analysis is the spatial normalisation step. The transformation between subject anatomies for spatial normalisation can be ill defined in many regions. Critically, in regions of uniform tissue (for example in uniform white matter), the local orientation may be poorly defined. In our orientation based analysis this can introduce significant unwanted variance into the serial deformation tensor morphometry data (derived from within subject registration). We have therefore used a pre-filtering step on the deformation field, using a Gaussian kernel applied to the three directional components just prior to calculation of the derviatives used to form J_Rn. (we note that this does not influence the spatial location since that uses the unfiltered deformation field). In this initial work we choose a filter size experimentally to reduce orientation variance and improve the final quality of the fitting.

2.4 Application to the Study of Recovery from Alcoholism

We applied the analysis to a study of brain volume changes in alcohol abuse and recovery. The data consisted of 24 pairs of high resolution T1W MPRAGE MRI scans of a group of subjects recovering from alcohol abuse, imaged using a 1.5T MRI scanner. The subjects were imaged twice, approximately 8 months apart. The baseline study was conducted within a week of entering treatment for alcoholism. The 24 subjects were divided into 16 consistent abstainers (188 ± 66 days since last drink), and 8 relapsers (8 ± 6) days since last drink) who failed to abstain from alcohol. Collectively they had a mean age of 48 years. We analyzed the data using deformation tensor morphometry and formed a voxelwise multivariate analysis with the grouping as the variable of interest, and age as a covariate.

3 Results

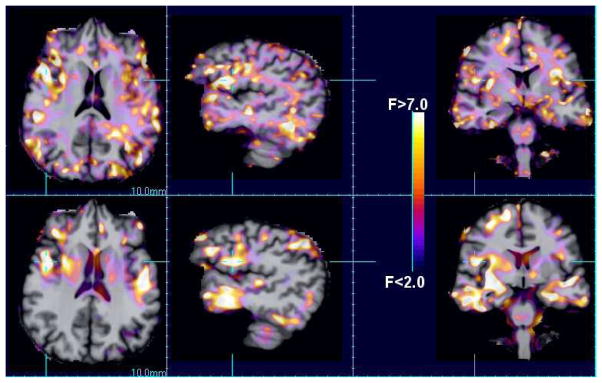
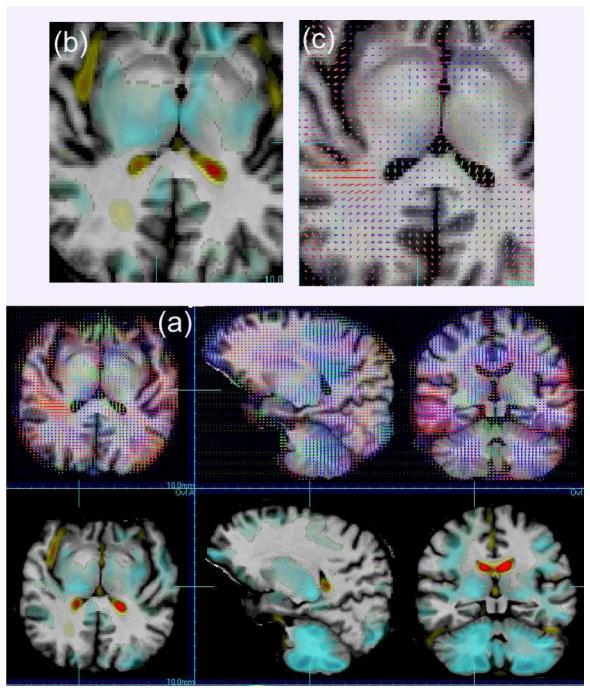
Figure 2 shows a comparison of F statistic maps of the relationship between the grouping (abstainer vs relapser) to the deformation parameters: using the Jacobian determinant (scalar) and the full deformation tensor. Larger areas of improved model fitting are shown for the model containing directional information. Figure 3 shows the corresponding maps of the estimated group effect for the scalar determinant model and the direction effects. For the directional effects, differing directional patterns of volume change are revealed in the deeper white matter and sub-cortical grey matter structures.

Fig. 2.

A comparison of the voxel F statistics showing the local quality of fits for conventional analyses using the scalar Jacobian determinant (bottom row) and the individual Jacobian matrix elements (top row).

Fig. 3.

(a) A comparison of the effect maps for the difference between groups (abstainers vs relapsers) for the scalar volume change maps (bottom) and the directional models (top). Directional effects are shown by three effect vectors whose length indicates the relative size of the effect and the colour indicates direction of effect. Enlargements of an area are shown for one slice in (b) and (c).

4 Discussion

We have described an approach to population based analysis of directional information in deformation tensor morphometry data from multi-subject serial MRI studies. The approach takes into account the reorientation of deformation tensors evaluated in subject coordinates and maps them into a common space for analysis. We then employ a multivariate linear model to examine relationships between clinical variables and directional volume changes. One step in this process is to transform deformation tensors to a common coordinate system. We use approaches derived from the transformation and analysis of diffusion tensor data. An alternative for this step is to examine the transformation of the underlying deformation fields as in [19]. However we have focussed on the deformation tensor because of the underlying interest in volume changes, rather than displacements.

By using directional information about the volume changes over time, we may reveal additional relationships with underlying tissue properties, and additionally provide an improved model fitting in regions of anatomy for which volume changes are poorly constrained, because of anatomical structure, in one or more axes. Preliminary results on an imaging study of brain changes in recovering alcoholics show both improved significance of model fits and the ability to reveal hidden directional characteristics in the volume changes over time. It is also not clear for which clinical applications this methodology will be most useful: it will certainly depend on the disease being studied and how it influences brain tissue. Our aim in this paper is simply to present the methodology. Further work is underway to examine how these directional patterns relate to the shape of regional brain anatomy and to any underlying tissue properties.