Abstract
Background
Annuloplasty ring or band implantation during surgical mitral valve repair perturbs mitral annular dimensions, dynamics and shape, which have been associated with changes in anterior mitral leaflet (AML) strain patterns and suboptimal long-term repair durability. We hypothesized that rigid rings with non-physiological 3-D shapes, but not saddle-shaped rigid rings or flexible bands, increase AML strains.
Methods and Results
Sheep had 23 radiopaque markers inserted: 7 along the anterior mitral annulus and 16 equally spaced on the AML. True-sized Edwards Cosgrove flexible, partial band (COS, n=12), rigid, complete St. Jude saddle-shaped annuloplasty ring (RSAR, n=12), Carpentier-Edwards Physio (PHYSIO, n=12), Edwards IMR ETlogix (ETL, n=11) and Edwards GeoForm (GEO, n=12) annuloplasty rings were implanted in a releasable fashion. Under acute open-chest conditions, four-dimensional marker coordinates were obtained using biplane videofluoroscopy along with hemodynamic parameters with the ring inserted and after release. Marker coordinates were triangulated and the largest maximum principal AML strains were determined during isovolumetric relaxation (IVR). No relevant changes in hemodynamics occurred. Compared to the respective Control state, strains increased significantly with RSAR, PHYSIO, ETL and GEO (0.14±0.05 vs. 0.16±0.05, p=0.024, 0.15±0.03 vs. 0.18±0.04, p=0.020, 0.11±0.05 vs. 0.14±0.05, p=0.042 and 0.13±0.05 vs. 0.16±0.05, p=0.009), but not with COS (0.15±0.05 vs. 0.15±0.04,p=0.973).
Conclusions
Regardless of 3-D shape, rigid, complete annuloplasty rings, but not a flexible, partial band, increased AML strains in the normal beating ovine heart. Clinical studies are needed to determine if annuloplasty rings affect AML strains in patients, and, if so, whether ring-induced perturbations in leaflet strain states are linked to repair failure.
Keywords: mitral valve, physiology, mitral regurgitation, surgery
INTRODUCTION
Surgical mitral valve repair most commonly includes the insertion of an annuloplasty band or ring. While bands are flexible devices that spare the anterior, fibrous portion of the mitral annulus, rings encircle the entire annulus and may be either flexible, semi-rigid or rigid. Rigid rings are available in various shapes. The most commonly used ring (Carpentier-Edwards Physio) is flat, semi-rigid and D-shaped. Recently, saddle shaped, rigid, complete annuloplasty rings have been introduced (e.g. Saint Jude Medical RSAR, Medtronic Profile 3-D or Carpentier-Edwards Physio II) in order to account for the physiological 3-D shape of the mitral annulus [1, 2]. Furthermore, rigid rings with non-physiological shapes and dimensions have been designed specifically for patients with functional/ischemic mitral regurgitation (e.g. Edwards GeoForm and IMR ETLogix). These rings aim to counteract the main determinants of functional/ischemic mitral regurgitation (i.e. mitral annular dilatation, left ventricular (LV) dilatation and papillary muscle displacement) on an annular level via their specific designs, all of which include disproportionate annular septal-lateral downsizing [3]. While some studies demonstrate that such rings may reduce mitral leaflet strains in the diseased heart [4], other studies suggest that, by perturbing the natural mitral annular saddle-shape, disease-specific or non-physiologically shaped rings may increase leaflet strains in the normal heart [5-7]. Due to these results from in vitro measurements the authors speculate that such perturbations in mitral leaflet strain patterns could be associated with impaired long-term results after mitral valve repair [5-7]. Our goal was, therefore, to assess the effects of one flexible partial band and four different, complete annuloplasty rings on anterior mitral leaflet strains in healthy, beating ovine hearts. We tested the hypothesis that rigid, complete rings with non-physiological 3-D shapes, but not saddle-shaped rigid rings or flexible partial bands, increase maximum principal strains across the anterior mitral leaflet.
METHODS
All animals received humane care in compliance with the Principles of Laboratory Animal Care formulated by the National Society for Medical Research and the Guide for Care and Use of Laboratory Animals prepared by the National Academy of Sciences and published by the National Institutes of Health (DHEW [NIH] Publication 85 to 23, revised 1985). This study was approved by the Stanford Medical Center Laboratory Research Animal Review Committee and conducted according to Stanford University policy.
Surgical Preparation
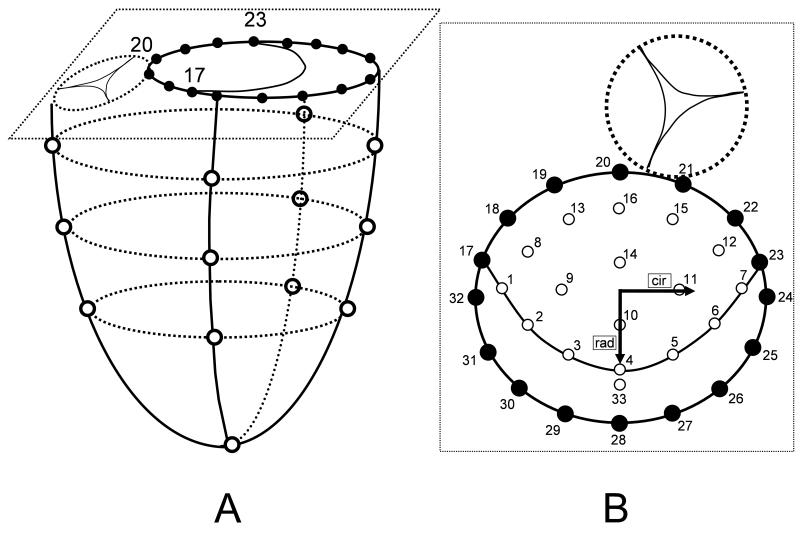
Fifty nine adult, Dorsett-hybrid, male sheep (49±5kg) were premedicated with ketamine (25mg/kg intramuscularly), anesthetized with sodium thiopental (6.8mg/kg intravenously), intubated and mechanically ventilated with inhalational isoflurane (1.0-2.5%). A left thoracotomy was performed and the heart was suspended in a pericardial cradle. Thirteen miniature radiopaque tantalum markers were surgically implanted into the sub-epicardium to silhouette the LV chamber at the intersections of two longitudinal and three crosswise meridians as shown in Figure 1A. Using cardiopulmonary bypass and cardioplegic arrest a total of 33 radiopaque tantalum markers were sewn to the following sites (Figure 1B): 16 around the mitral annulus (17-32, Fig 2A, B), 16 equally spaced on the atrial aspect of the anterior mitral leaflet (AML, 1-16, Fig 2B) and 1 on the central edge of the middle scallop of the posterior mitral leaflet (PML, 33, Fig 2B). A single tantalum loop (0.6mm ID, 1.1mm OD, 3.2 mg) was used for each leaflet marker.
Fig 1.
A: Schematic illustrating ventricular and annular marker locations. Marker #20 represents the mitral annular saddle horn marker and markers #17 and #23 the anterior and posterior commissural markers, respectively. B: Schematic magnification of a top view of the mitral valve showing annular as well as leaflet markers. Sixteen markers were placed on the mitral annulus (#17-#32), 16 markers were placed on the anterior mitral leaflet (#1-#16) and one marker was placed on the free edge of the mid part of the posterior leaflet (#33). Inset shows the radial (rad) and circumferential (cir) directions used for strain definitions.
Fig 2.
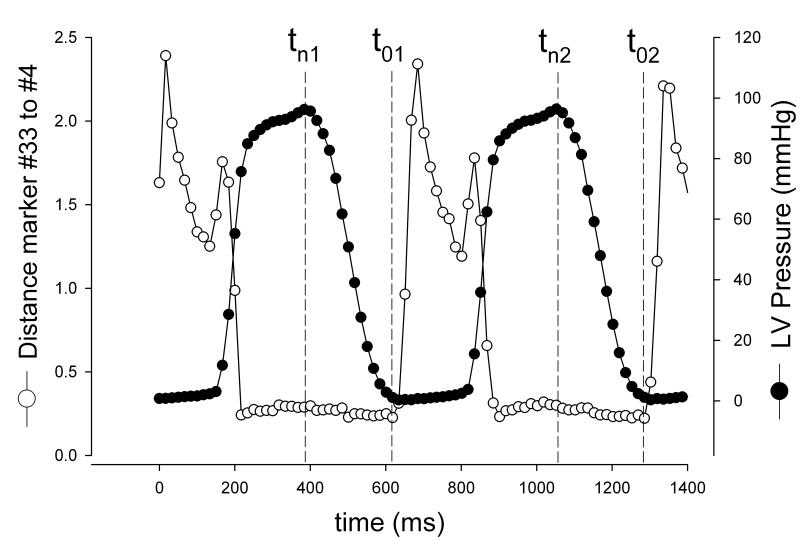
Illustration of time point definitions. Time point tn (strained state) was defined as maximum LV pressure for beat 1 (tn1) and beat 2 (tn2). Time point t0 (reference state) was defined as last time frame before mitral leaflet separation (as represented by the rapid increase in plotted curve of distances (cm) between marker #33 and #4, see Fig 1) for beat 1 (t01) and beat 2 (t02).
After marker placement, five different annuloplasty ring models, the Cosgrove-Edwards band (COS, Edwards Lifesciences, Irvine, CA, USA, n=12), St. Jude Medical rigid saddle ring (RSAR, St. Jude Medical Inc, St. Paul, MN, USA, n=12), Carpentier-Edwards Physio (PHYSIO, n=12), Edwards IMR ETlogix (ETL, n=11) and Edwards GeoForm (GEO, n=12, all three Edwards Lifesciences, Irvine, CA, USA) were implanted in a releasable fashion as described earlier [8]. In brief, the annuloplasty devices were prepared before the operation in the following manner: The middle parts of eight double-armed polyester braided sutures were stitched evenly spaced around the ring or band from the bottom to the top side using a “spring eye” needle. The resulting loops were “locked” with two polypropylene sutures. The polyester sutures were stitched equidistantly in a perpendicular direction from the ventricular to the atrial side through the mitral annulus. The annuloplasty devices were secured to the mitral annulus by tying these sutures. The “locking sutures” (polypropylene) and the drawstrings were exteriorized before closing the atrium. Ring and band sizes were determined by assessing the entire area of the anterior mitral leaflet using a sizer from Edwards Lifesciences. All annuloplasty devices were true-sized (as all animals had similarly sized leaflets, each received size 28 rings or bands). The left atrium (LA) was closed and the left circumflex artery (LCx) was encircled with a vessel loop for a parallel study [9]. Data from mitral annular and leaflet geometry using this dataset have been published earlier [8-11]. The animals were then transferred to the experimental catheterization laboratory for data acquisition under acute open-chest conditions.
Data Acquisition
Videofluoroscopic images (60 frames/sec) of all radiopaque markers were acquired using biplane videofluoroscopy (Philips Medical Systems, North America, Pleasanton, CA, USA). First, images were acquired under baseline conditions with the ring inserted (COS, RSAR, PHYSIO, ETL, GEO). Following the data acquisition under baseline conditions, 90sec of ischemia were induced, for a parallel study, by tightening the encircling LCx vessel loop with a tourniquet. Thereafter, the “locking sutures” were pulled out and the ring was lifted away from the mitral annulus towards the left atrial roof using the drawstrings. After hemodynamic values returned to baseline, a third data acquisition was performed and images were acquired under baseline conditions with the ring released (COS-CTRL, RSAR-CTRL, PHYSIO-CTRL, ETL-CTRL, GEO-CTRL). Marker coordinates from two consecutive sinus rhythm heart beats from each of the biplane views were then digitized and merged to yield the 3-D coordinates of each marker centroid in each frame using semi-automated image processing and digitization software [12]. Simultaneously, analog left ventricular pressures (LVP) as well as electrocardiogram (ECG) signals were recorded in real-time on the video images during data acquisition.
Hemodynamic Parameters and Cardiac Cycle Timing
For each beat, the end-diastolic videofluoroscopic frame was defined as the frame that coincided with the peak of the R-wave on the ECG. In order to calculate leaflet strains, a reference configuration during diastole and a deformed configuration during peak systole were determined for each beat (t0 and tn, respectively, Figure 2). When defining these configurations the goal was to quantify strains with the mitral valve closed in both configurations and maximize the LVP difference between the two time points. To identify the reference configuration, the distance between AML central edge (#4, Figure 1B) and PML edge marker (#33, Figure 1B) was plotted throughout the cardiac cycle for each animal. For each heartbeat the time point of leaflet opening was defined as the time point immediately before the AML and PML started to separate (Figure 2), thereby defining the reference state for beat 1 (t01, Figure 2) and beat 2 (t02, Figure 2). To identify the deformed configuration, LVP curves were plotted throughout the cardiac cycle. The time point of maximum LVP for each heartbeat was defined as the deformed state (tn1 and tn2, respectively, Figure 2). The embedded period between these two states closely reflects the period of isovolumetric relaxation (IVR, Figure 2). Maximum systolic dP/dt (dP/dtmax) was calculated for each beat for each animal. LV volumes (LVV) were calculated from space-filling tetrahedral fit between all LV markers at each beat at end-diastole (LVEDV), tn1, tn2, t01 and t02 (See Ref [13] for details). Changes in LVP and LVV (ΔLVP and ΔLVV, respectively) from t01 to tn1 and from t02 to tn2 were calculated as LVPtn1 – LVPt01 , LVPtn2 – LVPt02, and LVVtn1 – LVVt01 , LVVtn2 – LVVt02 ,respectively.
Mitral Annular Dimensions
At tn1, tn2, t01 and t02 distances between markers #20 and #28 and those between #32 and #24 (Figure 1B) were calculated to determine septal-lateral (S-L) and commissure-commissure (C-C) annular dimensions, respectively. Changes in mitral annular S-L and C-C dimensions (ΔS-L and ΔC-C, respectively) from t01 to tn1 and from t02 to tn2 were calculated as tn1 – t01 and tn2 – t02.
Global Maximum Principal (global εmax), Radial (global εrad) and Circumferential (global εcir) Strains
In order to determine the largest (global) maximum principal, radial and circumferential strains across the entire leaflet, the 16 AML mitral leaflet markers (#1-#16, Figure 1B) and the seven mitral annular markers (#17-#23, Figure 1B) were triangulated and 30 triangular membrane elements were generated. For each triangle, the co- and contravariant base vectors at time points t01, tn1, t02, and tn2, were calculated to determine the corresponding metric tensors and the resulting Euler-Almansi strain tensors for beats 1 and 2. The direction defined by the belly markers #9 and 11# (Figure 1B) in the deformed configuration, i.e., at times tn1 and tn2 for beat 1 and beat 2, respectively, was interpreted as the circumferential direction. The radial direction was defined orthogonal to the circumferential axis, passing through belly marker #10 (see Fig 1B). The largest projections of the Euler-Almansi strain tensor onto the circumferential and radial directions were defined as global maximum circumferential strain (global εcir) and global maximum radial strain (global εrad), respectively. These values were determined for two beats in each animal, and each state (with and without annuloplasty device implanted). The animal global maximum principal strain (global εmax) was calculated as the two-beat average for each animal and each state by solving the eigenvalue problem for the Euler-Almansi strain tensor.
Maximum Principal (εmax,), Radial (εrad ) and Circumferential (εcir ) Strains Across the Entire Anterior Mitral Leaflet
In order to provide a qualitative description of changes in strain patterns across the entire AML with and without annuloplasty device implanted, the two-beat averages of εmax, εrad and εcir values of each triangular element were calculated for each animal in each state. These values were averaged for all animals (by extrapolating constant average element strains to the individual marker positions using super-convergent patch recovery to obtain smoothly varying strain profiles) and plotted onto color mapped schematics.
Statistical Analysis
Average values of all animals in the respective groups were reported as mean ± 1 SD. All data reported for individual animals and all data used for quantitative statistical comparisons are two beat averages. Data with and without annuloplasty ring (or band) were compared using 1-way repeated-measures analysis of variance with a Holm–Sidak post hoc test (Sigmaplot 11.0, Systat Software Inc). To look at strain differences between the ring groups, maximum principal (εmax,), radial (εrad ) and circumferential (εcir ) strains with rings (COS, RSAR, PHYSIO, ETL and GEO) were compared using 1-way analysis of variance. A P value of less than .05 was considered statistically significant.
RESULTS
Heart rate, LVEDV and dP/dtmax
Group mean heart rates, LVEDVs and dP/dtmax are shown in Table 1. No significant differences were found between ring and Control states in all five groups (except for Cosgrove, where dP/dtmax was slightly higher compared to Control).
TABLE 1.
Heart rate (HR), LV end-diastolic volume (LVEDV) and dP/dtmax
| Animal no | Mean±1SD | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | HR (min−1) |
P vs. CTRL | LVEDV (ml) |
P vs. CTRL | dP/dtmax (mmHg) |
P vs. CTRL | ||
| COS- CTRL |
HR (min−1) | 89 | 104 | 124 | 103 | 87 | 76 | 114 | 90 | 100 | 113 | 85 | 94 | 98±14 | |||||
|
| |||||||||||||||||||
| LVEDV (ml) | 109 | 104 | 107 | 137 | 136 | 111 | 132 | 100 | 113 | 122 | 149 | 122 | 120±15 | ||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 979 | 1619 | 1289 | 1069 | 1853 | 1514 | 1742 | 1238 | 1478 | 1564 | 846 | 1128 | 1360±317 | ||||||
| COS | HR (min−1) | 97 | 111 | 118 | 101 | 87 | 73 | 114 | 90 | 97 | 111 | 86 | 94 | 98±13 | .914 | ||||
|
| |||||||||||||||||||
| LVEDV (ml) | 109 | 100 | 118 | 139 | 137 | 117 | 132 | 100 | 111 | 122 | 149 | 119 | 121±16 | .392 | |||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1280 | 1905 | 1309 | 1100 | 2018 | 1635 | 2196 | 1294 | 1739 | 1636 | 970 | 1240 | 1527±386 | .001 | |||||
| RSAR- CTRL |
HR (min−1) | 74 | 122 | 113 | 94 | 71 | 88 | 88 | 86 | 106 | 66 | 87 | 77 | 89±17 | |||||
|
| |||||||||||||||||||
| LVEDV (ml) | 91 | 80 | 135 | 100 | 122 | 112 | 140 | 156 | 113 | 136 | 123 | 138 | 121±22 | ||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1309 | 2296 | 1267 | 1109 | 1055 | 1794 | 1082 | 1381 | 1039 | 1232 | 708 | 1125 | 1283±409 | ||||||
| RSAR | HR (min−1) | 77 | 113 | 114 | 96 | 73 | 90 | 89 | 85 | 104 | 67 | 85 | 74 | 89±15 | .853 | ||||
|
| |||||||||||||||||||
| LVEDV (ml) | 96 | 85 | 139 | 103 | 124 | 110 | 138 | 149 | 111 | 133 | 123 | 140 | 121±20 | .714 | |||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1202 | 1817 | 1313 | 1312 | 1145 | 1692 | 1131 | 1011 | 1087 | 1111 | 682 | 1212 | 1226±297 | .340 | |||||
| PHYSIO- CTRL |
HR (min−1) | 84 | 118 | 107 | 80 | 99 | 84 | 88 | 82 | 88 | 100 | 87 | 90 | 92±12 | |||||
|
| |||||||||||||||||||
| LVEDV (ml) | 174 | 136 | 112 | 136 | 126 | 87 | 124 | 119 | 99 | 126 | 120 | 128 | 124±21 | ||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1694 | 1187 | 1307 | 841 | 1343 | 1551 | 1014 | 1116 | 1948 | 1239 | 888 | 1560 | 1307±333 | ||||||
| PHYSIO | HR (min−1) | 84 | 111 | 107 | 78 | 103 | 83 | 88 | 82 | 91 | 99 | 88 | 88 | 92±11 | .517 | ||||
|
| |||||||||||||||||||
| LVEDV (ml) | 178 | 138 | 118 | 139 | 116 | 80 | 125 | 118 | 96 | 128 | 123 | 128 | 124±24 | .934 | |||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1896 | 1186 | 1290 | 835 | 1683 | 1757 | 1166 | 1056 | 1426 | 1362 | 913 | 1606 | 1348±337 | .523 | |||||
| ETL- CTRL |
HR (min−1) | 87 | 79 | 85 | 76 | 76 | 79 | 78 | 80 | 91 | 94 | 74 | 82±6 | ||||||
|
| |||||||||||||||||||
| LVEDV (ml) | 145 | 105 | 96 | 147 | 115 | 94 | 120 | 140 | 125 | 148 | 139 | 125±20 | |||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1879 | 681 | 1630 | 1064 | 1091 | 1348 | 1085 | 821 | 728 | 1322 | 1207 | 1169±368 | |||||||
| ETL | HR (min−1) | 60 | 79 | 83 | 81 | 75 | 80 | 78 | 83 | 91 | 96 | 74 | 80±9 | .531 | |||||
|
| |||||||||||||||||||
| LVEDV (ml) | 150 | 104 | 96 | 147 | 120 | 98 | 117 | 139 | 123 | 145 | 137 | 125±20 | .833 | ||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1860 | 686 | 1591 | 1053 | 1098 | 1399 | 1073 | 874 | 772 | 1492 | 1188 | 1190±363 | .259 | ||||||
| GEO- CTRL |
HR (min−1) | 80 | 82 | 94 | 100 | 96 | 106 | 106 | 86 | 85 | 106 | 84 | 82 | 92±10 | |||||
|
| |||||||||||||||||||
| LVEDV (ml) | 89 | 113 | 120 | 114 | 122 | 131 | 131 | 107 | 113 | 95 | 109 | 130 | 114±13 | ||||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1030 | 1238 | 1298 | 1248 | 1469 | 1043 | 1163 | 1392 | 1138 | 1342 | 2221 | 1180 | 1313±315 | ||||||
| GEO | HR (min−1) | 83 | 79 | 95 | 103 | 97 | 104 | 109 | 91 | 99 | 96 | 84 | 79 | 93±10 | .492 | ||||
|
| |||||||||||||||||||
| LVEDV (ml) | 89 | 116 | 119 | 105 | 119 | 130 | 129 | 101 | 107 | 104 | 106 | 129 | 113±13 | .223 | |||||
|
| |||||||||||||||||||
| dP/dtmax (mmHg) | 1070 | 1259 | 1398 | 1144 | 1569 | 1181 | 1372 | 1509 | 1110 | 1321 | 2586 | 1131 | 1388±41 | .070 | |||||
All values from individual animals are two beat averages, COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL= Edwards IMR ETlogix, GEO=Edwards GeoForm, SD=standard deviation
LV Pressures and Volumes at Reference State (t0) and Deformed State (tn)
Table 2 shows LVPs and LVVs at t0 and tn as well as ΔLVP and ΔLVV. ΔLVP and ΔLVV are also graphically depicted in Figure 3 (top row). A significant increase in LVPs by approximately 80mmHg (note that changes in LVP and LVV (ΔLVP and ΔLVV) are described from t0 to tn, i.e. backward in time) occurred in both ring and Control states from t0 to tn, while no relevant LVV changes were observed.
TABLE 2.
Left ventricular pressures and volumes at reference state (t0) and strained state (tn)
| Animal no | Mean±1SD | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LVP (mmHg) | LVV (ml) | |||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | t0 | P vs. CTRL | tn | P vs. CTRL | Δtn-t0 | P vs. CTRL | t0 | P vs. CTRL | tn | P vs. CTRL | Δtn-t0 | P vs. CTRL | |||
| COS- CTRL |
LVP (mmHg) |
t0 | 20 | 10 | 45 | 17 | 24 | 12 | 15 | 9 | 7 | 6 | 18 | 7 | 16±11 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 87 | 97 | 82 | 105 | 109 | 100 | 95 | 87 | 103 | 94 | 88 | 103 | 96±8 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 68 | 88 | 37 | 89 | 85 | 88 | 79 | 78 | 96 | 88 | 69 | 96 | 80±16 | |||||||||||||
| LVV (ml) |
t0 | 87 | 78 | 88 | 122 | 94 | 81 | 86 | 72 | 91 | 102 | 108 | 99 | 92±14 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 91 | 85 | 89 | 124 | 97 | 82 | 92 | 80 | 92 | 101 | 112 | 102 | 96±13 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 4.1 | 6.7 | 1.1 | 1.6 | 3.7 | 1.8 | 6.1 | 7.6 | 0.9 | −0.6 | 4.0 | 3.0 | 3.3±2.5 | |||||||||||||
| COS | LVP (mmHg) |
t0 | 13 | 10 | 18 | 17 | 24 | 17 | 15 | 10 | 5 | 2 | 12 | 6 | 12±6 | .188 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 90 | 99 | 90 | 100 | 109 | 107 | 98 | 91 | 100 | 97 | 92 | 97 | 97±6 | .218 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 77 | 89 | 71 | 84 | 85 | 90 | 83 | 81 | 94 | 95 | 81 | 91 | 85±7 | .132 | ||||||||||||
| LVV (ml) |
t0 | 90 | 76 | 101 | 126 | 89 | 81 | 80 | 72 | 87 | 101 | 109 | 97 | 92±15 | .940 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 93 | 81 | 102 | 126 | 94 | 85 | 88 | 80 | 88 | 101 | 116 | 99 | 96±14 | .708 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 3.6 | 5.6 | 0.8 | 0.6 | 4.4 | 3.9 | 8.0 | 7.6 | 0.9 | −0.1 | 7.3 | 2.2 | 3.7±2.9 | .323 | ||||||||||||
| RSAR - CTRL |
LVP (mmHg) |
t0 | 39 | 4 | 12 | 21 | 11 | 15 | 25 | 19 | 14 | 7 | 17 | 14 | 16±9 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 100 | 96 | 101 | 91 | 97 | 125 | 107 | 107 | 95 | 98 | 95 | 96 | 101±9 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 61 | 92 | 89 | 71 | 86 | 109 | 82 | 87 | 80 | 91 | 78 | 82 | 84±12 | |||||||||||||
| LVV (ml) |
t0 | 75 | 63 | 113 | 77 | 83 | 81 | 109 | 113 | 90 | 102 | 103 | 101 | 92±17 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 74 | 68 | 120 | 79 | 93 | 89 | 113 | 117 | 94 | 108 | 106 | 106 | 97±17 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.1 | 5.7 | 6.6 | 1.7 | 10.3 | 8.4 | 3.5 | 3.7 | 4.3 | 6.2 | 2.9 | 4.6 | 4.7±3.0 | |||||||||||||
| RSAR | LVP (mmHg) |
t0 | 33 | 7 | 10 | 21 | 10 | 13 | 18 | 18 | 13 | 7 | 8 | 11 | 14±7 | .040 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 92 | 91 | 102 | 95 | 102 | 109 | 95 | 101 | 95 | 97 | 94 | 98 | 98±5 | .144 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 59 | 83 | 92 | 75 | 92 | 96 | 77 | 82 | 83 | 90 | 86 | 87 | 83±10 | .752 | ||||||||||||
| LVV (ml) |
t0 | 75 | 67 | 120 | 81 | 85 | 81 | 110 | 115 | 88 | 102 | 102 | 103 | 94±17 | .027 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 75 | 75 | 124 | 83 | 95 | 89 | 114 | 121 | 92 | 107 | 107 | 107 | 99±17 | .022 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.2 | 7.9 | 4.1 | 2.4 | 10.7 | 7.5 | 3.5 | 6.0 | 4.0 | 4.8 | 5.4 | 3.5 | 5.0±2.9 | .639 | ||||||||||||
| PHYSIO- CTRL |
LVP (mmHg) |
t0 | 32 | 2 | 24 | 6 | 13 | 41 | 33 | 5 | 2 | 37 | 10 | 12 | 18±14 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 95 | 81 | 85 | 83 | 108 | 97 | 95 | 96 | 101 | 101 | 95 | 97 | 95±8 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 63 | 79 | 61 | 77 | 95 | 56 | 62 | 91 | 99 | 64 | 85 | 85 | 76±15 | |||||||||||||
| LVV (ml) |
t0 | 123 | 102 | 94 | 113 | 96 | 72 | 88 | 95 | 66 | 105 | 93 | 97 | 95±16 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 122 | 109 | 94 | 116 | 98 | 69 | 88 | 100 | 70 | 100 | 95 | 102 | 97±16 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.1 | 6.4 | −0.1 | 2.7 | 1.5 | −2.2 | −0.1 | 5.6 | 4.1 | −4.5 | 2.2 | 4.4 | 1.6±3.3 | |||||||||||||
| PHYSIO | LVP (mmHg) |
t0 | 28 | 2 | 26 | 4 | 7 | 46 | 29 | 3 | 2 | 33 | 11 | 8 | 17±15 | .124 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 97 | 83 | 86 | 87 | 103 | 98 | 97 | 96 | 95 | 99 | 99 | 97 | 95±6 | .949 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 69 | 81 | 60 | 83 | 96 | 52 | 67 | 93 | 92 | 65 | 89 | 89 | 78±15 | .221 | ||||||||||||
| LVV (ml) |
t0 | 123 | 107 | 97 | 119 | 95 | 62 | 87 | 98 | 71 | 105 | 97 | 99 | 97±17 | .285 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 123 | 112 | 100 | 122 | 95 | 61 | 87 | 100 | 75 | 102 | 101 | 103 | 98±18 | .236 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.6 | 5.8 | 3.4 | 3.4 | 0.4 | −1.6 | 0.4 | 1.9 | 4.1 | −2.8 | 3.4 | 3.8 | 1.8±2.6 | .657 | ||||||||||||
| ETL- CTRL |
LVP (mmHg) |
t0 | 10 | 19 | 10 | 15 | 17 | 13 | 15 | 11 | 14 | 11 | 21 | 14±4 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 95 | 93 | 98 | 92 | 90 | 89 | 105 | 91 | 91 | 98 | 103 | 95±5 | ||||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 85 | 74 | 88 | 77 | 73 | 75 | 89 | 80 | 77 | 86 | 81 | 81±6 | ||||||||||||||
| LVV (ml) |
t0 | 96 | 87 | 64 | 110 | 87 | 68 | 90 | 104 | 104 | 107 | 110 | 93±16 | |||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 123 | 89 | 77 | 115 | 95 | 70 | 91 | 112 | 105 | 115 | 120 | 101±18 | ||||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 26.9 | 2.1 | 12.3 | 5.6 | 8.0 | 2.9 | 0.9 | 7.5 | 0.7 | 7.1 | 9.2 | 7.6±7.4 | ||||||||||||||
| ETL | LVP (mmHg) |
t0 | 11 | 11 | 8 | 9 | 13 | 12 | 13 | 10 | 12 | 12 | 15 | 11±2 | .010 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 98 | 93 | 103 | 90 | 93 | 94 | 101 | 95 | 94 | 98 | 98 | 96±4 | .306 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 87 | 82 | 95 | 80 | 79 | 82 | 88 | 85 | 83 | 87 | 83 | 85±4 | .080 | |||||||||||||
| LVV (ml) |
t0 | 97 | 91 | 66 | 114 | 93 | 72 | 89 | 106 | 107 | 104 | 115 | 96±16 | .015 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 123 | 94 | 77 | 115 | 101 | 74 | 91 | 114 | 106 | 113 | 122 | 103±17 | .034 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 25.2 | 2.7 | 11.0 | 1.6 | 7.7 | 2.2 | 1.8 | 8.1 | −1.2 | 9.1 | 6.8 | 6.8±7.2 | .186 | |||||||||||||
| GEO- CTRL |
LVP (mmHg) |
t0 | 18 | 13 | 33 | 16 | 17 | 8 | 11 | 1 | 3 | 3 | 3 | 15 | 12±9 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 98 | 91 | 100 | 111 | 105 | 105 | 86 | 96 | 96 | 88 | 93 | 88 | 96±8 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 81 | 77 | 67 | 95 | 88 | 98 | 75 | 95 | 93 | 85 | 90 | 72 | 85±10 | |||||||||||||
| LVV (ml) |
t0 | 70 | 74 | 99 | 86 | 102 | 118 | 99 | 84 | 88 | 75 | 81 | 90 | 89±14 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 77 | 88 | 103 | 93 | 99 | 125 | 101 | 92 | 90 | 74 | 85 | 99 | 94±14 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 7.0 | 14.0 | 4.1 | 7.7 | −3.9 | 7.8 | 2.3 | 7.8 | 2.4 | −1.0 | 3.6 | 9.0 | 5.1±4.8 | |||||||||||||
| GEO | LVP (mmHg) |
t0 | 17 | 10 | 24 | 15 | 14 | 8 | 8 | 1 | 2 | 7 | 6 | 8 | 10±6 | .175 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 93 | 90 | 96 | 110 | 101 | 111 | 92 | 96 | 99 | 92 | 96 | 88 | 97±7 | .589 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 76 | 81 | 73 | 95 | 87 | 103 | 83 | 95 | 97 | 85 | 90 | 81 | 87±9 | .088 | ||||||||||||
| LVV (ml) |
t0 | 74 | 77 | 102 | 86 | 98 | 122 | 98 | 83 | 91 | 92 | 82 | 91 | 91±13 | .131 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 78 | 92 | 105 | 92 | 97 | 130 | 101 | 90 | 91 | 78 | 82 | 102 | 95±14 | .289 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 4.0 | 14.6 | 2.6 | 6.1 | −1.6 | 7.9 | 2.5 | 7.0 | 0.6 | −14.7 | 0.7 | 10.6 | 3.4±7.3 | .175 | ||||||||||||
All values from individual animals are two beat averages, tn=strained state (time point of maximum LVP), t0=reference strain state (time point before mitral valve opening, see METHODS), COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL= Edwards IMR ETlogix, GEO=Edwards GeoForm, SD=standard deviation
Fig 3.
Changes in LV pressure and volumes (ΔLVP and ΔLVV, respectively (top row), mitral annular dimensions (middle row) from reference state (t0) to strained state (tn) as well as global maximum principal (εmax), radial (εrad) and circumferential (εcir) (bottom row). Note that changes from t0 to tn include a calculation from a time point later in the cardiac cycle (t0) to an earlier time point of the cardiac cycle (tn). COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL=Edwards IMR ETlogix, GEO=Edwards GeoForm. Values are mean±1SD.
Mitral Annular Dimensions at Reference State (t0) and Deformed State (tn)
Table 3 shows the mitral annular S-L and C-C dimensions at tn and t0 as well as ΔS-L and ΔC-C. ΔS-L and ΔC-C are also graphically depicted in Figure 3 (middle row). Again, please note that ΔS-L and ΔC-C are described from t0 to tn, i.e. backward in time. Consequently, negative ΔS-L and ΔC-C represent an increase, whereas positive ΔS-L and ΔC-C represent a decrease in the respective dimension during the regular cardiac cycle. Relative to Control, implantation of either complete, rigid rings (RSAR, PHYSIO, ETL or GEO) or the flexible band (COS) resulted in significantly smaller mitral annular S-L and C-C dimensions. Decreases in S-L and C-C diameters from t0 to tn (negative ΔS-L and ΔC-C, Table 3) were observed for the Control cases (all groups). With the annuloplasty device implanted, the S-L dimension became slightly smaller from t0 to tn with COS (ΔS-L: −0.9±0.5mm, Table 3 and Figure3, middle row) while no relevant decreases in S-L and C-C diameters from t0 to tn were found with RSAR, PHYSIO, ETL or GEO.
TABLE 3.
Mitral annular septal-lateral (S-L) and commissure-commissure (C-C) dimensions at reference state (t0) and strained state (tn)
| Animal no | Mean±1SD | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-L | C-C | |||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | t0 | P vs. CTRL | tn | P vs. CTRL | Δtn-t0 | P vs. CTRL | t0 | P vs. CTRL | tn | P vs. CTRL | Δtn-t0 | P vs. CTRL | |||
| COS- CTRL |
S-L | t0 | 29.3 | 29.9 | 27.2 | 33.2 | 27.2 | 24.6 | 32.7 | 28.8 | 27.1 | 25.9 | 35.7 | 29.8 | 29.3±3.3 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 27.9 | 27.4 | 26.3 | 28.7 | 23.0 | 22.7 | 30.5 | 27.5 | 24.9 | 26.1 | 34.6 | 26.9 | 27.2±3.2 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.4 | −2.4 | −1.0 | −4.5 | −4.2 | −1.9 | −2.2 | −1.3 | −2.2 | 0.2 | −1.1 | −2.9 | −2.1±1.3 | |||||||||||||
| C-C | t0 | 36.2 | 36.9 | 34.6 | 37.2 | 36.9 | 33.8 | 40.4 | 41.6 | 42.4 | 36.5 | 38.9 | 39.0 | 37.8±2.7 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 35.7 | 36.2 | 34.1 | 36.3 | 34.1 | 33.1 | 39.8 | 40.6 | 40.8 | 35.7 | 38.0 | 37.9 | 36.8±2.6 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.4 | −0.7 | −0.5 | −1.0 | −2.8 | −0.7 | −0.6 | −1.0 | −1.6 | −0.8 | −0.9 | −1.1 | −1.0±0.6 | |||||||||||||
| COS | S-L | t0 | 23.5 | 26.1 | 26.0 | 29.7 | 23.9 | 24.2 | 30.6 | 25.9 | 24.5 | 26.1 | 32.2 | 27.5 | 26.7±2.8 | <.001 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 22.9 | 25.5 | 25.2 | 29.1 | 22.5 | 22.9 | 28.9 | 25.7 | 23.7 | 25.5 | 31.8 | 26.2 | 25.8±2.8 | .008 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.6 | −0.6 | −0.9 | −0.6 | −1.5 | −1.3 | −1.7 | −0.2 | −0.7 | −0.6 | −0.4 | −1.3 | −0.9±0.5 | .006 | ||||||||||||
| C-C | t0 | 30.6 | 32.7 | 32.0 | 34.6 | 32.6 | 33.6 | 38.3 | 38.8 | 38.0 | 35.9 | 35.2 | 37.9 | 35.0±2.8 | .004 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 30.4 | 32.6 | 31.7 | 34.4 | 32.3 | 33.4 | 38.1 | 38.3 | 38.1 | 35.2 | 34.8 | 37.6 | 34.7±2.8 | .001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.3 | 0.0 | −0.3 | −0.1 | −0.3 | −0.2 | −0.2 | −0.5 | 0.0 | −0.7 | −0.4 | −0.3 | −0.3±0.2 | .002 | ||||||||||||
| RSAR- CTRL |
S-L | t0 | 30.5 | 23.3 | 27.5 | 27.3 | 27.6 | 29.7 | 29.1 | 30.8 | 27.5 | 33.9 | 28.5 | 30.4 | 28.8±2.6 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 30.0 | 22.9 | 26.4 | 27.3 | 25.9 | 28.3 | 27.7 | 27.1 | 25.3 | 30.5 | 26.6 | 28.7 | 27.2±2.1 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.5 | −0.3 | −1.1 | 0.0 | −1.7 | −1.4 | −1.4 | −3.8 | −2.2 | −3.5 | −1.9 | −1.7 | −1.6±1.1 | |||||||||||||
| C-C | t0 | 37.6 | 32.7 | 32.9 | 35.2 | 37.7 | 35.6 | 36.4 | 40.1 | 36.7 | 42.1 | 38.6 | 40.4 | 37.2±2.9 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 36.6 | 32.5 | 32.5 | 34.7 | 36.3 | 34.1 | 35.5 | 38.0 | 36.7 | 41.1 | 37.3 | 40.0 | 36.3±2.7 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.1 | −0.2 | −0.5 | −0.5 | −1.4 | −1.6 | −0.9 | −2.2 | 0.0 | −1.0 | −1.3 | −0.5 | −0.9±0.6 | |||||||||||||
| RSAR | S-L | t0 | 25.4 | 23.7 | 24.9 | 24.1 | 24.6 | 25.8 | 24.8 | 25.0 | 23.5 | 26.5 | 24.7 | 24.6 | 24.8±0.8 | <.001 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 25.2 | 24.0 | 24.6 | 23.9 | 24.5 | 25.7 | 24.6 | 24.9 | 22.9 | 26.4 | 24.8 | 24.4 | 24.6±0.9 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.2 | 0.3 | −0.3 | −0.3 | −0.1 | −0.1 | −0.2 | −0.2 | −0.6 | −0.1 | 0.1 | −0.2 | −0.2±0.2 | .001 | ||||||||||||
| C-C | t0 | 34.5 | 33.4 | 33.7 | 33.8 | 33.8 | 34.6 | 34.3 | 33.1 | 31.1 | 33.0 | 31.8 | 33.8 | 33.4±1.0 | .009 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 34.3 | 33.6 | 33.7 | 33.8 | 33.8 | 34.5 | 34.5 | 33.4 | 31.3 | 33.1 | 31.8 | 33.9 | 33.5±1.0 | .002 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.2 | 0.2 | 0.0 | 0.0 | 0.0 | −0.1 | 0.2 | 0.3 | 0.1 | 0.1 | −0.1 | 0.0 | 0.1±0.1 | <.001 | ||||||||||||
| PHYSIO- CTRL |
S-L | t0 | 30.1 | 26.9 | 26.5 | 30.5 | 27.7 | 25.3 | 30.5 | 35.6 | 27.7 | 31.2 | 33.1 | 30.2 | 29.6±3.0 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 28.6 | 26.1 | 24.0 | 27.6 | 25.7 | 24.5 | 28.4 | 33.5 | 25.2 | 29.6 | 31.4 | 27.3 | 27.7±2.9 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.5 | −0.9 | −2.4 | −2.9 | −2.0 | −0.8 | −2.1 | −2.1 | −2.5 | −1.7 | −1.7 | −3.0 | −2.0±0.7 | |||||||||||||
| C-C | t0 | 42.6 | 37.7 | 39.0 | 42.0 | 40.5 | 36.7 | 40.0 | 43.6 | 38.9 | 37.9 | 40.5 | 39.6 | 39.9±2.1 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 41.2 | 39.1 | 37.5 | 41.4 | 39.9 | 35.7 | 39.4 | 43.2 | 37.1 | 37.9 | 39.3 | 38.4 | 39.1±2.1 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.4 | 1.4 | −1.6 | −0.6 | −0.6 | −1.1 | −0.6 | −0.4 | −1.9 | 0.0 | −1.2 | −1.3 | −0.8±0.9 | |||||||||||||
| PHYSIO | S-L | t0 | 24.2 | 24.2 | 24.6 | 24.1 | 23.5 | 23.3 | 25.0 | 28.1 | 24.1 | 26.1 | 25.9 | 26.1 | 24.9±1.4 | <.001 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 23.9 | 24.0 | 24.2 | 23.8 | 22.8 | 23.1 | 24.6 | 28.2 | 23.8 | 25.9 | 25.9 | 25.9 | 24.7±1.5 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.2 | −0.2 | −0.4 | −0.2 | −0.7 | −0.2 | −0.4 | 0.1 | −0.4 | −0.2 | 0.0 | −0.3 | −0.3±0.2 | <.001 | ||||||||||||
| C-C | t0 | 33.0 | 33.1 | 32.7 | 34.9 | 32.8 | 32.7 | 32.7 | 33.7 | 32.7 | 32.6 | 31.5 | 32.6 | 32.9±0.8 | <.001 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 33.1 | 33.1 | 32.7 | 34.8 | 32.8 | 32.6 | 32.8 | 33.9 | 32.9 | 32.9 | 31.7 | 32.9 | 33.0±0.8 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 0.0 | 0.0 | 0.0 | −0.1 | 0.1 | −0.1 | 0.2 | 0.1 | 0.1 | 0.2 | 0.2 | 0.3 | 0.1±0.1 | .007 | ||||||||||||
| ETL- CTRL |
S-L | t0 | 29.2 | 32.1 | 28.0 | 27.5 | 29.8 | 26.2 | 33.3 | 32.6 | 32.6 | 30.6 | 28.7 | 30.1±2.4 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 27.9 | 31.4 | 24.8 | 25.8 | 27.9 | 27.1 | 31.1 | 30.5 | 31.1 | 27.5 | 27.0 | 28.4±2.3 | ||||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.3 | −0.7 | −3.3 | −1.7 | −1.9 | 0.9 | −2.3 | −2.1 | −1.6 | −3.1 | −1.7 | −1.7±1.1 | ||||||||||||||
| C-C | t0 | 34.0 | 39.8 | 35.6 | 39.6 | 40.4 | 43.6 | 36.8 | 38.8 | 41.0 | 40.7 | 41.5 | 39.2±2.8 | |||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 34.0 | 39.0 | 35.4 | 38.3 | 39.5 | 43.0 | 36.6 | 38.3 | 40.8 | 39.7 | 39.8 | 38.6±2.5 | ||||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 0.0 | −0.7 | −0.2 | −1.3 | −1.0 | −0.7 | −0.2 | −0.5 | −0.2 | −1.0 | −1.7 | −0.7±0.5 | ||||||||||||||
| ETL | S-L | t0 | 23.1 | 25.5 | 20.7 | 24.5 | 24.3 | 21.0 | 22.9 | 24.2 | 24.1 | 24.2 | 23.5 | 23.4±1.5 | <.001 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 23.6 | 25.3 | 20.5 | 23.1 | 23.9 | 20.8 | 22.7 | 23.9 | 24.0 | 24.0 | 23.1 | 23.2±1.4 | <.001 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 0.5 | −0.1 | −0.2 | −1.3 | −0.4 | −0.1 | −0.2 | −0.4 | −0.1 | −0.2 | −0.4 | −0.3±0.4 | .002 | |||||||||||||
| C-C | t0 | 29.0 | 32.3 | 29.9 | 30.6 | 33.3 | 33.9 | 32.3 | 33.2 | 32.8 | 32.7 | 32.7 | 32.1±1.5 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 29.3 | 32.2 | 30.1 | 30.8 | 33.0 | 33.9 | 32.5 | 33.1 | 32.7 | 32.7 | 32.7 | 32.1±1.4 | <.001 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | 0.3 | −0.1 | 0.2 | 0.2 | −0.2 | 0.0 | 0.2 | −0.1 | −0.2 | 0.1 | 0.0 | 0.0±0.2 | .001 | |||||||||||||
| GEO- CTRL |
S-L | t0 | 27.6 | 29.8 | 26.0 | 29.8 | 27.5 | 27.2 | 31.1 | 29.6 | 30.9 | 28.3 | 24.8 | 30.1 | 28.6±2.0 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 25.8 | 28.5 | 25.2 | 27.9 | 23.5 | 23.2 | 29.0 | 26.6 | 27.0 | 27.6 | 22.8 | 28.1 | 26.3±2.2 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.8 | −1.3 | −0.9 | −1.9 | −4.1 | −4.0 | −2.2 | −2.9 | −3.9 | −0.7 | −2.0 | −2.0 | −2.3±1.2 | |||||||||||||
| C-C | t0 | 36.6 | 34.8 | 34.2 | 35.7 | 36.6 | 36.8 | 38.3 | 38.5 | 42.5 | 41.0 | 37.4 | 43.0 | 37.9±2.9 | ||||||||||||
|
| ||||||||||||||||||||||||||
| tn | 35.1 | 35.2 | 33.2 | 34.9 | 33.9 | 36.2 | 37.9 | 37.8 | 40.4 | 40.0 | 36.4 | 41.7 | 36.9±2.7 | |||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −1.5 | 0.4 | −1.0 | −0.8 | −2.6 | −0.6 | −0.4 | −0.7 | −2.1 | −0.9 | −1.0 | −1.3 | −1.0±0.8 | |||||||||||||
| GEO | S-L | t0 | 19.9 | 19.6 | 19.6 | 20.6 | 19.7 | 19.1 | 21.0 | 20.7 | 21.6 | 18.7 | 18.7 | 19.7 | 19.9±0.9 | <.001 | ||||||||||
|
| ||||||||||||||||||||||||||
| tn | 19.8 | 19.8 | 19.5 | 20.7 | 19.5 | 18.9 | 21.1 | 20.5 | 21.1 | 18.7 | 18.9 | 19.7 | 19.8±0.8 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.1 | 0.2 | −0.1 | 0.2 | −0.3 | −0.2 | 0.1 | −0.2 | −0.5 | −0.1 | 0.2 | −0.1 | −0.1±0.2 | <.001 | ||||||||||||
| C-C | t0 | 33.4 | 33.4 | 31.5 | 34.9 | 34.8 | 33.7 | 35.8 | 36.5 | 35.7 | 35.4 | 35.7 | 36.2 | 34.7±1.5 | .001 | |||||||||||
|
| ||||||||||||||||||||||||||
| tn | 33.2 | 33.7 | 31.4 | 34.7 | 34.1 | 33.3 | 36.1 | 36.4 | 35.7 | 35.3 | 35.6 | 36.1 | 34.6±1.5 | <.001 | ||||||||||||
|
| ||||||||||||||||||||||||||
| Δ tn-t0 | −0.2 | 0.3 | −0.1 | −0.2 | −0.7 | −0.4 | 0.3 | −0.1 | 0.0 | 0.0 | −0.1 | −0.1 | −0.1±0.3 | <.001 | ||||||||||||
All values from individual animals are in mm and two beat averages, tn=strained state (time point of maximum LVP), t0=reference strain state (time point before mitral valve opening, see METHODS), COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL= Edwards IMR ETlogix, GEO=Edwards GeoForm, SD=standard deviation
Global Maximum Principal (global εmax), Radial (global εrad) and Circumferential (global εcir) Strains
Table 4 shows global εmax, εrad and εcir for all five groups with and without annuloplasty devices implanted. Global εmax, εrad and εcir (average from all animals) are also graphically displayed in Figure 3 (bottom row). Compared to the respective Control state, strains increased significantly with RSAR, PHYSIO, ETL and GEO (0.14±0.05 vs. 0.16±0.05, p=0.024, 0.15±0.03 vs. 0.18±0.04, p=0.020, 0.11±0.05 vs. 0.14±0.05, p=0.042 and 0.13±0.05 vs. 0.16±0.05, p=0.009, respectively, all p<0.05), but not with COS (0.15±0.05 vs. 0.15±0.04, n.s., p=0.973). Global εrad increased significantly compared to the Control state only with RSAR, while greater global εcir values were found with RSAR, PHYSIO, ETL and GEO (however, insignificant for GEO, Table 4). No significant changes in global εrad or εcir were found with COS compared to the Control state. With no annuloplasty device implanted, global εrad was greater than global εcir in all five groups (COS-CTRL, RSAR-CTRL, PHYSIO-CTRL, ETL-CTRL, GEO-CTRL, Table 4 and Figure 3, bottom row). With annuloplasty device implanted, global εrad values were either greater than global εcir (COS, RSAR), smaller (PHYSIO) or similar (ETL, GEO, Table 4 and Figure 3, bottom row). No differences in εmax (p=0.331, F=1.178), εrad (p=0.188, F=1.598) or εcir (p=0.160, F=1.716) with rings implanted were found between the groups (COS, RSAR, PHYSIO, ETL and GEO).
TABLE 4.
Global maximum principal (global εmax), radial (global εrad) and circumferential (global εcir) strains
| Animal no | Mean±1SD | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | global εmax | P vs. CTRL | global εrad | P vs. CTRL | global εcir | P vs. CTRL | ||
| COS- CTRL |
global εmax | 0.08 | 0.20 | 0.06 | 0.12 | 0.14 | 0.22 | 0.19 | 0.15 | 0.11 | 0.23 | 0.11 | 0.16 | 0.15±0.05 | |||||
|
| |||||||||||||||||||
| global εrad | 0.03 | 0.12 | 0.04 | 0.08 | 0.08 | 0.17 | 0.10 | 0.09 | 0.08 | 0.10 | 0.05 | 0.12 | 0.09±0.04 | ||||||
|
| |||||||||||||||||||
| global εcir | 0.04 | 0.11 | 0.04 | 0.05 | 0.07 | 0.08 | 0.07 | 0.09 | 0.04 | 0.07 | 0.03 | 0.10 | 0.07±0.03 | ||||||
| COS | global εmax | 0.19 | 0.19 | 0.07 | 0.13 | 0.14 | 0.14 | 0.15 | 0.14 | 0.12 | 0.16 | 0.12 | 0.21 | 0.15±0.04 | .973 | ||||
|
| |||||||||||||||||||
| global εrad | 0.08 | 0.15 | 0.05 | 0.10 | 0.11 | 0.11 | 0.06 | 0.09 | 0.09 | 0.13 | 0.07 | 0.12 | 0.10±0.03 | .425 | |||||
|
| |||||||||||||||||||
| global εcir | 0.08 | 0.08 | 0.04 | 0.05 | 0.07 | 0.04 | 0.08 | 0.06 | 0.05 | 0.10 | 0.03 | 0.13 | 0.07±0.03 | .858 | |||||
| RSAR- CTRL |
global εmax | 0.08 | 0.19 | 0.24 | 0.08 | 0.18 | 0.09 | 0.17 | 0.16 | 0.08 | 0.14 | 0.07 | 0.14 | 0.14±0.05 | |||||
|
| |||||||||||||||||||
| global εrad | 0.04 | 0.15 | 0.20 | 0.05 | 0.10 | 0.03 | 0.10 | 0.16 | 0.04 | 0.09 | 0.05 | 0.07 | 0.09±0.05 | ||||||
|
| |||||||||||||||||||
| global εcir | 0.03 | 0.13 | 0.07 | 0.02 | 0.06 | 0.04 | 0.04 | 0.05 | 0.03 | 0.06 | 0.02 | 0.07 | 0.05±0.03 | ||||||
| RSAR | global εmax | 0.15 | 0.17 | 0.24 | 0.09 | 0.21 | 0.09 | 0.18 | 0.18 | 0.10 | 0.15 | 0.09 | 0.23 | 0.16±0.05 | .024 | ||||
|
| |||||||||||||||||||
| global εrad | 0.12 | 0.15 | 0.20 | 0.06 | 0.12 | 0.06 | 0.15 | 0.17 | 0.03 | 0.10 | 0.06 | 0.16 | 0.11±0.05 | .010 | |||||
|
| |||||||||||||||||||
| global εcir | 0.06 | 0.09 | 0.09 | 0.05 | 0.11 | 0.05 | 0.07 | 0.04 | 0.06 | 0.06 | 0.05 | 0.11 | 0.07±0.02 | .022 | |||||
| PHYSIO- CTRL |
global εmax | 0.17 | 0.15 | 0.19 | 0.20 | 0.17 | 0.12 | 0.16 | 0.14 | 0.18 | 0.09 | 0.11 | 0.17 | 0.15±0.03 | |||||
|
| |||||||||||||||||||
| global εrad | 0.11 | 0.04 | 0.08 | 0.09 | 0.14 | 0.04 | 0.12 | 0.08 | 0.10 | 0.03 | 0.07 | 0.13 | 0.08±0.04 | ||||||
|
| |||||||||||||||||||
| global εcir | 0.05 | 0.11 | 0.11 | 0.09 | 0.07 | 0.08 | 0.06 | 0.07 | 0.03 | 0.03 | 0.05 | 0.07 | 0.07±0.03 | ||||||
| PHYSIO | global εmax | 0.21 | 0.18 | 0.21 | 0.19 | 0.20 | 0.12 | 0.20 | 0.20 | 0.14 | 0.14 | 0.11 | 0.24 | 0.18±0.04 | .020 | ||||
|
| |||||||||||||||||||
| global εrad | 0.14 | 0.03 | 0.10 | 0.13 | 0.14 | 0.04 | 0.14 | 0.11 | 0.09 | 0.04 | 0.05 | 0.13 | 0.09±0.05 | .102 | |||||
|
| |||||||||||||||||||
| global εcir | 0.10 | 0.13 | 0.10 | 0.10 | 0.10 | 0.05 | 0.11 | 0.13 | 0.04 | 0.08 | 0.06 | 0.15 | 0.10±0.03 | .010 | |||||
| ETL- CTRL |
global εmax | 0.21 | 0.08 | 0.09 | 0.12 | 0.07 | 0.10 | 0.07 | 0.08 | 0.09 | 0.20 | 0.06 | 0.11±0.05 | ||||||
|
| |||||||||||||||||||
| global εrad | 0.15 | 0.07 | 0.06 | 0.11 | 0.02 | 0.04 | 0.04 | 0.07 | 0.03 | 0.15 | 0.03 | 0.07±0.05 | |||||||
|
| |||||||||||||||||||
| global εcir | 0.13 | 0.02 | 0.03 | 0.05 | 0.05 | 0.06 | 0.04 | 0.03 | 0.02 | 0.12 | 0.03 | 0.05±0.04 | |||||||
| ETL | global εmax | 0.19 | 0.11 | 0.17 | 0.24 | 0.06 | 0.11 | 0.15 | 0.11 | 0.12 | 0.17 | 0.09 | 0.14±0.05 | .042 | |||||
|
| |||||||||||||||||||
| global εrad | 0.10 | 0.08 | 0.08 | 0.17 | 0.03 | 0.03 | 0.05 | 0.10 | 0.07 | 0.11 | 0.06 | 0.08±0.04 | .349 | ||||||
|
| |||||||||||||||||||
| global εcir | 0.14 | 0.05 | 0.11 | 0.12 | 0.04 | 0.08 | 0.07 | 0.04 | 0.05 | 0.09 | 0.06 | 0.08±0.03 | .017 | ||||||
| GEO- CTRL |
global εmax | 0.13 | 0.15 | 0.04 | 0.17 | 0.06 | 0.08 | 0.19 | 0.17 | 0.11 | 0.13 | 0.16 | 0.13 | 0.13±0.05 | |||||
|
| |||||||||||||||||||
| global εrad | 0.08 | 0.10 | 0.02 | 0.12 | 0.02 | 0.03 | 0.08 | 0.11 | 0.06 | 0.09 | 0.06 | 0.07 | 0.07±0.03 | ||||||
|
| |||||||||||||||||||
| global εcir | 0.07 | 0.10 | 0.01 | 0.07 | 0.02 | 0.02 | 0.11 | 0.03 | 0.07 | 0.05 | 0.05 | 0.06 | 0.06±0.03 | ||||||
| GEO | global εmax | 0.14 | 0.21 | 0.05 | 0.22 | 0.16 | 0.07 | 0.17 | 0.20 | 0.16 | 0.16 | 0.18 | 0.19 | 0.16±0.05 | .009 | ||||
|
| |||||||||||||||||||
| global εrad | 0.07 | 0.15 | 0.01 | 0.12 | 0.09 | 0.04 | 0.05 | 0.14 | 0.07 | 0.05 | 0.00 | 0.11 | 0.07±0.05 | .581 | |||||
|
| |||||||||||||||||||
| global εcir | 0.09 | 0.11 | 0.02 | 0.13 | 0.02 | 0.02 | 0.08 | 0.04 | 0.10 | 0.07 | 0.07 | 0.07 | 0.07±0.04 | .065 | |||||
All values from individual animals are two beat averages, COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL= Edwards IMR ETlogix, GEO=Edwards GeoForm, SD=standard deviation
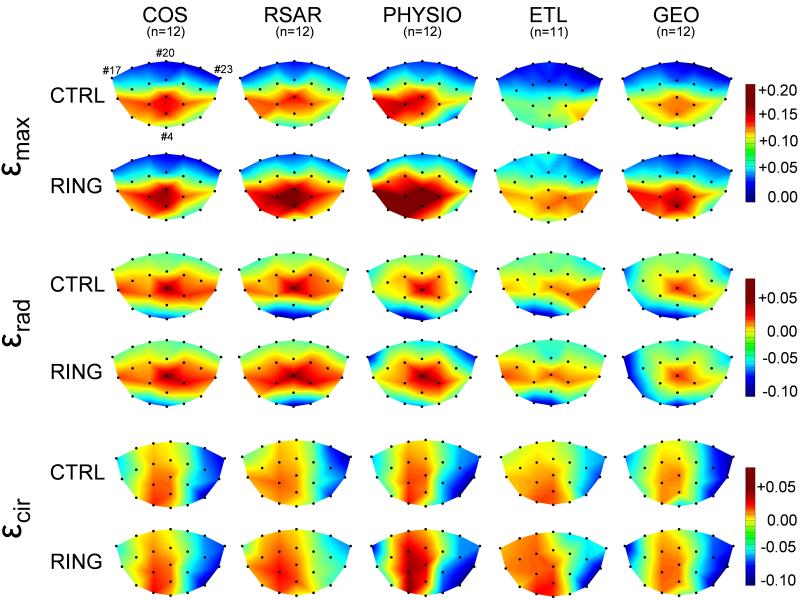
Maximum Principal (εmax), Radial (εrad) and Circumferential (εcir) Strains Across the Entire Anterior Mitral Leaflet
Figure 4 shows εmax, εrad and εcir across the entire AML for both states, with and without annuloplasty device implanted in all five groups. Increases in εmax can be appreciated with RSAR, PHYSIO, ETL and GEO compared to the respective Control state and predominantly occur in the belly and edge region of the anterior mitral leaflet. No major changes in strain patterns (εmax, εrad or εcir) were observed with COS. εmax values across the AML of the respective Control states were slightly different between groups with COS-CTRL, RSAR-CTRL and PHYSIO-CTRL being more strained than GEO-CTRL and ETL-CTRL.
Fig 4.
Color-mapped schematics of maximum principal (εmax, two top rows), radial (εrad, two middle rows) and circumferential (εcir, two bottom rows) strains across the entire anterior mitral leaflet for the Control state (CTRL) and with annuloplasty device implanted (RING). Markers #17 and #23 depict anterior and posterior commissures, respectively, marker #20 represents the mid-septal mitral annulus (saddle horn, see Figure 1). COS=Edwards Cosgrove band, RSAR=St Jude Medical rigid saddle-shaped annuloplasty ring, ETL=Edwards IMR ETlogix, GEO=Edwards GeoForm.
DISCUSSION
The principle finding of this study was that, with no relevant changes in hemodynamics, implantation of rigid, complete annuloplasty rings (RSAR, PHYSIO, ETL and GEO), but not of the flexible partial band (COS), increased global maximum principal strains of the AML. These changes predominantly occurred in the region of the AML belly and edge.
Several studies have determined mitral leaflet strains and stretches using a variety of different techniques [4-7, 14-19]. In vitro studies have been employed to characterize dynamic stretches on the anterior and posterior leaflet of excised porcine mitral valves using a left heart simulator [6, 14-17]. In vivo studies, using sonomicrometer technology, quantified AML strains in the beating ovine heart [16] and lastly, finite element studies investigated strain patterns across the AML [4, 5, 18, 19].
Salgo et al. demonstrated in a numerical simulation that the native mitral annular shape is important to minimize stresses acting on the leaflet [5]. In a previous analysis from the same dataset we demonstrated that implantation of the Physio, IMR ETLogix and GeoForm, but not RSAR, perturbed the physiological saddle-shape of the mitral annulus [11]. The increased maximum principal leaflet strains observed with these three rings are therefore consistent with engineering intuition quantified through the results of Salgo et al.. However, to our surprise, the supposedly physiologically shaped RSAR also led to an increase in maximum principal leaflet strains. Assuming that the shape of this ring is physiological it could be speculated that the dynamic motion of the mitral annulus rather than its 3-D shape is of major importance to preserve AML strain distribution. This hypothesis, however, is contrary to previous studies that suggested changes in the physiological mitral annular 3-D saddle shape lead to increases in leaflet strains [6]. It may therefore also be speculated that the shape of the RSAR does not fully represent the natural 3-D annular shape and that, as discussed earlier [6], increased strains are also a result of a non-physiological annular shape.
The partial, flexible band (COS) has been found to preserve the mitral annular saddle shape [11] and allow minimal mitral annular S-L dynamics (Figure 3, middle row) during the observed time period (from t0 to tn). However, COS significantly reduced mitral annular dimensions compared to the Controlstate (Table 3 and Ref [11]). Since COS did not affect AML strains (Figure 3, bottom row) we speculate that preserving physiologic mitral annular dynamics and shape rather than absolute mitral annular dimensions are the key components to maintaining a physiological strain distribution across the AML.
To our knowledge, Votta et al. were the only group that quantified the effects of annuloplasty rings (GeoForm and Physio) on mitral leaflet strains and stresses [4]. The group used a finite element model and demonstrated that the GeoForm, but not the Physio, reduced maximum principal mitral leaflet stresses during simulated functional mitral regurgitation [4]. In our study we found that all rigid rings (RSAR, PHYSIO, ETL and GEO) increased maximum principal AML strains, irrespective of their 3-D shape. However, unlike Votta et al., we used an in vivo model of the normal, beating heart. We therefore cannot comment on the potential effects of FMR/IMR rings in the diseased state and it is possible that these rings restore a physiological strain distribution in hearts with dilated LVs.
In our study we report the effect of different annuloplasty devices on radial and circumferential strains. While global εrad was only greater with RSAR, global εcir was greater with all rigid, complete rings (RSAR, PHYSIO, ETL and GEO, Table 4) compared to the Control state (however, insignificantly for GEO), suggesting that rigid, complete annuloplasty devices affect circumferential strains more than radial strains. The reason for the insignificant increase in global εcir observed with GEO could be a result of the larger commissure to commissure dimension of this ring compared to RSAR, PHYSIO or ETL [3], suggesting that the physiological circumferential AML strain distribution is sensitive to the amount of mitral annular C-C decrease.
Study Limitations
Several limitations should be addressed to allow a better interpretation of these data. First, the data were acquired from open-chest, anesthetized ovine hearts with normal preoperative anatomy. Considerable caution must therefore be exercised when extrapolating these findings to the human heart. This is especially true for the GeoForm and IMR ETLogix rings that have been designed for patients with IMR/FMR (with distorted annular, leaflet and ventricular geometry and function). As mentioned above, if these rings are implanted in the setting of FMR/IMR, it could well be that they reduce (or restore physiological) leaflet strains as demonstrated by Votta and colleagues in a computer simulation [4]. In future analyses we aim to use our experimental in vivo data to determine whether these two FMR/IMR-specific rings (GEO and ETL) are more efficient than conventional rings in terms of reducing leaflet strains during acute myocardial ischemia. Second, AML strains were quantified for only the IVR phase of the cardiac cycle and it could be that the rings affect strain patterns differently in other phases of the cardiac cycle [20]. Third, although perturbed leaflet strains have been associated with impaired mitral valve repair durability [6, 7] currently no study exists that proves causation. Consequently, it remains to be determined whether perturbations in AML strains impair long-term function of the mitral valve after repair. Fourth, when radial and circumferential strains were plotted onto color mapped schematics (Figure 4), we did not only observe tensile, but also compressive strains in both Control states and with rings implanted (green and blue areas, Figure 4). Compressive strains do not occur, e.g., in purely computational models that use simplified AML shapes with the leaflet being entirely convex to the left ventricle [4] and, thus, may be a result of the complex AML shape [21] that was included in our analyses. The finding of compressive strains warrants further investigation; however, we focused on the tensile aspects of strain in this manuscript and did not perform detailed analyses of compressive strain patterns. Fifth, no statistically significant differences in strains were found between the different ring types. We therefore cannot draw any conclusions from these data whether one ring design is superior to another; however, this study was not adequately powered to demonstrate differences between the different ring types. Sixth, we only studied a partial, flexible band. Since no complete, flexible ring was examined in this experiment it is not possible to distinguish whether the observed lack of increase in AML strains with a partial band is due to its partial design, its flexibility, or due to a combination of the two. Lastly, strain patterns may change with varying annuloplasty device sizes [4]. Since only size 28mm annuloplasty rings were used in this study, we are unable to draw any conclusions about the impact of ring or band size on leaflet strains.
Conclusions
In conclusion, regardless of their three-dimensional shape, rigid, complete annuloplasty rings (RSAR, PHYSIO, ETL, GEO), but not a partial flexible band (COS), increased maximum principal anterior mitral leaflet strains predominantly in the belly and edge regions in the normal beating ovine heart. Large, randomized, clinical trials are needed to answer the question whether the observed ring-induced alterations in mitral leaflet strain states exist in patients, and if so, whether they adversely affect long-term mitral valve repair durability.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the expert technical assistance of Paul Chang, Maggie Brophy, Sigurd Hartnett, Erin Schultz and George T. Daughters as well as the inspiring suggestions of Frank Langer.
FUNDING SOURCES D. Craig Miller, M.D.: R01 research grant, NHLBI, National Institutes of Health HL29589 (1982-2008), R01 research grant, NHLBI, National Institutes of Health HL67025 (2001-2010) Wolfgang Bothe, M.D.: Research Grant S/06/07, Deutsche Herzstiftung, Frankfurt, Germany Ellen Kuhl, Ph.D.: NSF CAREER Award CMMI-0952021
John-Peder Escobar Kvitting, M.D.:U.S.-Norway Fulbright Foundation, the Swedish Heart-Lung Foundation and the Swedish Society for Medical Research.
Julia C. Swanson, M.D.: Western States Affiliate AHA Postdoctoral Fellowship
Footnotes
DISCLOSURES D. Craig Miller, M.D.: Consultant, Medtronic CardioVascular Division; Consultant, St. Jude Medical, Inc.; PARTNER U.S. Pivotal Trial Executive Committee, Edwards Lifesciences (uncompensated); PARTNER U.S. pivot trial site PI, Edwards Lifesciences (uncompensated); Consultant, Abbott Vascular (MitraClip).
This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Ryan LP, Jackson BM, Hamamoto H, Eperjesi TJ, Plappert TJ, St John-Sutton M, Gorman RC, Gorman JH., 3rd The influence of annuloplasty ring geometry on mitral leaflet curvature. Ann Thorac Surg. 2008;86:749–60. doi: 10.1016/j.athoracsur.2008.03.079. discussion 749-60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Accola KD, Scott ML, Thompson PA, Palmer GJ, 3rd, Sand ME, Ebra G. Midterm outcomes using the physio ring in mitral valve reconstruction: experience in 492 patients. Ann Thorac Surg. 2005;79:1276–83. doi: 10.1016/j.athoracsur.2004.09.035. discussion 1276-83. [DOI] [PubMed] [Google Scholar]
- 3.Bothe W, Swanson JC, Ingels NB, Miller DC. How much septal-lateral mitral annular reduction do you get with new ischemic/functional mitral regurgitation annuloplasty rings? J Thorac Cardiovasc Surg. 2010;140:117–21. 121 e1–3. doi: 10.1016/j.jtcvs.2009.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Votta E, Maisano F, Bolling SF, Alfieri O, Montevecchi FM, Redaelli A. The Geoform disease-specific annuloplasty system: a finite element study. Ann Thorac Surg. 2007;84:92–101. doi: 10.1016/j.athoracsur.2007.03.040. [DOI] [PubMed] [Google Scholar]
- 5.Salgo IS, Gorman JH, 3rd, Gorman RC, Jackson BM, Bowen FW, Plappert T, St John Sutton MG, Edmunds LH., Jr. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106:711–7. doi: 10.1161/01.cir.0000025426.39426.83. [DOI] [PubMed] [Google Scholar]
- 6.Jimenez JH, Liou SW, Padala M, He Z, Sacks M, Gorman RC, Gorman JH, 3rd, Yoganathan AP. A saddle-shaped annulus reduces systolic strain on the central region of the mitral valve anterior leaflet. J Thorac Cardiovasc Surg. 2007;134:1562–8. doi: 10.1016/j.jtcvs.2007.08.037. [DOI] [PubMed] [Google Scholar]
- 7.Padala M, Hutchison RA, Croft LR, Jimenez JH, Gorman RC, Gorman JH, 3rd, Sacks MS, Yoganathan AP. Saddle shape of the mitral annulus reduces systolic strains on the P2 segment of the posterior mitral leaflet. Ann Thorac Surg. 2009;88:1499–504. doi: 10.1016/j.athoracsur.2009.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bothe W, Chang PA, Swanson JC, Itoh A, Arata K, Ingels NB, Miller DC. Releasable annuloplasty ring insertion--a novel experimental implantation model. Eur J Cardiothorac Surg. 2009;36:830–2. doi: 10.1016/j.ejcts.2009.06.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bothe W, Kvitting JP, Stephens EH, Swanson JC, Liang DH, Ingels NB, Jr., Miller DC. Effects of different annuloplasty ring types on mitral leaflet tenting area during acute myocardial ischemia. J Thorac Cardiovasc Surg. 2011;141:345–53. doi: 10.1016/j.jtcvs.2010.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bothe W, Kvitting JP, Swanson JC, Goktepe S, Vo KN, Ingels NB, Miller DC. How do annuloplasty rings affect mitral leaflet dynamic motion? Eur J Cardiothorac Surg. 2010;38:340–9. doi: 10.1016/j.ejcts.2010.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bothe W, Kvitting JP, Swanson JC, Hartnett S, Ingels NB, Jr., Miller DC. Effects of different annuloplasty rings on anterior mitral leaflet dimensions. J Thorac Cardiovasc Surg. 139:1114–22. doi: 10.1016/j.jtcvs.2009.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Niczyporuk MA, Miller DC. Automatic tracking and digitization of multiple radiopaque myocardial markers. Comput Biomed Res. 1991;24:129–42. doi: 10.1016/0010-4809(91)90025-r. [DOI] [PubMed] [Google Scholar]
- 13.Moon MR, DeAnda A, Jr., Daughters GT, 2nd, Ingels NB, Jr., Miller DC. Experimental evaluation of different chordal preservation methods during mitral valve replacement. Ann Thorac Surg. 1994;58:931–43. doi: 10.1016/0003-4975(94)90436-7. discussion 943-4. [DOI] [PubMed] [Google Scholar]
- 14.He Z, Sacks MS, Baijens L, Wanant S, Shah P, Yoganathan AP. Effects of papillary muscle position on in-vitro dynamic strain on the porcine mitral valve. J Heart Valve Dis. 2003;12:488–94. [PubMed] [Google Scholar]
- 15.He S, Jimenez J, He Z, Yoganathan AP. Mitral leaflet geometry perturbations with papillary muscle displacement and annular dilatation: an in-vitro study of ischemic mitral regurgitation. J Heart Valve Dis. 2003;12:300–7. [PubMed] [Google Scholar]
- 16.Sacks MS, He Z, Baijens L, Wanant S, Shah P, Sugimoto H, Yoganathan AP. Surface strains in the anterior leaflet of the functioning mitral valve. Ann Biomed Eng. 2002;30:1281–90. doi: 10.1114/1.1529194. [DOI] [PubMed] [Google Scholar]
- 17.Jimenez JH, Soerensen DD, He Z, He S, Yoganathan AP. Effects of a saddle shaped annulus on mitral valve function and chordal force distribution: an in vitro study. Ann Biomed Eng. 2003;31:1171–81. doi: 10.1114/1.1616929. [DOI] [PubMed] [Google Scholar]
- 18.Kunzelman KS, Reimink MS, Cochran RP. Annular dilatation increases stress in the mitral valve and delays coaptation: a finite element computer model. Cardiovasc Surg. 1997;5:427–34. doi: 10.1016/s0967-2109(97)00045-8. [DOI] [PubMed] [Google Scholar]
- 19.Votta E, Maisano F, Soncini M, Redaelli A, Montevecchi FM, Alfieri O. 3-D computational analysis of the stress distribution on the leaflets after edge-to-edge repair of mitral regurgitation. J Heart Valve Dis. 2002;11:810–22. [PubMed] [Google Scholar]
- 20.Itoh A, Krishnamurthy G, Swanson JC, Ennis DB, Bothe W, Kuhl E, Karlsson M, Davis LR, Miller DC, Ingels NB., Jr. Active stiffening of mitral valve leaflets in the beating heart. Am J Physiol Heart Circ Physiol. 2009;296:H1766–73. doi: 10.1152/ajpheart.00120.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ryan LP, Jackson BM, Eperjesi TJ, Plappert TJ, St John-Sutton M, Gorman RC, Gorman JH., 3rd A methodology for assessing human mitral leaflet curvature using real-time 3-dimensional echocardiography. J Thorac Cardiovasc Surg. 2008;136:726–34. doi: 10.1016/j.jtcvs.2008.02.073. [DOI] [PMC free article] [PubMed] [Google Scholar]