Variable Helix Elongation as a Tool to Modulate RNA Alignment and Motional Couplings

Abstract

The application of residual dipolar couplings (RDCs) in studies of RNA structure and dynamics can be complicated by the presence of couplings between collective helix motions and overall alignment and by the inability to modulate overall alignment of the molecule by changing the ordering medium. Here, we show for a 27-nt TAR RNA construct that variable levels of helix elongation can be used to alter both overall alignment and couplings to collective helix motions in a semi-predictable manner. In the absence of elongation, a four base-pair helix II capped by a UUCG apical loop exhibits a higher degree of order compared to a six base-pair helix I (ϑ_I/ϑ_II = 0.56±0.1). The principal S_zz direction is nearly parallel to the axis of helix II but deviates by ∼40° relative to the axis of helix I. Elongating helix I by three base-pairs equalizes the alignment of the two helices and pushes the RNA into the motional coupling limit such that the two helices have comparable degrees of order (ϑ_I/ϑ_II = 0.92±0.04) and orientations relative to S_zz (∼17°). Increasing the length of elongation further to twenty-two base-pairs pushes the RNA into the motional decoupling limit in which helix I dominates alignment (ϑ_II/ϑ_I = 0.45±0.05), with S_zz orientated nearly parallel to its helix axis. Many of these trends can be rationalized using PALES simulations that employ a previously proposed three-state dynamic ensemble of TAR. Our results provide new insights into motional couplings, offer guidelines for assessing their extent, and suggest that variable degrees of helix elongation can allow access to independent sets of RDCs for characterizing RNA structural dynamics.

1. Introduction

There is great interest in utilizing NMR residual dipolar couplings (RDCs) [1,2] to characterize the structure and dynamics of biomolecules [3-5]. RDCs can be measured in molecules that are partially aligned, either spontaneously when they have a significant magnetic susceptibility anisotropy [1,6] or, more commonly, by dissolution in an appropriate ordering medium [2,7-10]. Several studies have established the utility of measuring RDCs under multiple linearly independent alignment conditions [11] to increase the spatial resolution with which structure and dynamics can be simultaneously characterized [12-18].

Two challenges can arise when using RDCs to characterize the conformational dynamics of nucleic acids, particularly globally flexible RNAs. First, it cannot be generally assumed, as is done in most formalisms, that internal motions do not lead to coupled changes in overall alignment [12,13,19]. Rather, rigid-body collective movements of helical domains about flexible junctions can lead to significant changes in the RNA overall molecular shape and thus global alignment [20,21]. Second, though the alignment of proteins can be modulated by changing the alignment medium and altering the balance between electrostatic and steric forces governing alignment [11,22], this has proven difficult if not impossible for nucleic acids because their uniform charge distribution closely follows that of their molecular shape [23-28]. Although spontaneous magnetic field alignment can yield one additional independent alignment [26,28], the degree of order generally remains unfavorably small under current magnetic field strengths.

Recently, we showed that correlations between internal motions and overall alignment could be reduced and overall alignment altered by chemically perturbing the overall RNA molecular shape [20]. In particular, the alignment of the transactivation response element (TAR) RNA from HIV-1 dissolved in the Pf1 phage ordering medium [8,9] was modulated by independently elongating each of its two helices by twenty-two Watson-Crick base-pairs [20,29]. The elongation renders the overall molecular shape, and consequently overall alignment, far less sensitive to collective motions of helices. It also serves to predefine overall alignment by fixing the principal axis of order (S_zz) to be nearly parallel to the elongated helix axis. A similar mutagenesis strategy that serves to alter the surface electrostatic properties has successfully been used by Bax and co-workers to modulate the alignment of proteins [30].

In RNA, extensive helix elongation (>20 base-pairs) is generally required to adequately decouple internal and overall motions. However, this results in an unfavorable increase in the size of the RNA under study and also necessitates preparation of two specifically labeled samples to minimize spectral overcrowding from elongation residues [29]. Many RNAs, including TAR bound to ligands [31] or at high monovalent and divalent ion concentrations [32], are globally rigid and may not require extensive helix elongation to decouple motions. In these cases, moderate degrees of elongation may offer an approach for modulating alignment. Even for globally flexible RNAs, moderate elongation may help expose collective helix motions and provide physical insights into the motional couplings themselves [33]. Here, we examine the utility of moderate degrees of helix elongation in modulating both the alignment and degree of motional couplings in a TAR mutant, EI(3)-TAR_m, in which the apical wild-type loop has been replaced with a UUCG loop and in which the terminal helix is elongated by three base-pairs (Figure 1a).

Figure 1.

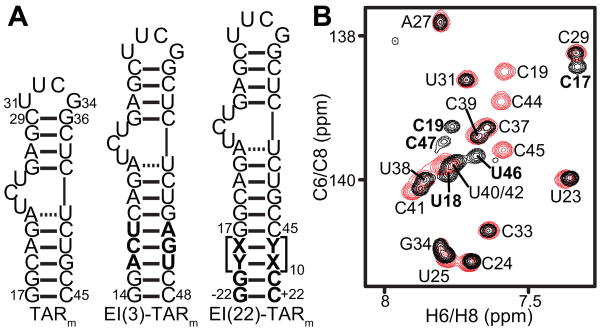
TAR_m constructs. (a) Secondary structures of TAR_m, EI(3)-TAR_m, and EI(22)-TAR_m. Differences between constructs are shown in bold. (b) 2D ¹H-¹³C HSQC spectrum of EI(3)-TAR_m (black) overlaid on the corresponding spectrum of TAR_m (red). TAR_m resonances are labeled in black, while peaks that belong only to EI(3)-TAR_m are shown in bold. All EI(3)-TAR_m experiments were conducted in NMR buffer (15 mM sodium phosphate, 25 mM sodium chloride, 0.1 mM EDTA and pH 6.4) at 298 K on an Avance Bruker 600 MHz NMR spectrometer equipped with a triple-resonance 5 mm cryogenic probe. ¹H, ¹³C, and ¹⁵N resonances were assigned by spectra overlay [29,43] and using standard homonuclear and heteronuclear 2D experiments, including an exchangeable NOESY and a 2D HCN experiment that correlates intranucleotide H8/H6 to N1/N9 to H1′.

2. Results and Discussion

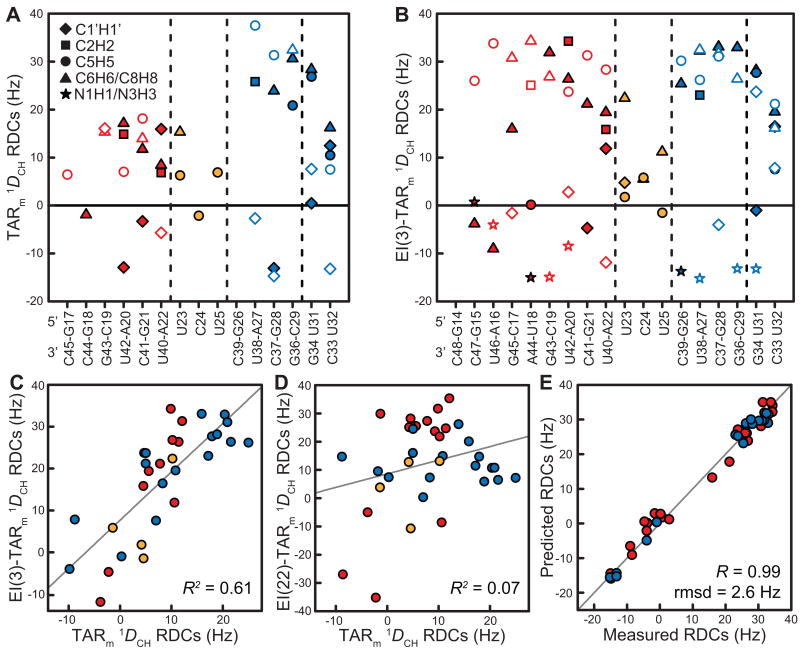
We prepared uniformly ¹³C/¹⁵N labeled EI(3)-TAR_m by in vitro transcription as previously described [34]. As shown in Figure 1b, spectra of EI(3)-TAR_m are in excellent agreement with those of non-elongated TAR_m, indicating that the elongation does not affect its structural and dynamical integrity, as reported previously for a twenty-two base-pair elongated TAR sample (EI(22)-TAR_m, Figure 1a) [20,29]. A total of 9 N-H and 53 C-H RDCs (Table S1) were measured in sugar (C1′H1′) and base (C2H2, C5H5, C6H6, C8H8, N1H1, and N3H3) moieties of EI(3)-TAR_m using ∼22 mg/ml of Pf1 phage as an ordering medium [8,35]. A plot of RDCs as a function of secondary structure is shown in Figure 2a and 2b for TAR_m and EI(3)-TAR_m, respectively. The RDCs measured in helix I of TAR_m are consistently attenuated relative to counterparts in helix II. This has previously been attributed to inter-helical motions and a smaller degree of order for helix I compared to helix II [36]. Differences between helix RDCs are far less pronounced in EI(3)-TAR_m, indicating that elongation of helix I by three base-pairs increases its degree of order relative to helix II. The poor agreement (R²=0.61) observed between the EI(3)-TAR_m and TAR_m RDCs (Figure 2c) qualitatively suggests that the three-base pair elongation modulates overall alignment and/or motional couplings. An even poorer correlation (R²=0.07) is observed upon elongating helix I by twenty-two base-pairs (Figure 2d), consistent with elongation-dependent modulation of alignment and/or motional couplings.

Figure 2.

Measurement of RDCs in EI(3)-TAR_m. One bond RDCs (¹D_CH and ¹D_NH) measured in (a) TAR_m and (b) EI(3)-TAR_m as a function of residue/secondary structure. Filled and open circles represent RDCs measured on the 5′and 3′ strand, respectively. RDCs have been normalized to those of EI(3)-TAR_m by the ratio of the ϑ_II values of EI(3)-TAR_m and TAR_m. See inset in Figure 2a for key. (c-d) Correlation plots between (c) TAR_m and EI(3)-TAR_m and (d) TAR_m and EI(22)-TAR_m RDCs. (e) Comparison of EI(3)-TAR_m RDCs measured in helix I (red) and helix II (blue) with values back-predicted using the best-fit order tensor and an idealized A-form helix and X-ray structure of the loop.

To characterize the alignment of EI(3)-TAR_m in phage, we used the RDCs measured in non-terminal Watson-Crick base-pairs and structurally stable loop residues to determine order tensors for each helix. The order tensors were determined by fitting measured RDCs to an idealized A-form helical geometry and an X-ray structure of the loop[37] as described previously [38-40]. An excellent fit was observed between the measured and back-predicted RDCs, indicating that both EI(3)-TAR_m helices are accurately modeled using an idealized A-form geometry as described previously for non-elongated [36] and elongated [20] TAR (Figure 2e).

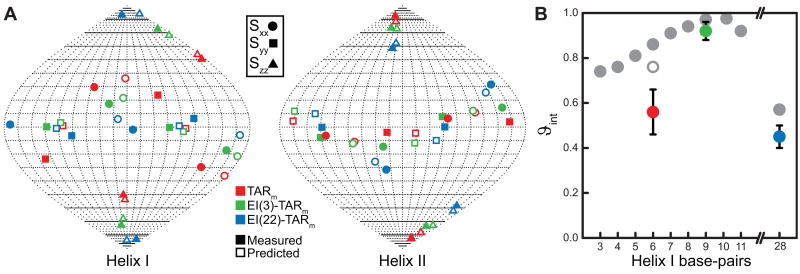
In Figure 3a, we use a Sauson-Flamsteed map to depict the best-fit principal orientational solutions (S_xx, S_yy, and S_zz) obtained for each helix in EI(3)-TAR_m. The orientational solutions are shown relative to a molecular frame in which the helix axis is oriented along the molecular z direction. For comparison, the corresponding order tensors reported previously for TAR_m [36] and EI(22)-TAR_m [20] are also shown. The estimated uncertainty in the S_zz orientations determined for helix I/II using the program Aform-RDC [39] is 7°/6°, 2°/2°, and 2°/4° for TAR_m, EI(3)-TAR_m, and EI(22)-TAR_m, respectively. In TAR_m, S_zz deviates by only ∼7° from the helix II axis but deviates by ∼40° from the helix I axis. As expected, elongation of helix I by three base-pairs tips S_zz towards its helical axis such that S_zz deviates by only ∼17° and is nearly fully aligned with the axis following a twenty-two base-pair elongation (∼7°). The three S_zz directions in TAR_m, EI(3)-TAR_m, and EI(22)-TAR_m do not fall along a common plane, most likely because the A-form helices deviate from perfect cylindrical axial symmetry (Figure 3a). The three base-pair elongation has an opposite, albeit smaller effect on helix II. The angle between S_zz and the helix II axis increases from ∼7° to ∼16° to ∼32° upon elongation by three and twenty-two base-pairs, respectively (Figure 3a). Changes are also observed in the S_xx and S_yy orientations (Figure 3a) and the asymmetry parameter (η) (Figure S1a, S1b), indicating that elongation modulates all five elements of the order tensor.

Figure 3.

Measured and predicted alignment of variable elongated TAR. (a) Sauson-Flamsteed maps showing the best-fit measured (filled symbols) and PALES-predicted (open symbols) order tensor frames (S_xx, S_yy, and S_zz) for helices I and II. Solutions are depicted relative to a molecular frame in which the helix axis is oriented along the z direction. (b) Measured (in color) and PALES-predicted (in gray) ϑ_int values (ϑ_int = ϑ_II/ϑ_I) as a function of helix I length. Note that the value for EI(22)-TAR_m corresponds to ϑ_int = ϑ_I/ϑ_II. The open circle corresponds to the predicted ϑ_int value of TAR_m when the two terminal base-pairs are excluded.

Elongation of helix I leads to changes in relative degrees of helix order that mirror those observed for the principal S_zz direction. In TAR_m, helix II dominates overall alignment, yielding an internal generalized degree of order ϑ_int = ϑ_I/ϑ_II = 0.56±0.1 that is consistent with large amplitude, inter-helical motions [36]. Elongating helix I by three base-pairs increases its level of order compared to helix II such that both helices now have comparable degrees of order (ϑ_int = ϑ_I/ϑ_II = 0.92±0.04). This, together with the similar angles between the S_zz direction and the two helical axes (Figure 3a), strongly suggests that the three base-pair elongation equalizes contributions of the two helices to overall alignment and pushes TAR into the motional coupling limit. Extending the elongation of helix I to twenty-two base-pairs drives the system towards the decoupling limit in which helix I dominates alignment (ϑ_int = ϑ_II/ϑ_I = 0.45±0.05). Because RNA helices are often not coaxially stacked, moderate degrees of elongation are expected to modulate alignment. This was verified using PALES simulations on a variety of RNAs following elongation of the terminal helix by three base-pairs (data not shown). The combination of helix-elongation with measurements of magnetic field-induced RDCs [26,28] may make it possible to access the maximum of five linearly independent sets of RDCs in nucleic acids. Access to such measurements will make it possible to more fully characterize the structural dynamics of RNA.

To rationalize the observed trends in the alignment of TAR as a function of elongation, we used the three-state dynamical ensemble determined previously using RDCs [20] in conjunction with electrostatic-induced alignment simulations using the program PALES [23,41] to simulate TAR alignment in phage at varying lengths of helix I elongation. The three-state ensemble is a discrete approximation of what is likely a continuous distribution involving many conformations. While we do not expect to observe quantitative agreement between measured alignment parameters and values predicted using this three-state ensemble approximation, we would like to obtain insights into the general trends observed for orientation and alignment upon helix elongation. An elongated helix I was superimposed onto each of the three TAR conformers of the ensemble, and PALES was used to predict the RDCs for each conformer. Bulge residues were not included in the three-state dynamical ensemble, so they were not included in PALES calculations. The three sets of RDCs simulated for each conformer were then averaged and used to compute order tensors for each helix. As shown in Figure 3a, we observe very good agreement between measured and predicted S_zz directions. The deviations range between 2-11° and 6-8°, for helices I and II, respectively. The simulations reproduce the observed non-planar approach of the S_zz direction towards the helix I axis with increasing elongation. Interestingly, the S_xx and S_yy directions (Figure 3a) and the asymmetry (Figure S1) are also reasonably well reproduced considering their much larger experimental uncertainty and given that exclusion of the bulge has a strong effect on these predicted values (data not shown). The simulations reproduce the increase in the helix I order compared to helix II upon helix I elongation (Figure 3b). Also, the simulated ϑ_int values reflect the observed trend. The larger discrepancy in TAR_m could arise from neglect of the bulge and fraying motions at terminal base-pairs which are likely to have a bigger effect on the small TAR_m compared to the other elongated constructs. Indeed, better agreement is observed for TAR_m when excluding the two terminal base-pairs in helix I (Figure 3b).

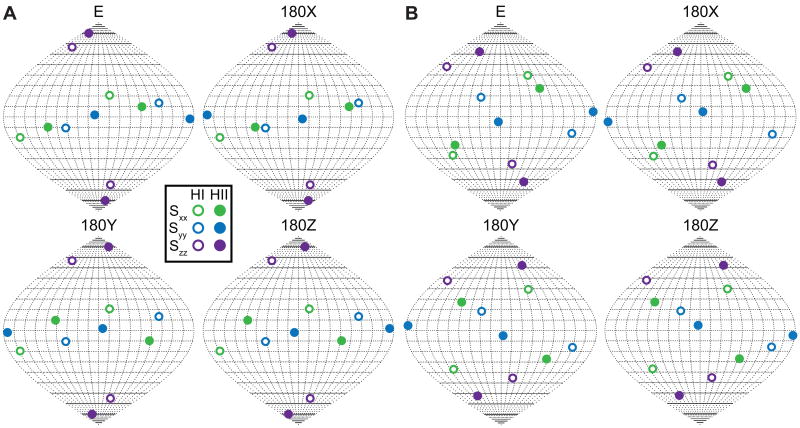
Independent RDC data sets are often used to overcome the 4^n-1 fold orientational degeneracy arising from superposition of the order tensors of n domains [11,22]. One of the consequences of having differential motional averaging effects due to inter-domain motions is that two sets of RDCs may not be reconcilable with a single inter-domain orientation [42]. This is the case for the RDC datasets measured in TAR_m, EI(3)-TAR_m, and EI(22)-TAR_m. As shown in Figure 4a, none of the four inter-helix structures assembled using the RDCs measured in TAR_m satisfy the orientational solutions obtained using the EI(3)-TAR_m RDCs. Similarly, a common solution does not exist when using RDCs from EI(22)-TAR_m (Figure 4b). Thus, the inability to reconcile RDCs measured in differentially elongated RNAs in this manner may be an indication that inter-helix motions are present. However, other sources of experimental uncertainty should also be ruled out.

Figure 4.

Difficulty in resolving degeneracies in determining the average orientation of TAR helices using multiple RDC data sets. Shown are the experimental order tensor frames (S_xx, S_yy, and S_zz, in green, blue, and purple, respectively) determined for helix I (open circles) and II (filled circles) using (a) EI(3)-TAR_m and (b) EI(22)-TAR_m RDCs shown relative to the PAS of the order tensor determined using the TAR_m RDCs. The different orientational solutions were generated by rotating helix II in the TAR_m PAS 180° degrees about the x, y, and z axis.

3. Conclusion

In conclusion, we show that modest degrees of helix-elongation can be used to modulate both overall alignment of RNA and the degree of motional couplings in a semi-predictable manner. Our results underscore the importance of exercising caution in interpreting similar levels of order for two domains (ϑ_int ∼1) in terms of inter-domain rigidity. In general, motional couplings obscure inter-domain motion and will often result in underestimated dynamics. Our data suggest that even moderate degrees of helix elongation may be used to push an RNA system outside the motionally coupled regime, though the degree of elongation needed will obviously vary from RNA to RNA.