Probing the folding transition state of ubiquitin mutants by temperature-jump induced downhill unfolding

Abstract

Crucial to revealing mechanistic details of protein folding is a characterization of the transition state ensemble and its structural dynamics. To probe the transition state of ubiquitin thermal unfolding, we examine unfolding dynamics and kinetics of wildtype and mutant ubiquitin using time-resolved nonlinear infrared spectroscopy after a nanosecond temperature jump. We observe spectral changes on two different timescales. A fast nonexponential microsecond phase is attributed to downhill unfolding from the transition state region, which is induced by a shift of the barrier due to the rapid temperature change. Slow millisecond changes arise from thermally activated folding and unfolding kinetics. Mutants that stabilize or destabilize the β strands III – V lead to decreased or increased amplitude of the μs phase, indicating that the disruption or weakening of these strands occurs in the transition state. Unfolding features from μs to ms can be explained by temperature-dependent changes of a two-dimensional free energy surface constructed by the native contacts between β strands of the protein. In addition, the results support the possibility of an intermediate state in thermal unfolding.

Introduction

One of the most striking features in protein folding is its cooperativity. Many small proteins consisting of less than 100 residues show a single step folding transition (1–3), which can be described by simple thermally-activated two-state chemical kinetics. In this picture, folding and unfolding can be understood by characterizing the folded and unfolded states, and the transition state between them. A characterization of the transition state is at the heart of describing the folding dynamics, the time-evolution of the protein structure, and the mechanistic details of folding.

Unfortunately, the short lifetime and small population prevent a direct observation of the transition state. Alternate strategies to characterizing the transition state involve understanding how the manipulation of microscopic variables influences the free energy surface. Of these approaches, Φ value analysis has been most widely used to map the transition state (4–6). In this method, the effect of a given point mutation can be quantified by the ratio of the free energy change of the transition state to that of the folded state (Φ value). A series of point mutations is used to deduce the involvement of each residue in the transition state. As a complementary method, ψ value analysis has been developed, which is useful for investigating the role of pair-wise interactions in the folding transition state (7–9). In this method, two histidine mutations (bi-His) are introduced in such a way that the two mutated residues can be linked by coordination to a metal ion. The stability of the bound residues can be controlled continuously by varying the concentration of divalent metal ions. This method has proven effective for stabilizing two β strands or a turn of an α helix.

Both Φ and ψ value analyses are indirect ways to map the transition state. Direct dynamic information of the transition state is hidden under the larger changes of the folded and unfolded state. An alternative approach is to observe the folding or unfolding dynamics directly using downhill folders for which no barrier to folding exists (10–12). Many small proteins, of which folding rates are close to the “folding speed limit” (13), show global (14, 15) or conditional downhill unfolding features (16), although some of the interpretations of these results remain controversial (17–19).

Ubiquitin is a 76-residue protein consisting of one α helix and five β strands (Fig. 1a), with folding behavior often interpreted in the context of two-state kinetics. However, several observations suggest a deviation from the simple two-state picture depending on experimental conditions. In spite of its small size, ubiquitin is divided into stable and less stable regions. A fragment study has reported that the N-terminal peptides (1–35) show a small population having a native-like structure while C-terminal peptides (36–76) form a nonnative structure (20, 21). Also a partially folded structure of ubiquitin including strands I and II and the α helix has been observed in the organic solvent and water mixture (22–24). The Φ value analysis has described the transition state of ubiquitin folding as localized in the β hairpin (strands I and II) and the α helix (25), a conclusion supported by molecular dynamics simulations (26). The extension of the transition state to strands V and III has been reported using ψ-value analysis (8, 9). In spite of these issues, all of these results suggest a sequential folding scenario in which folding of the more stable part N-terminal β hairpin and helix is followed by the rest.

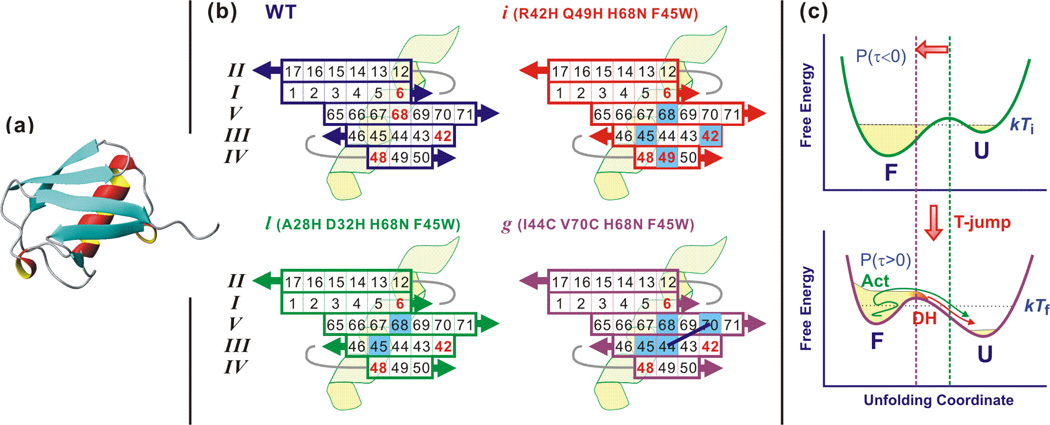
Figure 1.

Structure of ubiquitin, mutations, and T-jump experiment. (a) Crystal structure of wildtype ubiquitin composed of five β strands and one α helix. (PDB id: 1UBQ) (63)(b) Projection of the β-sheet registry of ubiquitin. Amino acid residue numbers are indicated in the β sheet. Positively charged residues are marked with red figures. Mutated residues are indicated with blue-filled square boxes. For mutant l, there are two more mutations at residue 28 and 32 located in the C-terminus (upper right part) of the α helix, which are not shown. Residue 44 and 70 in mutant g are covalently linked as connected with black lines. (c) A T-jump not only changes the relative stability of the folded and unfolded state but also induce a barrier shift towards the folded state. The latter prepares a small population near the barrier (transition state) that show non-exponential relaxation (downhill unfolding, DH) and the former appear as ms activated unfolding (Act).

The ability to observe sequential folding or unfolding dynamics of ubiquitin would benefit from fast initiation and detection methods. A ns temperature jump (T-jump) technique has been used to watch a time-evolution of the species from the transition state. The experimental concept is illustrated in Fig. 1c. A rapid T-jump induces a shift of the free energy barrier towards the folded well according to the Hammond postulate (27), positioning a small folded population near the barrier (A). This subensemble unfolds in a downhill manner. Unfolding of this species is temporally isolated (μs) from the main unfolding phase (ms) and provides direct information of the unfolding dynamics. The unfolding dynamics of ubiquitin’s β sheet has been probed using this rapid initiation followed by a structure-sensitive nonlinear infrared probe such as dispersed vibrational echo (DVE) (28) and two-dimensional infrared (2D IR) spectroscopy (29). As other experimental observations, these studies supported a sequential folding/unfolding scenario in that unfolding of less stable strands III-V precedes unfolding of the stable strands I and II (see Fig. 1b). Sequential unfolding has also been observed in the high temperature unfolding simulation (30). Based on these results, a two-dimensional free energy surface was proposed and calculated (31) consisting of two reaction coordinates, the number of native contacts between stable strands I and II and between less stable strands III – V. Finally, a temperature-dependent T-jump study has suggested an increased heterogeneity of the transition state at high temperature, namely multiple unfolding routes (32).

In this paper, we report dispersed vibrational echo (DVE) probed T-jump experiments to better understand the transition state and unfolding dynamics of ubiquitin. Three ubiquitin mutants are investigated. Two mutants have bihistidine substitutions in either the helix (Mutant l, residues 28,32) or across β strands III and IV (Mutant i, residues 42,49) (8). A third, bicysteine mutant (g, residues 44,70) uses a stabilizing synthetic crosslink across strands III and V (33). The change in the downhill unfolding amplitude that occurs by destabilizing or stabilizing strands III – V reveals the involvement of these strands in the transition state. The μs downhill unfolding and ms barrier crossing are described in the picture of the two-dimensional free energy surface. The increased and decreased downhill unfolding amplitude of mutant i and g support the presence of an intermediate state on the native-side of the rate-limiting barrier.

Materials and Methods

Materials

Wildtype ubiquitin (WT) was purchased from Sigma-Aldrich (U6253) and used without further purification. We use three of an extensive series of mutants that has been cloned in the studies of ubiquitin folding (8, 9, 33). These mutants, named i, l and g, have the following substitutions: i: R42H Q49H H68N F45W, l: A28H D32H H68N F45W, g: I44C V70C H68N F45W. To remove a trace of trifluoroacetic acid (TFA) added in the purification step, mutant samples were lyophilized under acidic conditions (0.18% DCl in D₂O). About 5 mg of each mutant sample was lyophilized twice more after dissolving in 500 – 800 mL of D₂O. The experiment was performed at a sample concentration of 30 mg/mL in the 0.35% DCl solution. The solution is loaded between two 1-mm thick CaF₂ windows separated by a 50-µm thick Teflon spacer, which is mounted on a temperature controlled brass cell. Temperature is controlled within 0.1°C by water circulation.

The experiments were performed in acidic condition for reversible thermal unfolding. Therefore, all side chain amine groups, indicated by red numbers in Fig. 1b, are positively charged. In WT, there are five positively charged residues in the β sheet. Since the side chains of Lys 6, Arg 42, and His 68 are oriented outward from the hydrophobic core, while those of the residue Lys 11 and Lys 48 penetrate inward, the repulsion between side chains of the strands I and II (Lys6 – Lys11), and III and IV (Arg42 – Lys48) would presumably be small and would not affect the stability of proteins. However, the repulsion between residues 6, 68, and 42, the side chains of which are on the same side, destabilizes the protein and lowers the melting temperature relative to neutral pH (34, 35).

Three different mutants are named according to the convention in Ref. (8) and (33). The locations of mutated residues are shown with blue-colored boxes in the projected β sheet in Fig. 1b. Mutant i and l are bi-His mutants of the β sheet and α helix, respectively, which were originally designed for ψ-analysis (8). However, we cannot utilize the metal-ion-induced ligation of the mutated residues because of the lower pH than the pK_a of His (6.5). At this condition, required for reversible unfolding, the side chain of the His residue is protonated and cannot bind to the metal ion. Instead, the mutation affects the protein stability by charge-charge repulsion and disrupting structure-stabilizing hydrogen bonding networks for the water in the vicinity of those residues. In all mutants, Phe 45 was mutated to Trp to allow fluorescence detection and His 68 is mutated to Gln to avoid an unwanted metal ion induced linkage in the original ψ-value analysis experiments (8, 9). The Trp mutation at residue 45 is known to destabilize the protein slightly by ~ 0.4 kcal/mol (36). On the other hand, removal of the charged His 68 stabilizes the protein.

Mutant g differs from i and l in that the β sheet is stabilized through a covalent linkage. In this mutant, residues 44 and 70 in strands III and V are mutated to Cys and then cross-linked with dichloroacetone to form a covalent -S-CH₂-CO-CH₂-S- bridge (33, 37). Therefore, the stability of the strands III and V is greatly increased. Control experiments with the unlinked bi-Cys mutant under excess dithiothreitol (DTT) were attempted; however, thermal aggregation occurred too rapidly at 58 °C (near the melting temperature) to obtain meaningful data. A quoted “mutant g” indicates the covalently linked version in this paper.

Equilibrium and transient data of WT were adopted from our previous study (32) for comparison with those of mutants.

Amide I vibrational spectroscopy

Amide I vibrational spectroscopy has extensively been used in protein folding research because of its spectral isolation from most sidechain vibrations and its sensitivity to the protein secondary structures (38). Amide I vibration is primarily a carbonyl stretching of the peptide backbone but characteristic collective modes are formed by electrostatic couplings according to the symmetries of secondary structures (39–44). These couplings induce a big splitting between two vibrations of the anti-parallel β sheet, ν_⊥ and ν_‖ mode located <1650 cm⁻¹ and >1680 cm⁻¹, respectively. The intensity and the position (or red-shift) of the ν_⊥ mode reflect the size of the β sheet and reports on the number of β strands in contact (41). The ν_‖ mode is insensitive to the size of the β sheet, but it provides the evidence of the presence of at least two β strands, the β hairpin. Vibrations of the α helix are also composed of A and E₁ vibrations, but the two modes are not resolved due to the small splitting compared to the wide intrinsic linewidth of the infrared spectrum. Also, vibrations of the random coil component overlap spectrally with the α helical peak. Empirical assignments of the α helical and the random coil vibrations are 1640 cm⁻¹ and 1650 cm⁻¹, respectively (45, 46). In this paper, we will focus on the β sheet vibrations, especially the ν_⊥ mode.

Nonlinear infrared spectroscopy

Thermal unfolding of proteins was monitored by DVE spectroscopy (47, 48). Three temporally coincident femtosecond pulses (90 fs in FWHM, λ = 6 µm) are focused on the sample (100 µm diam.) and the emitted third-order nonlinear signal is dispersed onto the liquid nitrogen cooled HgCdTe (MCT) array detector by a monochromator. The DVE spectrum is a one-dimensional projection of the 2D IR spectrum, which monitors couplings between vibrations by cross-peak formation. Recently, transient 2D IR spectroscopy has been reported (29, 49) but we performed transient DVE spectroscopy in this paper due to the fast aggregation of mutant ubiquitin. In spite of its one-dimensional nature, DVE spectroscopy differs from FTIR because of its sensitivity to vibrational couplings, and has been used to equilibrium and transient thermal unfolding of proteins and peptides (28, 48, 50, 51). Experimental details of ultrafast nonlinear IR spectroscopy have been described elsewhere (47).

Laser temperature jump

The laser T-jump has been widely used to monitor fast folding/unfolding kinetics of various proteins and peptides (10, 11, 51–55). In this paper, approximately 10°C was jumped from the temperature near the melting points of proteins. A 5 mJ, 7 ns T-jump laser pulse (λ = 2 µm) is generated from a BBO-based optical parametric oscillator (OPO) pumped by a frequency doubled Q-switched Nd:YAG laser. A T-jump pulse is focused (500 µm diam.) and overlapped with probe (6 µm) pulses. The pulse excites the first overtone of the D₂O solvent’s O-D stretching vibration, and subsequent ps vibrational relaxation results in the temperature rise on the same timescale of the T-jump pulse duration of 7 ns. A fine delay τ between the T-jump pulse and the first probe pulse is controlled by an electronic delay generator with 2 ns accuracy. Since the T-jump laser and the 6 µm femtosecond probe are run by 20 Hz and 1 kHz, respectively, 50 pulses can probe spectral changes from τ to 49 ms + τ with a 1 ms interval after a T-jump. Details of the T-jump experiments including delay controls have been reported elsewhere (49).

Results

Equilibrium thermal unfolding

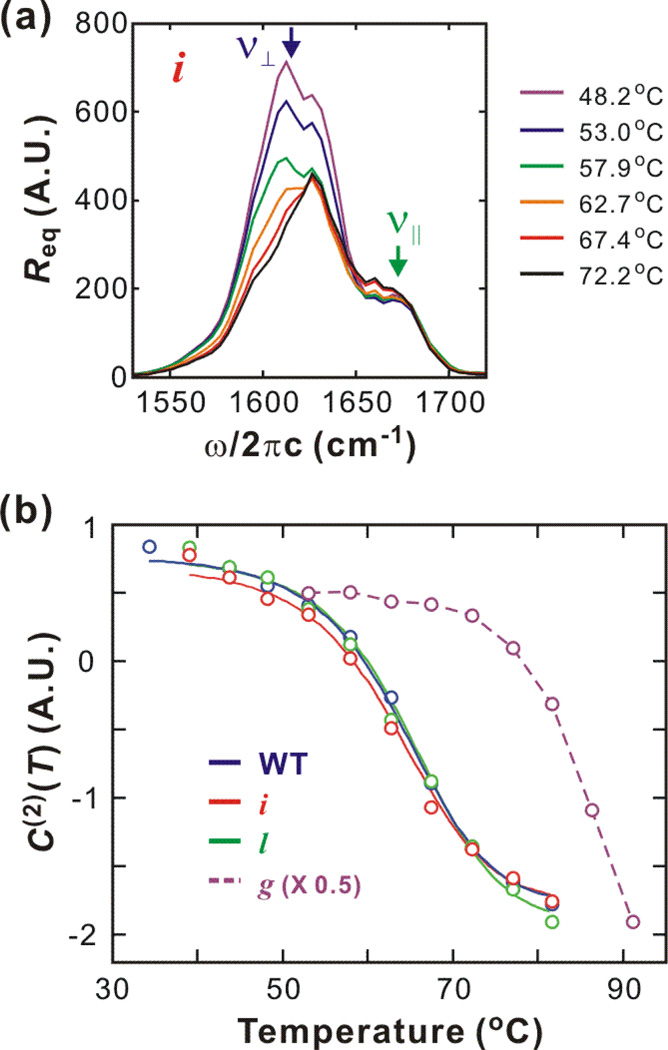
The representative equilibrium thermal unfolding of ubiquitin monitored through their DVE spectra are shown with melting curves in Fig. 2. Temperature dependent spectra of WT and three mutants are similar though only DVE spectra of mutant i are shown in Fig. 2a. The spectral intensity in the ν_⊥ region decreases and the peak shifts to the blue side as a result of the disruption of the β sheet. Also, the random coil component between the ν_⊥ and ν_‖ modes slightly increases. The melting curves are constructed from C⁽²⁾(T), the second component from singular value decomposition (SVD) (Fig. 2b). A sigmoid shape is fitted to the equations below (56) to obtain the thermodynamic parameters summarized in Table 1

$$\begin{array}{cc}\hfill K& =\frac{P_{\mathrm{U}}}{P_{\mathrm{F}}}=\text{exp}(-\mathrm{\Delta }G(T)/\mathit{\text{RT}}),\hfill \\ \hfill \mathrm{\Delta }G(T)& =\mathrm{\Delta }H(T)-T\mathrm{\Delta }S(T)\hfill \\ & \approx -\mathrm{\Delta }{S}_{\mathrm{m}}(T-T_{\mathrm{m}})-\frac{\mathrm{\Delta }{C}_{\mathrm{p}}}{2T_{\mathrm{m}}}{(T-T_{\mathrm{m}})}^2.\hfill \end{array}$$ (1)

Here, ΔH = ΔH_m + ΔC_p (T - T_m) and ΔS = ΔS_m + ΔC_p ln (T - T_m)are temperature-dependent enthalpy and entropy of unfolding. ΔH_m and ΔS_m are the enthalpy and entropy of unfolding at the melting temperature T_m (= ΔH_m/ΔS_m), respectively. Higher-order temperature terms are ignored in the Taylor expansion of ΔS. The fractional population of the unfolded and folded state, P_U and P_F satisfy a relation P_U + P_F = 1. The heat capacity change, ΔC_p is assumed to be constant for the mutants, as a result of the large uncertainty in its determination relative to the other variables. Floating ΔC_p for all mutants resulted in unreasonable variation. Assuming that the variation of ΔC_p is smaller than the error for WT, we used the same fixed value for mutant i and l. The similar errors for other variables confirm the validity of this procedure.

Figure 2.

Equilibrium thermal unfolding of wildtype ubiquitin and three mutants, i, l, and g. (a) Temperature-dependent equilibrium DVE spectra of mutant i. (b) Melting curves (solid line) are constructed by thermodynamic fitting (two-state) to the SVD 2nd components (open circle). For mutant g, thermodynamic analysis is not possible due to incomplete unfolding, and a dashed line is added to assist the reader.

Table 1.

Thermodynamic parameters of wildtype and mutant ubiquitin.

	Tm (°C)	ΔHm (kcal/mol)	ΔSm (cal/mol·K)	ΔCp (cal/mol·K)
WT	64.0 (± 0.4)	40.9 (± 1.4)	121 (± 4)	1300 (± 200)
i	63.2 (± 0.4)	39.4 (± 1.4)	117 (± 4)	1300a
l	64.9 (± 0.4)	40.9 (± 1.4)	121 (± 4)	1300a

^aFitting was conducted with ΔC_p fixed to the WT value.

The melting temperatures of WT, mutant l, and mutant i are similar. The melting curve of mutant g shows that thermal unfolding is not complete even at 91°C. Therefore, thermodynamic parameters cannot be obtained from mutant g.

Transient thermal unfolding

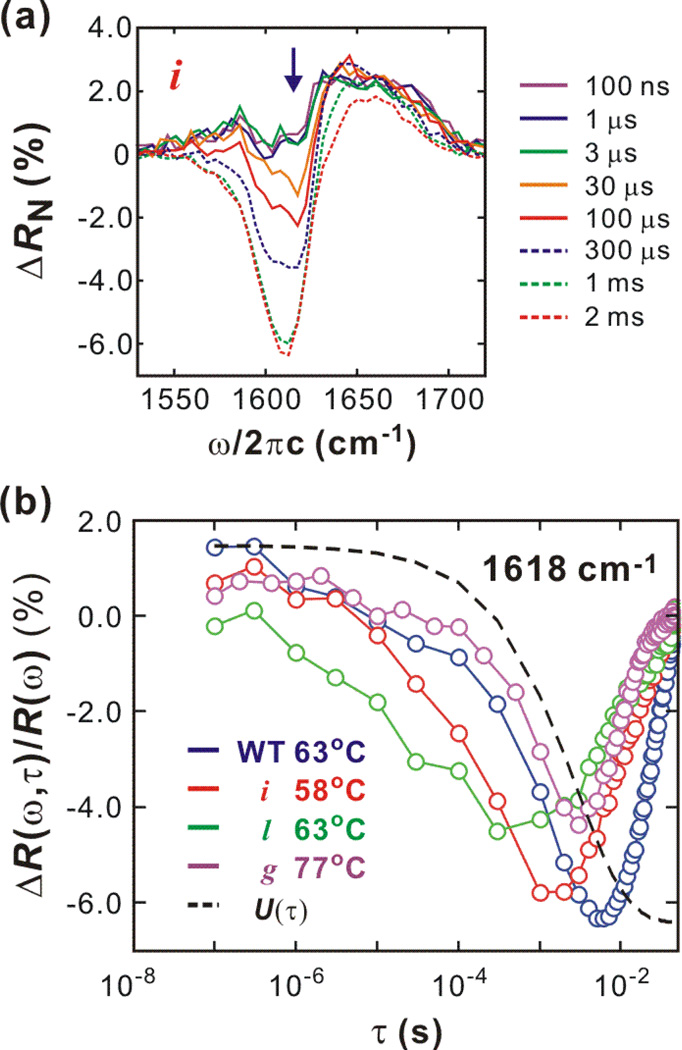
Typical transient spectral changes from 100 ns to 2 ms are shown in Fig. 3a. DVE difference spectra ΔR(ω,τ) = R(ω,τ) − R_ref(ω,T_i) are normalized by the maximum of the reference spectrum R_ref(T_i) obtained by the two probe pulses preceding a T-jump pulse. (Note that there are 50 probe pulses between two T-jump pulses.) At the earliest delay (100 ns), there are positive changes over the whole spectral range, which result from the increased solvent transmission of the 6 µm probe beam at the elevated temperature. A gradual signal loss in the ν_⊥ region and an increase in the random coil region indicate thermal unfolding of the β-sheet as seen in the equilibrium changes in Fig. 2a.

Figure 3.

Transient thermal unfolding initiated by a T-jump. (a) Shown are transient DVE difference spectra of mutant i (57.9°C → 68.2°C). (b) Spectral change of ν_⊥ mode (1618 cm⁻¹) indicated with a arrow in (Fig. 3a) and the temperature relaxation profile U(τ). The upturn on the ms time-scale is due to the temperature recovery of the observation cell.

Transient spectral changes of the ν_⊥ region (ω = 1618 cm⁻¹) from nanosecond to millisecond time scales are plotted in Fig. 3b along with the temperature relaxation profile, U(τ). The data show a variation of unfolding timescales between mutants. The spectral difference is normalized by the reference signal at the same frequency as ΔR(ω,τ)/R_ref(ω,T_i). In general, the proteins unfold over time scales from several μs to several ms. As the temperature of the cell re-equilibrates (τ_r = 2.7 ms), the protein begins to refold before unfolding is complete. The system refolds after reaching a balanced position (k_uP_F = k_fP_U) where incomplete unfolding balances with refolding. However, the timescales of unfolding and refolding, and the unfolding spectral features are different for each protein. The unfolding of the WT consists of two distinct relaxations on the μs and ms timescale. On the other hand, those two components are not clearly resolved in mutant i and l. Also, they show faster unfolding than WT. Unfolding of mutant g occur mostly on the ms timescale. The crossover to refolding kinetics at the balanced position differs by several ms.

Unfolding kinetics

We describe here the analysis methods briefly. The details for WT have been described in Ref. (32). For the improvement of the signal-to-noise ratio, transient data of the ν_⊥ region (1582 – 1651 cm⁻¹) of each mutant are extracted using SVD. Since the temperature relaxation is faster than ms unfolding, the slow unfolding part is complicated by the temperature-dependent transmission change. We assume that the temperature-dependent part is a product of the temperature profile, U(τ), and the difference spectrum at the earliest delay, 100 ns and subtract this from the DVE difference spectra prior to SVD (32).

$$\mathrm{\Delta }\mathrm{\Delta }R(\omega ,\tau )=\mathrm{\Delta }R(\omega ,\tau )-U(\tau )·\mathrm{\Delta }R(\omega ,\tau =100\text{ ns}).$$ (2)

$U(\tau )=\text{exp }\left[-{(\tau /{\tau }_r)}^{\beta }\right]$ (β = 0.68 and τ_r = 2.7 ms) is obtained from the transmission changes at 6 µm. Then, the relative spectral relaxation profile is constructed using the first SVD component coefficient C⁽¹⁾(τ), the first component spectrum $R_{\text{SVD}}^{(1)}$ and equilibrium difference ΔR_eq,

$$\mathrm{\Delta }{R}_{\text{rel}}(\tau )=C^{(1)}(\tau )·\frac{\text{Max}\left|R_{\text{SVD}}^{(1)}\right|}{\text{Max}\left|\mathrm{\Delta }{R}_{\text{eq}}\right|}.$$ (3)

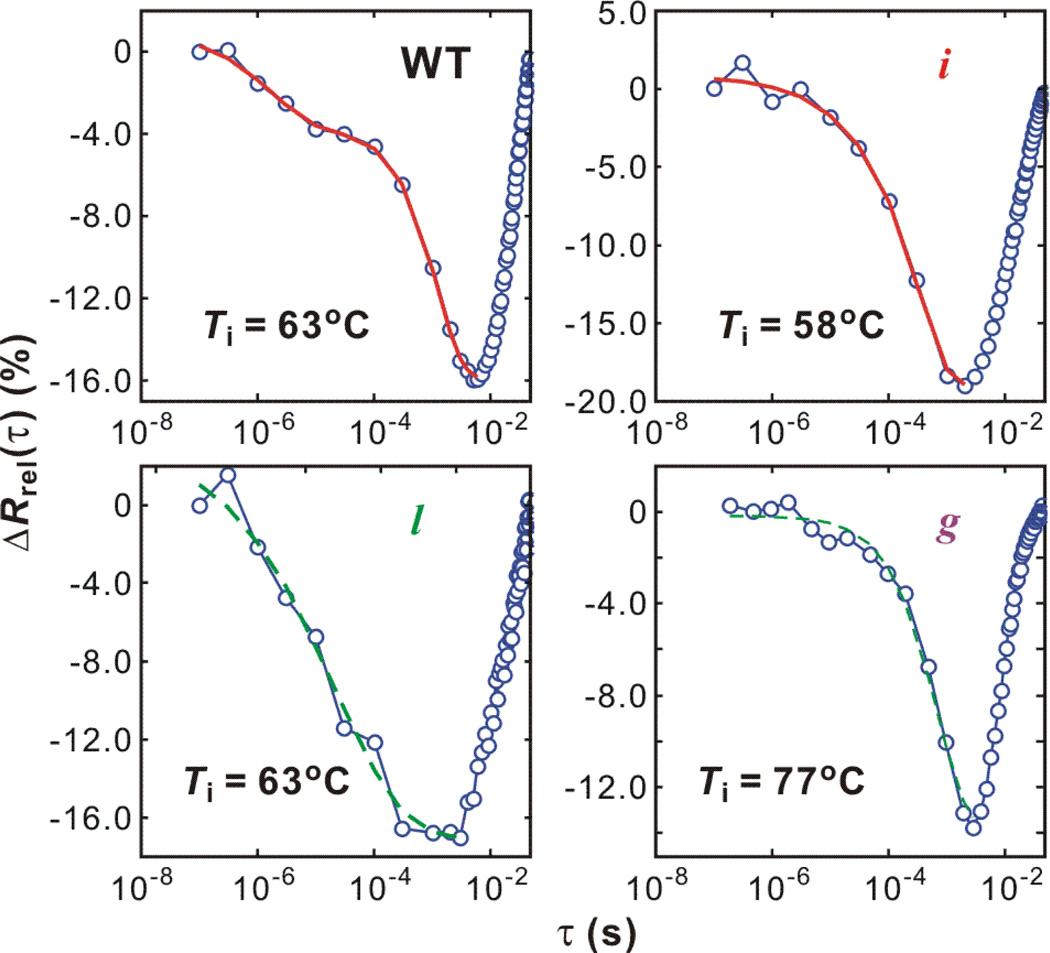
The results are shown in Fig. 4 and are described below.

Figure 4.

Relaxations of the ν_⊥ region (1582 – 1651 cm⁻¹) of the wildtype ubiquitin and mutants. The unfolding part are fitted with stretched exponential + exponential (red) or a single stretched exponential (green dashed) function.

The most important feature of WT unfolding is the relaxation on two different timescales. The faster period occurs on several μs, which is close to the speed limit of protein folding (32) and is attributed to the barrier-free unfolding from the transition state (28, 32). The slow unfolding part on the ms timescale is an activated, barrier-crossing process. To obtain exact timescales, the unfolding part is fitted with a sum of stretched exponential (μs) and exponential (ms) functions.

$$\mathrm{\Delta }{R}_{\text{rel}}(\tau )=A_{\mathrm{\mu }\mathrm{s}}\text{ exp }\left[-{(\tau /{\tau }_{\mathrm{\mu }\mathrm{s}})}^{\beta }\right]+A_{\text{ms}}\text{ exp}[-\tau /{\tau }_{\text{ms}}],$$ (4)

where τ is the delay time ranging from 100 ns to the time when ΔR_rel(τ) reaches its minimum, the balanced position. Fitting results are summarized in Table 2. Also, the relative folded population near the barrier (P_μs/P_F) at T_i is calculated from P_μs = A_μs·(P_F(T_i) − P_F(T_f)). The equilibrium population P_F(T) is calculated using Eq. (1). τ_μs provides the stretched exponential unfolding rate constant of 1/(1.8 μs). Due to the temperature change on the ms timescale, the activated unfolding time (1/k_u) cannot be obtained from the 1–10 millisecond window. As a result of the time-scale separation, In Eq. (4) we use the exponential function for the ms unfolding only as a guide function to help obtain exact μs unfolding parameters. A more careful analysis of the ms behavior follows.

Table 2.

Relaxation parameters obtained from the unfolding portion of the SVD analysis on the ν_┴ region (1582 – 1651 cm⁻¹)^a

	Ti – Tf (°C)	βb	τµs (µs)b	Aµs (%)c	Aµs + Ams (%)c	Pµs/PF (%)d
WT	62.7 – 74.3	0.62 (± 0.24)	1.8 (± 0.5)	4.8 (± 0.6)	17.0 (± 0.6)	3.8 (± 0.5)
i	53.0 – 63.3	0.61 (± 0.33)	9.3 (± 4)	4.3 (± 1.3)	13.2 (± 1.5)	1.8 (± 0.6)
	57.9 – 68.2	0.57 (± 0.95)	45.3 (± 24.9)	6.3 (± 3.8)	19.8 (± 4.8)	3.8 (± 2.3)
	62.7 – 74.5	0.83 (± 0.44)	20.7 (± 28.6)	11.9 (± 6.8)	22.6 (± 11.9)	9.4 (± 5.4)
l	57.9 – 67.3	0.29 (± 0.07)	76 (± 56)	8.9 (± 1.3)	–	3.2 (± 0.5)
	62.7 – 71.9	0.38 (± 0.09)	21 (± 10)	20.5 (± 2.5)	–	7.2 (± 0.9)
g	72.2 – 83.8	0.95 (± 0.11)	646 (± 57)	9.8 (± 0.2)	–	–
	77.0 – 88.6	0.87 (± 0.08)	725 (± 60)	13.6 (± 0.2)	–	–

^aUnfolding traces of WT and mutant i are fit to the sum of a stretched exponential (µs part) and an exponential (ms part) function (A_µs·exp(−(τ/τ_µs)^β) + A_ms·exp(−τ/τ_ms)) while the whole unfolding traces of mutant l and g are fit to a stretched exponential function.

^bβ and τ_µs are the stretched exponential parameters for the µs relaxation part.

^cA_µs and A_ms are the relative amplitudes of the µs and ms relaxation compared to the expected, equilibrium-determined change to the final temperature of the T-jump.

^dP_µs/P_F is the relative amplitude change during the µs relaxation to the folded population at the initial temperature.

Compared to WT, the barrierless unfolding of mutant i is slower (9 – 45 μs) but its amplitude is bigger than that of WT at similar temperature (Table 2). The unfolding transients of mutant l and g are fit to a single stretched exponential because either the μs component or ms component is small. Unfolding of mutant l is highly heterogeneous (β < 0.4) whereas the high β value of mutant g indicates that the fast barrierless unfolding is minimal. This indicates that the stabilization of the strands III and V by crosslinking removes the barrier shift and downhill unfolding relaxation present in the WT. Such an observation is expected if disorder of the III-V strand contacts determines the position of the WT transition state and leads to the μs downhill unfolding population.

Refolding kinetics

Although the determination of the ms unfolding kinetics cannot be made accurately, we can still obtain the refolding kinetics after the temperature re-equilibrates. The temperature after 10 ms is approximately same as T_i (less than 1°C difference), and the folding and unfolding rates are essentially constant. In this case, an exponential fit of the refolding part gives the relaxation rate that is the sum of the folding and unfolding rates. (k_r = k_f + k_u) Using this value and the equilibrium constant (K = k_u/k_f) obtained from the equilibrium measurement, folding and unfolding rates can be obtained. These values are summarized in Table 3.

Table 3.

Parameters for refolding kinetics obtained from the refolding portion of the transients after temperature re-equilibration.

	T (°C)	τr (ms)	kf (s−1)	ku (s−1)
WT	62.7	16.7 (± 0.6)	33 (± 2)	27 (± 3)
i	53.0	14.9 (± 0.4)	55 (± 2)	12 (± 3)
	57.9	14.1 (± 0.3)	50 (± 2)	21 (± 2)
	62.7	11.8 (± 0.4)	44 (± 2)	41 (± 3)
l	57.9	18.9 (± 1.1)	40 (± 2)	13 (± 4)
	62.7	17.3 (± 1.0)	33 (± 2)	23 (± 4)
g	72.2	8.3 (± 0.2)	–	–
	77.0	8.4 (± 0.1)	–	–

The relaxation rate (k_r) of mutant g is the fastest. This increase may be due to the experiment being performed at the elevated melting point where solvent viscosity is decreased and chain diffusion is faster. The barrier to unfolding of mutant i is lower than that of WT as seen from the faster unfolding rate and the higher unfolding population near the barrier. On the other hand, the refolding relaxation of mutant l is slower than those of WT and mutant i indicating the higher barrier, which is contradictory to fast μs unfolding of mutant l. Because the melting temperatures of mutant l and WT are very close, ms unfolding (barrier crossing) of mutant l will be slower than that of WT as its slower refolding. As explained earlier, the faster temperature re-equilibration (τ_r = 2.7 ms) than barrier-crossing unfolding makes thermal unfolding incomplete, and slower unfolding of mutant l results in the smaller ms unfolding amplitude. In fact, the timescale and amplitude obtained from the global fit (a single stretched exponential) of mutant l unfolding (Table 2) are similar to those of μs unfolding of mutant i. Therefore, the unfolding phase of mutant l is dominated by a barrierless process and the amount of the ms unfolding is very small due to the higher barrier.

Discussion

Unfolding mechanism and origin of microsecond unfolding

A temperature dependent barrier shift illustrated in Fig. 1c is the basis of our interpretation of unfolding on the two distinct timescales: μs downhill process and ms barrier crossing. However, this one-dimensional picture does not provide any structural information during unfolding. In earlier work, a two-dimensional free energy surface of thermal unfolding of ubiquitin was proposed based on the observation of non-coincident relaxation of the ν_⊥ and ν_‖ modes on the μs timescale (28). This free energy surface is illustrated in Fig. 5a for WT. Signal changes of these two vibrational modes report on the reduction of size of the β sheet following by disappearance of the β hairpin, which indicates a sequential unfolding of the β sheet. This observation and the numerous experimental and theoretical results supporting the stability of the β hairpin consisting of the strands I and II (20–26) suggest a free energy surface consists of two reaction coordinates: the number of native contacts between the stable β strands (I and II) and between the less stable β strands (III – V). The temperature dependence of this free energy surface of ubiquitin unfolding has been investigated by statistical mechanical calculations (31).

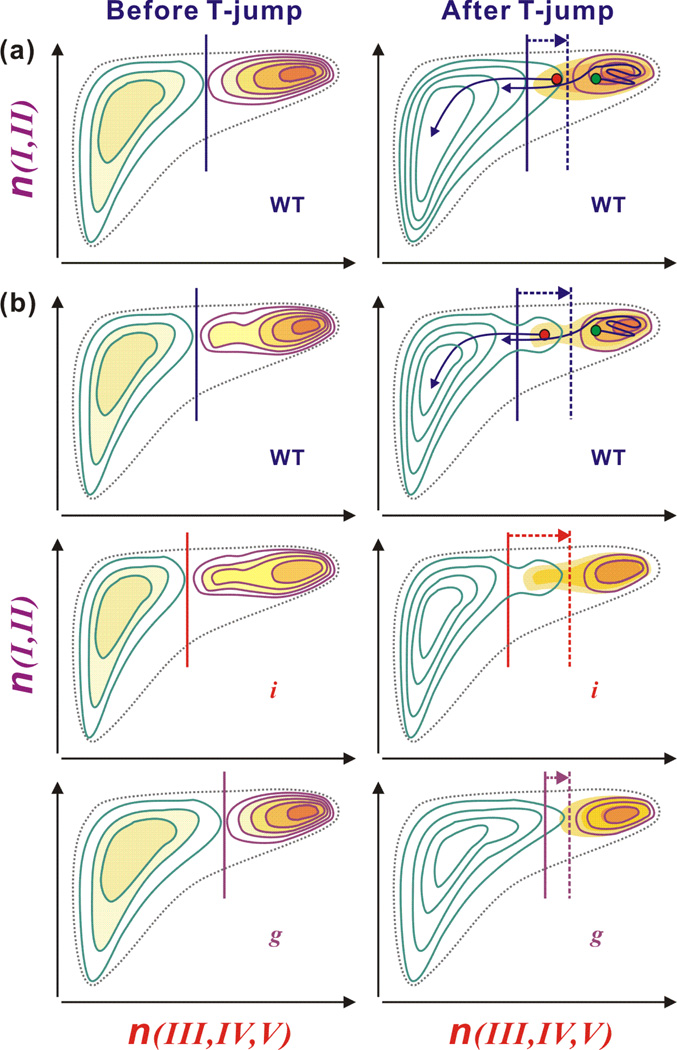
Figure 5.

Proposed free energy surfaces. Vertical and horizontal axes indicate the number of native contacts between the stable strands I and II (n(I, II)) and between the less stable strands III to V (n(III, IV, V)), respectively. Vertical solid and vertical dashed lines indicate the barrier position before and after the T-jump, respectively. (a) Free energy surfaces for WT in the absence of the intermediate state. The barrier shift by a rapid temperature jump towards the folded well induces downhill unfolding of the folded population located in the unfolded side of the new barrier (red dot), which is followed by ms unfolding from the folded well (green dot) across the barrier. (b) Free energy surfaces in the presence of the intermediate state where strands III and V are partially folded. For WT, the intermediate state belongs to the folded side before the temperature jump and the barrier is formed between the intermediate state and the unfolded state. At higher temperature after the T-jump, the intermediate state belongs to the unfolded side with a negligible barrier and the major barrier is formed between the intermediate state and the folded state. In this case, the partially unfolded protein at the intermediate state unfolds in a downhill manner on the μs timescale, which is also followed by ms unfolding. For mutant i, the unfolding features is similar to those of WT, but the intermediate state is more populated due to the destabilization of the strands III and IV in the folded state. The more populated intermediate state results in the μs unfolding of larger amplitude. In the case of mutant g, the intermediate state almost disappears because of the stabilization of the strands III and V, which removes the barrier between the intermediate state and the folded state at all temperature.

In the proposed free energy surface, the transition state is characterized by fully folded stable strands I and II and partially folded strands III and V, consistent with the extended transition state identified using ψ value analysis (8, 9). Upon T-jump, the transition state moves towards the folded well along the coordinate n(III, IV, V) and the population positioned around the barrier unfolds in a downhill manner, first along n(III, IV, V) (unfolding of the strands III – V) and then along n(I, II) (unfolding of the remaining β hairpin). In this picture, therefore, the amplitude of this fast phase will be dependent on the stability of strands III – V. This is consistent with the increased (decreased) amplitude of the μs component for mutant i (g) upon destabilization (stabilization) of strands III – V. In Ref. (8), the ψ-values for mutant l and i were unity and near zero, respectively. For mutant g, the ϕ^crosslink value was fractional while the ψ-value for a biHis analog was near unity (33). These results indicate that in the TES, the c-terminal portion of the helix is native-like while the strands III and V are associated in a near-native arrangement but strands III and IV are not associated. However, this transition state cannot explain the amplitude variation of the μs unfolding in mutant i and g in thermal unfolding. Therefore, we conclude that both strand III and V are partially folded in the transition state at high temperature and low pH.

Intermediate state

The presence of the intermediate state in ubiquitin folding has long been under debate because of the controversial results from similar experiments (57–61). In stopped-flow measurements, the roll-over at low denaturant concentration in the chevron plot is used to argue for an early intermediate state. For ubiquitin, this roll-over appears depending on experimental conditions such as the concentration of the protein and the stabilizing salt and temperature (60). Sosnick and co-workers have pointed out that this roll-over can result from an artifact in fitting when the relaxation rate is close to the dead time of the apparatus and is affected by the burst phase (58, 59). In addition, results are also affected by the method of probing and the location of the chromophore. Recently, folding of different part of ubiquitin has been monitored by multiple tryptophan substitutions, which is interpreted as the presence of the late but misfolded intermediate state (62).

In a previous temperature-dependent thermal unfolding study of WT ubiquitin, we noted that the μs unfolding population is much larger than the amount deduced from the barrier height of 7 kcal/mol (32), which may indicate the presence of the intermediate state on the native-side of the barrier in the thermal unfolding case as well. In Fig. 5b, we illustrate an alternate free energy surface in the presence of the intermediate state, consistent with the present experiments and ψ-analysis. An on-pathway intermediate located between the folded and unfolded state has strands III and V partially disordered, while strand IV is unfolded. At low temperature, the intermediate state is the part of the folded well and the rate limiting folding barrier is located between the intermediate state and the unfolded state. The barrier between the intermediate state and the folded state is small or negligible. The μs unfolding also originates from a barrier shift towards the folded well upon T-jump. However, in this case, the presence of the intermediate state can lead to a larger barrier shift that positions the major folding barrier between the intermediate and the folded state. (See Fig. 5b) Also, the barrier between the intermediate and unfolded state becomes small or negligible, which induces a barrierless unfolding with bigger amplitude than expected in the two-state system.

For mutant i, the situation is similar but the intermediate state is more populated because the energy difference between the intermediate state and the folded state is smaller than that of WT due to the destabilization of the strands III and IV. The more populated intermediated state results in the bigger amplitude of μs unfolding. On the other hand, the stabilization of the strands III and V by crosslinking removes the barrier between the intermediate state and the folded state at all temperatures, resulting in negligible μs unfolding of mutant g (Fig. 5b).

Conclusions

The transition state of thermal unfolding of ubiquitin has been investigated by a combination of site-specific mutations and a laser T-jump experiment probed by DVE spectroscopy. We compare the amplitudes of the non-exponential μs unfolding relaxation between mutants and WT, which reflects population changes near the transition state. The destabilization of the β strands III and IV (mutant i) induces an increased μs unfolding amplitude whereas the stabilization of contacts between strands III and V (mutant g) results in its decrease. Based on these observations, we conclude that the transition state of WT is extended to strands V and III at the thermal melting temperature. Also, the observation of a larger μs unfolding amplitude than expected from two-state kinetics supports the presence of an intermediate state. These observations were discussed in terms of a modified two-dimensional free energy surface. In addition, several observations in mutant l such as the origin of faster unfolding in spite of a higher barrier compared to the mutant i and WT remain unanswered but more through mutation studies are required for quantitative analyses.

Abbreviations

DVE

Dispersed Vibrational Echo

T-jump

temperature jump

SVD

singular value decomposition

2D IR

two-dimensional infrared

WT

wildtype