Abstract
Many recently discovered non-coding RNAs do not fold into a single native conformation, but rather, sample many different conformations along their free energy landscape to carry out their biological function. Unprecedented insights into the RNA dynamic structure landscape are provided by solution-state NMR techniques that measure the structural, kinetic, and thermodynamic characteristics of motions spanning picosecond to second timescales at atomic resolution. From these studies a basic description of the RNA dynamic structure landscape is emerging, bringing new insights into how RNA structures change to carry out their function as well as applications in RNA-targeted drug discovery and RNA bioengineering.
Introduction
Accompanying the discovery of non-coding RNAs (ncRNAs) as abundant players in gene expression and regulation is the growing realization that most ncRNA sequences do not code for a single native conformation, but rather sample many different conformations from their free energy landscape1,2 to carry out their biological function. For example, many ncRNAs function as genetic switches by transitioning between entirely different secondary structural forms in response to a wide range of cellular stimuli3,4. Not only do the structural characteristics of the different states have to be optimized to carry out distinct functions, transitions between them have to occur at dedicated timescales and be triggered by specific cellular signals. Thus, a deep molecular understanding of how ncRNAs perform their functions requires insights into how RNA dynamically samples different conformations along its energy landscape and how this landscape is in turn modulated by cellular cues2.
Beyond understanding function, there are a multitude reasons that are motivating studies of RNA dynamics at atomic resolution. First, RNA is exploding in its importance as a drug target5 and a broader dynamic view of the conformations populating the energy landscape1 is now widely recognized as essential for successfully implementing structure-based approaches in lead compound discovery and optimization2,6. Second, experimental data probing the dynamic aspects of RNA structure is also urgently required for the continued testing and improvement of computational force fields, which remain severely underdeveloped for nucleic acids as compared to proteins7. Third, a predictive understanding of RNA dynamics will also enable the design of RNA-based devices whose functionality often depends on dynamic transitions in structure.
The free energy landscape1 provides a unified and complete description regarding the dynamic properties of RNA that are relevant for understanding function (Fig. 1, landscape). Here, the free energy is specified for every conformation that can be adopted by the RNA. The fractional population of a given conformer then depends on its relative free energy, whereas the rate with which two conformers interconvert depends on the free energy barrier that separates them. Cellular cues perturb the free energy landscape, diminishing barriers and/or stabilizing conformers that are otherwise unfavorable, and thereby redistribute the conformer populations to effect specific biological outcomes. While rich in information, the free energy landscape is very complex, and cannot be measured experimentally. Fortunately, important insights into biological function can be obtained by focusing on a sub-set of conformers that populate minima along the energy landscape. Studies increasingly show that such ‘low-hanging fruit’ conformers are often the ones that are stabilized by cellular cues to carry out biological function8–10. These more appreciably populated conformers are also more amenable to experimental characterization using spectroscopic techniques that probe dynamic fluctuations in structure along the energy landscape. We will refer to this partial energy landscape as the ‘dynamic structure landscape’.
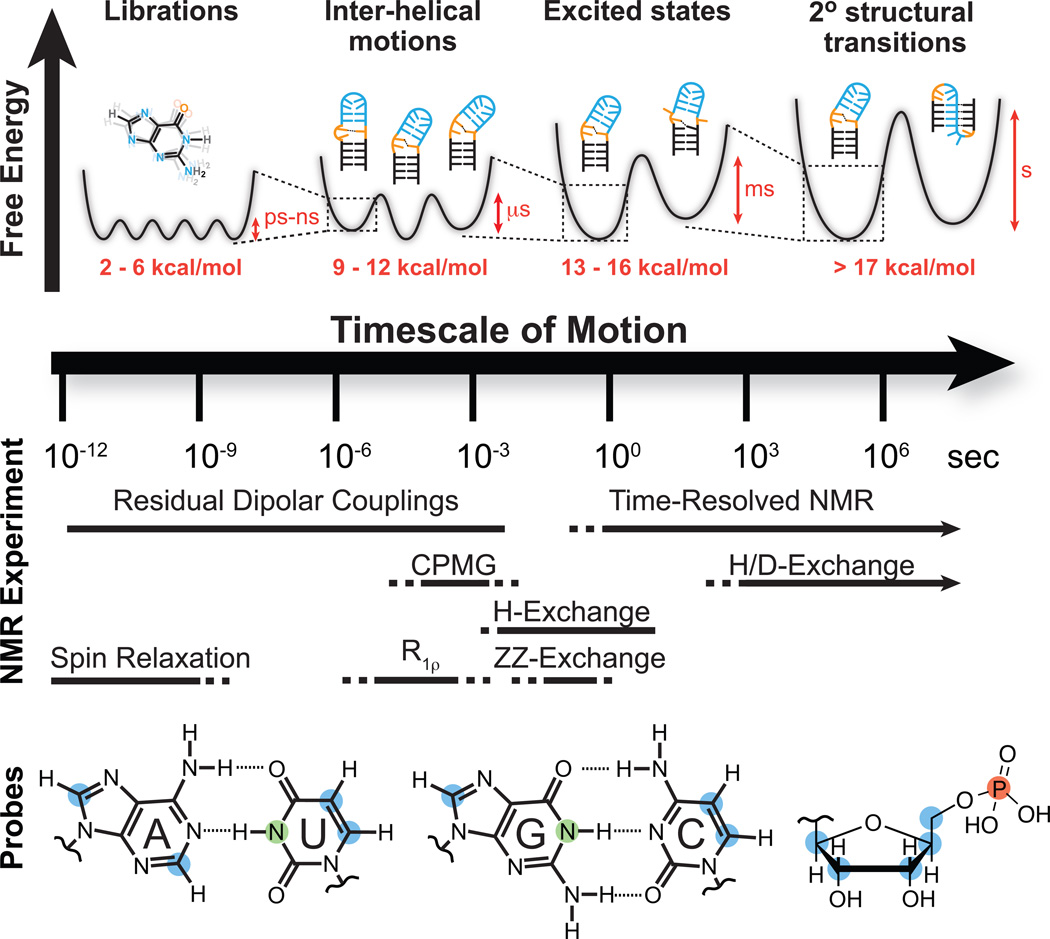
Figure 1.
NMR techniques and site-specific probes for characterizing motional modes that carry RNA structure along various regions of the dynamic structure landscape. Dynamic Structure Landscape: Transition free energies (red, kcal/mol) corresponding to typical timescales of interconversion were estimated using transition state theory at 25 °C. NMR Experiments: Solid lines indicate the timescales at which each NMR experiment is optimally suited for, while the dotted lines indicate timescales that are difficult to probe. Probes: Nuclei most commonly used for RNA dynamics measurements: protonated carbons (blue), imino protons (green), backbone phosphorus (red).
Among many techniques that are now being developed to study RNA dynamics, solution-state NMR spectroscopy, which has contributed significantly toward the characterization of protein dynamics11, has a unique role to play (Fig. 1, NMR). First, NMR can be used to measure dynamics at atomic resolution, comprehensively for sugar, base, and backbone moieties across different residues (Fig. 1, probes). Second, multiple interactions can be measured at a given site to deduce structural, kinetic, and thermodynamic characteristics of not one, but many motional modes occurring at different timescales. Third, NMR enjoys broad sensitivity to motions spanning picosecond to second and longer timescales (Fig. 1, NMR) and can be used to characterize very subtle changes in conformation, including those involving minutely populated conformers (on the order of ~ 10−7 %) that have exceptionally short lifetimes (on the order of nanoseconds). Last but not least, NMR provides a powerful approach for exploring how the dynamic structure landscape is modulated by cellular cues and time-resolved methods can be used to follow these perturbations in real time.
Here, we review solution-state NMR methods for studying RNA dynamics and highlight some of the new insights that have been obtained regarding the RNA dynamic structure landscape and its relationship to function.
NMR interactions used to study nucleic acid dynamics
The basic NMR experiment can be simplistically described as follows. Nuclei behave as tiny magnets and because of the quantization of the nuclear spin angular momentum, they align either parallel (α state) or anti-parallel (β state) relative to the applied magnetic field. Since the parallel (or anti-parallel, depending the nucleus) alignment is energetically more favorable, a net bulk magnetization over an ensemble of nuclei builds up parallel to the magnetic field. Radiofrequency (RF) pulses are then used to realign this bulk magnetization along a direction perpendicular to the magnetic field. The bulk magnetization then precesses about the magnetic field at a characteristic NMR resonance frequency called the “chemical shift” and gives rise to a detectable oscillating magnetic field. This non-equilibrium magnetization ultimately relaxes back to the equilibrium, parallel state. The time-domain spectrum is Fourier transformed to yield the standard frequency-domain NMR spectrum, in which unique signals at characteristic chemical shift frequencies are observed for different types of nuclei. For nucleic acid applications, one is typically interested in the NMR active nuclei 1H, 13C, 15N, 2H, and 31P, with 13C, 15N, and 2H introduced during synthesis, typically by using labeled nucleotide triphosphates (NTPs) by in vitro transcription reactions (Fig. 1, probes).
The NMR chemical shift (Box 1) is proportional to the energy gap between the α and β states and the static applied magnetic field. However, electronic clouds surrounding nuclei can “shield” or “deshield” them from the external magnetic field by variable amounts dependent on the electronic structure. This leads to a wide range of chemical shifts that makes it possible to measure dynamics with site-specific resolution. Furthermore, changes in chemical shift arising due to local fluctuations in the electronic environment form the basis for relaxation dispersion experiments to measure exchange processes occurring at micro- to millisecond timescales, ZZ-exchange spectroscopy to measure motions at millisecond to second timescales, and time-resolved NMR experiments to follow transitions occurring at timescales longer than a few seconds.
Box 1 Basic NMR interactions.
Chemical shifts
Chemical shifts report on the local electronic environment surrounding nuclei and are highly sensitive to local geometry (e.g. syn versus anti conformations, sugar puckers, etc.) and intermolecular interactions including hydrogen-bonding, stacking, and metal interactions.
Scalar couplings (J-couplings)
Scalar couplings arise from coupled interactions between the electron and nuclear spins of bonded nuclei that result in the splitting of NMR signals. Scalar couplings depend on the type of nuclei involved (typically larger for larger γ nuclei), number of bonds separating them (typically smaller the larger the number of bonds), and the dihedral angle in the case of three bond scalar couplings (3J).
Dipolar couplings
The dipolar coupling between two nuclei i and j depends on γiγj (γ values for 1H, 13C, and 15N follow the ratio 1.00:0.2515:−0.1014) and the inverse cubic distance between the two nuclei. For relaxation, which is a second order perturbation, this prefactor is squared, leading to a γ2γ2r−6 dependence.
Chemical shift anisotropy (CSA)
This interaction results from the anisotropic electronic environment, which “shields” or “deshields” nuclei from the external magnetic field in an orientation dependent manner. The CSA contribution to spin relaxation scales quadratically with the external magnetic field and is usually less significant than the dipolar interaction.
In the NMR experiment, interactions such as the dipolar coupling (Box 1) and chemical shift anisotropy (CSA) (Box 1) modulate the effective field experienced by a given nucleus in an orientation-dependent manner, thereby perturbing the energy gap between the α and β states and the observed NMR spectrum. Many NMR experiments that probe dynamics take advantage of these so-called ‘anisotropic’ interactions. In solution, the orientation dependence of anisotropic interactions gives rise to a time-dependent fluctuating field (Fig. 2a), which in turn influences the rate at which the magnetization relaxes back to equilibrium. The contribution to so-called transverse relaxation (R2) is encoded within the linewidth of the NMR signal, with faster motions leading to narrower lines. Spin relaxation measurements take advantage of these effects to probe internal motions of bond vectors at picosecond to tens of nanosecond timescales.
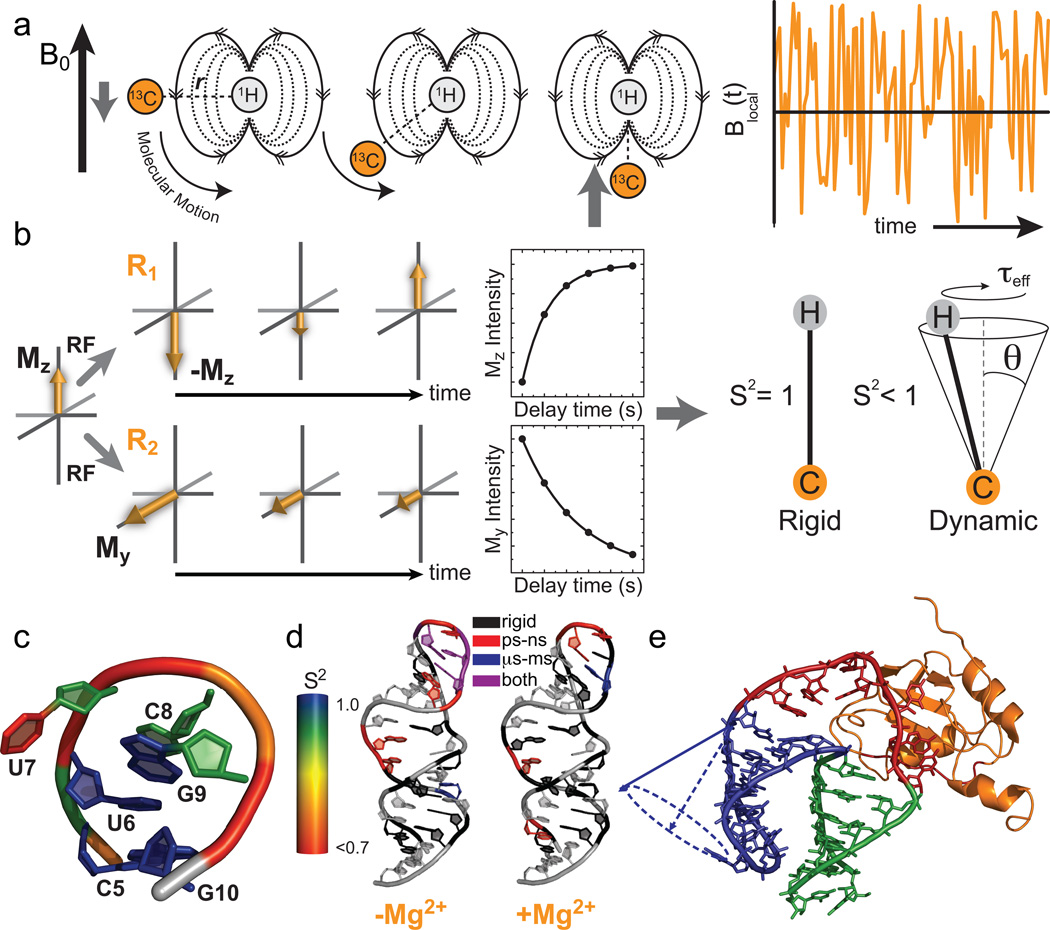
Figure 2.
Characterization of pico- to nanosecond motions using spin relaxation. (a) Reorientation of bond vectors leads to an oscillating local field at the nucleus of interest that influences relaxation. Shown is an example involving a 13C-1H dipolar interaction. (b) Model free analysis of longitudinal (R1) and transverse (R2) spin relaxation data yield an order parameter (S2) describing the amplitude of motion and a constant (τeff) describing its timescale. (c–e) Example applications of spin relaxation in studies of RNA dynamics, (c) Site-specific UUCG tetraloop dynamics. Note, the sugar and nucleobase order parameters17,32 were determined at 298 K while the phosphate backbone order parameters18 were determined at 310 K. (d) Re-distribution of motional modes in the catalytic domain 5 RNA of a group II intron upon addition of Mg2+ (Adapted from ref. 33 with permission from Elsevier). (e) RNA inter-helical motions persist when bound to the human U1A protein (Reprinted with permission from ref. 39. Copyright 2007 American Chemical Society).
Though they influence relaxation, and thus the apparent linewidth of the NMR signal, anisotropic interactions average to zero due to random tumbling of the molecule in solution and therefore do not affect the time-averaged effective field experienced by the nucleus and the observed time-averaged chemical shift frequency. However, these anisotropic interactions can be resurrected in solution by inducing a small degree of alignment, allowing the direct measurement of residual dipolar couplings (RDCs) and residual chemical shift anisotropies (RCSAs) (Box 2) which manifest as frequency off-sets or added splittings when comparing unaligned and aligned samples that can be used to probe motions at sub-millisecond timescales.
Box 2 The NMR dynamics toolkit.
Spin relaxation
Types of Dynamics Measured
Provides information about the amplitude and timescale of motions that reorient bond vectors (typically C-H and N-H) at pico- to nanosecond timescales.
Pros
Provides both amplitude and timescale information for multiple motional modes occurring at different timescales involving the sugars, bases and phosphodiester backbone. There is an incredible wealth of information, the full scope of which has yet to be obtained by recording data at varying field strengths and for varying types of nuclei and interactions.
Cons
Contributions from overall motions can be difficult to quantitatively disentangle from those due to internal motions. Little information is typically obtained about the directionality of the motion and fluctuations slower than overall tumbling can only partially be characterized. Complicating 13C-13C dipolar interactions grow significantly with increasing RNA size13–16.
Residual dipolar couplings
Types of dynamics measured
Provides information about the amplitude of motions that reorient bond vectors (typically C-H and N-H) at timescales faster than ~10 milliseconds.
Pros
Can be measured in great abundance to probe dynamics of directly bonded and non-bonded inter-nuclear vectors. Provides exquisite sensitivity to the orientation distribution of bond vectors spanning broad timescales and can be integrated with computational methods to steer MD or construct atomic-resolution ensembles. There is an incredible wealth of information the full scope of which has yet to be obtained by recording data under different alignment conditions49, using different frames of reference54, and by exploiting motional couplings48.
Cons
Contributions from overall motions can be difficult to quantitatively disentangle from those due to internal motions. Little to no information is obtained about motional timescales. Typically requires use of a potentially perturbing ordering medium. Limited sensitivity to small amplitude (<15°) motions.
Relaxation dispersion
Types of dynamics measured
Provides information about micro- to millisecond transitions.
Pros
Can be used to characterize transitions to minutely populated excited state conformations (with populations ranging between ~1–5 0 %) that have very short lifetimes (hundreds of microseconds to 1 millisecond). Under favorable conditions, a complete thermodynamic and kinetic description of the transition can be obtained, along with the chemical shift of the excited state, which can be used to obtain insights into its structural features. There is an incredible wealth of information, which has yet to be obtained, by measuring RDC and RCSA based relaxation dispersion for directly determining structures of excited states96.
Cons
Chemical shift based relaxation dispersion is only sensitive to conformational transitions that lead to changes in chemical shift. Analysis of data in terms of more than two states can be difficult and typically requires mutations to minimize the number of states. Data acquisition can be very time consuming.
ZZ-Exchange
Types of dynamics measured
Provides rate information regarding transitions occurring at 10’s of milliseconds to ~ 1 second timescales.
Pros
Can be used to directly determine the forward and reverse rate constant for a transition under equilibrium conditions and is in principle not restricted to a particular atom type as in the H and H/D exchange. Recent methods developed for proteins might extend the sensitivity of ZZ-exchange experiments to highly skewed populations in RNA systems100.
Cons
The exchanging species must be sufficiently populated (> 30%) and exchange within a narrow window of timescales. If imino protons are used to probe exchange, the possibility of imino proton exchange with water during the mixing period should be considered.
Time-resolved
Types of dynamics measured
Can be used to monitor a non-equilibrium state relax to equilibrium at timescales > a few seconds.
Pros
Can be used to dissect complex transitions involving multiple steps and different sites on a molecule. Kinetic initiation within the magnet with special hardware (laser or rapid mixing) allows for very short (~1–2 s) dead times. There is an incredible wealth of information which has yet to be obtained, for example by measuring RDC and other NMR interactions in a time-resolved manner73.
Cons
Without special hardware, mixing outside of the NMR magnet has long dead times (> ~20 seconds), thus reducing the time sensitivity window. For laser initiation studies, chemical synthesis is required to attach photolabile groups to either small molecules or phosphoramidites. Laser based studies are also limited by low sample concentrations in order to achieve full cleavage via short laser irradiation.
H and H/D exchange
Types of dynamics measured
Provides information regarding base-pair opening kinetics and thermodynamics.
Pros
Can be used to probe exchange timescales over a broad range spanning 1 millisecond up to years. Data can be used to measure base-pair and open state lifetimes, as well as free energy differences.
Cons
Experiments are limited to detectable imino and amino protons. H/D-exchange experiments typically have dead times of ~3–5 minutes and cannot access base-pair open state lifetimes and thermodynamics. H-exchange assumes the exchange from the open state equals that of mononucleotides and neglects differences in accessibility and electrostatics.
The above interactions form the basis for many of the NMR techniques used to probe nucleic acid dynamics that are reviewed here. Note that other types of NMR interactions, including NOEs (nuclear Overhauser effect), ROEs (rotating-frame Overhauser effect), scalar couplings, and cross-correlated relaxation, can also be used to probe unique aspects of nucleic acid dynamics12, they have so far primarily been used in structure determination and will therefore not be reviewed here.
Sample preparation
Many important advances in solution NMR methods to study RNA dynamics involve sample preparation. NMR dynamics measurements, particularly those involving the measurement of pico- to nanosecond motions by spin relaxation and micro- to millisecond motions by relaxation dispersion, require the ability to isolate and measure specific interactions from what can be a complex network of interactions involving many nuclei. In general, the unwanted NMR interactions increase with the gyromagnetic ratio (γ) of the nuclei involved, with decreasing distance of separation, and are difficult to suppress between nuclei of the same kind. Studies of protein dynamics have taken advantage of low γ backbone amide nitrogens, which enjoy simple relaxation mechanisms. In nucleic acids, corresponding imino nitrogens (Fig. 1, probes) are available for only guanines and uridines, and seldom in flexible residues of interest owing to rapid exchange of the imino protons with solvent. This has made it necessary to rely on carbon nuclei (Fig. 1, probes), which suffer from extensive 13C-13C interactions that complicate measurements and analysis of data, particularly for larger RNAs13–16. The preparation of nucleotide triphosphates (NTPs) with site-specifically labeled carbons has helped isolate specific carbon nuclei, thus simplifying and in some cases enabling dynamics measurements that would otherwise be intractable. Examples of specific carbon labeling schemes that harness bacterial nucleotide biosynthetic pathways are shown in Supplementary Table 1.
Methods have also been developed to incorporate other types of nuclei that have desirable spectroscopic properties. For example, deuterium enjoys relatively simple relaxation mechanisms17 that that can be exploited in spin relaxation studies of pico- to nanosecond dynamics. RNA samples can be prepared using commercially available NTPs that are site-specifically deuterated at desirable ribose and/or nucleobase sites (Supplementary Table 1). Deuterated NTPs have also been used to simplify the spin relaxation mechanisms of 31P as a unique probe of pico- to nanosecond backbone motions18. The site-specific introduction of 13C labeled methyl probes has also been used to simplify the measurement and interpretation of 13C based dynamics data and may potentially allow for application to much larger RNAs19 (Supplementary Table 1).
Many NMR techniques for dynamics measurements, including spin relaxation and RDCs, probe the reorientation of bond vectors (C-H or N-H) relative to the external applied magnetic field. The ability to extract information regarding internal motions hinges on being able to disentangle these small spectroscopic contributions from the much larger contributions due to overall motions. While this is typically accomplished by invoking the so-called ‘decoupling approximation’ and the assumption that internal and overall motions are not correlated to one another20, studies increasingly show that the decoupling approximation breaks down in many flexible RNA systems21–24. Here, collective motions of helices can give rise to large changes in overall shape, and thus the overall motions, resulting in motional coupling that severely complicate data analysis. This problem has recently been addressed with the introduction of a domain-elongation strategy22 (Supplementary Table 1, see RDC section). Here, an RNA terminal helix is elongated using a stretch of isotopically unlabelled Watson-Crick (WC) base-pairs designed to adopt an A-form helix structure. The resulting elongated RNA has an overall shape, and thus overall motions, that are far less sensitive to internal motions occurring in other parts of the molecule. Domain-elongation also broadens the time-scale sensitivity of spin relaxation data, expands the amount of RDC data that can be measured, and makes it possible to accurately compute RDC and spin relaxation data from molecular dynamics (MD) simulations.
Pico- to nanosecond motions from spin relaxation
Spin relaxation measurements (Box 2) of pico- to nanosecond motions take advantage of the fact that anisotropic interactions such as dipolar couplings and CSA (Box 1) modulate the effective field experienced by a given nucleus in an orientation-dependent manner, thus influencing the rate at which the bulk magnetization relaxes back to equilibrium. Let us consider how the dipolar interaction between a carbon and proton nucleus in a C-H bond modulates the effective magnetic field at the carbon nucleus (Fig. 2a). The carbon nucleus experiences both the static external magnetic field and the much smaller (~10−4) magnetic field generated by the proton nucleus. Because the nuclear bar magnets are always quantized parallel (or anti-parallel) to the magnetic field, the proton field experienced by the carbon nucleus will vary as the C-H bond changes orientation relative to the magnetic field, either due to internal or overall motions; in some orientations the proton field adds to the external magnetic field, in other orientations it subtracts or has no contribution (Fig. 2a). In the case of CSA, electrons oppose the magnetic field in a manner dependent on the orientation of the molecule relative to the field. As a result, internal and overall motions give rise to an oscillating magnetic field (Fig. 2a) at the carbon nucleus with a frequency comparable to the NMR transition frequency, thus stimulating relaxation. Note that internal motions occurring at timescales slower than overall motions will have only a small effect on the fluctuating field because the molecule will reorient many times before the internal motion has any effect. As a result, spin relaxation data is much less sensitive to motions occurring at timescales much slower than overall tumbling and are best-suited for measuring dynamics on the picosecond to tens of nanosecond timescales, depending on the size of the nucleic acid.
Typically R1 and R2 relaxation rates (Fig. 2b) are measured, together with heteronuclear NOE, which is a measure of the rate at which proton magnetization transfers to the heteronucleus due to the dipolar interaction, and the data is analyzed using the model free formalism20, which yields an order parameter (S2) describing the amplitude of motion of the C-H or N-H bond vector, ranging between 0 and 1 for maximum and minimum disorder, respectively, and a time constant (τeff) describing the rate of internal motions (Fig. 2b). More sophisticated models can be used to obtain amplitude and time constants for many distinct internal motional modes provided that they have sufficiently different timescales and data is collected at multiple fields25. Alternatively, data can be analyzed using spectral density mapping approaches that directly map out components of the oscillating magnetic field26. The recent determination of the large nucleobase carbon CSAs, which are necessary for interpretation of spin relaxation data, has also addressed a considerable element of uncertainty in data analysis27–29. For domain-elongated RNAs, qualitative dynamic information can be obtained by simply comparing the intensity of NMR signals for a given nucleus type in multi-dimensional spectra22.
The nuclei that are most commonly targeted for spin relaxation studies include imino nitrogens in the guanine and uridine nucleobases and the protonated carbons in the nucleobases and sugars of all four nucleotides (Fig. 1, probes). For 13C relaxation measurements, unwanted 13C-13C interactions are suppressed by using site-specific (Supplementary Table 1) or fractional carbon labeling schemes, performing experiments at natural abundance, or by use of appropriate pulse schemes. TROSY-detected pulse sequences can be used to acquire nucleobase 13C relaxation data on large RNAs up to ~ 150 nt in size16.
Common themes are beginning to emerge regarding RNA dynamics at pico- to nanosecond timescales from spin relaxation studies of a wide range of RNA systems17,30–35. Watson-Crick as well as non-canonical base-pairs tend to experience limited motions (S2 >0.85) with amplitudes that are comparable to the static variations seen in X-ray structures of A-form helices36. Non-canonical residues typically undergo larger, more variable amplitude local motions that tend to be inversely correlated with the extent of stacking17,30–35. These motions can occur at timescales comparable to, or slower than, overall tumbling, i.e. in the tens to hundreds of nanosecond timescale22,37. Interestingly, the dynamics of the sugars often, but not always34, follow the dynamics of the nucleobases whereas recent 31P relaxation data suggest that the amplitude of backbone motions exceeds that of both the sugar and base moieties18. Many of these trends are illustrated in spin relaxation studies of the structurally well characterized U6U7C8G9 tetraloop in which limited mobility (S2~1) is observed for the G-U non-canonical base-pair which stacks on the helix, whereas much greater mobility (S2 = 0.68–0.83) is observed for the looped out U7 and partially looped out C817,18,32 (Fig. 2c). Furthermore, studies show that helices can undergo large amplitude collective motions (S2 = 0.6–0.8)16,22,37. These inter-helical motions, are however, not fully captured by spin relaxation because they occur at timescales slower than overall tumbling. Rather, they have been quantitatively characterized with the use of RDCs (see next section).
High pico- to nanosecond mobility is often observed in regions that undergo conformational adjustments during catalysis and recognition. For example, analysis of 13C relaxation data using reduced spectral density mapping revealed extensive pico- to nanosecond mobility in key functional groups of the D5 domain from the group II intron that are implicated in binding magnesium ions and catalysis33 (Fig. 2d). A quantitative correlation has been observed between the amplitude of pico- to nanosecond motions at a given site of the HIV-1 transactivation response (TAR) element and the extent to which that site undergoes changes in conformation on binding seven distinct ligands16,22.
A surprising theme emerging from spin relaxation studies is that RNA recognition does not necessarily lead to conformational stabilization, but more typically, the reorganization of motional modes, reflecting broader changes across the dynamic structure landscape33,37,38. For example, binding of the U1A protein to its cognate RNA target does not lead to the arrest of inter-helical motions, and induces mobility in regions of the RNA that are in direct contact with the protein39 (Fig. 2e). In contrast, binding of the ligand argininamide to TAR leads to the total arrest of inter-helical motions and an increase in the local dynamics of two out of three bulge residues in the inter-helical junction16.
Sub-millisecond motions from residual dipolar couplings
The introduction of partial alignment methods for measuring residual anisotropic interactions – RDCs and RCSAs–, which normally average to zero in the solution-state40,41, has extended the timescales of motions that are accessible by NMR beyond those which can be measured by spin relaxation to include all timescales that are faster than ~ 10 milliseconds. Despite this broader timescale sensitivity, RDCs do not replace spin relaxation measurements, but rather complement them. In particular, RDCs are somewhat less sensitive to the amplitude of motions since they scale with S rather than S2 and also do not provide information about motional timescales. Thus, RDCs are most effectively used when applied in concert with spin relaxation and also relaxation dispersion techniques for quantifying micro- to millisecond exchange (see below). Studies employing all of these techniques reveal that a given site in RNA can experience multiple motional modes simultaneously, highlighting the complexity of RNA dynamics33,38,42 (Fig. 2d).
To understand how RDCs can be measured via partial alignment, let us consider a C-H bond vector. As mentioned previously, the carbon nucleus experiences the sum of the external magnetic field and the field generated by the proton nucleus. The latter contribution varies as the molecule tumbles – in some orientations the proton field adds to the external magnetic field, whereas in other orientations, it opposes it. This angular dependence is described by
| (1) |
where θ is the angle between the inter-nuclear vector and the magnetic field, and the angular brackets denotes a time-average over all orientations sampled at a rate faster than the dipolar coupling (Fig. 3a). Under conditions of random Brownian rotational diffusion, the angular term averages to zero and the proton does not modify the average field at the carbon nucleus and therefore the observed carbon chemical shift remains unchanged. However, by imparting a small degree of order on the molecule, on the tune of 1 in 103–105 molecules being completely aligned, the angular term no longer averages to zero, and the carbon nucleus experiences a residual proton field in addition to the external magnetic field. Since half of the proton nuclei are aligned parallel and the other half anti-parallel to the field, the proton fields add to the external field for half of the carbon nuclei and subtracts for the other half. Consequently, the carbon resonance frequency splits into a doublet, reflecting the addition and subtraction of the average proton field. The magnitude of this splitting is referred to as a ‘residual dipolar coupling’40,41. A wide range of RDCs involving the base, sugar and backbone moieties can be measured in nucleic acids as reviewed elsewhere43.
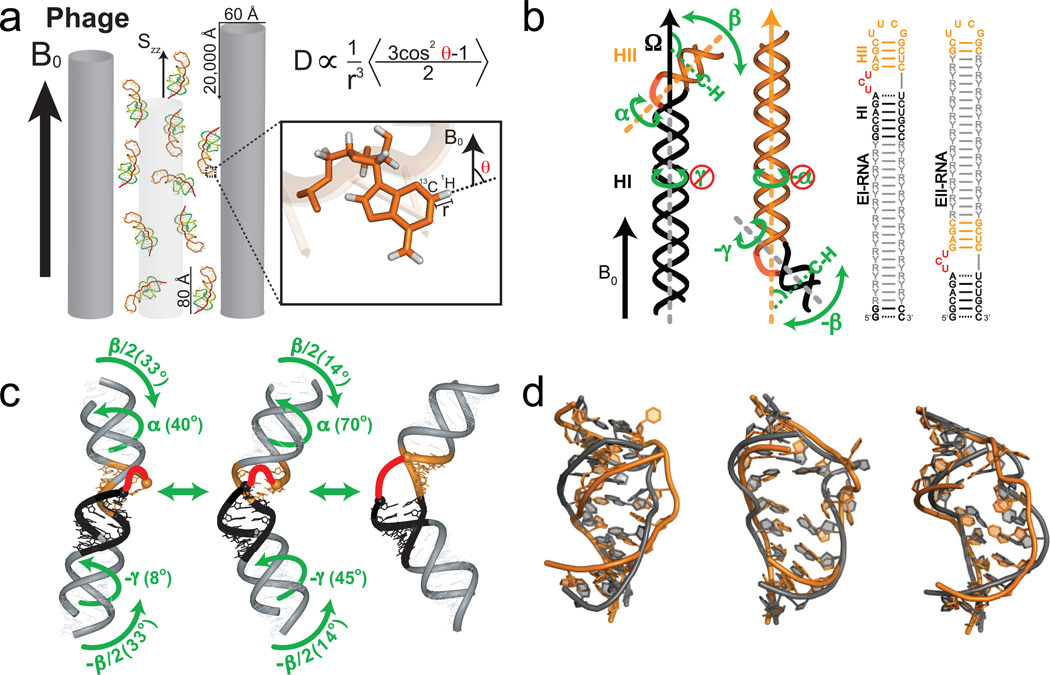
Figure 3.
Characterizing motions over sub-millisecond timescales using residual dipolar couplings. (a) Partial alignment of RNA using Pf1 phage shown as gray rods (left) (Adapted from ref. 43). (b) Domain-elongation for decoupling internal and overall motions allows measurement of bond vector dynamics relative to the elongated helix. An isotopic labeling strategy is used to render elongation residues (R-Y) NMR invisible (adapted from ref. 52). (c) Spatially correlated inter-helical motions observed using RDCs involving correlated changes in the inter-helical twist (α and γ) and bend (β) angles (adapted from ref. 52). (d) Combining domain-elongation RDCs and MD simulations in the construction of atomic-resolution dynamic ensembles of TAR reveals conformations (in gray) very similar to those observed in ligand bound states (in orange) (Adapted from ref. 55 by permission of Oxford University Press).
The desired optimum degree of alignment (~10−3) can be achieved by dissolving molecules in magnetically or mechanically ordered media41,44 that transmit their order to the solute by a combination of steric and electrostatic mechanisms. For nucleic acids, the most widely used medium is filamentous bacteriophage (Pf1)45, which is negatively charged thus minimizing unwanted interactions with the nucleic acid, has good tolerance to high ionic strength, and is commercially available (Fig. 3a). RDCs are typically measured as the difference in splittings observed in the absence and presence of the Pf1 phage medium. Although less commonly used, a smaller (10−5) less ideal degree of alignment can be achieved based on spontaneous alignment of nucleic acids due to interactions with the magnetic field itself40,46. Magnetic field alignment also has a simple dependence on nucleic acid structure, which can be exploited in a number of unique applications21,46–48. By changing the alignment of the solute, up to five independent sets of RDCs can be measured, which can be used to probe motions with greater spatial resolution49,50. In proteins, changing alignment can be accomplished by changing the ordering medium44,51. This has proven difficult in nucleic acids, because their polyanionic nature results in similar steric and electrostatic interactions with different ordering media. Differential domain-elongation and magnetic field alignment offer alterative approaches for modulating the alignment of RNA48,52.
The angular dependence of RDCs, equation 1, is time averaged over both internal and overall motions. Separating and quantifying these two contributions can be difficult in highly flexible systems43,53. The interpretation of RDCs is considerably simplified by elongating the RNA so that the overall alignment can be fixed on the elongated helix and used as a reference for measuring averaging contributions due to internal motions in other parts of the RNA52 (Fig. 3b). Furthermore, by altering which helix is elongated, multiple sets of RDCs can be measured to improve the spatial sensitivity to the dynamics54 (Fig. 3b). Such RDC approaches have revealed collective inter-helical motions that are not fully captured by spin relaxation data. For example, the amplitude of inter-helical motions measured in TAR using RDCs 52 far exceed those observed by spin relaxation (S2 ~0.74)22, most likely because the inter-helical motions include fluctuations at the nano- to microsecond timescale that are inaccessible to spin relaxation22,42. Moreover, the measurement of RDCs in two domain-elongated TAR samples (Fig. 3b) made it possible to map out its inter-helical dynamic trajectory in 3D. Results revealed a highly choreographed trajectory in which the two helices bend and twist in a spatially correlated manner52 (Fig. 3c).
By combining domain-elongation RDCs with MD simulations, Frank et al. extended the dynamic ensemble description of RNA to the atomic level55. Here, RDCs measured in elongated RNAs were used to guide selection of conformers from a pool generated using MD simulations. The ensemble of TAR constructed in this manner was shown to include many conformations that resemble those of TAR observed in various ligand-bound states, providing support for recognition via conformational selection (Fig. 3d). More recently, the RDC-derived TAR ensemble was subjected to computational screening to identify anti-HIV therapies that broadly target the TAR dynamic structure landscape56. This made it possible to overcome the difficulty in computationally modeling changes in RNA structure that take place on small molecule binding and led to de novo discovery of six small molecules that bind TAR, one of which inhibited HIV replication in T cell lines in vivo with an IC50 of ~20 µM.
Characterizing excited states using relaxation dispersion
Thus far, we have focused on techniques that can be used to study dynamic excursions about the dominant ‘ground state’ conformation. Much less often, biomolecules transition into different conformational sub-states, often referred to as ‘excited states’, that populate different local minima along the energy landscape, and that require loss of key stabilizing interactions that are partially restored by formation of new ones (Fig. 1, landscape). NMR relaxation dispersion techniques (Box 2) provide a rare opportunity to characterize the population, lifetime, and conformation of these lowly populated (as low as 1%) and transient (lifetimes <1 ms) excited states57,58.
To understand relaxation dispersion, consider a nucleus that exchanges between a major ground (G) and minor (E) excited state with chemical shifts, ωG and ωE, respectively. In the absence of exchange, two NMR peaks are observed with chemical shifts ωG and ωE with integrated volumes that reflect their relative populations (Fig. 4a). Now consider what happens when G and E states exchange at a rate (kex = kGE + kEG) comparable to their NMR frequency difference (Δω = ωG − ωE). In this case, the frequency of a given nucleus stochastically fluctuates between ωG and ωE. Because nuclei in different molecules spend varying amounts of time in the G and E state, their magnetization no longer precess in synchrony (Fig. 4b). The resulting ‘fanning out’ of the magnetization leads to a decay in the net oscillating signal and an additional exchange contribution (Rex) to transverse relaxation (R2) (Fig. 4c). The broadening of both the excited state and observed peaks is a function of the kinetics and populations of the exchange process. Further, this line broadening can result in the total disappearance of the E signal (Fig. 4a). Relaxation dispersion experiments probe the invisible E state by measuring the exchange broadening contribution to the visible G state signal following the application of a series of RF pulses in the Carr-Purcell-Meiboom-Gill (CPMG) experiment, or constant RF field in the R1ρ experiment, which are designed to suppress the exchange broadening (Fig. 4b). For example, in the CPMG experiment, a series of 180° pulses reverse the precession of magnetization at constant time intervals, τcp; as a result, any dephasing that accrues prior to the 180° pulse is partly refocused in the following period, with the extent of refocusing increasing with shorter τcp delays (Fig. 4b). The exchange contribution is measured as a function of τcp in CPMG and the power and frequency of RF field in R1ρ. The resulting relaxation dispersion curve (Fig. 4c) is typically fit to a two-state model. For slow (kex ≪ |Δω|) to intermediate (kex ~ |Δω|) exchange, this yields the population (pE), lifetime (τex = 1/kex), and chemical shift (ωE) of the excited state, the latter carrying structural information, whereas for fast exchange (kex ≫ |Δω|), only τex and Φ = pGpEΔω2 can be determined and additional experiments are needed to resolve Δω and pE. The CPMG experiment only yields the absolute difference in chemical shift |ωE − ωG|, and additional experiments59,60 are typically needed to determine ωE.
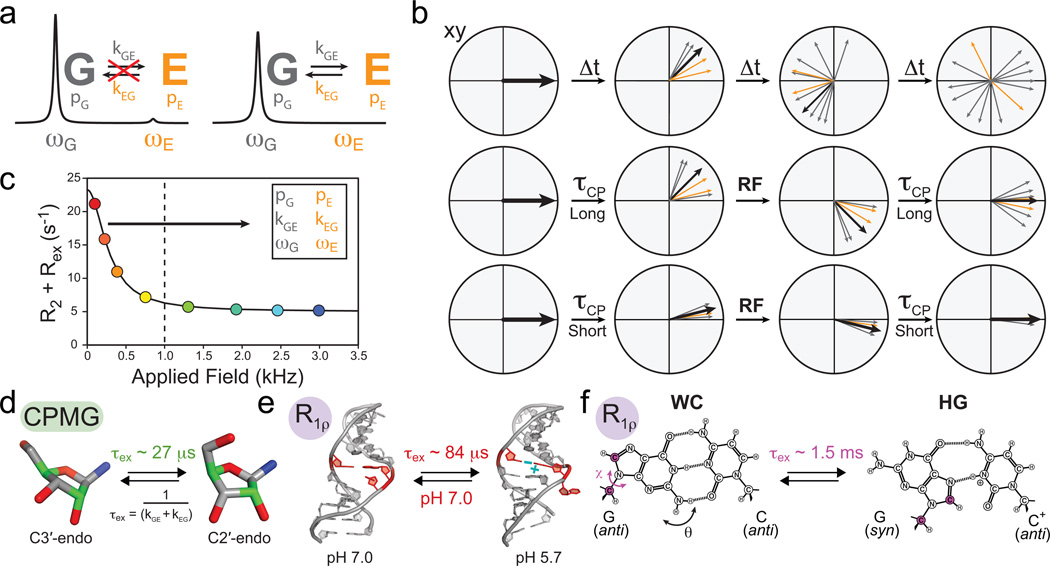
Figure 4.
Characterizing micro- to millisecond exchange by relaxation dispersion. (a) Exchange between ground (G) and excited (E) states leads to broadening of the G signal and disappearance of the E signal. (b) Fanning out of bulk magnetization due to exchange can be suppressed by application of RF fields. (c) Characteristic relaxation dispersion curve showing the power dependence of Rex which can be used to extract in favorable cases the populations (p), exchange rates (k) and chemical shifts (ω) of G and E. (d–f) Examples of conformational exchange characterized by CPMG and R1ρ carbon relaxation dispersion. (d) Sugar repuckering in a GCAA tetraloop using selectively labeled C2' and C4' (green) probes61. (e) Transition toward an excited state structure in the U6 RNA involving a CA+ base-pair and looping out of a uridine bulge68. (f) Transition to Hoogsteen (HG) GC+ base-pairs in canonical duplex DNA (Adapted from ref. 70).
CPMG relaxation dispersion can be used to probe exchange processes occurring at microsecond to tens of millisecond timescales57,58. The CPMG experiment proves difficult to apply to nucleic acids because 13C experiments are complicated by extensive 13C-13C scalar couplings that are difficult to suppress due to challenges in achieving selective carbon excitation with hard 180° pulses13,61. This problem was recently addressed by preparing RNA samples that are specifically 13C labeled at the C2' and C4' sugar positions61 (Fig. 4d, green). CPMG experiments on these samples led to the observation of excited state sugar conformations in the GCAA tetraloop with populations of 15–30% and lifetimes of 30–42 microseconds that most likely correspond to exchange between C3'-endo and C2'-endo sugar pucker conformations61 (Fig. 4d).
The R1ρ experiment measures line broadening as a function of the power and frequency offset of a constant RF spin lock field62. The R1ρ experiment has been more widely used than CPMG in studies of nucleic acids because spin lock fields can be used more selectively to reduce or eliminate unwanted 13C-13C interactions. Additional benefits include the ability to directly determine ωE at a single magnetic field strength without the need for additional experiments63. The upper limit for motional timescale is comparable to, if not greater than that of the CPMG experiment (tens to hundreds of microseconds) and is limited by the amount of RF power that can be dissipated into the probe. While technical considerations have traditionally limited the lowest RF spin lock strength to ~1,000 Hz (Fig. 4c) and the timescales to exchange processes faster than ~500 microseconds, recent advances permit use of much lower spin lock fields64–66 (on the order of 100 Hz) extending the timescale sensitivity to tens of milliseconds.
Some of the earliest R1ρ studies revealed microsecond timescale exchange processes involving an excited state CA+ base-pair within the active site of the lead-dependent ribozyme that may be important for catalysis67. More recent studies suggest that excited states that are coupled to protonation of nucleobases may be quite common. For example, Blad et al. uncovered a microsecond timescale exchange processes directed towards an excited state structure involving a CA+ base-pair within a functionally important region of the U6 RNA element from the spliceosome which is accompanied by the looping out of a uridine bulge68,69 (Fig. 4e), whereas Nikolova et al. uncovered an even slower millisecond exchange process directed towards excited state GC+ Hoogsteen base-pairs in canonical duplex DNA70 (Fig. 4f). The above two studies provide rare examples in which the structure of the excited state could be determined. In both cases, this was accomplished by trapping the excited state, either by lowering the pH or by introducing chemical modifications. With these structures in hand, the authors were able to gain insights into the conformational pathway linking the ground and excited states using various computational methods70,71, highlighting another important area of synergy between NMR and computation.
Following transitions at > millisecond timescales using ZZ-exchange and time-resolved NMR
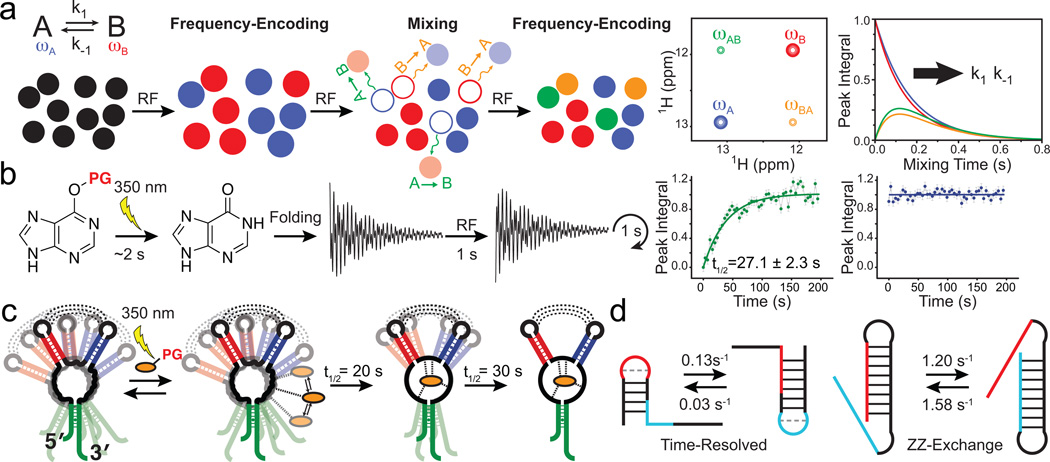
Many RNA dynamic transitions involve changes in secondary structure, which in turn require disruption of several base-pairs, and can occur at timescales slower than milliseconds. Such transitions can yield separate well-resolved NMR signals for the exchanging species, and in such cases, can be studied using a combination of ZZ-exchange and time-resolved NMR.
ZZ-exchange spectroscopy can be used to characterize transitions occurring between ~10 millisecond and 1 second timescales. The exchanging species must have well-resolved and detectable NMR signals, and must therefore typically be >30% populated. The transition has to be slow enough to avoid extensive exchange broadening, but fast enough to allow multiple exchange events to take place while magnetization is stored along the Z-axis during the ZZ-exchange experiment (i.e. exchange has to be fast compared to longitudinal relaxation, R1). Here, an initial frequency-encoding period is used to label the exchanging species, A and B, with their NMR frequencies, ωA and ωB (Fig. 5a). This is followed by a variable ‘mixing period’ during which magnetization is stored along the Z-axis (parallel to the magnetic field) and species allowed to exchange. This is followed by a second frequency-encoding period. A two dimensional (2D) spectrum is constructed correlating the frequencies observed in the two periods (Fig. 5a). Molecules that do not exchange during the mixing period, or that exchange multiple times back to the original state, appear as diagonal cross peaks with frequencies ωA/ωA and ωB/ωB, whereas molecules that exchange to a different A or B state appear as off-diagonal cross peaks with frequencies ωA/ωB and ωB/ωA. The peak intensities of all cross peaks are measured as a function of the mixing period (Fig. 5a) and are fit to appropriate equations to obtain the forward and reverse rate constants (k1 and k−1) for the A to B inter-conversion. The experiment is optimally carried out using nuclei with long R1 relaxation times, typically imino protons, or as demonstrated more recently using imino nitrogens which enjoy approximately ten fold slower R1 relaxation, thus extending sensitivity to slower processes72. Alternatively, 13C labeled methyl groups which enjoy high sensitivity, spectral resolution, and minimal 13C-13C interactions can be introduced onto the 2' OH groups of uridines and used in 13C ZZ-exchange experiments for studying transitions in large RNAs19.
Figure 5.
Characterizing conformational transitions occurring at millisecond and longer timescales by ZZ-exchange and time-resolved NMR. Schematic of the (a) ZZ-exchange and (b) time-resolved NMR experiment. (c) Visualizing a multi-step ligand-induced conformational transition in the guanine sensing riboswitch using laser induced time-resolved NMR (Adapted from ref. 76, copyright 2007 National Academy of Sciences, USA). (d) Characterizing slow and fast RNA refolding rates by time-resolved and ZZ-exchange NMR, respectively.
Time-resolved NMR experiments can be used to monitor transitions from a non-equilibrium to equilibrium state by repeatedly acquiring 1D or 2D NMR spectra with repetition rates that are on the order of ~2 seconds. This permits characterization of processes occurring at second and slower timescales73. Simple mixing of the RNA with suitable reagents can be used to monitor transitions occurring at slower than 1 minute timescales. Faster processes (<1 minute) require laser excitation or rapid mixing which reduce dead times to ~1 second73,74. In the former, a bulky photolabile group (Fig. 5b, PG) is used to protect a ligand or bias an RNA structure towards one of many competing conformations. One typically follows the appearance and disappearance of imino proton signals because they enjoy high spectral resolution and directly report on formation and loss of base-pairs, and therefore RNA secondary structure (Fig. 5b). Site-specific isotopic labeling schemes or the acquisition of multidimensional spectra using new ultrafast methods can help alleviate spectral congestion, which becomes increasingly important for larger RNAs74.
ZZ-exchange and time-resolved NMR have allowed the characterization of ligand-induced structural transitions occurring over a wide range of timescales and involving distinct mechanisms. For example, 1H ZZ-exchange revealed that the theophylline RNA aptamer exchanges between its free and structurally more ordered ligand-bound form at second timescales75. By contrast, time-resolved NMR allowed the kinetic and site specific resolution of two distinct kinetic steps occurring on the order of tens of seconds during the ligand induced structural transition of a 73 nt guanine-sensing riboswitch76 (Fig. 5c). The two steps follow rapid formation of an encounter complex and likely involve insertion of the ligand into the binding pocket within the three-way junction followed by formation of tertiary loop-loop interactions that stabilize the ligand-bound structure (Fig. 5c).
ZZ-exchange and time-resolved NMR have also allowed the characterization of RNA-refolding transitions occurring over a wide range of timescales and involving distinct mechanisms. These studies have targeted model bistable RNAs which fold into two distinct but nearly energetically equivalent secondary structures. For example, time-resolved NMR experiments revealed that the bistable 20 nt RNA shown in Figure 5d (time-resolved)77 re-folds at second timescales, whereas 15N imino nitrogen ZZ-exchange experiments reveled even faster re-folding rates at hundreds of milliseconds for the large 34 nt sequence shown in Figure 5d (ZZ-exchange)72. Together, these studies suggest that the rate of RNA secondary structural transitions is governed both by the number of bases that have to be disrupted during the transition77–79, and also, the RNA topology72,73 and relative spatial placement of strands that have to exchange. Further insights into refolding mechanisms have been obtained from combining these experiments with hydrogen and hydrogen/deuterium exchange experiments described below.
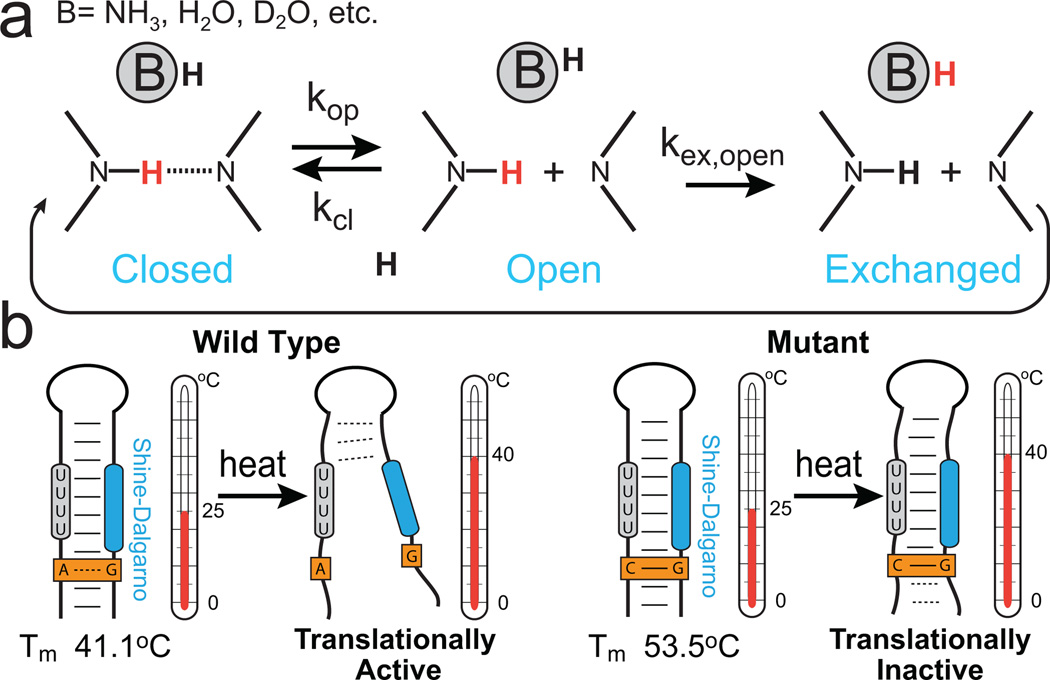
Base-pair opening dynamics from hydrogen and hydrogen/deuterium exchange
Many genetic RNA switches, including those that involve change in secondary structure outlined above, require the melting or annealing of strands. At the microscopic level, the underlying dynamics involve the opening of individual base-pairs. Characterizing base-pair opening dynamics is extremely challenging given that the open state typically has miniscule populations that are on the order of 10−5 to 10−9 with exceptionally short lifetimes on the order of nanoseconds. NMR experiments probing hydrogen exchange (H-exchange) and hydrogen/deuterium exchange (H/D-exchange) provide a unique opportunity to characterize base-opening dynamics with site-specific resolution80,81. H and H/D-exchange measurements have a long history of probing nucleic acid stability, providing some of the earliest NMR dynamics measurements of DNA and RNA. The experiments take advantage of the fact that when individual base-pairs open, imino or amino protons (Fig. 6a, red) can exchange with solvent (Fig. 6a, black)82, resulting in a perturbation of the observed NMR signal. Analogous to ZZ-exchange and time-resolved NMR methods, two experimental schemes are used to probe exchange at different timescales80,81. Exchange times slower than ~102 – 103 seconds can be measured by rapidly immersing a protonated RNA sample into D2O buffer and monitoring the disappearance of imino proton signals over time using 1D or 2D NMR (similar to time-resolved). Faster exchange rates ranging between ~ 10 seconds to 5 milliseconds can be measured by selectively perturbing the magnetization of water protons and following how this perturbation is transmitted to exchangeable RNA protons during a variable mixing period (similar to ZZ-exchange). Data is typically collected as a function of base catalyst concentration to extract individual opening and closing rate constants and the base-pair opening equilibrium constant (Kop = τcl /τop) permitting determination of the opening and activation free energies.
Figure 6.
Characterizing base-pair opening dynamics by imino proton exchange. (a) Schematic of a two-step (direct or water-mediated) imino proton exchange for an RNA base pair catalyzed by a proton acceptor B, followed by reversible base-pair formation. H exchange experiments can be used to measure rate constants in each step. (b) Imino proton exchange study of the wild-type (left) Salmonella FourU RNA thermometer and its translationally inactive GA-to-GC mutant (right), showed a correlation between changes in local base-pair stabilities and changes in global melting profiles of the wild-type and mutant constructs91.
H and H/D-exchange experiments reveal that base-pair lifetimes can range from < 1 millisecond to many days, with short (1–50 ms) lifetimes typically observed for A-form helical AU and GC/GU base-pairs83,84, intermediate lifetimes of several seconds for poly(G)-poly(C)85, up to minutes for base-pairs and triplets part of tertiary folds86, and even longer lifetimes on the order of days for hydrogen-bonding interactions involved in DNA and RNA quadruplexes87,88 and stable tertiary networks89. Lifetimes for the open base-pair state range between ~ 1 to 200 nanoseconds for internal duplex residues83, with longer lifetimes up to 1 – 2 microseconds observed for base-pairs at the 5' end of AU-tracts84 or near loops and bulges, which are often believed to be sites for triggering secondary structural rearrangements.
The measured base-pair opening equilibrium constants typically span a large range between 10−9 to 10−5 for WC83,84,90,91 and surprisingly stable GG mismatch base-pairs90 and up to ~10−3 for less stable AU and GU base-pairs91, GA mismatches92, and bulged or syn G imino protons stabilized by contacts with backbone or tertiary H-bond acceptors90. The corresponding opening free energies range between ~3 to 10 kcal/mol. Base-pair opening is accompanied by a large increase in both enthalpy and entropy, up to ~10-fold larger than the change in free energy, signifying loss of favorable interaction energy with neighboring nucleotides and gain of favorable entropy arising in part from conformational flexibility in the open state.
H-exchange experiments, when combined with time-resolved and ZZ-exchange experiments, provide insights into the refolding mechanism of bistable RNAs. Dissociative refolding mechanisms involve partial unfolding of the RNA followed by formation of stabilizing contacts that lead to a competing secondary structure while associative mechanisms involve an intermediate where structural elements join to form contacts of the competing secondary structure followed by dissociation of existing stabilizing contacts. The refolding mechanisms of two 20 nt RNAs77,78, highlighted previously, were deduced by comparing imino proton exchange rates measured for sequences able and unable to refold. Similar imino proton exchange rate patterns are indicative of dissociative mechanisms, whereas enhanced exchange rates near the site of association in the RNA suggest an associative mechanism. The authors found that the mechanism type is encoded by the particular topology of refolding RNA sequences73.
In another example utilizing H-exchange experiments, Rinnenthal et al. studied the temperature labile Salmonella FourU RNA thermometer, which regulates gene expression at the translational level by undergoing a melting transition in response to changes in temperature91 (Fig. 6b). An inactive single-point mutant was used to deconstruct differences in macroscopic RNA unfolding in terms of microscopic unfolding events (Fig. 6b). The authors observe strong enthalpy-entropy compensation, which argues that global unfolding occurs when microscopic base-pair stabilities are equalized. A single GA to GC Watson-Crick mutation was observed to stabilize base-pairs close and far-removed from the site of mutation, possibly via an extended hydration network, which globally translates into an enhanced overall hairpin thermostability and folding cooperativity providing an explanation for its lack of in vivo activity at physiological temperatures.
Summary and future perspective
Thanks to many developments in solution-state NMR methodology that have taken place over the past decade, new aspects of the RNA dynamic structure landscape are beginning to emerge, at least in outline (Fig. 1, landscape). A characteristic feature of the dynamic structure landscape is that it is punctuated by several local minima corresponding to very distinct but energetically comparable RNA structures that can be separated by vastly different barriers leading to exchange times spanning picoseconds to seconds. These local minima along the landscape constitute specific ‘low hanging fruit’ conformations that are stabilized by cellular cues to effect conformational changes that are important for biological function.
We have outlined avenues for future technical developments in NMR methods for dynamics measurements in Box 2. We would also like to identify three challenges for the future. First, the accessible experimental data is not sufficient to comprehensively and unambiguously characterize the RNA dynamic structure landscape at atomic resolution. To overcome this challenge, other sources of NMR information have to be tapped, including chemical shifts93,94, paramagnetic relaxation enhancement95 (PRE), RDC/RCSA relaxation dispersion experiments96 and also, powerful information that can be obtained from solid-state NMR methods97. Solution state NMR methods are also hindered by size limitations due to spectral overcrowding of resonances and enhanced line broadening with increasing molecular weight. Therefore, data from other techniques including small-angle X-ray scattering98 and chemical footprinting99 will also be important for enabling studies of much larger RNAs. Most importantly, input from computational methods will be critical and there is an urgent need to continue to test and develop nucleic acid force fields using NMR32,55. Second, there is a need to better understand how the RNA dynamic structure landscape depends on sequence, secondary and tertiary structure, and metals. To meet this goal, the dynamic properties of RNA structure have to be more systematically pursued using a range of strategically well-chosen RNA systems and conditions. Last but not least, this dynamic description of RNA has to be translated into a better more predictive understanding of function. The link between RNA dynamics and function remains vague and qualitative. Regions that have to change during functional cycles tend to be flexible; in few cases, aspects of sequence and secondary structure seem to have evolutionally conserved dynamic roles. To make this relationship more quantitative, kinetic, thermodynamic and structural properties of RNA dynamics have to be surgically perturbed with the use of mutagenesis, chemical modifications, or external agents, and the consequences on functional read-outs firmly established. Likewise, there is a need to better characterize and understand how cellular cues broadly affect the RNA dynamic structure landscape.
But perhaps most importantly, the current rejuvenated interest in solution-state NMR spectroscopy of RNA will very likely lead to unanticipated advances and discoveries regarding the basic physical behavior of RNA. We hope that this review will help enable many of these future applications.
Supplementary Material
Acknowledgments
We thank members of the Al-Hashimi lab for insightful comments and A. Kurochkin for maintenance of the NMR instruments. We would like to acknowledge collaborations with the groups of C. Fierke (University of Michigan), I. Andricioaei (University of California - Irvine), and C. Brooks (University of Michigan). The authors gratefully acknowledge the Michigan Economic Development Cooperation and the Michigan Technology Tri-Corridor for the support of the purchase of a 600 MHz spectrometer. This work was supported by the US National Institutes of Health (R01 AI066975 and R01 GM089846) and the US National Science Foundation (NSF Career Award CHE-0918817).
Footnotes
Competing financial interests
H.M.A. is an advisor to and holds an ownership interest in Nymirum, an RNA-based drug-discovery company.
Supplementary Information
Supplementary Table 1 RNA labeling schemes for dynamics measurements.
References
- 1.Frauenfelder H, Sligar SG, Wolynes PG. The Energy Landscapes and Motions of Proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 2.Cruz JA, Westhof E. The Dynamic Landscapes of RNA Architecture. Cell. 2009;136:604–609. doi: 10.1016/j.cell.2009.02.003. [DOI] [PubMed] [Google Scholar]
- 3.Blount KF, Breaker RR. Riboswitches as antibacterial drug targets. Nat. Biotechnol. 2006;24:1558–1564. doi: 10.1038/nbt1268. [DOI] [PubMed] [Google Scholar]
- 4.Micura R, Hobartner C. On secondary structure rearrangements and equilibria of small RNAs. Chembiochem. 2003;4:984–990. doi: 10.1002/cbic.200300664. [DOI] [PubMed] [Google Scholar]
- 5.Cooper TA, Wan LL, Dreyfuss G. Rna and Disease. Cell. 2009;136:777–793. doi: 10.1016/j.cell.2009.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hermann T. Rational ligand design for RNA: the role of static structure and conformational flexibility in target recognition. Biochimie. 2002;84:869–875. doi: 10.1016/s0300-9084(02)01460-8. [DOI] [PubMed] [Google Scholar]
- 7.Banas P, et al. Performance of Molecular Mechanics Force Fields for RNA Simulations: Stability of UUCG and GNRA Hairpins. J. Chem. Theory Comput. 2010;6:3836–3849. doi: 10.1021/ct100481h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boehr DD, Nussinov R, Wright PE. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leulliot N, Varani G. Current topics in RNA-protein recognition: Control of specificity and biological function through induced fit and conformational capture. Biochemistry. 2001;40:7947–7956. doi: 10.1021/bi010680y. [DOI] [PubMed] [Google Scholar]
- 10.Al-Hashimi HM, Walter NG. RNA dynamics: it is about time. Curr. Opin. Struc. Biol. 2008;18:321–329. doi: 10.1016/j.sbi.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chem. Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 12.Furtig B, Richter C, Wohnert J, Schwalbe H. NMR spectroscopy of RNA. Chembiochem. 2003;4:936–962. doi: 10.1002/cbic.200300700. [DOI] [PubMed] [Google Scholar]
- 13.Yamazaki T, Muhandiram R, Kay LE. Nmr Experiments for the Measurement of Carbon Relaxation Properties in Highly Enriched, Uniformly C-13,N-15-Labeled Proteins - Application to C-13(Alpha) Carbons. J. Am. Chem. Soc. 1994;116:8266–8278. [Google Scholar]
- 14.Boisbouvier J, Wu Z, Ono A, Kainosho M, Bax A. Rotational diffusion tensor of nucleic acids from 13C NMR relaxation. J. Biomol. NMR. 2003;27:133–142. doi: 10.1023/a:1024931619957. [DOI] [PubMed] [Google Scholar]
- 15.Johnson JE, Jr, Julien KR, Hoogstraten CG. Alternate-site isotopic labeling of ribonucleotides for NMR studies of ribose conformational dynamics in RNA. J. Biomol. NMR. 2006;35:261–274. doi: 10.1007/s10858-006-9041-x. [DOI] [PubMed] [Google Scholar]
- 16.Hansen AL, Al-Hashimi HM. Dynamics of large elongated RNA by NMR carbon relaxation. J. Am. Chem. Soc. 2007;129:16072–16082. doi: 10.1021/ja0757982. [DOI] [PubMed] [Google Scholar]
- 17.Vallurupalli P, Kay LE. A suite of 2H NMR spin relaxation experiments for the measurement of RNA dynamics. J. Am. Chem. Soc. 2005;127:6893–6901. doi: 10.1021/ja0427799. [DOI] [PubMed] [Google Scholar]
- 18.Rinnenthal J, et al. RNA phosphodiester backbone dynamics of a perdeuterated cUUCGg tetraloop RNA from phosphorus-31 NMR relaxation analysis. J. Biomol. NMR. 2009;45:143–155. doi: 10.1007/s10858-009-9343-x. [DOI] [PubMed] [Google Scholar]
- 19.Kloiber K, Spitzer R, Tollinger M, Konrat R, Kreutz C. Probing RNA dynamics via longitudinal exchange and CPMG relaxation dispersion NMR spectroscopy using a sensitive 13C-methyl label. Nucleic Acids Res. 2011;39:4340–4351. doi: 10.1093/nar/gkq1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lipari G, Szabo A. Model-Free Approach to the Interpretation of Nuclear Magnetic-Resonance Relaxation in Macromolecules .1. Theory and Range of Validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 21.Zhang Q, Throolin R, Pitt SW, Serganov A, Al-Hashimi HM. Probing motions between equivalent RNA domains using magnetic field induced residual dipolar couplings: Accounting for correlations between motions and alignment. J. Am. Chem. Soc. 2003;125:10530–10531. doi: 10.1021/ja0363056. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Q, Sun X, Watt ED, Al-Hashimi HM. Resolving the motional modes that code for RNA adaptation. Science. 2006;311:653–656. doi: 10.1126/science.1119488. [DOI] [PubMed] [Google Scholar]
- 23.Showalter SA, Baker NA, Tang CG, Hall K. Iron responsive element RNA flexibility described by NMR and isotropic reorientational eigenmode dynamics. J Biomol NMR. 2005;32:179–193. doi: 10.1007/s10858-005-7948-2. [DOI] [PubMed] [Google Scholar]
- 24.Showalter SA, Hall KB. Correlated motions in the U1 snRNA stem/loop 2: U1A RBD1 complex. Biophys. J. 2005;89:2046–2058. doi: 10.1529/biophysj.104.058032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clore GM, et al. Deviations from the Simple 2-Parameter Model-Free Approach to the Interpretation of N-15 Nuclear Magnetic-Relaxation of Proteins. J. Am. Chem. Soc. 1990;112:4989–4991. [Google Scholar]
- 26.Peng JW, Wagner G. Mapping of the spectral densities of N-H bond motions in eglin c using heteronuclear relaxation experiments. Biochemistry. 1992;31:8571–8586. doi: 10.1021/bi00151a027. [DOI] [PubMed] [Google Scholar]
- 27.Stueber D, Grant DM. 13C and (15)N chemical shift tensors in adenosine, guanosine dihydrate, 2'-deoxythymidine, and cytidine. J. Am. Chem. Soc. 2002;124:10539–10551. doi: 10.1021/ja012485c. [DOI] [PubMed] [Google Scholar]
- 28.Hansen AL, Al-Hashimi HM. Insight into the CSA tensors of nucleobase carbons in RNA polynucleotides from solution measurements of residual CSA: Towards new long-range orientational constraints. J. Magn. Reson. 2006;179:299–307. doi: 10.1016/j.jmr.2005.12.012. [DOI] [PubMed] [Google Scholar]
- 29. Ying JF, Grishaev A, Bryce DL, Bax A. Chemical shift tensors of protonated base carbons in helical RNA and DNA from NMR relaxation and liquid crystal measurements. J. Am. Chem. Soc. 2006;128:11443–11454. doi: 10.1021/ja061984g. This study reports the determination of the nucleobase carbon CSA tensors in helical RNA and DNA which are necessary for properly interpreting carbon spin relaxtion data in terms of fast picosecond-to-nanosecond dynamics.
- 30.Akke M, Fiala R, Jiang F, Patel D, Palmer AG., 3rd Base dynamics in a UUCG tetraloop RNA hairpin characterized by 15N spin relaxation: correlations with structure and stability. RNA. 1997;3:702–709. [PMC free article] [PubMed] [Google Scholar]
- 31.Duchardt E, Schwalbe H. Residue specific ribose and nucleobase dynamics of the cUUCGg RNA tetraloop motif by MNMR 13C relaxation. J. Biomol. NMR. 2005;32:295–308. doi: 10.1007/s10858-005-0659-x. [DOI] [PubMed] [Google Scholar]
- 32.Ferner J, et al. NMR and MD studies of the temperature-dependent dynamics of RNA YNMG-tetraloops. Nucleic Acids Res. 2008;36:1928–1940. doi: 10.1093/nar/gkm1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Eldho NV, Dayie KT. Internal bulge and tetraloop of the catalytic domain 5 of a group II intron ribozyme are flexible: implications for catalysis. J. Mol. Biol. 2007;365:930–944. doi: 10.1016/j.jmb.2006.10.037. This paper highlights the complexity of the RNA structure dynamic landscape. The authors report motions occuring at fast (ps-ns) and slow (ms-ms) timescales that are modulated by the presence of Mg2+ ions.
- 34.Oberstrass FC, Allain FH, Ravindranathan S. Changes in dynamics of SRE-RNA on binding to the VTS1p-SAM domain studied by 13C NMR relaxation. J. Am. Chem. Soc. 2008;130:12007–12020. doi: 10.1021/ja8023115. [DOI] [PubMed] [Google Scholar]
- 35.Ampt KAM, van der Werf RM, Nelissen FHT, Tessari M, Wijmenga SS. The Unstable Part of the Apical Stem of Duck Hepatitis B Virus Epsilon Shows Enhanced Base Pair Opening but Not Pico- to Nanosecond Dynamics and Is Essential for Reverse Transcriptase Binding. Biochemistry. 2009;48:10499–10508. doi: 10.1021/bi9011385. [DOI] [PubMed] [Google Scholar]
- 36.Musselman C, et al. Impact of static and dynamic A-form heterogeneity on the determination of RNA global structural dynamics using NMR residual dipolar couplings. J. Biomol. NMR. 2006;36:235–249. doi: 10.1007/s10858-006-9087-9. [DOI] [PubMed] [Google Scholar]
- 37.Sun X, Zhang Q, Al-Hashimi HM. Resolving fast and slow motions in the internal loop containing stem-loop 1 of HIV-1 that are modulated by Mg2+ binding: role in the kissing-duplex structural transition. Nucleic Acids Res. 2007;35:1698–1713. doi: 10.1093/nar/gkm020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bardaro MF, Shajani Z, Patora-Komisarska K, Robinson JA, Varani G. How binding of small molecule and peptide ligands to HIV-1 TAR alters the RNA motional landscape. Nucleic Acids Res. 2009;37:1529–1540. doi: 10.1093/nar/gkn1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Shajani Z, Drobny G, Varani G. Binding of U1A protein changes RNA dynamics as observed by 13C NMR relaxation studies. Biochemistry. 2007;46:5875–5883. doi: 10.1021/bi602658x. This study highlights the complex manner in which protein binding transforms the RNA dynamic structure landscape. Interhelical motions are minimally perturbed while residues that directly interact with the protein are either rigidified or become more flexible.
- 40.Tolman JR, Flanagan JM, Kennedy MA, Prestegard JH. Nuclear Magnetic Dipole Interactions in Field-Oriented Proteins - Information for Structure Determination in Solution. Proc. Natl. Acad. Sci. USA. 1995;92:9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1697–1697. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 42.Dethoff EA, et al. Characterizing complex dynamics in the transactivation response element apical loop and motional correlations with the bulge by NMR, molecular dynamics, and mutagenesis. Biophys. J. 2008;95:3906–3915. doi: 10.1529/biophysj.108.140285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Getz M, Sun X, Casiano-Negroni A, Zhang Q, Al-Hashimi HM. NMR studies of RNA dynamics and structural plasticity using NMR residual dipolar couplings. Biopolymers. 2007;86:384–402. doi: 10.1002/bip.20765. [DOI] [PubMed] [Google Scholar]
- 44.Tolman JR, Ruan K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem. Rev. 2006;106:1720–1736. doi: 10.1021/cr040429z. [DOI] [PubMed] [Google Scholar]
- 45.Hansen MR, Mueller L, Pardi A. Tunable alignment of macromolecules by filamentous phage yields dipolar coupling interactions. Nat. Struct. Biol. 1998;5:1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- 46.Kung HC, Wang KY, Goljer I, Bolton PH. Magnetic alignment of duplex and quadruplex DNAs. J. Magn. Reson. B. 1995;109:323–325. doi: 10.1006/jmrb.1995.9987. [DOI] [PubMed] [Google Scholar]
- 47.Tjandra N, Omichinski JG, Gronenborn AM, Clore GM, Bax A. Use of dipolar H-1-N-15 and H-1-C-13 couplings in the structure determination of magnetically oriented macromolecules in solution. Nat. Struct. Biol. 1997;4:732–738. doi: 10.1038/nsb0997-732. [DOI] [PubMed] [Google Scholar]
- 48.Zhang Q, Al-Hashimi HM. Extending the NMR spatial resolution limit for RNA by motional couplings. Nat. Methods. 2008;5:243–245. doi: 10.1038/nmeth.1180. [DOI] [PubMed] [Google Scholar]
- 49.Peti W, Meiler J, Bruschweiler R, Griesinger C. Model-free analysis of protein backbone motion from residual dipolar couplings. J. Am. Chem. Soc. 2002;124:5822–5833. doi: 10.1021/ja011883c. [DOI] [PubMed] [Google Scholar]
- 50.Fisher CK, Al-Hashimi HM. Approximate Reconstruction of Continuous Spatially Complex Domain Motions by Multialignment NMR Residual Dipolar Couplings. J. Phys. Chem. B. 2009;113:6173–6176. doi: 10.1021/jp900411z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ramirez BE, Bax A. Modulation of the alignment tensor of macromolecules dissolved in a dilute liquid crystalline medium. J. Am. Chem. Soc. 1998;120:9106–9107. [Google Scholar]
- 52. Zhang Q, Stelzer AC, Fisher CK, Al-Hashimi HM. Visualizing spatially correlated dynamics that directs RNA conformational transitions. Nature. 2007;450:1263–1267. doi: 10.1038/nature06389. This study combined domain elongation and RDCs to construct a 3D trajectory of the interhelical motions in TAR RNA. The inter-helical trajectory shows that TAR can dynamically sample seven distinct ligamd bound states in the absence of ligands.
- 53.Tolman JR, Ruan K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem. Rev. 2006;106:1720–1736. doi: 10.1021/cr040429z. [DOI] [PubMed] [Google Scholar]
- 54.Fisher CK, Zhang Q, Stelzer A, Al-Hashimi HM. Ultrahigh Resolution Characterization of Domain Motions and Correlations by Multialignment and Multireference Residual Dipolar Coupling NMR. J. Phys. Chem. B. 2008;112:16815–16822. doi: 10.1021/jp806188j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Frank AT, Stelzer AC, Al-Hashimi HM, Andricioaei I. Constructing RNA dynamical ensembles by combining MD and motionally decoupled NMR RDCs: new insights into RNA dynamics and adaptive ligand recognition. Nucleic Acids Res. 2009;37:3670–3679. doi: 10.1093/nar/gkp156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Stelzer AC, et al. Discovery of selective bioactive small molecules by targeting an RNA dynamic ensemble. Nat. Chem. Biol. 2011 doi: 10.1038/nchembio.596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Palmer AG, Kroenke CD, Loria JP. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Method. Enzymol. 2001;339:204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- 58.Korzhnev DM, Kay LE. Probing invisible, low-populated states of protein molecules by relaxation dispersion NMR spectroscopy: An application to protein folding. Accounts Chem. Res. 2008;41:442–451. doi: 10.1021/ar700189y. [DOI] [PubMed] [Google Scholar]
- 59.Skrynnikov NR, Dahlquist FW, Kay LE. Reconstructing NMR spectra of "invisible" excited protein states using HSQC and HMQC experiments. J. Am. Chem. Soc. 2002;124:12352–12360. doi: 10.1021/ja0207089. [DOI] [PubMed] [Google Scholar]
- 60.Auer R, et al. Measurement of signs of chemical shift differences between ground and excited protein states: a comparison between H(S/M)QC and R-1 rho methods. J. Biomol. NMR. 2010;46:205–216. doi: 10.1007/s10858-009-9394-z. [DOI] [PubMed] [Google Scholar]
- 61. Johnson JE, Jr, Hoogstraten CG. Extensive backbone dynamics in the GCAA RNA tetraloop analyzed using 13C NMR spin relaxation and specific isotope labeling. J. Am. Chem. Soc. 2008;130:16757–16769. doi: 10.1021/ja805759z. Site-specific carbon labelling makes it possible to apply carbon CPMG relaxation dispersion experiments and lead to the observation of conformational exchange within the sugars of an apical loop.
- 62.Palmer AG, Massi F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem. Rev. 2006;106:1700–1719. doi: 10.1021/cr0404287. [DOI] [PubMed] [Google Scholar]
- 63.Trott O, Palmer AG. R-1 rho relaxation outside of the fast-exchange limit. J. Magn. Reson. 2002;154:157–160. doi: 10.1006/jmre.2001.2466. [DOI] [PubMed] [Google Scholar]
- 64.Massi F, Johnson E, Wang CY, Rance M, Palmer AG. NMR R-1 rho rotating-frame relaxation with weak radio frequency fields. J. Am. Chem. Soc. 2004;126:2247–2256. doi: 10.1021/ja038721w. [DOI] [PubMed] [Google Scholar]
- 65.Korzhnev DM, Orekhov VY, Kay LE. Off-resonance R1(p) NMR studies of exchange dynamics in proteins with low spin-lock fields: An application to a fyn SH3 domain. J. Am. Chem. Soc. 2005;127:713–721. doi: 10.1021/ja0446855. [DOI] [PubMed] [Google Scholar]
- 66. Hansen AL, Nikolova EN, Casiano-Negroni A, Al-Hashimi HM. Extending the range of microsecond-to-millisecond chemical exchange detected in labeled and unlabeled nucleic acids by selective carbon R(1rho) NMR spectroscopy. J. Am. Chem. Soc. 2009;131:3818–3819. doi: 10.1021/ja8091399. This paper describes application of low spin lock power R1p experiments for characterizing slow millisecond exchange processes in DNA and RNA.
- 67.Hoogstraten CG, Wank JR, Pardi A. Active site dynamics in the lead-dependent ribozyme. Biochemistry. 2000;39:9951–9958. doi: 10.1021/bi0007627. [DOI] [PubMed] [Google Scholar]
- 68. Blad H, Reiter NJ, Abildgaard F, Markley JL, Butcher SE. Dynamics and metal ion binding in the U6 RNA intramolecular stem-loop as analyzed by NMR. J. Mol. Biol. 2005;353:540–555. doi: 10.1016/j.jmb.2005.08.030. This study combines NMR relaxation dispersion measurements with complementary structural data to propose an RNA excited state.
- 69.Reiter NJ, Blad H, Abildgaard F, Butcher SE. Dynamics in the U6 RNA intramolecular stem-loop: a base flipping conformational change. Biochemistry. 2004;43:13739–13747. doi: 10.1021/bi048815y. [DOI] [PubMed] [Google Scholar]
- 70.Nikolova EN, et al. Transient Hoogsteen base pairs in canonical duplex DNA. Nature. 2011;470:498–502. doi: 10.1038/nature09775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Venditti V, Clos L, Niccolai N, Butcher SE. Minimum-Energy Path for a U6 RNA Conformational Change Involving Protonation, Base-Pair Rearrangement and Base Flipping. J. Mol. Biol. 2009;391:894–905. doi: 10.1016/j.jmb.2009.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wenter P, Bodenhausen G, Dittmer J, Pitsch S. Kinetics of RNA refolding in dynamic equilibrium by 1H-detected 15N exchange NMR spectroscopy. J. Am. Chem. Soc. 2006;128:7579–7587. doi: 10.1021/ja060344a. [DOI] [PubMed] [Google Scholar]
- 73.Furtig B, et al. Time-resolved NMR studies of RNA folding. Biopolymers. 2007;86:360–383. doi: 10.1002/bip.20761. [DOI] [PubMed] [Google Scholar]
- 74.Lee MK, Gal M, Frydman L, Varani G. Real-time multidimensional NMR follows RNA folding with second resolution. Proc. Natl. Acad. Sci. USA. 2010;107:9192–9197. doi: 10.1073/pnas.1001195107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Latham MP, Zimmermann GR, Pardi A. NMR chemical exchange as a probe for ligand-binding kinetics in a theophylline-binding RNA aptamer. J. Am. Chem. Soc. 2009;131:5052–5053. doi: 10.1021/ja900695m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Buck J, Furtig B, Noeske J, Wohnert J, Schwalbe H. Time-resolved NMR methods resolving ligand-induced RNA folding at atomic resolution. Proc. Natl. Acad. Sci. USA. 2007;104:15699–15704. doi: 10.1073/pnas.0703182104. Time-resolved NMR is used to monitor conformational changes in an aptamer domain of an RNA riboswitch that are triggered following ligand binding.
- 77.Wenter P, Furtig B, Hainard A, Schwalbe H, Pitsch S. Kinetics of photoinduced RNA refolding by real-time NMR spectroscopy. Angew. Chem. Int. Ed. 2005;44:2600–2603. doi: 10.1002/anie.200462724. [DOI] [PubMed] [Google Scholar]
- 78.Wenter P, Furtig B, Hainard A, Schwalbe H, Pitsch S. A caged uridine for the selective preparation of an RNA fold and determination of its refolding kinetics by real-time NMR. Chembiochem. 2006;7:417–420. doi: 10.1002/cbic.200500468. [DOI] [PubMed] [Google Scholar]
- 79.Furtig B, et al. Conformational dynamics of bistable RNAs studied by time-resolved NMR spectroscopy. J. Am. Chem. Soc. 2007;129:16222–16229. doi: 10.1021/ja076739r. [DOI] [PubMed] [Google Scholar]
- 80.Gueron M, Leroy JL. Studies of base pair kinetics by NMR measurement of proton exchange. Methods in enzymology. 1995;261:383–413. doi: 10.1016/s0076-6879(95)61018-9. [DOI] [PubMed] [Google Scholar]
- 81.Russu IM. Probing site-specific energetics in proteins and nucleic acids by hydrogen exchange and nuclear magnetic resonance spectroscopy. Methods in enzymology. 2004;379:152–175. doi: 10.1016/S0076-6879(04)79009-6. [DOI] [PubMed] [Google Scholar]
- 82.Gueron M, Kochoyan M, Leroy JL. A single mode of DNA base-pair opening drives imino proton exchange. Nature. 1987;328:89–92. doi: 10.1038/328089a0. [DOI] [PubMed] [Google Scholar]
- 83.Snoussi K, Leroy JL. Imino proton exchange and base-pair kinetics in RNA duplexes. Biochemistry. 2001;40:8898–8904. doi: 10.1021/bi010385d. [DOI] [PubMed] [Google Scholar]
- 84.Huang Y, Weng X, Russu IM. Enhanced base-pair opening in the adenine tract of a RNA double helix. Biochemistry. 2011;50:1857–1863. doi: 10.1021/bi1014997. [DOI] [PubMed] [Google Scholar]
- 85.Mirau PA, Kearns DR. Effect of environment, conformation, sequence and base substituents on the imino proton exchange rates in guanine and inosine-containing DNA, RNA, and DNA-RNA duplexes. J. Mol. Biol. 1984;177:207–227. doi: 10.1016/0022-2836(84)90453-4. [DOI] [PubMed] [Google Scholar]
- 86.Vermeulen A, McCallum SA, Pardi A. Comparison of the global structure and dynamics of native and unmodified tRNAval. Biochemistry. 2005;44:6024–6033. doi: 10.1021/bi0473399. [DOI] [PubMed] [Google Scholar]
- 87.Smith FW, Feigon J. Quadruplex structure of Oxytricha telomeric DNA oligonucleotides. Nature. 1992;356:164–168. doi: 10.1038/356164a0. [DOI] [PubMed] [Google Scholar]
- 88.Cheong C, Moore PB. Solution structure of an unusually stable RNA tetraplex containing G- and U-quartet structures. Biochemistry. 1992;31:8406–8414. doi: 10.1021/bi00151a003. [DOI] [PubMed] [Google Scholar]
- 89.Figueroa N, et al. NMR study of slowly exchanging imino protons in yeast tRNAasp. Proc. Natl. Acad. Sci. USA. 1983;80:4330–4333. doi: 10.1073/pnas.80.14.4330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Nonin S, Jiang F, Patel DJ. Imino proton exchange and base-pair kinetics in the AMP-RNA aptamer complex. J. Mol. Biol. 1997;268:359–374. doi: 10.1006/jmbi.1997.0986. [DOI] [PubMed] [Google Scholar]
- 91. Rinnenthal J, Klinkert B, Narberhaus F, Schwalbe H. Direct observation of the temperature-induced melting process of the Salmonella fourU RNA thermometer at base-pair resolution. Nucleic Acids Res. 2010 doi: 10.1093/nar/gkq124. This paper reveals enthalpy-entropy compensation in RNA base-pair opening and argues that global unfolding of an RNA thermosensor occurs when microscopic stabilities of base-pairs are equalized.
- 92.Chen C, Jiang L, Michalczyk R, Russu IM. Structural energetics and base-pair opening dynamics in sarcin-ricin domain RNA. Biochemistry. 2006;45:13606–13613. doi: 10.1021/bi060908n. [DOI] [PubMed] [Google Scholar]
- 93.Dejaegere RA, Bryce RA, Case DA. Modeling NMR Chemical Shifts. In: Facelli JC, de Dios AC, editors. Ch. An Emipirical Analysis of Proton Chemical Shifts in Nucleic Acids. American Chemical Society; 1999. pp. 194–206. [Google Scholar]
- 94.Cromsigt JA, Hilbers CW, Wijmenga SS. Prediction of proton chemical shifts in RNA. Their use in structure refinement and validation. J. Biomol. NMR. 2001;21:11–29. doi: 10.1023/a:1011914132531. [DOI] [PubMed] [Google Scholar]
- 95.Clore GM, Tang C, Iwahara J. Elucidating transient macromolecular interactions using paramagnetic relaxation enhancement. Curr Opin Struc Biol. 2007;17:603–616. doi: 10.1016/j.sbi.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Hansen DF, Vallurupalli P, Kay LE. Using relaxation dispersion NMR spectroscopy to determine structures of excited, invisible protein states. J. Biomol. NMR. 2008;41:113–120. doi: 10.1007/s10858-008-9251-5. [DOI] [PubMed] [Google Scholar]
- 97.Olsen GL, et al. Solid-state deuterium NMR studies reveal mu s-ns motions in the HIV-1 Transactivation response RNA recognition site. J. Am. Chem. Soc. 2008;130:2896–2897. doi: 10.1021/ja0778803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Wang YX, Zuo XB, Wang JB, Yu P, Butcher SE. Rapid global structure determination of large RNA and RNA complexes using NMR and small-angle X-ray scattering. Methods. 2010;52:180–191. doi: 10.1016/j.ymeth.2010.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Gherghe CM, Shajani Z, Wilkinson KA, Varani G, Weeks KM. Strong correlation between SHAPE chemistry and the generalized NMR order parameter (S-2) in RNA. J. Am. Chem. Soc. 2008;130 doi: 10.1021/ja804541s. 12244-+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Sugase K. Elucidating slow binding kinetics of a protein without observable bound resonances by longitudinal relaxation NMR spectroscopy. J. Biomol. NMR. 2011 doi: 10.1007/s10858-011-9511-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.