Ultra-High Resolution Characterization of Domain Motions and Correlations by Multi-Alignment and Multi-Reference RDC NMR

Abstract

Nuclear Magnetic Resonance (NMR) residual dipolar couplings (RDC) provide a unique opportunity for spatially characterizing complex motions in biomolecules with timescale sensitivity extending up to milliseconds. Up to five motionally averaged Wigner rotation elements, $\langle D_{0k}^2(\alpha \beta )\rangle$, can be determined experimentally using RDCs measured in five linearly independent alignment conditions and applied to define motions of axially symmetric bond vectors. Here, we show that up to twenty-five motionally averaged Wigner rotation elements, $\langle D_{\mathit{\text{mk}}}^2(\alpha \beta \gamma )\rangle$, can be determined experimentally from multi-alignment RDCs and used to characterize rigid-body motions of chiral domains. The twenty-five $\langle D_{\mathit{\text{mk}}}^2(\alpha \beta \gamma )\rangle$ elements form a basis set that allows one to measure motions of a domain relative to an isotropic distribution of reference frames anchored on a second domain (and vice versa), thus expanding the 3D spatial resolution with which motions can be characterized. The twenty-five $\langle D_{\mathit{\text{mk}}}^2(\alpha \beta \gamma )\rangle$ elements can also be used to fit an ensemble consisting of up to eight equally or six unequally populated states. For more than two domains, changing the identity of the domain governing alignment allows access to new information regarding the correlated nature of the domain fluctuations. Example simulations are provided that validate the theoretical derivation and illustrate the high spatial resolution with which rigid-body domain motions can be characterized using multi-alignment and multi-reference RDCs. Our results further motivate the development of experimental approaches for both modulating alignment and anchoring it on specifically targeted domains.

Introduction

An important challenge in biophysics is to reconstruct the dynamics of biomolecules on the basis of experimental measurements^1,2. There has been great interest in recent years in harnessing the broad time-scale sensitivity of NMR residual dipolar couplings (RDCs)^3,4 in visualizing the dynamics of complex biomolecules^5–7. RDCs can be measured in molecules that are partially aligned, either spontaneously when they have a significant magnetic susceptibility anisotropy^3,8 or, more generally, by dissolution in an appropriate ordering medium^4,9. The RDC observed between two nuclei depends on $\langle \frac{3{\text{cos}}^2\theta -1}{2}\rangle$, where θ is the angle between the inter-nuclear bond vector and the magnetic field and the angular brackets denote a time average over all orientations that are sampled at a rate faster than the inverse of the dipolar interaction (typically 10–100 ms).

Several frameworks have been introduced that allow the interpretation of RDCs in terms of the average orientation and dynamics of bond vectors (reviewed in^5,6). The direct interpretation of dipolar couplings (DIDC)^10,11 and model-free^12,13 formalisms allow the determination of five independent parameters per bond vector based on the measurement of RDCs under five linearly independent alignment conditions¹⁴. The five parameters correspond to motionally averaged Wigner rotation elements, $\langle D_{0l}^2(\alpha \beta )\rangle$, where α and β are polar angles defining the orientation of a bond relative to a molecule-fixed chiral frame that typically corresponds to the principal axis system (PAS) of the overall alignment tensor. The five parameters describe the mean bond vector orientation, the amplitude of motion, and the direction and degree of any motional asymmetry. Collections of co-planar RDCs can also be combined in the dynamic-meccano approach and used to simultaneously determine the relative orientation and dynamics of peptide planes¹⁵. Alternatively, multi-alignment RDCs can be included along with other experimental and non-experimental restraints in the simulated annealing protocol to refine an ensemble of inter-converting conformations¹⁶.

The information that can be retrieved regarding bond vector dynamics is limited by the axially symmetric nature of the dipolar interaction, which is inherently insensitive to one of three rotational degrees of freedom involving rotations around the bond vector itself. However, motions of chiral domains can be complex and involve all three degrees of rotational freedom^17,18. Such motions can, in principle, be characterized with greater spatial resolution since many RDC vectors spanning different orientations can serve as reporters of the underlying motional trajectory¹⁹. Stated differently, the alignment tensor of a chiral domain, which can be determined experimentally using collections of RDCs, can deviate from axial symmetry, allowing motions to be characterized with more complete 3D rotational sensitivity.

Several studies have used RDCs in characterizing rigid-body motions of chiral structural fragments, including secondary structural elements¹⁹ and intact domains in proteins^20–23, sugar moieties in carbohydrates²⁴, and A-form helices in RNA^25,26. The order tensor formalism^27–29 and related frameworks have been widely used in interpreting RDCs in terms of the relative orientation and dynamics of domains. When the overall alignment is axially symmetric³⁰, the five motionally averaged order tensor elements can easily be interpreted in terms of five parameters describing the average orientation and dynamics of a domain, in analogy to the five parameters obtained for axially symmetric bond vectors using multi-alignment RDCs. However, the interpretation is not straightforward when the overall alignment departs from axial symmetry and the intrinsic spatial sensitivity to domain motions is extended from two to three rotational degrees of freedom. Other approaches have been developed that characterize the conformational space in terms of maximum allowed probabilities for any conformation so to be consistent with the measured RDCs³¹. The analysis of domain motions has largely been limited to RDCs measured in one or two alignments and is complicated by potential deviations from the “decoupling approximation,” the assumption that domain motions do not affect the overall alignment.

Here, we present a theoretical framework that extracts the maximum information from RDCs in characterizing rigid-body domain motions. We show that a set of twenty-five motionally averaged Wigner rotation elements can be determined experimentally from RDCs measured under five linearly independent alignment conditions and used to characterize rigid-body domain motions. Compared to the five parameter description of bond vector dynamics, the twenty-five parameters afford 3D rather than 2D rotational sensitivity and offer stronger restraints on the domain orientational distribution; thus sharpening the resolution with which motions can be characterized. Furthermore, we show that changing the identity of the reference domain governing overall alignment in multi-domain molecules provides access to new information regarding the correlated nature of the domain fluctuations that is inaccessible from simply changing alignment.

Theory

We show in what follows that all twenty-five $D_{\mathit{\text{mn}}}^2(\alpha \beta \gamma )$ elements representing the second rank approximation to the orientational probability distribution function (OPDF)³⁸ describing the dynamics of a domain relative to a reference domain can be determined experimentally from analysis of collections of five or more independent RDCs measured under five linearly independent alignment conditions. We assume that domain motions do not alter overall alignment, which is dominated entirely by a “reference” domain. This situation applies for any domain whose motion does not alter the overall alignment. Alternatively, a reference domain can deliberately be established by, for example, introducing a paramagnetic metal^3,22 or tag^39,40 or by other chemical modifications, such as elongating a domain so that its becomes more anisotropic⁴¹. We consider two domains (I and II) that are linked by a flexible hinge. Unless stated otherwise, domain I will be the reference domain dominating alignment. We ignore the effects of local motions of bond vectors, which are assumed to lead to uniform scaling of the measured RDCs, and also assume that the mean orientation of RDC targeted bond vectors within each domain is known.

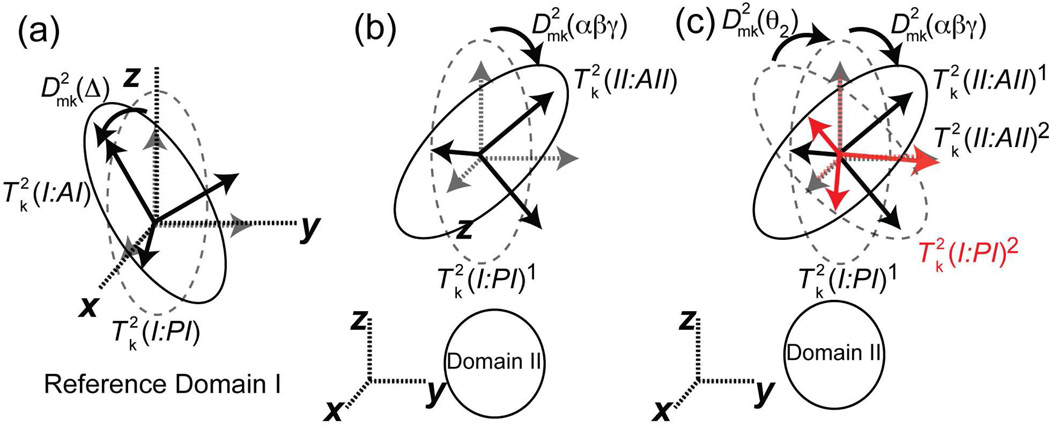
Let $T_k^2(I:\mathit{\text{PI}})$ be elements of the domain I overall alignment tensor expressed in its overall PAS (PI). The motionally averaged alignment tensors measured for domains I $\langle T_k^2(I:\mathit{\text{AI}})\rangle \text{ and II }\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ expressed in arbitrary frames (AI and AII) are given by (Figure 1),

$$\begin{array}{c}\langle T_k^2(I:\mathit{\text{AI}})\rangle =T_k^2(I:\mathit{\text{AI}})={\displaystyle \sum _{m=-2}^2}{T}_m^2(I:\mathit{\text{PI}})D_{\mathit{\text{mk}}}^2(\mathrm{\Delta })\hfill \\ \langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle ={\displaystyle \sum _{m=-2}^2}{T}_m^2(I:\mathit{\text{PI}})\langle D_{\mathit{\text{mk}}}^2(\alpha \beta \gamma )\rangle \hfill \end{array},$$ (1)

where $D_{\mathit{\text{mk}}}^2(\mathrm{\Delta })$ transforms domain I from its alignment tensor PAS to the arbitrary molecular frame, AI (Figure 1(a)). The $T_k^2(I:\mathit{\text{AI}})$ elements are obtained experimentally by determining the domain I alignment tensor using RDCs and established protocols^25,28,42. $D_{\mathit{\text{mk}}}^2(\alpha \beta \gamma )$ is a time-dependent Wigner rotation that transforms the reference domain I alignment tensor from its PAS to its instantaneous orientation relative to the domain II arbitrary frame, AII (Figure 1(b)). The angular brackets denote a time average over all orientations sampled at a rate faster than the inverse of the dipolar interaction. In the PAS $T_{\pm 1}^2(I:\mathit{\text{PI}})=0$ and the fifteen $\langle D_{0k}^2(\alpha \beta \gamma )\rangle ,\langle D_{2k}^2(\alpha \beta \gamma )\rangle ,\text{and }\langle D_{-2k}^2(\alpha \beta \gamma )\rangle$ elements are required to relate $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle \text{ to }{T}_m^2(I:\mathit{\text{PI}})$. For an axially symmetric domain I alignment, $T_{\pm 1}^2(I:\mathit{\text{PI}})=T_{\pm 2}^2(I:\mathit{\text{PI}})=0$, and only five elements, $\langle D_{0k}^2(\alpha \beta )\rangle$, are relevant. In the general case, eq 1 is underdetermined since there are fifteen unknown Wigner elements and only five experimentally determined $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ elements. Additional measurements can be obtained by changing the alignment of the reference domain I¹⁴ and acquiring a new set of RDCs. Changing the orientation of alignment will, however, necessarily lead to deviations from the original alignment PAS, requiring a new set of $\langle D_{\mathit{\text{mk}}}^2({\alpha }_l{\beta }_l{\gamma }_l)\rangle$ elements relating the orientation of the l^th domain I alignment PAS relative to domain II,

$${\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle }^l={\displaystyle \sum _{m=-2}^2}{T}_m^2{(I:\mathit{\text{PI}})}^l\langle D_{\mathit{\text{mk}}}^2({\alpha }_l{\beta }_l{\gamma }_l)\rangle$$ (2)

To effectively take advantage of the new set of RDC measurements, we use the closure relationship to break down $\langle D_{\mathit{\text{mk}}}^2({\alpha }_l{\beta }_l{\gamma }_l)\rangle$ into two rotations,

$$\langle D_{\mathit{\text{mk}}}^2({\alpha }_l{\beta }_l{\gamma }_l)\rangle =\langle {\displaystyle \sum _{n=-2}^2}{D}_{\mathit{\text{mn}}}^2({\theta }_l)D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle ={\displaystyle \sum _{n=-2}^2}{D}_{\mathit{\text{mn}}}^2({\theta }_l)\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle ,$$ (3)

where $D_{\mathit{\text{mn}}}^2({\theta }_l)$ transforms domain I from the PAS of the l^th alignment to an arbitrary common reference frame (e.g. in this case the PAS of the l=1 alignment) and $D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )$ from the reference frame to the instantaneous orientation relative to domain II in its arbitrary frame, as is diagrammatically illustrated in Figure 1(c). Note that any arbitrary common reference frame can be chosen and that the elements of $D_{\mathit{\text{mn}}}^2({\theta }_l)$ will be known for every l^th alignment based on determination of the domain I alignment tensor and that the averaging is performed over the time-dependent matrix elements only. This yields the following expression for ${\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle }^l$ measured under the l^th alignment:

$${\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle }^l={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}{T}_m^2{(I:\mathit{\text{PI}})}^l{D}_{\mathit{\text{mn}}}^2({\theta }_l)\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle .$$ (4)

Figure 1.

Molecular frames and rotations used in the analytical treatment of motions for the (a) reference domain dominating alignment and (b, c) moving domain under (b) one and (c) multiple reference domain I alignments.

Since the domain motions no longer originate from the PAS for every alignment, all twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ Wigner matrix elements are necessary to describe the system of equations. These elements can be numerically solved for using eq 4 by experimentally determining $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ under five linearly independent reference domain I alignments. Note that with the determination of $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$, one has also determined the inverse Wigner elements $\langle D_{\mathit{\text{kn}}}^{2*}(\alpha \beta \gamma )\rangle$ and therefore the corresponding dynamics of the reference domain relative to the chiral domain.

It has recently been shown⁴³ that a sub-set of elements, $\langle D_{0k}^2(\alpha \beta )\rangle \text{ and }\langle D_{k0}^{2*}(\beta \gamma )\rangle$, can be determined experimentally under the limiting case of having axially symmetric reference alignments anchored independently onto domains I and II,

$$\begin{array}{c}\langle T_k^2(\mathit{\text{II}}:\mathit{\text{PII}})\rangle =T_0^2(I:\mathit{\text{PI}})\langle D_{0k}^2(\alpha \beta )\rangle \hfill \\ \langle T_k^2(I:\mathit{\text{PI}})\rangle =T_0^2(\mathit{\text{II}}:\mathit{\text{PII}})\langle D_{k0}^{2*}(\beta \gamma )\rangle \hfill \end{array}$$ (5)

Interpreting $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$

The twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements obtained from five independent alignments provide a more complete 3D description of domain motions when compared to the ten sub-elements $\langle D_{0l}^2(\alpha \beta )\rangle \text{ and }\langle D_{l0}^{2*}(\beta \gamma )\rangle$ that have been measured previously⁴³. A unique feature of the $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements is that they contain several elements (n and k ≠ 0) that are simultaneously sensitive to all three rotational degrees freedom (αβγ) and therefore any correlations between them. In contrast, $\langle D_{0l}^2(\alpha \beta )\rangle \text{ and }\langle D_{l0}^{2*}(\beta \gamma )\rangle$ are insensitive to one rotational degree of freedom and, even when combined, remain insensitive to any correlations between α and γ when β does not vary. The elements of $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ are also not subject to the 180° inversion degeneracy that arises for $\langle D_{0l}^2(\alpha \beta )\rangle \text{ and }\langle D_{l0}^{2*}(\beta \gamma )\rangle$, as first demonstrated by Prestegard and co-workers⁴⁴.

The elements of $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ constitute internal order parameters with 3D rotational sensitivity. We define a chiral generalized internal order parameter, $S_{\mathit{\text{CL}}}^2$, that ranges between 0 to 1 for maximum and minimum domain motional amplitudes:

$$S_{\mathit{\text{CL}}}^2=\frac{1}{5}{\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}\langle D_{\mathit{\text{mn}}}^{2*}(\alpha \beta \gamma )\rangle \langle D_{\mathit{\text{mn}}}^2(\alpha \beta \gamma )\rangle .$$ (6)

$S_{\mathit{\text{CL}}}^2$ provides a frame independent measure of domain motional amplitudes. In contrast, conventional order parameters do not sense motions around the axially symmetric interactions and typically probe reorientation of the bonds relative to a molecule-fixed alignment or diffusion tensor.

The twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ allow one to compute motions of a given chiral domain relative to any reference alignment frame anchored on a second domain (and vice versa), even though experimental measurements are made relative to only five distinct alignments. This is because eq 4 and the twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements can be used to compute motionally averaged alignment tensors for a domain $(\langle T_k^2\rangle )$ given any reference domain alignment tensor $(T_m^2{D}_{\mathit{\text{mn}}}^2(\theta ))$. For example, one can compute motionally averaged alignment tensors for a domain given an isotropic distribution of axially symmetric alignment tensors anchored onto the reference domain. In this way, one can obtain five independent parameters describing motions of a domain relative to every direction on the second domain.

The twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements can also be fit to a dynamical ensemble of n distinct inter-domain conformations each defined by three Euler angles αⁿβⁿγⁿ. Such an ensemble based approach was first proposed by Clore and co-workers in the analysis of bond vector orientation¹⁶. The added spatial sensitivity afforded by determining the full Wigner matrix is self-evident here as it allows construction of ensembles defined by a larger number of parameters. For example, assuming equal populations for various members of the ensemble, a maximum of eight states (25/3 rounded down to the nearest integer) can be used to fit the twenty-five independent Wigner elements. For unequal populations, an n state ensemble will require 3n spatial and n-1 weighting parameters allowing fitting to a maximum of six states. Of course, it is preferable to find an ensemble that has the smallest number of independent parameters that can explain the data. It is possible in such analyses that more than one degenerate solution exists that can reproduce the average $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements to within statistical significance, particularly in the presence of experimental uncertainty, and it is therefore critical to vastly explore the parameter space during the fitting procedure. In simulations, we were able to perfectly reproduce equally populated discrete states for n up to 8 (data not shown) on the basis of RDCs measured under five linearly independent alignment conditions. No degeneracies were observed in our simulations, though we did not attempt to fit models involving different populations and did not perform a brute force search algorithm to explore all local minima of the fitting landscape.

Multiple Domains

The treatment for more than two domains readily follows from the framework presented above. As an example, we consider three domains (I II and III) with domain I as a reference. The motionally averaged alignment tensors for the three domains are given by,

$$\begin{array}{c}\langle T_k^2(I:\mathit{\text{AI}})\rangle =T_k^2(I:\mathit{\text{AI}})={\displaystyle \sum _{m=-2}^2}{T}_m^2(I:\mathit{\text{PI}})D_{\mathit{\text{mk}}}^2(\mathrm{\Delta })\hfill \\ \langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle ={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}{T}_m^2(I:\mathit{\text{PI}})D_{\mathit{\text{mn}}}^2(\theta )\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{II}})\rangle \hfill \\ \langle T_k^2(\mathit{\text{III}}:\mathit{\text{AIII}})\rangle ={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}{T}_m^2(I:\mathit{\text{PI}})D_{\mathit{\text{mn}}}^2(\theta \prime )\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{III}})\rangle \hfill \end{array},$$ (7)

where $D_{\mathit{\text{nk}}}^2(i\to j)$ transforms domain i from its arbitrary frame to its instantaneous orientation relative to the domain j. The fifty $\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{II}})\rangle \text{ and }\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{III}})\rangle$ elements can be experimentally determined from five linearly independent domain I alignments. However, no direct information is obtained regarding the relative motions of domains II and III, as given by $\langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle$.

If we assume that the relative motions of domain I and domain II are completely independent of the relative motions of domain III and domain II then, by eq 3,

$$\langle D_{\mathit{\text{mk}}}^2(I\to \mathit{\text{III}})\rangle ={\displaystyle \sum _{n=-2}^2}\langle D_{\mathit{\text{mn}}}^2(I\to \mathit{\text{II}})\rangle \langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle ,$$ (8)

and $\langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle$ can be determined from $\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{II}})\rangle \text{ and }\langle D_{\mathit{\text{nk}}}^2(I\to \mathit{\text{III}})\rangle$ using eq 8. If the domain motions are not independent, all seventy-five Wigner rotation elements are required to describe the dynamics. The additional twenty-five elements can be measured by changing the reference domain. The system of equations when making domain II a reference is given by,

$$\begin{array}{c}\langle T_k^2(I:\mathit{\text{PI}})\rangle ={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}{T}_m^2(\mathit{\text{II}}:\mathit{\text{PII}})D_{\mathit{\text{mn}}}^2(\theta )\langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to I)\rangle \hfill \\ \langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle =T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})={\displaystyle \sum _{m=-2}^2}{T}_m^2(\mathit{\text{II}}:\mathit{\text{PII}})D_{\mathit{\text{mk}}}^2(\mathrm{\Delta }\text{'})\hfill \\ \langle T_k^2(\mathit{\text{III}}:\mathit{\text{AIII}})\rangle ={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}{T}_m^2(\mathit{\text{II}}:\mathit{\text{PII}})D_{\mathit{\text{mn}}}^2(\theta \prime )\langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle \hfill \end{array},$$ (9)

in which $\langle D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle$ can be determined in the same manner as discussed above. Thus for n domains, RDCs need to be measured under five linearly independent alignment conditions for n-1 different reference domains in order to solve for the $25{\displaystyle \sum _{i=1}^n}(n-i)$ Wigner elements.

Correlated Domain Motion

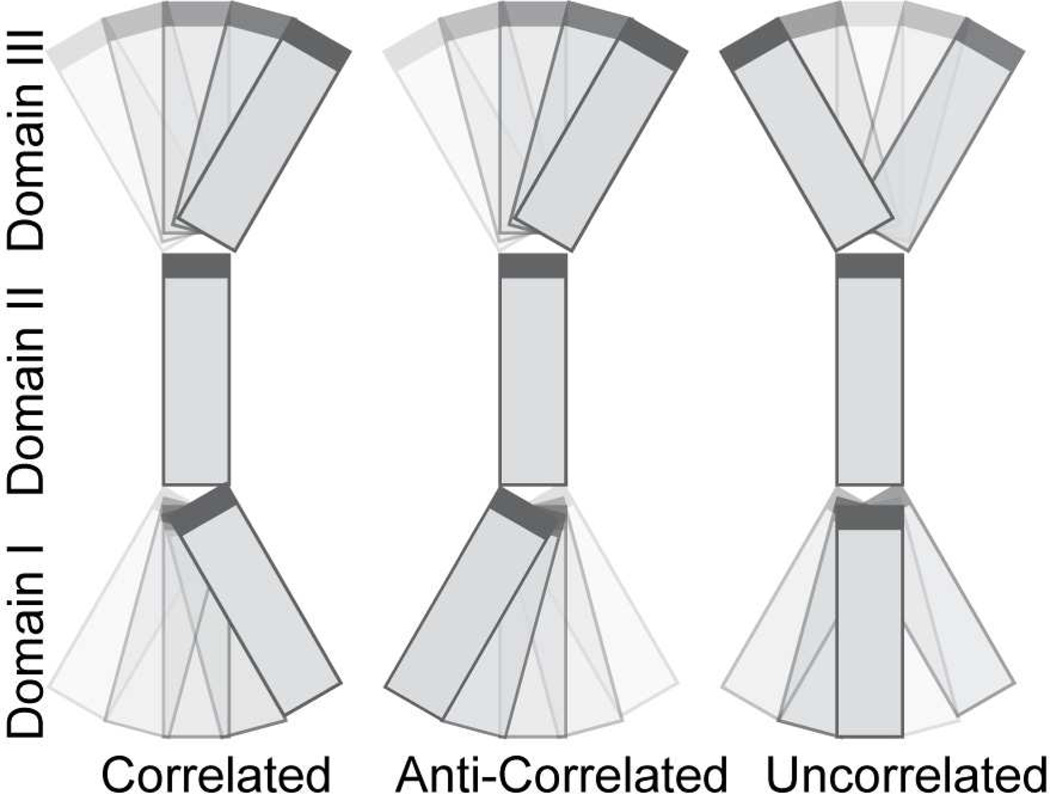
Changing the reference domain provides the basis for resolving the correlated nature of motions between two or more domains. To illustrate this, we consider three domains (I II and III). Assuming that motions of the domains are not correlated to one another (Figure 2), by eq 8, the chiral order parameters describing relative motions of the domains I and III $(S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}}))$ can be expressed in terms of the product of successive order parameters describing motions of domain I relative domain II $(S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}}))$ and domain II relative to domain III $(S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}}))$,

$$S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})=S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}}).$$ (10)

Figure 2.

Depiction of correlated, anti-correlated and uncorrelated motions between domains I and III in a three-domain system.

If the motions of domains I and III are correlated (Figure 2), the motional amplitude of one domain from the reference frame of the other appears exaggerated as compared to the non-correlated case and,

$$S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})<S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}}).$$ (11)

For anti-correlated motions (Figure 2) between domains I and III the motional amplitude of one domain from the reference frame of the other domain appears diminished compared to the non-correlated case and,

$$S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})>S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})$$ (12)

The degree to which the domain motions are correlated or anti-correlated can be assessed by the deviation from non-correlated behavior with a correlation parameter, H_corr, defined as,

$$H_{\mathit{\text{corr}}}=\frac{S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})-S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})}{S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})}.$$ (13)

The value of H_corr is a percentage deviation from non-correlated motion, but is dependent on the motional model and therefore should only serve as a qualitative measure of motional correlations. A positive value of H_corr implies correlated motion, a negative value anti-correlated motion, and H_corr approximately equal to zero implies little motional correlation.

Characterization of motion: Examples from simulations

We preformed several simulations using Mathematica® Version 5.2 to establish the utility of $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ in characterizing domain motions. We present results for three illustrative domain motions (i) continuous single axis rotation of a domain by ± 25° about a fixed arbitrary axis (ii) a motional model comprising collective motions of two helical domains as derived from a previously reported 65 ns molecular dynamics simulation of the HIV-1 transactivation response element (TAR)^25,34 and (iii) ± 30° correlated, anti-correlated and uncorrelated bending motions involving three domains (Figure 2).

In these simulations, five linearly independent alignments were generated for a reference domain using the Gram-Schmidt orthonormalization³⁶ procedure on five arbitrarily chosen alignment tensors. For the third motional model, five independent alignments were constructed independently when having domain I and II as the reference domain. The relative orientations were defined using Euler angles and unit quaternions. The latter are 4-dimensional complex numbers that represent an orientation as a single axis rotation³². The relationship between the quaternions and the Euler angles is given by,

$$q_{\alpha \beta \gamma }=\left[\text{cos}\left(\frac{\beta }{2}\right)\text{cos}\left(\frac{\alpha +\gamma }{2}\right),\text{sin}\left(\frac{\beta }{2}\right)\text{sin}\left(\frac{-\alpha +\gamma }{2}\right),\text{sin}\left(\frac{\beta }{2}\right)\text{cos}\left(\frac{-\alpha +\gamma }{2}\right),\text{cos}\left(\frac{\beta }{2}\right)\text{sin}\left(\frac{\alpha +\gamma }{2}\right)\right]$$ (14)

For motional models (i) and (iii), the “real” average Wigner rotation elements ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}$ were computed by averaging over 10001 equally spaced states along the trajectory. For motional model (ii) inter-helical Euler angles were calculated for each picosecond in the 64.998 ns simulation of the transactivation response element (TAR) RNA^33,34 as described previously³⁵ and ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}$ were computed by averaging over all states. The motionally averaged alignment tensor elements ${\langle T_k^2(\mathit{\text{II}})\rangle }_{\mathit{\text{real}}}$ were determined using eqs 4, 7, and 9. The elements of ${\langle T_k^2(\mathit{\text{II}})\rangle }_{\mathit{\text{real}}}$ determined under each of the five alignment conditions were then used to solve for the “experimental” ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\text{exp}}$ elements by minimizing the root mean square deviation between 〈T(II)〉_real and 〈T(II)〉_exp in the Cartesian representation using the Nelder-Mead algorithm⁴⁵ implemented in Mathematica®.

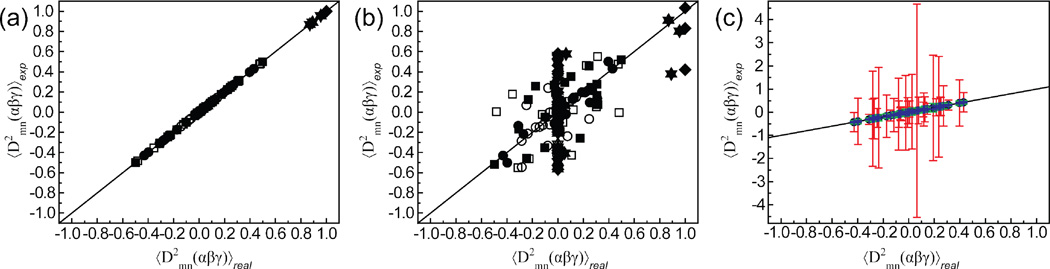
As shown in Figure 3(a), we observe perfect agreement between ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}\text{ and }{\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\text{exp}}$ for all three motional models examined, demonstrating that all twenty-five matrix elements can be determined experimentally using RDCs measured under five linearly independent alignments. In contrast, as shown in Figure 3(b), substantial deviations are observed when solving for $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ using five alignments, only four of which are linearly independent as the fifth alignment was constructed from a linear combination of the initial four.

Figure 3.

Comparison of “real” ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}$ Wigner rotation elements with “experimental” ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\text{exp}}$ values computed using Equations 4, 7, and 9 based on (a) five and (b) four linearly independent alignment conditions. Results are shown for three motional models; continuous rotation of a domain by ± 25° about an arbitrary axis (square); collective motions of two helical domains in a 65 ns molecular dynamics simulation of TAR RNA^25,34(circle); and ± 30° anti-correlated bending motions for domains I–II (triangle up), II–III (triangle down), and I–III (diamond). (c) The effects of RDC error and structural noise on Wigner elements determined from the MD trajectory for three levels of uncertainty in the alignment tensors, (blue error bars) ≤ 5° uncertainty in orientation and ≤ 5 % uncertainty in magnitude, (green error bars) 5°–10° uncertainty in orientation and 5–10 % uncertainty in magnitude, (red error bars) 10°–15° uncertainty in orientation and 10–15 % uncertainty in magnitude. Error bars represent the RMSD calculated over 100 random iterations.

We explored the effects of experimental uncertainty by randomly perturbing the alignment tensors calculated from the MD trajectory and using the resulting tensors to back-predict the Wigner matrix. The alignment tensors were perturbed by a random rotation and scaling in a manner analogous to that described in ref 25. Three different levels of error were explored; (small) ≤ 5° uncertainty in orientation and ≤ 5 % uncertainty in magnitude, (medium) 5°–10° uncertainty in orientation and 5–10 % uncertainty in magnitude, (large) 10°–15° uncertainty in orientation and 10–15 % uncertainty in magnitude. The latter error ranges account for both RDC uncertainty and structural heterogeneity in the domain structure. For RNA A-form helices, the small range corresponds to values expected based on typical RDC uncertainty and documented deviations from the idealized A-form structure as described previously²⁵. The impact of the error on the “experimental” Wigner elements was assessed by computing the RMSD between the “real” and “experimental” values over 100 iterations.

As shown in Figure 3(c) the Wigner elements can be accurately determined in the presence of uncertainty levels even greater than those typically encountered in experimental studies. The errors observed at “medium” levels of alignment tensor uncertainty were roughly twice those observed at “small” levels of uncertainty. However, “large” errors in the alignment tensors led to a breakdown in the ability to resolve the Wigner matrix, resulting in very large errors and leading to mathematically impossible values in our unconstrained fitting procedure. For these cases, a more comprehensive and thorough analysis of the effects of uncertainty is clearly required but is beyond the scope of the current work.

We used different approaches to interpret the $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements for each motional model. A model-free approach was used to analyze the rotation around and an axis model. Here, the twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements are used to determine alignment tensors for the mobile domain II $(\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle )$ given any arbitrary alignment tensor on the reference domain $(T_m^2(I:\mathit{\text{PI}})D_{\mathit{\text{mn}}}^2(\theta ))$. In particular, we computed the entire family of $(\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle )$ elements for an isotropic distribution of axially symmetric alignment tensors, with principal values of −0.0005, −0.0005, and 0.001 for the x, y and z components, on the reference domain. Each five $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ elements provide a description of the orientational ordering of a designated reference domain I direction relative to the chiral domain II. In analogy to the description of bond vector dynamics, the five parameters describe the average orientation of that direction relative to the chiral domain, the amplitude of its motion (but not twisting motion around the long axis in case of axial symmetry) and the direction and degree of motional asymmetry. In this manner, a five parameter description regarding orientational ordering of every direction on reference domain I relative to chiral domain II can be obtained.

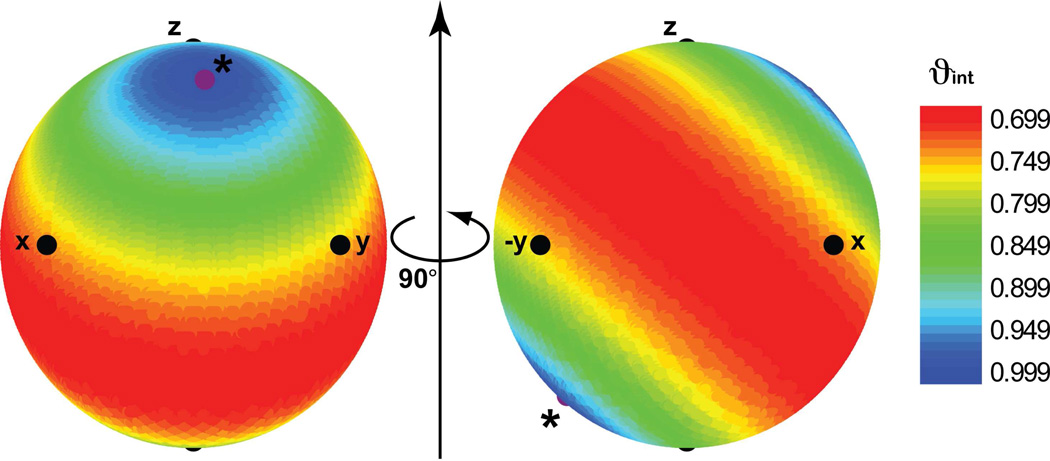
The twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements were used compute the family of $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ using eq 4 for an isotropic distribution of axially symmetric alignment tensors on the reference domain I. The $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ elements were then converted into the familiar Cartesian form. The value of the ϑ_int²⁹, which describes the amplitude of motion for a given direction (but not twisting dynamics around it) ranging between 0 and 1 for maximum and minimum motions, was computed for each starting alignment tensor. Here, each direction relative to the domain I arbitrary frame (AI) is represented as a point on the globe. The amplitude of motion for each direction is then represented by coloring the ϑ_int value.

We observe a symmetric distribution of decreasing ϑ_int values around a maximum value of 1 observed for a direction inclined at 40° and 50° relative to the domain I arbitrary frame z and x axes, respectively (Figure 4). Thus, this direction does not change its orientation relative to the chiral domain II. As expected, this direction exactly corresponds to the rotation axis of the domain motion. The $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ elements obtained for this direction yield a T_zz direction relative to domain II that is also in perfect coincidence with the axis of motion. As expected, maximum motional amplitudes are observed for directions orthogonal to the rotation axis (Figure 4). In this manner, the nature of the motion i.e. rotation around a single axis, can be inferred de novo. Note that delineating the type of motion in this way is only feasible with a uniform distribution of reference frames and hence requires all twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements. One could also visualize in an analogous manner the average orientation, degree and direction of motional asymmetry for every direction examined and employ axially asymmetric tensors for the reference domain I, in which case the $\langle T_k^2(\mathit{\text{II}}:\mathit{\text{AII}})\rangle$ elements will also be sensitive to rotational motions around each chosen axis.

Figure 4.

Diagram of domain motions by multi-alignment RDCs. Globe showing the internal generalized degree of order (ϑ_int) for domain II for an isotropic distribution of axially symmetric alignment tensors centered on reference domain I, for a motional model involving rotation of domain II about an arbitrary axis direction relative to reference domain I. Each point on the globe represents a specific direction relative to reference domain I. The value of the ϑ_int is color-coded for each direction with ϑ_int increasing in value (and motions therefore decreasing in amplitude) from red to blue for 0.699 and 1, respectively. The ϑ_int value provides a measure of the extent to which a given direction undergoes reorientational dynamics relative to the chiral domain II. The smallest degree of motion is observed for a direction around which the rotational motions occur. The axis of rotation is denoted by *.

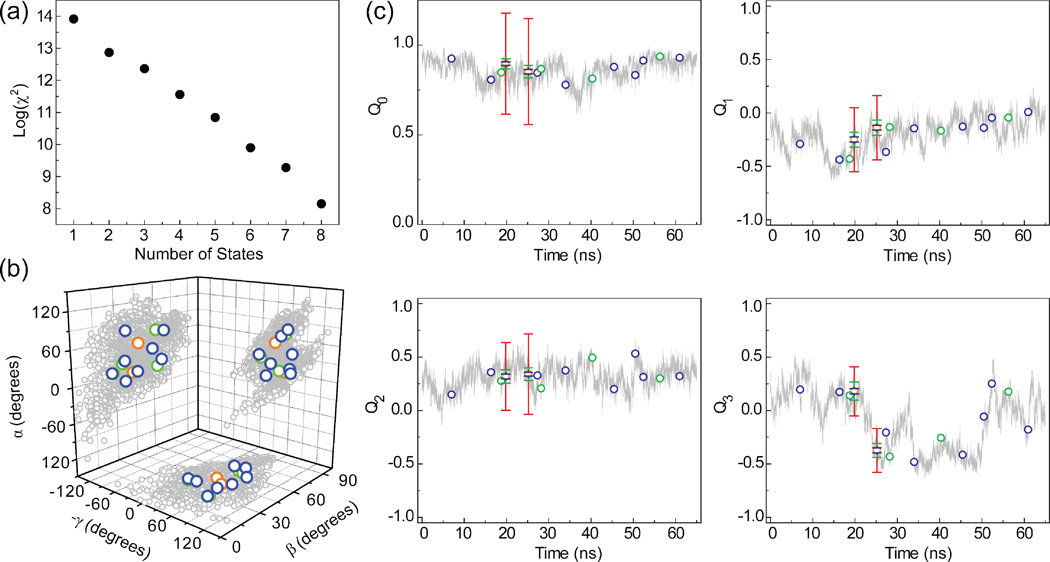
The $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements obtained for the motional model derived from the MD trajectory were analyzed using an n-state ensemble method. Here, we fit the twenty-five $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements to n equally populated states. A χ² given by, ${\chi }^2={\displaystyle \sum _{m=-2}^2}{\displaystyle \sum _{n=-2}^2}\frac{{|{\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}-{\langle D_{\mathit{\text{nk}}}^2(q_{\alpha \beta \gamma })\rangle }_{\mathit{\text{ensemble}}}|}^2}{{\mathit{\text{error}}}^2}$, where the error was set to 10⁻⁷ to account for numerical imprecision based on the accuracy with which randomly generated states could be back-predicted (data not shown) and unit quaternions were used to specify orientation, was optimized using the Differential Evolution³⁷ genetic algorithm provided in Mathematica®.

As shown in Figure 5(a), the χ² agreement between measured and back-predicted $\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle$ elements improved continuously when increasing n from 1 to 8. The Euler angles describing the inter-helical orientations for the MD and best fit n-state ensembles (where α, γ and β define twisting about domains II and I and inter-helical bending, respectively) are shown in Figure 5(b) for n = 2, 4 and 8. In each case, the distinct states draw out a trajectory similar in 3D spatial distribution to that observed by the MD.

Figure 5.

n-state ensemble fit to ${\langle D_{\mathit{\text{nk}}}^2(\alpha \beta \gamma )\rangle }_{\mathit{\text{real}}}$ computed for a motional model involving collective motions of two helical domains in a 65 ns molecular dynamics simulation of TAR RNA^25,34. (a) χ² value as a function of the number of states in the ensemble. (b) Comparison of the MD trajectory (shown in gray) and 2 (orange circles), 4 (green circles) and 8 (blue circles) state fits using an Euler angle representation described previously⁴³. (c) Comparison of the fitted states to 64,998 state MD trajectory. Color coding is as in (b). Each state defined as an inter-helical domain orientation is represented using a unit quaternion; a 4-dimensional complex number that represents an orientation as a single axis rotation from the z-axis. The relationship between the quaternions and the Euler angles is given in Equation 14. Shown are the values for the four quaternion components; Q₀, Q₁, Q₂, and Q₃. Q₀ encodes the rotational amplitude and Q₁, Q₂, and Q₃ encode the x, y and z components of the rotation axis, respectively. Error bars are shown for the 2 state fit and represent the RMSD calculated over 100 random iterations. Color coding is as Figure 3. The order of the two states was chosen to minimize the overall RMSD compared to the zero error ensemble.

In Figure 5(c), we compare the best fit states to 64,998 states in the MD trajectory. To aid presentation, each state and the MD trajectory are represented using unit quaternions with a time ordering. The position of each of the best fit states along the time axis was determined as the point in time where each state most closely intersects the MD trajectory. As can be seen in Figure 5(c), all of the 2, 4 and 8 states fall along the MD motional trajectory sampling distinct conformations nearly over the entire 65 ns time frame. This supports the validity of using discrete n-state ensembles to capture salient 3D spatial features of what might otherwise be a highly complex continuous motional trajectory⁴³.

To examine the effects of experimental uncertainty, the fits were also preformed after noise corrupting the alignment tensors with three levels of uncertainty. The error bars for the 2 state fit in Figure 5(c) represents the RMSD calculated over 100 iterations for each level of alignment tensor error. Due to the higher computational cost associated with fitting models with larger numbers of states, only 10 iterations were performed for the 4 and 8 state models. To illustrate the range of variation for the 4 and 8 state ensembles the points from all 10 iterations were plotted for each level of error (Figures S1 and S2). As might be expected, the robustness of the analysis increases with decreasing number of states and alignment tensor error. For the relatively low alignment tensor uncertainty expected in the analysis of A-form RNA helices, the analysis appears to be robust up to 8 states (Figures 5(c), S1 and S2). However, larger alignment tensor uncertainty can lead to a great deal of error particularly when fitting a large number (>4) of states. The latter likely arises from a combination of the lower ratio of measurements to degrees of freedom and difficulty in sampling and converging towards a single unique correct solution. Thus, the inclusion of other inter-domain constraints¹⁶, such as the simple steric restraints implemented in ref. 43 will be important in carrying out such analyses using experimental data.

Finally, we simulated the correlated, anti-correlated and uncorrelated ± 30° bending about the y-axis motion for a three domain system. Average Wigner matrices were constructed by averaging over 10001 equally spaced states along motional trajectory for a given domain, with the matrix elements describing reorientation of domain I relative to domain III as,

$$\langle D_{\mathit{\text{mk}}}^2(I\to \mathit{\text{III}})\rangle ={\displaystyle \sum _{n=-2}^2}\langle D_{\mathit{\text{mn}}}^2(I\to \mathit{\text{II}})D_{\mathit{\text{nk}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})\rangle .$$ (15)

For the uncorrelated case, conformations were generated over the entire trajectory and then randomly permuted. The $S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}}),S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}}),S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})$ and H_corr were calculated for all three motional models. Since the motion of domain I relative to domain II is equal in amplitude and character to motion of domain II relative to domain III, we observe $S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{II}})=S_{\mathit{\text{CL}}}^2(\mathit{\text{II}}\to \mathit{\text{III}})=0.838$ for the correlated, anti-correlated and uncorrelated models. However, the three models can be distinguished by their $S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})$ and H_corr, shown in Table 1. The $S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})$ for the correlated motion is significantly less than that of the uncorrelated case, which is significantly less than for the anti-correlated motion. As a result, the H_corr for the uncorrelated motion is two orders of magnitude smaller than that of the correlated and anti-correlated motions.

Table 1.

Analysis of motional correlations in a three domain system.

	Correlated	Anti-Correlated	Uncorrelated	Uncorrelated (Ideal)
$S_{\mathit{\text{CL}}}^2(I\to \mathit{\text{III}})$	0.542	1.000	0.723	0.702
Hcorr	0.229	−0.423	−0.029	0.000

Conclusions

We have presented a theoretical approach to the analysis of domain motions using multi-alignment and multi-reference RDCs that is applicable to any system of rigid domains where the decoupling approximation is not violated. Using five independent alignments, twenty-five internal order parameters can be measured providing 3D rotational sensitivity. The twenty-five Wigner matrix elements provide a means to characterize domain motions with unprecedented resolution, as demonstrated by an eight state ensemble fit to a 65 ns molecular dynamics simulation of HIV-1 TAR. In addition, we have shown that changing the identity of the reference domain in a multi-domain molecule provides insight into correlated domain motions that is inaccessible by simply modulating alignment.

Our results motivate the development of novel experimental strategies for obtaining linearly independent alignments and for establishing reference domains in multi-domain molecules. The inclusion of other restraints in interpreting the Wigner elements will be important for overcoming the effects of experimental uncertainty, which will require a more thorough exploration than presented here. Finally, development of new theoretical methods for interpreting the measured internal order parameters in terms of continuous motional models may enhance the ability to characterize highly complex motional trajectories.